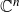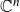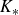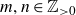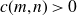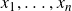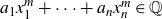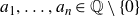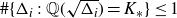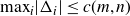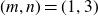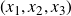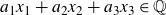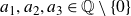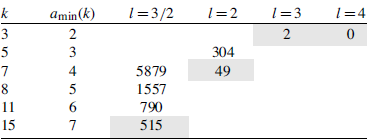1. Introduction
A singular modulus is the j-invariant of an elliptic curve with complex multiplication. The discriminant of a singular modulus is defined to be the discriminant of the imaginary quadratic order isomorphic to the endomorphism ring of the corresponding elliptic curve. In particular, the discriminant is a negative integer. There are only finitely many singular moduli of a given discriminant and these may be computed effectively [ Reference Cox10 , section 13].
Identify
![]() ${\mathbb{C}}$
with the modular curve Y(1) via the j-invariant. A point
${\mathbb{C}}$
with the modular curve Y(1) via the j-invariant. A point
![]() $(x_1, \ldots, x_n) \in {\mathbb{C}}^n$
such that
$(x_1, \ldots, x_n) \in {\mathbb{C}}^n$
such that
![]() $x_1, \ldots, x_n$
are all singular moduli is called, in the terminology of Shimura varieties, a special point of
$x_1, \ldots, x_n$
are all singular moduli is called, in the terminology of Shimura varieties, a special point of
![]() ${\mathbb{C}}^n$
. A special point is a zero-dimensional special subvariety of
${\mathbb{C}}^n$
. A special point is a zero-dimensional special subvariety of
![]() ${\mathbb{C}}^n$
(see [
Reference Pila24
, definition 4·10] for the general definition of a special subvariety of
${\mathbb{C}}^n$
(see [
Reference Pila24
, definition 4·10] for the general definition of a special subvariety of
![]() ${\mathbb{C}}^n$
).
${\mathbb{C}}^n$
).
The André–Oort conjecture, which was proved for
![]() ${\mathbb{C}}^n$
by Pila [
Reference Pila22
], states that a subvariety
${\mathbb{C}}^n$
by Pila [
Reference Pila22
], states that a subvariety
![]() $V \subset {\mathbb{C}}^n$
contains only finitely many maximal special subvarieties. In particular, a subvariety V contains only finitely many special points which do not lie on the union of all the positive-dimensional special subvarieties of V. Pila’s proof of André–Oort has a strong uniformity, as illustrated by the following theorem. This result is a direct consequence of Pila’s uniform André–Oort theorem [
Reference Pila22
, theorem 13·2] and a result of Binyamini [
Reference Binyamini8
, corollary 4]. The result is ineffective, due to the ineffectivity of Pila’s proof of André–Oort (see [
Reference Pila22
, section 13]).
$V \subset {\mathbb{C}}^n$
contains only finitely many maximal special subvarieties. In particular, a subvariety V contains only finitely many special points which do not lie on the union of all the positive-dimensional special subvarieties of V. Pila’s proof of André–Oort has a strong uniformity, as illustrated by the following theorem. This result is a direct consequence of Pila’s uniform André–Oort theorem [
Reference Pila22
, theorem 13·2] and a result of Binyamini [
Reference Binyamini8
, corollary 4]. The result is ineffective, due to the ineffectivity of Pila’s proof of André–Oort (see [
Reference Pila22
, section 13]).
Theorem 1·1. Let
![]() $m, n, d \in {\mathbb{Z}}_{\gt0}$
. There exists an ineffective constant
$m, n, d \in {\mathbb{Z}}_{\gt0}$
. There exists an ineffective constant
![]() $c(m, n, d) \gt 0$
with the following property:
$c(m, n, d) \gt 0$
with the following property:
Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli and write
$x_1, \ldots, x_n$
be pairwise distinct singular moduli and write
![]() $\Delta_i$
for the discriminant of
$\Delta_i$
for the discriminant of
![]() $x_i$
. If
$x_i$
. If
for some
![]() $a_1, \ldots, a_n \in {\overline{\mathbb{Q}}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\overline{\mathbb{Q}}} \setminus \{0\}$
and
![]() $b \in {\overline{\mathbb{Q}}}$
with
$b \in {\overline{\mathbb{Q}}}$
with
then
Notably, the constant c(m, n, d) in Theorem 1·1 does not depend on the height of the coefficients
![]() $a_1, \ldots, a_n, b$
. In particular, given
$a_1, \ldots, a_n, b$
. In particular, given
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
, there are only finitely many n-tuples
$m, n \in {\mathbb{Z}}_{\gt0}$
, there are only finitely many n-tuples
![]() $(x_1, \ldots, x_n)$
of pairwise distinct singular moduli
$(x_1, \ldots, x_n)$
of pairwise distinct singular moduli
![]() $x_1, \ldots, x_n$
such that there exist
$x_1, \ldots, x_n$
such that there exist
![]() $a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $b \in {\mathbb{Q}}$
with
$b \in {\mathbb{Q}}$
with
Theorem 1·1 is known effectively only when
![]() $n \leq 2$
. For
$n \leq 2$
. For
![]() $n = 1$
, this is a consequence of a result due to Goldfeld [
Reference Goldfeld14
] and Gross and Zagier [
Reference Gross and Zagier15
] (see Proposition 2·7). For
$n = 1$
, this is a consequence of a result due to Goldfeld [
Reference Goldfeld14
] and Gross and Zagier [
Reference Gross and Zagier15
] (see Proposition 2·7). For
![]() $n = 2$
, an effective version of Theorem 1·1 follows from a theorem of Kühne [
Reference Kühne17
, theorem 4] combined with the aforementioned result of Goldfeld–Gross–Zagier.
$n = 2$
, an effective version of Theorem 1·1 follows from a theorem of Kühne [
Reference Kühne17
, theorem 4] combined with the aforementioned result of Goldfeld–Gross–Zagier.
1·1. Main results
The first main result of this paper is the following effective partial version of Theorem 1·1 in the case that
![]() $d=1$
, i.e. for equations over
$d=1$
, i.e. for equations over
![]() ${\mathbb{Q}}$
. Throughout this paper,
${\mathbb{Q}}$
. Throughout this paper,
![]() $K_*$
denotes a fixed imaginary quadratic field, the definition of which is given just before Proposition 2·2. Briefly,
$K_*$
denotes a fixed imaginary quadratic field, the definition of which is given just before Proposition 2·2. Briefly,
![]() $K_*$
is the single exceptional field arising from an application of Tatuzawa’s effective version [
Reference Tatuzawa29
] of Siegel’s lower bound [
Reference Siegel28
] for the class number of an imaginary quadratic field.
$K_*$
is the single exceptional field arising from an application of Tatuzawa’s effective version [
Reference Tatuzawa29
] of Siegel’s lower bound [
Reference Siegel28
] for the class number of an imaginary quadratic field.
Theorem 1·2. Let
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
. There exists an effective constant c(m, n) with the following property:
$m, n \in {\mathbb{Z}}_{\gt0}$
. There exists an effective constant c(m, n) with the following property:
Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli and write
$x_1, \ldots, x_n$
be pairwise distinct singular moduli and write
![]() $\Delta_i$
for the discriminant of
$\Delta_i$
for the discriminant of
![]() $x_i$
. If
$x_i$
. If
for some
![]() $a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $b \in {\mathbb{Q}}$
and
$b \in {\mathbb{Q}}$
and
then
An effective bound, depending only on m, n, for all those discriminants
![]() $\Delta_i$
such that
$\Delta_i$
such that
![]() ${\mathbb{Q}}(\sqrt{\Delta_i}) \neq K_*$
is given by a result of Binyamini [
Reference Binyamini8
, theorem 1]. If there is at most one i such that
${\mathbb{Q}}(\sqrt{\Delta_i}) \neq K_*$
is given by a result of Binyamini [
Reference Binyamini8
, theorem 1]. If there is at most one i such that
![]() ${\mathbb{Q}}(\sqrt{\Delta_i}) = K_*$
, then
${\mathbb{Q}}(\sqrt{\Delta_i}) = K_*$
, then
![]() $\max \{ \lvert \Delta_1 \rvert, \ldots, \lvert \Delta_n \rvert\}$
is effectively bounded in terms of m, n by [
Reference Binyamini8
, corollary 1]. Our Theorem 1·2 improves on these prior results by allowing any number of the discriminants
$\max \{ \lvert \Delta_1 \rvert, \ldots, \lvert \Delta_n \rvert\}$
is effectively bounded in terms of m, n by [
Reference Binyamini8
, corollary 1]. Our Theorem 1·2 improves on these prior results by allowing any number of the discriminants
![]() $\Delta_1, \ldots, \Delta_n$
to be such that
$\Delta_1, \ldots, \Delta_n$
to be such that
![]() ${\mathbb{Q}}(\sqrt{\Delta_i}) = K_*$
, provided that all these exceptional
${\mathbb{Q}}(\sqrt{\Delta_i}) = K_*$
, provided that all these exceptional
![]() $\Delta_i$
are themselves equal to one another.
$\Delta_i$
are themselves equal to one another.
The second main result of this paper shows that, under a more restrictive condition on the discriminants involved, we can make the constant c(m, n) uniform in m and also write down this constant explicitly.
Theorem 1·3. Let
![]() $n \in {\mathbb{Z}}_{\gt0}$
. There exist explicit constants
$n \in {\mathbb{Z}}_{\gt0}$
. There exist explicit constants
![]() $c_1(n), c_2(n)$
with the following properties:
$c_1(n), c_2(n)$
with the following properties:
Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli such that
$x_1, \ldots, x_n$
be pairwise distinct singular moduli such that
for some
![]() $m \in {\mathbb{Z}}_{\gt0}$
and
$m \in {\mathbb{Z}}_{\gt0}$
and
![]() $a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $b \in {\mathbb{Q}}$
. Write
$b \in {\mathbb{Q}}$
. Write
![]() $\Delta_i$
for the discriminant of
$\Delta_i$
for the discriminant of
![]() $x_i$
.
$x_i$
.
-
(i) If
 $k \in \{1, \ldots, n\}$
is such that
$k \in \{1, \ldots, n\}$
is such that
 ${\mathbb{Q}}(\sqrt{\Delta_k}) \neq K_*$
and
then
${\mathbb{Q}}(\sqrt{\Delta_k}) \neq K_*$
and
then \[ \quad \# \left \{ \Delta_i \;:\; i \in \left \{1, \ldots, n\right \} \mbox{ such that } {\mathbb{Q}}\left(\sqrt{\Delta_i}\right) = {\mathbb{Q}}\left(\sqrt{\Delta_k}\right) \right \} = 1,\]
\[ \quad \# \left \{ \Delta_i \;:\; i \in \left \{1, \ldots, n\right \} \mbox{ such that } {\mathbb{Q}}\left(\sqrt{\Delta_i}\right) = {\mathbb{Q}}\left(\sqrt{\Delta_k}\right) \right \} = 1,\]
 $\lvert \Delta_k \rvert \leq c_1(n)$
.
$\lvert \Delta_k \rvert \leq c_1(n)$
.
-
(ii) If, for every
 $k \in \{1, \ldots, n\}$
,
then
$k \in \{1, \ldots, n\}$
,
then \[ \quad \# \left \{ \Delta_i \;:\; i \in \left \{1, \ldots, n\right \} \mbox{ such that } {\mathbb{Q}}\left(\sqrt{\Delta_i}\right) = {\mathbb{Q}}\left(\sqrt{\Delta_k}\right) \right \} = 1,\]
\[ \quad \# \left \{ \Delta_i \;:\; i \in \left \{1, \ldots, n\right \} \mbox{ such that } {\mathbb{Q}}\left(\sqrt{\Delta_i}\right) = {\mathbb{Q}}\left(\sqrt{\Delta_k}\right) \right \} = 1,\]
 $ \max \{ \lvert \Delta_i \rvert \;:\; i=1, \ldots, n\} \leq c_2(n)$
.
$ \max \{ \lvert \Delta_i \rvert \;:\; i=1, \ldots, n\} \leq c_2(n)$
.
An explicit form for the constant
![]() $c_1(n)$
is given in Proposition 6·2, while an explicit form for the constant
$c_1(n)$
is given in Proposition 6·2, while an explicit form for the constant
![]() $c_2(n)$
appears at the end of Section 6·2.
$c_2(n)$
appears at the end of Section 6·2.
As steps in the proofs of Theorems 1·2 and Theorem 1·3, we also prove the following two results, which may have some independent interest. The first of them is also used in the proof of Theorem 1·6.
Theorem 1·4. Let
![]() $n \in {\mathbb{Z}}_{\gt0}$
. Let
$n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli which are all of discriminant
$x_1, \ldots, x_n$
be pairwise distinct singular moduli which are all of discriminant
![]() $\Delta$
. Denote by
$\Delta$
. Denote by
![]() $h(\Delta)$
the class number of the imaginary quadratic order of discriminant
$h(\Delta)$
the class number of the imaginary quadratic order of discriminant
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $K = {\mathbb{Q}}(\sqrt{\Delta})$
. If
$K = {\mathbb{Q}}(\sqrt{\Delta})$
. If
for some
![]() $a_1, \ldots, a_n \in K \setminus \{0\}$
and
$a_1, \ldots, a_n \in K \setminus \{0\}$
and
![]() $m \in {\mathbb{Z}}_{\gt0}$
, then either
$m \in {\mathbb{Z}}_{\gt0}$
, then either
or
![]() $h(\Delta) = n$
and
$h(\Delta) = n$
and
![]() $a_1 = \cdots = a_n$
.
$a_1 = \cdots = a_n$
.
The second is a result on the fields generated by linear combinations of powers of singular moduli of the same discriminant.
Theorem 1·5. Let
![]() $n \in {\mathbb{Z}}_{\gt0}$
. Let
$n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli which are all of discriminant
$x_1, \ldots, x_n$
be pairwise distinct singular moduli which are all of discriminant
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $K = {\mathbb{Q}}(\sqrt{\Delta})$
. Then either
$K = {\mathbb{Q}}(\sqrt{\Delta})$
. Then either
or
for all
![]() $a_1, \ldots, a_n \in K \setminus \{0\}$
and every
$a_1, \ldots, a_n \in K \setminus \{0\}$
and every
![]() $m \in {\mathbb{Z}}_{\gt0}$
.
$m \in {\mathbb{Z}}_{\gt0}$
.
We emphasise that Theorems 1·4 and 1·5 apply to all discriminants
![]() $\Delta$
, including those with
$\Delta$
, including those with
![]() ${\mathbb{Q}}(\sqrt{\Delta}) = K_*$
. Note also that Theorems 1·4 and 1·5 are uniform in the exponent m, as well as in
${\mathbb{Q}}(\sqrt{\Delta}) = K_*$
. Note also that Theorems 1·4 and 1·5 are uniform in the exponent m, as well as in
![]() $a_1, \ldots, a_n$
. For discussion of whether such uniformity in m may also hold in Theorem 1·1, see Section 3·1.
$a_1, \ldots, a_n$
. For discussion of whether such uniformity in m may also hold in Theorem 1·1, see Section 3·1.
The final main result of this paper is a completely explicit version of Theorem 1·1 for the case where
![]() $m= d=1$
and
$m= d=1$
and
![]() $n=3$
. The analogous result for
$n=3$
. The analogous result for
![]() $n=2$
is due to Allombert, Bilu and Pizarro–Madariaga [
Reference Allombert, Bilu and Pizarro-Madariaga1
, theorem 1·2].
$n=2$
is due to Allombert, Bilu and Pizarro–Madariaga [
Reference Allombert, Bilu and Pizarro-Madariaga1
, theorem 1·2].
Theorem 1·6. Let x, y, z be pairwise distinct singular moduli and
![]() $A, B, C \in {\mathbb{Q}} \setminus \{0\}$
. Then
$A, B, C \in {\mathbb{Q}} \setminus \{0\}$
. Then
if and only if (up to permuting x, y, z) one of the following holds:
-
(i)
 $x, y, z \in {\mathbb{Q}}$
;
$x, y, z \in {\mathbb{Q}}$
;-
(ii) (a)
 $x \in {\mathbb{Q}}$
,
$x \in {\mathbb{Q}}$
, -
(b)
 ${\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
,
${\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
, -
(c)
 $[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 2$
, and
$[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 2$
, and -
(d)
 $B/C = -(z-z')/(y-y')$
, where y′, z′ are the unique non-trivial Galois conjugates of y, z over
$B/C = -(z-z')/(y-y')$
, where y′, z′ are the unique non-trivial Galois conjugates of y, z over
 ${\mathbb{Q}}$
respectively;
${\mathbb{Q}}$
respectively;
-
(iii) (a)
 ${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
,
${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
, -
(b)
 $[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 2$
, and
$[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 2$
, and -
(c) writing x′, y′, z′ for the unique non-trivial Galois conjugates over
 ${\mathbb{Q}}$
of x, y, z respectively, we have that
${\mathbb{Q}}$
of x, y, z respectively, we have that
 \[A = -\frac{B(y-y')+C(z-z')}{x-x'};\]
\[A = -\frac{B(y-y')+C(z-z')}{x-x'};\]
-
(iv) (a)
 $[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 3$
,
$[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 3$
, -
(b) x, y, z are all conjugate over
 ${\mathbb{Q}}$
, and
${\mathbb{Q}}$
, and -
(c)
 $A= B = C$
;
$A= B = C$
;
-
(v) (a)
 ${\mathbb{Q}}(x) \subset {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
,
${\mathbb{Q}}(x) \subset {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
, -
(b)
 $[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = 2$
and
$[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = 2$
and
 $[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 4$
,
$[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}] = [{\mathbb{Q}}(z) \;:\; {\mathbb{Q}}] = 4$
, -
(c) y, z are conjugate over
 ${\mathbb{Q}}$
, and
${\mathbb{Q}}$
, and -
(d) writing x′ for the unique non-trivial Galois conjugate of x over
 ${\mathbb{Q}}$
and v, w for the other two Galois conjugates of y, z over
${\mathbb{Q}}$
and v, w for the other two Galois conjugates of y, z over
 ${\mathbb{Q}}$
, we have that
${\mathbb{Q}}$
, we have that
 \[\frac{A}{B} = \frac{A}{C} = - \frac{(y+z) - (v+w)}{x - x'}.\]
\[\frac{A}{B} = \frac{A}{C} = - \frac{(y+z) - (v+w)}{x - x'}.\]
-
Note that it is straightforward to compute the list of all the triples of singular moduli satisfying one of the conditions (i)–(v) in Theorem 1·6. The proof of Theorem 1·6 involves some computations in PARI [ 30 ]. These computations were carried out using a standard desktop computerFootnote 1 ; the scripts are available from: https://github.com/guyfowler/sums_of_powers.
1·2. Related results
Riffaut [
Reference Riffaut25
] and, jointly, Luca and Riffaut [
Reference Luca and Riffaut19
] proved an effective (indeed, completely explicit) version [
Reference Luca and Riffaut19
, theorem 1·3] of Theorem 1·1 in the case where
![]() $d = 1$
and
$d = 1$
and
![]() $n = 2$
. For
$n = 2$
. For
![]() $d=1$
and
$d=1$
and
![]() $n = 3$
, an explicit version of Theorem 1·1 in the special case that
$n = 3$
, an explicit version of Theorem 1·1 in the special case that
![]() $\lvert a_1 \rvert = \lvert a_2 \rvert = \lvert a_3 \rvert$
was proved by the author in a previous paper [
Reference Fowler13
, theorem 1·1].
$\lvert a_1 \rvert = \lvert a_2 \rvert = \lvert a_3 \rvert$
was proved by the author in a previous paper [
Reference Fowler13
, theorem 1·1].
Binyamini [
Reference Binyamini8
] proved a version of Theorem 1·1 which is effective, but not uniform in the height of the coefficients
![]() $a_1, \ldots, a_n, b$
. He proved [
Reference Binyamini8
, corollary 4] that if
$a_1, \ldots, a_n, b$
. He proved [
Reference Binyamini8
, corollary 4] that if
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
and
$m, n \in {\mathbb{Z}}_{\gt0}$
and
![]() $x_1, \ldots, x_n$
are pairwise distinct singular moduli of respective discriminants
$x_1, \ldots, x_n$
are pairwise distinct singular moduli of respective discriminants
![]() $\Delta_1, \ldots, \Delta_n$
such that
$\Delta_1, \ldots, \Delta_n$
such that
then
where c(m, n, d, h) is an effective constant which depends only on m, n,
and also
Here
![]() $H(\!\cdot\!)$
denotes the absolute multiplicative Weil height, see e.g. [
Reference Bombieri and Gubler9
, section 1·5]. In the
$H(\!\cdot\!)$
denotes the absolute multiplicative Weil height, see e.g. [
Reference Bombieri and Gubler9
, section 1·5]. In the
![]() $m=1$
case, the same result was proved independently by Bilu and Kühne [
Reference Bilu and Kühne4
, lemma 3·1], who even gave an explicit form [
Reference Bilu and Kühne4
, (42)] for the constant c(1, n, d, h). The dependence of the constant c(m, n, d, h) on h means that [
Reference Binyamini8
, corollary 4] and [
Reference Bilu and Kühne4
, lemma 3·1] do not, for example, give an effective bound on the n-tuples
$m=1$
case, the same result was proved independently by Bilu and Kühne [
Reference Bilu and Kühne4
, lemma 3·1], who even gave an explicit form [
Reference Bilu and Kühne4
, (42)] for the constant c(1, n, d, h). The dependence of the constant c(m, n, d, h) on h means that [
Reference Binyamini8
, corollary 4] and [
Reference Bilu and Kühne4
, lemma 3·1] do not, for example, give an effective bound on the n-tuples
![]() $(x_1, \ldots, x_n)$
of pairwise distinct singular moduli
$(x_1, \ldots, x_n)$
of pairwise distinct singular moduli
![]() $x_1, \ldots, x_n$
which satisfy (1·1) with
$x_1, \ldots, x_n$
which satisfy (1·1) with
![]() $a_1, \ldots, a_n, b \in {\mathbb{Q}}$
.
$a_1, \ldots, a_n, b \in {\mathbb{Q}}$
.
It is also worth noting that it is possible to obtain (ineffective) bounds on the number of maximal special subvarieties which are uniform across definable families of subvarieties and do not depend on (the degree of) the field of definition of the subvariety. Scanlon’s results on automatic uniformity [
Reference Scanlon27
, theorem 4·2] imply that, for every
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
, there exists an ineffective constant
$m, n \in {\mathbb{Z}}_{\gt0}$
, there exists an ineffective constant
![]() $c(m, n) \gt 0$
with the following property: if
$c(m, n) \gt 0$
with the following property: if
![]() $a_1, \ldots, a_n \in {\mathbb{C}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{C}} \setminus \{0\}$
and
![]() $b \in {\mathbb{C}}$
, then there are at most c(m, n) distinct n-tuples
$b \in {\mathbb{C}}$
, then there are at most c(m, n) distinct n-tuples
![]() $(x_1, \ldots, x_n)$
of pairwise distinct singular moduli
$(x_1, \ldots, x_n)$
of pairwise distinct singular moduli
![]() $x_1, \ldots, x_n$
such that
$x_1, \ldots, x_n$
such that
In the case where
![]() $m=1$
and
$m=1$
and
![]() $n=2$
, Bilu, Luca, and Masser [
Reference Bilu, Luca and Masser5
, theorem 1·1] proved that there are only (ineffectively) finitely many distinct, non-special linear subvarieties of
$n=2$
, Bilu, Luca, and Masser [
Reference Bilu, Luca and Masser5
, theorem 1·1] proved that there are only (ineffectively) finitely many distinct, non-special linear subvarieties of
![]() ${\mathbb{C}}^2$
which contain at least 3 distinct special points.
${\mathbb{C}}^2$
which contain at least 3 distinct special points.
1·3. Structure of this paper
In Section 2, we recall some facts needed throughout the paper. In Section 3, we explain how Theorem 1·1 follows from the results of Pila [ Reference Pila22 ] and Binyamini [ Reference Binyamini8 ]. Theorems 1·4 and 1·5 are proved in Sections 4 and 5 respectively. The proofs of Theorems 1·2 and 1·3 are then carried out in Section 6. Section 7 contains some properties of singular moduli, which are then used for the proof of Theorem 1·6 in Section 8.
2. Preliminaries
2·1. Properties of singular moduli
We collect here some well-known properties of singular moduli which we will need throughout the paper.
Let
![]() $j \colon {\mathbb{H}} \to {\mathbb{C}}$
denote the modular j-function, where
$j \colon {\mathbb{H}} \to {\mathbb{C}}$
denote the modular j-function, where
![]() ${\mathbb{H}}$
is the complex upper half plane. A singular modulus is a complex number
${\mathbb{H}}$
is the complex upper half plane. A singular modulus is a complex number
![]() $j(\tau)$
, where
$j(\tau)$
, where
![]() $\tau \in {\mathbb{H}}$
is such that
$\tau \in {\mathbb{H}}$
is such that
![]() $[{\mathbb{Q}}(\tau) \;:\; {\mathbb{Q}}] = 2$
. The discriminant
$[{\mathbb{Q}}(\tau) \;:\; {\mathbb{Q}}] = 2$
. The discriminant
![]() $\Delta$
of a singular modulus
$\Delta$
of a singular modulus
![]() $j(\tau)$
is given by
$j(\tau)$
is given by
![]() $\Delta = b^2-4ac$
, where
$\Delta = b^2-4ac$
, where
![]() $a, b, c \in {\mathbb{Z}}$
, not all zero, are such that
$a, b, c \in {\mathbb{Z}}$
, not all zero, are such that
![]() $a \tau^2 + b \tau + c = 0$
and
$a \tau^2 + b \tau + c = 0$
and
![]() $\gcd(a, b, c) = 1$
. In particular,
$\gcd(a, b, c) = 1$
. In particular,
![]() $\Delta \lt 0$
and
$\Delta \lt 0$
and
![]() $\Delta \equiv 0, 1 \bmod 4$
. Hence,
$\Delta \equiv 0, 1 \bmod 4$
. Hence,
![]() $\lvert \Delta \rvert \geq 3$
always.
$\lvert \Delta \rvert \geq 3$
always.
Note that
![]() ${\mathbb{Q}}(\tau) = {\mathbb{Q}}(\sqrt{\Delta})$
. The fundamental discriminant D of
${\mathbb{Q}}(\tau) = {\mathbb{Q}}(\sqrt{\Delta})$
. The fundamental discriminant D of
![]() $j(\tau)$
is defined to be the discriminant of the imaginary quadratic field
$j(\tau)$
is defined to be the discriminant of the imaginary quadratic field
![]() ${\mathbb{Q}}(\tau) = {\mathbb{Q}}(\sqrt{\Delta})$
. One has that
${\mathbb{Q}}(\tau) = {\mathbb{Q}}(\sqrt{\Delta})$
. One has that
![]() $\Delta = f^2 D$
for some
$\Delta = f^2 D$
for some
![]() $f \in {\mathbb{Z}}_{\gt0}$
.
$f \in {\mathbb{Z}}_{\gt0}$
.
Write
![]() $F_j$
for the standard fundamental domain for the action (by fractional linear transformations) of
$F_j$
for the standard fundamental domain for the action (by fractional linear transformations) of
![]() ${\mathrm{SL}_2({\mathbb{Z}})}$
on
${\mathrm{SL}_2({\mathbb{Z}})}$
on
![]() ${\mathbb{H}}$
, i.e.
${\mathbb{H}}$
, i.e.
 \begin{align*} {}F_j = &\left\{ z \in {\mathbb{H}} \;:\; -\frac{1}{2} \leq {\mathrm{Re}} z \lt \frac{1}{2} \mbox{ and } \lvert z \rvert \gt 1\right\}\\ {}&\cup \left\{ z \in {\mathbb{H}} \;:\; -\frac{1}{2} \leq {\mathrm{Re}} z \leq 0 \mbox{ and } \lvert z \rvert = 1\right\}.\end{align*}
\begin{align*} {}F_j = &\left\{ z \in {\mathbb{H}} \;:\; -\frac{1}{2} \leq {\mathrm{Re}} z \lt \frac{1}{2} \mbox{ and } \lvert z \rvert \gt 1\right\}\\ {}&\cup \left\{ z \in {\mathbb{H}} \;:\; -\frac{1}{2} \leq {\mathrm{Re}} z \leq 0 \mbox{ and } \lvert z \rvert = 1\right\}.\end{align*}
The j-function restricts to a bijection
![]() $F_j \to {\mathbb{C}}$
. Therefore, for
$F_j \to {\mathbb{C}}$
. Therefore, for
![]() $\Delta \lt 0$
such that
$\Delta \lt 0$
such that
![]() $\Delta \equiv 0, 1 \bmod 4$
, the map
$\Delta \equiv 0, 1 \bmod 4$
, the map
is a bijection between the set
and the set of singular moduli of discriminant
![]() $\Delta$
. For each such
$\Delta$
. For each such
![]() $\Delta$
, there exists a unique triple
$\Delta$
, there exists a unique triple
![]() $(a, b, c) \in T_\Delta$
with
$(a, b, c) \in T_\Delta$
with
![]() $a=1$
, given by
$a=1$
, given by
where
![]() $k \in \{0, 1\}$
is such that
$k \in \{0, 1\}$
is such that
![]() $k \equiv \Delta \bmod 2$
; we call the corresponding singular modulus the dominant singular modulus of discriminant
$k \equiv \Delta \bmod 2$
; we call the corresponding singular modulus the dominant singular modulus of discriminant
![]() $\Delta$
.
$\Delta$
.
If x is a singular modulus of discriminant
![]() $\Delta$
, then, see [
Reference Cox10
, lemma 9·3 and theorem 11·1], the field
$\Delta$
, then, see [
Reference Cox10
, lemma 9·3 and theorem 11·1], the field
![]() ${\mathbb{Q}}(\sqrt{\Delta}, x)$
is a Galois extension of both
${\mathbb{Q}}(\sqrt{\Delta}, x)$
is a Galois extension of both
![]() ${\mathbb{Q}}(\sqrt{\Delta})$
and
${\mathbb{Q}}(\sqrt{\Delta})$
and
![]() ${\mathbb{Q}}$
and
${\mathbb{Q}}$
and
where
![]() ${\mathrm{cl}}(\Delta)$
denotes the class group of the unique imaginary quadratic order of discriminant
${\mathrm{cl}}(\Delta)$
denotes the class group of the unique imaginary quadratic order of discriminant
![]() $\Delta$
.
$\Delta$
.
Let
![]() $x_1, \ldots, x_n$
be all the distinct singular moduli of some discriminant
$x_1, \ldots, x_n$
be all the distinct singular moduli of some discriminant
![]() $\Delta$
. Then, by [
Reference Cox10
, theorem 11·1 and proposition 13·2], the polynomial
$\Delta$
. Then, by [
Reference Cox10
, theorem 11·1 and proposition 13·2], the polynomial
has coefficients in
![]() ${\mathbb{Z}}$
and is irreducible over
${\mathbb{Z}}$
and is irreducible over
![]() ${\mathbb{Q}}$
and over
${\mathbb{Q}}$
and over
![]() ${\mathbb{Q}}(\sqrt{\Delta})$
. Hence, for every
${\mathbb{Q}}(\sqrt{\Delta})$
. Hence, for every
![]() $i \in \{1, \ldots, n\}$
, we have that
$i \in \{1, \ldots, n\}$
, we have that
where
![]() $h(\Delta)$
denotes the class number of the imaginary quadratic order of discriminant
$h(\Delta)$
denotes the class number of the imaginary quadratic order of discriminant
![]() $\Delta$
.
$\Delta$
.
The class numbers of small discriminants may be computed straightforwardly in PARI. We will make use of the following consequence of this.
Lemma 2·1. Let x be a singular modulus of discriminant
![]() $\Delta$
. If
$\Delta$
. If
![]() $\lvert \Delta \rvert \lt 15$
, then
$\lvert \Delta \rvert \lt 15$
, then
![]() $x \in {\mathbb{Q}}$
. If
$x \in {\mathbb{Q}}$
. If
![]() $\lvert \Delta \rvert \lt 39$
, then
$\lvert \Delta \rvert \lt 39$
, then
![]() $h(\Delta) \leq 3$
.
$h(\Delta) \leq 3$
.
We will also need the following bound on singular moduli.
Proposition 2·2. Let x be a singular modulus of discriminant
![]() $\Delta$
which corresponds to a triple
$\Delta$
which corresponds to a triple
![]() $(a, b, c) \in T_\Delta$
. Then
$(a, b, c) \in T_\Delta$
. Then
Proof. Let
![]() $(a, b, c) \in T_\Delta$
be the triple corresponding to x. Then
$(a, b, c) \in T_\Delta$
be the triple corresponding to x. Then
![]() $x = j(\tau)$
, where
$x = j(\tau)$
, where
The result follows immediately, since Bilu, Masser and Zannier [
Reference Bilu, Masser and Zannier7
, lemma 1] proved that if
![]() $z \in F_j$
, then
$z \in F_j$
, then
This bound has the following consequence.
Lemma 2·3. Let x, y be distinct singular moduli of the same discriminant
![]() $\Delta$
. Suppose that x is dominant. Then
$\Delta$
. Suppose that x is dominant. Then
 \[\lvert y \rvert \leq \frac{6 \lvert x \rvert}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}.\]
\[\lvert y \rvert \leq \frac{6 \lvert x \rvert}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}.\]
Proof. There are at least two distinct singular moduli of discriminant
![]() $\Delta$
, so
$\Delta$
, so
![]() $\lvert \Delta \rvert \geq 15$
by Lemma 2·1. Since x is dominant, y is not dominant. Thus, Proposition 2·2 implies that
$\lvert \Delta \rvert \geq 15$
by Lemma 2·1. Since x is dominant, y is not dominant. Thus, Proposition 2·2 implies that
 \begin{align*} {} {}\frac{\lvert y \rvert}{\lvert x \rvert} &\leq \frac{1}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)} \frac{1 + 2079 \exp\left(\frac{-\pi \lvert \Delta \rvert^{1/2}}{2}\right)}{1 - 2079 \exp\left(- \pi \lvert \Delta \rvert^{1/2}\right)}\\ {} {}&\leq \frac{1}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)} \frac{1 + 2079 \exp\left(\frac{-\pi \sqrt{15}}{2}\right)}{1 - 2079 \exp\left(- \pi \sqrt{15}\right)}\\ {} {}&\leq \frac{6}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}. {}\end{align*}
\begin{align*} {} {}\frac{\lvert y \rvert}{\lvert x \rvert} &\leq \frac{1}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)} \frac{1 + 2079 \exp\left(\frac{-\pi \lvert \Delta \rvert^{1/2}}{2}\right)}{1 - 2079 \exp\left(- \pi \lvert \Delta \rvert^{1/2}\right)}\\ {} {}&\leq \frac{1}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)} \frac{1 + 2079 \exp\left(\frac{-\pi \sqrt{15}}{2}\right)}{1 - 2079 \exp\left(- \pi \sqrt{15}\right)}\\ {} {}&\leq \frac{6}{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}. {}\end{align*}
2·2. Effective bounds for the class number
A theorem of Tatuzawa [ Reference Tatuzawa29 , theorem 1] and Dirichlet’s class number formula together imply the following result. It shows that Siegel’s [ Reference Siegel28 ] ineffective lower bound for the class number of imaginary quadratic fields may be made effective, apart from at most one possible exceptional imaginary quadratic field.
Theorem 2·4 ([
Reference Tatuzawa29
, theorem 1]). Let
![]() $\epsilon \in (0, 1/2)$
. Let
$\epsilon \in (0, 1/2)$
. Let
![]() $K_1, K_2$
be imaginary quadratic fields with respective discriminants
$K_1, K_2$
be imaginary quadratic fields with respective discriminants
![]() $D_1, D_2$
. If
$D_1, D_2$
. If
then
![]() $K_1 = K_2$
.
$K_1 = K_2$
.
In other words, for a fixed
![]() $\epsilon \in (0, 1/2)$
, there is at most one imaginary quadratic field K for which the bound
$\epsilon \in (0, 1/2)$
, there is at most one imaginary quadratic field K for which the bound
is false, where D denotes the discriminant of K. It is possible (indeed, it would follow from GRH) that, for some
![]() $\epsilon \in (0, 1/2)$
, the bound (2·1) in fact holds for every imaginary quadratic field K. In such a case, the results of [
Reference Binyamini8
] would imply an effective version of Theorem 1·1.
$\epsilon \in (0, 1/2)$
, the bound (2·1) in fact holds for every imaginary quadratic field K. In such a case, the results of [
Reference Binyamini8
] would imply an effective version of Theorem 1·1.
Throughout this paper, we fix
![]() $\epsilon_* = 1/12$
and denote by
$\epsilon_* = 1/12$
and denote by
![]() $K_*$
the unique imaginary quadratic field for which the corresponding bound (2·1) is false. Denote by
$K_*$
the unique imaginary quadratic field for which the corresponding bound (2·1) is false. Denote by
![]() $D_*$
the discriminant of
$D_*$
the discriminant of
![]() $K_*$
. If no such field
$K_*$
. If no such field
![]() $K_*$
exists, then we adopt the notational convention that the inequalities
$K_*$
exists, then we adopt the notational convention that the inequalities
![]() $K \neq K_*$
and
$K \neq K_*$
and
![]() $D \neq D_*$
hold for every imaginary quadratic field K with discriminant D. We have the following consequence of Tatuzawa’s result.
$D \neq D_*$
hold for every imaginary quadratic field K with discriminant D. We have the following consequence of Tatuzawa’s result.
Proposition 2·5 ([
Reference Bilu and Kühne4
, (17)]). Let
![]() $\Delta \lt 0$
be such that
$\Delta \lt 0$
be such that
![]() $\Delta \equiv 0, 1 \bmod 4$
and let
$\Delta \equiv 0, 1 \bmod 4$
and let
![]() $K = {\mathbb{Q}}(\sqrt{\Delta})$
. If
$K = {\mathbb{Q}}(\sqrt{\Delta})$
. If
![]() $K \neq K_*$
, then
$K \neq K_*$
, then
For discriminants
![]() $\Delta$
with
$\Delta$
with
![]() ${\mathbb{Q}}(\sqrt{\Delta}) = K_*$
, the known effective bounds for the class number are much weaker.
${\mathbb{Q}}(\sqrt{\Delta}) = K_*$
, the known effective bounds for the class number are much weaker.
Proposition 2·6. Let
![]() $D \lt 0$
be a fundamental discriminant. Then
$D \lt 0$
be a fundamental discriminant. Then
Proof. Oesterlé [ Reference Oesterlé20 , théorème 1 and section 5·1], building on work of Goldfeld [ Reference Goldfeld14 ] and Gross–Zagier [ Reference Gross and Zagier15 , theorem 8·1], proved that
where
and this product is taken over all the primes p which divide D except the largest. Let
![]() $\omega(D)$
denote the number of distinct prime divisors of D. So there are
$\omega(D)$
denote the number of distinct prime divisors of D. So there are
![]() $\omega(D) - 1$
terms in the product defining F(D). By the theory of genera, see e.g. [
Reference Cox10
, proposition 3·11 and theorem 6·1], we have that
$\omega(D) - 1$
terms in the product defining F(D). By the theory of genera, see e.g. [
Reference Cox10
, proposition 3·11 and theorem 6·1], we have that
In particular,
![]() $2^{\omega(D) -1} \mid h(D)$
. So
$2^{\omega(D) -1} \mid h(D)$
. So
![]() $\omega(D) - 1 \leq v_2(h(D))$
, where
$\omega(D) - 1 \leq v_2(h(D))$
, where
![]() $ v_2(h(D))$
denotes the largest integer k such that
$ v_2(h(D))$
denotes the largest integer k such that
![]() $2^k \mid h(D)$
. Hence, there are at most
$2^k \mid h(D)$
. Hence, there are at most
![]() $v_2(h(D))$
terms appearing in the product defining F(D).
$v_2(h(D))$
terms appearing in the product defining F(D).
Observe that
if
![]() $p \geq 11$
. Hence,
$p \geq 11$
. Hence,
Since
![]() $h(D) \geq 2^{v_2(h(D))}$
by definition, we obtain that
$h(D) \geq 2^{v_2(h(D))}$
by definition, we obtain that
Proposition 2·7. Let
![]() $\Delta \lt 0$
be such that
$\Delta \lt 0$
be such that
![]() $\Delta \equiv 0, 1 \bmod 4$
and let
$\Delta \equiv 0, 1 \bmod 4$
and let
![]() $k \in {\mathbb{Z}}_{\gt 0}$
. If
$k \in {\mathbb{Z}}_{\gt 0}$
. If
![]() $h(\Delta) \leq k$
, then
$h(\Delta) \leq k$
, then
Proof. Write
![]() $\Delta = f^2 D$
, where D is the discriminant of
$\Delta = f^2 D$
, where D is the discriminant of
![]() ${\mathbb{Q}}(\sqrt{\Delta})$
. Suppose that
${\mathbb{Q}}(\sqrt{\Delta})$
. Suppose that
![]() $h(\Delta) \leq k$
. Assume first that
$h(\Delta) \leq k$
. Assume first that
![]() $D \notin \{-3, -4\}$
. The class number formula in [
Reference Cox10
, theorem 7·24] gives that
$D \notin \{-3, -4\}$
. The class number formula in [
Reference Cox10
, theorem 7·24] gives that
 \[ h(\Delta) = h(D) f \prod_{p \mid f} \left(1 - \left(\frac{D}{p}\right)\frac{1}{p}\right),\]
\[ h(\Delta) = h(D) f \prod_{p \mid f} \left(1 - \left(\frac{D}{p}\right)\frac{1}{p}\right),\]
where
![]() $(D/p)$
denotes the Kronecker symbol. Hence,
$(D/p)$
denotes the Kronecker symbol. Hence,
![]() $h(D) \mid h(\Delta)$
and
$h(D) \mid h(\Delta)$
and
where
![]() $\varphi(\!\cdot\!)$
denotes Euler’s totient function. Hence,
$\varphi(\!\cdot\!)$
denotes Euler’s totient function. Hence,
Proposition 2·6 then implies that
while the classical bound
![]() $\varphi(\,f) \geq \sqrt{f/2}$
implies that
$\varphi(\,f) \geq \sqrt{f/2}$
implies that
![]() $f \leq 2k^2$
. Hence,
$f \leq 2k^2$
. Hence,
Now assume
![]() $D \in \{-3, -4\}$
. Then
$D \in \{-3, -4\}$
. Then
![]() $h(D) = 1$
. In this case, the class number formula from [
Reference Cox10
, theorem 7·24] implies that
$h(D) = 1$
. In this case, the class number formula from [
Reference Cox10
, theorem 7·24] implies that
Hence,
![]() $\varphi(\,f) \leq 3 k$
and so
$\varphi(\,f) \leq 3 k$
and so
![]() $f \leq 18 k^2$
. Thus, clearly,
$f \leq 18 k^2$
. Thus, clearly,
Finally, we will also need an upper bound for the class number. This bound is a straightforward consequence of Dirichlet’s class number formula.
Proposition 2·8. If
![]() $\Delta \lt 0$
is such that
$\Delta \lt 0$
is such that
![]() $\Delta \equiv 0, 1 \bmod 4$
, then
$\Delta \equiv 0, 1 \bmod 4$
, then
![]() $h(\Delta) \leq \lvert \Delta \rvert^{2/3}$
.
$h(\Delta) \leq \lvert \Delta \rvert^{2/3}$
.
Proof. By [ Reference Paulin21 , proposition 2·2], we have that
It then suffices to note that, for every
![]() $x\gt0$
,
$x\gt0$
,
3. Deducing Theorem 1·1
In this section, we explain how Theorem 1·1 may be deduced from the results of Pila [
Reference Pila22
, theorem 13·2] and Binyamini [
Reference Binyamini8
, corollary 4]. A direct proof of the
![]() $m = 1$
case of Theorem 1·1 was given by Pila [
Reference Pila23
, theorem 7·7].
$m = 1$
case of Theorem 1·1 was given by Pila [
Reference Pila23
, theorem 7·7].
For the definition of a special subvariety of
![]() ${\mathbb{C}}^n$
, see e.g. [
Reference Pila22
, definition 1·3], [
Reference Binyamini8
, (1·1)], or [
Reference Pila24
, definition 4·10]. For a subvariety
${\mathbb{C}}^n$
, see e.g. [
Reference Pila22
, definition 1·3], [
Reference Binyamini8
, (1·1)], or [
Reference Pila24
, definition 4·10]. For a subvariety
![]() $V \subset {\mathbb{C}}^n$
, denote by
$V \subset {\mathbb{C}}^n$
, denote by
![]() $V^\mathrm{sp}$
the union of all the positive-dimensional special subvarieties of V.
$V^\mathrm{sp}$
the union of all the positive-dimensional special subvarieties of V.
Let
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
. For
$m, n \in {\mathbb{Z}}_{\gt0}$
. For
![]() $a = (a_1, \ldots, a_n) \in {\mathbb{C}}^n$
and
$a = (a_1, \ldots, a_n) \in {\mathbb{C}}^n$
and
![]() $b \in {\mathbb{C}}$
, let
$b \in {\mathbb{C}}$
, let
Lemma 3·1. Let
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
. Let
$m, n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli. Suppose that
$x_1, \ldots, x_n$
be pairwise distinct singular moduli. Suppose that
![]() $a = (a_1, \ldots, a_n) \in ({\overline{\mathbb{Q}}} \setminus \{0\})^n$
and
$a = (a_1, \ldots, a_n) \in ({\overline{\mathbb{Q}}} \setminus \{0\})^n$
and
![]() $b \in {\overline{\mathbb{Q}}}$
are such that
$b \in {\overline{\mathbb{Q}}}$
are such that
Then
Proof. Clearly,
Suppose that
for some positive-dimensional special subvariety S of
![]() $V_{a, b}$
. We show that this is impossible.
$V_{a, b}$
. We show that this is impossible.
The subvariety
![]() $V_{a, b}$
is, in the terminology of [
Reference Binyamini8
, definition 2], a hereditarily degree non-degenerate (hdnd) hypersurface. Hence, by [
Reference Binyamini8
, corollary 4], the special subvariety S may be defined by equations solely of the form
$V_{a, b}$
is, in the terminology of [
Reference Binyamini8
, definition 2], a hereditarily degree non-degenerate (hdnd) hypersurface. Hence, by [
Reference Binyamini8
, corollary 4], the special subvariety S may be defined by equations solely of the form
![]() $z_i = z_k$
and
$z_i = z_k$
and
![]() $z_l = x_l$
. Since
$z_l = x_l$
. Since
![]() $x_1, \ldots, x_n$
are pairwise distinct, no non-trivial equations
$x_1, \ldots, x_n$
are pairwise distinct, no non-trivial equations
![]() $z_i = z_k$
hold on S. Thus, up to reordering the coordinates,
$z_i = z_k$
hold on S. Thus, up to reordering the coordinates,
for some
![]() $k \in \{1, \ldots, n-1\}$
and
$k \in \{1, \ldots, n-1\}$
and
![]() $I \subset \{1, \ldots, n\}$
with
$I \subset \{1, \ldots, n\}$
with
![]() $\lvert I \rvert = k$
. So
$\lvert I \rvert = k$
. So
for all
![]() $z_i \in {\mathbb{C}}$
, which is clearly absurd since the
$z_i \in {\mathbb{C}}$
, which is clearly absurd since the
![]() $a_i$
are non-zero.
$a_i$
are non-zero.
Proof of Theorem
1·1. Let
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
. Define
$m, n \in {\mathbb{Z}}_{\gt0}$
. Define
![]() $V_{a, b} \subset {\mathbb{C}}^n$
as above. Let
$V_{a, b} \subset {\mathbb{C}}^n$
as above. Let
View
![]() $\mathbb{V}$
as a definable family of subvarieties of
$\mathbb{V}$
as a definable family of subvarieties of
![]() ${\mathbb{C}}^n$
with fibres
${\mathbb{C}}^n$
with fibres
![]() $V_{a, b}$
. Note that the definition of
$V_{a, b}$
. Note that the definition of
![]() $\mathbb{V}$
depends only on m, n.
$\mathbb{V}$
depends only on m, n.
By Pila’s Uniform André–Oort for
![]() ${\mathbb{C}}^n$
[
Reference Pila22
, theorem 13·2] applied to
${\mathbb{C}}^n$
[
Reference Pila22
, theorem 13·2] applied to
![]() $\mathbb{V}$
, for every
$\mathbb{V}$
, for every
![]() $d \in {\mathbb{Z}}_{\gt0}$
, there exists an ineffective constant
$d \in {\mathbb{Z}}_{\gt0}$
, there exists an ineffective constant
![]() $c(m, n, d)\gt0$
with the following property. Let
$c(m, n, d)\gt0$
with the following property. Let
![]() $x_1, \ldots, x_n$
be singular moduli and write
$x_1, \ldots, x_n$
be singular moduli and write
![]() $\Delta_i$
for the discriminant of
$\Delta_i$
for the discriminant of
![]() $x_i$
. Let
$x_i$
. Let
![]() $a = (a_1, \ldots, a_n) \in ({\overline{\mathbb{Q}}} \setminus \{0\})^n$
and
$a = (a_1, \ldots, a_n) \in ({\overline{\mathbb{Q}}} \setminus \{0\})^n$
and
![]() $b \in {\overline{\mathbb{Q}}}$
. If
$b \in {\overline{\mathbb{Q}}}$
. If
and
then
3·1. Uniformity in Theorem 1·1
Recall, from Section 2·1, that the singular moduli of a given discriminant
![]() $\Delta$
form a complete set of Galois conjugates over
$\Delta$
form a complete set of Galois conjugates over
![]() ${\mathbb{Q}}$
. Moreover, by Proposition 2·7, the number of distinct singular moduli of discriminant
${\mathbb{Q}}$
. Moreover, by Proposition 2·7, the number of distinct singular moduli of discriminant
![]() $\Delta$
is
$\Delta$
is
![]() $\geq c_1 (\log \lvert \Delta \rvert)^{c_2}$
for some absolute effective constants
$\geq c_1 (\log \lvert \Delta \rvert)^{c_2}$
for some absolute effective constants
![]() $c_1, c_2\gt0$
. Therefore, if m, n are fixed, then
$c_1, c_2\gt0$
. Therefore, if m, n are fixed, then
![]() $c(m, n, d) \to \infty$
as
$c(m, n, d) \to \infty$
as
![]() $d \to \infty$
, where c(m, n, d) is the constant in Theorem 1·1. Similarly, if m, d are fixed, then
$d \to \infty$
, where c(m, n, d) is the constant in Theorem 1·1. Similarly, if m, d are fixed, then
![]() $c(m, n, d) \to \infty$
as
$c(m, n, d) \to \infty$
as
![]() $n \to \infty$
.
$n \to \infty$
.
On the other hand, if n, d are fixed, then it is not obvious what happens to the constant c(m, n, d) as
![]() $m \to \infty$
. Since singular moduli are algebraic, one cannot bound the discriminants associated to a special point lying on a general hypersurface in
$m \to \infty$
. Since singular moduli are algebraic, one cannot bound the discriminants associated to a special point lying on a general hypersurface in
![]() ${\mathbb{C}}^n$
solely in terms of n and the minimal degree of a field of definition of the hypersurface. However, it may be possible to obtain bounds that are uniform in m for the specific family of hypersurfaces considered in Theorem 1·1, i.e. those defined by equations of the form
${\mathbb{C}}^n$
solely in terms of n and the minimal degree of a field of definition of the hypersurface. However, it may be possible to obtain bounds that are uniform in m for the specific family of hypersurfaces considered in Theorem 1·1, i.e. those defined by equations of the form
Indeed, the constant c(m, n, d) in Theorem 1·1 may be taken to be uniform in m if either
![]() $n = 1$
or
$n = 1$
or
![]() $(d, n) = (1, 2)$
. If x is a singular modulus of discriminant
$(d, n) = (1, 2)$
. If x is a singular modulus of discriminant
![]() $\Delta$
such that
$\Delta$
such that
for some
![]() $a, b \in {\overline{\mathbb{Q}}} \setminus \{0\}$
and
$a, b \in {\overline{\mathbb{Q}}} \setminus \{0\}$
and
![]() $m \in {\mathbb{Z}}_{\gt0}$
, then
$m \in {\mathbb{Z}}_{\gt0}$
, then
![]() $\lvert \Delta \rvert$
may be bounded solely in terms of
$\lvert \Delta \rvert$
may be bounded solely in terms of
![]() $[{\mathbb{Q}}(a, b) \;:\; {\mathbb{Q}}]$
, thanks to Proposition 2·7 and the fact [
Reference Riffaut25
, lemma 2·6] that
$[{\mathbb{Q}}(a, b) \;:\; {\mathbb{Q}}]$
, thanks to Proposition 2·7 and the fact [
Reference Riffaut25
, lemma 2·6] that
![]() ${\mathbb{Q}}(x^m) = {\mathbb{Q}}(x)$
. If
${\mathbb{Q}}(x^m) = {\mathbb{Q}}(x)$
. If
![]() $x_1, x_2$
are distinct singular moduli of respective discriminants
$x_1, x_2$
are distinct singular moduli of respective discriminants
![]() $\Delta_1, \Delta_2$
such that
$\Delta_1, \Delta_2$
such that
for some
![]() $a_1, a_2 \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, a_2 \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $m_1, m_2 \in {\mathbb{Z}}_{\gt0}$
, then
$m_1, m_2 \in {\mathbb{Z}}_{\gt0}$
, then
![]() $\max \{\lvert \Delta_1 \rvert, \lvert \Delta_2 \rvert \} \leq 427$
by [
Reference Luca and Riffaut19
, theorem 1·3] (see also [
Reference Riffaut25
, theorem 1·5]). For
$\max \{\lvert \Delta_1 \rvert, \lvert \Delta_2 \rvert \} \leq 427$
by [
Reference Luca and Riffaut19
, theorem 1·3] (see also [
Reference Riffaut25
, theorem 1·5]). For
![]() $n = 3$
, we have the previous result of the author [
Reference Fowler13
, theorem 1·1]: if
$n = 3$
, we have the previous result of the author [
Reference Fowler13
, theorem 1·1]: if
![]() $x_1, x_2, x_3$
are pairwise distinct singular moduli of respective discriminants
$x_1, x_2, x_3$
are pairwise distinct singular moduli of respective discriminants
![]() $\Delta_1, \Delta_2, \Delta_3$
such that
$\Delta_1, \Delta_2, \Delta_3$
such that
for some
![]() $m \in {\mathbb{Z}}_{\gt0}$
and
$m \in {\mathbb{Z}}_{\gt0}$
and
![]() $a_1, a_2, a_3 \in {\mathbb{Q}} \setminus \{0\}$
with
$a_1, a_2, a_3 \in {\mathbb{Q}} \setminus \{0\}$
with
![]() $\lvert a_1 \rvert = \lvert a_2 \rvert = \lvert a_3 \rvert$
, then
$\lvert a_1 \rvert = \lvert a_2 \rvert = \lvert a_3 \rvert$
, then
![]() $\max \{\lvert \Delta_1 \rvert, \lvert \Delta_2 \rvert, \lvert \Delta_3 \rvert \} \leq 907$
.
$\max \{\lvert \Delta_1 \rvert, \lvert \Delta_2 \rvert, \lvert \Delta_3 \rvert \} \leq 907$
.
4. Equations in singular moduli of the same discriminant
In this section, we prove Theorem 1·4.
Proof of Theorem
1·4. Let
![]() $n \in {\mathbb{Z}}_{\gt0}$
. Let
$n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli of discriminant
$x_1, \ldots, x_n$
be pairwise distinct singular moduli of discriminant
![]() $\Delta$
. In particular,
$\Delta$
. In particular,
![]() $h(\Delta) \geq n$
. Write
$h(\Delta) \geq n$
. Write
![]() $K = {\mathbb{Q}}(\sqrt{\Delta})$
. Suppose that
$K = {\mathbb{Q}}(\sqrt{\Delta})$
. Suppose that
for some
![]() $a_1, \ldots, a_n \in K \setminus \{0\}$
,
$a_1, \ldots, a_n \in K \setminus \{0\}$
,
![]() $b \in K$
, and
$b \in K$
, and
![]() $m \in {\mathbb{Z}}_{\gt0}$
.
$m \in {\mathbb{Z}}_{\gt0}$
.
Suppose first that
![]() $h(\Delta) \geq n+1$
. The singular moduli of discriminant
$h(\Delta) \geq n+1$
. The singular moduli of discriminant
![]() $\Delta$
form a complete set of Galois conjugates over K. Hence, there must exist K-conjugates
$\Delta$
form a complete set of Galois conjugates over K. Hence, there must exist K-conjugates
of
![]() $(x_1, \ldots, x_n)$
, where
$(x_1, \ldots, x_n)$
, where
![]() $i \in \{1, \ldots, n+1\}$
, with the property that:
$i \in \{1, \ldots, n+1\}$
, with the property that:
Note that
for every
![]() $i \in \{1, \ldots, n+1\}$
. Therefore,
$i \in \{1, \ldots, n+1\}$
. Therefore,
 \begin{align*} {}\begin{vmatrix} {} {}1 & \cdots & 1\\ {} {}x_{1, 1}^m & \cdots & x_{1, n+1}^m\\ {} {}\vdots & & \vdots\\ {} {}x_{n, 1}^m & \cdots & x_{n, n+1}^m {}\end{vmatrix} {}=0.\end{align*}
\begin{align*} {}\begin{vmatrix} {} {}1 & \cdots & 1\\ {} {}x_{1, 1}^m & \cdots & x_{1, n+1}^m\\ {} {}\vdots & & \vdots\\ {} {}x_{n, 1}^m & \cdots & x_{n, n+1}^m {}\end{vmatrix} {}=0.\end{align*}
Expanding this determinant, we have that
Let
![]() $\tau$
be the unique element of
$\tau$
be the unique element of
![]() $S_{n+1}$
such that
$S_{n+1}$
such that
![]() $\tau(i+1) = i$
for every
$\tau(i+1) = i$
for every
![]() $i \in \{1, \ldots, n\}$
. Then
$i \in \{1, \ldots, n\}$
. Then
 \begin{align} {}\lvert x_{1, 1} \cdots x_{n, n} \rvert^m = \left \lvert \sum_{\sigma \in S_{n+1} \setminus \{ \tau\}} \mathrm{sgn}(\sigma) (x_{1, \sigma(2)} \cdots x_{n, \sigma(n+1)})^m \right\rvert.\end{align}
\begin{align} {}\lvert x_{1, 1} \cdots x_{n, n} \rvert^m = \left \lvert \sum_{\sigma \in S_{n+1} \setminus \{ \tau\}} \mathrm{sgn}(\sigma) (x_{1, \sigma(2)} \cdots x_{n, \sigma(n+1)})^m \right\rvert.\end{align}
Note that
since
![]() $x_{i, i}$
is the unique dominant singular modulus of discriminant
$x_{i, i}$
is the unique dominant singular modulus of discriminant
![]() $\Delta$
for every
$\Delta$
for every
![]() $i \in \{1, \ldots, n\}$
. Observe also that if
$i \in \{1, \ldots, n\}$
. Observe also that if
![]() $\sigma \in S_{n+1} \setminus \{ \tau\}$
, then
$\sigma \in S_{n+1} \setminus \{ \tau\}$
, then
![]() $\sigma(i+1) \neq i$
for some
$\sigma(i+1) \neq i$
for some
![]() $i \in \{1, \ldots, n\}$
and hence at least one of
$i \in \{1, \ldots, n\}$
and hence at least one of
is not dominant. Therefore, by Lemma 2·3,
 \begin{align} {}&\left\lvert {}\sum_{\sigma \in S_{n+1} \setminus \{ \tau\}} \mathrm{sgn}(\sigma) (x_{1, \sigma(2)} \cdots x_{n, \sigma(n+1)})^m \right\rvert \nonumber\\ {}&\quad \leq (n+1)! \left(\frac{6 }{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) } \right)^m\lvert x_{1, 1} \rvert^{mn}.\end{align}
\begin{align} {}&\left\lvert {}\sum_{\sigma \in S_{n+1} \setminus \{ \tau\}} \mathrm{sgn}(\sigma) (x_{1, \sigma(2)} \cdots x_{n, \sigma(n+1)})^m \right\rvert \nonumber\\ {}&\quad \leq (n+1)! \left(\frac{6 }{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) } \right)^m\lvert x_{1, 1} \rvert^{mn}.\end{align}
Then (4·1) and (4·2) together imply that
 \[\left(\frac{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}{6}\right)^m \leq (n+1)!\]
\[\left(\frac{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}{6}\right)^m \leq (n+1)!\]
Since
![]() $\lvert \Delta \rvert \geq 3$
for every discriminant
$\lvert \Delta \rvert \geq 3$
for every discriminant
![]() $\Delta$
, we have that
$\Delta$
, we have that
 \[ \exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) \geq \exp\left(\frac{\pi \sqrt{3}}{2}\right) = 15.190\ldots \gt 6.\]
\[ \exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) \geq \exp\left(\frac{\pi \sqrt{3}}{2}\right) = 15.190\ldots \gt 6.\]
Thus,
 \[\frac{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}{6} \leq (n+1)!\]
\[\frac{\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}{6} \leq (n+1)!\]
For every
![]() $k \in {\mathbb{Z}}_{\gt0}$
, Stirling’s formula [
Reference Robbins26
, (1), (2)] implies that
$k \in {\mathbb{Z}}_{\gt0}$
, Stirling’s formula [
Reference Robbins26
, (1), (2)] implies that
Hence,
 \begin{align*} {}\lvert \Delta \rvert^{1/2} &\leq \frac{1}{\pi} \left((2n+3) \log(n+1) -2(n+1) +\log(72 \pi) + \frac{1}{6}\right)\\ {}&\leq \frac{1}{\pi} \left(\left(2n+3\right) \log\left(n+1\right) -2n +4\right).\end{align*}
\begin{align*} {}\lvert \Delta \rvert^{1/2} &\leq \frac{1}{\pi} \left((2n+3) \log(n+1) -2(n+1) +\log(72 \pi) + \frac{1}{6}\right)\\ {}&\leq \frac{1}{\pi} \left(\left(2n+3\right) \log\left(n+1\right) -2n +4\right).\end{align*}
Now suppose that
![]() $h(\Delta) = n$
. So
$h(\Delta) = n$
. So
![]() $x_1, \ldots, x_n$
are a complete set of Galois conjugates over K. Newton’s identities thus imply that
$x_1, \ldots, x_n$
are a complete set of Galois conjugates over K. Newton’s identities thus imply that
Hence,
If
![]() $a_1, \ldots, a_n$
are not all equal, then
$a_1, \ldots, a_n$
are not all equal, then
![]() $a_i \neq a_1$
for some
$a_i \neq a_1$
for some
![]() $i \in \{2, \ldots, n\}$
. Let
$i \in \{2, \ldots, n\}$
. Let
Since
![]() $l \lt n$
, we have that
$l \lt n$
, we have that
![]() $h(\Delta) \geq l+1$
. We may then apply, for l singular moduli, the already proved case of the theorem to obtain that
$h(\Delta) \geq l+1$
. We may then apply, for l singular moduli, the already proved case of the theorem to obtain that
 \begin{align*} {}\lvert \Delta \rvert^{1/2} &\leq \frac{1}{\pi} \left((2l+3) \log(l+1) -2l +4\right)\\ {}&\leq \frac{1}{\pi} \left((2n+3) \log(n+1) -2n +4\right).\end{align*}
\begin{align*} {}\lvert \Delta \rvert^{1/2} &\leq \frac{1}{\pi} \left((2l+3) \log(l+1) -2l +4\right)\\ {}&\leq \frac{1}{\pi} \left((2n+3) \log(n+1) -2n +4\right).\end{align*}
Remark 4·1. In the proof of Theorem 1·4, it is crucial that every singular modulus of discriminant
![]() $\Delta$
is conjugate over K to the dominant singular modulus of discriminant
$\Delta$
is conjugate over K to the dominant singular modulus of discriminant
![]() $\Delta$
. Thus, the above proof does not extend to equations over an arbitrary number field L. In contrast, the deduction, in the next two sections, of Theorem 1·5 and then Theorem 1·2 from Theorem 1·4 would go through over a general number field L.
$\Delta$
. Thus, the above proof does not extend to equations over an arbitrary number field L. In contrast, the deduction, in the next two sections, of Theorem 1·5 and then Theorem 1·2 from Theorem 1·4 would go through over a general number field L.
5. Fields generated by singular moduli
Theorem 1·5 may be deduced from Theorem 1·4, as we now show.
Proof of Theorem
1·5. Let
![]() $n \in {\mathbb{Z}}_{\gt0}$
. Let
$n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli of the same discriminant
$x_1, \ldots, x_n$
be pairwise distinct singular moduli of the same discriminant
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $K = {\mathbb{Q}}(\sqrt{\Delta})$
. Suppose that
$K = {\mathbb{Q}}(\sqrt{\Delta})$
. Suppose that
![]() $a_1, \ldots, a_n \in K \setminus \{0\}$
and
$a_1, \ldots, a_n \in K \setminus \{0\}$
and
![]() $m \in {\mathbb{Z}}_{\gt0}$
are such that
$m \in {\mathbb{Z}}_{\gt0}$
are such that
We will show that the desired bound holds on
![]() $\lvert \Delta \rvert$
.
$\lvert \Delta \rvert$
.
Recall that
![]() $K(x_1) / K$
is a Galois extension. In particular,
$K(x_1) / K$
is a Galois extension. In particular,
since
![]() $x_1, \ldots, x_n$
are all conjugate over K. Let
$x_1, \ldots, x_n$
are all conjugate over K. Let
![]() $G = {\mathrm{Gal}}(K(x_1) / K)$
and let
$G = {\mathrm{Gal}}(K(x_1) / K)$
and let
So
by assumption. In particular, there exists some
![]() $\sigma \in H$
such that
$\sigma \in H$
such that
Since
![]() $\sigma$
fixes
$\sigma$
fixes
![]() $K(a_1 x_1^m + \cdots + a_n x_n^m)$
, we have that
$K(a_1 x_1^m + \cdots + a_n x_n^m)$
, we have that
The
![]() $x_1, \ldots, x_n$
are pairwise distinct and the
$x_1, \ldots, x_n$
are pairwise distinct and the
![]() $\sigma(x_1), \ldots, \sigma(x_n)$
are pairwise distinct too. Cancelling terms as necessary, there must exist some
$\sigma(x_1), \ldots, \sigma(x_n)$
are pairwise distinct too. Cancelling terms as necessary, there must exist some
![]() $k \in \{2, \ldots, 2n\}$
and pairwise distinct singular moduli
$k \in \{2, \ldots, 2n\}$
and pairwise distinct singular moduli
![]() $y_1, \ldots, y_k$
of discriminant
$y_1, \ldots, y_k$
of discriminant
![]() $\Delta$
such that
$\Delta$
such that
for some
![]() $b_1, \ldots, b_k \in K \setminus \{0\}$
. Here we used that
$b_1, \ldots, b_k \in K \setminus \{0\}$
. Here we used that
![]() $\sigma(x_1) \notin \{x_1, \ldots, x_n\}$
. Hence, by Theorem 1·4, either:
$\sigma(x_1) \notin \{x_1, \ldots, x_n\}$
. Hence, by Theorem 1·4, either:
![]() $\lvert \Delta \rvert^{1/2} \leq c_1(k)$
and so certainly
$\lvert \Delta \rvert^{1/2} \leq c_1(k)$
and so certainly
![]() $\lvert \Delta \rvert^{1/2} \leq c_1(2n)$
as desired (where
$\lvert \Delta \rvert^{1/2} \leq c_1(2n)$
as desired (where
![]() $c_1(\!\cdot\!)$
denotes the constant from Theorem 1·4), or:
$c_1(\!\cdot\!)$
denotes the constant from Theorem 1·4), or:
![]() $h(\Delta) = k$
and
$h(\Delta) = k$
and
![]() $b_1 = \cdots = b_k$
.
$b_1 = \cdots = b_k$
.
Suppose then that
![]() $h(\Delta) = k$
and
$h(\Delta) = k$
and
![]() $b_1 = \cdots = b_k$
. Re-indexing the
$b_1 = \cdots = b_k$
. Re-indexing the
![]() $y_i$
as necessary, we may assume that
$y_i$
as necessary, we may assume that
![]() $y_1$
is dominant. Note also that
$y_1$
is dominant. Note also that
![]() $y_1 \neq 0$
and
$y_1 \neq 0$
and
![]() $\lvert \Delta \rvert \geq 15$
, by Lemma 2·1 since
$\lvert \Delta \rvert \geq 15$
, by Lemma 2·1 since
![]() $k \geq 2$
. Then, by Lemma 2·3 and Proposition 2·8,
$k \geq 2$
. Then, by Lemma 2·3 and Proposition 2·8,
 \begin{align*} {}&\lvert b_1 y_1^m + \cdots + b_k y_k^m \rvert\\ & \quad \geq \left\lvert b_1 \right\rvert \left( \left\lvert y_1 \right\rvert^m - \left( \left\lvert y_2 \right\rvert^m + \cdots + \left\rvert y_k \right\rvert^m \right) \right) \\ & \quad {}\geq \left\lvert b_1 \right \rvert \left \lvert y_1 \right\rvert^m \left(1- \frac{\lvert \Delta \rvert^{1/2} (2 + \log \lvert \Delta \rvert)}{\pi}\left(\frac{6}{ \exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}\right)^m\right)\\ {} & \quad \geq \left\lvert b_1 \right \rvert \left \lvert y_1 \right\rvert^m \left(1- \frac{6 \lvert \Delta \rvert^{1/2} (2 + \log \lvert \Delta \rvert) }{ \pi \exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}\right)\\ {} & \quad \gt0,\end{align*}
\begin{align*} {}&\lvert b_1 y_1^m + \cdots + b_k y_k^m \rvert\\ & \quad \geq \left\lvert b_1 \right\rvert \left( \left\lvert y_1 \right\rvert^m - \left( \left\lvert y_2 \right\rvert^m + \cdots + \left\rvert y_k \right\rvert^m \right) \right) \\ & \quad {}\geq \left\lvert b_1 \right \rvert \left \lvert y_1 \right\rvert^m \left(1- \frac{\lvert \Delta \rvert^{1/2} (2 + \log \lvert \Delta \rvert)}{\pi}\left(\frac{6}{ \exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}\right)^m\right)\\ {} & \quad \geq \left\lvert b_1 \right \rvert \left \lvert y_1 \right\rvert^m \left(1- \frac{6 \lvert \Delta \rvert^{1/2} (2 + \log \lvert \Delta \rvert) }{ \pi \exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right)}\right)\\ {} & \quad \gt0,\end{align*}
which is a contradiction. So we must have that
![]() $\lvert \Delta \rvert^{1/2} \leq c_1(2n)$
.
$\lvert \Delta \rvert^{1/2} \leq c_1(2n)$
.
6. The proof of Theorems 1·2 and 1·3
6·1. Completing the proof of Theorem 1·2
In this section, we complete the proof of Theorem 1·2. We start by recalling Binyamini’s [
Reference Binyamini8
] “almost” effective André–Oort result for
![]() ${\mathbb{C}}^n$
. For the definition of a special subvariety of
${\mathbb{C}}^n$
. For the definition of a special subvariety of
![]() ${\mathbb{C}}^n$
, see e.g. [
Reference Binyamini8
, (1·1)] or [
Reference Pila24
, definition 4·10]. For a subvariety
${\mathbb{C}}^n$
, see e.g. [
Reference Binyamini8
, (1·1)] or [
Reference Pila24
, definition 4·10]. For a subvariety
![]() $V \subset {\mathbb{C}}^n$
, we denote by
$V \subset {\mathbb{C}}^n$
, we denote by
![]() $\deg V$
the degree of V with respect to the projective embedding
$\deg V$
the degree of V with respect to the projective embedding
![]() ${\mathbb{C}}^n \subset \mathbb{P}^n$
. Binyamini proved the following theoremFootnote
2
. (Recall that
${\mathbb{C}}^n \subset \mathbb{P}^n$
. Binyamini proved the following theoremFootnote
2
. (Recall that
![]() $K_*$
denotes the exceptional imaginary quadratic field that was defined above Proposition 2·5.)
$K_*$
denotes the exceptional imaginary quadratic field that was defined above Proposition 2·5.)
Theorem 6·1 ([
Reference Binyamini8
, theorem 1]). Let
![]() $n, d, l \in {\mathbb{Z}}_{\gt0}$
. There exists an effective constant
$n, d, l \in {\mathbb{Z}}_{\gt0}$
. There exists an effective constant
![]() $c(n, d, l)\gt0$
with the following property:
$c(n, d, l)\gt0$
with the following property:
Let
![]() $V \subset {\mathbb{C}}^n$
be a subvariety defined over some number field L with
$V \subset {\mathbb{C}}^n$
be a subvariety defined over some number field L with
![]() $[L \;:\; {\mathbb{Q}}] \leq d$
and
$[L \;:\; {\mathbb{Q}}] \leq d$
and
![]() $\deg V \leq l$
. Denote by
$\deg V \leq l$
. Denote by
![]() $V^\mathrm{sp}$
the union of all the positive-dimensional special subvarieties of V. If
$V^\mathrm{sp}$
the union of all the positive-dimensional special subvarieties of V. If
![]() $x_1, \ldots, x_n$
are singular moduli with respective discriminants
$x_1, \ldots, x_n$
are singular moduli with respective discriminants
![]() $\Delta_1, \ldots, \Delta_n$
such that
$\Delta_1, \ldots, \Delta_n$
such that
then, for every
![]() $i \in \{1, \ldots, n\}$
, either
$i \in \{1, \ldots, n\}$
, either
or
Let
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
. For
$m, n \in {\mathbb{Z}}_{\gt0}$
. For
![]() $a = (a_1, \ldots, a_n) \in ({\mathbb{Q}} \setminus \{0\})^n$
and
$a = (a_1, \ldots, a_n) \in ({\mathbb{Q}} \setminus \{0\})^n$
and
![]() $b \in {\mathbb{Q}}$
, let
$b \in {\mathbb{Q}}$
, let
Since the
![]() $V_{a, b}$
are all defined over
$V_{a, b}$
are all defined over
![]() ${\mathbb{Q}}$
and have degree m, the constant in Theorem 6·1 is uniform (for the given m, n) across the
${\mathbb{Q}}$
and have degree m, the constant in Theorem 6·1 is uniform (for the given m, n) across the
![]() $V_{a, b}$
.
$V_{a, b}$
.
Proof of Theorem
1·2. Let
![]() $m, n \in {\mathbb{Z}}_{\gt0}$
. Let
$m, n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $c_1(m, n)\gt0$
be the effective constant given by Theorem 6·1 applied to the family of linear subvarieties
$c_1(m, n)\gt0$
be the effective constant given by Theorem 6·1 applied to the family of linear subvarieties
![]() $V_{a, b} \subset {\mathbb{C}}^n$
, where
$V_{a, b} \subset {\mathbb{C}}^n$
, where
![]() $a \in ({\mathbb{Q}} \setminus \{0\})^n$
and
$a \in ({\mathbb{Q}} \setminus \{0\})^n$
and
![]() $b \in {\mathbb{Q}}$
(i.e.
$b \in {\mathbb{Q}}$
(i.e.
![]() $c_1(m, n) = c(n, 1, m)$
for the constant c(n, d, l) in the statement of Theorem 6·1).
$c_1(m, n) = c(n, 1, m)$
for the constant c(n, d, l) in the statement of Theorem 6·1).
Suppose that
![]() $x_1, \ldots, x_n$
are pairwise distinct singular moduli such that
$x_1, \ldots, x_n$
are pairwise distinct singular moduli such that
for some
![]() $a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $b \in {\mathbb{Q}}$
. Then, by Lemma 3·1,
$b \in {\mathbb{Q}}$
. Then, by Lemma 3·1,
Hence, by Theorem 6·1, for every
![]() $i \in \{1, \ldots, n\}$
, either
$i \in \{1, \ldots, n\}$
, either
or
If there is no i such that
![]() ${\mathbb{Q}}(\sqrt{\Delta_i}) = K_*$
, then we are done. We may thus assume that there exists a discriminant
${\mathbb{Q}}(\sqrt{\Delta_i}) = K_*$
, then we are done. We may thus assume that there exists a discriminant
![]() $\Delta_*$
such that
$\Delta_*$
such that
![]() ${\mathbb{Q}}(\sqrt{\Delta_*}) = K_*$
and, for every
${\mathbb{Q}}(\sqrt{\Delta_*}) = K_*$
and, for every
![]() $i \in \{1, \ldots, n\}$
, either
$i \in \{1, \ldots, n\}$
, either
![]() $\Delta_i = \Delta_*$
or
$\Delta_i = \Delta_*$
or
![]() ${\mathbb{Q}}(\sqrt{\Delta_i}) \neq K_*$
. Relabelling as necessary, we may assume that there exists some
${\mathbb{Q}}(\sqrt{\Delta_i}) \neq K_*$
. Relabelling as necessary, we may assume that there exists some
![]() $k \in \{1, \ldots, n\}$
such that
$k \in \{1, \ldots, n\}$
such that
In particular, if
![]() $k+1 \leq i \leq n$
, then
$k+1 \leq i \leq n$
, then
![]() ${\mathbb{Q}}(\sqrt{\Delta_i}) \neq K_*$
and so
${\mathbb{Q}}(\sqrt{\Delta_i}) \neq K_*$
and so
Observe that
 \[ \sum_{i=1}^k a_i x_i^m = b - \sum_{i = k+1}^n a_i x_i^m,\]
\[ \sum_{i=1}^k a_i x_i^m = b - \sum_{i = k+1}^n a_i x_i^m,\]
where the sum on the right-hand side may be empty. Hence,
Since the
![]() $\lvert \Delta_i \rvert$
are effectively bounded (solely in terms of m, n) for
$\lvert \Delta_i \rvert$
are effectively bounded (solely in terms of m, n) for
![]() $i \geq k+1$
, there exists, by Proposition 2·8, an effective constant
$i \geq k+1$
, there exists, by Proposition 2·8, an effective constant
![]() $c_2(m, n)\gt0$
such that
$c_2(m, n)\gt0$
such that
Hence,
Since
![]() $\Delta_1 = \cdots = \Delta_k = \Delta_*$
, we may apply Theorem 1·5 to see that there exists an effective constant
$\Delta_1 = \cdots = \Delta_k = \Delta_*$
, we may apply Theorem 1·5 to see that there exists an effective constant
![]() $c_3(n)\gt0$
such that either
$c_3(n)\gt0$
such that either
or
In the first case, we are done. So assume then that
Then
 \begin{align*} {}h(\Delta_*) &= {}[{\mathbb{Q}}(x_1) \;:\; {\mathbb{Q}}]\\ {}&\leq [{\mathbb{Q}}(x_1, a_1 x_1^m + \cdots + a_k x_k^m) \;:\; {\mathbb{Q}}]\\ {}&= [{\mathbb{Q}}(x_1, a_1 x_1^m + \cdots + a_k x_k^m) \;:\; {\mathbb{Q}}(a_1 x_1^m + \cdots + a_k x_k^m)]\\ {}&\quad \times [{\mathbb{Q}}(a_1 x_1^m + \cdots + a_k x_k^m) \;:\; {\mathbb{Q}}]\\ {}&\leq 2n c_2(m, n).\end{align*}
\begin{align*} {}h(\Delta_*) &= {}[{\mathbb{Q}}(x_1) \;:\; {\mathbb{Q}}]\\ {}&\leq [{\mathbb{Q}}(x_1, a_1 x_1^m + \cdots + a_k x_k^m) \;:\; {\mathbb{Q}}]\\ {}&= [{\mathbb{Q}}(x_1, a_1 x_1^m + \cdots + a_k x_k^m) \;:\; {\mathbb{Q}}(a_1 x_1^m + \cdots + a_k x_k^m)]\\ {}&\quad \times [{\mathbb{Q}}(a_1 x_1^m + \cdots + a_k x_k^m) \;:\; {\mathbb{Q}}]\\ {}&\leq 2n c_2(m, n).\end{align*}
Thus, by Proposition 2·7, there exists an effective constant
![]() $c_4(m, n) \gt 0$
, which depends only on m, n, such that
$c_4(m, n) \gt 0$
, which depends only on m, n, such that
![]() $\lvert \Delta_* \rvert \leq c_4(m, n)$
.
$\lvert \Delta_* \rvert \leq c_4(m, n)$
.
6·2. The proof of Theorem 1·3
The first part of Theorem 1·3 (i.e. the existence of the constant
![]() $c_1(n)$
) is given by the following proposition. It follows from Theorem 1·5 by an argument of Bilu and Kühne [
Reference Bilu and Kühne4
, section 3, step 4], which in turn relies on an earlier result of Kühne [
Reference Kühne18
, corollary 1·2].
$c_1(n)$
) is given by the following proposition. It follows from Theorem 1·5 by an argument of Bilu and Kühne [
Reference Bilu and Kühne4
, section 3, step 4], which in turn relies on an earlier result of Kühne [
Reference Kühne18
, corollary 1·2].
Proposition 6·2. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli such that
$x_1, \ldots, x_n$
be pairwise distinct singular moduli such that
for some
![]() $m \in {\mathbb{Z}}_{\gt0}$
and
$m \in {\mathbb{Z}}_{\gt0}$
and
![]() $a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $b \in {\mathbb{Q}}$
. Write
$b \in {\mathbb{Q}}$
. Write
![]() $\Delta_i$
for the discriminant of
$\Delta_i$
for the discriminant of
![]() $x_i$
and
$x_i$
and
![]() $D_i$
for the fundamental discriminant. Suppose that
$D_i$
for the fundamental discriminant. Suppose that
![]() $k \in \{1, \ldots, n\}$
is such that
$k \in \{1, \ldots, n\}$
is such that
![]() $D_k \neq D_*$
and
$D_k \neq D_*$
and
Then
Proof. Let
![]() $k \in \{1, \ldots, n\}$
be such that
$k \in \{1, \ldots, n\}$
be such that
![]() $D_k \neq D_*$
and
$D_k \neq D_*$
and
Let
Suppose first that
![]() $r=1$
. Then
$r=1$
. Then
![]() $\Delta_1 = \cdots = \Delta_n$
by assumption. Hence, by Theorem 1·4, either
$\Delta_1 = \cdots = \Delta_n$
by assumption. Hence, by Theorem 1·4, either
or
![]() $h(\Delta) = n$
. In the latter case, since
$h(\Delta) = n$
. In the latter case, since
![]() $D_k \neq D_*$
, Proposition 2·2 implies that
$D_k \neq D_*$
, Proposition 2·2 implies that
Thus, in either case, the desired bound on
![]() $\lvert \Delta_k \rvert^{1/2}$
evidently holds.
$\lvert \Delta_k \rvert^{1/2}$
evidently holds.
So we may assume that
![]() $r \geq 2$
. Relabelling as necessary, we may assume that
$r \geq 2$
. Relabelling as necessary, we may assume that
![]() $k = 1$
and there are
$k = 1$
and there are
![]() $0 = n_0 \lt n_1 \lt \ldots \lt n_r = n$
such that
$0 = n_0 \lt n_1 \lt \ldots \lt n_r = n$
such that
 \begin{align*} {}D_{n_0 + 1} = &\ldots = D_{n_1},\\ {}D_{n_1 + 1} = &\ldots = D_{n_2},\\ {}&\ldots\\ {}D_{n_{r-1} + 1} = &\ldots = D_{n_r}.\end{align*}
\begin{align*} {}D_{n_0 + 1} = &\ldots = D_{n_1},\\ {}D_{n_1 + 1} = &\ldots = D_{n_2},\\ {}&\ldots\\ {}D_{n_{r-1} + 1} = &\ldots = D_{n_r}.\end{align*}
For
![]() $i \in \{1, \ldots, r\}$
, let
$i \in \{1, \ldots, r\}$
, let
![]() $K_i = {\mathbb{Q}}(\sqrt{D_{n_i}})$
and
$K_i = {\mathbb{Q}}(\sqrt{D_{n_i}})$
and
By assumption,
![]() $\Delta_{1} = \cdots = \Delta_{n_1}$
. We may also assume that
$\Delta_{1} = \cdots = \Delta_{n_1}$
. We may also assume that
since otherwise the desired bound already holds. Hence, by Theorem 1·5,
Since
![]() $D_1 \neq D_*$
, one may now argue exactly as below [
Reference Bilu and Kühne4
, (39)] to obtain that
$D_1 \neq D_*$
, one may now argue exactly as below [
Reference Bilu and Kühne4
, (39)] to obtain that
The second part of Theorem 1·3 is an easy consequence of Theorem 1·5 and Proposition 6·2.
Proof of Theorem
1·3. Let
![]() $n \in {\mathbb{Z}}_{\gt0}$
. Let
$n \in {\mathbb{Z}}_{\gt0}$
. Let
![]() $x_1, \ldots, x_n$
be pairwise distinct singular moduli. Write
$x_1, \ldots, x_n$
be pairwise distinct singular moduli. Write
![]() $\Delta_i$
for the discriminant of
$\Delta_i$
for the discriminant of
![]() $x_i$
and
$x_i$
and
![]() $D_i$
for the fundamental discriminant. Suppose that
$D_i$
for the fundamental discriminant. Suppose that
for some
![]() $m \in {\mathbb{Z}}_{\gt0}$
and
$m \in {\mathbb{Z}}_{\gt0}$
and
![]() $a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
$a_1, \ldots, a_n \in {\mathbb{Q}} \setminus \{0\}$
and
![]() $b \in {\mathbb{Q}}$
. Suppose that, for every
$b \in {\mathbb{Q}}$
. Suppose that, for every
![]() $k \in \{1, \ldots, n\}$
,
$k \in \{1, \ldots, n\}$
,
Hence, by Proposition 6·2, if
![]() $i \in \{1, \ldots, n\}$
is such that
$i \in \{1, \ldots, n\}$
is such that
![]() $D_i \neq D_*$
, then
$D_i \neq D_*$
, then
So if
![]() $D_* \notin \{D_1, \ldots, D_n\}$
, then we are done.
$D_* \notin \{D_1, \ldots, D_n\}$
, then we are done.
Without loss of generality, assume then that
![]() $D_1 = D_*$
. For
$D_1 = D_*$
. For
![]() $i \geq 2$
, either
$i \geq 2$
, either
![]() $\Delta_i = \Delta_1$
, or
$\Delta_i = \Delta_1$
, or
![]() $D_i \neq D_*$
and so
$D_i \neq D_*$
and so
![]() $\lvert \Delta_i \rvert$
is bounded as above. Relabelling as necessary, there exists
$\lvert \Delta_i \rvert$
is bounded as above. Relabelling as necessary, there exists
![]() $k \in \{1, \ldots, n\}$
such that:
$k \in \{1, \ldots, n\}$
such that:
and if
![]() $i \gt k$
, then
$i \gt k$
, then
![]() $D_i \neq D_*$
and hence
$D_i \neq D_*$
and hence
Hence, by Proposition 2·8, if
![]() $i \gt k$
, then
$i \gt k$
, then
Let
We may and do assume that
Since
![]() $\Delta_1 = \cdots = \Delta_k$
, Theorem 1·5 implies that
$\Delta_1 = \cdots = \Delta_k$
, Theorem 1·5 implies that
Thus,
Since
 \[ a_1 x_1^m + \cdots + a_k x_k^m = b - \sum_{i = k + 1}^n a_{i} x_{i}^m ,\]
\[ a_1 x_1^m + \cdots + a_k x_k^m = b - \sum_{i = k + 1}^n a_{i} x_{i}^m ,\]
we have that
Hence,
 \[ [L \;:\; {\mathbb{Q}}] \leq \prod_{i=k+1}^n [{\mathbb{Q}}(x_i) \;:\; {\mathbb{Q}}] \leq \left( \left((3.8 \times 10^{10})(2.1 \times 10^4)^n (n+1)^{4n+6}\right)^{4/3} \right)^n,\]
\[ [L \;:\; {\mathbb{Q}}] \leq \prod_{i=k+1}^n [{\mathbb{Q}}(x_i) \;:\; {\mathbb{Q}}] \leq \left( \left((3.8 \times 10^{10})(2.1 \times 10^4)^n (n+1)^{4n+6}\right)^{4/3} \right)^n,\]
and so
Hence, if we write
for convenience, then Proposition 2·7 implies that
7. Some more properties of singular moduli
In this section, we collect some more facts about singular moduli, which we will use for the proof of Theorem 1·6 in Section 8.
Recall, from Section 2·1, that a singular modulus x of discriminant
![]() $\Delta$
corresponds to a unique triple
$\Delta$
corresponds to a unique triple
![]() $(a, b, c) \in T_\Delta$
. Call the number a the denominator of the corresponding singular modulus. A singular modulus is called dominant (respectively subdominant) if it has denominator 1 (respectively 2). This terminology is adopted from [
Reference Bilu, Gun and Tron3, Reference Faye and Riffaut11, Reference Riffaut25
]. We need the following result on the number of singular moduli of a given discriminant with small denominators.
$(a, b, c) \in T_\Delta$
. Call the number a the denominator of the corresponding singular modulus. A singular modulus is called dominant (respectively subdominant) if it has denominator 1 (respectively 2). This terminology is adopted from [
Reference Bilu, Gun and Tron3, Reference Faye and Riffaut11, Reference Riffaut25
]. We need the following result on the number of singular moduli of a given discriminant with small denominators.
Proposition 7·1 ([
Reference Bilu, Luca and Pizarro-Madariaga6
, proposition 2·6] and [
Reference Fowler13
, lemma 2·1]). Let
![]() $\Delta \lt 0$
be such that
$\Delta \lt 0$
be such that
![]() $\Delta \equiv 0, 1 \bmod 4$
. Then:
$\Delta \equiv 0, 1 \bmod 4$
. Then:
-
(i) there exists exactly one dominant singular modulus of discriminant
 $\Delta$
;
$\Delta$
; -
(ii) for each
 $a \in \{2, 3, 4, 5\}$
, there exist at most two singular moduli of discriminant
$a \in \{2, 3, 4, 5\}$
, there exist at most two singular moduli of discriminant
 $\Delta$
with denominator a;
$\Delta$
with denominator a; -
(iii) there exist at most four singular moduli of discriminant
 $\Delta$
with denominator 6;
$\Delta$
with denominator 6; -
(iv) if
 $\Delta \equiv 1 \bmod 8$
and
$\Delta \equiv 1 \bmod 8$
and
 $\Delta \notin \{-7, -15\}$
, then there exist exactly two subdominant singular moduli of discriminant
$\Delta \notin \{-7, -15\}$
, then there exist exactly two subdominant singular moduli of discriminant
 $\Delta$
;
$\Delta$
; -
(v) if
 $\Delta \equiv 4 \bmod 32$
, then there are no subdominant singular moduli of discriminant
$\Delta \equiv 4 \bmod 32$
, then there are no subdominant singular moduli of discriminant
 $\Delta$
.
$\Delta$
.
The absolute value of the difference of two distinct singular moduli is bounded below in terms of the corresponding discriminants.
Proposition 7·2 ([
Reference Bilu, Faye and Zhu2
, theorem 1·1]). Let x, y be distinct singular moduli of respective discriminants
![]() $\Delta_x, \Delta_y$
. Then
$\Delta_x, \Delta_y$
. Then
The discriminants of small class number may be bounded by an explicit computation in PARI. We will use the following bounds.
Proposition 7·3. Let
![]() $\Delta \lt 0$
be such that
$\Delta \lt 0$
be such that
![]() $\Delta \equiv 0, 1 \bmod 4$
. If
$\Delta \equiv 0, 1 \bmod 4$
. If
![]() $h(\Delta) \leq 6$
, then
$h(\Delta) \leq 6$
, then
![]() $\lvert \Delta \rvert \leq 4075$
. If
$\lvert \Delta \rvert \leq 4075$
. If
![]() $h(\Delta) \leq 32$
, then
$h(\Delta) \leq 32$
, then
![]() $\lvert \Delta \rvert \leq 166147$
.
$\lvert \Delta \rvert \leq 166147$
.
Proof. For each
![]() $k \in \{1, \ldots, 100\}$
, Watkins [
Reference Watkins31
, table 4] computed the largest (in absolute value) fundamental discriminant D with
$k \in \{1, \ldots, 100\}$
, Watkins [
Reference Watkins31
, table 4] computed the largest (in absolute value) fundamental discriminant D with
![]() $h(D) = k$
. As explained in [
Reference Bilu, Gun and Tron3
, proposition 2·1], one may then use this and the class number formula [
Reference Cox10
, theorem 7·24] to obtain an upper bound c(k) such that
$h(D) = k$
. As explained in [
Reference Bilu, Gun and Tron3
, proposition 2·1], one may then use this and the class number formula [
Reference Cox10
, theorem 7·24] to obtain an upper bound c(k) such that
![]() $\lvert \Delta \rvert \leq c(k)$
for all
$\lvert \Delta \rvert \leq c(k)$
for all
![]() $\Delta \lt 0$
such that
$\Delta \lt 0$
such that
![]() $\Delta \equiv 0, 1 \bmod 4$
and
$\Delta \equiv 0, 1 \bmod 4$
and
![]() $h(\Delta) \leq k$
. To find the largest (in absolute value) discriminant with
$h(\Delta) \leq k$
. To find the largest (in absolute value) discriminant with
![]() $h(\Delta) \leq k$
, we then need only compute in PARI the class numbers of all discriminants
$h(\Delta) \leq k$
, we then need only compute in PARI the class numbers of all discriminants
![]() $\Delta$
with
$\Delta$
with
![]() $\lvert \Delta \rvert \leq c(k)$
. This computation is essentially instant for
$\lvert \Delta \rvert \leq c(k)$
. This computation is essentially instant for
![]() $k=6$
and takes about 3 minutes for
$k=6$
and takes about 3 minutes for
![]() $k=32$
. The bounds we compute agree with those in [
Reference Bilu, Gun and Tron3
, proposition 2·1] and with those given by Klaise [
Reference Klaise16
, p.19].
$k=32$
. The bounds we compute agree with those in [
Reference Bilu, Gun and Tron3
, proposition 2·1] and with those given by Klaise [
Reference Klaise16
, p.19].
7·1. Fields generated by singular moduli
The fields generated by
![]() ${\mathbb{Q}}$
-linear combinations of two singular moduli may be described explicitly.
${\mathbb{Q}}$
-linear combinations of two singular moduli may be described explicitly.
Theorem 7·4 ([
Reference Bilu, Faye and Zhu2
, theorem 1·5] and [
Reference Faye and Riffaut11
, theorem 4·1]). Let
![]() $\alpha \in {\mathbb{Q}} \setminus \{0\}$
. Let x, y be distinct singular moduli of respective discriminants
$\alpha \in {\mathbb{Q}} \setminus \{0\}$
. Let x, y be distinct singular moduli of respective discriminants
![]() $\Delta_x, \Delta_y$
. If
$\Delta_x, \Delta_y$
. If
then one of the following holds:
-
(i)
 $\alpha = 1$
and
$\alpha = 1$
and
 $\Delta_x = \Delta_y$
. In this case,
$\Delta_x = \Delta_y$
. In this case,
 \[ [{\mathbb{Q}}(x, y) \;:\; {\mathbb{Q}}(x + y)] = 2;\]
\[ [{\mathbb{Q}}(x, y) \;:\; {\mathbb{Q}}(x + y)] = 2;\]
-
(ii)
 $\Delta_x \neq \Delta_y$
,
$\Delta_x \neq \Delta_y$
,
 ${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
and this field has degree 2 over
${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
and this field has degree 2 over
 ${\mathbb{Q}}$
, and
where x′, y′ are the non-trivial
${\mathbb{Q}}$
, and
where x′, y′ are the non-trivial \[ \alpha = -\frac{x - x'}{y - y'},\]
\[ \alpha = -\frac{x - x'}{y - y'},\]
 ${\mathbb{Q}}$
-conjugates of x, y respectively. In this case,
${\mathbb{Q}}$
-conjugates of x, y respectively. In this case,
 \[ {\mathbb{Q}}(x + \alpha y) = {\mathbb{Q}}.\]
\[ {\mathbb{Q}}(x + \alpha y) = {\mathbb{Q}}.\]
We also need the following results describing when singular moduli x, y satisfy either
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
or
${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
or
![]() ${\mathbb{Q}}(x) \subset {\mathbb{Q}}(y)$
with
${\mathbb{Q}}(x) \subset {\mathbb{Q}}(y)$
with
![]() $[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}(x)] = 2$
.
$[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}(x)] = 2$
.
Proposition 7·5 ([
Reference Allombert, Bilu and Pizarro-Madariaga1
, corollary 4·2]). Let x, y be singular moduli with discriminants
![]() $\Delta_x, \Delta_y$
and fundamental discriminants
$\Delta_x, \Delta_y$
and fundamental discriminants
![]() $D_x, D_y$
respectively. If
$D_x, D_y$
respectively. If
then all the possible fields
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
and the corresponding possible discriminants
${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
and the corresponding possible discriminants
![]() $\Delta_x, \Delta_y$
are listed in [
Reference Allombert, Bilu and Pizarro-Madariaga1
, table 2].
$\Delta_x, \Delta_y$
are listed in [
Reference Allombert, Bilu and Pizarro-Madariaga1
, table 2].
Proposition 7·6. Let x, y be singular moduli with discriminants
![]() $\Delta_x, \Delta_y$
and fundamental discriminants
$\Delta_x, \Delta_y$
and fundamental discriminants
![]() $D_x, D_y$
respectively. If
$D_x, D_y$
respectively. If
then there are only finitely many possibilities for the pair
![]() $(\Delta_x, \Delta_y)$
and these may be listed explicitly.
$(\Delta_x, \Delta_y)$
and these may be listed explicitly.
This is an explicit version of [
Reference Bilu, Gun and Tron3
, corollary 2·13(2)]. To give a proof, we need the following terminology from [
Reference Bilu, Gun and Tron3
]. Let G be a finite abelian group, written multiplicatively. Say that G is 2-elementary if every element of G has order
![]() $\leq 2$
. Say that G is almost 2-elementary if there exists a subgroup
$\leq 2$
. Say that G is almost 2-elementary if there exists a subgroup
![]() $H \leq G$
such that H is 2-elementary and
$H \leq G$
such that H is 2-elementary and
![]() $[G \;:\; H] = 2$
. Denote by
$[G \;:\; H] = 2$
. Denote by
![]() $\rho_2(G)$
the dimension of
$\rho_2(G)$
the dimension of
![]() $G / G^2$
as an
$G / G^2$
as an
![]() $\mathbb{F}_2$
-vector space, where
$\mathbb{F}_2$
-vector space, where
![]() $G^2 = \{g^2 \;:\; g \in G\}$
.
$G^2 = \{g^2 \;:\; g \in G\}$
.
Proof. Suppose that
Then
![]() $h(\Delta_x) \leq 16$
and
$h(\Delta_x) \leq 16$
and
![]() $h(\Delta_y) \leq 32$
by [
Reference Bilu, Gun and Tron3
, corollary 2·13]. So
$h(\Delta_y) \leq 32$
by [
Reference Bilu, Gun and Tron3
, corollary 2·13]. So
![]() $\lvert \Delta_x \rvert, \lvert \Delta_y \rvert \leq 166147$
by Proposition 7·3. The proof of [
Reference Bilu, Gun and Tron3
, corollary 2·13] also shows that the class group
$\lvert \Delta_x \rvert, \lvert \Delta_y \rvert \leq 166147$
by Proposition 7·3. The proof of [
Reference Bilu, Gun and Tron3
, corollary 2·13] also shows that the class group
![]() ${\mathrm{cl}}(\Delta_x)$
is 2-elementary (and hence also almost 2-elementary) and that the class group
${\mathrm{cl}}(\Delta_x)$
is 2-elementary (and hence also almost 2-elementary) and that the class group
![]() ${\mathrm{cl}}(\Delta_y)$
is almost 2-elementary.
${\mathrm{cl}}(\Delta_y)$
is almost 2-elementary.
One may then compute in PARI all the almost 2-elementary discriminants
![]() $\Delta$
with
$\Delta$
with
![]() $\lvert \Delta \rvert \leq 166147$
and
$\lvert \Delta \rvert \leq 166147$
and
![]() $h(\Delta) \leq 32$
and then, among those, compute all the 2-elementary discriminants
$h(\Delta) \leq 32$
and then, among those, compute all the 2-elementary discriminants
![]() $\Delta$
with
$\Delta$
with
![]() $h(\Delta) \leq 16$
. To do this, we use the following two characterisations [
Reference Bilu, Gun and Tron3
, (2·9), (2·10)]:
$h(\Delta) \leq 16$
. To do this, we use the following two characterisations [
Reference Bilu, Gun and Tron3
, (2·9), (2·10)]:
and the classical fact (see e.g. [ Reference Cox10 , proposition 3·11] and the isomorphism in [ Reference Cox10 , (3·19)]) that
 \[ \rho_2({\mathrm{cl}}(\Delta)) = \begin{cases} {}\omega(\Delta) & \mbox{if } \Delta \equiv 0 \bmod 32\\ {}\omega(\Delta)-2 & \mbox{if } \Delta \equiv 4 \bmod 16\\ {}\omega(\Delta) - 1 & \mbox{otherwise,}\end{cases} \]
\[ \rho_2({\mathrm{cl}}(\Delta)) = \begin{cases} {}\omega(\Delta) & \mbox{if } \Delta \equiv 0 \bmod 32\\ {}\omega(\Delta)-2 & \mbox{if } \Delta \equiv 4 \bmod 16\\ {}\omega(\Delta) - 1 & \mbox{otherwise,}\end{cases} \]
where
![]() $\omega(\Delta)$
denotes the number of distinct prime divisors of
$\omega(\Delta)$
denotes the number of distinct prime divisors of
![]() $\Delta$
as usual.
$\Delta$
as usual.
Let
![]() $\Delta_y$
be an almost 2-elementary discriminant such that
$\Delta_y$
be an almost 2-elementary discriminant such that
![]() $h(\Delta_y)\leq 32$
and
$h(\Delta_y)\leq 32$
and
![]() $\Delta_x$
a 2-elementary discriminant such that
$\Delta_x$
a 2-elementary discriminant such that
![]() $h(\Delta_x) \leq 16$
. One may then check in PARI whether the conditions in (7·1) are satisfied by the pair
$h(\Delta_x) \leq 16$
. One may then check in PARI whether the conditions in (7·1) are satisfied by the pair
![]() $(\Delta_x, \Delta_y)$
. One finds in this way that there are 873 different possibilities for
$(\Delta_x, \Delta_y)$
. One finds in this way that there are 873 different possibilities for
![]() $(\Delta_x, \Delta_y)$
. The computations take about 30 minutes in total.
$(\Delta_x, \Delta_y)$
. The computations take about 30 minutes in total.
Proposition 7·7 ([
Reference Allombert, Bilu and Pizarro-Madariaga1
, proposition 4·3] and [
Reference Bilu, Luca and Pizarro-Madariaga6
, section 3·2·2]). Let x, y be singular moduli with respective discriminants
![]() $\Delta_x, \Delta_y$
and respective fundamental discriminants
$\Delta_x, \Delta_y$
and respective fundamental discriminants
![]() $D_x, D_y$
. Suppose that
$D_x, D_y$
. Suppose that
![]() $D_x = D_y$
and
$D_x = D_y$
and
![]() $x, y \notin {\mathbb{Q}}$
. Suppose further that
$x, y \notin {\mathbb{Q}}$
. Suppose further that
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
. Then
${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
. Then
![]() $\Delta_x/ \Delta_y \in \{1, 4, 1/4\}$
and if
$\Delta_x/ \Delta_y \in \{1, 4, 1/4\}$
and if
![]() $\Delta_x / \Delta_y = 4$
, then
$\Delta_x / \Delta_y = 4$
, then
![]() $\Delta_y \equiv 1 \bmod 8$
.
$\Delta_y \equiv 1 \bmod 8$
.
Proposition 7·8 ([
Reference Fowler12
, lemma 2·3]). Let x, y be singular moduli with respective discriminants
![]() $\Delta_x, \Delta_y$
and respective fundamental discriminants
$\Delta_x, \Delta_y$
and respective fundamental discriminants
![]() $D_x, D_y$
. Suppose that
$D_x, D_y$
. Suppose that
Then
![]() $\Delta_y/ \Delta_x \in \{9/4, 4, 9, 16\}$
. In addition, if
$\Delta_y/ \Delta_x \in \{9/4, 4, 9, 16\}$
. In addition, if
![]() $\Delta_y / \Delta_x = 9/4$
, then
$\Delta_y / \Delta_x = 9/4$
, then
![]() $\Delta_x \equiv 0, 4 \bmod 16$
.
$\Delta_x \equiv 0, 4 \bmod 16$
.
The “in addition” part of Proposition 7·8 is not stated in [
Reference Fowler12
, lemma 2·3], but is a trivial consequence of the fact that
![]() $\Delta_x, \Delta_y \equiv 0, 1 \bmod 4$
.
$\Delta_x, \Delta_y \equiv 0, 1 \bmod 4$
.
8. The proof of Theorem 1·6
The “if” direction is clear. We prove the “only if”. The proof is rather lengthy and involves considering several cases; we split the argument into a series of claims for the reader’s convenience.
Let x, y, z be pairwise distinct singular moduli. Suppose that
for some
![]() $A, B, C \in {\mathbb{Q}} \setminus \{0\}$
. Write
$A, B, C \in {\mathbb{Q}} \setminus \{0\}$
. Write
![]() $\Delta_x, \Delta_y, \Delta_z$
for the discriminants and
$\Delta_x, \Delta_y, \Delta_z$
for the discriminants and
![]() $D_x, D_y, D_z$
for the fundamental discriminants of x, y, z respectively.
$D_x, D_y, D_z$
for the fundamental discriminants of x, y, z respectively.
Claim 8·1. We may assume
![]() $x, y, z \notin {\mathbb{Q}}$
.
$x, y, z \notin {\mathbb{Q}}$
.
Proof. If at least one of x, y, z is in
![]() ${\mathbb{Q}}$
, then [
Reference Allombert, Bilu and Pizarro-Madariaga1
, theorem 1·2] implies that either case (i) or case (ii) of Theorem 1·6 holds.
${\mathbb{Q}}$
, then [
Reference Allombert, Bilu and Pizarro-Madariaga1
, theorem 1·2] implies that either case (i) or case (ii) of Theorem 1·6 holds.
Hence, we assume subsequently that
![]() $x, y, z \notin {\mathbb{Q}}$
. We thus cannot be in either of cases (i) or (ii) of Theorem 1·6.
$x, y, z \notin {\mathbb{Q}}$
. We thus cannot be in either of cases (i) or (ii) of Theorem 1·6.
Claim 8·2. We may assume that
![]() $\Delta_x, \Delta_y, \Delta_z$
are not all equal.
$\Delta_x, \Delta_y, \Delta_z$
are not all equal.
Proof. Suppose that
![]() $\Delta_x = \Delta_y = \Delta_z$
. Write
$\Delta_x = \Delta_y = \Delta_z$
. Write
![]() $\Delta$
for this common discriminant. By Theorem 1·4, either
$\Delta$
for this common discriminant. By Theorem 1·4, either
or
![]() $h(\Delta) = 3$
and
$h(\Delta) = 3$
and
![]() $A = B = C$
. If
$A = B = C$
. If
![]() $\lvert \Delta \rvert \lt 12$
, then
$\lvert \Delta \rvert \lt 12$
, then
![]() $x \in {\mathbb{Q}}$
by Lemma 2·1, contradicting Claim 8·1. If
$x \in {\mathbb{Q}}$
by Lemma 2·1, contradicting Claim 8·1. If
![]() $h(\Delta) = 3$
and
$h(\Delta) = 3$
and
![]() $A=B=C$
, then case (iv) of Theorem 1·6 holds.
$A=B=C$
, then case (iv) of Theorem 1·6 holds.
We may thus assume subsequently that
![]() $\Delta_x, \Delta_y, \Delta_z$
are not all equal. In particular, x, y, z are not all conjugate over
$\Delta_x, \Delta_y, \Delta_z$
are not all equal. In particular, x, y, z are not all conjugate over
![]() ${\mathbb{Q}}$
and so case (iv) of Theorem 1·6 does not hold.
${\mathbb{Q}}$
and so case (iv) of Theorem 1·6 does not hold.
8·1. Controlling the fields
Claim 8·3. Either:
or:
Proof. Observe that
The same holds permuting x, y, z.
Suppose then that
Note that
We apply Theorem 7·4 to the field
Since
![]() $x \notin {\mathbb{Q}}$
by Claim 8·1, case (ii) of Theorem 7·4 is not possible. Thus, we must have that
$x \notin {\mathbb{Q}}$
by Claim 8·1, case (ii) of Theorem 7·4 is not possible. Thus, we must have that
![]() $B = C$
,
$B = C$
,
![]() $\Delta_y = \Delta_z$
, and
$\Delta_y = \Delta_z$
, and
Suppose, in addition, that
Then, by the same argument, we must have that
![]() $A = C$
and
$A = C$
and
![]() $\Delta_x = \Delta_z$
. Thus,
$\Delta_x = \Delta_z$
. Thus,
![]() $\Delta_x = \Delta_y = \Delta_z$
, which contradicts Claim 8·2. Similarly, if
$\Delta_x = \Delta_y = \Delta_z$
, which contradicts Claim 8·2. Similarly, if
![]() ${\mathbb{Q}}(z) \subsetneq {\mathbb{Q}}(x, y)$
.
${\mathbb{Q}}(z) \subsetneq {\mathbb{Q}}(x, y)$
.
We are thus left with the following two possibilities. Either:
or, up to permuting x, y, z:
Hence, either:
or:
Claim 8·4. If
then we may assume that this field has degree at least 3 over
![]() ${\mathbb{Q}}$
.
${\mathbb{Q}}$
.
Proof. Suppose not. Then
and, by Claim 8·1, this field must be a degree 2 extension of
![]() ${\mathbb{Q}}$
. Write x
′, y
′, z
′ for the unique non-trivial
${\mathbb{Q}}$
. Write x
′, y
′, z
′ for the unique non-trivial
![]() ${\mathbb{Q}}$
-conjugates of x, y, z respectively. Then
${\mathbb{Q}}$
-conjugates of x, y, z respectively. Then
Hence,
and so we must be in case (iii) of Theorem 1·6.
Claim 8·5. If
then we may assume that
Proof. Suppose that
Suppose, in addition, that
We will show that we must then be in case (v) of Theorem 1·6.
Since
![]() ${\mathbb{Q}}(x) \subsetneq {\mathbb{Q}}(y, z)$
, we must have that
${\mathbb{Q}}(x) \subsetneq {\mathbb{Q}}(y, z)$
, we must have that
![]() $B=C$
and
$B=C$
and
![]() $\Delta_y = \Delta_z$
. Let x
′ denote the unique non-trivial Galois conjugate of x over
$\Delta_y = \Delta_z$
. Let x
′ denote the unique non-trivial Galois conjugate of x over
![]() ${\mathbb{Q}}$
. Let v, w be the other (along with y, z) two singular moduli of discriminant
${\mathbb{Q}}$
. Let v, w be the other (along with y, z) two singular moduli of discriminant
![]() $\Delta_y$
. Since
$\Delta_y$
. Since
there are then
![]() $y', z' \in \{y, z, v, w\}$
such that
$y', z' \in \{y, z, v, w\}$
such that
So
Suppose that
![]() $\{y, z\} \cap \{y', z'\} \neq \emptyset$
. Without loss of generality, we may assume that
$\{y, z\} \cap \{y', z'\} \neq \emptyset$
. Without loss of generality, we may assume that
![]() $y = y'$
. So
$y = y'$
. So
and hence
We thus have that
where the second equality is by Theorem 7·4 and the third equality holds since
![]() $[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = 2$
. In particular,
$[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = 2$
. In particular,
![]() $z \neq z'$
, and so, by Theorem 7·4 again,
$z \neq z'$
, and so, by Theorem 7·4 again,
Hence,
This is a contradiction, since
![]() $[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = 2$
, but
$[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] = 2$
, but
Therefore, we must have that
![]() $\{y', z'\} = \{v, w\}$
and so
$\{y', z'\} = \{v, w\}$
and so
We are thus in case (v) of Theorem 1·6.
Claim 8·6. We may assume that we are not in any of cases (i)–(v) of Theorem 1·6.
Proof. By Claim 8·3, either
or:
If
then, by Claim 8·4, this field has degree at least 3 over
![]() ${\mathbb{Q}}$
, and hence we are not in any of cases (i)–(v) of Theorem 1·6. (Recall that, by Claim 8·2, we are not in case (iv) of Theorem 1·6.) If
${\mathbb{Q}}$
, and hence we are not in any of cases (i)–(v) of Theorem 1·6. (Recall that, by Claim 8·2, we are not in case (iv) of Theorem 1·6.) If
then, by Claim 8·5,
and hence we are not in any of cases (i)–(v) of Theorem 1·6.
8·2. Controlling the discriminants
Claim 8·7. We may assume that
![]() $D_x = D_y = D_z$
.
$D_x = D_y = D_z$
.
Proof. By Claim 8·3, either:
or:
In either case, if the fundamental discriminants
![]() $D_x, D_y, D_z$
are not all equal, then all the possibilities for
$D_x, D_y, D_z$
are not all equal, then all the possibilities for
![]() $(\Delta_x, \Delta_y, \Delta_z)$
are given by Propositions 7·5 and 7·6. These possibilities will be dealt with in Section 8·4.
$(\Delta_x, \Delta_y, \Delta_z)$
are given by Propositions 7·5 and 7·6. These possibilities will be dealt with in Section 8·4.
Claim 8·8. If
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
, then we may assume that either:
${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
, then we may assume that either:
-
(i)
 $\Delta_x = 4 \Delta$
and
$\Delta_x = 4 \Delta$
and
 $\Delta_y = \Delta_z = \Delta$
for some
$\Delta_y = \Delta_z = \Delta$
for some
 $\Delta \equiv 1 \bmod 8$
; or
$\Delta \equiv 1 \bmod 8$
; or -
(ii)
 $\Delta_x = \Delta_y = 4 \Delta$
and
$\Delta_x = \Delta_y = 4 \Delta$
and
 $\Delta_z = \Delta$
for some
$\Delta_z = \Delta$
for some
 $\Delta \equiv 1 \bmod 8$
.
$\Delta \equiv 1 \bmod 8$
.
Proof. Suppose that
Without loss of generality, we assume that
![]() $\lvert \Delta_x \rvert \geq \lvert \Delta_y \rvert \geq \lvert \Delta_z \rvert$
. Hence,
$\lvert \Delta_x \rvert \geq \lvert \Delta_y \rvert \geq \lvert \Delta_z \rvert$
. Hence,
![]() $\lvert \Delta_x \rvert \gt \lvert \Delta_z \rvert$
by Claim 8·2. By Claim 8·7,
$\lvert \Delta_x \rvert \gt \lvert \Delta_z \rvert$
by Claim 8·2. By Claim 8·7,
![]() $D_x = D_y = D_z$
. Hence, Proposition 7·6 implies that there are the following two possibilities:
$D_x = D_y = D_z$
. Hence, Proposition 7·6 implies that there are the following two possibilities:
-
(1)
 $\Delta_x = 4 \Delta$
and
$\Delta_x = 4 \Delta$
and
 $\Delta_y = \Delta_z = \Delta$
for some
$\Delta_y = \Delta_z = \Delta$
for some
 $\Delta \equiv 1 \bmod 8$
;
$\Delta \equiv 1 \bmod 8$
; -
(2)
 $\Delta_x = \Delta_y = 4 \Delta$
and
$\Delta_x = \Delta_y = 4 \Delta$
and
 $\Delta_z = \Delta$
for some
$\Delta_z = \Delta$
for some
 $\Delta \equiv 1 \bmod 8$
.
$\Delta \equiv 1 \bmod 8$
.
Claim 8·9. If
then
![]() $\Delta_x = \Delta$
and
$\Delta_x = \Delta$
and
![]() $\Delta_y = \Delta_z = l^2 \Delta$
for some
$\Delta_y = \Delta_z = l^2 \Delta$
for some
![]() $\Delta$
, where
$\Delta$
, where
![]() $l \in \{3/2, 2, 3, 4\}$
. If
$l \in \{3/2, 2, 3, 4\}$
. If
![]() $l = 3/2$
, then
$l = 3/2$
, then
![]() $\Delta \equiv 0, 4 \bmod 16$
.
$\Delta \equiv 0, 4 \bmod 16$
.
Proof. Since
Theorem 7·4 and Claim 8·1 together imply that
![]() $\Delta_y = \Delta_z$
and
$\Delta_y = \Delta_z$
and
![]() $B=C$
. Proposition 7·7 then implies that we may write
$B=C$
. Proposition 7·7 then implies that we may write
![]() $\Delta_x = \Delta$
and
$\Delta_x = \Delta$
and
![]() $\Delta_y = \Delta_z = l^2 \Delta$
, where
$\Delta_y = \Delta_z = l^2 \Delta$
, where
![]() $l \in \{3/2, 2, 3, 4\}$
, and also that
$l \in \{3/2, 2, 3, 4\}$
, and also that
![]() $\Delta \equiv 0, 4 \bmod 16$
if
$\Delta \equiv 0, 4 \bmod 16$
if
![]() $l = 3/2$
.
$l = 3/2$
.
8·3. Bounding the discriminants
Let
So
![]() $\alpha \in {\mathbb{Q}}$
by assumption. Suppose that
$\alpha \in {\mathbb{Q}}$
by assumption. Suppose that
![]() $(x_i, y_i, z_i)$
, where
$(x_i, y_i, z_i)$
, where
![]() $i=1, \ldots, 4$
, are Galois conjugates of (x, y, z) over
$i=1, \ldots, 4$
, are Galois conjugates of (x, y, z) over
![]() ${\mathbb{Q}}$
. Then
${\mathbb{Q}}$
. Then
for
![]() $i=1, 2, 3, 4$
. In particular, we have that
$i=1, 2, 3, 4$
. In particular, we have that
 \begin{align}\begin{vmatrix} {}1 & 1 & 1 & 1\\ {}x_1 & x_2 & x_3 & x_4\\ {}y_1 & y_2 & y_3 & y_4\\ {}z_1 & z_2 & z_3 & z_4\end{vmatrix}= 0.\end{align}
\begin{align}\begin{vmatrix} {}1 & 1 & 1 & 1\\ {}x_1 & x_2 & x_3 & x_4\\ {}y_1 & y_2 & y_3 & y_4\\ {}z_1 & z_2 & z_3 & z_4\end{vmatrix}= 0.\end{align}
In this section, we will establish effective bounds on
![]() $(\Delta_x, \Delta_y, \Delta_z)$
by showing that, if these discriminants are too large (in absolute value), then one may find conjugates
$(\Delta_x, \Delta_y, \Delta_z)$
by showing that, if these discriminants are too large (in absolute value), then one may find conjugates
![]() $(x_i, y_i, z_i)$
such that the determinant on the left-hand side of (8·1) is non-zero. Typically, we will do this by showing that there exists a permutation
$(x_i, y_i, z_i)$
such that the determinant on the left-hand side of (8·1) is non-zero. Typically, we will do this by showing that there exists a permutation
![]() $\tau \in S_4$
such that
$\tau \in S_4$
such that
We will make repeated use (without special reference) of the bound on singular moduli given in Proposition 2·2, the description of the conjugates of a singular modulus in Subsection 2·1, and the bound on the number of singular moduli of a given discriminant and denominator in Proposition 7·1. The bounds themselves were calculated in PARI; this took only a few seconds.
8·3·1. The case where
 ${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
In this section, we assume that
By Claim 8·4, the field
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
has degree at least 3 over
${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
has degree at least 3 over
![]() ${\mathbb{Q}}$
. Each singular modulus of discriminant
${\mathbb{Q}}$
. Each singular modulus of discriminant
![]() $\Delta_x$
occurs precisely once among the first coordinates of the distinct
$\Delta_x$
occurs precisely once among the first coordinates of the distinct
![]() ${\mathbb{Q}}$
-conjugates of (x, y, z). Correspondingly for the singular moduli of discriminant
${\mathbb{Q}}$
-conjugates of (x, y, z). Correspondingly for the singular moduli of discriminant
![]() $\Delta_y$
among the second coordinates, and for the singular moduli of discriminant
$\Delta_y$
among the second coordinates, and for the singular moduli of discriminant
![]() $\Delta_z$
among the third coordinates.
$\Delta_z$
among the third coordinates.
Claim 8·10. If
![]() $\Delta_x = 4 \Delta$
and
$\Delta_x = 4 \Delta$
and
![]() $\Delta_y = \Delta_z = \Delta$
, where
$\Delta_y = \Delta_z = \Delta$
, where
![]() $\Delta \equiv 1 \bmod 8$
, then
$\Delta \equiv 1 \bmod 8$
, then
![]() $h(\Delta) \leq 6$
.
$h(\Delta) \leq 6$
.
Proof. Suppose that
![]() $\Delta_x = 4 \Delta$
and
$\Delta_x = 4 \Delta$
and
![]() $\Delta_y = \Delta_z = \Delta$
, where
$\Delta_y = \Delta_z = \Delta$
, where
![]() $\Delta \equiv 1 \bmod 8$
. Assume that
$\Delta \equiv 1 \bmod 8$
. Assume that
![]() $h(\Delta) \geq 7$
. In particular,
$h(\Delta) \geq 7$
. In particular,
![]() $\Delta \notin \{-7, -15\}$
by Lemma 2·1. Thus there are exactly two subdominant singular moduli of discriminant
$\Delta \notin \{-7, -15\}$
by Lemma 2·1. Thus there are exactly two subdominant singular moduli of discriminant
![]() $\Delta$
and no subdominant singular moduli of discriminant
$\Delta$
and no subdominant singular moduli of discriminant
![]() $4 \Delta$
. Let
$4 \Delta$
. Let
![]() $(x_1, y_1, z_1)$
be the unique conjugate of (x, y, z) with
$(x_1, y_1, z_1)$
be the unique conjugate of (x, y, z) with
![]() $x_1$
dominant. We distinguish two subcases.
$x_1$
dominant. We distinguish two subcases.
Subcase 1: neither of
![]() $y_1, z_1$
is dominant. In this case, we may take
$y_1, z_1$
is dominant. In this case, we may take
![]() $(x_2, y_2, z_2), (x_3, y_3, z_3)$
to be the unique conjugates such that
$(x_2, y_2, z_2), (x_3, y_3, z_3)$
to be the unique conjugates such that
![]() $y_2, z_3$
are dominant. Then
$y_2, z_3$
are dominant. Then
Since
![]() $h(\Delta) \geq 7$
, we may take
$h(\Delta) \geq 7$
, we may take
![]() $(x_4, y_4, z_4)$
to be a conjugate with none of
$(x_4, y_4, z_4)$
to be a conjugate with none of
![]() $x_4, y_4, z_4$
dominant. Then, for
$x_4, y_4, z_4$
dominant. Then, for
![]() $\sigma \in S_4$
such that
$\sigma \in S_4$
such that
![]() $\sigma(2, 3, 4) \neq (1, 2, 3)$
, we have that either:
$\sigma(2, 3, 4) \neq (1, 2, 3)$
, we have that either:
![]() $\sigma(2)=1$
and
$\sigma(2)=1$
and
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)(\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)\nonumber \\ {}&\quad \times \left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right),\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)(\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)\nonumber \\ {}&\quad \times \left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right),\end{align}
or:
![]() $\sigma(2) \neq 1$
and
$\sigma(2) \neq 1$
and
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{2 \pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right)(\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)^2.\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{2 \pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right)(\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)^2.\end{align}
The bounds (8·2), (8·3) and (8·4) are incompatible with (8·1) if
![]() $\lvert \Delta \rvert \geq 10$
. By Lemma 2·1,
$\lvert \Delta \rvert \geq 10$
. By Lemma 2·1,
![]() $\lvert \Delta \rvert \leq 9$
is impossible since
$\lvert \Delta \rvert \leq 9$
is impossible since
![]() $z \notin {\mathbb{Q}}$
.
$z \notin {\mathbb{Q}}$
.
Subcase 2: one of
![]() $y_1, z_1$
is dominant. Without loss of generality, suppose that
$y_1, z_1$
is dominant. Without loss of generality, suppose that
![]() $y_1$
is dominant. Let
$y_1$
is dominant. Let
![]() $(x_2, y_2, z_2)$
be the unique conjugate with
$(x_2, y_2, z_2)$
be the unique conjugate with
![]() $z_2$
dominant. There also exists a conjugate
$z_2$
dominant. There also exists a conjugate
![]() $(x_3, y_3, z_3)$
with
$(x_3, y_3, z_3)$
with
![]() $y_3$
subdominant and
$y_3$
subdominant and
![]() $x_3, z_3$
not dominant. There exists a conjugate
$x_3, z_3$
not dominant. There exists a conjugate
![]() $(x_4, y_4, z_4)$
with neither of
$(x_4, y_4, z_4)$
with neither of
![]() $y_4, z_4$
dominant or subdominant. Note that
$y_4, z_4$
dominant or subdominant. Note that
![]() $x_4$
is thus not dominant as well. Hence,
$x_4$
is thus not dominant as well. Hence,
 \begin{align} {}&\lvert x_1 y_3 z_2 \rvert \nonumber\\ {}&\quad \geq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) - 2079)\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) - 2079\right) \nonumber \\ {}&\qquad \times (\!\exp(\pi \lvert \Delta \rvert^{1/2}) - 2079).\end{align}
\begin{align} {}&\lvert x_1 y_3 z_2 \rvert \nonumber\\ {}&\quad \geq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) - 2079)\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) - 2079\right) \nonumber \\ {}&\qquad \times (\!\exp(\pi \lvert \Delta \rvert^{1/2}) - 2079).\end{align}
Now let
![]() $\sigma \in S_4$
be such that
$\sigma \in S_4$
be such that
![]() $\sigma(2, 3, 4) \neq (1, 3, 2)$
. If
$\sigma(2, 3, 4) \neq (1, 3, 2)$
. If
![]() $\sigma(2) \neq 1$
, then
$\sigma(2) \neq 1$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{2 \pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right)(\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)^2.\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{2 \pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right)(\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)^2.\end{align}
If
![]() $\sigma(2) = 1$
and
$\sigma(2) = 1$
and
![]() $\sigma(4) = 2$
, then
$\sigma(4) = 2$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right) \nonumber \\ {}&\qquad \times (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079).\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right) \nonumber \\ {}&\qquad \times (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079).\end{align}
If
![]() $\sigma(2) = 1$
and
$\sigma(2) = 1$
and
![]() $\sigma(4) \neq 2$
, then
$\sigma(4) \neq 2$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)^2.\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)^2.\end{align}
The bounds (8·5), (8·6), (8·7) and (8·8) are incompatible with (8·1) if
![]() $\lvert \Delta \rvert \geq 32$
. By Lemma 2·1,
$\lvert \Delta \rvert \geq 32$
. By Lemma 2·1,
![]() $\lvert \Delta \rvert \leq 31$
is impossible since
$\lvert \Delta \rvert \leq 31$
is impossible since
![]() $h(\Delta) \geq 7$
by assumption.
$h(\Delta) \geq 7$
by assumption.
We must therefore have that
![]() $h(\Delta) \leq 6$
.
$h(\Delta) \leq 6$
.
Claim 8·11. If
![]() $\Delta_x = \Delta_y = 4 \Delta$
and
$\Delta_x = \Delta_y = 4 \Delta$
and
![]() $\Delta_z = \Delta$
, where
$\Delta_z = \Delta$
, where
![]() $\Delta \equiv 1 \bmod 8$
, then
$\Delta \equiv 1 \bmod 8$
, then
![]() $h(\Delta) \leq 5$
.
$h(\Delta) \leq 5$
.
Proof. Suppose that
![]() $\Delta_x = \Delta_y = 4 \Delta$
and
$\Delta_x = \Delta_y = 4 \Delta$
and
![]() $\Delta_z = \Delta$
, where
$\Delta_z = \Delta$
, where
![]() $\Delta \equiv 1 \bmod 8$
. Assume further that
$\Delta \equiv 1 \bmod 8$
. Assume further that
![]() $h(\Delta) \geq 6$
. In particular,
$h(\Delta) \geq 6$
. In particular,
![]() $\Delta \notin \{-7, -15\}$
by Lemma 2·1. Thus there are exactly two subdominant singular moduli of discriminant
$\Delta \notin \{-7, -15\}$
by Lemma 2·1. Thus there are exactly two subdominant singular moduli of discriminant
![]() $\Delta$
and no subdominant singular moduli of discriminant
$\Delta$
and no subdominant singular moduli of discriminant
![]() $4 \Delta$
. Let
$4 \Delta$
. Let
![]() $(x_1, y_1, z_1), (x_2, y_2, z_2)$
be the unique conjugates of (x, y, z) such that
$(x_1, y_1, z_1), (x_2, y_2, z_2)$
be the unique conjugates of (x, y, z) such that
![]() $x_1, y_2$
are dominant. There must also exist a conjugate
$x_1, y_2$
are dominant. There must also exist a conjugate
![]() $(x_3, y_3, z_3)$
such that
$(x_3, y_3, z_3)$
such that
![]() $z_3$
is either dominant or subdominant and neither of
$z_3$
is either dominant or subdominant and neither of
![]() $x_3, y_3$
is dominant.
$x_3, y_3$
is dominant.
Then
There exists a conjugate
![]() $(x_4, y_4, z_4)$
such that neither of
$(x_4, y_4, z_4)$
such that neither of
![]() $x_4, y_4$
is dominant and
$x_4, y_4$
is dominant and
![]() $z_4$
is neither dominant nor subdominant. Let
$z_4$
is neither dominant nor subdominant. Let
![]() $\sigma \in S_4$
be such that
$\sigma \in S_4$
be such that
![]() $\sigma(2, 3, 4) \neq (1, 2, 3)$
. If
$\sigma(2, 3, 4) \neq (1, 2, 3)$
. If
![]() $\sigma(2)=1$
and
$\sigma(2)=1$
and
![]() $\sigma(3)=2$
, then
$\sigma(3)=2$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)^2\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right).\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)^2\left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right).\end{align}
If either
![]() $\sigma(2) \neq 1$
or
$\sigma(2) \neq 1$
or
![]() $\sigma(3) \neq 2$
, then
$\sigma(3) \neq 2$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{2 \pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right) \nonumber \\ {}&\qquad \times (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079).\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(2 \pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{2 \pi \lvert \Delta \rvert^{1/2}}{3}\right) + 2079\right) \nonumber \\ {}&\qquad \times (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079).\end{align}
The bounds (8·9), (8·10), and (8·11) are incompatible with (8·1) if
![]() $\lvert \Delta \rvert \geq 29$
. By Lemma 2·1, there are no discriminants
$\lvert \Delta \rvert \geq 29$
. By Lemma 2·1, there are no discriminants
![]() $\Delta$
with
$\Delta$
with
![]() $\lvert \Delta \rvert \leq 28$
and
$\lvert \Delta \rvert \leq 28$
and
![]() $h(\Delta) \geq 6$
. Hence, we must have that
$h(\Delta) \geq 6$
. Hence, we must have that
![]() $h(\Delta) \leq 5$
.
$h(\Delta) \leq 5$
.
8·3·2. The case where
 ${\mathbb{Q}}(x) \subsetneq {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
${\mathbb{Q}}(x) \subsetneq {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
In this section, we assume that
By Claim 8·9, we have that
![]() $\Delta_x = \Delta$
and
$\Delta_x = \Delta$
and
![]() $\Delta_y = \Delta_z = l^2 \Delta$
, where
$\Delta_y = \Delta_z = l^2 \Delta$
, where
![]() $l \in \{3/2, 2, 3, 4\}$
. Also, by Claims 8·3 and 8·5,
$l \in \{3/2, 2, 3, 4\}$
. Also, by Claims 8·3 and 8·5,
So
![]() $h(\Delta) \geq 3$
.
$h(\Delta) \geq 3$
.
Each singular modulus of discriminant
![]() $\Delta$
occurs exactly twice among the first coordinates of the distinct
$\Delta$
occurs exactly twice among the first coordinates of the distinct
![]() ${\mathbb{Q}}$
-conjugates of (x, y, z). Each singular modulus of discriminant
${\mathbb{Q}}$
-conjugates of (x, y, z). Each singular modulus of discriminant
![]() $l^2 \Delta$
occurs exactly once among the second coordinates of the distinct
$l^2 \Delta$
occurs exactly once among the second coordinates of the distinct
![]() ${\mathbb{Q}}$
-conjugates of (x, y, z) and exactly once among the third coordinates. Let
${\mathbb{Q}}$
-conjugates of (x, y, z) and exactly once among the third coordinates. Let
![]() $(x_1, y_1, z_1), (x_2, y_2, z_2)$
be the conjugates such that
$(x_1, y_1, z_1), (x_2, y_2, z_2)$
be the conjugates such that
![]() $y_1, z_2$
are dominant.
$y_1, z_2$
are dominant.
Claim 8·12. Both of
![]() $x_1, x_2$
are dominant.
$x_1, x_2$
are dominant.
Proof. Suppose that at least one of
![]() $x_1, x_2$
is not dominant. There is then a conjugate
$x_1, x_2$
is not dominant. There is then a conjugate
![]() $(x_3, y_3, z_3)$
with
$(x_3, y_3, z_3)$
with
![]() $x_3$
dominant and neither of
$x_3$
dominant and neither of
![]() $y_3, z_3$
dominant. Then
$y_3, z_3$
dominant. Then
Since
![]() $h(\Delta) \geq 3$
, there is a conjugate
$h(\Delta) \geq 3$
, there is a conjugate
![]() $(x_4, y_4, z_4)$
with none of
$(x_4, y_4, z_4)$
with none of
![]() $x_4, y_4, z_4$
dominant. Now let
$x_4, y_4, z_4$
dominant. Now let
![]() $\sigma \in S_4$
be such that
$\sigma \in S_4$
be such that
![]() $\sigma(2, 3, 4) \neq (3, 1, 2)$
. If
$\sigma(2, 3, 4) \neq (3, 1, 2)$
. If
![]() $\sigma(3) = 1$
and
$\sigma(3) = 1$
and
![]() $\sigma(4) = 2$
, then
$\sigma(4) = 2$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)(\!\exp(l \pi \lvert \Delta \rvert^{1/2}) + 2079)^2.\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)(\!\exp(l \pi \lvert \Delta \rvert^{1/2}) + 2079)^2.\end{align}
If either
![]() $\sigma(3) \neq 1$
or
$\sigma(3) \neq 1$
or
![]() $\sigma(4) \neq 2$
, then
$\sigma(4) \neq 2$
, then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)(\!\exp(l \pi \lvert \Delta \rvert^{1/2}) + 2079) \nonumber \\ {}& \qquad \times \left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right).\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)(\!\exp(l \pi \lvert \Delta \rvert^{1/2}) + 2079) \nonumber \\ {}& \qquad \times \left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right).\end{align}
For every
![]() $l \in \{3/2, 2, 3, 4\}$
, the bounds (8·12), (8·13) and (8·14) are incompatible with (8·1) if
$l \in \{3/2, 2, 3, 4\}$
, the bounds (8·12), (8·13) and (8·14) are incompatible with (8·1) if
![]() $\lvert \Delta \rvert \geq 8$
. By Lemma 2·1,
$\lvert \Delta \rvert \geq 8$
. By Lemma 2·1,
![]() $\lvert \Delta \rvert \leq 7$
is impossible since
$\lvert \Delta \rvert \leq 7$
is impossible since
![]() $x \notin {\mathbb{Q}}$
.
$x \notin {\mathbb{Q}}$
.
Note that
![]() $x_1 = x_2$
, since
$x_1 = x_2$
, since
![]() $x_1, x_2$
are both dominant. We therefore rearrange (8·1) to obtain that
$x_1, x_2$
are both dominant. We therefore rearrange (8·1) to obtain that
 \begin{align}y_1 z_2 (x_3 - x_4) = \sum_{\substack{\sigma \in S_4\\ \sigma(3, 4) \neq (1, 2)}} \mathrm{sgn}(\sigma) x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)}.\end{align}
\begin{align}y_1 z_2 (x_3 - x_4) = \sum_{\substack{\sigma \in S_4\\ \sigma(3, 4) \neq (1, 2)}} \mathrm{sgn}(\sigma) x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)}.\end{align}
We may then use Proposition 7·2 to obtain the lower bound
Claim 8·13. We have that
![]() $l \in \{3/2, 2\}$
and:
$l \in \{3/2, 2\}$
and:
-
(i) if
 $l = 3/2$
, then one of the following holds:
$l = 3/2$
, then one of the following holds:-
(a)
 $h(\Delta_x) \leq 6$
;
$h(\Delta_x) \leq 6$
; -
(b)
 $h(\Delta_x) \in \{7, 8\}$
and
$h(\Delta_x) \in \{7, 8\}$
and
 $\lvert \Delta_x \rvert \leq 5879$
;
$\lvert \Delta_x \rvert \leq 5879$
; -
(c)
 $h(\Delta_x) \in \{9, 10\}$
and
$h(\Delta_x) \in \{9, 10\}$
and
 $\lvert \Delta_x \rvert \leq 1557$
;
$\lvert \Delta_x \rvert \leq 1557$
; -
(d)
 $h(\Delta_x) \in \{11, 12, 13, 14\}$
and
$h(\Delta_x) \in \{11, 12, 13, 14\}$
and
 $\lvert \Delta_x \rvert \leq 790$
.
$\lvert \Delta_x \rvert \leq 790$
.
-
-
(ii) if
 $l = 2$
, then one of the following holds:
$l = 2$
, then one of the following holds:-
(a)
 $h(\Delta_x) \leq 4$
;
$h(\Delta_x) \leq 4$
; -
(b)
 $h(\Delta_x) \in \{5, 6\}$
and
$h(\Delta_x) \in \{5, 6\}$
and
 $\lvert \Delta_x \rvert \leq 304$
;
$\lvert \Delta_x \rvert \leq 304$
;
-
Proof. For each
![]() $k \in \{3, 5, 7, 9, 11, 15\}$
, there is some
$k \in \{3, 5, 7, 9, 11, 15\}$
, there is some
![]() $a_\mathrm{min}(k)$
, the value of which is given in Table 1, with the property that: for every
$a_\mathrm{min}(k)$
, the value of which is given in Table 1, with the property that: for every
![]() $l \in \{3/2, 2, 3, 4\}$
, if
$l \in \{3/2, 2, 3, 4\}$
, if
![]() $h(\Delta) \geq k$
, then there exist conjugates
$h(\Delta) \geq k$
, then there exist conjugates
![]() $(x_3, y_3, z_3), (x_4, y_4, z_4)$
such that
$(x_3, y_3, z_3), (x_4, y_4, z_4)$
such that
![]() $x_3 \neq x_4$
and
$x_3 \neq x_4$
and
where
![]() $a(y_i)$
(respectively
$a(y_i)$
(respectively
![]() $a(z_i)$
) denotes the denominator of
$a(z_i)$
) denotes the denominator of
![]() $y_i$
(respectively
$y_i$
(respectively
![]() $z_i$
).
$z_i$
).
Fix some
![]() $l \in \{3/2, 2, 3, 4\}$
. Next, let
$l \in \{3/2, 2, 3, 4\}$
. Next, let
![]() $k \in \{3, 5, 7, 9, 11, 15\}$
, and take the corresponding value of
$k \in \{3, 5, 7, 9, 11, 15\}$
, and take the corresponding value of
![]() $a_\mathrm{min}(k)$
from Table 1. Now let
$a_\mathrm{min}(k)$
from Table 1. Now let
![]() $\sigma \in S_4$
be such that
$\sigma \in S_4$
be such that
![]() $\sigma(3, 4) \neq (1, 2)$
. If either
$\sigma(3, 4) \neq (1, 2)$
. If either
![]() $\sigma(3) = 1$
or
$\sigma(3) = 1$
or
![]() $\sigma(4) = 2$
(note there are 8 such
$\sigma(4) = 2$
(note there are 8 such
![]() $\sigma$
), then
$\sigma$
), then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)(\!\exp(l \pi \lvert \Delta \rvert^{1/2}) + 2079) \nonumber \\ {}&\qquad \times\left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{a_\mathrm{min}(k)}\right) + 2079\right).\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)(\!\exp(l \pi \lvert \Delta \rvert^{1/2}) + 2079) \nonumber \\ {}&\qquad \times\left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{a_\mathrm{min}(k)}\right) + 2079\right).\end{align}
If
![]() $\sigma(3) = 2$
and
$\sigma(3) = 2$
and
![]() $\sigma(4) = 1$
(note there are 2 such
$\sigma(4) = 1$
(note there are 2 such
![]() $\sigma$
), then
$\sigma$
), then
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)\left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)^2.\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq \left(\exp\left(\frac{\pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)\left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right)^2.\end{align}
Otherwise (i.e. for the 12 remaining
![]() $\sigma$
),
$\sigma$
),
 \begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right) \nonumber \\ {}&\qquad \times \left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{a_\mathrm{min}(k)}\right) + 2079\right).\end{align}
\begin{align} {}&\lvert x_{\sigma(2)} y_{\sigma(3)} z_{\sigma(4)} \rvert \nonumber \\ {}&\quad \leq (\!\exp(\pi \lvert \Delta \rvert^{1/2}) + 2079)\left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{2}\right) + 2079\right) \nonumber \\ {}&\qquad \times \left(\exp\left(\frac{l \pi \lvert \Delta \rvert^{1/2}}{a_\mathrm{min}(k)}\right) + 2079\right).\end{align}
If k is suitably large (for the given l), then the bounds (8·16), (8·17), (8·18) and (8·19) are incompatible with (8·15) for large enough
![]() $\lvert \Delta \rvert$
. The entries in Table 1 are the upper bounds on
$\lvert \Delta \rvert$
. The entries in Table 1 are the upper bounds on
![]() $\lvert \Delta \rvert$
which are obtained for a given l when
$\lvert \Delta \rvert$
which are obtained for a given l when
![]() $h(\Delta) \geq k$
by taking suitable conjugates
$h(\Delta) \geq k$
by taking suitable conjugates
![]() $(x_3, y_3, z_3), (x_4, y_4, z_4)$
with
$(x_3, y_3, z_3), (x_4, y_4, z_4)$
with
![]() $x_3 \neq x_4$
and
$x_3 \neq x_4$
and
Note that for
![]() $l = 3/2$
(respectively, for
$l = 3/2$
(respectively, for
![]() $l=2$
) no upper bound on
$l=2$
) no upper bound on
![]() $\lvert \Delta \rvert$
is obtained if
$\lvert \Delta \rvert$
is obtained if
![]() $k \lt 7$
(respectively if
$k \lt 7$
(respectively if
![]() $k \lt 5$
). An entry b in a row k and column l of Table 1 is in a grey-shaded cell if there are no discriminants
$k \lt 5$
). An entry b in a row k and column l of Table 1 is in a grey-shaded cell if there are no discriminants
![]() $\Delta$
satisfying:
$\Delta$
satisfying:
-
(1)
 $h(\Delta) \geq k$
;
$h(\Delta) \geq k$
; -
(2)
 $\lvert \Delta \rvert \leq b$
; and
$\lvert \Delta \rvert \leq b$
; and -
(3) if
 $l=3/2$
, then
$l=3/2$
, then
 $\Delta \equiv 0, 4 \bmod 16$
.
$\Delta \equiv 0, 4 \bmod 16$
.
(These conditions are easily checked in PARI.) In particular, this implies that
![]() $l \in \{3, 4\}$
is impossible, since
$l \in \{3, 4\}$
is impossible, since
![]() $h(\Delta) \geq 3$
by Claim 8·5. For
$h(\Delta) \geq 3$
by Claim 8·5. For
![]() $l \in \{3/2, 2\}$
, we must be in one of the cases stated in the claim.
$l \in \{3/2, 2\}$
, we must be in one of the cases stated in the claim.
Table 1. Upper bounds on
![]() $\lvert \Delta \rvert$
when
$\lvert \Delta \rvert$
when
![]() $h(\Delta) \geq k$
for a given
$h(\Delta) \geq k$
for a given
![]() $l \in \{3/2, 2, 3, 4\}$
$l \in \{3/2, 2, 3, 4\}$

8·4. Eliminating the discriminants
So far in Section 8, we have shown that if x, y, z are pairwise distinct singular moduli of respective discriminants
![]() $\Delta_x, \Delta_y, \Delta_z$
such that
$\Delta_x, \Delta_y, \Delta_z$
such that
for some
![]() $A, B, C \in {\mathbb{Q}} \setminus \{0\}$
, then either we are in one of cases (1)–(5) of Theorem 1·6 or (without loss of generality) one of the following situations occurs:
$A, B, C \in {\mathbb{Q}} \setminus \{0\}$
, then either we are in one of cases (1)–(5) of Theorem 1·6 or (without loss of generality) one of the following situations occurs:
-
(1)
 ${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
and this field, denote it L, is an extension of
${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
and this field, denote it L, is an extension of
 ${\mathbb{Q}}$
of degree at least 3 and one of the following holds:
${\mathbb{Q}}$
of degree at least 3 and one of the following holds:-
(a)
 $(\Delta_x, \Delta_y, \Delta_z) = (4 \Delta, \Delta, \Delta)$
, where
$(\Delta_x, \Delta_y, \Delta_z) = (4 \Delta, \Delta, \Delta)$
, where
 $\Delta \equiv 1 \bmod 8$
and
$\Delta \equiv 1 \bmod 8$
and
 $h(\Delta) \leq 6$
;
$h(\Delta) \leq 6$
; -
(b)
 $(\Delta_x, \Delta_y, \Delta_z) = (4 \Delta, 4 \Delta, \Delta)$
, where
$(\Delta_x, \Delta_y, \Delta_z) = (4 \Delta, 4 \Delta, \Delta)$
, where
 $\Delta \equiv 1 \bmod 8$
and
$\Delta \equiv 1 \bmod 8$
and
 $h(\Delta) \leq 5$
;
$h(\Delta) \leq 5$
; -
(c) the field L and the discriminants
 $\Delta_x, \Delta_y, \Delta_z$
are given in [
Reference Allombert, Bilu and Pizarro-Madariaga1
, table 2];
$\Delta_x, \Delta_y, \Delta_z$
are given in [
Reference Allombert, Bilu and Pizarro-Madariaga1
, table 2];
-
-
(2)
 ${\mathbb{Q}}(x) \subset {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
,
${\mathbb{Q}}(x) \subset {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
,
 $[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}(x)] = 2$
,
$[{\mathbb{Q}}(y) \;:\; {\mathbb{Q}}(x)] = 2$
,
 $[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] \geq 3$
,
$[{\mathbb{Q}}(x) \;:\; {\mathbb{Q}}] \geq 3$
,
 $\Delta_y = \Delta_z$
, and one of the following holds:
$\Delta_y = \Delta_z$
, and one of the following holds:-
(a)
 $9 \Delta_x = 4 \Delta_y$
and
$9 \Delta_x = 4 \Delta_y$
and
 $\Delta_x \equiv 0, 4 \bmod 16$
and one of the following holds:
$\Delta_x \equiv 0, 4 \bmod 16$
and one of the following holds:-
(i)
 $h(\Delta_x) \leq 6$
;
$h(\Delta_x) \leq 6$
; -
(ii)
 $h(\Delta_x) \in \{7, 8\}$
and
$h(\Delta_x) \in \{7, 8\}$
and
 $\lvert \Delta_x \rvert \leq 5879$
;
$\lvert \Delta_x \rvert \leq 5879$
; -
(iii)
 $h(\Delta_x) \in \{9, 10\}$
and
$h(\Delta_x) \in \{9, 10\}$
and
 $\lvert \Delta_x \rvert \leq 1557$
;
$\lvert \Delta_x \rvert \leq 1557$
; -
(iv)
 $h(\Delta_x) \in \{11, 12, 13, 14\}$
and
$h(\Delta_x) \in \{11, 12, 13, 14\}$
and
 $\lvert \Delta_x \rvert \leq 790$
;
$\lvert \Delta_x \rvert \leq 790$
;
-
-
-
(b)
 $4 \Delta_x = \Delta_y$
and one of the following holds:
$4 \Delta_x = \Delta_y$
and one of the following holds:-
(i)
 $h(\Delta_x) \leq 4$
;
$h(\Delta_x) \leq 4$
; -
(ii)
 $h(\Delta_x) \in \{5, 6\}$
and
$h(\Delta_x) \in \{5, 6\}$
and
 $\lvert \Delta_x \rvert \leq 304$
;
$\lvert \Delta_x \rvert \leq 304$
;
-
-
(c)
 $(\Delta_x, \Delta_y)$
is one of the 873 pairs given in Proposition 7·5.
$(\Delta_x, \Delta_y)$
is one of the 873 pairs given in Proposition 7·5.
Here (1)(a) arises from Claim 8·10, (1)(b) arises from Claim 8·11, 1(c) and (2)(c) arise from Claim 8·7, and (2)(a) and (2)(b) arise from Claim 8·13.
The corresponding list of all such
![]() $(\Delta_x, \Delta_y, \Delta_z)$
may be generated straightforwardly in PARI. Here we make use of Proposition 7·3, whence
$(\Delta_x, \Delta_y, \Delta_z)$
may be generated straightforwardly in PARI. Here we make use of Proposition 7·3, whence
![]() $h(\Delta) \leq 6$
implies that
$h(\Delta) \leq 6$
implies that
![]() $\lvert \Delta \rvert \leq 4075$
. For each triple of discriminants
$\lvert \Delta \rvert \leq 4075$
. For each triple of discriminants
![]() $(\Delta_x, \Delta_y, \Delta_z)$
belonging to this list, we then use PARI to show that there are no pairwise distinct singular moduli x, y, z of the corresponding discriminants such that the set
$(\Delta_x, \Delta_y, \Delta_z)$
belonging to this list, we then use PARI to show that there are no pairwise distinct singular moduli x, y, z of the corresponding discriminants such that the set
![]() $\{1, x, y, z\}$
is linearly dependent over
$\{1, x, y, z\}$
is linearly dependent over
![]() ${\mathbb{Q}}$
. The necessary computations take about 40 minutes to run. This completes the proof of Theorem 1·6.
${\mathbb{Q}}$
. The necessary computations take about 40 minutes to run. This completes the proof of Theorem 1·6.
One might expect that, in analogy to case (iii) of Theorem 1·6, there would be an additional case in Theorem 1·6, namely one where x, y, z all generate the same number field of degree 3 over
![]() ${\mathbb{Q}}$
. In fact, this cannot occur, for reasons that we now explain.
${\mathbb{Q}}$
. In fact, this cannot occur, for reasons that we now explain.
Suppose that x, y are distinct singular moduli such that
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
and this field has degree 3 over
${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
and this field has degree 3 over
![]() ${\mathbb{Q}}$
. In particular, by [
Reference Allombert, Bilu and Pizarro-Madariaga1
, corollary 3·3], the field
${\mathbb{Q}}$
. In particular, by [
Reference Allombert, Bilu and Pizarro-Madariaga1
, corollary 3·3], the field
![]() ${\mathbb{Q}}(x)$
is not a Galois extension of
${\mathbb{Q}}(x)$
is not a Galois extension of
![]() ${\mathbb{Q}}$
. Propositions 7·5 and 7·7, together with the list of discriminants
${\mathbb{Q}}$
. Propositions 7·5 and 7·7, together with the list of discriminants
![]() $\Delta$
with
$\Delta$
with
![]() $h(\Delta) = 3$
, imply that either
$h(\Delta) = 3$
, imply that either
![]() $\Delta_x = \Delta_y$
or
$\Delta_x = \Delta_y$
or
![]() $\{\Delta_x, \Delta_y\} \in \{ \{-23, -92\}, \{-31, -124\} \}$
.
$\{\Delta_x, \Delta_y\} \in \{ \{-23, -92\}, \{-31, -124\} \}$
.
Hence, if x, y, z are pairwise distinct singular moduli such that
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
and this field has degree 3 over
${\mathbb{Q}}(x) = {\mathbb{Q}}(y) = {\mathbb{Q}}(z)$
and this field has degree 3 over
![]() ${\mathbb{Q}}$
, then at least two of x, y, z have the same discriminant. Suppose that x, y have the same discriminant. Then the equality
${\mathbb{Q}}$
, then at least two of x, y, z have the same discriminant. Suppose that x, y have the same discriminant. Then the equality
![]() ${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
implies that
${\mathbb{Q}}(x) = {\mathbb{Q}}(y)$
implies that
![]() ${\mathbb{Q}}(x)$
is a Galois extension of
${\mathbb{Q}}(x)$
is a Galois extension of
![]() ${\mathbb{Q}}$
, which is a contradiction.
${\mathbb{Q}}$
, which is a contradiction.
Acknowledgements
I would like to thank Sebastian Eterović and Ziyang Gao for helpful comments. The author has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 945714).