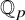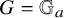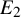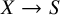1 Introduction
1.1 The Hodge–Tate decomposition
Let X be a proper smooth rigid space over a complete algebraically closed field extension K of
![]() $\mathbb {Q}_p$
. The Hodge–Tate decomposition, first conjectured by Tate in his celebrated article [Reference Tate51, §4.1], asserts the existence of an isomorphism
$\mathbb {Q}_p$
. The Hodge–Tate decomposition, first conjectured by Tate in his celebrated article [Reference Tate51, §4.1], asserts the existence of an isomorphism
that is Galois-equivariant when X admits a model over a discretely valued subfield of K. The algebraic case is due to Faltings [Reference Faltings13, III Thm. 4.1] and was reproven via different methods by Tsuji [Reference Tsuji52] and Nizioł [Reference Nizioł42]. The existence of the decomposition in full generality was first proven in [Reference Bhatt, Morrow and Scholze7, Thm. 13.3], building on [Reference Scholze45, §3.3]. In this article, we prove the following generalization of the Hodge–Tate decomposition.
Theorem 1.1 (Theorem 3.37)
Let X be a proper smooth rigid space over K and let G be a locally p-divisible rigid group. Then a choice of a
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
-lift
${\mathrm {B_{dR}^+}}/\xi ^2$
-lift
![]() $\mathbb {X}$
of X and the datum of an exponential
$\mathbb {X}$
of X and the datum of an exponential
![]() $\operatorname {\mathrm {Exp}}$
for K induce a Hodge–Tate decomposition with G-coefficients, natural in
$\operatorname {\mathrm {Exp}}$
for K induce a Hodge–Tate decomposition with G-coefficients, natural in
![]() $\mathbb {X}$
and G
$\mathbb {X}$
and G
We recover (1.1) as the case
![]() $G=\mathbb {G}_a$
using the Primitive Comparison Theorem [Reference Scholze44, Thm. 5.1]. By an exponential, we mean a continuous homomorphism
$G=\mathbb {G}_a$
using the Primitive Comparison Theorem [Reference Scholze44, Thm. 5.1]. By an exponential, we mean a continuous homomorphism
![]() $\operatorname {\mathrm {Exp}} \colon K \rightarrow 1+{\mathfrak {m}}_K$
splitting the logarithm map
$\operatorname {\mathrm {Exp}} \colon K \rightarrow 1+{\mathfrak {m}}_K$
splitting the logarithm map
![]() $\log \colon 1+{\mathfrak {m}}_K \rightarrow K$
and extending the exponential power series. The locally p-divisible rigid groups form a class of commutative rigid groups, recently introduced in [Reference Heuer, Werner and Zhang32, §6], of which examples are
$\log \colon 1+{\mathfrak {m}}_K \rightarrow K$
and extending the exponential power series. The locally p-divisible rigid groups form a class of commutative rigid groups, recently introduced in [Reference Heuer, Werner and Zhang32, §6], of which examples are
![]() $G=\mathbb {G}_a,\mathbb {G}_m$
, and more generally any connected commutative algebraic group over K. This also includes nonalgebraic groups, such as abeloid varieties and analytic p-divisible groups in the sense of Fargues [Reference Fargues14, §2]. As we explain below, we also prove a more general relative version of this result (Theorem 1.6) and give applications to rigid analytic Brauer groups (Example 3.51) and nonabelian p-adic Hodge theory (§1.3). We also deduce a formula for the cohomology groups
$G=\mathbb {G}_a,\mathbb {G}_m$
, and more generally any connected commutative algebraic group over K. This also includes nonalgebraic groups, such as abeloid varieties and analytic p-divisible groups in the sense of Fargues [Reference Fargues14, §2]. As we explain below, we also prove a more general relative version of this result (Theorem 1.6) and give applications to rigid analytic Brauer groups (Example 3.51) and nonabelian p-adic Hodge theory (§1.3). We also deduce a formula for the cohomology groups
![]() $H_{v}^n(X,\mathbb {B}^{\varphi =p})$
, where
$H_{v}^n(X,\mathbb {B}^{\varphi =p})$
, where
![]() $\mathbb {B}$
is the v-sheaf analog of the ring of analytic functions on the “punctured Fargues–Fontaine disc”
$\mathbb {B}$
is the v-sheaf analog of the ring of analytic functions on the “punctured Fargues–Fontaine disc”
![]() $\operatorname {\mathrm {Spa}}(A_{\inf },A_{\inf })\backslash V(p[p^{\flat }])$
(Theorem 3.43).
$\operatorname {\mathrm {Spa}}(A_{\inf },A_{\inf })\backslash V(p[p^{\flat }])$
(Theorem 3.43).
For the proof of Theorem 1.1, generalizing an idea of Faltings and Scholze, we construct a spectral sequence, natural in X and G
 $$ \begin{align} E_2^{ij} = \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X, \Omega_X^j)(-j)\otimes_{K} \operatorname{\mathrm{Lie}}(G) \quad &\text{if }j>0\\ &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X, G) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_v^{i+j}(X,G). \end{align} $$
$$ \begin{align} E_2^{ij} = \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X, \Omega_X^j)(-j)\otimes_{K} \operatorname{\mathrm{Lie}}(G) \quad &\text{if }j>0\\ &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X, G) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_v^{i+j}(X,G). \end{align} $$
We call it the Hodge–Tate spectral sequence with G -coefficients. We then show the following.
Theorem 1.2 (Corollary 3.30)
Let X be a proper smooth rigid space over K and let G be a locally p-divisible rigid group. Then the Hodge–Tate spectral sequence with G-coefficients (1.3) degenerates at the
![]() $E_2$
-page.
$E_2$
-page.
For
![]() $G=\mathbb {G}_a$
, the sequence (1.3) is the Hodge–Tate spectral sequence of Scholze [Reference Scholze45, Thm. 3.20]. For
$G=\mathbb {G}_a$
, the sequence (1.3) is the Hodge–Tate spectral sequence of Scholze [Reference Scholze45, Thm. 3.20]. For
![]() $G=\mathbb {G}_m$
, this sequence is already defined by Ben Heuer in [Reference Heuer26, §2.4], where it is called the “multiplicative Hodge–Tate spectral sequence.” This last sequence is also the subject of recent work of Ertl–Gilles–Nizioł [Reference Ertl, Gilles and Nizioł11] where it is studied for X a smooth Stein space.
$G=\mathbb {G}_m$
, this sequence is already defined by Ben Heuer in [Reference Heuer26, §2.4], where it is called the “multiplicative Hodge–Tate spectral sequence.” This last sequence is also the subject of recent work of Ertl–Gilles–Nizioł [Reference Ertl, Gilles and Nizioł11] where it is studied for X a smooth Stein space.
1.2 The geometric Hodge–Tate spectral sequence
The key idea for proving Theorem 1.2 is to upgrade the Hodge–Tate spectral sequence (1.3) to a geometric analog. For this, we generalize the approach of [Reference Heuer22]. We allow K to be an arbitrary perfectoid field extension of
![]() $\mathbb {Q}_p$
and we let
$\mathbb {Q}_p$
and we let
![]() $\pi \colon X \rightarrow \operatorname {\mathrm {Spa}}(K)$
denote the structure map. We consider the category
$\pi \colon X \rightarrow \operatorname {\mathrm {Spa}}(K)$
denote the structure map. We consider the category
![]() $\operatorname {\mathrm {Perf}}_K$
of affinoid perfectoid spaces over K. We then define for a locally p-divisible rigid group G the diamantine higher direct images
$\operatorname {\mathrm {Perf}}_K$
of affinoid perfectoid spaces over K. We then define for a locally p-divisible rigid group G the diamantine higher direct images
where
![]() $\tau $
is either the étale or the v-topology. Explicitly, this is the
$\tau $
is either the étale or the v-topology. Explicitly, this is the
![]() $\tau $
-sheafification of the presheaf
$\tau $
-sheafification of the presheaf
When
![]() $G=\mathbb {G}_m$
and
$G=\mathbb {G}_m$
and
![]() $n=1$
, this recovers the diamantine Picard functors
$n=1$
, this recovers the diamantine Picard functors
![]() ${\mathbf {Pic}}_{X,\tau }$
of [Reference Heuer22].
${\mathbf {Pic}}_{X,\tau }$
of [Reference Heuer22].
The étale Picard functor is often representable by a rigid group and is expected to be so in general. We refer the reader to the introduction of [Reference Heuer22] for an exposition of some known cases. This holds in particular when
![]() $\pi \colon X \rightarrow \operatorname {\mathrm {Spa}}(K)$
is the analytification of a proper smooth algebraic variety
$\pi \colon X \rightarrow \operatorname {\mathrm {Spa}}(K)$
is the analytification of a proper smooth algebraic variety
![]() $\pi ^{\operatorname {\mathrm {alg}}}\colon X^{\operatorname {\mathrm {alg}}} \rightarrow \operatorname {\mathrm {Spec}}(K)$
, in which case
$\pi ^{\operatorname {\mathrm {alg}}}\colon X^{\operatorname {\mathrm {alg}}} \rightarrow \operatorname {\mathrm {Spec}}(K)$
, in which case
![]() ${\mathbf {Pic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
is the analytification of the Picard variety of
${\mathbf {Pic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
is the analytification of the Picard variety of
![]() $X^{\operatorname {\mathrm {alg}}}$
. For the higher pushforwards, the situation is different: Let
$X^{\operatorname {\mathrm {alg}}}$
. For the higher pushforwards, the situation is different: Let
![]() $\pi _{\operatorname {\mathrm {\acute {E}t}}}^{\operatorname {\mathrm {alg}}}\colon \operatorname {\mathrm {Sch}}_{X^{\operatorname {\mathrm {alg}}},\operatorname {\mathrm {\acute {e}t}}} \rightarrow \operatorname {\mathrm {Sch}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
denote the map of big étale sites, then the sheaves
$\pi _{\operatorname {\mathrm {\acute {E}t}}}^{\operatorname {\mathrm {alg}}}\colon \operatorname {\mathrm {Sch}}_{X^{\operatorname {\mathrm {alg}}},\operatorname {\mathrm {\acute {e}t}}} \rightarrow \operatorname {\mathrm {Sch}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
denote the map of big étale sites, then the sheaves
are generally not representable by smooth group schemes for
![]() $n\geq 2$
(see Remark 3.55). Moreover, the analytification of this sheaf and the analytic higher direct image are generally not isomorphic. This is exemplified in rank
$n\geq 2$
(see Remark 3.55). Moreover, the analytification of this sheaf and the analytic higher direct image are generally not isomorphic. This is exemplified in rank
![]() $n=2$
where the analytic Brauer group
$n=2$
where the analytic Brauer group
![]() $H_{\operatorname {\mathrm {\acute {e}t}}}^2(X,\mathbb {G}_m)$
typically contains nontorsion elements, in contrast with the algebraic Brauer group
$H_{\operatorname {\mathrm {\acute {e}t}}}^2(X,\mathbb {G}_m)$
typically contains nontorsion elements, in contrast with the algebraic Brauer group
![]() $H_{\operatorname {\mathrm {\acute {e}t}}}^2(X^{\operatorname {\mathrm {alg}}},\mathbb {G}_m)$
which is torsion [Reference Milne39, Cor. IV.2.6]. This mirrors phenomena appearing in complex geometry: For X a projective smooth variety over
$H_{\operatorname {\mathrm {\acute {e}t}}}^2(X^{\operatorname {\mathrm {alg}}},\mathbb {G}_m)$
which is torsion [Reference Milne39, Cor. IV.2.6]. This mirrors phenomena appearing in complex geometry: For X a projective smooth variety over
![]() $\mathbb {C}$
,
$\mathbb {C}$
,
![]() $H_{\operatorname {\mathrm {an}}}^2(X(\mathbb {C}),\mathbb {G}_m)$
is typically nontorsion, as can be seen using the exponential sequence.
$H_{\operatorname {\mathrm {an}}}^2(X(\mathbb {C}),\mathbb {G}_m)$
is typically nontorsion, as can be seen using the exponential sequence.
Nevertheless, we obtain the following: Given a locally p-divisible rigid group G, we let
![]() $\widehat {G} \subseteq G$
denote the open subgroup of p-topological torsion of G, see Definition 2.16.
$\widehat {G} \subseteq G$
denote the open subgroup of p-topological torsion of G, see Definition 2.16.
Proposition 1.3 (Proposition 3.39)
Let X be a proper smooth rigid space and let G be a locally p-divisible rigid group. Then for all
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
, the sheaf
$\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
, the sheaf
![]() ${\mathbf {Bun}}_{\widehat {G},\tau }^n$
is representable by a locally p-divisible rigid group with Lie algebra
${\mathbf {Bun}}_{\widehat {G},\tau }^n$
is representable by a locally p-divisible rigid group with Lie algebra
![]() $H_{\tau }^n(X, \mathcal {O}_X\otimes _K \operatorname {\mathrm {Lie}}(G))$
.
$H_{\tau }^n(X, \mathcal {O}_X\otimes _K \operatorname {\mathrm {Lie}}(G))$
.
For
![]() $G\neq \widehat {G}$
and
$G\neq \widehat {G}$
and
![]() $n\geq 2$
, the sheaves
$n\geq 2$
, the sheaves
![]() ${\mathbf {Bun}}_{G,\tau }^n$
need not be representable by smooth rigid groups. We provide a counterexample in Corollary 3.54.
${\mathbf {Bun}}_{G,\tau }^n$
need not be representable by smooth rigid groups. We provide a counterexample in Corollary 3.54.
As an application, we obtain a new perspective on the presence of nontorsion elements in Brauer groups of proper smooth rigid analytic varieties (cf. Example 3.51): The p-adic exponential yields an open subgroup
![]() $U \subseteq {\mathbf {Bun}}_{\widehat {\mathbb {G}}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
isomorphic to a rigid polydisc
$U \subseteq {\mathbf {Bun}}_{\widehat {\mathbb {G}}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
isomorphic to a rigid polydisc
![]() $U\cong \mathbb {B}^d$
, where
$U\cong \mathbb {B}^d$
, where
![]() $d=h^2(X,\mathcal {O}_X)$
. Moreover, we show in Proposition 3.49 that the kernel of the map of sheaves
$d=h^2(X,\mathcal {O}_X)$
. Moreover, we show in Proposition 3.49 that the kernel of the map of sheaves
is a discrete group, so that the image of U is not torsion, as soon as
![]() $d>0$
. This generalizes to any locally p-divisible group G and any degree
$d>0$
. This generalizes to any locally p-divisible group G and any degree
![]() $n\geq 1$
.
$n\geq 1$
.
In this article, we construct an
![]() $E_2$
-spectral sequence of étale sheaves on
$E_2$
-spectral sequence of étale sheaves on
![]() $\operatorname {\mathrm {Perf}}_K$
$\operatorname {\mathrm {Perf}}_K$
 $$ \begin{align} \mathbf{E}_2^{ij}(G) = \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\Omega_X^j)(-j)\otimes \operatorname{\mathrm{Lie}}(G)\otimes_K \mathbb{G}_a \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{G,\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow {\mathbf{Bun}}_{G,v}^{i+j}, \end{align} $$
$$ \begin{align} \mathbf{E}_2^{ij}(G) = \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\Omega_X^j)(-j)\otimes \operatorname{\mathrm{Lie}}(G)\otimes_K \mathbb{G}_a \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{G,\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow {\mathbf{Bun}}_{G,v}^{i+j}, \end{align} $$
that we call the geometric Hodge–Tate spectral sequence with G-coefficients. We obtain the following.
Theorem 1.4 (Theorem 3.29)
Let X be a proper smooth rigid space over a perfectoid field extension K of
![]() $\mathbb {Q}_p$
and let G be a locally p-divisible rigid group. Then the geometric Hodge–Tate spectral sequence (1.4) degenerates at the
$\mathbb {Q}_p$
and let G be a locally p-divisible rigid group. Then the geometric Hodge–Tate spectral sequence (1.4) degenerates at the
![]() $E_2$
-page.
$E_2$
-page.
In particular, setting ![]() , Theorem 1.4 yields a natural short exact sequence on
, Theorem 1.4 yields a natural short exact sequence on
![]() $\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
This reproves the existence of the exact sequence in [Reference Heuer22, Thm. 2.7] for
![]() $G=\mathbb {G}_m$
and geometrizes the short exact sequence [Reference Heuer, Werner and Zhang32, Thm. 7.3.(1)]. In particular, this yields evidence for a new instance of the geometric p-adic Simpson correspondence, as we explain further below.
$G=\mathbb {G}_m$
and geometrizes the short exact sequence [Reference Heuer, Werner and Zhang32, Thm. 7.3.(1)]. In particular, this yields evidence for a new instance of the geometric p-adic Simpson correspondence, as we explain further below.
For algebraically closed K, taking the K-rational points of the geometric spectral sequence (1.4) gives back the group-theoretic spectral sequence (1.3). Hence Theorem 1.4 implies Theorem 1.2. This was one motivation for introducing the moduli-theoretic spectral sequences (1.4), as it is the geometry that makes the proof of the degeneration available.
Moreover, we also exploit the geometric properties of the sheaves
![]() ${\mathbf {Bun}}_{G,\tau }^n$
in order to split the sequence (1.3). Indeed, we recall the following result.
${\mathbf {Bun}}_{G,\tau }^n$
in order to split the sequence (1.3). Indeed, we recall the following result.
Lemma 1.5 [Reference Heuer, Werner and Zhang32, Thm. 6.12]
Let H be a locally p-divisible rigid group over K and assume that K is algebraically closed. Then a choice of exponential
![]() $\operatorname {\mathrm {Exp}}$
for K induces a natural exponential
$\operatorname {\mathrm {Exp}}$
for K induces a natural exponential
Given a
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
-lift
${\mathrm {B_{dR}^+}}/\xi ^2$
-lift
![]() $\mathbb {X}$
of X and an exponential
$\mathbb {X}$
of X and an exponential
![]() $\operatorname {\mathrm {Exp}}$
for K, we therefore obtain two splittings of the maps below
$\operatorname {\mathrm {Exp}}$
for K, we therefore obtain two splittings of the maps below
whose composition is the required splitting. This yields the Hodge–Tate decomposition and concludes the proof of Theorem 1.1.
We also extend our results to a class of smooth families of commutative adic groups
![]() $\mathcal {G} \rightarrow X$
. These are the so-called admissible locally p-divisible X-groups, see Definition 2.23 for the precise definition. In addition to constant families
$\mathcal {G} \rightarrow X$
. These are the so-called admissible locally p-divisible X-groups, see Definition 2.23 for the precise definition. In addition to constant families
![]() $G\times _K X$
, where G is a locally p-divisible rigid group, this also includes vector bundles, families of analytic p-divisible groups [Reference Fargues15, Def. 4.1] as well as
$G\times _K X$
, where G is a locally p-divisible rigid group, this also includes vector bundles, families of analytic p-divisible groups [Reference Fargues15, Def. 4.1] as well as
![]() $\mathcal {G} = B^{\times }$
, for B a finite locally free commutative
$\mathcal {G} = B^{\times }$
, for B a finite locally free commutative
![]() $\mathcal {O}_X$
-algebra. This last example appears naturally in the context of abelianization in the p-adic Simpson correspondence [Reference Heuer29] [Reference Heuer and Xu33]. An admissible locally p-divisible group
$\mathcal {O}_X$
-algebra. This last example appears naturally in the context of abelianization in the p-adic Simpson correspondence [Reference Heuer29] [Reference Heuer and Xu33]. An admissible locally p-divisible group
![]() $\mathcal {G} \rightarrow X$
defines a v-sheaf on X and we show that analogs of all aforementioned results hold for such groups
$\mathcal {G} \rightarrow X$
defines a v-sheaf on X and we show that analogs of all aforementioned results hold for such groups
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
We further extend our results to the relative setting of proper smooth morphisms
![]() $\pi \colon X\rightarrow S$
of rigid spaces. Relative variant of the Hodge–Tate spectral sequence were considered, for example, in [Reference Caraiani and Scholze9, §2.2], [Reference Abbes and Gros2], [Reference Gaisin and Koshikawa19, §7.1] and [Reference Heuer28]. In the latter, which is the closest to our technical setup, Heuer shows that, for reduced S, we have a spectral sequence of v-vector bundles [Reference Heuer28, Cor. 5.12, Thm. 5.7.3]
$\pi \colon X\rightarrow S$
of rigid spaces. Relative variant of the Hodge–Tate spectral sequence were considered, for example, in [Reference Caraiani and Scholze9, §2.2], [Reference Abbes and Gros2], [Reference Gaisin and Koshikawa19, §7.1] and [Reference Heuer28]. In the latter, which is the closest to our technical setup, Heuer shows that, for reduced S, we have a spectral sequence of v-vector bundles [Reference Heuer28, Cor. 5.12, Thm. 5.7.3]
that degenerates at
![]() $E_2$
.
$E_2$
.
In our situation, we also have a relative variant of the geometric Hodge–Tate spectral sequences. Let
![]() $\pi \colon X\rightarrow S$
be a proper smooth morphism of seminormal rigid spaces. We define analogously
$\pi \colon X\rightarrow S$
be a proper smooth morphism of seminormal rigid spaces. We define analogously
where
![]() $\tau $
is either the étale or the v-topology. Our most general statement is the following.
$\tau $
is either the étale or the v-topology. Our most general statement is the following.
Theorem 1.6 (Theorem 3.29, Corollary 3.32)
Let
![]() $\pi \colon X \rightarrow S$
be a proper smooth morphism of seminormal rigid spaces over a perfectoid field extension K of
$\pi \colon X \rightarrow S$
be a proper smooth morphism of seminormal rigid spaces over a perfectoid field extension K of
![]() $\mathbb {Q}_p$
, and let
$\mathbb {Q}_p$
, and let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group. Assume that
$\mathcal {G}$
be an admissible locally p-divisible X-group. Assume that
![]() $S=\operatorname {\mathrm {Spa}}(K)$
or that
$S=\operatorname {\mathrm {Spa}}(K)$
or that
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G})$
comes via pullback from a vector bundle on S. Then there is an
$\operatorname {\mathrm {Lie}}(\mathcal {G})$
comes via pullback from a vector bundle on S. Then there is an
![]() $E_2$
-spectral sequence of sheaves on
$E_2$
-spectral sequence of sheaves on
![]() $\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
 $$ \begin{align} \mathbf{E}_2^{ij}(\mathcal{G}) = \left\{\begin{aligned} &R^i\pi_{\operatorname{\mathrm{\acute{E}t}},*}(\Omega_X^j\otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G}))(-j) \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{\mathcal{G},X/S,\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow {\mathbf{Bun}}_{\mathcal{G},X/S,v}^{i+j}. \end{align} $$
$$ \begin{align} \mathbf{E}_2^{ij}(\mathcal{G}) = \left\{\begin{aligned} &R^i\pi_{\operatorname{\mathrm{\acute{E}t}},*}(\Omega_X^j\otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G}))(-j) \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{\mathcal{G},X/S,\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow {\mathbf{Bun}}_{\mathcal{G},X/S,v}^{i+j}. \end{align} $$
Moreover, this spectral sequence degenerates at the
![]() $E_2$
-page.
$E_2$
-page.
The degeneration of the relative Hodge–Tate spectral sequence (1.6) is an essential ingredient for our proof of Theorem 1.6. As a corollary, we obtain the following.
1.3 Application to nonabelian p-adic Hodge theory
At last, we connect our results to the p-adic Simpson correspondence. Let X a proper smooth connected rigid space over an algebraically closed field
![]() $K/\mathbb {Q}_p$
and fix
$K/\mathbb {Q}_p$
and fix
![]() $x\in X(K)$
. The field of nonabelian p-adic Hodge theory arose from the wish to find a p-adic analog of the Corlette–Simpson correspondence in complex geometry. Initiated by Deninger–Werner [Reference Deninger and Werner10] and Faltings [Reference Faltings12] independently, it was first envisaged (in their respective settings) as a correspondence between continuous K-linear (generalized) representations of the étale fundamental group
$x\in X(K)$
. The field of nonabelian p-adic Hodge theory arose from the wish to find a p-adic analog of the Corlette–Simpson correspondence in complex geometry. Initiated by Deninger–Werner [Reference Deninger and Werner10] and Faltings [Reference Faltings12] independently, it was first envisaged (in their respective settings) as a correspondence between continuous K-linear (generalized) representations of the étale fundamental group
![]() $\pi _1(X,x)$
and Higgs bundles
$\pi _1(X,x)$
and Higgs bundles
![]() $(E,\theta )$
on X satisfying certain properties. Reformulated in terms of Scholze’s perfectoid foundations for p-adic Hodge theory, it is now understood as an equivalence of categories [Reference Heuer29, Thm. 1.1]
$(E,\theta )$
on X satisfying certain properties. Reformulated in terms of Scholze’s perfectoid foundations for p-adic Hodge theory, it is now understood as an equivalence of categories [Reference Heuer29, Thm. 1.1]
depending on choice of
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
-lift
${\mathrm {B_{dR}^+}}/\xi ^2$
-lift
![]() $\mathbb {X}$
of X and an exponential
$\mathbb {X}$
of X and an exponential
![]() $\operatorname {\mathrm {Exp}}$
for K. A first instance of this modern formulation is the isomorphism [Reference Heuer23, Thm. 5.7]
$\operatorname {\mathrm {Exp}}$
for K. A first instance of this modern formulation is the isomorphism [Reference Heuer23, Thm. 5.7]
where
![]() $\operatorname {\mathrm {Pic}}_{\operatorname {\mathrm {\acute {e}t}},\operatorname {\mathrm {prof\acute {e}t}}}(X)$
consists of those étale line bundles that are trivialized by a pro-finite-étale cover
$\operatorname {\mathrm {Pic}}_{\operatorname {\mathrm {\acute {e}t}},\operatorname {\mathrm {prof\acute {e}t}}}(X)$
consists of those étale line bundles that are trivialized by a pro-finite-étale cover
![]() $\widetilde {X} \rightarrow X$
. From loc. cit, one can also deduce a decomposition
$\widetilde {X} \rightarrow X$
. From loc. cit, one can also deduce a decomposition
underlying a p-adic Simpson correspondence for line bundles. These two decompositions were later generalized [Reference Heuer, Werner and Zhang32, Thm. 7.3-4] to locally p-divisible rigid group G in place of
![]() $\mathbb {G}_m$
, and it is shown there that it induces a p-adic Simpson correspondence for G-torsors. The Hodge–Tate decomposition of Theorem 1.1 recovers (1.10) and its extensions to general G as the special case
$\mathbb {G}_m$
, and it is shown there that it induces a p-adic Simpson correspondence for G-torsors. The Hodge–Tate decomposition of Theorem 1.1 recovers (1.10) and its extensions to general G as the special case
![]() $n=1$
. Moreover, our decomposition with
$n=1$
. Moreover, our decomposition with
![]() $n> 1$
$n> 1$
 $$\begin{align*}H_v^n(X,\mathbb{G}_m) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathbb{G}_m) \oplus \bigoplus_{i=0}^{n-1}H^i(X,\Omega_X^{n-i})(i-n)\end{align*}$$
$$\begin{align*}H_v^n(X,\mathbb{G}_m) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathbb{G}_m) \oplus \bigoplus_{i=0}^{n-1}H^i(X,\Omega_X^{n-i})(i-n)\end{align*}$$
is new already for
![]() $\mathbb {G}_m$
and the author is not aware of an analogous result in complex geometry. We suspect that it is an instance of a higher analogue of the p-adic Simpson correspondence, involving étale and v-topological n-gerbes. We also obtain a version of the decomposition involving the étale fundamental group
$\mathbb {G}_m$
and the author is not aware of an analogous result in complex geometry. We suspect that it is an instance of a higher analogue of the p-adic Simpson correspondence, involving étale and v-topological n-gerbes. We also obtain a version of the decomposition involving the étale fundamental group
![]() $\pi _1(X,x)$
in the case where X is either a curve of genus
$\pi _1(X,x)$
in the case where X is either a curve of genus
![]() $g\geq 1$
or an abeloid variety, cf. Theorem 3.48.
$g\geq 1$
or an abeloid variety, cf. Theorem 3.48.
Moreover, the perspective of moduli spaces in nonabelian p-adic Hodge theory was explored in [Reference Heuer25] and [Reference Heuer and Xu33], where Heuer–Xu show that the p-adic Simpson correspondence can be upgraded from an equivalence of categories to a comparison of small v-stacks. Our results yield a new instance of this geometric p-adic Simpson correspondence. Namely, the sequence (1.5) can be interpreted geometrically as saying that the coarse moduli space
![]() ${\mathbf {Bun}}_{G,v}$
of v-G-torsors on X is a
${\mathbf {Bun}}_{G,v}$
of v-G-torsors on X is a
![]() ${\mathbf {Bun}}_{G,\operatorname {\mathrm {\acute {e}t}}}$
-torsor over the “Hitchin base”
${\mathbf {Bun}}_{G,\operatorname {\mathrm {\acute {e}t}}}$
-torsor over the “Hitchin base”
![]() $H^0(X,\widetilde {\Omega }_X^1)(-1) \otimes \operatorname {\mathrm {Lie}}(G)\otimes _K \mathbb {G}_a$
. We claim that, under mild assumptions on G, one can derive from (1.5) a geometric p-adic Simpson correspondence for G-torsors, following the strategy of [Reference Heuer25].
$H^0(X,\widetilde {\Omega }_X^1)(-1) \otimes \operatorname {\mathrm {Lie}}(G)\otimes _K \mathbb {G}_a$
. We claim that, under mild assumptions on G, one can derive from (1.5) a geometric p-adic Simpson correspondence for G-torsors, following the strategy of [Reference Heuer25].
Finally, it was discovered in [Reference Heuer29] that the more difficult higher rank correspondence could be tackled by trading the nonabelian p-adic Hodge theory of the group
![]() $\operatorname {\mathrm {GL}}_n$
for the relative p-adic Hodge theory of smooth families of abelian groups
$\operatorname {\mathrm {GL}}_n$
for the relative p-adic Hodge theory of smooth families of abelian groups
![]() $\mathcal {G} \rightarrow X$
, through the process of abelianization. Our approach yields a systematic study of smooth commutative relative groups and their Hodge–Tate theory in a more general setting. Given a finite locally free commutative
$\mathcal {G} \rightarrow X$
, through the process of abelianization. Our approach yields a systematic study of smooth commutative relative groups and their Hodge–Tate theory in a more general setting. Given a finite locally free commutative
![]() $\mathcal {O}_X$
-algebra B on a proper smooth rigid space X over K, Theorem 1.4 yields a short exact sequence
$\mathcal {O}_X$
-algebra B on a proper smooth rigid space X over K, Theorem 1.4 yields a short exact sequence
This recovers [Reference Heuer29, Thm. 1.5]. Note that via the canonical decomposition of Theorem 1.1
we recover the association
![]() $\theta \in H^0(X,\Omega _X^1 \otimes B)(-1) \mapsto [\mathcal {L}_{\theta }] \in H_v^1(X,B^{\times })$
of [Reference Heuer29, Reference Bhatt and Hansen4] at least when B is locally free. We note that it would be interesting to extend the methods of this article to more general sheaves of groups over X such as
$\theta \in H^0(X,\Omega _X^1 \otimes B)(-1) \mapsto [\mathcal {L}_{\theta }] \in H_v^1(X,B^{\times })$
of [Reference Heuer29, Reference Bhatt and Hansen4] at least when B is locally free. We note that it would be interesting to extend the methods of this article to more general sheaves of groups over X such as
![]() $B^{\times }$
, for B a coherent commutative
$B^{\times }$
, for B a coherent commutative
![]() $\mathcal {O}_X$
-algebra.
$\mathcal {O}_X$
-algebra.
Notations and conventions
-
○ We fix a prime number p. We denote by K a nonarchimedean field extension of
 $\mathbb {Q}_p$
, with ring of integers
$\mathbb {Q}_p$
, with ring of integers
 $\mathcal {O}_K$
and subspace of topologically nilpotent elements
$\mathcal {O}_K$
and subspace of topologically nilpotent elements
 ${\mathfrak {m}}$
. More generally, we consider open and bounded valuation subrings
${\mathfrak {m}}$
. More generally, we consider open and bounded valuation subrings
 $K^+ \subseteq K$
contained in
$K^+ \subseteq K$
contained in
 $\mathcal {O}_K$
. Such a pair
$\mathcal {O}_K$
. Such a pair
 $(K,K^+)$
will sometimes be referred to as a nonarchimedean field. Throughout, we will work with analytic adic spaces in the sense of Huber [Reference Huber31]. For simplicity, we will simply talk about adic spaces over K when dealing with adic spaces over
$(K,K^+)$
will sometimes be referred to as a nonarchimedean field. Throughout, we will work with analytic adic spaces in the sense of Huber [Reference Huber31]. For simplicity, we will simply talk about adic spaces over K when dealing with adic spaces over
 $\operatorname {\mathrm {Spa}}(K,K^+)$
.
$\operatorname {\mathrm {Spa}}(K,K^+)$
. -
○ A rigid space over K will mean for us an adic space locally of topologically finite type over K. When
 $K^+=\mathcal {O}_K$
, there is an equivalence of categories between (quasi-)separated rigid analytic varieties in the sense of Tate and (quasi-)separated rigid spaces in the above sense [Reference Huber31, (1.1.11)].
$K^+=\mathcal {O}_K$
, there is an equivalence of categories between (quasi-)separated rigid analytic varieties in the sense of Tate and (quasi-)separated rigid spaces in the above sense [Reference Huber31, (1.1.11)]. -
○ We work with perfectoid spaces in the sense of [Reference Scholze43]. We let
 $\operatorname {\mathrm {Perf}}_K$
denote the category of affinoid perfectoid spaces over K, or equivalently of perfectoid
$\operatorname {\mathrm {Perf}}_K$
denote the category of affinoid perfectoid spaces over K, or equivalently of perfectoid
 $(K,K^+)$
-algebras. We may equip it with the étale or the v-topology, and we denote the resulting sites by
$(K,K^+)$
-algebras. We may equip it with the étale or the v-topology, and we denote the resulting sites by
 $\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
and
$\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
and
 $\operatorname {\mathrm {Perf}}_{K,v}$
.
$\operatorname {\mathrm {Perf}}_{K,v}$
. -
○ Throughout we will often work with sousperfectoid adic spaces over
 $\mathbb {Q}_p$
, that is, adic spaces that are locally of the form
$\mathbb {Q}_p$
, that is, adic spaces that are locally of the form
 $\operatorname {\mathrm {Spa}}(R,R^+)$
where R is sousperfectoid [Reference Scholze and Weinstein50, §6.3]. This contains both perfectoid spaces and smooth rigid spaces over perfectoid fields.
$\operatorname {\mathrm {Spa}}(R,R^+)$
where R is sousperfectoid [Reference Scholze and Weinstein50, §6.3]. This contains both perfectoid spaces and smooth rigid spaces over perfectoid fields. -
○ If X is either a sousperfectoid space or a rigid space, the étale site
 $X_{\operatorname {\mathrm {\acute {e}t}}}$
of Kedlaya–Liu [Reference Kedlaya and Liu35, Def. 8.2.19] consists only of sheafy adic spaces. A map
$X_{\operatorname {\mathrm {\acute {e}t}}}$
of Kedlaya–Liu [Reference Kedlaya and Liu35, Def. 8.2.19] consists only of sheafy adic spaces. A map
 $f\colon Y \rightarrow X$
is called standard-étale if X and Y are affinoid and f can be written as a composition of finite-étale maps and rational open immersions. These form a basis of the étale site. More generally, the theory of smooth adic spaces over sousperfectoid spaces is well-behaved, see [Reference Fargues and Scholze17, §IV.4.1]. In particular, this produces sousperfectoid spaces again. A map
$f\colon Y \rightarrow X$
is called standard-étale if X and Y are affinoid and f can be written as a composition of finite-étale maps and rational open immersions. These form a basis of the étale site. More generally, the theory of smooth adic spaces over sousperfectoid spaces is well-behaved, see [Reference Fargues and Scholze17, §IV.4.1]. In particular, this produces sousperfectoid spaces again. A map
 $Y\rightarrow X$
is called standard-smooth if it can be written as a composition of finite-étale maps, rational open immersions, and projections
$Y\rightarrow X$
is called standard-smooth if it can be written as a composition of finite-étale maps, rational open immersions, and projections
 $\mathbb {B}_S^1=\mathbb {B}^1 \times _{\operatorname {\mathrm {Spa}}(\mathbb {Q}_p)} S \rightarrow S$
, where
$\mathbb {B}_S^1=\mathbb {B}^1 \times _{\operatorname {\mathrm {Spa}}(\mathbb {Q}_p)} S \rightarrow S$
, where
 $\mathbb {B}^1=\operatorname {\mathrm {Spa}}(\mathbb {Q}_p\langle T \rangle )$
.
$\mathbb {B}^1=\operatorname {\mathrm {Spa}}(\mathbb {Q}_p\langle T \rangle )$
. -
○ Scholze’s diamond functor [Reference Scholze47, §15] associates to any adic space X over
 $\mathbb {Q}_p$
a diamond
$\mathbb {Q}_p$
a diamond
 $X^{\diamondsuit }$
over
$X^{\diamondsuit }$
over
 $\operatorname {\mathrm {Spd}}(\mathbb {Q}_p)$
. Under the equivalence
$\operatorname {\mathrm {Spd}}(\mathbb {Q}_p)$
. Under the equivalence
 $\operatorname {\mathrm {Perf}}_{\mathbb {F}_p, /\operatorname {\mathrm {Spd}}(\mathbb {Q}_p)} \cong \operatorname {\mathrm {Perf}}_{\mathbb {Q}_p}$
, sending a characteristic p perfectoid space
$\operatorname {\mathrm {Perf}}_{\mathbb {F}_p, /\operatorname {\mathrm {Spd}}(\mathbb {Q}_p)} \cong \operatorname {\mathrm {Perf}}_{\mathbb {Q}_p}$
, sending a characteristic p perfectoid space
 $S\rightarrow \operatorname {\mathrm {Spd}}(\mathbb {Q}_p)$
to the corresponding untilt
$S\rightarrow \operatorname {\mathrm {Spd}}(\mathbb {Q}_p)$
to the corresponding untilt
 $S^{\sharp } \rightarrow \operatorname {\mathrm {Spa}}(\mathbb {Q}_p)$
, we may equivalently consider
$S^{\sharp } \rightarrow \operatorname {\mathrm {Spa}}(\mathbb {Q}_p)$
, we may equivalently consider
 $X^{\diamondsuit }$
as a sheaf on
$X^{\diamondsuit }$
as a sheaf on
 $\operatorname {\mathrm {Perf}}_{\mathbb {Q}_p,v}$
, namely the functor of points. By [Reference Scholze47, Lemma 15.6], for any adic space X over
$\operatorname {\mathrm {Perf}}_{\mathbb {Q}_p,v}$
, namely the functor of points. By [Reference Scholze47, Lemma 15.6], for any adic space X over
 $\mathbb {Q}_p$
, we have an equivalence of sites
$\mathbb {Q}_p$
, we have an equivalence of sites
 $X_{\operatorname {\mathrm {\acute {e}t}}} \cong X_{\operatorname {\mathrm {\acute {e}t}}}^{\diamondsuit }$
. Furthermore, we will often restrict to a situation where the functor
$X_{\operatorname {\mathrm {\acute {e}t}}} \cong X_{\operatorname {\mathrm {\acute {e}t}}}^{\diamondsuit }$
. Furthermore, we will often restrict to a situation where the functor
 $(\cdot )^{\diamondsuit }$
is fully faithful. Thus, we will freely switch back and forth between adic spaces and their associated diamonds, and we will sometimes omit the diamond symbol when the context is clear.
$(\cdot )^{\diamondsuit }$
is fully faithful. Thus, we will freely switch back and forth between adic spaces and their associated diamonds, and we will sometimes omit the diamond symbol when the context is clear. -
○ We will also require to work with various big sites over adic spaces. If X is an adic space over
 $\mathbb {Q}_p$
, we denote by
$\mathbb {Q}_p$
, we denote by
 $X_v = \operatorname {\mathrm {LSD}}_{X,v}$
the v-site of X, with underlying category all locally spatial diamonds over
$X_v = \operatorname {\mathrm {LSD}}_{X,v}$
the v-site of X, with underlying category all locally spatial diamonds over
 $X^{\diamondsuit }$
[Reference Scholze47, §14]. We will occasionally also equip this category with the étale topology and denote it by
$X^{\diamondsuit }$
[Reference Scholze47, §14]. We will occasionally also equip this category with the étale topology and denote it by
 $\operatorname {\mathrm {LSD}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
. We will also denote by
$\operatorname {\mathrm {LSD}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
. We will also denote by
 $\operatorname {\mathrm {Perf}}_X$
the category of affinoid perfectoid spaces living over X, which we can equip either with the étale or the v-topology. Note that
$\operatorname {\mathrm {Perf}}_X$
the category of affinoid perfectoid spaces living over X, which we can equip either with the étale or the v-topology. Note that
 $\operatorname {\mathrm {Perf}}_X$
need not be a slice category. If X is a sousperfectoid space or a rigid space, we also set
$\operatorname {\mathrm {Perf}}_X$
need not be a slice category. If X is a sousperfectoid space or a rigid space, we also set
 $\operatorname {\mathrm {Sm}}_{/X,\operatorname {\mathrm {\acute {e}t}}}$
to be the category of adic spaces smooth over X, equipped with the étale topology.
$\operatorname {\mathrm {Sm}}_{/X,\operatorname {\mathrm {\acute {e}t}}}$
to be the category of adic spaces smooth over X, equipped with the étale topology. -
○ Given a morphism of adic space
 $\pi \colon X\rightarrow S$
, we have an associated morphism of small étale site
$\pi \colon X\rightarrow S$
, we have an associated morphism of small étale site
 $\pi _{\operatorname {\mathrm {\acute {e}t}}}\colon X_{\operatorname {\mathrm {\acute {e}t}}} \rightarrow S_{\operatorname {\mathrm {\acute {e}t}}}$
. We will also consider the induced morphism between big étale sites, for a choice of big étale site, for example,
$\pi _{\operatorname {\mathrm {\acute {e}t}}}\colon X_{\operatorname {\mathrm {\acute {e}t}}} \rightarrow S_{\operatorname {\mathrm {\acute {e}t}}}$
. We will also consider the induced morphism between big étale sites, for a choice of big étale site, for example,
 $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
or
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
or
 $\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
. To emphasize this difference, we will denote this morphism by
$\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
. To emphasize this difference, we will denote this morphism by
 $\pi _{\operatorname {\mathrm {\acute {E}t}}}$
.
$\pi _{\operatorname {\mathrm {\acute {E}t}}}$
. -
○ This article is primarily concerned with commutative groups. Therefore, all groups will be taken to be commutative, unless mentioned otherwise.
2 Preliminaries
2.1 Good adic spaces
We define a class of adic spaces that we will be working with throughout the paper.
Definition 2.1. Let X be an adic space over
![]() $\mathbb {Q}_p$
that is either a sousperfectoid space or a rigid space over some nonarchimedean field
$\mathbb {Q}_p$
that is either a sousperfectoid space or a rigid space over some nonarchimedean field
![]() $(K,K^+)$
. We say that X is good if the natural map
$(K,K^+)$
. We say that X is good if the natural map
is an isomorphism, where
![]() $\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
is the natural map of sites. We denote by
$\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
is the natural map of sites. We denote by
![]() $\operatorname {\mathrm {Adic}}_{\mathbb {Q}_p}$
the category of good adic spaces over
$\operatorname {\mathrm {Adic}}_{\mathbb {Q}_p}$
the category of good adic spaces over
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Example 2.2.
-
1. Any perfectoid space is a good adic space.
-
2. Let X be a rigid space over a nonarchimedean field
 $(K,K^+)$
over
$(K,K^+)$
over
 $\mathbb {Q}_p$
. Then by [Reference Hansen and Kedlaya30, Thm. 10.3, Lemma 6.4], X is good if and only if it is seminormal.
$\mathbb {Q}_p$
. Then by [Reference Hansen and Kedlaya30, Thm. 10.3, Lemma 6.4], X is good if and only if it is seminormal.
Remark 2.3. A similar condition on adic spaces was recently introduced in [Reference Graham, van Hoften and Howe18, Def. 3.1.9] under the name locally fiercely v-complete adic spaces. We show below in Proposition 2.5 that good adic spaces over
![]() $\mathbb {Q}_p$
are stable under smooth maps. It follows that the good adic spaces over
$\mathbb {Q}_p$
are stable under smooth maps. It follows that the good adic spaces over
![]() $\mathbb {Q}_p$
are exactly the locally fiercely v-complete spaces that are either sousperfectoid or rigid spaces. We do not know whether any sousperfectoid space over
$\mathbb {Q}_p$
are exactly the locally fiercely v-complete spaces that are either sousperfectoid or rigid spaces. We do not know whether any sousperfectoid space over
![]() $\mathbb {Q}_p$
is good.
$\mathbb {Q}_p$
is good.
Proposition 2.4. Let X be a good adic space over
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
-
1. Let
 $\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
denote the natural map of sites, then we have isomorphisms
$\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
denote the natural map of sites, then we have isomorphisms  $$\begin{align*}\mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+ \xrightarrow{\cong} \nu_*\mathcal{O}_{X_v}^+, \quad \mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+/p^n \xrightarrow{\cong} \nu_*(\mathcal{O}_{X_v}^+/p^n), \quad \mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+ = \varprojlim_n \mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+/p^n .\end{align*}$$
$$\begin{align*}\mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+ \xrightarrow{\cong} \nu_*\mathcal{O}_{X_v}^+, \quad \mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+/p^n \xrightarrow{\cong} \nu_*(\mathcal{O}_{X_v}^+/p^n), \quad \mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+ = \varprojlim_n \mathcal{O}_{X_{\operatorname{\mathrm{\acute{e}t}}}}^+/p^n .\end{align*}$$
-
2. For Y another good adic space over
 $\mathbb {Q}_p$
, we have a natural isomorphism
$\mathbb {Q}_p$
, we have a natural isomorphism  $$\begin{align*}\operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{Spa}}(\mathbb{Q}_p)}(X,Y) \xrightarrow{\cong} \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{Spd}}(\mathbb{Q}_p)}(X^{\diamondsuit},Y^{\diamondsuit}).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{Spa}}(\mathbb{Q}_p)}(X,Y) \xrightarrow{\cong} \operatorname{\mathrm{Hom}}_{\operatorname{\mathrm{Spd}}(\mathbb{Q}_p)}(X^{\diamondsuit},Y^{\diamondsuit}).\end{align*}$$
Proof. To prove the second point, we may work locally on
![]() $\vert Y \vert = \vert Y^{\diamondsuit } \vert $
and assume that
$\vert Y \vert = \vert Y^{\diamondsuit } \vert $
and assume that
![]() $Y=\operatorname {\mathrm {Spa}}(B,B^+)$
is affinoid. We have the following adjunction, left to the reader
$Y=\operatorname {\mathrm {Spa}}(B,B^+)$
is affinoid. We have the following adjunction, left to the reader
It thus remains to show that the natural map
is an isomorphism, so that it suffices to show the first point. The isomorphism
![]() $\nu _*(\mathcal {O}_{X_v}^+/p^n) = \mathcal {O}_{X_{\operatorname {\mathrm {\acute {e}t}}}}^+/p^n$
is [Reference Mann and Werner41, Prop. 2.8, Prop. 2.13] when X is a rigid space and [Reference Heuer24, Corollary 2.15] when X is sousperfectoid. The isomorphism
$\nu _*(\mathcal {O}_{X_v}^+/p^n) = \mathcal {O}_{X_{\operatorname {\mathrm {\acute {e}t}}}}^+/p^n$
is [Reference Mann and Werner41, Prop. 2.8, Prop. 2.13] when X is a rigid space and [Reference Heuer24, Corollary 2.15] when X is sousperfectoid. The isomorphism
![]() $\nu _*\mathcal {O}_{X_v}^+ = \mathcal {O}_{X_{\operatorname {\mathrm {\acute {e}t}}}}^+$
follows from
$\nu _*\mathcal {O}_{X_v}^+ = \mathcal {O}_{X_{\operatorname {\mathrm {\acute {e}t}}}}^+$
follows from
![]() $\nu _*\mathcal {O}_{X_v} = \mathcal {O}_{X_{\operatorname {\mathrm {\acute {e}t}}}}$
. Finally, to show the last isomorphism, it is enough to show the isomorphism
$\nu _*\mathcal {O}_{X_v} = \mathcal {O}_{X_{\operatorname {\mathrm {\acute {e}t}}}}$
. Finally, to show the last isomorphism, it is enough to show the isomorphism
This can be checked on affinoid perfectoids Y. Injectivity is clear. For surjectivity, given a collection
![]() $(s_n)_{n\geq 1}$
of compatible sections
$(s_n)_{n\geq 1}$
of compatible sections
![]() $s_n \in \mathcal {O}_v^+/p^n(Y)$
, let
$s_n \in \mathcal {O}_v^+/p^n(Y)$
, let
![]() $c_n\in H_v^1(Y,\mathcal {O}_v^+)$
be the obstruction class to lifting
$c_n\in H_v^1(Y,\mathcal {O}_v^+)$
be the obstruction class to lifting
![]() $s_n$
to a section in
$s_n$
to a section in
![]() $\mathcal {O}^+(Y)/p^n$
. Then
$\mathcal {O}^+(Y)/p^n$
. Then
![]() $c_n = pc_{n+1}$
. Since
$c_n = pc_{n+1}$
. Since
![]() $H_v^1(Y,\mathcal {O}_v^+)$
is almost zero, by [Reference Scholze47, Prop. 8.8], it is in particular annihilated by p. Hence
$H_v^1(Y,\mathcal {O}_v^+)$
is almost zero, by [Reference Scholze47, Prop. 8.8], it is in particular annihilated by p. Hence
![]() $c_n$
vanishes and
$c_n$
vanishes and
![]() $(s_n)_n$
is in the image of the above map, as required. This concludes the proof.
$(s_n)_n$
is in the image of the above map, as required. This concludes the proof.
Proposition 2.5. Let X be a good adic space over
![]() $\mathbb {Q}_p$
and let
$\mathbb {Q}_p$
and let
![]() $f\colon X'\rightarrow X$
be a smooth map. Then
$f\colon X'\rightarrow X$
be a smooth map. Then
![]() $X'$
is a good adic space.
$X'$
is a good adic space.
Proof. The claim is local on
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}$
. Therefore, we may assume that
$X_{\operatorname {\mathrm {\acute {e}t}}}$
. Therefore, we may assume that
![]() $X=\operatorname {\mathrm {Spa}}(A,A^+)$
,
$X=\operatorname {\mathrm {Spa}}(A,A^+)$
,
![]() $X'=\operatorname {\mathrm {Spa}}(B,B^+)$
, and f is standard-smooth, that is, a composition of finite-étale maps, rational open immersions, and projections
$X'=\operatorname {\mathrm {Spa}}(B,B^+)$
, and f is standard-smooth, that is, a composition of finite-étale maps, rational open immersions, and projections
![]() $\mathbb {B}_S^1 \rightarrow S$
. We may further assume that
$\mathbb {B}_S^1 \rightarrow S$
. We may further assume that
![]() $X'=\mathbb {B}_X^1$
, so that
$X'=\mathbb {B}_X^1$
, so that
![]() $B=A\langle T \rangle $
. Fix a pro-étale presentation
$B=A\langle T \rangle $
. Fix a pro-étale presentation
![]() $X^{\diamondsuit } = Y/R$
for perfectoids Y and
$X^{\diamondsuit } = Y/R$
for perfectoids Y and
![]() $R\subseteq Y\times Y$
. By Proposition 2.4.1, we have left exact sequences, for each
$R\subseteq Y\times Y$
. By Proposition 2.4.1, we have left exact sequences, for each
![]() $n\geq 1$
$n\geq 1$
Upon adjoining a polynomial variable, taking the inverse limit over n and inverting p, we obtain the left exact sequence
By a
![]() $5$
-lemma argument, to show that
$5$
-lemma argument, to show that
it is enough to show that
Hence, we may assume that X is affinoid perfectoid. In that case, X is diamantine, in the sense of [Reference Hansen and Kedlaya30, Def. 11.1], so that the result follows from [Reference Hansen and Kedlaya30, Thm. 11.18].
We denote by
![]() $\operatorname {\mathrm {Adic}}_{X}$
the category of good adic spaces over a fixed good adic space X. By Proposition 2.5, we may endow it with the étale topology, and we denote by
$\operatorname {\mathrm {Adic}}_{X}$
the category of good adic spaces over a fixed good adic space X. By Proposition 2.5, we may endow it with the étale topology, and we denote by
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
the resulting site. We will also sometimes consider v-sheaves on
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
the resulting site. We will also sometimes consider v-sheaves on
![]() $\operatorname {\mathrm {Adic}}_{X}$
. These are defined to be presheaves
$\operatorname {\mathrm {Adic}}_{X}$
. These are defined to be presheaves
![]() $\mathcal {F}$
such that, for any v-cover
$\mathcal {F}$
such that, for any v-cover
![]() $Y' \rightarrow Y$
of good adic spaces over X (i.e., a map that induces a v-cover
$Y' \rightarrow Y$
of good adic spaces over X (i.e., a map that induces a v-cover
![]() $Y^{\prime \diamondsuit } \rightarrow Y^{\diamondsuit }$
) and for any v-cover
$Y^{\prime \diamondsuit } \rightarrow Y^{\diamondsuit }$
) and for any v-cover
![]() $Y" \rightarrow Y^{\prime \diamondsuit } \times _{Y^{\diamondsuit }}Y^{\prime \diamondsuit }$
from a good adic space
$Y" \rightarrow Y^{\prime \diamondsuit } \times _{Y^{\diamondsuit }}Y^{\prime \diamondsuit }$
from a good adic space
![]() $Y"$
, we have
$Y"$
, we have
These are equivalent to sheaves on the site
![]() $X_v$
.
$X_v$
.
2.2 Smoothoid spaces
Fix a perfectoid field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
. We recall some facts about smoothoid spaces, introduced in [Reference Heuer27], which form a subclass of good adic spaces over K admitting a well-behaved notion of differentials. All the results of this section are taken from [Reference Heuer27, §2].
$\mathbb {Q}_p$
. We recall some facts about smoothoid spaces, introduced in [Reference Heuer27], which form a subclass of good adic spaces over K admitting a well-behaved notion of differentials. All the results of this section are taken from [Reference Heuer27, §2].
Definition 2.6 [Reference Heuer27, Def. 2.2]
An adic space X over K is called smoothoid if it admits an open cover by adic spaces that are smooth over a perfectoid space Y over K. We denote by
![]() $\operatorname {\mathrm {Smd}}_K$
the category of smoothoid spaces over K.
$\operatorname {\mathrm {Smd}}_K$
the category of smoothoid spaces over K.
Example 2.7. Given a smooth morphism of rigid spaces
![]() $X\rightarrow S$
over K and a morphism
$X\rightarrow S$
over K and a morphism
![]() $Y\rightarrow S$
from a perfectoid space Y, the fiber product
$Y\rightarrow S$
from a perfectoid space Y, the fiber product
![]() $X\times _S Y$
is smoothoid.
$X\times _S Y$
is smoothoid.
By [Reference Heuer27, Lemma 2.6], any smoothoid space over K is sousperfectoid and a good adic space in the sense of Definition 2.1. Moreover, the category
![]() $\operatorname {\mathrm {Smd}}_K$
of smoothoid spaces is clearly closed under taking small étale sites. We may thus turn
$\operatorname {\mathrm {Smd}}_K$
of smoothoid spaces is clearly closed under taking small étale sites. We may thus turn
![]() $\operatorname {\mathrm {Smd}}_K$
into a site by equipping it with the étale topology, which we denote by
$\operatorname {\mathrm {Smd}}_K$
into a site by equipping it with the étale topology, which we denote by
![]() $\operatorname {\mathrm {Smd}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
.
$\operatorname {\mathrm {Smd}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
.
Definition 2.8 [Reference Heuer27, Def. 2.10]
Let X be a smoothoid space and let
![]() $\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
be the natural map of sites. We set, for any
$\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
be the natural map of sites. We set, for any
![]() $n\geq 0$
$n\geq 0$
Example 2.9.
-
1. For X a smooth rigid space, we have [Reference Scholze45, Prop. 3.23]
where $$\begin{align*}\widetilde{\Omega}_X^1 = \Omega_{X/K}^1\{-1\},\end{align*}$$
$$\begin{align*}\widetilde{\Omega}_X^1 = \Omega_{X/K}^1\{-1\},\end{align*}$$
 $\Omega _{X/K}^1$
is the sheaf of relative differentials of Huber [Reference Huber31, (1.6.2)] and
$\Omega _{X/K}^1$
is the sheaf of relative differentials of Huber [Reference Huber31, (1.6.2)] and
 $\{-1\}$
denotes a Breuil–Kisin–Fargues twist [Reference Heuer23, Def. 2.24]. If K contains
$\{-1\}$
denotes a Breuil–Kisin–Fargues twist [Reference Heuer23, Def. 2.24]. If K contains
 $\mathbb {Q}_p(\mu _{p^{\infty }})$
, this is canonically isomorphic to a Tate twist, by adapting the proof of [Reference Scholze44, Prop. 6.7]. In general, if C denotes a completed algebraic closure of K, we have a canonical,
$\mathbb {Q}_p(\mu _{p^{\infty }})$
, this is canonically isomorphic to a Tate twist, by adapting the proof of [Reference Scholze44, Prop. 6.7]. In general, if C denotes a completed algebraic closure of K, we have a canonical,
 $\operatorname {\mathrm {Gal}}_K$
-equivariant isomorphism
$\operatorname {\mathrm {Gal}}_K$
-equivariant isomorphism  $$\begin{align*}\widetilde{\Omega}_X^1 \otimes_K C \cong \Omega_{X/K}^1\otimes_K C(-1).\end{align*}$$
$$\begin{align*}\widetilde{\Omega}_X^1 \otimes_K C \cong \Omega_{X/K}^1\otimes_K C(-1).\end{align*}$$
-
2. Let Y be a perfectoid space over K, then by v-acyclicity of affinoid perfectoid spaces [Reference Scholze47, Prop. 8.8],
 $\widetilde {\Omega }_Y^n = 0$
.
$\widetilde {\Omega }_Y^n = 0$
. -
3. Given a diagram
where
 $\pi $
is a smooth morphism of rigid spaces and Y is any perfectoid space, we have [Reference Heuer27, Prop. 2.9.(2)]
$\pi $
is a smooth morphism of rigid spaces and Y is any perfectoid space, we have [Reference Heuer27, Prop. 2.9.(2)]  $$\begin{align*}\widetilde{\Omega}_{X\times_S Y}^1 = g^*\Omega_{X/S}^1\{-1\}.\end{align*}$$
$$\begin{align*}\widetilde{\Omega}_{X\times_S Y}^1 = g^*\Omega_{X/S}^1\{-1\}.\end{align*}$$
This generalizes the two previous examples.
For a general smoothoid space X, the sheaf
![]() $\widetilde {\Omega }_X^n$
is a vector bundle [Reference Heuer27, Prop. 2.9.(1)], satisfying all the compatibility properties of the Kähler differentials. The assignment
$\widetilde {\Omega }_X^n$
is a vector bundle [Reference Heuer27, Prop. 2.9.(1)], satisfying all the compatibility properties of the Kähler differentials. The assignment
defines a sheaf for the étale topology and we have
where
![]() $\mu \colon K_v \rightarrow \operatorname {\mathrm {Smd}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
is the natural map of sites [Reference Heuer27, Lemma 2.12].
$\mu \colon K_v \rightarrow \operatorname {\mathrm {Smd}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
is the natural map of sites [Reference Heuer27, Lemma 2.12].
2.3 Zariski-constructible sheaves
We recall the notion of Zariski-constructible sheaves on rigid spaces in characteristic
![]() $0$
and some of their basic properties. Let X be a rigid space over a nonarchimedean field
$0$
and some of their basic properties. Let X be a rigid space over a nonarchimedean field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
. Recall that X comes with a natural Zariski topology
$\mathbb {Q}_p$
. Recall that X comes with a natural Zariski topology
![]() $X_{\operatorname {\mathrm {Zar}}}$
[Reference Johansson and Newton34, §2.1].
$X_{\operatorname {\mathrm {Zar}}}$
[Reference Johansson and Newton34, §2.1].
Definition 2.10 [Reference Hansen21]
A sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}$
is Zariski-constructible if there exists a locally finite stratification
$X_{\operatorname {\mathrm {\acute {e}t}}}$
is Zariski-constructible if there exists a locally finite stratification
![]() $X=\coprod _i X_i$
where each
$X=\coprod _i X_i$
where each
![]() $X_i$
is locally closed in X in the Zariski topology and
$X_i$
is locally closed in X in the Zariski topology and
![]() $\mathcal {F}|_{X_i}$
is étale-locally constant finite. The sheaf
$\mathcal {F}|_{X_i}$
is étale-locally constant finite. The sheaf
![]() $\mathcal {F}$
is ind-Zariski-constructible if it can be written as a filtered colimit of Zariski-constructible étale sheaves.
$\mathcal {F}$
is ind-Zariski-constructible if it can be written as a filtered colimit of Zariski-constructible étale sheaves.
Remark 2.11. The Zariski-constructible sheaves on
![]() $\operatorname {\mathrm {Spa}}(L,L^+)$
are exactly the finite étale-locally constant sheaves. Hence any Zariski-constructible sheaf
$\operatorname {\mathrm {Spa}}(L,L^+)$
are exactly the finite étale-locally constant sheaves. Hence any Zariski-constructible sheaf
![]() $\mathcal {F}$
on a rigid space X is overconvergent [Reference Huber31, Def. 8.2.1]. In particular, if
$\mathcal {F}$
on a rigid space X is overconvergent [Reference Huber31, Def. 8.2.1]. In particular, if
![]() $X_0 = X\times _{\operatorname {\mathrm {Spa}}(K,K^+)} \operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
and we let
$X_0 = X\times _{\operatorname {\mathrm {Spa}}(K,K^+)} \operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
and we let
![]() $i\colon X_0 \rightarrow X$
denote the induced inclusion, we have
$i\colon X_0 \rightarrow X$
denote the induced inclusion, we have
![]() $i_*i^*\mathcal {F} = \mathcal {F}$
. Moreover, the maps
$i_*i^*\mathcal {F} = \mathcal {F}$
. Moreover, the maps
![]() $i_*$
and
$i_*$
and
![]() $i^*$
are immediately seen to define an equivalence of categories between the respective categories of Zariski-constructible sheaves. This allows us to transport to our setup many results from [Reference Hansen21] and [Reference Bhatt and Hansen4], where there is a standing assumption that
$i^*$
are immediately seen to define an equivalence of categories between the respective categories of Zariski-constructible sheaves. This allows us to transport to our setup many results from [Reference Hansen21] and [Reference Bhatt and Hansen4], where there is a standing assumption that
![]() $K^+=\mathcal {O}_K$
.
$K^+=\mathcal {O}_K$
.
Theorem 2.12 [Reference Bhatt and Hansen4, Thm. 3.10, Thm. 3.15]
Let
![]() $\pi \colon X \rightarrow S$
be a proper map of rigid spaces over K. Let
$\pi \colon X \rightarrow S$
be a proper map of rigid spaces over K. Let
![]() $\mathcal {F}$
be an ind-Zariski-constructible abelian sheaf on
$\mathcal {F}$
be an ind-Zariski-constructible abelian sheaf on
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}$
. Fix any
$X_{\operatorname {\mathrm {\acute {e}t}}}$
. Fix any
![]() $n\geq 0$
.
$n\geq 0$
.
-
1. The sheaf
 $R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {F}$
is an ind-Zariski-constructible sheaf on
$R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {F}$
is an ind-Zariski-constructible sheaf on
 $S_{\operatorname {\mathrm {\acute {e}t}}}$
. It is Zariski-constructible if
$S_{\operatorname {\mathrm {\acute {e}t}}}$
. It is Zariski-constructible if
 $\mathcal {F}$
is.
$\mathcal {F}$
is. -
2. Let
 $Y\rightarrow S$
be any morphism from a rigid space over K and form the pullback diagram
$Y\rightarrow S$
be any morphism from a rigid space over K and form the pullback diagram 
Then we have a natural isomorphism of sheaves on
 $Y_{\operatorname {\mathrm {\acute {e}t}}}$
$Y_{\operatorname {\mathrm {\acute {e}t}}}$
 $$\begin{align*}g^*R^n\pi_{\operatorname{\mathrm{\acute{e}t}},*}\mathcal{F} \cong R^n\pi^{\prime}_{\operatorname{\mathrm{\acute{e}t}},*}(g^{\prime*}\mathcal{F}). \end{align*}$$
$$\begin{align*}g^*R^n\pi_{\operatorname{\mathrm{\acute{e}t}},*}\mathcal{F} \cong R^n\pi^{\prime}_{\operatorname{\mathrm{\acute{e}t}},*}(g^{\prime*}\mathcal{F}). \end{align*}$$
Proof. Let us write
![]() $\mathcal {F} = \varinjlim _{i\in I} \mathcal {F}_i$
where I is cofiltered and the
$\mathcal {F} = \varinjlim _{i\in I} \mathcal {F}_i$
where I is cofiltered and the
![]() $\mathcal {F}_i$
are Zariski-constructible. As
$\mathcal {F}_i$
are Zariski-constructible. As
![]() $\pi \colon X \rightarrow S$
is qcqs, we have, by [48, Tag 0739]
$\pi \colon X \rightarrow S$
is qcqs, we have, by [48, Tag 0739]
From this, we reduce to the case where
![]() $\mathcal {F} = \mathcal {F}_i$
is Zariski-constructible. Let
$\mathcal {F} = \mathcal {F}_i$
is Zariski-constructible. Let
![]() $X_0,S_0,Y_0$
denote the respective base change along
$X_0,S_0,Y_0$
denote the respective base change along
![]() $\operatorname {\mathrm {Spa}}(K,\mathcal {O}_K) \rightarrow \operatorname {\mathrm {Spa}}(K,K^+)$
. By [Reference Huber31, Prop. 8.2.3(ii)], the sheaves
$\operatorname {\mathrm {Spa}}(K,\mathcal {O}_K) \rightarrow \operatorname {\mathrm {Spa}}(K,K^+)$
. By [Reference Huber31, Prop. 8.2.3(ii)], the sheaves
![]() $R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {F}$
are overconvergent. Furthermore, their formations are easily seen to commute with base change along
$R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {F}$
are overconvergent. Furthermore, their formations are easily seen to commute with base change along
![]() $S_0 \subseteq S$
. Hence, we may assume that
$S_0 \subseteq S$
. Hence, we may assume that
![]() $K^+=\mathcal {O}_K$
, in which case this is [Reference Bhatt and Hansen4, Thm. 3.10, Thm. 3.15].
$K^+=\mathcal {O}_K$
, in which case this is [Reference Bhatt and Hansen4, Thm. 3.10, Thm. 3.15].
2.4 Locally p-divisible groups
We now introduce locally p-divisible groups, which will be the central objects of focus of this paper. At the same time, we will recall some facts about smooth relative adic groups, logarithms and exponentials that we will need throughout. We fix an adic space X over
![]() $\mathbb {Q}_p$
that is either a sousperfectoid space or a rigid space over some nonarchimedean field
$\mathbb {Q}_p$
that is either a sousperfectoid space or a rigid space over some nonarchimedean field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Definition 2.13. A smooth relative group over X is a group object
![]() $\mathcal {G} \rightarrow X$
in the category of adic spaces smooth over X.
$\mathcal {G} \rightarrow X$
in the category of adic spaces smooth over X.
Example 2.14.
-
1. Let G be a rigid group over a nonarchimedean field K. Then G is smooth by [Reference Fargues14, Prop. 1]. Whenever X lives over K, the product
 defines a smooth relative group over X. We may for example take
defines a smooth relative group over X. We may for example take
 $G=\mathbb {G}_a$
,
$G=\mathbb {G}_a$
,
 $\mathbb {G}_m$
, or
$\mathbb {G}_m$
, or  the closed unit ball. We will sometimes write G for
the closed unit ball. We will sometimes write G for
 $G_X$
, as it will be clear from context which base we are considering. We refer to [Reference Fargues14] and [Reference Heuer24] for more background on rigid groups.
$G_X$
, as it will be clear from context which base we are considering. We refer to [Reference Fargues14] and [Reference Heuer24] for more background on rigid groups. -
2. Let V be a finite dimensional K-vector space, then we have the smooth adic group
 $V \otimes _K \mathbb {G}_a$
. We call a relative group of this form a vector group. More generally, if E is a finite locally free
$V \otimes _K \mathbb {G}_a$
. We call a relative group of this form a vector group. More generally, if E is a finite locally free
 $\mathcal {O}_X$
-module, the corresponding vector bundle
$\mathcal {O}_X$
-module, the corresponding vector bundle
 $E \otimes _{\mathcal {O}_X} \mathbb {G}_a$
is a smooth relative group over X.
$E \otimes _{\mathcal {O}_X} \mathbb {G}_a$
is a smooth relative group over X. -
3. Let
 $\mathcal {G}^{\operatorname {\mathrm {alg}}}$
be a smooth group scheme over a finite type K-scheme
$\mathcal {G}^{\operatorname {\mathrm {alg}}}$
be a smooth group scheme over a finite type K-scheme
 $X^{\operatorname {\mathrm {alg}}}$
. Then its analytification
$X^{\operatorname {\mathrm {alg}}}$
. Then its analytification
 $(\mathcal {G} \rightarrow X) = (\mathcal {G}^{\operatorname {\mathrm {alg}}} \rightarrow X^{\operatorname {\mathrm {alg}}})^{\operatorname {\mathrm {an}}}$
is a smooth relative group.
$(\mathcal {G} \rightarrow X) = (\mathcal {G}^{\operatorname {\mathrm {alg}}} \rightarrow X^{\operatorname {\mathrm {alg}}})^{\operatorname {\mathrm {an}}}$
is a smooth relative group. -
4. Assume that X is a rigid space over K and let
 ${\mathfrak {X}}$
be an admissible formal scheme over
${\mathfrak {X}}$
be an admissible formal scheme over
 $\operatorname {\mathrm {Spf}}(K^+)$
with adic generic fiber X. Let
$\operatorname {\mathrm {Spf}}(K^+)$
with adic generic fiber X. Let
 $\mathfrak {S}$
be a smooth formal group scheme over
$\mathfrak {S}$
be a smooth formal group scheme over
 ${\mathfrak {X}}$
, then its adic generic fiber
${\mathfrak {X}}$
, then its adic generic fiber
 $\mathfrak {S}_{\eta }$
is a smooth relative group over X. A smooth X-group is said to have good reduction if it is of this form.
$\mathfrak {S}_{\eta }$
is a smooth relative group over X. A smooth X-group is said to have good reduction if it is of this form.
Definition 2.15. Given a smooth relative group
![]() $\mathcal {G} \rightarrow X$
with identity section
$\mathcal {G} \rightarrow X$
with identity section
![]() $e\colon X \rightarrow \mathcal {G}$
, its Lie algebra is defined to be
$e\colon X \rightarrow \mathcal {G}$
, its Lie algebra is defined to be
It is a finite-dimensional locally free
![]() $\mathcal {O}_X$
-module and we let
$\mathcal {O}_X$
-module and we let
denote the underlying geometric vector bundle.
We now move to logarithms. Given a commutative rigid group G, Fargues [Reference Fargues14, Théorème 1.2] defines the subgroup
![]() $\widehat {G}$
of p-topological torsion of G and shows that it is the domain of a logarithm map, functorially associated with G. These definitions were later recast by Heuer in terms of v-sheaves [Reference Heuer25, Def. 2.6] and generalized by Heuer–Xu to relative groups [Reference Heuer and Xu33, §3].
$\widehat {G}$
of p-topological torsion of G and shows that it is the domain of a logarithm map, functorially associated with G. These definitions were later recast by Heuer in terms of v-sheaves [Reference Heuer25, Def. 2.6] and generalized by Heuer–Xu to relative groups [Reference Heuer and Xu33, §3].
Definition 2.16 [Reference Heuer25, Def. 2.6]
Let
![]() $\mathcal {F}$
be an abelian sheaf on
$\mathcal {F}$
be an abelian sheaf on
![]() $X_v$
. The p-topological torsion subsheaf
$X_v$
. The p-topological torsion subsheaf
![]() $\widehat {\mathcal {F}} \subseteq \mathcal {F}$
is defined to be the image as sheaves on
$\widehat {\mathcal {F}} \subseteq \mathcal {F}$
is defined to be the image as sheaves on
![]() $X_v$
of the map
$X_v$
of the map
where
![]() $\underline {\mathbb {Z}_p}$
denotes the profinite sheaf
$\underline {\mathbb {Z}_p}$
denotes the profinite sheaf
![]() $\varprojlim _n \, \underline {\mathbb {Z}/p^n}$
.
$\varprojlim _n \, \underline {\mathbb {Z}/p^n}$
.
Lemma 2.17 [Reference Heuer and Xu33, Prop. 3.2.4]
Let
![]() $\mathcal {G} \rightarrow X$
be a commutative smooth relative group.
$\mathcal {G} \rightarrow X$
be a commutative smooth relative group.
-
1. The v-sheaf
 $\widehat {\mathcal {G}}$
is representable by an open subgroup of
$\widehat {\mathcal {G}}$
is representable by an open subgroup of
 $\mathcal {G}$
and evaluation at
$\mathcal {G}$
and evaluation at
 $1$
defines an isomorphism of v-sheaves
$1$
defines an isomorphism of v-sheaves  $$\begin{align*}\underline{\operatorname{\mathrm{Hom}}}(\underline{\mathbb{Z}_p},\mathcal{G}) \xrightarrow{\cong} \widehat{\mathcal{G}}. \end{align*}$$
$$\begin{align*}\underline{\operatorname{\mathrm{Hom}}}(\underline{\mathbb{Z}_p},\mathcal{G}) \xrightarrow{\cong} \widehat{\mathcal{G}}. \end{align*}$$
-
2. There is a unique homomorphism of adic groups
whose derivative is $$\begin{align*}\log_{\mathcal{G}}\colon \widehat{\mathcal{G}} \rightarrow {\mathfrak{g}}\end{align*}$$
$$\begin{align*}\log_{\mathcal{G}}\colon \widehat{\mathcal{G}} \rightarrow {\mathfrak{g}}\end{align*}$$
 $D(\log _{\mathcal {G}}) = \operatorname {\mathrm {id}}\colon \operatorname {\mathrm {Lie}}(\mathcal {G})\rightarrow \operatorname {\mathrm {Lie}}(\mathcal {G})$
. The map
$D(\log _{\mathcal {G}}) = \operatorname {\mathrm {id}}\colon \operatorname {\mathrm {Lie}}(\mathcal {G})\rightarrow \operatorname {\mathrm {Lie}}(\mathcal {G})$
. The map
 $\log _{\mathcal {G}}$
is natural in
$\log _{\mathcal {G}}$
is natural in
 $\mathcal {G}$
and fits in an exact sequence of smooth X-groups (2.2)
$\mathcal {G}$
and fits in an exact sequence of smooth X-groups (2.2)
-
3. If
 $[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is étale, so is
$[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is étale, so is
 $\log _{\mathcal {G}}$
.
$\log _{\mathcal {G}}$
.
Remark 2.18. When X is a smooth rigid space,
![]() $[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is automatically étale by [Reference Heuer and Xu33, Lemma 3.2.2].
$[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is automatically étale by [Reference Heuer and Xu33, Lemma 3.2.2].
Definition 2.19. Let
![]() $\mathcal {G} \rightarrow X$
be a smooth commutative group. We define the sheaf
$\mathcal {G} \rightarrow X$
be a smooth commutative group. We define the sheaf
![]() $\overline {\mathcal {G}}$
on
$\overline {\mathcal {G}}$
on
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
to be the quotient sheaf
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
to be the quotient sheaf
Remark 2.20. As we will see later in Proposition 3.12,
![]() $\overline {\mathcal {G}}$
is a v-sheaf, such that we get the same result if we compute the quotient in the category of v-sheaves instead.
$\overline {\mathcal {G}}$
is a v-sheaf, such that we get the same result if we compute the quotient in the category of v-sheaves instead.
We now introduce a relative variant of the locally p-divisible rigid groups of [Reference Heuer, Werner and Zhang32, §6].
Definition 2.21. Let
![]() $\mathcal {G}$
be a commutative smooth X-group.
$\mathcal {G}$
be a commutative smooth X-group.
-
1. We say that
 $\mathcal {G}$
is an analytic p-divisible X-group if
$\mathcal {G}$
is an analytic p-divisible X-group if
 $\mathcal {G}=\widehat {\mathcal {G}}$
and
$\mathcal {G}=\widehat {\mathcal {G}}$
and
 $[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is finite étale and surjective ([Reference Fargues15, Def. 4.1]).
$[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is finite étale and surjective ([Reference Fargues15, Def. 4.1]). -
2. We say that
 $\mathcal {G}$
is a locally p-divisible X-group if
$\mathcal {G}$
is a locally p-divisible X-group if
 $\log _{\mathcal {G}}\colon \widehat {\mathcal {G}} \rightarrow {\mathfrak {g}}$
is étale and surjective.
$\log _{\mathcal {G}}\colon \widehat {\mathcal {G}} \rightarrow {\mathfrak {g}}$
is étale and surjective.
Example 2.22.
-
1. Any analytic p-divisible group (e.g., a vector bundle) is locally p-divisible [Reference Fargues15, §4].
-
2. Let G be a (locally) p-divisible rigid group over K, then
 $G_X$
is a (locally) p-divisible X-group. Examples of locally p-divisible rigid groups include
$G_X$
is a (locally) p-divisible X-group. Examples of locally p-divisible rigid groups include
 $G=\mathbb {G}_a$
,
$G=\mathbb {G}_a$
,
 $\mathbb {G}_m$
, or more generally all commutative connected algebraic groups G over K [Reference Heuer, Werner and Zhang32, Example 6.9].
$\mathbb {G}_m$
, or more generally all commutative connected algebraic groups G over K [Reference Heuer, Werner and Zhang32, Example 6.9]. -
3. If
 $\mathcal {G}$
contains an open subgroup
$\mathcal {G}$
contains an open subgroup
 $U\subseteq \mathcal {G}$
with
$U\subseteq \mathcal {G}$
with
 $[p]\colon U \rightarrow U$
étale surjective, then
$[p]\colon U \rightarrow U$
étale surjective, then
 $\mathcal {G}$
is locally p-divisible [Reference Heuer and Xu33, Prop. 3.2.4(3)]. If
$\mathcal {G}$
is locally p-divisible [Reference Heuer and Xu33, Prop. 3.2.4(3)]. If
 $X=\operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
for algebraically closed K, the converse is true [Reference Heuer, Werner and Zhang32, Prop. 6.10].
$X=\operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
for algebraically closed K, the converse is true [Reference Heuer, Werner and Zhang32, Prop. 6.10]. -
4. Let X be a rigid space and
 $\mathcal {A} \rightarrow X$
be a relative abeloid variety, that is, a proper smooth commutative X-group with geometrically connected fibers. Then
$\mathcal {A} \rightarrow X$
be a relative abeloid variety, that is, a proper smooth commutative X-group with geometrically connected fibers. Then
 $[p]\colon \mathcal {A} \rightarrow \mathcal {A}$
is surjective, such that
$[p]\colon \mathcal {A} \rightarrow \mathcal {A}$
is surjective, such that
 $\mathcal {A}$
is locally p-divisible, by the previous point.
$\mathcal {A}$
is locally p-divisible, by the previous point. -
5. Let
 $\mathcal {G} \rightarrow X$
denote the analytification of a smooth commutative group scheme
$\mathcal {G} \rightarrow X$
denote the analytification of a smooth commutative group scheme
 $\mathcal {G}^{\operatorname {\mathrm {alg}}} \rightarrow X^{\operatorname {\mathrm {alg}}}$
where
$\mathcal {G}^{\operatorname {\mathrm {alg}}} \rightarrow X^{\operatorname {\mathrm {alg}}}$
where
 $X^{\operatorname {\mathrm {alg}}}$
is an algebraic variety over K. Then
$X^{\operatorname {\mathrm {alg}}}$
is an algebraic variety over K. Then
 $\mathcal {G}$
is locally p-divisible [Reference Heuer and Xu33, Lemma 3.2.6].
$\mathcal {G}$
is locally p-divisible [Reference Heuer and Xu33, Lemma 3.2.6].
We will restrict to the locally p-divisible groups satisfying a minor technical assumption.
Definition 2.23. Let
![]() $\mathcal {G} \rightarrow X$
be a locally p-divisible X-group.
$\mathcal {G} \rightarrow X$
be a locally p-divisible X-group.
-
1. If X is a rigid space, the group
 $\mathcal {G}$
is said to be admissible if
$\mathcal {G}$
is said to be admissible if
 $\mathcal {G}[p^{\infty }]$
is ind-Zariski-constructible.
$\mathcal {G}[p^{\infty }]$
is ind-Zariski-constructible. -
2. If X is a sousperfectoid space, the group
 $\mathcal {G}$
is admissible if it arises as the pullback of an admissible locally p-divisible group
$\mathcal {G}$
is admissible if it arises as the pullback of an admissible locally p-divisible group
 $\mathcal {G}' \rightarrow X'$
along a map
$\mathcal {G}' \rightarrow X'$
along a map
 $X\rightarrow X'$
, where
$X\rightarrow X'$
, where
 $X'$
is a rigid space.
$X'$
is a rigid space.
By
![]() $\mathcal {G}[p^{\infty }]$
being ind-Zariski-constructible, we mean that there exists an ind-Zariski-constructible sheaf
$\mathcal {G}[p^{\infty }]$
being ind-Zariski-constructible, we mean that there exists an ind-Zariski-constructible sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}$
such that
$X_{\operatorname {\mathrm {\acute {e}t}}}$
such that
![]() $\mathcal {G}[p^{\infty }] = \nu ^*\mathcal {F}$
, where
$\mathcal {G}[p^{\infty }] = \nu ^*\mathcal {F}$
, where
![]() $\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
is the natural map of sites. There is no meaningful notion of Zariski-constructible sheaves on general sousperfectoid spaces, which is the reason for this roundabout definition. We will be mainly interested in the case where the base X is a rigid space, but even so, some proofs will require to consider groups
$\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
is the natural map of sites. There is no meaningful notion of Zariski-constructible sheaves on general sousperfectoid spaces, which is the reason for this roundabout definition. We will be mainly interested in the case where the base X is a rigid space, but even so, some proofs will require to consider groups
![]() $\mathcal {G}$
over bases of the shape
$\mathcal {G}$
over bases of the shape
![]() $X\times _S Y$
, where
$X\times _S Y$
, where
![]() $X\rightarrow S$
is a smooth morphism of rigid spaces and Y is a perfectoid space over S.
$X\rightarrow S$
is a smooth morphism of rigid spaces and Y is a perfectoid space over S.
All locally p-divisible groups appearing in Example 2.22 except
![]() $(3)$
are admissibleFootnote
1
. One more important example is the following. By
$(3)$
are admissibleFootnote
1
. One more important example is the following. By
![]() $\operatorname {\mathrm {Sm}}_{/X, \operatorname {\mathrm {\acute {e}t}}}$
, we denote the site of all rigid spaces smooth over X, endowed with the étale topology.
$\operatorname {\mathrm {Sm}}_{/X, \operatorname {\mathrm {\acute {e}t}}}$
, we denote the site of all rigid spaces smooth over X, endowed with the étale topology.
Lemma 2.24. Let X be a smooth rigid space and let B be a finite locally free commutative
![]() $\mathcal {O}_X$
-algebra. Then the sheaf
$\mathcal {O}_X$
-algebra. Then the sheaf
is represented by an admissible locally p-divisible X-group.
Remark 2.25. This is the prime example of a locally p-divisible group
![]() $\mathcal {G}$
where the torsion subgroups
$\mathcal {G}$
where the torsion subgroups
![]() $\mathcal {G}[p^m]$
need not be finite étale over X, and which motivates the generality in Definition 2.23.
$\mathcal {G}[p^m]$
need not be finite étale over X, and which motivates the generality in Definition 2.23.
Proof. Let
![]() $\mathbb {B} \rightarrow X$
denote the vector bundle underlying the locally free sheaf B. The norm map
$\mathbb {B} \rightarrow X$
denote the vector bundle underlying the locally free sheaf B. The norm map
![]() $\operatorname {\mathrm {Nr}}\colon B \rightarrow \mathcal {O}_X$
induces a map of X-spaces
$\operatorname {\mathrm {Nr}}\colon B \rightarrow \mathcal {O}_X$
induces a map of X-spaces
![]() $N\colon \mathbb {B} \rightarrow \mathbb {G}_{a,X}$
and
$N\colon \mathbb {B} \rightarrow \mathbb {G}_{a,X}$
and
![]() $B^{\times }$
is easily seen to be represented by the open subspace
$B^{\times }$
is easily seen to be represented by the open subspace
![]() $N^{-1}(\mathbb {G}_{m,X})$
. Let
$N^{-1}(\mathbb {G}_{m,X})$
. Let
![]() $f\colon X' \rightarrow X$
denote the finite flat morphism associated with B. It is clear that
$f\colon X' \rightarrow X$
denote the finite flat morphism associated with B. It is clear that
where
is the natural map of sites. By Theorem 2.12.1,
![]() $B^{\times }[p^m] = f_{\operatorname {\mathrm {\acute {E}t}},*}^{\operatorname {\mathrm {rig}}}\mu _{p^m}$
is Zariski-constructible. Moreover,
$B^{\times }[p^m] = f_{\operatorname {\mathrm {\acute {E}t}},*}^{\operatorname {\mathrm {rig}}}\mu _{p^m}$
is Zariski-constructible. Moreover,
![]() $f_{\operatorname {\mathrm {\acute {E}t}},*}^{\operatorname {\mathrm {rig}}}$
is exact, by [Reference Huber31, Cor. 2.6.6], such that
$f_{\operatorname {\mathrm {\acute {E}t}},*}^{\operatorname {\mathrm {rig}}}$
is exact, by [Reference Huber31, Cor. 2.6.6], such that
It follows that
![]() $[p]\colon B^{\times } \rightarrow B^{\times }$
is surjective, and it is also étale by Remark 2.18. In particular
$[p]\colon B^{\times } \rightarrow B^{\times }$
is surjective, and it is also étale by Remark 2.18. In particular
![]() $B^{\times }$
is locally p-divisible, as required.
$B^{\times }$
is locally p-divisible, as required.
We will occasionally use the p-adic exponential, which converges on an open subgroup of the Lie algebra and defines a natural section of the logarithm.
Lemma 2.26. Let X be a qcqs rigid space over
![]() $(K,\mathcal {O}_K)$
and let
$(K,\mathcal {O}_K)$
and let
![]() $\mathcal {G}$
be a commutative smooth X-group. Then there exists an open
$\mathcal {G}$
be a commutative smooth X-group. Then there exists an open
![]() $\mathcal {O}_X^+$
-subvector bundle
$\mathcal {O}_X^+$
-subvector bundle
![]() ${\mathfrak {g}}^{\circ } \subseteq {\mathfrak {g}}$
and an open embedding of X-groups
${\mathfrak {g}}^{\circ } \subseteq {\mathfrak {g}}$
and an open embedding of X-groups
that is a section of the logarithm
![]() $\log _{\mathcal {G}}$
. The exponential is functorial in
$\log _{\mathcal {G}}$
. The exponential is functorial in
![]() $\mathcal {G}$
(i.e., the obvious diagram commutes after shrinking
$\mathcal {G}$
(i.e., the obvious diagram commutes after shrinking
![]() ${\mathfrak {g}}^{\circ }$
).
${\mathfrak {g}}^{\circ }$
).
Remark 2.27. The lemma stays valid if X is any quasi-compact rigid space over
![]() $(K,K^+)$
or sousperfectoid space, assuming that the Lie algebra
$(K,K^+)$
or sousperfectoid space, assuming that the Lie algebra
![]() ${\mathfrak {g}}$
comes from an
${\mathfrak {g}}$
comes from an
![]() $\mathcal {O}_X^+$
-vector bundle, for example, if
$\mathcal {O}_X^+$
-vector bundle, for example, if
![]() ${\mathfrak {g}}$
is trivial.
${\mathfrak {g}}$
is trivial.
Proof. We start by showing that there exists a finite locally free
![]() $\mathcal {O}_X^+$
-submodule
$\mathcal {O}_X^+$
-submodule
![]() $E \subseteq \operatorname {\mathrm {Lie}}(\mathcal {G})$
such that
$E \subseteq \operatorname {\mathrm {Lie}}(\mathcal {G})$
such that
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G}) = E[\frac {1}{p}]$
. For this, we view X as a coherent rigid space in the sense of [Reference Abbes1, Def. 4.1.6] and thus we find a formal model
$\operatorname {\mathrm {Lie}}(\mathcal {G}) = E[\frac {1}{p}]$
. For this, we view X as a coherent rigid space in the sense of [Reference Abbes1, Def. 4.1.6] and thus we find a formal model
![]() ${\mathfrak {X}}$
of X topologically of finite presentation over
${\mathfrak {X}}$
of X topologically of finite presentation over
![]() $\operatorname {\mathrm {Spf}}(\mathcal {O}_K)$
. By [Reference Abbes1, Thm. 4.8.18.(ii)], the
$\operatorname {\mathrm {Spf}}(\mathcal {O}_K)$
. By [Reference Abbes1, Thm. 4.8.18.(ii)], the
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G})$
admits a coherent formal model
$\operatorname {\mathrm {Lie}}(\mathcal {G})$
admits a coherent formal model
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() ${\mathfrak {X}}$
. By Raynaud–Gruson’s flattening, see [Reference Abbes1, Thm. 5.8.1], up to replacing
${\mathfrak {X}}$
. By Raynaud–Gruson’s flattening, see [Reference Abbes1, Thm. 5.8.1], up to replacing
![]() ${\mathfrak {X}}$
by an admissible formal blowup, we may assume that
${\mathfrak {X}}$
by an admissible formal blowup, we may assume that
![]() $\mathcal {F}$
is locally free. Then
$\mathcal {F}$
is locally free. Then
![]() $E =\mathcal {F} \otimes _{\mathcal {O}_{{\mathfrak {X}}}} \mathcal {O}_X^+$
is as required.
$E =\mathcal {F} \otimes _{\mathcal {O}_{{\mathfrak {X}}}} \mathcal {O}_X^+$
is as required.
Next, we consider the induced open subgroup
By [Reference Heuer and Xu33, Prop. 3.2.1], we can find an open cover of X by affinoid opens
![]() $X_i \subseteq X$
and open subgroups
$X_i \subseteq X$
and open subgroups
![]() $V_i \subseteq {\mathfrak {g}}_{X_i}$
such that the logarithm restricts to an isomorphism
$V_i \subseteq {\mathfrak {g}}_{X_i}$
such that the logarithm restricts to an isomorphism
![]() $\log _{\mathcal {G}}^{-1}(V_i) \xrightarrow {\cong } V_i$
. By [Reference Heuer and Xu33, Lemma 3.1.2], there exists integers
$\log _{\mathcal {G}}^{-1}(V_i) \xrightarrow {\cong } V_i$
. By [Reference Heuer and Xu33, Lemma 3.1.2], there exists integers
![]() $n_i\geq 0$
such that
$n_i\geq 0$
such that
![]() $p^{n_i}{\mathfrak {h}}_{X_i} \subseteq V_i$
for each i. As X is quasi-compact, we can replace the open cover
$p^{n_i}{\mathfrak {h}}_{X_i} \subseteq V_i$
for each i. As X is quasi-compact, we can replace the open cover
![]() $\{X_i\}_i$
by a finite subcover, and we find that
$\{X_i\}_i$
by a finite subcover, and we find that ![]() is as required, for
is as required, for
![]() $n \gg 0$
.
$n \gg 0$
.
We now fix a nonarchimedean field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
. We recall from [Reference Heuer, Werner and Zhang32, §6] how a choice of exponential for K induces a compatible system of exponentials on K-rational points for admissible locally p-divisible rigid groups G.
$\mathbb {Q}_p$
. We recall from [Reference Heuer, Werner and Zhang32, §6] how a choice of exponential for K induces a compatible system of exponentials on K-rational points for admissible locally p-divisible rigid groups G.
Definition 2.28. An exponential for K is a continuous group morphism
extending the usual analytic exponential function and splitting the logarithm map
![]() $\log \colon 1+{\mathfrak {m}} \rightarrow K$
.
$\log \colon 1+{\mathfrak {m}} \rightarrow K$
.
Exponentials for K exist as soon as K is algebraically closed [Reference Heuer, Werner and Zhang32, Lemma 6.2].
Proposition 2.29. Let K be an algebraically closed complete extension of
![]() $\mathbb {Q}_p$
and let G be an admissible locally p-divisible rigid group over K. Then a choice of exponential
$\mathbb {Q}_p$
and let G be an admissible locally p-divisible rigid group over K. Then a choice of exponential
![]() $\operatorname {\mathrm {Exp}}$
for K induces a continuous section
$\operatorname {\mathrm {Exp}}$
for K induces a continuous section
to the logarithm map
![]() $\log _G$
on K-points. For fixed
$\log _G$
on K-points. For fixed
![]() $\operatorname {\mathrm {Exp}}$
, the map
$\operatorname {\mathrm {Exp}}$
, the map
![]() $\operatorname {\mathrm {Exp}}_G$
is natural in G.
$\operatorname {\mathrm {Exp}}_G$
is natural in G.
Proof. Let
![]() $G'= G \times _{\operatorname {\mathrm {Spa}}(K,K^+)}\operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
be the associated locally p-divisible group over
$G'= G \times _{\operatorname {\mathrm {Spa}}(K,K^+)}\operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
be the associated locally p-divisible group over
![]() $(K,\mathcal {O}_K)$
. By [Reference Heuer, Werner and Zhang32, Thm. 6.12], we get an exponential, functorial in
$(K,\mathcal {O}_K)$
. By [Reference Heuer, Werner and Zhang32, Thm. 6.12], we get an exponential, functorial in
![]() $G'$
$G'$
It remains to show that
![]() $\widehat {G}(K,\mathcal {O}_K) = \widehat {G}(K,K^+)$
. By the logarithm sequence (2.2), it is enough to show that
$\widehat {G}(K,\mathcal {O}_K) = \widehat {G}(K,K^+)$
. By the logarithm sequence (2.2), it is enough to show that
![]() $G[p^{\infty }](K,\mathcal {O}_K) = G[p^{\infty }](K,K^+)$
. This follows from the fact that
$G[p^{\infty }](K,\mathcal {O}_K) = G[p^{\infty }](K,K^+)$
. This follows from the fact that
![]() $G[p^{\infty }]$
is ind-Zariski-constructible and hence overconvergent, by Remark 2.11.
$G[p^{\infty }]$
is ind-Zariski-constructible and hence overconvergent, by Remark 2.11.
3 Hodge–Tate spectral sequences
With these preparations, we are now ready to define and study the Hodge–Tate spectral sequences with locally p-divisible coefficients and their geometric counterparts.
3.1 The group theoretic spectral sequence
We fix a perfectoid field extension
![]() $(K,K^+)$
of
$(K,K^+)$
of
![]() $\mathbb {Q}_p$
. Let X be a smoothoid space over K (cf. §2.2).
$\mathbb {Q}_p$
. Let X be a smoothoid space over K (cf. §2.2).
Definition 3.1. Let
![]() $\mathcal {G}$
be a commutative smooth X-group, viewed as a v-sheaf on X. We define the Hodge–Tate spectral sequence with
$\mathcal {G}$
be a commutative smooth X-group, viewed as a v-sheaf on X. We define the Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients to be the Leray spectral sequence associated to
$\mathcal {G}$
-coefficients to be the Leray spectral sequence associated to
![]() $\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
$\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
Remark 3.2. When
![]() $\mathcal {G}=\mathbb {G}_a$
and X is a smooth rigid space, this recovers the Hodge–Tate spectral sequence [Reference Scholze45, Thm. 3.20].
$\mathcal {G}=\mathbb {G}_a$
and X is a smooth rigid space, this recovers the Hodge–Tate spectral sequence [Reference Scholze45, Thm. 3.20].
We have the following result, generalizing the commutative case of [Reference Heuer27, Thm. 4.1]. We delay the proof to the next section.
Proposition 3.3. Let X be a smoothoid space over K and let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group. Then
$\mathcal {G}$
be an admissible locally p-divisible X-group. Then
![]() $\nu _*\mathcal {G} = \mathcal {G}$
and we have for each
$\nu _*\mathcal {G} = \mathcal {G}$
and we have for each
![]() $j>0$
a canonical isomorphism of sheaves on
$j>0$
a canonical isomorphism of sheaves on
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}$
, natural in X and
$X_{\operatorname {\mathrm {\acute {e}t}}}$
, natural in X and
![]() $\mathcal {G}$
$\mathcal {G}$
Using Proposition 3.3, the Hodge–Tate spectral sequence takes the following form
 $$ \begin{align} E_2^{ij}(\mathcal{G})= \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\widetilde{\Omega}_X^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\mathcal{G}) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_{v}^{i+j}(X,\mathcal{G}). \end{align} $$
$$ \begin{align} E_2^{ij}(\mathcal{G})= \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\widetilde{\Omega}_X^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\mathcal{G}) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_{v}^{i+j}(X,\mathcal{G}). \end{align} $$
We will prove later in Corollary 3.30 that the Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients degenerates in the proper smooth case. For now, we treat the case where
$\mathcal {G}$
-coefficients degenerates in the proper smooth case. For now, we treat the case where
![]() $\mathcal {G}={\mathfrak {g}}$
is a vector bundle, in which case it essentially follows from the case
$\mathcal {G}={\mathfrak {g}}$
is a vector bundle, in which case it essentially follows from the case
![]() $\mathcal {G}=\mathbb {G}_a$
and is due to Scholze [Reference Scholze45, Thm. 3.20] and Bhatt–Morrow–Scholze [Reference Bhatt, Morrow and Scholze7, Thm. 13.3.(ii)].
$\mathcal {G}=\mathbb {G}_a$
and is due to Scholze [Reference Scholze45, Thm. 3.20] and Bhatt–Morrow–Scholze [Reference Bhatt, Morrow and Scholze7, Thm. 13.3.(ii)].
Proposition 3.4. Let X be a proper smooth rigid space and E a finite locally free
![]() $\mathcal {O}_X$
-module. Then the Hodge–Tate spectral sequence
$\mathcal {O}_X$
-module. Then the Hodge–Tate spectral sequence
degenerates at
![]() $E_2$
. If K is algebraically closed, a
$E_2$
. If K is algebraically closed, a
![]() ${\mathrm {B_{dR}^+}} /\xi ^2$
-lift
${\mathrm {B_{dR}^+}} /\xi ^2$
-lift
![]() $\mathbb {X}$
of X induces a splitting of the spectral sequence and hence a decomposition, natural in
$\mathbb {X}$
of X induces a splitting of the spectral sequence and hence a decomposition, natural in
![]() $\mathbb {X}$
$\mathbb {X}$
 $$\begin{align*}H_v^n(X,E) = \bigoplus_{i=0}^{n}H^i(X,\widetilde{\Omega}_X^{n-i} \otimes_{\mathcal{O}_X} E).\end{align*}$$
$$\begin{align*}H_v^n(X,E) = \bigoplus_{i=0}^{n}H^i(X,\widetilde{\Omega}_X^{n-i} \otimes_{\mathcal{O}_X} E).\end{align*}$$
Proof. Let C be a completed algebraic closure of K and let
![]() $C^+$
denote the completion of the integral closure of
$C^+$
denote the completion of the integral closure of
![]() $K^+$
in C. We denote by
$K^+$
in C. We denote by
![]() $X_C$
(resp.
$X_C$
(resp.
![]() $E_C$
) the base change of X (resp. E) from K to C. By [Reference Heuer28, Cor. 3.10], we have
$E_C$
) the base change of X (resp. E) from K to C. By [Reference Heuer28, Cor. 3.10], we have
As the degeneration can be deduced from a dimension count, we may assume without loss that K is algebraically closed. By the projection formula, we have
Now by [Reference Guo20, Prop. 7.2.5], any lift
![]() $\mathbb {X}$
of X to
$\mathbb {X}$
of X to
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
induces a splitting in the derived category
${\mathrm {B_{dR}^+}}/\xi ^2$
induces a splitting in the derived category
![]() $D(X_{\operatorname {\mathrm {\acute {e}t}}})$
, natural in
$D(X_{\operatorname {\mathrm {\acute {e}t}}})$
, natural in
![]() $\mathbb {X}$
$\mathbb {X}$
There is thus a trivial Cartan–Eilenberg resolution of the complex
![]() $R\nu _*E$
given by
$R\nu _*E$
given by
where
![]() $J_i$
is an injective resolution of
$J_i$
is an injective resolution of
![]() $\widetilde {\Omega }_X^i \otimes E$
in
$\widetilde {\Omega }_X^i \otimes E$
in
![]() $D(X_{\operatorname {\mathrm {\acute {e}t}}})$
. It follows that the Hodge–Tate spectral sequence for E decomposes as the direct sum of the spectral sequence associated to the
$D(X_{\operatorname {\mathrm {\acute {e}t}}})$
. It follows that the Hodge–Tate spectral sequence for E decomposes as the direct sum of the spectral sequence associated to the
![]() $1$
-column bicomplexes
$1$
-column bicomplexes
![]() $J_i^{\bullet }$
, and this decomposition is natural in
$J_i^{\bullet }$
, and this decomposition is natural in
![]() $\mathbb {X}$
. The result follows.
$\mathbb {X}$
. The result follows.
Remark 3.5. For
![]() $E=\mathcal {O}_X$
and algebraically closed K, this recovers the Hodge–Tate decomposition
$E=\mathcal {O}_X$
and algebraically closed K, this recovers the Hodge–Tate decomposition
via Scholze’s Primitive Comparison Theorem [Reference Scholze44, Thm. 5.1].
3.2 Rigid approximation
In this technical section, we prove Proposition 3.3. We will need a technique of approximation by rigid spaces, developed in [Reference Heuer24], that we improve upon. The results of this section will also be used extensively later on.
We first recall the notions of tilde-limits of adic spaces.
Definition 3.6 [Reference Huber31, (2.4.1)], [49, §2.4]
Let
![]() $(Y_i)_{i \in I}$
denote an inverse system of adic spaces with quasi-compact and quasi-separated (in short, qcqs) transition maps and let Y be an adic space together with maps
$(Y_i)_{i \in I}$
denote an inverse system of adic spaces with quasi-compact and quasi-separated (in short, qcqs) transition maps and let Y be an adic space together with maps
![]() $f_i\colon Y\rightarrow Y_i$
compatible with the transition maps. We say that Y is a tilde-limit of the inverse system
$f_i\colon Y\rightarrow Y_i$
compatible with the transition maps. We say that Y is a tilde-limit of the inverse system
![]() $(Y_i)_i$
and we write
$(Y_i)_i$
and we write
if the following conditions are satisfied:
-
1. The induced map
 $\vert Y \vert \rightarrow \varprojlim _i \vert Y_i \vert $
is a homeomorphism, and
$\vert Y \vert \rightarrow \varprojlim _i \vert Y_i \vert $
is a homeomorphism, and -
2. There exists an open cover of Y by affinoids U such that the map
 $\varinjlim \mathcal {O}(U_i) \rightarrow \mathcal {O}(U)$
has dense image, where the direct limit runs over all
$\varinjlim \mathcal {O}(U_i) \rightarrow \mathcal {O}(U)$
has dense image, where the direct limit runs over all
 $i\in I$
and all affinoid opens
$i\in I$
and all affinoid opens
 $U_i \subseteq Y_i$
through which the map
$U_i \subseteq Y_i$
through which the map
 $U \rightarrow Y_i$
factors.
$U \rightarrow Y_i$
factors.
Assume moreover that all
![]() $Y_i$
and Y are affinoid. We write
$Y_i$
and Y are affinoid. We write
if, in addition, already
![]() $\varinjlim _i \mathcal {O}(Y_i) \rightarrow \mathcal {O}(Y)$
has dense image.
$\varinjlim _i \mathcal {O}(Y_i) \rightarrow \mathcal {O}(Y)$
has dense image.
Lemma 3.7. Let
![]() $Y \sim \varprojlim _i Y_i$
and assume that all
$Y \sim \varprojlim _i Y_i$
and assume that all
![]() $Y_i$
and Y are qcqs.
$Y_i$
and Y are qcqs.
-
1. On the level of diamonds, we have
 $$\begin{align*}Y^{\diamondsuit} = \varprojlim_i Y_i^{\diamondsuit}.\end{align*}$$
$$\begin{align*}Y^{\diamondsuit} = \varprojlim_i Y_i^{\diamondsuit}.\end{align*}$$
-
2. For the associated qcqs étale sites, we have

Proof. For the first point, see [Reference Scholze and Weinstein49, Prop. 2.4.5]. The second point then follows from [Reference Scholze47, Prop. 11.23].
Definition 3.8 [Reference Heuer24, Def. 2.13]
Let X be any good adic space over
![]() $\mathbb {Q}_p$
. A sheaf of sets
$\mathbb {Q}_p$
. A sheaf of sets
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
is said to satisfy the approximation property if, for any affinoid perfectoid tilde-limit
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
is said to satisfy the approximation property if, for any affinoid perfectoid tilde-limit
![]() $Y \approx \varprojlim _i Y_i$
of good affinoid adic spaces
$Y \approx \varprojlim _i Y_i$
of good affinoid adic spaces
![]() $Y_i$
over X, we have
$Y_i$
over X, we have
Remark 3.9. A similar condition recently appeared in [Reference Scholze46], where such sheaves are called finitary.
Example 3.10.
-
1. Let
 $\mathcal {F}$
be a sheaf on
$\mathcal {F}$
be a sheaf on
 $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
that arises as the pullback of a sheaf on
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
that arises as the pullback of a sheaf on
 $X_{\operatorname {\mathrm {\acute {e}t}}}$
along the natural map of sites
$X_{\operatorname {\mathrm {\acute {e}t}}}$
along the natural map of sites
 $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}} \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
. Then
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}} \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
. Then
 $\mathcal {F}$
has the approximation property, by adapting the proof of [Reference Scholze47, Prop. 14.9].
$\mathcal {F}$
has the approximation property, by adapting the proof of [Reference Scholze47, Prop. 14.9]. -
2. Let
 $Y \rightarrow X$
be an étale morphism, then Y viewed as a sheaf on
$Y \rightarrow X$
be an étale morphism, then Y viewed as a sheaf on
 $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
has the approximation property. This is a special case of the first point.
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
has the approximation property. This is a special case of the first point. -
3. Let G be a (not necessarily commutative) rigid group over a nonarchimedean field extension K of
 $\mathbb {Q}_p$
, and let
$\mathbb {Q}_p$
, and let
 $U \subseteq G$
be any open subgroup. Then the sheaf of cosets
$U \subseteq G$
be any open subgroup. Then the sheaf of cosets
 $G/U$
on
$G/U$
on
 $\operatorname {\mathrm {Adic}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
has the approximation property, by [Reference Heuer24, Prop. 4.1]. We generalize this in Proposition 3.12 below.
$\operatorname {\mathrm {Adic}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
has the approximation property, by [Reference Heuer24, Prop. 4.1]. We generalize this in Proposition 3.12 below.
The decisive property satisfied by sheaves with the approximating property is the following.
Proposition 3.11. Let X be a good adic space over
![]() $\mathbb {Q}_p$
and let
$\mathbb {Q}_p$
and let
![]() $\mathcal {F}$
be a sheaf of sets on
$\mathcal {F}$
be a sheaf of sets on
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property.
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property.
-
1.
 $\mathcal {F}$
is a v-sheaf. In particular,
$\mathcal {F}$
is a v-sheaf. In particular,
 $\mathcal {F}$
extends uniquely to a sheaf on
$\mathcal {F}$
extends uniquely to a sheaf on
 $X_v$
.
$X_v$
. -
2. For any inverse limit of spatial diamonds
 $Y = \varprojlim _i Y_i$
with qcqs transition maps, we have
$Y = \varprojlim _i Y_i$
with qcqs transition maps, we have  $$\begin{align*}\mathcal{F}(Y) = \varinjlim_i \mathcal{F}(Y_i).\end{align*}$$
$$\begin{align*}\mathcal{F}(Y) = \varinjlim_i \mathcal{F}(Y_i).\end{align*}$$
-
3. Let
 $\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
denote the natural map of sites. If
$\nu \colon X_v \rightarrow X_{\operatorname {\mathrm {\acute {e}t}}}$
denote the natural map of sites. If
 $\mathcal {F}$
is a sheaf of groups (resp. of abelian groups), then
$\mathcal {F}$
is a sheaf of groups (resp. of abelian groups), then
 $R^n\nu _*\mathcal {F} = 0$
for
$R^n\nu _*\mathcal {F} = 0$
for
 $n=1$
(resp. for all
$n=1$
(resp. for all
 $n\geq 1$
). In particular, for
$n\geq 1$
). In particular, for $$\begin{align*}H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathcal{F}) = H_{v}^n(X,\mathcal{F}),\end{align*}$$
$$\begin{align*}H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathcal{F}) = H_{v}^n(X,\mathcal{F}),\end{align*}$$
 $n=0,1$
(resp. for all
$n=0,1$
(resp. for all
 $n\geq 0$
).
$n\geq 0$
).
Proof. This is proven in [Reference Heuer24, Prop. 2.14, Lemma 2.20] for
![]() $X=\operatorname {\mathrm {Spa}}(K,K^+)$
, but the proof extends without change to the general case.
$X=\operatorname {\mathrm {Spa}}(K,K^+)$
, but the proof extends without change to the general case.
Our main new input is the following characterization of sheaves with the approximation property.
Proposition 3.12. Let X be a good adic space over
![]() $\mathbb {Q}_p$
and let
$\mathbb {Q}_p$
and let
![]() $\mathcal {F}$
be a sheaf on
$\mathcal {F}$
be a sheaf on
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
. Then the following are equivalent:
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
. Then the following are equivalent:
-
1.
 $\mathcal {F}$
satisfies the approximation property, and
$\mathcal {F}$
satisfies the approximation property, and -
2.
 $\mathcal {F}$
admits a presentation as an étale quotient sheaf where V is an adic space smooth over X and
$\mathcal {F}$
admits a presentation as an étale quotient sheaf where V is an adic space smooth over X and $$\begin{align*}\mathcal{F} = V/R,\end{align*}$$
$$\begin{align*}\mathcal{F} = V/R,\end{align*}$$
 $R\subseteq V\times _X V$
is an open equivalence relation.
$R\subseteq V\times _X V$
is an open equivalence relation.
In that case, the following additional statements hold: For any map
![]() $V \rightarrow \mathcal {F}$
from a smooth X-space V, the diamond
$V \rightarrow \mathcal {F}$
from a smooth X-space V, the diamond
![]() $R = V \times _{\mathcal {F}} V$
is open in
$R = V \times _{\mathcal {F}} V$
is open in
![]() $V\times _X V$
.
$V\times _X V$
.
With this result in hand, we can prove Proposition 3.3.
Proof of Proposition 3.3
By Proposition 3.12, the sheaf
![]() $\overline {\mathcal {G}} = \mathcal {G}/\widehat {\mathcal {G}}$
has the approximation property. It follows from Proposition 3.11.3 that
$\overline {\mathcal {G}} = \mathcal {G}/\widehat {\mathcal {G}}$
has the approximation property. It follows from Proposition 3.11.3 that
![]() $R\nu _*\overline {\mathcal {G}} =\overline {\mathcal {G}}$
, such that
$R\nu _*\overline {\mathcal {G}} =\overline {\mathcal {G}}$
, such that
Moreover, recall that the logarithm defines an exact sequence
The étale X-group
![]() $\mathcal {G}[p^{\infty }]$
also satisfies the approximation property, by Example 3.10.2. Hence we also have
$\mathcal {G}[p^{\infty }]$
also satisfies the approximation property, by Example 3.10.2. Hence we also have
![]() $R\nu _*\mathcal {G}[p^{\infty }] =\mathcal {G}[p^{\infty }]$
and
$R\nu _*\mathcal {G}[p^{\infty }] =\mathcal {G}[p^{\infty }]$
and
Finally, we have
where we use the projection formula for the first equality.
Proof of Proposition 3.12
-
○
 $\underline{(1) \Rightarrow (2)\colon} $
$\underline{(1) \Rightarrow (2)\colon} $
Let
 $\mathcal {F}$
have the approximation property. We may assume that X is affinoid. By arguing as in [Reference Fargues and Scholze17, Prop. III.1.3], we find that
$\mathcal {F}$
have the approximation property. We may assume that X is affinoid. By arguing as in [Reference Fargues and Scholze17, Prop. III.1.3], we find that
 $\mathcal {F}$
is a small v-sheaf. Let
$\mathcal {F}$
is a small v-sheaf. Let
 $T \rightarrow \mathcal {F}$
be a surjection from a perfectoid space T and fix an open cover of T by affinoid perfectoids
$T \rightarrow \mathcal {F}$
be a surjection from a perfectoid space T and fix an open cover of T by affinoid perfectoids
 $T_i$
. We may write by [Reference Heuer22, Prop. 3.17] where each
$T_i$
. We may write by [Reference Heuer22, Prop. 3.17] where each $$\begin{align*}T_i \approx \varprojlim_j U_{ij} \rightarrow X,\end{align*}$$
$$\begin{align*}T_i \approx \varprojlim_j U_{ij} \rightarrow X,\end{align*}$$
 $U_{ij}$
is affinoid smooth over X. Applying the approximation property, we find that
$U_{ij}$
is affinoid smooth over X. Applying the approximation property, we find that
 $T_i \rightarrow \mathcal {F}$
factors through
$T_i \rightarrow \mathcal {F}$
factors through  for some
for some
 $j=j(i)$
. Then we obtain a surjection of v-sheaves
$j=j(i)$
. Then we obtain a surjection of v-sheaves
 $q\colon V = \coprod _{i} V_i \rightarrow \mathcal {F}$
from a smooth X-space. It remains to show that
$q\colon V = \coprod _{i} V_i \rightarrow \mathcal {F}$
from a smooth X-space. It remains to show that
 $R = V\times _{\mathcal {F}} V \subseteq V\times _X V$
is an open subspace, for any such map q. Let
$R = V\times _{\mathcal {F}} V \subseteq V\times _X V$
is an open subspace, for any such map q. Let
 $y\in R$
with its associated geometric point
$y\in R$
with its associated geometric point
 $\overline {y}\colon \operatorname {\mathrm {Spa}}(C,C^+) \rightarrow V\times _X V$
. We may write where the limit ranges over all affinoid spaces
$\overline {y}\colon \operatorname {\mathrm {Spa}}(C,C^+) \rightarrow V\times _X V$
. We may write where the limit ranges over all affinoid spaces $$\begin{align*}\operatorname{\mathrm{Spa}}(C,C^+) \approx \varprojlim_k W_k,\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Spa}}(C,C^+) \approx \varprojlim_k W_k,\end{align*}$$
 $W_k$
étale over
$W_k$
étale over
 $V\times _X V$
together with a factorization
$V\times _X V$
together with a factorization 
Then the two following compositions
are equal. By the approximation property, we deduce that already the compositions agree for
agree for
 $k\gg 0$
. This shows that the map
$k\gg 0$
. This shows that the map
 $W_k \rightarrow V \times _X V$
factors through
$W_k \rightarrow V \times _X V$
factors through
 $R \subseteq V \times _X V$
and its image is an open neighborhood of
$R \subseteq V \times _X V$
and its image is an open neighborhood of
 $y \in V \times _X V$
contained in R. We deduce that R is open in
$y \in V \times _X V$
contained in R. We deduce that R is open in
 $V \times _X V$
, as required. This shows the first implication and the last part of the statement.
$V \times _X V$
, as required. This shows the first implication and the last part of the statement.
-
○
 $\underline{(2) \Rightarrow (1)\colon}$
$\underline{(2) \Rightarrow (1)\colon}$
Fix an affinoid perfectoid tilde-limit
 $Y\approx \varprojlim _i Y_i$
of good affinoid adic spaces. We first show that the natural map is injective. Let
$Y\approx \varprojlim _i Y_i$
of good affinoid adic spaces. We first show that the natural map is injective. Let $$\begin{align*}\phi\colon \varinjlim_i \mathcal{F}(Y_i) \rightarrow \mathcal{F}(Y).\end{align*}$$
$$\begin{align*}\phi\colon \varinjlim_i \mathcal{F}(Y_i) \rightarrow \mathcal{F}(Y).\end{align*}$$
 $i_0\in I$
and
$i_0\in I$
and
 $\overline {s},\overline {t}\in \mathcal {F}(Y_{i_0})$
be such that
$\overline {s},\overline {t}\in \mathcal {F}(Y_{i_0})$
be such that
 $\overline {s}|_{Y}=\overline {t}|_{Y}$
. We need to show that already
$\overline {s}|_{Y}=\overline {t}|_{Y}$
. We need to show that already
 $\overline {s}|_{Y_i}=\overline {t}|_{Y_i}$
for
$\overline {s}|_{Y_i}=\overline {t}|_{Y_i}$
for
 $i\gg i_0$
. This may be checked after taking a standard-étale cover of
$i\gg i_0$
. This may be checked after taking a standard-étale cover of
 $Y_{i_0}$
(replacing
$Y_{i_0}$
(replacing
 $Y_i$
and Y by their respective pullbacks along this cover). Hence we may assume that the given sections admit lifts
$Y_i$
and Y by their respective pullbacks along this cover). Hence we may assume that the given sections admit lifts
 $s,t\in V(Y_{i_0})$
. By assumption, the following diagram commutes so that
$s,t\in V(Y_{i_0})$
. By assumption, the following diagram commutes so that
 $(s,t)|_{Y}$
has image in
$(s,t)|_{Y}$
has image in
 $R \subseteq V\times _X V$
. By Lemma 3.13 below, we deduce that already
$R \subseteq V\times _X V$
. By Lemma 3.13 below, we deduce that already
 $(s,t)|_{Y_i}$
maps in R, for
$(s,t)|_{Y_i}$
maps in R, for
 $i\gg i_0$
, such that
$i\gg i_0$
, such that
 $\overline {s}|_{Y_i} = \overline {t}|_{Y_i}$
. This shows injectivity.
$\overline {s}|_{Y_i} = \overline {t}|_{Y_i}$
. This shows injectivity.
We now show that
 $\phi $
is surjective. Let
$\phi $
is surjective. Let
 $\overline {s} \in \mathcal {F}(Y)$
. Assume that
$\overline {s} \in \mathcal {F}(Y)$
. Assume that
 $\overline {s}$
is in the image of
$\overline {s}$
is in the image of
 $\varphi $
after replacing Y by an étale cover, then we can conclude. Indeed, let
$\varphi $
after replacing Y by an étale cover, then we can conclude. Indeed, let
 $Y' \rightarrow Y$
be a quasi-compact étale cover, corresponding to an étale cover
$Y' \rightarrow Y$
be a quasi-compact étale cover, corresponding to an étale cover
 $Y_{i_0}' \rightarrow Y_{i_0}$
for some
$Y_{i_0}' \rightarrow Y_{i_0}$
for some
 $i_0\in I$
, and let
$i_0\in I$
, and let
 $\overline {s_i'} \in \mathcal {F}(Y_i')$
be a section for
$\overline {s_i'} \in \mathcal {F}(Y_i')$
be a section for
 $i\geq i_0$
mapping to
$i\geq i_0$
mapping to
 $\overline {s}|_{Y'}$
. We claim that the section
$\overline {s}|_{Y'}$
. We claim that the section
 $\overline {s_i'}$
descends to a section
$\overline {s_i'}$
descends to a section
 $\overline {s_i} \in \mathcal {F}(Y_i)$
(which is then automatically mapped to
$\overline {s_i} \in \mathcal {F}(Y_i)$
(which is then automatically mapped to
 $\overline {s}$
), up to increasing i: For this, it is enough to show that
$\overline {s}$
), up to increasing i: For this, it is enough to show that
 $p_1^*\overline {s_i'} = p_2^*\overline {s_i'} \in \mathcal {F}(Y_i' \times _{Y_i} Y_i')$
: This holds after pullback to
$p_1^*\overline {s_i'} = p_2^*\overline {s_i'} \in \mathcal {F}(Y_i' \times _{Y_i} Y_i')$
: This holds after pullback to
 $Y' \times _Y Y'$
, hence it holds after increasing i, by the injectivity step.
$Y' \times _Y Y'$
, hence it holds after increasing i, by the injectivity step.Next we reduce to the case where
 $Y=\operatorname {\mathrm {Spa}}(C,C^+)$
for a complete algebraically closed field C. Let
$Y=\operatorname {\mathrm {Spa}}(C,C^+)$
for a complete algebraically closed field C. Let
 $y\in \vert Y \vert $
and let
$y\in \vert Y \vert $
and let
 $\{ (U_j,u_j) \}_j$
denote the cofiltered inverse system of quasi-compact étale maps
$\{ (U_j,u_j) \}_j$
denote the cofiltered inverse system of quasi-compact étale maps
 $U_j \rightarrow Y$
together with a lift
$U_j \rightarrow Y$
together with a lift
 $u_j \in \vert U_j \vert $
of y. Then the corresponding geometric point
$u_j \in \vert U_j \vert $
of y. Then the corresponding geometric point
 $\operatorname {\mathrm {Spa}}(C(y),C(y)^+) \rightarrow Y$
satisfies
$\operatorname {\mathrm {Spa}}(C(y),C(y)^+) \rightarrow Y$
satisfies
 $\operatorname {\mathrm {Spa}}(C(y),C(y)^+) \approx \varprojlim _j U_j$
. Consider the cofiltered category consisting of triplets
$\operatorname {\mathrm {Spa}}(C(y),C(y)^+) \approx \varprojlim _j U_j$
. Consider the cofiltered category consisting of triplets
 $(i,j,U_{ij}\rightarrow Y_i)$
, where
$(i,j,U_{ij}\rightarrow Y_i)$
, where
 $U_{ij}\rightarrow Y_i$
is an étale map with
$U_{ij}\rightarrow Y_i$
is an étale map with
 $U_j = U_{ij}\times _{Y_i}Y$
. Then it follows from [Reference Heuer22, Lemma 3.13] (or alternatively Lemma 3.19.2 below) that
$U_j = U_{ij}\times _{Y_i}Y$
. Then it follows from [Reference Heuer22, Lemma 3.13] (or alternatively Lemma 3.19.2 below) that  $$\begin{align*}U_j \approx \varprojlim_{i} U_{ij}. \end{align*}$$
$$\begin{align*}U_j \approx \varprojlim_{i} U_{ij}. \end{align*}$$
By sequential approximation, we deduce that also
 $$\begin{align*}\operatorname{\mathrm{Spa}}(C(y),C(y)^+) \approx \varprojlim_{i,j} U_{ij}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Spa}}(C(y),C(y)^+) \approx \varprojlim_{i,j} U_{ij}.\end{align*}$$
Suppose that
 $\overline {s}(y)\in \mathcal {F}(C(y),C(y)^+)$
coincides with
$\overline {s}(y)\in \mathcal {F}(C(y),C(y)^+)$
coincides with
 $\overline {s}_{ij}(y)$
for some
$\overline {s}_{ij}(y)$
for some
 $\overline {s}_{ij}\in \mathcal {F}(U_{ij})$
. Then
$\overline {s}_{ij}\in \mathcal {F}(U_{ij})$
. Then
 $\overline {s}|_{U_j}$
and
$\overline {s}|_{U_j}$
and
 $\overline {s}_{ij}|_{U_j}$
map to the same element of
$\overline {s}_{ij}|_{U_j}$
map to the same element of
 $\mathcal {F}(C(y),C(y)^+)$
. By the injectivity step, these two sections are equal, up to increasing j. Hence, if surjectivity of
$\mathcal {F}(C(y),C(y)^+)$
. By the injectivity step, these two sections are equal, up to increasing j. Hence, if surjectivity of
 $\phi $
holds for points, for each
$\phi $
holds for points, for each
 $y\in \vert Y \vert $
, the restriction of
$y\in \vert Y \vert $
, the restriction of
 $\overline {s}$
to some étale neighborhood of y is in the image of
$\overline {s}$
to some étale neighborhood of y is in the image of
 $\phi $
, which concludes, by the previous reduction step.
$\phi $
, which concludes, by the previous reduction step.From these two reduction steps, we can without loss assume that
 $Y=\operatorname {\mathrm {Spa}}(C,C^+)$
,
$Y=\operatorname {\mathrm {Spa}}(C,C^+)$
,
 $\overline {s}$
admits a lift
$\overline {s}$
admits a lift
 $s\in V(Y)$
, X is affinoid and V is standard-smooth over X. Hence, we may write
$s\in V(Y)$
, X is affinoid and V is standard-smooth over X. Hence, we may write
 $V\rightarrow X$
as a composition where g is standard-étale,
$V\rightarrow X$
as a composition where g is standard-étale, $$\begin{align*}V \xrightarrow{g} B \rightarrow X,\end{align*}$$
$$\begin{align*}V \xrightarrow{g} B \rightarrow X,\end{align*}$$
 $B=\mathbb {B}_X^n$
and the last map is the canonical projection. We write
$B=\mathbb {B}_X^n$
and the last map is the canonical projection. We write  $$\begin{align*}\mathcal{O}(B) = \mathcal{O}(X)\langle T_1, \ldots, T_n\rangle.\end{align*}$$
$$\begin{align*}\mathcal{O}(B) = \mathcal{O}(X)\langle T_1, \ldots, T_n\rangle.\end{align*}$$
Here,
 $T_1,\ldots T_n$
are Tate variables and we abbreviate these by
$T_1,\ldots T_n$
are Tate variables and we abbreviate these by
 $\underline {T}$
. Let
$\underline {T}$
. Let  $$\begin{align*}\underline{t} = g(s)\in B(Y) \cong (C^+)^{\oplus n}.\end{align*}$$
$$\begin{align*}\underline{t} = g(s)\in B(Y) \cong (C^+)^{\oplus n}.\end{align*}$$
By definition of tilde-limits
has dense image. Hence we may find $$\begin{align*}\theta\colon \varinjlim_i \mathcal{O}^+(Y_i) \rightarrow \mathcal{O}^+(Y)=C^+ \end{align*}$$
$$\begin{align*}\theta\colon \varinjlim_i \mathcal{O}^+(Y_i) \rightarrow \mathcal{O}^+(Y)=C^+ \end{align*}$$
 $\underline {t_i} \in \mathcal {O}^+(Y_i)^{\oplus n}$
such that
$\underline {t_i} \in \mathcal {O}^+(Y_i)^{\oplus n}$
such that
 $\theta (\underline {t_i}) \cong \underline {t} \, (\, \operatorname {\mathrm {mod}} \varpi ^N)$
, where
$\theta (\underline {t_i}) \cong \underline {t} \, (\, \operatorname {\mathrm {mod}} \varpi ^N)$
, where
 $\varpi \in K^+$
is a pseudo-uniformizer and
$\varpi \in K^+$
is a pseudo-uniformizer and
 $N\gg 0$
is a large integer. We write
$N\gg 0$
is a large integer. We write
 $\underline {t'} = \theta (\underline {t_i}) \in (C^+)^{\oplus n}$
.
$\underline {t'} = \theta (\underline {t_i}) \in (C^+)^{\oplus n}$
.
It remains to construct a lift
 $s' \in V(Y)$
of
$s' \in V(Y)$
of
 $\underline {t'} \in B(Y)$
that is R-equivalent to the original section
$\underline {t'} \in B(Y)$
that is R-equivalent to the original section
 $s \in V(Y)$
. Note that
$s \in V(Y)$
. Note that
 $s'$
will automatically live in finite level, that is, arise from a section
$s'$
will automatically live in finite level, that is, arise from a section
 $s_i \in V(Y_i)$
that lifts
$s_i \in V(Y_i)$
that lifts
 $\underline {t_i} \in B(Y_i)$
, up to increasing i. This follows from the fact that
$\underline {t_i} \in B(Y_i)$
, up to increasing i. This follows from the fact that
 $V \rightarrow B$
is étale, such that by [Reference Scholze47, Prop. 14.9],
$V \rightarrow B$
is étale, such that by [Reference Scholze47, Prop. 14.9],  $$\begin{align*}\operatorname{\mathrm{Hom}}_B(Y,V) = \varinjlim_i \operatorname{\mathrm{Hom}}_B(Y_i,V).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}_B(Y,V) = \varinjlim_i \operatorname{\mathrm{Hom}}_B(Y_i,V).\end{align*}$$
Let
 $U \subseteq R \subseteq V \times _X V$
be a rational open subset containing the image of
$U \subseteq R \subseteq V \times _X V$
be a rational open subset containing the image of
 $(s,s)\colon Y \rightarrow R$
. We form the following pullback diagram
$(s,s)\colon Y \rightarrow R$
. We form the following pullback diagram 
A lift
 $s'$
as above corresponds to a diagonal dotted arrow in the above diagram and thus a section to the étale map
$s'$
as above corresponds to a diagonal dotted arrow in the above diagram and thus a section to the étale map
 $Y' \rightarrow Y$
. Let
$Y' \rightarrow Y$
. Let
 $ W \subseteq (\operatorname {\mathrm {id}}\times g)(U)$
be a rational open neighborhood of the image of
$ W \subseteq (\operatorname {\mathrm {id}}\times g)(U)$
be a rational open neighborhood of the image of
 $(s,\underline {t})\colon Y \rightarrow V \times _X B$
in the open image
$(s,\underline {t})\colon Y \rightarrow V \times _X B$
in the open image
 $(\operatorname {\mathrm {id}}\times g)(U) \subseteq V\times _X B$
. We write
$(\operatorname {\mathrm {id}}\times g)(U) \subseteq V\times _X B$
. We write
 $W=U(\tfrac {F_1,\ldots ,F_r}{G})$
for
$W=U(\tfrac {F_1,\ldots ,F_r}{G})$
for
 $F_j,G\in \mathcal {O}^+(V\times _{X}B)$
and we let
$F_j,G\in \mathcal {O}^+(V\times _{X}B)$
and we let
 $f_j,g$
(resp.
$f_j,g$
(resp.
 $f_j', g'$
) denote their pullbacks in
$f_j', g'$
) denote their pullbacks in
 $\mathcal {O}^+(Y)=C^+$
under the map
$\mathcal {O}^+(Y)=C^+$
under the map
 $(s,\underline {t})$
(resp. the map
$(s,\underline {t})$
(resp. the map
 $(s,\underline {t'})$
). By assumption,
$(s,\underline {t'})$
). By assumption,
 $(s,\underline {t})(Y) \subseteq W$
such that where
$(s,\underline {t})(Y) \subseteq W$
such that where $$\begin{align*}\vert f_j\vert \leq \vert g \vert \neq 0, \,\, \forall j=1, \ldots r,\end{align*}$$
$$\begin{align*}\vert f_j\vert \leq \vert g \vert \neq 0, \,\, \forall j=1, \ldots r,\end{align*}$$
 $\vert \cdot \vert $
denotes the valuation on C. By construction of
$\vert \cdot \vert $
denotes the valuation on C. By construction of
 $\underline {t'}$
, we have that
$\underline {t'}$
, we have that
 $f_j\equiv f_j' \,(\, \operatorname {\mathrm {mod}} \varpi ^N)$
and
$f_j\equiv f_j' \,(\, \operatorname {\mathrm {mod}} \varpi ^N)$
and
 $g \equiv g' \,(\, \operatorname {\mathrm {mod}} \varpi ^N)$
. Hence, as soon as N is big enough,
$g \equiv g' \,(\, \operatorname {\mathrm {mod}} \varpi ^N)$
. Hence, as soon as N is big enough,  $$\begin{align*}\vert f_j'\vert = \vert f_j\vert \leq \vert g \vert= \vert g' \vert, \, \,\forall j=1, \ldots r.\end{align*}$$
$$\begin{align*}\vert f_j'\vert = \vert f_j\vert \leq \vert g \vert= \vert g' \vert, \, \,\forall j=1, \ldots r.\end{align*}$$
It follows that also
 $(s,\underline {t'})\colon Y \rightarrow V\times _X B$
has image in the open subspace
$(s,\underline {t'})\colon Y \rightarrow V\times _X B$
has image in the open subspace
 $W \subseteq V\times _X B$
. After passing to pullbacks, we deduce that the étale map
$W \subseteq V\times _X B$
. After passing to pullbacks, we deduce that the étale map
 $Y' \rightarrow Y$
is surjective. Since
$Y' \rightarrow Y$
is surjective. Since
 $Y=\operatorname {\mathrm {Spa}}(C,C^+)$
is strictly totally disconnected, the map
$Y=\operatorname {\mathrm {Spa}}(C,C^+)$
is strictly totally disconnected, the map
 $Y' \rightarrow Y$
thus admits a section, as required. This concludes the proof.
$Y' \rightarrow Y$
thus admits a section, as required. This concludes the proof.
The following lemma was used in the proof above.
Lemma 3.13. Let
![]() $Z= \varprojlim _{i \in I} Z_i$
be an inverse limit of spatial diamonds with qcqs transition maps. Let T be a locally spatial diamond and let
$Z= \varprojlim _{i \in I} Z_i$
be an inverse limit of spatial diamonds with qcqs transition maps. Let T be a locally spatial diamond and let
![]() $U\subseteq T$
be an open subdiamond. Let
$U\subseteq T$
be an open subdiamond. Let
![]() $t\in T(Z_{i_0})$
for some
$t\in T(Z_{i_0})$
for some
![]() $i_0 \in I$
and assume that the composition
$i_0 \in I$
and assume that the composition
![]() $Z\rightarrow Z_{i_0} \xrightarrow {t} T$
factors through
$Z\rightarrow Z_{i_0} \xrightarrow {t} T$
factors through
![]() $U \subseteq T$
. Then already the composition
$U \subseteq T$
. Then already the composition
![]() $Z_i \rightarrow Z_{i_0} \xrightarrow {t} T$
has image in U for
$Z_i \rightarrow Z_{i_0} \xrightarrow {t} T$
has image in U for
![]() $i\gg i_0$
.
$i\gg i_0$
.
Proof. Let us take an open cover
![]() $T=\bigcup _j T_j$
by open spatial subdiamonds and
$T=\bigcup _j T_j$
by open spatial subdiamonds and
![]() $Z_{i_0} = \bigcup _k Z_{i_0,k}$
an open cover by spatial subdiamonds subdividing the preimage of the
$Z_{i_0} = \bigcup _k Z_{i_0,k}$
an open cover by spatial subdiamonds subdividing the preimage of the
![]() $T_j$
. By quasi-compactness of
$T_j$
. By quasi-compactness of
![]() $Z_{i_0}$
, we may assume that there are finitely many k. Then letting
$Z_{i_0}$
, we may assume that there are finitely many k. Then letting
![]() $Z_{i,k},Z_k$
denote the inverse image of
$Z_{i,k},Z_k$
denote the inverse image of
![]() $Z_{i_0,k}$
in
$Z_{i_0,k}$
in
![]() $Z_i, Z$
, we obtain again inverse limits
$Z_i, Z$
, we obtain again inverse limits
![]() $Z_k = \varprojlim _{i \geq i_0} Z_{i,k}$
. Replacing Z by
$Z_k = \varprojlim _{i \geq i_0} Z_{i,k}$
. Replacing Z by
![]() $Z_k$
, we may assume that T is spatial. Let us take an open cover
$Z_k$
, we may assume that T is spatial. Let us take an open cover
![]() $U= \bigcup _{j} U_{j}$
by spatial subdiamonds. Again by quasi-compactness, finitely many
$U= \bigcup _{j} U_{j}$
by spatial subdiamonds. Again by quasi-compactness, finitely many
![]() $U_j$
cover the image of
$U_j$
cover the image of
![]() $Z \rightarrow U$
. Hence we may assume that U is quasi-compact and hence spatial. For
$Z \rightarrow U$
. Hence we may assume that U is quasi-compact and hence spatial. For
![]() $i\geq i_0$
, the preimage
$i\geq i_0$
, the preimage
![]() $V_i \subseteq Z_i$
of U under the composition
$V_i \subseteq Z_i$
of U under the composition
![]() $Z_i \rightarrow Z_{i_0} \xrightarrow {t} T$
are quasi-compact and
$Z_i \rightarrow Z_{i_0} \xrightarrow {t} T$
are quasi-compact and
![]() $\varprojlim _{i\geq i_0} V_i = Z$
. By [48, Tag 0A2W], it follows that
$\varprojlim _{i\geq i_0} V_i = Z$
. By [48, Tag 0A2W], it follows that
![]() $V_i=Z_i$
for
$V_i=Z_i$
for
![]() $i\gg i_0$
, as required.
$i\gg i_0$
, as required.
3.3 The diamantine higher direct images
In this section, we define the diamantine higher direct images and study their basic properties. Our definitions and choices for the presentation are heavily influenced by [Reference Heuer22].
Fix a nonarchimedean field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\pi \colon X \rightarrow S$
be a smooth morphism of seminormal rigid spaces over K. It induces maps of sites
$\pi \colon X \rightarrow S$
be a smooth morphism of seminormal rigid spaces over K. It induces maps of sites
Definition 3.14. Let
![]() $\mathcal {G}$
be a commutative smooth X-group and let
$\mathcal {G}$
be a commutative smooth X-group and let
![]() $\tau $
be either the étale or the v-topology. For
$\tau $
be either the étale or the v-topology. For
![]() $n\geq 0$
, the n-th diamantine higher direct image of
$n\geq 0$
, the n-th diamantine higher direct image of
![]() $\mathcal {G}$
is defined as the abelian sheaf
$\mathcal {G}$
is defined as the abelian sheaf
We will sometimes simplify the notation and write instead
![]() ${\mathbf {Bun}}_{\mathcal {G},\tau }^{n,\diamondsuit }$
or
${\mathbf {Bun}}_{\mathcal {G},\tau }^{n,\diamondsuit }$
or
![]() ${\mathbf {Bun}}_{\mathcal {G},\tau }^{n}$
when the context is clear.
${\mathbf {Bun}}_{\mathcal {G},\tau }^{n}$
when the context is clear.
We also have the following variant for the étale topology. Recall that in Lemma 2.24, we introduced the site
![]() $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
with underlying category all rigid spaces smooth over S, equipped with the étale topology. We have a morphism of sites
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
with underlying category all rigid spaces smooth over S, equipped with the étale topology. We have a morphism of sites
Definition 3.15. Let
![]() $n\geq 0$
, we define
$n\geq 0$
, we define
We may compare the two variants. We denote by
the morphism of sites induced by the functor
By Proposition 2.5, since S is a seminormal rigid space, this functor is fully faithful. We also have a morphism of sites
For any sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
, we define its diamantification to be
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
, we define its diamantification to be
This is consistent, since if
![]() $\mathcal {F}$
is representable by a smooth S-space V, then
$\mathcal {F}$
is representable by a smooth S-space V, then
![]() $\mathcal {F}^{\diamondsuit }$
coincides with
$\mathcal {F}^{\diamondsuit }$
coincides with
![]() $V^{\diamondsuit }$
. We have a commutative diagram
$V^{\diamondsuit }$
. We have a commutative diagram

It induces base-change morphisms, for any abelian sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\operatorname {\mathrm {LSD}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {LSD}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
We now summarize the main properties satisfied by the diamantine higher direct images. This generalizes [Reference Heuer22, Thm. 1.1], which is the case
![]() $\mathcal {G}=\mathbb {G}_m$
and
$\mathcal {G}=\mathbb {G}_m$
and
![]() $n=1$
.
$n=1$
.
Proposition 3.16. Let
![]() $\pi \colon X \rightarrow S$
be a proper smooth morphism of seminormal rigid spaces and let
$\pi \colon X \rightarrow S$
be a proper smooth morphism of seminormal rigid spaces and let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group. Assume either that
$\mathcal {G}$
be an admissible locally p-divisible X-group. Assume either that
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
or that
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
or that
![]() ${\mathfrak {g}}$
arises via pullback from a vector bundle on S.
${\mathfrak {g}}$
arises via pullback from a vector bundle on S.
-
1. For
 $\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
, the sheaf
$\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
, the sheaf
 ${\mathbf {Bun}}_{{\mathfrak {g}},\tau }^{n,\diamondsuit }$
is a
${\mathbf {Bun}}_{{\mathfrak {g}},\tau }^{n,\diamondsuit }$
is a
 $\tau $
-vector bundle on S. If
$\tau $
-vector bundle on S. If
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
and K is perfectoid, we further have
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
and K is perfectoid, we further have  $$\begin{align*}{\mathbf{Bun}}_{{\mathfrak{g}},\tau}^{n,\diamondsuit} = H_{\tau}^n(X,{\mathfrak{g}})\otimes \mathbb{G}_a.\end{align*}$$
$$\begin{align*}{\mathbf{Bun}}_{{\mathfrak{g}},\tau}^{n,\diamondsuit} = H_{\tau}^n(X,{\mathfrak{g}})\otimes \mathbb{G}_a.\end{align*}$$
-
2. For each
 $1 \leq m \leq \infty $
, we have and this sheaf is ind-Zariski-constructible. If
$1 \leq m \leq \infty $
, we have and this sheaf is ind-Zariski-constructible. If $$\begin{align*}{\mathbf{Bun}}_{\mathcal{G}[p^m],v}^{n,\diamondsuit} = {\mathbf{Bun}}_{\mathcal{G}[p^m],\operatorname{\mathrm{\acute{e}t}}}^{n,\diamondsuit} = \nu^* R^n\pi_{\operatorname{\mathrm{\acute{e}t}},*}\mathcal{G}[p^m]. \end{align*}$$
$$\begin{align*}{\mathbf{Bun}}_{\mathcal{G}[p^m],v}^{n,\diamondsuit} = {\mathbf{Bun}}_{\mathcal{G}[p^m],\operatorname{\mathrm{\acute{e}t}}}^{n,\diamondsuit} = \nu^* R^n\pi_{\operatorname{\mathrm{\acute{e}t}},*}\mathcal{G}[p^m]. \end{align*}$$
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
or
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
or
 $[p]\colon \widehat {\mathcal {G}} \rightarrow \widehat {\mathcal {G}}$
is finite étale surjective, then
$[p]\colon \widehat {\mathcal {G}} \rightarrow \widehat {\mathcal {G}}$
is finite étale surjective, then
 ${\mathbf {Bun}}_{\mathcal {G}[p^m],\operatorname {\mathrm {\acute {e}t}}}^{n,\diamondsuit }$
is representable by an étale group over S.
${\mathbf {Bun}}_{\mathcal {G}[p^m],\operatorname {\mathrm {\acute {e}t}}}^{n,\diamondsuit }$
is representable by an étale group over S.
-
3. For
 $\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
, we have a short exact sequence of sheaves on
$\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
, we have a short exact sequence of sheaves on
 $\operatorname {\mathrm {Perf}}_{S,\tau }$
(3.6)
$\operatorname {\mathrm {Perf}}_{S,\tau }$
(3.6)
-
4. The natural map (3.5) yields an isomorphism
 $$\begin{align*}({\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^{n,\operatorname{\mathrm{rig}}})^{\diamondsuit} \xrightarrow{\cong} {\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^{n,\diamondsuit}.\end{align*}$$
$$\begin{align*}({\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^{n,\operatorname{\mathrm{rig}}})^{\diamondsuit} \xrightarrow{\cong} {\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^{n,\diamondsuit}.\end{align*}$$
In particular,
 ${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\operatorname {\mathrm {rig}}}$
is representable by a smooth S-group
${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\operatorname {\mathrm {rig}}}$
is representable by a smooth S-group
 $\mathcal {H}$
if and only if
$\mathcal {H}$
if and only if
 ${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\diamondsuit }$
coincides with
${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\diamondsuit }$
coincides with
 $\mathcal {H}^{\diamondsuit }$
.
$\mathcal {H}^{\diamondsuit }$
.
Remark 3.17. Without further assumptions in
![]() $(2)$
, the sheaf
$(2)$
, the sheaf
![]() ${\mathbf {Bun}}_{\mathcal {G}[p^{m}],\operatorname {\mathrm {\acute {e}t}}}^{n}$
need a priori not be representable by an étale S-group. In general, one can show that a Zariski-constructible sheaf
${\mathbf {Bun}}_{\mathcal {G}[p^{m}],\operatorname {\mathrm {\acute {e}t}}}^{n}$
need a priori not be representable by an étale S-group. In general, one can show that a Zariski-constructible sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $S_{\operatorname {\mathrm {\acute {e}t}}}$
is represented by a diamond, using the equivalence of categories between constructible sheaves over a qcqs algebraic variety Y and algebraic spaces qcqs over Y [Reference Artin, Grothendieck and Verdier3, Exposé IX, Prop. 2.7]. However, this diamond need not be locally separated over S and thus may not come from an adic space, as can be seen by taking
$S_{\operatorname {\mathrm {\acute {e}t}}}$
is represented by a diamond, using the equivalence of categories between constructible sheaves over a qcqs algebraic variety Y and algebraic spaces qcqs over Y [Reference Artin, Grothendieck and Verdier3, Exposé IX, Prop. 2.7]. However, this diamond need not be locally separated over S and thus may not come from an adic space, as can be seen by taking
![]() $\mathcal {F}$
to be the skyscraper sheaf at the origin of the closed unit ball
$\mathcal {F}$
to be the skyscraper sheaf at the origin of the closed unit ball
![]() $S=\mathbb {B}_K^1$
.
$S=\mathbb {B}_K^1$
.
The main ingredient for the proof of Proposition 3.16 is the following result, generalizing [Reference Heuer22, Prop. 3.2].
Proposition 3.18. Let
![]() $\pi \colon X \rightarrow S$
be a qcqs smooth map of good adic spaces over
$\pi \colon X \rightarrow S$
be a qcqs smooth map of good adic spaces over
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\mathcal {F}$
be a sheaf of sets (resp. of groups, resp. of abelian groups) on
$\mathcal {F}$
be a sheaf of sets (resp. of groups, resp. of abelian groups) on
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property. Let
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property. Let
![]() $Y\approx \varprojlim _i Y_i$
be a tilde-limit of good affinoid adic spaces over S. Let
$Y\approx \varprojlim _i Y_i$
be a tilde-limit of good affinoid adic spaces over S. Let
![]() $i_0 \in I$
and let
$i_0 \in I$
and let
![]() $U_{i_0} \rightarrow X \times _S Y_{i_0}$
be a qcqs étale map. For all
$U_{i_0} \rightarrow X \times _S Y_{i_0}$
be a qcqs étale map. For all
![]() $i\geq i_0$
, form the products
$i\geq i_0$
, form the products
![]() $U_i = U_{i_0} \times _{Y_{i_0}}Y_i$
and
$U_i = U_{i_0} \times _{Y_{i_0}}Y_i$
and
![]() $U = U_{i_0}\times _{Y_{i_0}}Y$
. Then
$U = U_{i_0}\times _{Y_{i_0}}Y$
. Then
![]() $U \sim \underset {i\geq i_0}{\varprojlim }\, U_i$
and
$U \sim \underset {i\geq i_0}{\varprojlim }\, U_i$
and
for
![]() $n=0$
(resp. for
$n=0$
(resp. for
![]() $n=0,1$
, resp. for any
$n=0,1$
, resp. for any
![]() $n\geq 0$
).
$n\geq 0$
).
We will need the following lemma, which says that tilde-limits behave well under certain pullbacks.
Lemma 3.19. Let S be a good affinoid adic space over
![]() $\mathbb {Q}_p$
and let
$\mathbb {Q}_p$
and let
![]() $Y \approx \varprojlim _{i\in I} Y_i$
be a tilde-limit of good affinoid adic spaces over S.
$Y \approx \varprojlim _{i\in I} Y_i$
be a tilde-limit of good affinoid adic spaces over S.
-
1. Let
 $X \rightarrow S$
be a standard-smooth morphism from a good affinoid adic space X. Then we have a tilde-limit
$X \rightarrow S$
be a standard-smooth morphism from a good affinoid adic space X. Then we have a tilde-limit  $$\begin{align*}X\times_S Y \approx \varprojlim_i X\times_S Y_i.\end{align*}$$
$$\begin{align*}X\times_S Y \approx \varprojlim_i X\times_S Y_i.\end{align*}$$
-
2. Let
 $U \rightarrow Y$
be a standard-étale morphism, arising via pullback from
$U \rightarrow Y$
be a standard-étale morphism, arising via pullback from
 $U_{i_0} \rightarrow Y_{i_0}$
for some
$U_{i_0} \rightarrow Y_{i_0}$
for some
 $i_0\in I $
. Then if
$i_0\in I $
. Then if
 $U_i$
denotes the pullback of
$U_i$
denotes the pullback of
 $U_{i_0}$
along
$U_{i_0}$
along
 $Y_i \rightarrow Y_{i_0}$
for
$Y_i \rightarrow Y_{i_0}$
for
 $i\geq i_0$
, we have
$i\geq i_0$
, we have  $$\begin{align*}U \approx \varprojlim_{i\geq i_0} U_i.\end{align*}$$
$$\begin{align*}U \approx \varprojlim_{i\geq i_0} U_i.\end{align*}$$
Proof. The second point is [Reference Heuer22, Lemma 3.13]. In our case, it also follows from the first point if we redefine ![]() and
and ![]() . Let us now prove the first point. We claim that under our assumptions, the fiber products of diamonds
. Let us now prove the first point. We claim that under our assumptions, the fiber products of diamonds
![]() $X\times _S Y_i$
are representable by good affinoid adic spaces, namely the adic spectrum of
$X\times _S Y_i$
are representable by good affinoid adic spaces, namely the adic spectrum of
and similarly for Y. By assumption, the map
![]() $\mathcal {O}(S) \rightarrow \mathcal {O}(X)$
is a composition of rational open immersions, finite étale maps and adjunction of Tate variables. Then so is
$\mathcal {O}(S) \rightarrow \mathcal {O}(X)$
is a composition of rational open immersions, finite étale maps and adjunction of Tate variables. Then so is
![]() $\mathcal {O}(Y_i) \rightarrow \mathcal {O}(X)\, \widehat {\otimes }_{\mathcal {O}(S)} \,\mathcal {O}(Y_i)$
. It follows from Proposition 2.5 that the completed tensor product of Huber pairs above yields a good adic space, which then represents the diamond
$\mathcal {O}(Y_i) \rightarrow \mathcal {O}(X)\, \widehat {\otimes }_{\mathcal {O}(S)} \,\mathcal {O}(Y_i)$
. It follows from Proposition 2.5 that the completed tensor product of Huber pairs above yields a good adic space, which then represents the diamond
![]() $X\times _S Y_i$
.
$X\times _S Y_i$
.
Next, we want to show that the image of the map
is dense in its target. It is enough to show that the image of
is dense. This image is immediately seen to be dense in
![]() $\mathcal {O}(X)\otimes _{\mathcal {O}(S)} \mathcal {O}(Y)$
, which concludes.
$\mathcal {O}(X)\otimes _{\mathcal {O}(S)} \mathcal {O}(Y)$
, which concludes.
It remains to show the condition on topological spaces. The diamond functor commutes with fiber products and, on the level of sheaves, fiber products commute with inverse limits. It follows that
The topological spaces of an analytic adic space and its diamondification are identified [Reference Scholze47, Lemma 15.6]. On the level of diamonds, taking underlying topological spaces commutes with the inverse limit [Reference Scholze47, Lemma 11.22], which concludes.
Proof of Proposition 3.18
We start with the case
![]() $n=0$
.
$n=0$
.
Claim 3.20. In the situation of Proposition 3.18, assume furthermore that
![]() $U_{i_0}$
is standard-étale over
$U_{i_0}$
is standard-étale over
![]() $X'\times _{S'} Y_{i_0}$
where
$X'\times _{S'} Y_{i_0}$
where
![]() $X' \subseteq X$
and
$X' \subseteq X$
and
![]() $S'\subseteq S$
are affinoid open subspaces such that all
$S'\subseteq S$
are affinoid open subspaces such that all
![]() $Y,Y_i$
are defined over
$Y,Y_i$
are defined over
![]() $S'$
and the restriction
$S'$
and the restriction
![]() $\pi \colon X' \rightarrow S'$
is standard-smooth. Then we have an isomorphism
$\pi \colon X' \rightarrow S'$
is standard-smooth. Then we have an isomorphism
Proof. By Lemma 3.19.1-2, we find that
The claim now follows from Proposition 3.11.2.
Since standard-étale maps form a basis of the étale site of
![]() $X\times _S Y$
, it follows that we have an isomorphism of sheaves
$X\times _S Y$
, it follows that we have an isomorphism of sheaves
on the site
![]() , where
, where
![]() $q_i\colon X\times _S Y \rightarrow X\times _S Y_i$
denotes the projection and we denote the restriction of
$q_i\colon X\times _S Y \rightarrow X\times _S Y_i$
denotes the projection and we denote the restriction of
![]() $\mathcal {F}$
to the site
$\mathcal {F}$
to the site
![]() $(X \times _S Y)_{\operatorname {\mathrm {\acute {e}t}},\operatorname {\mathrm {qcqs}}}$
by the same symbol. The statement now follows from [48, Tag 09YP] in the abelian case, and the nonabelian case is deduced similarly.
$(X \times _S Y)_{\operatorname {\mathrm {\acute {e}t}},\operatorname {\mathrm {qcqs}}}$
by the same symbol. The statement now follows from [48, Tag 09YP] in the abelian case, and the nonabelian case is deduced similarly.
Corollary 3.21. Let
![]() $X \rightarrow S$
be a smooth qcqs morphism of good adic spaces over
$X \rightarrow S$
be a smooth qcqs morphism of good adic spaces over
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\mathcal {F}$
be a sheaf of sets (resp. groups, resp. abelian groups) on
$\mathcal {F}$
be a sheaf of sets (resp. groups, resp. abelian groups) on
![]() $\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property and let
$\operatorname {\mathrm {Adic}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property and let
![]() $n=0$
(resp.
$n=0$
(resp.
![]() $n=0,1$
, resp.
$n=0,1$
, resp.
![]() $n\geq 0$
).
$n\geq 0$
).
-
1. The sheaf
has the approximation property. $$\begin{align*}R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}\mathcal{F} \colon \operatorname{\mathrm{Adic}}_{S,\operatorname{\mathrm{\acute{e}t}}} \rightarrow \operatorname{\mathrm{Ab}} \end{align*}$$
$$\begin{align*}R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}\mathcal{F} \colon \operatorname{\mathrm{Adic}}_{S,\operatorname{\mathrm{\acute{e}t}}} \rightarrow \operatorname{\mathrm{Ab}} \end{align*}$$
-
2. We have
 $$\begin{align*}R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}\mathcal{F} \cong R^n\pi_{v,*}\mathcal{F}. \end{align*}$$
$$\begin{align*}R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}\mathcal{F} \cong R^n\pi_{v,*}\mathcal{F}. \end{align*}$$
-
3. The natural map (3.5) is an isomorphism
 $$\begin{align*}(R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\operatorname{\mathrm{rig}}}\mathcal{F})^{\diamondsuit} \xrightarrow{\cong} R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{F}.\end{align*}$$
$$\begin{align*}(R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\operatorname{\mathrm{rig}}}\mathcal{F})^{\diamondsuit} \xrightarrow{\cong} R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{F}.\end{align*}$$
Proof. Let
![]() $Y\approx \varprojlim _i Y_i$
be an affinoid perfectoid tilde-limit of good affinoid adic spaces over S. Let
$Y\approx \varprojlim _i Y_i$
be an affinoid perfectoid tilde-limit of good affinoid adic spaces over S. Let
![]() $V\rightarrow Y$
be a qcqs étale map, corresponding to a qcqs étale maps
$V\rightarrow Y$
be a qcqs étale map, corresponding to a qcqs étale maps
![]() $V_i \rightarrow Y_i$
for
$V_i \rightarrow Y_i$
for
![]() $i\gg 0$
. By Proposition 3.18, we have
$i\gg 0$
. By Proposition 3.18, we have
Sheafifying on Y yields
This proves that
![]() $R^n\pi _{\operatorname {\mathrm {\acute {E}t}},*}\mathcal {F}$
has the approximation property and is, in particular, a v-sheaf. Considering now
$R^n\pi _{\operatorname {\mathrm {\acute {E}t}},*}\mathcal {F}$
has the approximation property and is, in particular, a v-sheaf. Considering now
![]() $R^n\pi _{v,*}\mathcal {F}$
, which is the v-sheafification of the presheaf taking
$R^n\pi _{v,*}\mathcal {F}$
, which is the v-sheafification of the presheaf taking
![]() $Y \rightarrow S$
to
$Y \rightarrow S$
to
![]() $H_{v}^n(X\times _S Y,\mathcal {F})$
. By Proposition 3.11.3, we have
$H_{v}^n(X\times _S Y,\mathcal {F})$
. By Proposition 3.11.3, we have
We deduce that
Hence the first two points are proven. For the last point, we argue as in the proof of [Reference Heuer22, Cor. 3.16]. Namely, observe that the two sheaves under consideration are the étale sheafification of the following presheaves. The left-hand side comes from the presheaf
where the colimit runs over all factorization of
![]() $Y\rightarrow S$
into an adic space
$Y\rightarrow S$
into an adic space
![]() $Y_i$
smooth over S. Here we use that
$Y_i$
smooth over S. Here we use that
![]() so that it is enough to sheafify over Y. The right-hand side comes from the presheaf
so that it is enough to sheafify over Y. The right-hand side comes from the presheaf
By [Reference Heuer22, Prop. 3.17], we may write
where the limit ranges over all morphisms
![]() $Y \rightarrow Y_i$
into affinoid adic spaces smooth over S. It now follows from Proposition 3.18 that these two presheaves are isomorphic.
$Y \rightarrow Y_i$
into affinoid adic spaces smooth over S. It now follows from Proposition 3.18 that these two presheaves are isomorphic.
Proof of Proposition 3.16
-
1. Let us show that
 $$\begin{align*}R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}{\mathfrak{g}} = (R^n\pi_{\operatorname{\mathrm{\acute{e}t}},*}{\mathfrak{g}}) \otimes_{\mathcal{O}_{S_{\operatorname{\mathrm{\acute{e}t}}}}} \mathbb{G}_a.\end{align*}$$
$$\begin{align*}R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}{\mathfrak{g}} = (R^n\pi_{\operatorname{\mathrm{\acute{e}t}},*}{\mathfrak{g}}) \otimes_{\mathcal{O}_{S_{\operatorname{\mathrm{\acute{e}t}}}}} \mathbb{G}_a.\end{align*}$$
When
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, it follows from [Reference Heuer28, Cor. 3.10], which says that for any affinoid perfectoid Y over K
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, it follows from [Reference Heuer28, Cor. 3.10], which says that for any affinoid perfectoid Y over K  $$\begin{align*}H_{\operatorname{\mathrm{\acute{e}t}}}^n(X\times_K Y,{\mathfrak{g}}) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,{\mathfrak{g}}) \otimes_K \mathcal{O}(Y)\end{align*}$$
$$\begin{align*}H_{\operatorname{\mathrm{\acute{e}t}}}^n(X\times_K Y,{\mathfrak{g}}) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,{\mathfrak{g}}) \otimes_K \mathcal{O}(Y)\end{align*}$$
If K is perfectoid, loc. cit. also shows that
which yields $$\begin{align*}H_{v}^n(X\times_K Y,{\mathfrak{g}}) = H_{v}^n(X,{\mathfrak{g}}) \otimes_K \mathcal{O}(Y),\end{align*}$$
$$\begin{align*}H_{v}^n(X\times_K Y,{\mathfrak{g}}) = H_{v}^n(X,{\mathfrak{g}}) \otimes_K \mathcal{O}(Y),\end{align*}$$
 $$\begin{align*}R^n\pi_{v,*}^{\diamondsuit}{\mathfrak{g}} = H_v^n(X,{\mathfrak{g}}) \otimes_K \mathbb{G}_a.\end{align*}$$
$$\begin{align*}R^n\pi_{v,*}^{\diamondsuit}{\mathfrak{g}} = H_v^n(X,{\mathfrak{g}}) \otimes_K \mathbb{G}_a.\end{align*}$$
Assume now that S is arbitrary and that
 ${\mathfrak {g}}$
is the pullback of a vector bundle E on S. By the projection formula, we may assume that
${\mathfrak {g}}$
is the pullback of a vector bundle E on S. By the projection formula, we may assume that
 ${\mathfrak {g}}=\mathbb {G}_a$
. It now follows from the fact that
${\mathfrak {g}}=\mathbb {G}_a$
. It now follows from the fact that
 $R^n\pi _{\operatorname {\mathrm {an}},*}\mathcal {O}_X$
is an analytic vector bundle whose formation commutes with base change along any perfectoid space or rigid space
$R^n\pi _{\operatorname {\mathrm {an}},*}\mathcal {O}_X$
is an analytic vector bundle whose formation commutes with base change along any perfectoid space or rigid space
 $Y \rightarrow S$
[Reference Heuer28, Thm. 5.7.3]. Note that this proves the
$Y \rightarrow S$
[Reference Heuer28, Thm. 5.7.3]. Note that this proves the
 $4$
th point for
$4$
th point for
 $\mathcal {G}={\mathfrak {g}}$
.
$\mathcal {G}={\mathfrak {g}}$
. -
2. By Corollary 3.21.2-3, we have, for any
 $1\leq m \leq \infty $
$1\leq m \leq \infty $
 $$\begin{align*}R^n\pi_{v,*}^{\diamondsuit}\mathcal{G}[p^{m}] = R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{G}[p^{m}] = (R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\operatorname{\mathrm{rig}}}\mathcal{G}[p^{m}])^{\diamondsuit}.\end{align*}$$
$$\begin{align*}R^n\pi_{v,*}^{\diamondsuit}\mathcal{G}[p^{m}] = R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{G}[p^{m}] = (R^n\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\operatorname{\mathrm{rig}}}\mathcal{G}[p^{m}])^{\diamondsuit}.\end{align*}$$
By proper base change (Theorem 2.12.2, the sheaf
 $R^n\pi _{\operatorname {\mathrm {\acute {E}t}},*}^{\operatorname {\mathrm {rig}}}\mathcal {G}[p^{m}]$
arises from the ind-Zariski-constructible sheaf
$R^n\pi _{\operatorname {\mathrm {\acute {E}t}},*}^{\operatorname {\mathrm {rig}}}\mathcal {G}[p^{m}]$
arises from the ind-Zariski-constructible sheaf
 $R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {G}[p^{m}]$
via pullback along
$R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {G}[p^{m}]$
via pullback along
 $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}} \rightarrow S_{\operatorname {\mathrm {\acute {e}t}}}$
, which shows the first part of the statement. If
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}} \rightarrow S_{\operatorname {\mathrm {\acute {e}t}}}$
, which shows the first part of the statement. If
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, we conclude that the ind-Zariski-constructible sheaf
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, we conclude that the ind-Zariski-constructible sheaf
 $R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {G}[p^{m}]$
is representable by an étale-locally constant rigid group. Assume now that
$R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {G}[p^{m}]$
is representable by an étale-locally constant rigid group. Assume now that
 $[p]\colon \widehat {\mathcal {G}} \rightarrow \widehat {\mathcal {G}}$
is finite étale surjective. For
$[p]\colon \widehat {\mathcal {G}} \rightarrow \widehat {\mathcal {G}}$
is finite étale surjective. For
 $m< \infty $
, the group
$m< \infty $
, the group
 $\mathcal {G}[p^m] \rightarrow S$
is finite étale, such that
$\mathcal {G}[p^m] \rightarrow S$
is finite étale, such that
 $R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {G}[p^{m}]$
is a local system, by [Reference Scholze and Weinstein50, Thm. 10.5.1], and is thus easily seen to be representable by a finite étale S-group. By a standard limit argument (see the proof of [Reference Heuer28, Thm. 4.4]), we deduce that
$R^n\pi _{\operatorname {\mathrm {\acute {e}t}},*}\mathcal {G}[p^{m}]$
is a local system, by [Reference Scholze and Weinstein50, Thm. 10.5.1], and is thus easily seen to be representable by a finite étale S-group. By a standard limit argument (see the proof of [Reference Heuer28, Thm. 4.4]), we deduce that
 $\mathbb {M}^n = R^n\pi _{v,*}^{\diamondsuit }T_p\mathcal {G}$
is a lisse
$\mathbb {M}^n = R^n\pi _{v,*}^{\diamondsuit }T_p\mathcal {G}$
is a lisse
 $\mathbb {Z}_p$
-sheaf on
$\mathbb {Z}_p$
-sheaf on
 $S_v$
, where
$S_v$
, where
 $T_p\mathcal {G} = \varprojlim _m \mathcal {G}[p^m]$
is the Tate module. It remains to show that
$T_p\mathcal {G} = \varprojlim _m \mathcal {G}[p^m]$
is the Tate module. It remains to show that
 $R^n\pi _{\operatorname {\mathrm {\acute {E}t}},*}^{\diamondsuit }\mathcal {G}[p^{\infty }]$
is representable by an étale S-group. By writing
$R^n\pi _{\operatorname {\mathrm {\acute {E}t}},*}^{\diamondsuit }\mathcal {G}[p^{\infty }]$
is representable by an étale S-group. By writing
 $\mathcal {G}[p^{\infty }] = T_p\mathcal {G}[\tfrac {1}{p}]/T_p\mathcal {G}$
, we obtain a short exact sequence of v-sheaves over S where
$\mathcal {G}[p^{\infty }] = T_p\mathcal {G}[\tfrac {1}{p}]/T_p\mathcal {G}$
, we obtain a short exact sequence of v-sheaves over S where
 $\mathbb {M}_{\operatorname {\mathrm {tor}}}^{n+1}$
is the torsion subsheaf of
$\mathbb {M}_{\operatorname {\mathrm {tor}}}^{n+1}$
is the torsion subsheaf of
 $\mathbb {M}^{n+1}$
, a finite locally free abelian sheaf. Hence it is enough to show that
$\mathbb {M}^{n+1}$
, a finite locally free abelian sheaf. Hence it is enough to show that
 $\mathbb {M}^n[\tfrac {1}{p}]/\mathbb {M}^n$
is representable by a separated étale S-group. By [Reference Scholze47, Prop. 10.11.(iv)], this may be checked v-locally. Hence we may assume that S is strictly totally disconnected perfectoid space and
$\mathbb {M}^n[\tfrac {1}{p}]/\mathbb {M}^n$
is representable by a separated étale S-group. By [Reference Scholze47, Prop. 10.11.(iv)], this may be checked v-locally. Hence we may assume that S is strictly totally disconnected perfectoid space and
 $\mathbb {M}^n \cong \underline {M}$
for a finitely generated
$\mathbb {M}^n \cong \underline {M}$
for a finitely generated
 $\mathbb {Z}_p$
-module M, in which case it is clear.
$\mathbb {Z}_p$
-module M, in which case it is clear.
-
3. Applying
 $R\pi _{\tau ,*}^{\diamondsuit }$
to the logarithm exact sequence (2.2) yields a long exact sequence of sheaves on
$R\pi _{\tau ,*}^{\diamondsuit }$
to the logarithm exact sequence (2.2) yields a long exact sequence of sheaves on
 $\operatorname {\mathrm {Perf}}_{S,\tau }$
$\operatorname {\mathrm {Perf}}_{S,\tau }$

We claim that
 $\delta $
vanishes, for all
$\delta $
vanishes, for all
 $n\geq 0$
. For this, we use the following argument that we learned in [Reference Heuer and Xu33, Prop. 6.1.15]. Assume first that
$n\geq 0$
. For this, we use the following argument that we learned in [Reference Heuer and Xu33, Prop. 6.1.15]. Assume first that
 $\tau $
is the étale topology. By the first two points, the source of
$\tau $
is the étale topology. By the first two points, the source of
 $\delta $
is a vector bundle while its target comes from pullback from an ind-Zariski-constructible sheaf on
$\delta $
is a vector bundle while its target comes from pullback from an ind-Zariski-constructible sheaf on
 $S_{\operatorname {\mathrm {\acute {e}t}}}$
. Hence, by [Reference Huber31, Prop. 2.6.1], the vanishing of
$S_{\operatorname {\mathrm {\acute {e}t}}}$
. Hence, by [Reference Huber31, Prop. 2.6.1], the vanishing of
 $\delta $
may be checked on geometric fibers. We may thus assume that
$\delta $
may be checked on geometric fibers. We may thus assume that
 $S=\operatorname {\mathrm {Spa}}(C,C^+)$
for an algebraically closed field C, in which case for a discrete group
$S=\operatorname {\mathrm {Spa}}(C,C^+)$
for an algebraically closed field C, in which case for a discrete group $$\begin{align*}R^{n}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}{\mathfrak{g}} \cong \mathbb{G}_a^{\oplus r}, \quad R^{n+1}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{G}[p^{\infty}] = \underline{\Lambda},\end{align*}$$
$$\begin{align*}R^{n}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}{\mathfrak{g}} \cong \mathbb{G}_a^{\oplus r}, \quad R^{n+1}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{G}[p^{\infty}] = \underline{\Lambda},\end{align*}$$
 $\Lambda $
. Now there is no nonzero maps of groups from the connected rigid group
$\Lambda $
. Now there is no nonzero maps of groups from the connected rigid group
 $\mathbb {G}_a^{\oplus r}$
to a discrete group. This shows that
$\mathbb {G}_a^{\oplus r}$
to a discrete group. This shows that
 $\delta =0$
as required. When
$\delta =0$
as required. When
 $\tau =v$
, the vanishing of
$\tau =v$
, the vanishing of
 $\delta $
can be shown after pulling back along a pro-étale cover by a perfectoid space
$\delta $
can be shown after pulling back along a pro-étale cover by a perfectoid space
 $\widetilde {S} \rightarrow S$
. Then the above argument applies verbatim over
$\widetilde {S} \rightarrow S$
. Then the above argument applies verbatim over
 $\widetilde {S}$
, where
$\widetilde {S}$
, where
 $R^{n}\pi _{v,*}^{\diamondsuit }{\mathfrak {g}}$
is representable by an étale vector bundle, since étale and v-vector bundles on a perfectoid space agree [Reference Kedlaya and Liu36, Thm. 3.5.8].
$R^{n}\pi _{v,*}^{\diamondsuit }{\mathfrak {g}}$
is representable by an étale vector bundle, since étale and v-vector bundles on a perfectoid space agree [Reference Kedlaya and Liu36, Thm. 3.5.8].
-
4. To show that the natural map
is an isomorphism, it suffices, by the $$\begin{align*}(R^{n}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\operatorname{\mathrm{rig}}}\mathcal{G})^{\diamondsuit} \rightarrow R^{n}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{G}\end{align*}$$
$$\begin{align*}(R^{n}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\operatorname{\mathrm{rig}}}\mathcal{G})^{\diamondsuit} \rightarrow R^{n}\pi_{\operatorname{\mathrm{\acute{E}t}},*}^{\diamondsuit}\mathcal{G}\end{align*}$$
 $5$
-Lemma and Corollary 3.21.3 applied to the sheaf
$5$
-Lemma and Corollary 3.21.3 applied to the sheaf
 $\overline {\mathcal {G}} = \mathcal {G}/\widehat {\mathcal {G}}$
, to show the statement with
$\overline {\mathcal {G}} = \mathcal {G}/\widehat {\mathcal {G}}$
, to show the statement with
 $\mathcal {G}$
replaced by
$\mathcal {G}$
replaced by
 $\widehat {\mathcal {G}}$
. Applying again Corollary 3.21.3 to the sheaf
$\widehat {\mathcal {G}}$
. Applying again Corollary 3.21.3 to the sheaf
 $\mathcal {G}[p^{\infty }]$
, it is enough to show the statement for
$\mathcal {G}[p^{\infty }]$
, it is enough to show the statement for
 ${\mathfrak {g}}$
, which we have already seen in the proof of the first point. This completes the proof.
${\mathfrak {g}}$
, which we have already seen in the proof of the first point. This completes the proof.
3.4 The geometric spectral sequence
We now introduce the geometric Hodge–Tate spectral sequence. We fix a perfectoid field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\pi \colon X \rightarrow S$
be a smooth morphism of seminormal rigid spaces over K. From now on we will lighten the notation and write
$\pi \colon X \rightarrow S$
be a smooth morphism of seminormal rigid spaces over K. From now on we will lighten the notation and write
![]() $\pi _{\tau ,*}$
instead of
$\pi _{\tau ,*}$
instead of
![]() $\pi _{\tau ,*}^{\diamondsuit }$
for
$\pi _{\tau ,*}^{\diamondsuit }$
for
![]() $\tau \in \{\operatorname {\mathrm {\acute {E}t}},v\}$
. We recall that we denote by
$\tau \in \{\operatorname {\mathrm {\acute {E}t}},v\}$
. We recall that we denote by
![]() $\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
the category of smoothoid spaces Y (cf. Definition 2.6) together with a morphism
$\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
the category of smoothoid spaces Y (cf. Definition 2.6) together with a morphism
![]() $Y\rightarrow X$
, equipped with the étale topology. We have natural morphisms of sites fitting in a commutative diagram
$Y\rightarrow X$
, equipped with the étale topology. We have natural morphisms of sites fitting in a commutative diagram

Definition 3.22. Let
![]() $\mathcal {G}$
be a smooth commutative X-group, viewed as a sheaf on
$\mathcal {G}$
be a smooth commutative X-group, viewed as a sheaf on
![]() $X_v$
. We define the geometric Hodge–Tate spectral sequence with
$X_v$
. We define the geometric Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients to be the following Leray spectral sequence, consisting of sheaves on
$\mathcal {G}$
-coefficients to be the following Leray spectral sequence, consisting of sheaves on
![]() $\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
When
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, we may compare it to the group-theoretic Hodge–Tate spectral sequence (3.1).
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, we may compare it to the group-theoretic Hodge–Tate spectral sequence (3.1).
Lemma 3.23. Let
![]() $\pi \colon X \rightarrow S=Spa(K,K^+)$
be a smooth rigid space. The canonical maps given by étale sheafification
$\pi \colon X \rightarrow S=Spa(K,K^+)$
be a smooth rigid space. The canonical maps given by étale sheafification
commute with differentials. The induced maps on the
![]() $E_{\infty }$
-page are compatible with the natural maps on the abutments given by étale sheafification.
$E_{\infty }$
-page are compatible with the natural maps on the abutments given by étale sheafification.
If K is algebraically closed, the above maps are isomorphisms
Proof. We have a commutative diagram

By the usual comparison of cohomology between small and big étale sites, it is equivalent to work with
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}$
or
$X_{\operatorname {\mathrm {\acute {e}t}}}$
or
![]() $\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
to compute
$\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
to compute
![]() $E_{2}^{ij}$
. By construction of the Leray sequence, there is a collection of isomorphisms
$E_{2}^{ij}$
. By construction of the Leray sequence, there is a collection of isomorphisms
compatible with differentials, where
![]() $ I^{\bullet ,\bullet }$
is Cartan–Eilenberg resolution of
$ I^{\bullet ,\bullet }$
is Cartan–Eilenberg resolution of
![]() $R\mu _*\mathcal {G}$
. These isomorphisms are immediately seen to induce maps
$R\mu _*\mathcal {G}$
. These isomorphisms are immediately seen to induce maps
that coincide with étale sheafification for
![]() $r=2$
. Moreover, if K is assumed to be algebraically closed, taking
$r=2$
. Moreover, if K is assumed to be algebraically closed, taking
![]() $(K,K^+)$
-rational points is an exact functor, such that the comparison maps
$(K,K^+)$
-rational points is an exact functor, such that the comparison maps
![]() $E_r^{ij} \rightarrow \mathbf {E}_r^{ij}(K)$
are isomorphisms, for each
$E_r^{ij} \rightarrow \mathbf {E}_r^{ij}(K)$
are isomorphisms, for each
![]() $0\leq r \leq \infty $
. This concludes the proof.
$0\leq r \leq \infty $
. This concludes the proof.
The geometric Hodge–Tate spectral sequence takes the following explicit form.
Proposition 3.24. Let
![]() $\pi \colon X \rightarrow S$
be a proper smooth map of seminormal rigid spaces and let
$\pi \colon X \rightarrow S$
be a proper smooth map of seminormal rigid spaces and let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group. Assume either that
$\mathcal {G}$
be an admissible locally p-divisible X-group. Assume either that
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
or that
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
or that
![]() ${\mathfrak {g}}$
comes from a vector bundle on S. Then the geometric Hodge–Tate spectral sequence with
${\mathfrak {g}}$
comes from a vector bundle on S. Then the geometric Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients (3.8) has the following form
$\mathcal {G}$
-coefficients (3.8) has the following form
 $$ \begin{align} \mathbf{E}_2^{ij}(\mathcal{G}) = \left\{\begin{aligned} &R^i\pi_{\operatorname{\mathrm{\acute{E}t}},*}(\widetilde{\Omega}_{X/S}^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow R^{i+j}(\mu_* \pi_{v,*})\mathcal{G}. \end{align} $$
$$ \begin{align} \mathbf{E}_2^{ij}(\mathcal{G}) = \left\{\begin{aligned} &R^i\pi_{\operatorname{\mathrm{\acute{E}t}},*}(\widetilde{\Omega}_{X/S}^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow R^{i+j}(\mu_* \pi_{v,*})\mathcal{G}. \end{align} $$
Remark 3.25. We will prove later in Corollary 3.32 that the abutment satisfies
Remark 3.26. For
![]() $\mathcal {G} = \mathbb {G}_a$
, this recovers the relative Hodge–Tate spectral sequence of [Reference Heuer28]. Note that we require the base S to be seminormal, while loc. cit. allows reduced rigid spaces.
$\mathcal {G} = \mathbb {G}_a$
, this recovers the relative Hodge–Tate spectral sequence of [Reference Heuer28]. Note that we require the base S to be seminormal, while loc. cit. allows reduced rigid spaces.
In order to prove Proposition 3.24, we begin by recalling that Heuer’s Hodge–Tate logarithm map glues to the big étale site
![]() $\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
.
$\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
.
Lemma 3.27. Let X be a rigid space and let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group. Then we have a natural isomorphism of sheaves on
$\mathcal {G}$
be an admissible locally p-divisible X-group. Then we have a natural isomorphism of sheaves on
![]() $\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
 $$\begin{align*}R^j\mu_*\mathcal{G} =\begin{cases} \widetilde{\Omega}^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G}) \quad &\text{if }j>0\\ \mathcal{G} \quad &\text{if }j=0, \end{cases} \end{align*}$$
$$\begin{align*}R^j\mu_*\mathcal{G} =\begin{cases} \widetilde{\Omega}^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G}) \quad &\text{if }j>0\\ \mathcal{G} \quad &\text{if }j=0, \end{cases} \end{align*}$$
where
![]() $\widetilde {\Omega }^j$
is the sheaf on
$\widetilde {\Omega }^j$
is the sheaf on
![]() $\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
defined at (2.1).
$\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
defined at (2.1).
Proof. For
![]() $Z \in \operatorname {\mathrm {Smd}}_{X}$
, the isomorphism
$Z \in \operatorname {\mathrm {Smd}}_{X}$
, the isomorphism
![]() $\operatorname {\mathrm {HTlog}}_Z$
on
$\operatorname {\mathrm {HTlog}}_Z$
on
![]() $Z_{\operatorname {\mathrm {\acute {e}t}}}$
of Proposition 3.3 is natural in Z. This allows us to glue these isomorphisms to an isomorphism of sheaves on
$Z_{\operatorname {\mathrm {\acute {e}t}}}$
of Proposition 3.3 is natural in Z. This allows us to glue these isomorphisms to an isomorphism of sheaves on
![]() $\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
, as required.
$\operatorname {\mathrm {Smd}}_{X,\operatorname {\mathrm {\acute {e}t}}}$
, as required.
Proposition 3.24 now follows from the following result.
Proposition 3.28. Assume that we are in the situation of Proposition 3.24. Then for any
![]() $i\geq 0$
and
$i\geq 0$
and
![]() $j>0$
,
$j>0$
,
and this sheaf is an étale vector bundle on S. If
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, it is equal to
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, it is equal to
Proof. Let us take an affinoid perfectoid
![]() $Y\xrightarrow {g} S$
and form the following cartesian diagram of adic spaces
$Y\xrightarrow {g} S$
and form the following cartesian diagram of adic spaces

The sheaf
is the étale sheafification of the presheaf taking
![]() $Y \in \operatorname {\mathrm {Perf}}_S$
to
$Y \in \operatorname {\mathrm {Perf}}_S$
to
where we use Example 2.9. This shows that
and it remains to show that this sheaf is a vector bundle. In the case where
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, we have by [Reference Heuer28, Cor. 3.10.1],
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, we have by [Reference Heuer28, Cor. 3.10.1],
This shows that
Assume now that we are in the second case, so that
![]() $\operatorname {\mathrm {Lie}}(\mathcal {G}) = \pi ^*E$
for some vector bundle E on S. By the projection formula and the above observations, it is enough to show that
$\operatorname {\mathrm {Lie}}(\mathcal {G}) = \pi ^*E$
for some vector bundle E on S. By the projection formula and the above observations, it is enough to show that
![]() $R^i\pi _{\operatorname {\mathrm {\acute {E}t}},*}\widetilde {\Omega }_{X/S}^j$
is a vector bundle. It follows from the fact that
$R^i\pi _{\operatorname {\mathrm {\acute {E}t}},*}\widetilde {\Omega }_{X/S}^j$
is a vector bundle. It follows from the fact that
![]() $R^i\pi _{\operatorname {\mathrm {an}},*}\widetilde {\Omega }_{X/S}^j$
is a vector bundle whose formation commutes with pullbacks along perfectoid spaces
$R^i\pi _{\operatorname {\mathrm {an}},*}\widetilde {\Omega }_{X/S}^j$
is a vector bundle whose formation commutes with pullbacks along perfectoid spaces
![]() $Y \rightarrow S$
[Reference Heuer28, Thm. 5.7.3].
$Y \rightarrow S$
[Reference Heuer28, Thm. 5.7.3].
3.5 Degeneration
We now settle to prove the degeneration of the Hodge–Tate spectral sequences. We continue to denote by
![]() $(K,K^+)$
a fixed perfectoid field extension of
$(K,K^+)$
a fixed perfectoid field extension of
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Theorem 3.29. Let
![]() $\pi \colon X \rightarrow S$
be a proper smooth map of seminormal rigid space over K and let
$\pi \colon X \rightarrow S$
be a proper smooth map of seminormal rigid space over K and let
![]() $\mathcal {G}$
be an admissible locally p-divisible group over X. Assume either that
$\mathcal {G}$
be an admissible locally p-divisible group over X. Assume either that
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
or that
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
or that
![]() ${\mathfrak {g}}$
comes from a vector bundle on S. Then the geometric Hodge–Tate spectral sequence with
${\mathfrak {g}}$
comes from a vector bundle on S. Then the geometric Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients
$\mathcal {G}$
-coefficients
 $$ \begin{align*} \mathbf{E}_2^{ij}(\mathcal{G}) = \left\{\begin{aligned} &R^i\pi_{\operatorname{\mathrm{\acute{E}t}},*}(\widetilde{\Omega}_{X/S}^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow R^{i+j}(\mu_*\pi_{v,*})\mathcal{G} \end{align*} $$
$$ \begin{align*} \mathbf{E}_2^{ij}(\mathcal{G}) = \left\{\begin{aligned} &R^i\pi_{\operatorname{\mathrm{\acute{E}t}},*}(\widetilde{\Omega}_{X/S}^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &{\mathbf{Bun}}_{\mathcal{G},\operatorname{\mathrm{\acute{e}t}}}^i \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow R^{i+j}(\mu_*\pi_{v,*})\mathcal{G} \end{align*} $$
degenerates at the
![]() $E_2$
-page.
$E_2$
-page.
Before we pass to the proof of the theorem, we note that it immediately implies the following.
Corollary 3.30. Let X be a proper smooth rigid spaces over K with K algebraically closed, and let
![]() $\mathcal {G}$
be an admissible locally p-divisible group over X. Then the Hodge–Tate spectral sequence with
$\mathcal {G}$
be an admissible locally p-divisible group over X. Then the Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients
$\mathcal {G}$
-coefficients
 $$ \begin{align*} E_2^{ij}(\mathcal{G})= \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\widetilde{\Omega}_X^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\mathcal{G}) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_{v}^{i+j}(X,\mathcal{G}). \end{align*} $$
$$ \begin{align*} E_2^{ij}(\mathcal{G})= \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\widetilde{\Omega}_X^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\mathcal{G}) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_{v}^{i+j}(X,\mathcal{G}). \end{align*} $$
degenerates at
![]() $E_2$
.
$E_2$
.
Proof. This follows from Theorem 3.29 in the case
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
and the fact that the comparison maps (3.9) are isomorphisms, as K is assumed to be algebraically closed.
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
and the fact that the comparison maps (3.9) are isomorphisms, as K is assumed to be algebraically closed.
We now turn towards the proof of Theorem 3.29. We start with the case where
![]() $\mathcal {G}={\mathfrak {g}}$
is a vector bundle.
$\mathcal {G}={\mathfrak {g}}$
is a vector bundle.
Proposition 3.31. In the situation of Theorem 3.29, the geometric Hodge–Tate spectral sequence
degenerates at
![]() $E_2$
.
$E_2$
.
Proof. Let us first show that the abutment satisfies
By a Leray sequence argument, it is enough to show that
Let
![]() $Y \in \operatorname {\mathrm {Perf}}_S$
be an affinoid perfectoid space and let
$Y \in \operatorname {\mathrm {Perf}}_S$
be an affinoid perfectoid space and let
![]() $\nu \colon Y_v \rightarrow Y_{\operatorname {\mathrm {\acute {e}t}}}$
be the natural map. It is enough to show that
$\nu \colon Y_v \rightarrow Y_{\operatorname {\mathrm {\acute {e}t}}}$
be the natural map. It is enough to show that
We know by Proposition 3.16.1 that
![]() $E = {\mathbf {Bun}}_{{\mathfrak {g}},v}^{n}$
is represented by a v-vector bundle, but étale and v-vector bundles on Y agree by [Reference Kedlaya and Liu36, Thm. 5.3.8]. Therefore Proposition 3.3 applies and we find that
$E = {\mathbf {Bun}}_{{\mathfrak {g}},v}^{n}$
is represented by a v-vector bundle, but étale and v-vector bundles on Y agree by [Reference Kedlaya and Liu36, Thm. 5.3.8]. Therefore Proposition 3.3 applies and we find that
as required.
We now prove the degeneration of the sequence. Let us first assume that
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
. In that case, by [Reference Heuer28, Cor. 3.10.1], we further have, for any perfectoid space Y
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
. In that case, by [Reference Heuer28, Cor. 3.10.1], we further have, for any perfectoid space Y
This shows that
The geometric Hodge–Tate spectral sequence thus has the following shape
and its degeneration can clearly be checked on K-points, which is Proposition 3.4. Let us now assume that S is arbitrary and that
![]() ${\mathfrak {g}}$
comes from a vector bundle on S. In that case the statement follows from the projection formula and the degeneration of the relative Hodge–Tate spectral sequence for
${\mathfrak {g}}$
comes from a vector bundle on S. In that case the statement follows from the projection formula and the degeneration of the relative Hodge–Tate spectral sequence for
![]() $\mathcal {O}_X$
[Reference Heuer28, Cor. 5.12].
$\mathcal {O}_X$
[Reference Heuer28, Cor. 5.12].
Proof of Theorem 3.29
We have morphisms of X-groups and hence of v-sheaves
These induce morphisms between the
![]() $E_2$
-pages of their respective geometric Hodge–Tate spectral sequences. Moreover, these maps induce isomorphisms
$E_2$
-pages of their respective geometric Hodge–Tate spectral sequences. Moreover, these maps induce isomorphisms
for all
![]() $j\geq 1$
, by Lemma 3.27. These induce isomorphisms between the respective terms
$j\geq 1$
, by Lemma 3.27. These induce isomorphisms between the respective terms
![]() $\mathbf {E}_2^{ij}$
, for
$\mathbf {E}_2^{ij}$
, for
![]() $j\geq 1$
and any i. As a consequence, since the geometric Hodge–Tate spectral sequence for
$j\geq 1$
and any i. As a consequence, since the geometric Hodge–Tate spectral sequence for
![]() ${\mathfrak {g}}$
degenerates, by Proposition 3.31, we deduce that
${\mathfrak {g}}$
degenerates, by Proposition 3.31, we deduce that
![]() $\mathbf {d}_2^{ij}\colon \mathbf {E}_2^{ij}(\mathcal {G}) \rightarrow \mathbf {E}_2^{i+2,j-1}(\mathcal {G})$
is the zero map, for all
$\mathbf {d}_2^{ij}\colon \mathbf {E}_2^{ij}(\mathcal {G}) \rightarrow \mathbf {E}_2^{i+2,j-1}(\mathcal {G})$
is the zero map, for all
![]() $j\geq 2$
and all i. It remains to show that the differential
$j\geq 2$
and all i. It remains to show that the differential
vanishes, for all
![]() $i\geq 0$
. We have a commutative diagram
$i\geq 0$
. We have a commutative diagram

so that it is enough to show that
![]() $\mathbf {d}=\mathbf {d}_2^{i,1}(\widehat {\mathcal {G}}) =0$
. From the above diagram, we have a factorization
$\mathbf {d}=\mathbf {d}_2^{i,1}(\widehat {\mathcal {G}}) =0$
. From the above diagram, we have a factorization

As in the proof of Proposition 3.16.3, we deduce that, as the target of
![]() $\mathbf {d}'$
is an ind-Zariski-constructible sheaf on
$\mathbf {d}'$
is an ind-Zariski-constructible sheaf on
![]() $S_{\operatorname {\mathrm {\acute {e}t}}}$
(Proposition 3.16.3 and its source is fiberwise connected (Proposition 3.28), it must be the zero map. Hence
$S_{\operatorname {\mathrm {\acute {e}t}}}$
(Proposition 3.16.3 and its source is fiberwise connected (Proposition 3.28), it must be the zero map. Hence
![]() $\mathbf {d}=\mathbf {d}_2^{i,2}(\widehat {\mathcal {G}})$
vanishes, as required.
$\mathbf {d}=\mathbf {d}_2^{i,2}(\widehat {\mathcal {G}})$
vanishes, as required.
Corollary 3.32. Assume we are in the situation of Theorem 3.29. Then if
![]() $\mu \colon \operatorname {\mathrm {Perf}}_{S,v} \rightarrow \operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
denotes the natural map of sites,
$\mu \colon \operatorname {\mathrm {Perf}}_{S,v} \rightarrow \operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
denotes the natural map of sites,
In particular, the abutment of the geometric Hodge–Tate spectral sequence satisfies
Proof. The last equality in the statement follows from the first part, using the Leray sequence computing
![]() $R^{n}(\mu _*\pi _{v,*})\mathcal {G}$
. Let’s prove the first part, starting with the case
$R^{n}(\mu _*\pi _{v,*})\mathcal {G}$
. Let’s prove the first part, starting with the case
![]() $\mathcal {G}=\widehat {\mathcal {G}}$
. Let Y be any affinoid perfectoid space over S and consider the canonical map
$\mathcal {G}=\widehat {\mathcal {G}}$
. Let Y be any affinoid perfectoid space over S and consider the canonical map
![]() $\nu \colon Y_v \rightarrow Y_{\operatorname {\mathrm {\acute {e}t}}}$
. We need to show that
$\nu \colon Y_v \rightarrow Y_{\operatorname {\mathrm {\acute {e}t}}}$
. We need to show that
From the short exact sequence (3.6), it is enough to show that
By Corollary 3.21.1-2, the sheaf
![]() ${\mathbf {Bun}}_{\widehat {\mathcal {G}}[p^{\infty }],v}^{n}$
has the approximation property, hence it follows from Proposition 3.11.3 that the left term vanishes. The vanishing of the right term was already shown in the proof of Proposition 3.31.
${\mathbf {Bun}}_{\widehat {\mathcal {G}}[p^{\infty }],v}^{n}$
has the approximation property, hence it follows from Proposition 3.11.3 that the left term vanishes. The vanishing of the right term was already shown in the proof of Proposition 3.31.
We now treat the case of general
![]() $\mathcal {G}$
. For this, we need the following intermediary result.
$\mathcal {G}$
. For this, we need the following intermediary result.
Lemma 3.33. In the situation of Theorem 3.29, there exists a surjection
![]() $V \rightarrow {\mathbf {Bun}}_{\mathcal {G},v}^n$
of v-sheaves on
$V \rightarrow {\mathbf {Bun}}_{\mathcal {G},v}^n$
of v-sheaves on
![]() $\operatorname {\mathrm {Perf}}_{S}$
, where V is a smooth S-space.
$\operatorname {\mathrm {Perf}}_{S}$
, where V is a smooth S-space.
Let us assume the lemma. We have an exact sequence of v-sheaves on
![]() $\operatorname {\mathrm {Perf}}_{S,v}$
$\operatorname {\mathrm {Perf}}_{S,v}$
Those sheaves and the above exact sequence admit a natural extension to
![]() $\operatorname {\mathrm {Adic}}_{S,v}$
. By Corollary 3.21, the sheaves
$\operatorname {\mathrm {Adic}}_{S,v}$
. By Corollary 3.21, the sheaves
![]() ${\mathbf {Bun}}_{\overline {\mathcal {G}},v}^n$
satisfy the approximation property. We claim that the sheaves
${\mathbf {Bun}}_{\overline {\mathcal {G}},v}^n$
satisfy the approximation property. We claim that the sheaves
![]() $\operatorname {\mathrm {Ker}}(\delta _n)$
and
$\operatorname {\mathrm {Ker}}(\delta _n)$
and
![]() $\operatorname {\mathrm {Im}}(\delta _n)$
also satisfy the approximation property. Indeed, consider the composition
$\operatorname {\mathrm {Im}}(\delta _n)$
also satisfy the approximation property. Indeed, consider the composition
![]() $V\rightarrow {\mathbf {Bun}}_{\mathcal {G},v}^n \rightarrow {\mathbf {Bun}}_{\overline {\mathcal {G}},v}^n$
, where
$V\rightarrow {\mathbf {Bun}}_{\mathcal {G},v}^n \rightarrow {\mathbf {Bun}}_{\overline {\mathcal {G}},v}^n$
, where
![]() $V \rightarrow {\mathbf {Bun}}_{\mathcal {G},v}^n$
is as in Lemma 3.33. Then by Proposition 3.12, the diamond
$V \rightarrow {\mathbf {Bun}}_{\mathcal {G},v}^n$
is as in Lemma 3.33. Then by Proposition 3.12, the diamond
is open in
![]() $V \times _S V$
, such that the étale quotient
$V \times _S V$
, such that the étale quotient
![]() $V/^{\operatorname {\mathrm {\acute {e}t}}}R$
has the approximation property. In particular, it coincides with its v-sheafification
$V/^{\operatorname {\mathrm {\acute {e}t}}}R$
has the approximation property. In particular, it coincides with its v-sheafification
![]() $V/^{v}R = \operatorname {\mathrm {Ker}}(\delta _n)$
. We now consider the short exact sequence of étale sheaves
$V/^{v}R = \operatorname {\mathrm {Ker}}(\delta _n)$
. We now consider the short exact sequence of étale sheaves
where the first and second sheaves satisfy the approximation property. It is then easily seen that the third sheaf
![]() $\operatorname {\mathrm {Im}}_{\operatorname {\mathrm {\acute {e}t}}}(\delta _n)$
automatically satisfies the approximation property as well. In particular,
$\operatorname {\mathrm {Im}}_{\operatorname {\mathrm {\acute {e}t}}}(\delta _n)$
automatically satisfies the approximation property as well. In particular,
![]() $\operatorname {\mathrm {Im}}_{\operatorname {\mathrm {\acute {e}t}}}(\delta _n)$
is a v-sheaf and thus the above sequence is also right-exact in the v-topology.
$\operatorname {\mathrm {Im}}_{\operatorname {\mathrm {\acute {e}t}}}(\delta _n)$
is a v-sheaf and thus the above sequence is also right-exact in the v-topology.
We now consider the exact sequence of v-sheaves
Each sheaf
![]() $\mathcal {F}$
on the left or right of
$\mathcal {F}$
on the left or right of
![]() ${\mathbf {Bun}}_{\mathcal {G},v}^{n}$
in the above sequence satisfies
${\mathbf {Bun}}_{\mathcal {G},v}^{n}$
in the above sequence satisfies
![]() $R^m\mu _*\mathcal {F} = 0$
, by the case
$R^m\mu _*\mathcal {F} = 0$
, by the case
![]() $\mathcal {G}=\widehat {\mathcal {G}}$
and Proposition 3.11.3 respectively. By decomposing the above sequence into short exact sequences, we finally deduce that
$\mathcal {G}=\widehat {\mathcal {G}}$
and Proposition 3.11.3 respectively. By decomposing the above sequence into short exact sequences, we finally deduce that
which concludes the proof.
Proof of Lemma 3.33
By Theorem 3.29, we have a descending filtration
by étale sheaves on
![]() $\operatorname {\mathrm {Perf}}_{S}$
with
$\operatorname {\mathrm {Perf}}_{S}$
with
![]() ${\mathbf {Fil}}^n = {\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
and short exact sequences, for
${\mathbf {Fil}}^n = {\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
and short exact sequences, for
![]() $0\leq i < n$
$0\leq i < n$
where
![]() $\mathbf {V}_{i,n} = R^i\pi _{\operatorname {\mathrm {\acute {E}t}},*}(\widetilde {\Omega }_{X/S}^{n-i}\otimes \operatorname {\mathrm {Lie}}(\mathcal {G}))$
. By passing to the v-sheafification
$\mathbf {V}_{i,n} = R^i\pi _{\operatorname {\mathrm {\acute {E}t}},*}(\widetilde {\Omega }_{X/S}^{n-i}\otimes \operatorname {\mathrm {Lie}}(\mathcal {G}))$
. By passing to the v-sheafification
![]() $\mu ^*$
, we obtain a filtration by v-sheaves on
$\mu ^*$
, we obtain a filtration by v-sheaves on
![]() $\operatorname {\mathrm {Perf}}_S$
$\operatorname {\mathrm {Perf}}_S$
with short exact sequences
Here, we use the fact that
![]() $\mathbf {V}_{i,n}$
is a vector bundle and thus is already a v-sheaf. Observe that the sequence is already exact for the étale topology, using that the surjection of étale sheaves
$\mathbf {V}_{i,n}$
is a vector bundle and thus is already a v-sheaf. Observe that the sequence is already exact for the étale topology, using that the surjection of étale sheaves
![]() ${\mathbf {Fil}}^i \rightarrow \mathbf {V}_{i,n}$
factors through
${\mathbf {Fil}}^i \rightarrow \mathbf {V}_{i,n}$
factors through
![]() $\mu ^*{\mathbf {Fil}}^i$
. By Lemma 3.34 below, the map
$\mu ^*{\mathbf {Fil}}^i$
. By Lemma 3.34 below, the map
![]() $\mu ^*{\mathbf {Fil}}^i \rightarrow \mathbf {V}_{i,n}$
admits sections étale locally on
$\mu ^*{\mathbf {Fil}}^i \rightarrow \mathbf {V}_{i,n}$
admits sections étale locally on
![]() $\mathbf {V}_{i,n}$
. Hence, by arguing inductively, it is enough to show that each
$\mathbf {V}_{i,n}$
. Hence, by arguing inductively, it is enough to show that each
![]() $\mu ^*{\mathbf {Fil}}^i$
admits a surjection of v-sheaves from a smooth S-space, and we reduce to
$\mu ^*{\mathbf {Fil}}^i$
admits a surjection of v-sheaves from a smooth S-space, and we reduce to
![]() $i=n$
. For this, it is enough to show that
$i=n$
. For this, it is enough to show that
![]() ${\mathbf {Fil}}^n = {\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
admits a surjection of étale sheaves from a smooth S-space. By Proposition 3.16.4, it is enough to show that the sheaf
${\mathbf {Fil}}^n = {\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
admits a surjection of étale sheaves from a smooth S-space. By Proposition 3.16.4, it is enough to show that the sheaf
![]() ${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\operatorname {\mathrm {rig}}}$
on
${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\operatorname {\mathrm {rig}}}$
on
![]() $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
admits a surjection from a smooth S-space. This follows from the co-Yoneda Lemma, since the site
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
admits a surjection from a smooth S-space. This follows from the co-Yoneda Lemma, since the site
![]() $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
is essentially small.
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
is essentially small.
Lemma 3.34. Let S be a good adic space over
![]() $\mathbb {Q}_p$
and
$\mathbb {Q}_p$
and
![]() $\pi \colon \mathcal {F} \rightarrow \mathcal {G}$
be a map of v-sheaves on
$\pi \colon \mathcal {F} \rightarrow \mathcal {G}$
be a map of v-sheaves on
![]() $\operatorname {\mathrm {Perf}}_S$
. Suppose that
$\operatorname {\mathrm {Perf}}_S$
. Suppose that
![]() $\pi $
is a surjection of étale sheaves. Then for any good adic space Y over S and any map of v-sheaves
$\pi $
is a surjection of étale sheaves. Then for any good adic space Y over S and any map of v-sheaves
![]() $g\in \mathcal {G}(Y)$
, there exists an étale cover
$g\in \mathcal {G}(Y)$
, there exists an étale cover
![]() $Y'\rightarrow Y$
and a map
$Y'\rightarrow Y$
and a map
![]() $f\in \mathcal {F}(Y')$
such that
$f\in \mathcal {F}(Y')$
such that
![]() $\pi (f) = g|_{Y'}$
.
$\pi (f) = g|_{Y'}$
.
Proof. We may assume that Y is affinoid. By [Reference Scholze47, Lemma 15.3], there exists a v-cover
where
![]() $\widetilde {Y}$
is an affinoid perfectoid space,
$\widetilde {Y}$
is an affinoid perfectoid space,
![]() $Y_j$
are affinoid, finite étale over Y and each
$Y_j$
are affinoid, finite étale over Y and each
![]() $\widetilde {Y} \rightarrow Y_j$
is surjective. Since
$\widetilde {Y} \rightarrow Y_j$
is surjective. Since
![]() $\mathcal {F} \rightarrow \mathcal {G}$
is surjective for the étale topology on
$\mathcal {F} \rightarrow \mathcal {G}$
is surjective for the étale topology on
![]() $\operatorname {\mathrm {Perf}}_S$
, we may find a qcqs étale cover
$\operatorname {\mathrm {Perf}}_S$
, we may find a qcqs étale cover
![]() $\widetilde {Z} \rightarrow \widetilde {Y}$
and a map
$\widetilde {Z} \rightarrow \widetilde {Y}$
and a map
![]() $\widetilde {s}$
fitting in the following commutative diagram of sheaves on
$\widetilde {s}$
fitting in the following commutative diagram of sheaves on
![]() $\operatorname {\mathrm {Perf}}_S$
$\operatorname {\mathrm {Perf}}_S$

By Lemma 3.7.2,
![]() $\widetilde {Z}$
arises via pullback from an étale cover
$\widetilde {Z}$
arises via pullback from an étale cover
![]() $Z_j\rightarrow Y_j$
. Using that
$Z_j\rightarrow Y_j$
. Using that
![]() $\widetilde {Y} \rightarrow Y_j$
is surjective, it is easy to see that the map
$\widetilde {Y} \rightarrow Y_j$
is surjective, it is easy to see that the map
![]() $\widetilde {f}$
descends to a map
$\widetilde {f}$
descends to a map
![]() $f_j\colon Z_j \rightarrow \mathcal {F}$
satisfying the required properties.
$f_j\colon Z_j \rightarrow \mathcal {F}$
satisfying the required properties.
Remark 3.35. In situation of Theorem 3.29, there is therefore a filtration of
![]() ${\mathbf {Bun}}_{\mathcal {G},v}^n$
by subsheaves on
${\mathbf {Bun}}_{\mathcal {G},v}^n$
by subsheaves on
![]() $\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {Perf}}_{S,\operatorname {\mathrm {\acute {e}t}}}$
with
for each
![]() $0\leq i<n$
. In particular, since
$0\leq i<n$
. In particular, since
![]() ${\mathbf {Bun}}_{\mathcal {G},v}^n$
and
${\mathbf {Bun}}_{\mathcal {G},v}^n$
and
![]() $R^i\pi _{\operatorname {\mathrm {\acute {E}t}},*}(\widetilde {\Omega }_{X/S}^j\otimes \operatorname {\mathrm {Lie}}(\mathcal {G}))$
are small v-sheaves, we deduce, arguing inductively, that each
$R^i\pi _{\operatorname {\mathrm {\acute {E}t}},*}(\widetilde {\Omega }_{X/S}^j\otimes \operatorname {\mathrm {Lie}}(\mathcal {G}))$
are small v-sheaves, we deduce, arguing inductively, that each
![]() ${\mathbf {Fil}}^i$
is a small v-sheaf. In particular,
${\mathbf {Fil}}^i$
is a small v-sheaf. In particular,
![]() ${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
is a small v-sheaf on
${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
is a small v-sheaf on
![]() $\operatorname {\mathrm {Perf}}_S$
. We do not know whether its canonical extension to
$\operatorname {\mathrm {Perf}}_S$
. We do not know whether its canonical extension to
![]() $S_v$
agrees with
$S_v$
agrees with
![]() ${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\operatorname {\mathrm {rig}}}$
on
${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^{n,\operatorname {\mathrm {rig}}}$
on
![]() $\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
. When the latter is representable by a smooth S-group, this is an easy consequence of Proposition 3.16.4.
$\operatorname {\mathrm {Sm}}_{/S,\operatorname {\mathrm {\acute {e}t}}}$
. When the latter is representable by a smooth S-group, this is an easy consequence of Proposition 3.16.4.
Remark 3.36. Assume that
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
. Then arguing as in the proof of [Reference Heuer22, Thm. 2.7.3], we may use the exponential of Lemma 2.26 to produce a splitting of the short exact sequence
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
. Then arguing as in the proof of [Reference Heuer22, Thm. 2.7.3], we may use the exponential of Lemma 2.26 to produce a splitting of the short exact sequence
over an open subgroup of the form
![]() $\Lambda _i \otimes _{K^+} \mathbb {G}_a^+$
, where
$\Lambda _i \otimes _{K^+} \mathbb {G}_a^+$
, where
![]() $\Lambda _i \subseteq H^i(X,\widetilde {\Omega }_X^{n-i}\otimes \operatorname {\mathrm {Lie}}(\mathcal {G}))$
is an open
$\Lambda _i \subseteq H^i(X,\widetilde {\Omega }_X^{n-i}\otimes \operatorname {\mathrm {Lie}}(\mathcal {G}))$
is an open
![]() $K^+$
-lattice.
$K^+$
-lattice.
3.6 The Hodge–Tate decomposition
In this section, we prove the following Hodge–Tate decomposition with locally p-divisible coefficients.
Theorem 3.37. Let
![]() $(K,K^+)$
be an algebraically closed, nonarchimedean field extension of
$(K,K^+)$
be an algebraically closed, nonarchimedean field extension of
![]() $\mathbb {Q}_p$
. Let X be a proper smooth rigid space over K and let
$\mathbb {Q}_p$
. Let X be a proper smooth rigid space over K and let
![]() $\mathcal {G} \rightarrow X$
be an admissible locally p-divisible group. A choice of exponential for K and of a flat lift
$\mathcal {G} \rightarrow X$
be an admissible locally p-divisible group. A choice of exponential for K and of a flat lift
![]() $\mathbb {X}$
to
$\mathbb {X}$
to
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
induce a splitting of the Hodge–Tate spectral sequence with
${\mathrm {B_{dR}^+}}/\xi ^2$
induce a splitting of the Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients (3.2), natural in
$\mathcal {G}$
-coefficients (3.2), natural in
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathbb {X}$
, and thus a decomposition
$\mathbb {X}$
, and thus a decomposition
 $$ \begin{align} H_{v}^n(X,\mathcal{G}) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathcal{G}) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}\otimes_{\mathcal{O}_X}\operatorname{\mathrm{Lie}}(\mathcal{G})). \end{align} $$
$$ \begin{align} H_{v}^n(X,\mathcal{G}) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathcal{G}) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}\otimes_{\mathcal{O}_X}\operatorname{\mathrm{Lie}}(\mathcal{G})). \end{align} $$
To this end, we will use the results of the previous section to prove the representability of the diamantine higher direct images
![]() ${\mathbf {Bun}}_{\widehat {\mathcal {G}},\operatorname {\mathrm {\acute {e}t}}}^n$
. We start with the following lemma about extensions of smooth relative groups, generalizing [Reference Fargues14, Prop. 18].
${\mathbf {Bun}}_{\widehat {\mathcal {G}},\operatorname {\mathrm {\acute {e}t}}}^n$
. We start with the following lemma about extensions of smooth relative groups, generalizing [Reference Fargues14, Prop. 18].
Lemma 3.38. Let S be a good adic space over
![]() $\mathbb {Q}_p$
. Consider a short exact sequence of abelian sheaves on
$\mathbb {Q}_p$
. Consider a short exact sequence of abelian sheaves on
![]() $\operatorname {\mathrm {Perf}}_{S,v}$
$\operatorname {\mathrm {Perf}}_{S,v}$
where
![]() $\mathbf {V}$
is an étale vector bundle on S and
$\mathbf {V}$
is an étale vector bundle on S and
![]() $\Gamma $
is an étale separated S-group of
$\Gamma $
is an étale separated S-group of
![]() $p^{\infty }$
-torsion. Then the sheaf
$p^{\infty }$
-torsion. Then the sheaf
![]() $\mathcal {G}$
is represented by a locally p-divisible S-group,
$\mathcal {G}$
is represented by a locally p-divisible S-group,
![]() $\mathcal {G}= \widehat {\mathcal {G}}$
and the following diagram commutes
$\mathcal {G}= \widehat {\mathcal {G}}$
and the following diagram commutes

If we suppose furthermore that
![]() $[p]\colon \Gamma \rightarrow \Gamma $
is finite étale surjective, then
$[p]\colon \Gamma \rightarrow \Gamma $
is finite étale surjective, then
![]() $\mathcal {G}$
is an analytic p-divisible S-group.
$\mathcal {G}$
is an analytic p-divisible S-group.
Proof. Let
![]() $v\colon Y \rightarrow \mathbf {V}$
be any v-cover from a perfectoid space. By assumption, there exists a v-cover
$v\colon Y \rightarrow \mathbf {V}$
be any v-cover from a perfectoid space. By assumption, there exists a v-cover
![]() $Y' \rightarrow Y$
and a section
$Y' \rightarrow Y$
and a section
![]() $g\in \mathcal {G}(Y')$
such that
$g\in \mathcal {G}(Y')$
such that
![]() $f(g)=v|_{Y'}$
. Then
$f(g)=v|_{Y'}$
. Then
![]() $\mathcal {G} \times _{\mathbf {V}} Y' \cong \Gamma \times _S Y'$
is represented by an étale separated perfectoid space over
$\mathcal {G} \times _{\mathbf {V}} Y' \cong \Gamma \times _S Y'$
is represented by an étale separated perfectoid space over
![]() $Y'$
. By [Reference Scholze47, Prop. 10.11(iv)],
$Y'$
. By [Reference Scholze47, Prop. 10.11(iv)],
![]() $\mathcal {G} \rightarrow \mathbf {V}$
is étale. We deduce, using [Reference Scholze47, Lemma 15.6], that
$\mathcal {G} \rightarrow \mathbf {V}$
is étale. We deduce, using [Reference Scholze47, Lemma 15.6], that
![]() $\mathcal {G}$
is represented by an object of the small étale site
$\mathcal {G}$
is represented by an object of the small étale site
![]() $\mathbf {V}_{\operatorname {\mathrm {\acute {e}t}}}$
of
$\mathbf {V}_{\operatorname {\mathrm {\acute {e}t}}}$
of
![]() $\mathbf {V}$
considered as an adic space. This shows that
$\mathbf {V}$
considered as an adic space. This shows that
![]() $\mathcal {G}$
is represented by a smooth S-group.
$\mathcal {G}$
is represented by a smooth S-group.
Next, observe that the composition
is an étale morphism with
![]() $D(h) = \operatorname {\mathrm {id}}$
. By the unicity part of Lemma 2.17.1, we deduce that
$D(h) = \operatorname {\mathrm {id}}$
. By the unicity part of Lemma 2.17.1, we deduce that
![]() $h|_{\widehat {\mathcal {G}}}=\log _{\mathcal {G}}$
.
$h|_{\widehat {\mathcal {G}}}=\log _{\mathcal {G}}$
.
Let us now show that
![]() $\mathcal {G}=\widehat {\mathcal {G}}$
. This may be checked locally, such that we may assume that S is affinoid and
$\mathcal {G}=\widehat {\mathcal {G}}$
. This may be checked locally, such that we may assume that S is affinoid and
![]() $\mathbf {V}$
is a trivial vector bundle. Let Y be an affinoid perfectoid space over S and let
$\mathbf {V}$
is a trivial vector bundle. Let Y be an affinoid perfectoid space over S and let
![]() $g \in \mathcal {G}(Y)$
. It suffices to show that
$g \in \mathcal {G}(Y)$
. It suffices to show that
![]() $[p^n]g \in \widehat {\mathcal {G}}(Y)$
for some
$[p^n]g \in \widehat {\mathcal {G}}(Y)$
for some
![]() $n\geq 0$
, since the cokernel
$n\geq 0$
, since the cokernel
![]() $\overline {\mathcal {G}}$
of the inclusion
$\overline {\mathcal {G}}$
of the inclusion
![]() $\widehat {\mathcal {G}} \hookrightarrow \mathcal {G}$
is p-torsionfree, by [Reference Heuer25, Lemma 2.11.2]. Let
$\widehat {\mathcal {G}} \hookrightarrow \mathcal {G}$
is p-torsionfree, by [Reference Heuer25, Lemma 2.11.2]. Let
![]() $U \cong \mathbb {B}^n \subseteq \mathbf {V}$
denote an open subspace isomorphic to a closed ball where
$U \cong \mathbb {B}^n \subseteq \mathbf {V}$
denote an open subspace isomorphic to a closed ball where
![]() $\log _{\mathcal {G}}$
, and hence also f has a section, as in Lemma 2.26, see Remark 2.27. We have
$\log _{\mathcal {G}}$
, and hence also f has a section, as in Lemma 2.26, see Remark 2.27. We have
![]() $f([p^n]g)=p^nf(g) \in U$
for large enough n. Note that we have
$f([p^n]g)=p^nf(g) \in U$
for large enough n. Note that we have
![]() $f^{-1}(U) \cong \Gamma \times U$
as rigid groups, such that
$f^{-1}(U) \cong \Gamma \times U$
as rigid groups, such that
Since
![]() $[p^n]g \in \widehat {f^{-1}(U)} \subset \widehat {\mathcal {G}}$
, this proves that
$[p^n]g \in \widehat {f^{-1}(U)} \subset \widehat {\mathcal {G}}$
, this proves that
![]() $\mathcal {G}=\widehat {\mathcal {G}}$
, as required. In particular,
$\mathcal {G}=\widehat {\mathcal {G}}$
, as required. In particular,
![]() $\log _{\mathcal {G}} =h$
is étale and surjective, such that
$\log _{\mathcal {G}} =h$
is étale and surjective, such that
![]() $\mathcal {G}$
is locally p-divisible.
$\mathcal {G}$
is locally p-divisible.
For the last part of the statement, assume that
![]() $[p]\colon \Gamma \rightarrow \Gamma $
is surjective and finite étale. As
$[p]\colon \Gamma \rightarrow \Gamma $
is surjective and finite étale. As
![]() $[p]\colon \mathbf {V} \rightarrow \mathbf {V}$
is an isomorphism because
$[p]\colon \mathbf {V} \rightarrow \mathbf {V}$
is an isomorphism because
![]() $\mathbf {V}$
is a vector bundle, the assumption implies that
$\mathbf {V}$
is a vector bundle, the assumption implies that
![]() $[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is also a surjection with the kernel
$[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is also a surjection with the kernel
![]() $\mathcal {G}[p] = \Gamma [p]$
being finite étale over S, which concludes the proof.
$\mathcal {G}[p] = \Gamma [p]$
being finite étale over S, which concludes the proof.
Proposition 3.39. Let
![]() $\pi \colon X \rightarrow S$
be a proper smooth morphism of seminormal rigid spaces over K and let
$\pi \colon X \rightarrow S$
be a proper smooth morphism of seminormal rigid spaces over K and let
![]() $\mathcal {G} \rightarrow X$
be an admissible locally p-divisible group. Assume that we are in one of the following situations:
$\mathcal {G} \rightarrow X$
be an admissible locally p-divisible group. Assume that we are in one of the following situations:
-
○
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, or
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, or -
○ The Lie algebra
 ${\mathfrak {g}}$
comes from a vector bundle over S and
${\mathfrak {g}}$
comes from a vector bundle over S and
 $\widehat {\mathcal {G}} \xrightarrow {[p]}\widehat {\mathcal {G}}$
is finite étale surjective.
$\widehat {\mathcal {G}} \xrightarrow {[p]}\widehat {\mathcal {G}}$
is finite étale surjective.
-
1. For any
 $n\geq 0$
, the sheaf
$n\geq 0$
, the sheaf
 ${\mathbf {Bun}}_{\widehat {\mathcal {G}},\operatorname {\mathrm {\acute {e}t}}}^n$
is representable by an admissible locally p-divisible S-group of topological p-torsion, and the sequence (3.6) coincides with the logarithm sequence for this group. If
${\mathbf {Bun}}_{\widehat {\mathcal {G}},\operatorname {\mathrm {\acute {e}t}}}^n$
is representable by an admissible locally p-divisible S-group of topological p-torsion, and the sequence (3.6) coincides with the logarithm sequence for this group. If
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
, the analogous statement holds for
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
, the analogous statement holds for
 ${\mathbf {Bun}}_{\widehat {\mathcal {G}},v}^n$
.
${\mathbf {Bun}}_{\widehat {\mathcal {G}},v}^n$
.
-
2. Assume that
 $S=\operatorname {\mathrm {Spa}}(K,K^+)$
with K algebraically closed. A choice of exponential for K induces a splitting on K-points of the sequence (3.6), for
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
with K algebraically closed. A choice of exponential for K induces a splitting on K-points of the sequence (3.6), for
 $\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
(3.14)that is natural in
$\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
(3.14)that is natural in
 $\mathcal {G}$
.
$\mathcal {G}$
.
Proof. Let us prove the first part. We apply Lemma 3.38 to the exact sequence (3.6). This is possible, since
![]() ${\mathbf {Bun}}_{\widehat {\mathcal {G}},\operatorname {\mathrm {\acute {e}t}} }$
is a v-sheaf, by Remark 3.35. In the case
${\mathbf {Bun}}_{\widehat {\mathcal {G}},\operatorname {\mathrm {\acute {e}t}} }$
is a v-sheaf, by Remark 3.35. In the case
![]() $S=\operatorname {\mathrm {Spa}}(K,K^+)$
and
$S=\operatorname {\mathrm {Spa}}(K,K^+)$
and
![]() $\tau =v$
, Lemma 3.38 also applies to the exact sequence (3.6), as
$\tau =v$
, Lemma 3.38 also applies to the exact sequence (3.6), as
![]() ${\mathbf {Bun}}_{{\mathfrak {g}},v}^n = H_v^n(X,{\mathfrak {g}}) \otimes \mathbb {G}_a$
is an étale vector bundle, by Proposition 3.16.1. This proves the first point. The second point follows from Proposition 2.29.
${\mathbf {Bun}}_{{\mathfrak {g}},v}^n = H_v^n(X,{\mathfrak {g}}) \otimes \mathbb {G}_a$
is an étale vector bundle, by Proposition 3.16.1. This proves the first point. The second point follows from Proposition 2.29.
Proof of Theorem 3.37
We have a commutative diagram

Proposition 3.39 provides the splitting
![]() $s_{\exp }$
and hence yields a splitting
$s_{\exp }$
and hence yields a splitting
![]() $s_n$
of the left vertical map. For general
$s_n$
of the left vertical map. For general
![]() $i<n$
, we have a commutative diagram
$i<n$
, we have a commutative diagram

By descending induction on i, we have a section
![]() $s_{i+1}$
splitting the left vertical map. Since the left square above is a pushout square, we obtain a section
$s_{i+1}$
splitting the left vertical map. Since the left square above is a pushout square, we obtain a section
![]() $s_i$
of the middle vertical map. By Proposition 3.4, the lift
$s_i$
of the middle vertical map. By Proposition 3.4, the lift
![]() $\mathbb {X}$
induces a splitting
$\mathbb {X}$
induces a splitting
![]() $s_{\mathbb {X}}$
of the Hodge–Tate spectral sequence with
$s_{\mathbb {X}}$
of the Hodge–Tate spectral sequence with
![]() ${\mathfrak {g}}$
-coefficients. We may precompose
${\mathfrak {g}}$
-coefficients. We may precompose
![]() $s_i$
with
$s_i$
with
![]() $s_{\mathbb {X}}$
and postcompose it with the natural map
$s_{\mathbb {X}}$
and postcompose it with the natural map
This yields a map
![]() $H^i(X,\widetilde {\Omega }_X^{n-i} \otimes \operatorname {\mathrm {Lie}}(\mathcal {G})) \rightarrow \operatorname {\mathrm {Fil}}^iH_v^n(X,\mathcal {G})$
that splits the Hodge–Tate spectral sequence with
$H^i(X,\widetilde {\Omega }_X^{n-i} \otimes \operatorname {\mathrm {Lie}}(\mathcal {G})) \rightarrow \operatorname {\mathrm {Fil}}^iH_v^n(X,\mathcal {G})$
that splits the Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients, as required.
$\mathcal {G}$
-coefficients, as required.
3.7 Cohomology with coefficients in p-adic universal covers
In this section, we prove a Hodge–Tate decomposition with coefficients in the p-adic universal cover
![]() $\widetilde {\mathcal {G}}$
of locally p-divisible groups.
$\widetilde {\mathcal {G}}$
of locally p-divisible groups.
Definition 3.40. Let X be a good adic space over
![]() $\mathbb {Q}_p$
and let
$\mathbb {Q}_p$
and let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group. Assume that
$\mathcal {G}$
be an admissible locally p-divisible X-group. Assume that
![]() $[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is finite étale surjective. We define the p-adic universal cover of
$[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
is finite étale surjective. We define the p-adic universal cover of
![]() $\mathcal {G}$
to be
$\mathcal {G}$
to be
viewed as a group diamond over X. It fits in a short exact sequence of sheaves on
![]() $X_v$
$X_v$
where
![]() $T_p\mathcal {G} = \varprojlim _m \mathcal {G}[p^m]$
is the Tate module of
$T_p\mathcal {G} = \varprojlim _m \mathcal {G}[p^m]$
is the Tate module of
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
Remark 3.41. If
![]() $\mathcal {G} = \widehat {\mathcal {G}}$
is analytic p-divisible, we further have a short exact sequence of sheaves on
$\mathcal {G} = \widehat {\mathcal {G}}$
is analytic p-divisible, we further have a short exact sequence of sheaves on
![]() $X_v$
$X_v$
where
![]() $V_p\mathcal {G} = T_p\mathcal {G}[\tfrac {1}{p}]$
is the rational Tate module of
$V_p\mathcal {G} = T_p\mathcal {G}[\tfrac {1}{p}]$
is the rational Tate module of
![]() $\mathcal {G}$
. In particular,
$\mathcal {G}$
. In particular,
![]() $\widetilde {\mathcal {G}}$
then is an effective Banach–Colmez space [Reference Fontaine16, §4].
$\widetilde {\mathcal {G}}$
then is an effective Banach–Colmez space [Reference Fontaine16, §4].
Example 3.42. Let
![]() $\mathcal {G}= \widehat {\mathbb {G}}_m$
. Then by [Reference Fargues and Scholze17, Prop. II.2.2], we have
$\mathcal {G}= \widehat {\mathbb {G}}_m$
. Then by [Reference Fargues and Scholze17, Prop. II.2.2], we have
![]() $\widetilde {\widehat {\mathbb {G}}}_m= \mathbb {B}^{\varphi =p}$
, where
$\widetilde {\widehat {\mathbb {G}}}_m= \mathbb {B}^{\varphi =p}$
, where
![]() $\mathbb {B}$
is the v-sheaf on X defined by the formula
$\mathbb {B}$
is the v-sheaf on X defined by the formula
and the sequence (3.16) coincides with the fundamental exact sequence of p-adic Hodge theory
We obtain the following result.
Theorem 3.43. Let X be a proper smooth rigid space over an algebraically closed nonarchimedean field
![]() $(K,K^+)$
over
$(K,K^+)$
over
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\mathcal {G}$
be an admissible locally p-divisible X-group with
$\mathcal {G}$
be an admissible locally p-divisible X-group with
![]() $[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
finite étale surjective. Then there is a spectral sequence, natural in X and
$[p]\colon \mathcal {G} \rightarrow \mathcal {G}$
finite étale surjective. Then there is a spectral sequence, natural in X and
![]() $\mathcal {G}$
$\mathcal {G}$
 $$ \begin{align} E_2^{ij}= \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\widetilde{\Omega}_X^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &{\varprojlim}_{[p]}H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\mathcal{G}) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_{v}^{i+j}(X,\widetilde{\mathcal{G}}), \end{align} $$
$$ \begin{align} E_2^{ij}= \left\{\begin{aligned} &H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\widetilde{\Omega}_X^j \otimes_{\mathcal{O}_X} \operatorname{\mathrm{Lie}}(\mathcal{G})) \quad &\text{if }j>0\\ &{\varprojlim}_{[p]}H_{\operatorname{\mathrm{\acute{e}t}}}^i(X,\mathcal{G}) \quad &\text{if }j=0 \end{aligned}\right\} \Longrightarrow H_{v}^{i+j}(X,\widetilde{\mathcal{G}}), \end{align} $$
that lies over the Hodge–Tate spectral sequence with
![]() $\mathcal {G}$
-coefficients (3.2). Moreover, this spectral sequence degenerates at
$\mathcal {G}$
-coefficients (3.2). Moreover, this spectral sequence degenerates at
![]() $E_2$
. A choice of exponential for K and of a flat lift
$E_2$
. A choice of exponential for K and of a flat lift
![]() $\mathbb {X}$
to
$\mathbb {X}$
to
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
induce a decomposition, natural in
${\mathrm {B_{dR}^+}}/\xi ^2$
induce a decomposition, natural in
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\mathbb {X}$
$\mathbb {X}$
 $$ \begin{align} H_{v}^n(X,\widetilde{\mathcal{G}}) = \varprojlim_{[p]} H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathcal{G}) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}\otimes_{\mathcal{O}_X}\operatorname{\mathrm{Lie}}(\mathcal{G})). \end{align} $$
$$ \begin{align} H_{v}^n(X,\widetilde{\mathcal{G}}) = \varprojlim_{[p]} H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathcal{G}) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}\otimes_{\mathcal{O}_X}\operatorname{\mathrm{Lie}}(\mathcal{G})). \end{align} $$
Proof. The spectral sequence is obtained by taking the inverse limit over
![]() $[p]$
of the spectral sequence (3.2), which then is immediately seen to degenerate at
$[p]$
of the spectral sequence (3.2), which then is immediately seen to degenerate at
![]() $E_2$
, by Corollary 3.30. We claim that we have the following formula for the limiting term
$E_2$
, by Corollary 3.30. We claim that we have the following formula for the limiting term
As
![]() $\operatorname {\mathrm {Sh}}(X_v)$
is a replete topos, we have
$\operatorname {\mathrm {Sh}}(X_v)$
is a replete topos, we have
Hence
It remains to show that
for each
![]() $n\geq 0$
. We have a short exact sequence on
$n\geq 0$
. We have a short exact sequence on
![]() $X_v$
$X_v$
We end up with the following commutative diagram where the rows and the middle column are exact

Here, we use that
![]() $\overline {\mathcal {G}}$
is uniquely p-divisible, using our assumptions on
$\overline {\mathcal {G}}$
is uniquely p-divisible, using our assumptions on
![]() $\mathcal {G}$
and [Reference Heuer25, Lemma 2.11.2], such that
$\mathcal {G}$
and [Reference Heuer25, Lemma 2.11.2], such that
![]() $R^1\varprojlim _{[p]}H^{n}(X,\overline {\mathcal {G}})=0$
. By applying the Snake Lemma to the above diagram, we are reduced to showing that
$R^1\varprojlim _{[p]}H^{n}(X,\overline {\mathcal {G}})=0$
. By applying the Snake Lemma to the above diagram, we are reduced to showing that
Using the split short exact sequence (3.14), it is equivalent to show that
As
![]() $H_v^n(X,T_p\mathcal {G})$
is a finitely generated
$H_v^n(X,T_p\mathcal {G})$
is a finitely generated
![]() $\mathbb {Z}_p$
-module, by [Reference Scholze44, Thm. 5.1], it follows that we can write
$\mathbb {Z}_p$
-module, by [Reference Scholze44, Thm. 5.1], it follows that we can write
for some finite torsion group T. It follows that the system
is Mittag–Leffler, and the claim follows. The rest of the statement now follows by applying
![]() $\varprojlim _{[p]}$
to the Hodge–Tate decomposition with
$\varprojlim _{[p]}$
to the Hodge–Tate decomposition with
![]() $\mathcal {G}$
-coefficients (Theorem 3.37).
$\mathcal {G}$
-coefficients (Theorem 3.37).
As an application, we obtain the following deformation of the Hodge–Tate decomposition along Fontaine’s theta map.
Corollary 3.44. Let X be a proper smooth rigid space over a complete algebraically closed extension K of
![]() $\mathbb {Q}_p$
. Then a flat lift
$\mathbb {Q}_p$
. Then a flat lift
![]() $\mathbb {X}$
to
$\mathbb {X}$
to
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
and an exponential for K induce a decomposition, natural in
${\mathrm {B_{dR}^+}}/\xi ^2$
and an exponential for K induce a decomposition, natural in
![]() $\mathbb {X}$
$\mathbb {X}$
 $$ \begin{align} H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p}B^{\varphi =p} = \varprojlim_{[p]} H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\widehat{\mathbb{G}}_m) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}). \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p}B^{\varphi =p} = \varprojlim_{[p]} H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\widehat{\mathbb{G}}_m) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}). \end{align} $$
This lies over the classical Hodge–Tate decomposition (3.4) via Fontaine’s map
![]() $B^{\varphi =p} \xrightarrow {\theta } K$
.
$B^{\varphi =p} \xrightarrow {\theta } K$
.
Proof. By Theorem 3.43, all that remains to be shown is the isomorphism
Using the short exact sequence (3.17) and the
![]() $5$
-lemma, this follows from the primitive comparison Theorem [Reference Scholze44, Thm. 5.1].
$5$
-lemma, this follows from the primitive comparison Theorem [Reference Scholze44, Thm. 5.1].
3.8 The case of abeloid varieties and curves
Let
![]() $(K,K^+)$
be an algebraically closed nonarchimedean field over
$(K,K^+)$
be an algebraically closed nonarchimedean field over
![]() $\mathbb {Q}_p$
. Let X be either an abeloid variety or a smooth connected proper curve of genus
$\mathbb {Q}_p$
. Let X be either an abeloid variety or a smooth connected proper curve of genus
![]() $g\geq 1$
over K, and let
$g\geq 1$
over K, and let
![]() $x\in X(K)$
. In this section, we reformulate the Hodge–Tate decomposition of X with multiplicative coefficients in terms of continuous group cohomology of the étale fundamental group
$x\in X(K)$
. In this section, we reformulate the Hodge–Tate decomposition of X with multiplicative coefficients in terms of continuous group cohomology of the étale fundamental group
![]() $\pi _1(X,x)$
.
$\pi _1(X,x)$
.
Definition 3.45. The universal pro-finite-étale cover
![]() $\widetilde {X}$
of X is defined to be the diamond
$\widetilde {X}$
of X is defined to be the diamond
where the limit ranges over all connected finite étale covers
![]() $X' \rightarrow X$
together with a lift
$X' \rightarrow X$
together with a lift
![]() $x'\in X'(K)$
of x.
$x'\in X'(K)$
of x.
The map
![]() $\widetilde {X} \rightarrow X$
is a pro-étale torsor under the profinite group
$\widetilde {X} \rightarrow X$
is a pro-étale torsor under the profinite group
![]() $\pi _1(X,x)$
. Under our assumptions on X, it is moreover known that
$\pi _1(X,x)$
. Under our assumptions on X, it is moreover known that
![]() $\widetilde {X}$
is representable by a qcqs perfectoid space, see [Reference Blakestad, Gvirtz, Heuer, Shchedrina, Shimizu, Wear and Yao6, Cor. 5.7-8].
$\widetilde {X}$
is representable by a qcqs perfectoid space, see [Reference Blakestad, Gvirtz, Heuer, Shchedrina, Shimizu, Wear and Yao6, Cor. 5.7-8].
Lemma 3.46. For
![]() $\mathcal {F}$
any of the v-sheaves
$\mathcal {F}$
any of the v-sheaves
![]() $\mathbb {Z}/n\mathbb {Z}, \mathcal {O}^{+a}/p^m, \mathcal {O}^{+a},\mathcal {O}$
, we have
$\mathbb {Z}/n\mathbb {Z}, \mathcal {O}^{+a}/p^m, \mathcal {O}^{+a},\mathcal {O}$
, we have
 $$ \begin{align*} H_v^i(\widetilde{X},\mathcal{F}) = \begin{cases} \mathcal{F}(K) \quad &\text{if }i=0\\ 0\quad &\text{if }i>0. \end{cases} \end{align*} $$
$$ \begin{align*} H_v^i(\widetilde{X},\mathcal{F}) = \begin{cases} \mathcal{F}(K) \quad &\text{if }i=0\\ 0\quad &\text{if }i>0. \end{cases} \end{align*} $$
Here, the sheaf
![]() $\mathcal {O}^{+a}$
is the almost integral structure sheaf, sending a perfectoid pair
$\mathcal {O}^{+a}$
is the almost integral structure sheaf, sending a perfectoid pair
![]() $(R,R^+)$
to
$(R,R^+)$
to
![]() $R^{+,a}$
, where we use almost mathematics relative to
$R^{+,a}$
, where we use almost mathematics relative to
![]() $(\mathcal {O}_K,{\mathfrak {m}})$
.
$(\mathcal {O}_K,{\mathfrak {m}})$
.
Remark 3.47. If X is an arbitrary connected, proper, seminormal rigid space, the lemma holds for
![]() $i=0,1$
, see [Reference Heuer23, Prop. 4.9]. However, for
$i=0,1$
, see [Reference Heuer23, Prop. 4.9]. However, for
![]() $X=\mathbb {P}^n$
, we have
$X=\mathbb {P}^n$
, we have
![]() $\widetilde {X} = X$
and we immediately see that the statement need not hold for
$\widetilde {X} = X$
and we immediately see that the statement need not hold for
![]() $i \geq 2$
.
$i \geq 2$
.
Proof. In the abeloid case, this follows from [Reference Heuer26, Prop. 4.2] and its proof. For X a curve, we proceed as follows. First, Proposition 3.11.3 gives us
By [Reference Scholze47, Prop. 14.9], we have
The claim is thus clear for
![]() $i=0$
. By Poincaré duality [Reference Mann38, Thm. 1.1.1],
$i=0$
. By Poincaré duality [Reference Mann38, Thm. 1.1.1],
![]() $H^i(X',\mathbb {Z}/n\mathbb {Z}) =0$
for
$H^i(X',\mathbb {Z}/n\mathbb {Z}) =0$
for
![]() $i>2$
and
$i>2$
and
![]() $H^2(X',\mathbb {Z}/n\mathbb {Z}) \cong H^0(X',\mathbb {Z}/n\mathbb {Z}) = \mathbb {Z}/n\mathbb {Z}$
. Moreover, via this identification, the transition functions
$H^2(X',\mathbb {Z}/n\mathbb {Z}) \cong H^0(X',\mathbb {Z}/n\mathbb {Z}) = \mathbb {Z}/n\mathbb {Z}$
. Moreover, via this identification, the transition functions
![]() $f\colon X" \rightarrow X'$
induce
$f\colon X" \rightarrow X'$
induce
![]() $[\deg (f)]$
on
$[\deg (f)]$
on
![]() $\mathbb {Z}/n\mathbb {Z}$
. It follows that the colimit above vanishes. Finally, for
$\mathbb {Z}/n\mathbb {Z}$
. It follows that the colimit above vanishes. Finally, for
![]() $i=1$
, each class in
$i=1$
, each class in
![]() $H^1(X',\mathbb {Z}/n\mathbb {Z})$
represents an étale
$H^1(X',\mathbb {Z}/n\mathbb {Z})$
represents an étale
![]() $\mathbb {Z}/n\mathbb {Z}$
-torsor, and thus is trivialized by a finite étale cover
$\mathbb {Z}/n\mathbb {Z}$
-torsor, and thus is trivialized by a finite étale cover
![]() $X' \rightarrow X$
(alternatively, one could invoke [Reference Heuer25, Prop. 3.9]). Thus the colimit above vanishes as well and the statement is proven for
$X' \rightarrow X$
(alternatively, one could invoke [Reference Heuer25, Prop. 3.9]). Thus the colimit above vanishes as well and the statement is proven for
![]() $\mathcal {F}=\mathbb {Z}/n\mathbb {Z}$
. By the Primitive Comparison Theorem [Reference Scholze44, Thm. 5.1], we also get
$\mathcal {F}=\mathbb {Z}/n\mathbb {Z}$
. By the Primitive Comparison Theorem [Reference Scholze44, Thm. 5.1], we also get
 $$\begin{align*}H_v^i(\widetilde{X},\mathcal{O}^+/p^m) \overset{a}{=} \varinjlim H_{\operatorname{\mathrm{\acute{e}t}}}^i(X',\mathcal{O}^+/p^m) \overset{a}{=} \varinjlim H_{\operatorname{\mathrm{\acute{e}t}}}^i(X',\mathbb{Z}/p^m)\otimes K^+/p^m = \begin{cases} K^+/p^m \quad &\text{if }i=0\\ 0\quad &\text{if }i>0. \end{cases}\end{align*}$$
$$\begin{align*}H_v^i(\widetilde{X},\mathcal{O}^+/p^m) \overset{a}{=} \varinjlim H_{\operatorname{\mathrm{\acute{e}t}}}^i(X',\mathcal{O}^+/p^m) \overset{a}{=} \varinjlim H_{\operatorname{\mathrm{\acute{e}t}}}^i(X',\mathbb{Z}/p^m)\otimes K^+/p^m = \begin{cases} K^+/p^m \quad &\text{if }i=0\\ 0\quad &\text{if }i>0. \end{cases}\end{align*}$$
Since
![]() $\operatorname {\mathrm {Sh}}(X_v)$
is replete, it follows that
$\operatorname {\mathrm {Sh}}(X_v)$
is replete, it follows that
Hence the statement follows for
![]() $\mathcal {F}= \mathcal {O}^{+a},\mathcal {O}$
.
$\mathcal {F}= \mathcal {O}^{+a},\mathcal {O}$
.
We recall the definition of the topological torsion subgroup of
![]() $\mathbb {G}_m$
[Reference Heuer25, Def. 2.5]
$\mathbb {G}_m$
[Reference Heuer25, Def. 2.5]
Theorem 3.48. Let X be either an abeloid variety or a smooth connected proper curve of genus
![]() $g\geq 1$
over
$g\geq 1$
over
![]() $K=\overline {K}$
, and fix a point
$K=\overline {K}$
, and fix a point
![]() $x\in X(K)$
. Then a choice of exponential for K and of a flat lift
$x\in X(K)$
. Then a choice of exponential for K and of a flat lift
![]() $\mathbb {X}$
of X to
$\mathbb {X}$
of X to
![]() ${\mathrm {B_{dR}^+}}/\xi ^2$
induces a decomposition, natural in
${\mathrm {B_{dR}^+}}/\xi ^2$
induces a decomposition, natural in
![]() $\mathbb {X}$
, for any
$\mathbb {X}$
, for any
![]() $n\geq 0$
$n\geq 0$
 $$ \begin{align} H_{\operatorname{\mathrm{cts}}}^n(\pi_1(X,x),K^{\times}) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathbb{G}_m^{\operatorname{\mathrm{tt}}}) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}). \end{align} $$
$$ \begin{align} H_{\operatorname{\mathrm{cts}}}^n(\pi_1(X,x),K^{\times}) = H_{\operatorname{\mathrm{\acute{e}t}}}^n(X,\mathbb{G}_m^{\operatorname{\mathrm{tt}}}) \oplus \bigoplus_{i=0}^{n-1} H^i(X,\widetilde{\Omega}_X^{n-i}). \end{align} $$
Proof. Let
![]() $\mu = \bigcup _{n\geq 1}\mu _n \subseteq \mathbb {G}_m$
denote the sheaf of roots of unity on
$\mu = \bigcup _{n\geq 1}\mu _n \subseteq \mathbb {G}_m$
denote the sheaf of roots of unity on
![]() $X_v$
. The logarithm sequence extends to a short exact sequence on
$X_v$
. The logarithm sequence extends to a short exact sequence on
![]() $X_v$
[Reference Heuer, Werner and Zhang32, Lemma 6.7]
$X_v$
[Reference Heuer, Werner and Zhang32, Lemma 6.7]
By Lemma 3.46, we deduce that
Hence the Čech-to-derived spectral sequence yields an isomorphism
where
![]() $\mathbb {G}_m^{\operatorname {\mathrm {tt}}}(\widetilde {X})$
comes equipped with a natural topology [Reference Heuer, Werner and Zhang32, Lemma 2.11] and where we use [Reference Heuer, Werner and Zhang32, Lemma 5.4] for the second equality. Since
$\mathbb {G}_m^{\operatorname {\mathrm {tt}}}(\widetilde {X})$
comes equipped with a natural topology [Reference Heuer, Werner and Zhang32, Lemma 2.11] and where we use [Reference Heuer, Werner and Zhang32, Lemma 5.4] for the second equality. Since
![]() $\mathcal {O}(\widetilde {X}) = K$
, it follows that
$\mathcal {O}(\widetilde {X}) = K$
, it follows that
![]() $\mathbb {G}_m^{\operatorname {\mathrm {tt}}}(\widetilde {X}) = \mathbb {G}_m^{\operatorname {\mathrm {tt}}}(K)$
, in particular it is a trivial
$\mathbb {G}_m^{\operatorname {\mathrm {tt}}}(\widetilde {X}) = \mathbb {G}_m^{\operatorname {\mathrm {tt}}}(K)$
, in particular it is a trivial
![]() $\pi _1(X,x)$
-module. We now consider the short exact sequence of topological groups
$\pi _1(X,x)$
-module. We now consider the short exact sequence of topological groups
Since
![]() $\mathbb {G}_m/\mathbb {G}_m^{\operatorname {\mathrm {tt}}}(K)$
is discrete, the above induces a long exact sequence in continuous group cohomology. Moreover,
$\mathbb {G}_m/\mathbb {G}_m^{\operatorname {\mathrm {tt}}}(K)$
is discrete, the above induces a long exact sequence in continuous group cohomology. Moreover,
![]() $\mathbb {G}_m/\mathbb {G}_m^{\operatorname {\mathrm {tt}}}$
is uniquely divisible, by [Reference Heuer23, Lemma 2.16]. It follows that
$\mathbb {G}_m/\mathbb {G}_m^{\operatorname {\mathrm {tt}}}$
is uniquely divisible, by [Reference Heuer23, Lemma 2.16]. It follows that
The result now follows from the Hodge–Tate decomposition (Theorem 3.37) applied to the locally p-divisible group
![]() $\mathbb {G}_m^{\operatorname {\mathrm {tt}}}$
.
$\mathbb {G}_m^{\operatorname {\mathrm {tt}}}$
.
3.9 Application to analytic Brauer groups
In this section, we prove some additional facts on the diamantine higher direct images
![]() ${\mathbf {Bun}}_{\mathcal {G},\tau }^n$
for a proper smooth rigid space X over K, and we deduce some consequences for analytic Brauer groups. Here
${\mathbf {Bun}}_{\mathcal {G},\tau }^n$
for a proper smooth rigid space X over K, and we deduce some consequences for analytic Brauer groups. Here
![]() $(K,K^+)$
is any perfectoid field extension of
$(K,K^+)$
is any perfectoid field extension of
![]() $\mathbb {Q}_p$
. The main result is the following.
$\mathbb {Q}_p$
. The main result is the following.
Proposition 3.49. Let X be a proper smooth rigid space over K. Let
![]() $\mathcal {G} \rightarrow X$
be an admissible locally p-divisible group. Then there are étale rigid groups
$\mathcal {G} \rightarrow X$
be an admissible locally p-divisible group. Then there are étale rigid groups
![]() $(\Gamma _n)_{n \geq 0}$
and exact sequences on
$(\Gamma _n)_{n \geq 0}$
and exact sequences on
![]() $\operatorname {\mathrm {Perf}}_{K,\tau }$
, for
$\operatorname {\mathrm {Perf}}_{K,\tau }$
, for
![]() $\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
$\tau \in \{\operatorname {\mathrm {\acute {e}t}},v\}$
We begin by making preparations.
Lemma 3.50. Let
![]() $\mathcal {F}$
be an abelian sheaf on
$\mathcal {F}$
be an abelian sheaf on
![]() $\operatorname {\mathrm {Adic}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property and let H be a partially proper rigid group over K. Assume that K is algebraically closed. Then any morphism of sheaves
$\operatorname {\mathrm {Adic}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
with the approximation property and let H be a partially proper rigid group over K. Assume that K is algebraically closed. Then any morphism of sheaves
![]() $f\colon \mathcal {F} \rightarrow H$
factors through the locally constant sheaf
$f\colon \mathcal {F} \rightarrow H$
factors through the locally constant sheaf
Proof. Let Y be any good affinoid adic space over K. By [Reference Heuer22, Prop. 3.17], we can write
where each
![]() $Y_i$
is a smooth affinoid rigid space over K. We may apply Proposition 3.11.2 to obtain
$Y_i$
is a smooth affinoid rigid space over K. We may apply Proposition 3.11.2 to obtain
It is enough to show that f sends
![]() $\mathcal {F}(Y_i)$
in the set of locally constant functions
$\mathcal {F}(Y_i)$
in the set of locally constant functions
![]() $Y_i \rightarrow H(K,K^+)$
. Hence, we may assume that Y is a connected smooth affinoid rigid space. Given
$Y_i \rightarrow H(K,K^+)$
. Hence, we may assume that Y is a connected smooth affinoid rigid space. Given
![]() $s\in \mathcal {F}(Y)$
, it is enough to show that
$s\in \mathcal {F}(Y)$
, it is enough to show that
![]() $f(s) \in H(Y)$
restricts to a constant map on
$f(s) \in H(Y)$
restricts to a constant map on
![]() $Y' = Y\times _{\operatorname {\mathrm {Spa}}(K,K^+)} \operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
, using the valuative criterion. Therefore we may also assume that
$Y' = Y\times _{\operatorname {\mathrm {Spa}}(K,K^+)} \operatorname {\mathrm {Spa}}(K,\mathcal {O}_K)$
, using the valuative criterion. Therefore we may also assume that
![]() $K^+=\mathcal {O}_K$
.
$K^+=\mathcal {O}_K$
.
Let
![]() $s\in \mathcal {F}(Y)$
and
$s\in \mathcal {F}(Y)$
and
![]() $y\in Y(K)$
. We claim that there is an open neighborhood
$y\in Y(K)$
. We claim that there is an open neighborhood
![]() $y\in U \subseteq Y$
such that
$y\in U \subseteq Y$
such that
![]() $s|_{U}$
is constant equal to
$s|_{U}$
is constant equal to
![]() $s(y) \in \mathcal {F}(K)$
. We have morphisms of rigid spaces
$s(y) \in \mathcal {F}(K)$
. We have morphisms of rigid spaces
Up to replacing s by
![]() $s-q^*s(y)$
, we may assume that
$s-q^*s(y)$
, we may assume that
![]() $s(y)=0$
. One easily checks that
$s(y)=0$
. One easily checks that
where the limit ranges over all affinoid opens
![]() $U_i \subseteq Y$
containing y. Therefore, the approximation property applies and we deduce that already
$U_i \subseteq Y$
containing y. Therefore, the approximation property applies and we deduce that already
![]() $s|_{U_i} = 0$
for some i, as required. From this, we will deduce that
$s|_{U_i} = 0$
for some i, as required. From this, we will deduce that
![]() $f(s)\colon Y \rightarrow H$
is constant. Indeed, let
$f(s)\colon Y \rightarrow H$
is constant. Indeed, let
![]() $y\in Y(K)$
with image
$y\in Y(K)$
with image
![]() $h\in H(K)$
. We let
$h\in H(K)$
. We let
![]() $Y_h$
denote its fiber under
$Y_h$
denote its fiber under
![]() $f(s)$
$f(s)$

Then
![]() $Y_h$
is a Zariski-closed subset of Y containing y, and we claim that it equals all of Y. Indeed, by the above, there exists a rational open neighborhood
$Y_h$
is a Zariski-closed subset of Y containing y, and we claim that it equals all of Y. Indeed, by the above, there exists a rational open neighborhood
![]() $y\in U \subseteq Y$
contained in
$y\in U \subseteq Y$
contained in
![]() $Y_h$
. As
$Y_h$
. As
![]() $\mathcal {O}(Y) \rightarrow \mathcal {O}(U)$
is flat [Reference Bosch8, §4.1, Cor. 5] and
$\mathcal {O}(Y) \rightarrow \mathcal {O}(U)$
is flat [Reference Bosch8, §4.1, Cor. 5] and
![]() $\mathcal {O}(Y)$
is a domain, it follows that the surjection
$\mathcal {O}(Y)$
is a domain, it follows that the surjection
![]() $\mathcal {O}(Y) \twoheadrightarrow \mathcal {O}(Y_h)$
is an isomorphism, as required. This concludes the proof.
$\mathcal {O}(Y) \twoheadrightarrow \mathcal {O}(Y_h)$
is an isomorphism, as required. This concludes the proof.
Proof of Proposition 3.49
We start by taking
![]() $\tau $
to be the v-topology. By Proposition 3.11.1,
$\tau $
to be the v-topology. By Proposition 3.11.1,
![]() $\overline {\mathcal {G}}$
is a v-sheaf and we have a short exact sequence on
$\overline {\mathcal {G}}$
is a v-sheaf and we have a short exact sequence on
![]() $X_{v}$
$X_{v}$
Applying
![]() $R\pi _{v,*}$
yields the following long exact sequence of sheaves on
$R\pi _{v,*}$
yields the following long exact sequence of sheaves on
![]() $\operatorname {\mathrm {Adic}}_{K,v}$
$\operatorname {\mathrm {Adic}}_{K,v}$
We now let
![]() $\Gamma _n$
denote the image in v-sheaves on
$\Gamma _n$
denote the image in v-sheaves on
![]() $\operatorname {\mathrm {Adic}}_K$
of the map
$\operatorname {\mathrm {Adic}}_K$
of the map
![]() $\delta _n$
. To show that
$\delta _n$
. To show that
![]() $\Gamma _n$
is an étale rigid group, we may pass to a completed algebraic closure and therefore we assume that K is algebraically closed. Observe that
$\Gamma _n$
is an étale rigid group, we may pass to a completed algebraic closure and therefore we assume that K is algebraically closed. Observe that
![]() $H=R^{n+1}\pi _{v,*}\widehat {\mathcal {G}}$
is partially proper. Indeed, it is separated, as is any rigid group over K. To see that H is overconvergent, it is enough to show that
$H=R^{n+1}\pi _{v,*}\widehat {\mathcal {G}}$
is partially proper. Indeed, it is separated, as is any rigid group over K. To see that H is overconvergent, it is enough to show that
![]() $H[p^{\infty }] = R^{n+1}\pi _{v,*}\mathcal {G}[p^{\infty }]$
is overconvergent, which follows from Proposition 3.16.2. We may thus apply Lemma 3.50 to find that the sheaf
$H[p^{\infty }] = R^{n+1}\pi _{v,*}\mathcal {G}[p^{\infty }]$
is overconvergent, which follows from Proposition 3.16.2. We may thus apply Lemma 3.50 to find that the sheaf
![]() $\Gamma _n$
is a sub-v-sheaf of the locally constant sheaf
$\Gamma _n$
is a sub-v-sheaf of the locally constant sheaf
![]() $\underline {A}_K$
for some group A. By [Reference Scholze47, Prop. 10.5] applied to each open and closed component
$\underline {A}_K$
for some group A. By [Reference Scholze47, Prop. 10.5] applied to each open and closed component
![]() $\underline {\{a\}}_K$
, it follows that
$\underline {\{a\}}_K$
, it follows that
![]() $\Gamma _n$
is representable by an open subspace of
$\Gamma _n$
is representable by an open subspace of
![]() $\underline {A}_K$
and is therefore étale over K. This concludes, with
$\underline {A}_K$
and is therefore étale over K. This concludes, with
![]() $\tau $
being the v-topology.
$\tau $
being the v-topology.
We now treat the case
![]() $\tau =\operatorname {\mathrm {\acute {e}t}}$
. We define sheaves Q and
$\tau =\operatorname {\mathrm {\acute {e}t}}$
. We define sheaves Q and
![]() $Q'$
on
$Q'$
on
![]() $\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
as the following cokernels
$\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
as the following cokernels
From the degeneration of the geometric spectral sequences (Theorem 3.29), we obtain a commutative diagram of étale sheaves

where the rows are exact and the right vertical map is an isomorphism. From the snake Lemma, we deduce that
This concludes the proof.
Example 3.51. Assume that K is algebraically closed and let
![]() $X^{\operatorname {\mathrm {alg}}} \xrightarrow {\pi ^{\operatorname {\mathrm {alg}}}}\operatorname {\mathrm {Spec}}(K)$
be a proper smooth algebraic variety with analytification
$X^{\operatorname {\mathrm {alg}}} \xrightarrow {\pi ^{\operatorname {\mathrm {alg}}}}\operatorname {\mathrm {Spec}}(K)$
be a proper smooth algebraic variety with analytification
The exponential of Lemma 2.26 yields an open subgroup U of the locally p-divisible rigid group
![]() ${\mathbf {Bun}}_{\widehat {\mathbb {G}}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
isomorphic to the polydisc
${\mathbf {Bun}}_{\widehat {\mathbb {G}}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
isomorphic to the polydisc
![]() $\mathbb {B}^d$
, where
$\mathbb {B}^d$
, where
![]() $d= \dim _K H_{\operatorname {\mathrm {\acute {e}t}}}^2(X,\mathcal {O}_X)$
, and we assume that
$d= \dim _K H_{\operatorname {\mathrm {\acute {e}t}}}^2(X,\mathcal {O}_X)$
, and we assume that
![]() $d>0$
. Then the image of U in
$d>0$
. Then the image of U in
![]() ${\mathbf {Bun}}_{\mathbb {G}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
is not torsion, since U would otherwise be contained in the étale subgroup
${\mathbf {Bun}}_{\mathbb {G}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
is not torsion, since U would otherwise be contained in the étale subgroup
![]() $\bigcup _{n\geq 1} [n]^{-1}(\Gamma _1)$
. This gives a new perspective on why the Brauer group
$\bigcup _{n\geq 1} [n]^{-1}(\Gamma _1)$
. This gives a new perspective on why the Brauer group
![]() $H_{\operatorname {\mathrm {\acute {e}t}}}^2(X,\mathbb {G}_m)$
of smooth proper rigid analytic varieties typically contains nontorsion elements, in contrast with the algebraic Brauer group
$H_{\operatorname {\mathrm {\acute {e}t}}}^2(X,\mathbb {G}_m)$
of smooth proper rigid analytic varieties typically contains nontorsion elements, in contrast with the algebraic Brauer group
![]() $H_{\operatorname {\mathrm {\acute {e}t}}}^2(X^{\operatorname {\mathrm {alg}}},\mathbb {G}_m)$
which is torsion [Reference Milne39, Cor. IV.2.6]. This also shows that the GAGA principle fails for
$H_{\operatorname {\mathrm {\acute {e}t}}}^2(X^{\operatorname {\mathrm {alg}}},\mathbb {G}_m)$
which is torsion [Reference Milne39, Cor. IV.2.6]. This also shows that the GAGA principle fails for
![]() $\mathbb {G}_m$
-gerbes.
$\mathbb {G}_m$
-gerbes.
Example 3.52. We make the sequence (3.23) in low degree more explicit when
![]() $X = A$
is an abeloid variety over K with good reduction and
$X = A$
is an abeloid variety over K with good reduction and
![]() $\mathcal {G}=\mathbb {G}_m$
. We assume that
$\mathcal {G}=\mathbb {G}_m$
. We assume that
![]() $K^+=\mathcal {O}_K$
and that K is algebraically closed. By [Reference Heuer22, Lemma 4.11.2], we have a surjection
$K^+=\mathcal {O}_K$
and that K is algebraically closed. By [Reference Heuer22, Lemma 4.11.2], we have a surjection
![]() $\pi _*\mathbb {G}_m \twoheadrightarrow \pi _* \overline {\mathbb {G}}_m$
and thus
$\pi _*\mathbb {G}_m \twoheadrightarrow \pi _* \overline {\mathbb {G}}_m$
and thus
![]() $\Gamma _0 =0$
. We thus have an exact sequence of sheaves on
$\Gamma _0 =0$
. We thus have an exact sequence of sheaves on
![]() $\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
$\operatorname {\mathrm {Perf}}_{K,\operatorname {\mathrm {\acute {e}t}}}$
Here, the relative Picard functor
![]() ${\mathbf {Pic}}_{A,\operatorname {\mathrm {\acute {e}t}}} = R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\mathbb {G}_m$
is representable by a rigid group whose identity component is the dual abeloid variety
${\mathbf {Pic}}_{A,\operatorname {\mathrm {\acute {e}t}}} = R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\mathbb {G}_m$
is representable by a rigid group whose identity component is the dual abeloid variety
![]() $A^{\vee }$
[Reference Bosch and Lütkebohmert5, §6][Reference Heuer22, Cor. 2.9.(3), Cor. 5.4]. Applying the functor
$A^{\vee }$
[Reference Bosch and Lütkebohmert5, §6][Reference Heuer22, Cor. 2.9.(3), Cor. 5.4]. Applying the functor
![]() $\widehat {(\cdot )}$
(which is left exact on rigid groups by Proposition 2.17.1 yields an identification
$\widehat {(\cdot )}$
(which is left exact on rigid groups by Proposition 2.17.1 yields an identification
Claim 3.53. We have
where
![]() ${\mathbf {Pic}}_{A_0,\operatorname {\mathrm {\acute {e}t}}}$
is the Picard variety of the special fiber
${\mathbf {Pic}}_{A_0,\operatorname {\mathrm {\acute {e}t}}}$
is the Picard variety of the special fiber
![]() $A_0$
. See [Reference Heuer26, Def. 5.1] for the meaning of
$A_0$
. See [Reference Heuer26, Def. 5.1] for the meaning of
![]() $(\cdot )^{\diamondsuit }$
in this context.
$(\cdot )^{\diamondsuit }$
in this context.
Proof. First, [Reference Heuer26, Cor. 5.4] gives us
where
denotes the p-adic universal cover of A. Let
![]() $\widetilde {\pi }\colon \widetilde {A} \rightarrow \operatorname {\mathrm {Spa}}(K)$
denote the structure map. Combining [Reference Heuer26, Lemma 5.5] and the exponential sequence [Reference Heuer26, Lemma 2.12], we obtain
$\widetilde {\pi }\colon \widetilde {A} \rightarrow \operatorname {\mathrm {Spa}}(K)$
denote the structure map. Combining [Reference Heuer26, Lemma 5.5] and the exponential sequence [Reference Heuer26, Lemma 2.12], we obtain
Then by [Reference Heuer22, Prop. 4.12.2], it follows that
It remains to show that this colimit is equal to
![]() $R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\overline {\mathbb {G}}_m[\frac {1}{p}] =R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\overline {\mathbb {G}}_m$
. Consider the exact sequence
$R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\overline {\mathbb {G}}_m[\frac {1}{p}] =R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\overline {\mathbb {G}}_m$
. Consider the exact sequence
It is enough to show that, for
![]() $\mathcal {F}$
any sheaf on the left or right of
$\mathcal {F}$
any sheaf on the left or right of
![]() $R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\overline {\mathbb {G}}_m$
in the sequence above, we have
$R^1\pi _{\operatorname {\mathrm {\acute {E}t}},*}\overline {\mathbb {G}}_m$
in the sequence above, we have
For
![]() $\mathcal {F} = \widehat {{\mathbf {Pic}}}_{A,\operatorname {\mathrm {\acute {e}t}}}$
, this clear since
$\mathcal {F} = \widehat {{\mathbf {Pic}}}_{A,\operatorname {\mathrm {\acute {e}t}}}$
, this clear since
![]() $[p]^* = (\cdot )^{\otimes p}$
on
$[p]^* = (\cdot )^{\otimes p}$
on
![]() $A^{\vee }$
. For
$A^{\vee }$
. For
![]() $\mathcal {F} = {\mathbf {Pic}}_{A,\operatorname {\mathrm {\acute {e}t}}}$
, it follows from the fact that for a line bundle
$\mathcal {F} = {\mathbf {Pic}}_{A,\operatorname {\mathrm {\acute {e}t}}}$
, it follows from the fact that for a line bundle
![]() $\mathcal {L}$
on A, we have
$\mathcal {L}$
on A, we have
![]() $[p]^*\mathcal {L} \equiv \mathcal {L}^{\otimes p^{2}}(\operatorname {\mathrm {mod}} A^{\vee })$
: This is a consequence of the theorem of the cube [Reference Lütkebohmert37, Thm. 7.1.6. (a)], see [Reference Mumford40, II.8.(iv)]. For
$[p]^*\mathcal {L} \equiv \mathcal {L}^{\otimes p^{2}}(\operatorname {\mathrm {mod}} A^{\vee })$
: This is a consequence of the theorem of the cube [Reference Lütkebohmert37, Thm. 7.1.6. (a)], see [Reference Mumford40, II.8.(iv)]. For
![]() $\mathcal {F}= R^2\pi _{\operatorname {\mathrm {\acute {E}t}},*}\widehat {\mathbb {G}}_m$
, it follows from the exact sequence (3.6). Hence the claim is proven.
$\mathcal {F}= R^2\pi _{\operatorname {\mathrm {\acute {E}t}},*}\widehat {\mathbb {G}}_m$
, it follows from the exact sequence (3.6). Hence the claim is proven.
We now use the exact sequence [Reference Heuer26, Corollary 5.4]
Here,
![]() $\operatorname {\mathrm {NS}}(A)$
denotes the Neron–Severi group of A. We conclude that
$\operatorname {\mathrm {NS}}(A)$
denotes the Neron–Severi group of A. We conclude that
 $$\begin{align*}\Gamma_1 = \underline{\frac{\operatorname{\mathrm{NS}}(A_0)[\frac{1}{p}]}{\operatorname{\mathrm{NS}}(A)}}.\end{align*}$$
$$\begin{align*}\Gamma_1 = \underline{\frac{\operatorname{\mathrm{NS}}(A_0)[\frac{1}{p}]}{\operatorname{\mathrm{NS}}(A)}}.\end{align*}$$
In particular,
![]() $\Gamma _1$
is nonzero in that case.
$\Gamma _1$
is nonzero in that case.
Corollary 3.54. There exists a proper smooth rigid space X over K such that
![]() ${\mathbf {Bun}}_{\mathbb {G}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
is not representable by a rigid group.
${\mathbf {Bun}}_{\mathbb {G}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
is not representable by a rigid group.
Proof. We take K to be algebraically closed and
![]() $X = E\times E$
, for E an elliptic curve without complex multiplication, and with supersingular reduction
$X = E\times E$
, for E an elliptic curve without complex multiplication, and with supersingular reduction
![]() $E_0$
. Note that
$E_0$
. Note that
Similarly, one computes
![]() $\operatorname {\mathrm {rank}}_{\mathbb {Z}} \operatorname {\mathrm {NS}}(E_0 \times E_0) =6$
. Hence, by Example 3.52,
$\operatorname {\mathrm {rank}}_{\mathbb {Z}} \operatorname {\mathrm {NS}}(E_0 \times E_0) =6$
. Hence, by Example 3.52,
 $$\begin{align*}\Gamma_1 = \frac{\mathbb{Z}[\tfrac{1}{p}]^{\oplus 6}}{\mathbb{Z}^{\oplus 3}}= \mathbb{Z}[\tfrac{1}{p}]^{\oplus 3} \oplus (\mathbb{Q}_p/\mathbb{Z}_p)^{\oplus 3}. \end{align*}$$
$$\begin{align*}\Gamma_1 = \frac{\mathbb{Z}[\tfrac{1}{p}]^{\oplus 6}}{\mathbb{Z}^{\oplus 3}}= \mathbb{Z}[\tfrac{1}{p}]^{\oplus 3} \oplus (\mathbb{Q}_p/\mathbb{Z}_p)^{\oplus 3}. \end{align*}$$
We now apply the left exact functor
![]() $\underline {\operatorname {\mathrm {Hom}}}(\mathbb {Z}_p,-)$
to the exact sequence
$\underline {\operatorname {\mathrm {Hom}}}(\mathbb {Z}_p,-)$
to the exact sequence
Observe that
Hence we have a commutative diagram with exact rows

It follows that the right vertical map cannot be injective. By Lemma 2.17.1, in that case,
![]() ${\mathbf {Bun}}_{\mathbb {G}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
cannot be represented by a rigid group.
${\mathbf {Bun}}_{\mathbb {G}_m,\operatorname {\mathrm {\acute {e}t}}}^2$
cannot be represented by a rigid group.
Remark 3.55. Let
![]() $X^{\operatorname {\mathrm {alg}}}$
be an abelian variety of dimension
$X^{\operatorname {\mathrm {alg}}}$
be an abelian variety of dimension
![]() $g>1$
, Then the algebraic higher direct image
$g>1$
, Then the algebraic higher direct image
is not representable by an algebraic group. By contradiction, let H be such a group, which is automatically smooth, as K has characteristic
![]() $0$
. Let
$0$
. Let
![]() $X^{\operatorname {\mathrm {alg}}}[\epsilon ]$
denote the trivial thickening of
$X^{\operatorname {\mathrm {alg}}}[\epsilon ]$
denote the trivial thickening of
![]() $X^{\operatorname {\mathrm {alg}}}$
along
$X^{\operatorname {\mathrm {alg}}}$
along
![]() $\operatorname {\mathrm {Spec}}(K) \hookrightarrow \operatorname {\mathrm {Spec}}(K[\epsilon ])$
. There is a short exact sequence on
$\operatorname {\mathrm {Spec}}(K) \hookrightarrow \operatorname {\mathrm {Spec}}(K[\epsilon ])$
. There is a short exact sequence on
![]() $X_{\operatorname {\mathrm {\acute {e}t}}}^{\operatorname {\mathrm {alg}}}$
$X_{\operatorname {\mathrm {\acute {e}t}}}^{\operatorname {\mathrm {alg}}}$
We deduce that
Hence
![]() $\dim H = h^2(X^{\operatorname {\mathrm {alg}}},\mathcal {O}_{X^{\operatorname {\mathrm {alg}}}})>0$
, which contradicts the fact that
$\dim H = h^2(X^{\operatorname {\mathrm {alg}}},\mathcal {O}_{X^{\operatorname {\mathrm {alg}}}})>0$
, which contradicts the fact that
![]() $H(K)=H_{\operatorname {\mathrm {\acute {e}t}}}^2(X^{\operatorname {\mathrm {alg}}},\mathbb {G}_m)$
is torsion.
$H(K)=H_{\operatorname {\mathrm {\acute {e}t}}}^2(X^{\operatorname {\mathrm {alg}}},\mathbb {G}_m)$
is torsion.
Remark 3.56. Arguing as in the proof of [Reference Heuer22, Cor. 2.9.5], we can use the local splittings of Remark 3.36 to show that, for given
![]() $n \geq 0$
, the étale higher direct image
$n \geq 0$
, the étale higher direct image
![]() ${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
is representable by a rigid group if and only if
${\mathbf {Bun}}_{\mathcal {G},\operatorname {\mathrm {\acute {e}t}}}^n$
is representable by a rigid group if and only if
![]() ${\mathbf {Bun}}_{\mathcal {G},v}^n$
is representable by a rigid group.
${\mathbf {Bun}}_{\mathcal {G},v}^n$
is representable by a rigid group.
Acknowledgements
This project originated from a discussion with Ben Heuer, where the question of the degeneration of the multiplicative Hodge–Tate spectral sequence was raised. We thank him heartily for many helpful conversations, especially his suggestion to think about geometric Hodge–Tate spectral sequences, for answering all our questions and for carefully reading through the project’s early versions. The present work is part of the PhD thesis of the author. We thank our advisor, Annette Werner, for very helpful discussions and for her many insightful comments on early drafts of this article. We thank Annie Littler, Konrad Zou, and Jefferson Baudin for their comments and for interesting discussions. Finally, we thank the anonymous referee for helpful comments.
Competing interests
The author has no competing interest to declare.
Funding statement
This project was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through the Collaborative Research Centre TRR 326 Geometry and Arithmetic of Uniformized Structures – Project-ID 444845124. Our research was also partially supported by the Simons Foundation through the Simons Collaboration on Perfection in Algebra, Geometry, and Topology.