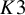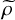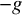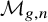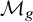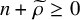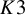1 Introduction
The theory of linear series on projective curves with prescribed ramification has been intensively studied since the appearance in the eighties of the groundbreaking results of Eisenbud and Harris [Reference Eisenbud and Harris13] see, for example, [Reference Cela, Pandharipande and Schmitt6, Reference Chan, Osserman and Pflueger7, Reference Chan, Martin, Pflueger and Bigas8, Reference Faber and Pandharipande15, Reference Farkas16, Reference Farkas and Lian17, Reference Farkas and Tarasca18, Reference Farkas and Tarasca19, Reference Janda, Pandharipande, Pixton and Zvonkine26, Reference Osserman34, Reference Osserman35, Reference Tevelev37, Reference Bigas38]. There is an adjusted Brill-Noether number
![]() $\widetilde {\rho }$
(see (2.3)) generalizing the classical Brill-Noether number
$\widetilde {\rho }$
(see (2.3)) generalizing the classical Brill-Noether number
![]() $\rho (g,r,d)$
, which in addition to
$\rho (g,r,d)$
, which in addition to
![]() $g,r,d$
also depends on the ramification profile. In [Reference Eisenbud and Harris13, Thm. 4.5 and its Rmk.] it is proved that a general pointed genus g curve carries a
$g,r,d$
also depends on the ramification profile. In [Reference Eisenbud and Harris13, Thm. 4.5 and its Rmk.] it is proved that a general pointed genus g curve carries a
![]() $g^r_d$
with prescribed ramifications at the marked points only if
$g^r_d$
with prescribed ramifications at the marked points only if
![]() $\widetilde {\rho }\geq 0$
. In contrast to the unramified case, the condition becomes sufficient provided that an intersection number of Schubert classes is nonzero, and, if so, the Brill-Noether loci have dimension
$\widetilde {\rho }\geq 0$
. In contrast to the unramified case, the condition becomes sufficient provided that an intersection number of Schubert classes is nonzero, and, if so, the Brill-Noether loci have dimension
![]() $\widetilde {\rho }$
. For pencils the conditions hold true by Osserman’s results [Reference Osserman35, Thms. 2.4 and 2.6].
$\widetilde {\rho }$
. For pencils the conditions hold true by Osserman’s results [Reference Osserman35, Thms. 2.4 and 2.6].
For negative
![]() $\widetilde {\rho }$
, comparatively little is known about the loci of curves in the moduli space of n-pointed curves
$\widetilde {\rho }$
, comparatively little is known about the loci of curves in the moduli space of n-pointed curves
![]() ${\mathcal M}_{g,n}$
carrying linear series with prescribed ramification, for instance their dimensions, and the dimension of the Brill-Noether varieties of the general members, even in the case of pencils. By contrast, in the classical case without ramification with
${\mathcal M}_{g,n}$
carrying linear series with prescribed ramification, for instance their dimensions, and the dimension of the Brill-Noether varieties of the general members, even in the case of pencils. By contrast, in the classical case without ramification with
![]() $\rho <0$
, it is known that the locus of curves in
$\rho <0$
, it is known that the locus of curves in
![]() ${\mathcal M}_g$
carrying a
${\mathcal M}_g$
carrying a
![]() $g^1_d$
is irreducible of codimension
$g^1_d$
is irreducible of codimension
![]() $-\rho $
and that its general element carries finitely many
$-\rho $
and that its general element carries finitely many
![]() $g^1_d$
s.
$g^1_d$
s.
The first main result of this paper generalizes the classical results on Brill-Noether theory of pencils to the case of prescribed ramification, under the condition
![]() $\widetilde {\rho } \geq -g$
. In Theorem 2.1, we prove that the moduli space of n-pointed curves with a
$\widetilde {\rho } \geq -g$
. In Theorem 2.1, we prove that the moduli space of n-pointed curves with a
![]() $g^1_k$
with prescribed ramification has codimension
$g^1_k$
with prescribed ramification has codimension
![]() $\min \{0,-\widetilde {\rho }\}$
in
$\min \{0,-\widetilde {\rho }\}$
in
![]() ${\mathcal M}_{g,n}$
, and that its general member carries a
${\mathcal M}_{g,n}$
, and that its general member carries a
![]() $\max \{0,\widetilde {\rho }\}$
-dimensional family of such pencils. When
$\max \{0,\widetilde {\rho }\}$
-dimensional family of such pencils. When
![]() $\widetilde {\rho } \geq 0$
, our result provides an alternative proof of the aforementioned existence results of Eisenbud-Harris [Reference Eisenbud and Harris13, Thm. 4.5 and its Rmk.] and Osserman [Reference Osserman35, Thms. 2.4 and 2.6], not relying on Schubert calculus. Most importantly, our result establishes the case of negative adjusted Brill-Noether number
$\widetilde {\rho } \geq 0$
, our result provides an alternative proof of the aforementioned existence results of Eisenbud-Harris [Reference Eisenbud and Harris13, Thm. 4.5 and its Rmk.] and Osserman [Reference Osserman35, Thms. 2.4 and 2.6], not relying on Schubert calculus. Most importantly, our result establishes the case of negative adjusted Brill-Noether number
![]() $\widetilde {\rho }$
.
$\widetilde {\rho }$
.
As a significant application, under the condition
![]() $\widetilde {\rho } \geq -g$
, in Theorem 2.3 we prove that the natural forgetful map from the Hurwitz space of covers with prescribed ramifications to
$\widetilde {\rho } \geq -g$
, in Theorem 2.3 we prove that the natural forgetful map from the Hurwitz space of covers with prescribed ramifications to
![]() ${\mathcal M}_g$
is dominant precisely when
${\mathcal M}_g$
is dominant precisely when
![]() $n+\widetilde {\rho }\geq 0$
. This answers a variation of the classical conjecture of Zariski [Reference Zariski41] expecting the map from the Hurwitz space with prescribed monodromies to
$n+\widetilde {\rho }\geq 0$
. This answers a variation of the classical conjecture of Zariski [Reference Zariski41] expecting the map from the Hurwitz space with prescribed monodromies to
![]() $\mathcal {M}_g$
to be dominant as soon as the dimension of the target is smaller and the covers are noncomposed. Such a variation has already been intensively studied in the past years and partial results can be found in some of the above mentioned papers.
$\mathcal {M}_g$
to be dominant as soon as the dimension of the target is smaller and the covers are noncomposed. Such a variation has already been intensively studied in the past years and partial results can be found in some of the above mentioned papers.
To prove the above results, we use degenerations to nodal rational curves, performed in §3. A refined version of this degeneration, performed in §4-5, allows us to exhibit curves having the desired properties as normalizations of nodal curves on
![]() $K3$
surfaces. In fact, in Theorem 2.6 we find loci of nodal curves on
$K3$
surfaces. In fact, in Theorem 2.6 we find loci of nodal curves on
![]() $K3$
surfaces whose normalizations carry a family of pencils with desired prescribed ramification of the expected dimension. We believe this result is of independent interest. For smooth curves, this extends to the ramified case Lazarsfeld’s famous result stating that smooth curves on general K3 surfaces are Brill-Noether general. For nodal curves, this extends the results without ramification in [Reference Ciliberto and Knutsen12] providing non-Brill-Noether general behavior.
$K3$
surfaces whose normalizations carry a family of pencils with desired prescribed ramification of the expected dimension. We believe this result is of independent interest. For smooth curves, this extends to the ramified case Lazarsfeld’s famous result stating that smooth curves on general K3 surfaces are Brill-Noether general. For nodal curves, this extends the results without ramification in [Reference Ciliberto and Knutsen12] providing non-Brill-Noether general behavior.
The last results of the paper, proved in §6, concern correspondences and cycles on K3 surfaces, and their relation to tautological points in
![]() ${\mathcal M}_{g,2}$
. Indeed, as an application of Theorem 2.6, we solve in full generality the problem of nonemptiness of components in the fibre over
${\mathcal M}_{g,2}$
. Indeed, as an application of Theorem 2.6, we solve in full generality the problem of nonemptiness of components in the fibre over
![]() $0$
of the difference map
$0$
of the difference map
![]() $X \times X\to CH_0(X)$
studied by Mumford [Reference Mumford33], obtained as n-torsion points in the Jacobian of curves in X, for a very general K3 surface X (see Theorem 2.8). We furthermore analyze these components with respect to Beauville-Voisin points and constant cycle curves (see Corollary 2.11). In view of Pandharipande and Schmitt’s result [Reference Pandharipande and Schmitt36] relating Beauville-Voisin points and tautological points, we construct cycles in
$X \times X\to CH_0(X)$
studied by Mumford [Reference Mumford33], obtained as n-torsion points in the Jacobian of curves in X, for a very general K3 surface X (see Theorem 2.8). We furthermore analyze these components with respect to Beauville-Voisin points and constant cycle curves (see Corollary 2.11). In view of Pandharipande and Schmitt’s result [Reference Pandharipande and Schmitt36] relating Beauville-Voisin points and tautological points, we construct cycles in
![]() ${\mathcal M}_{g,2}$
with a dense set of tautological points (see Corollary 2.12).
${\mathcal M}_{g,2}$
with a dense set of tautological points (see Corollary 2.12).
In the next section we will present the main results of this paper more precisely, and explain all necessary notation.
2 Setting and main results of the paper
In this section we will introduce notation and present the main results of the paper. We will divide the presentation in three parts:
-
○ results concerning Brill-Noether theory of pencils with prescribed ramification on pointed curves (§2.1),
-
○ results concerning Brill-Noether theory of pencils with prescribed ramification on normalizations of pointed nodal curves on
 $K3$
surfaces (§2.2),
$K3$
surfaces (§2.2), -
○ applications to cycles on
 $K3$
surfaces and tautological points in the moduli space of
$K3$
surfaces and tautological points in the moduli space of
 $2$
-pointed curves (§2.3).
$2$
-pointed curves (§2.3).
Throughout the paper,
![]() $g,k,n,e_1,\ldots ,e_n$
will be integers satisfying
$g,k,n,e_1,\ldots ,e_n$
will be integers satisfying
and we define
2.1 Moduli spaces of pointed curves with prescribed ramification
Let
![]() $ {\mathcal M}_{g,n}$
denote the moduli space of smooth n-pointed genus g curves. For
$ {\mathcal M}_{g,n}$
denote the moduli space of smooth n-pointed genus g curves. For
![]() $(C,x_1,\ldots , x_n) \in {\mathcal M}_{g,n}$
and
$(C,x_1,\ldots , x_n) \in {\mathcal M}_{g,n}$
and
![]() $\mathbf {e}=(e_1,\ldots ,e_n)$
we let
$\mathbf {e}=(e_1,\ldots ,e_n)$
we let
be the variety parametrizing
![]() $g^1_k$
s on C with ramification order
$g^1_k$
s on C with ramification order
![]() $e_i$
at
$e_i$
at
![]() $x_i$
. Note that
$x_i$
. Note that
(recall (2.2)) by Riemann-Hurwitz. In the classical (unramified) setting,
![]() $G^1_k(C)$
denotes the variety parametrizing
$G^1_k(C)$
denotes the variety parametrizing
![]() $g^1_k$
s on C. For a general curve C, a necessary and sufficient condition for
$g^1_k$
s on C. For a general curve C, a necessary and sufficient condition for
![]() $G^1_k(C)\neq \emptyset $
is
$G^1_k(C)\neq \emptyset $
is
![]() $\rho (g,1,k)\geq 0$
, where
$\rho (g,1,k)\geq 0$
, where
![]() $\rho $
is the Brill-Noether number.
$\rho $
is the Brill-Noether number.
Let
![]() ${\mathcal M}_{g,k,\mathbf {e}} \subset {\mathcal M}_{g,n}$
be the locus of n-pointed curves
${\mathcal M}_{g,k,\mathbf {e}} \subset {\mathcal M}_{g,n}$
be the locus of n-pointed curves
![]() $(C,x_1,\ldots ,x_n)$
such that
$(C,x_1,\ldots ,x_n)$
such that
![]() $G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n)) \neq \emptyset $
. A necessary and sufficient condition for such nonemptiness on a general n-pointed curve is that
$G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n)) \neq \emptyset $
. A necessary and sufficient condition for such nonemptiness on a general n-pointed curve is that
![]() $\widetilde {\rho }=\widetilde {\rho }(g,1,k;e_1,\ldots ,e_n)\geq 0$
, where
$\widetilde {\rho }=\widetilde {\rho }(g,1,k;e_1,\ldots ,e_n)\geq 0$
, where
 $$ \begin{align} \widetilde{\rho}=\widetilde{\rho}(g,1,k;e_1,\ldots,e_n):=\rho(g,1,k)-\sum_{i=1}^n(e_i-1)=2k-2-g-e+n \end{align} $$
$$ \begin{align} \widetilde{\rho}=\widetilde{\rho}(g,1,k;e_1,\ldots,e_n):=\rho(g,1,k)-\sum_{i=1}^n(e_i-1)=2k-2-g-e+n \end{align} $$
is the adjusted Brill-Noether number. In other words,
![]() ${\mathcal M}_{g,k,\mathbf {e}} ={\mathcal M}_{g,n}$
if and only if
${\mathcal M}_{g,k,\mathbf {e}} ={\mathcal M}_{g,n}$
if and only if
![]() $\widetilde {\rho }=\widetilde {\rho }(g,1,k;e_1,\ldots ,e_n)\geq 0$
. In contrast to the classical case (with no ramification), the ‘if statement’ relies on the computation of a nonzero intersection number of Schubert classes in the Chow ring of the Grassmannian
$\widetilde {\rho }=\widetilde {\rho }(g,1,k;e_1,\ldots ,e_n)\geq 0$
. In contrast to the classical case (with no ramification), the ‘if statement’ relies on the computation of a nonzero intersection number of Schubert classes in the Chow ring of the Grassmannian
![]() ${\mathbb G}(d -2, d)$
provided by Ossermann, cf., [Reference Harris and Morrison23, Thm. 5.42] and [Reference Osserman35, Thms. 2.4 and 2.6].
${\mathbb G}(d -2, d)$
provided by Ossermann, cf., [Reference Harris and Morrison23, Thm. 5.42] and [Reference Osserman35, Thms. 2.4 and 2.6].
We denote by
![]() ${\mathcal G}^1_{g,k,\mathbf {e}}$
the variety parametrizing pairs
${\mathcal G}^1_{g,k,\mathbf {e}}$
the variety parametrizing pairs
![]() $\left ((C,x_1,\ldots ,x_n),\mathfrak {g}\right )$
such that
$\left ((C,x_1,\ldots ,x_n),\mathfrak {g}\right )$
such that
![]() $(C,x_1,\ldots ,x_n) \in {\mathcal M}_{g,k,\mathbf {e}}$
and
$(C,x_1,\ldots ,x_n) \in {\mathcal M}_{g,k,\mathbf {e}}$
and
![]() $\mathfrak {g} \in G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
and by
$\mathfrak {g} \in G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
and by
the forgetful map, with fibre over
![]() $(C,x_1,\ldots ,x_n)$
being
$(C,x_1,\ldots ,x_n)$
being
![]() $G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
. This is related to the Hurwitz moduli space
$G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
. This is related to the Hurwitz moduli space
parametrizing degree k covers
![]() $X \to {\mathbb P}^1$
with X a smooth projective curve of genus g with points of ramification
$X \to {\mathbb P}^1$
with X a smooth projective curve of genus g with points of ramification
![]() $e_i$
over n ordered points of the target, and simple ramification over
$e_i$
over n ordered points of the target, and simple ramification over
![]() $r:=2(k-1+g)+n-e$
ordered points of the target completing the ramification profileFootnote 1, cf., for example, [Reference Harris and Mumford24, Reference Abramovich, Corti and Vistoli1, Reference Mochizuki31, Reference Faber and Pandharipande15]. We have a natural finiteFootnote 2 forgetful map dominating each componentFootnote 3
$r:=2(k-1+g)+n-e$
ordered points of the target completing the ramification profileFootnote 1, cf., for example, [Reference Harris and Mumford24, Reference Abramovich, Corti and Vistoli1, Reference Mochizuki31, Reference Faber and Pandharipande15]. We have a natural finiteFootnote 2 forgetful map dominating each componentFootnote 3
By Riemann’s Existence TheoremFootnote 4 (cf., e.g., [Reference Miranda30, III, Cor. 4.10]),
This, along with the classical result [Reference Eisenbud and Harris13, Thm. 4.5] of Eisenbud and Harris when
![]() $\widetilde {\rho } \geq 0$
, implies that all components of
$\widetilde {\rho } \geq 0$
, implies that all components of
![]() $G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
have dimension at least
$G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
have dimension at least
![]() $ \max \{0,\widetilde {\rho }\}$
, and if equality holds for some
$ \max \{0,\widetilde {\rho }\}$
, and if equality holds for some
![]() $(C,x_1,\ldots ,x_n)$
, then
$(C,x_1,\ldots ,x_n)$
, then
![]() ${\mathcal M}_{g,k,\mathbf {e}}$
has a component of codimension
${\mathcal M}_{g,k,\mathbf {e}}$
has a component of codimension
in
![]() ${\mathcal M}_{g,n}$
. We call this the expected codimension of
${\mathcal M}_{g,n}$
. We call this the expected codimension of
![]() ${\mathcal M}_{g,k,\mathbf {e}}$
. One of the main results of this paper proves the existence of a component of the expected codimension under the additional condition
${\mathcal M}_{g,k,\mathbf {e}}$
. One of the main results of this paper proves the existence of a component of the expected codimension under the additional condition
![]() $\widetilde {\rho } \geq -g$
:
$\widetilde {\rho } \geq -g$
:
Theorem 2.1. In the setting (2.1)-(2.2), assume that
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
. Then
$\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
. Then
![]() ${\mathcal M}_{g,k,\mathbf {e}}$
has a component of the expected codimension
${\mathcal M}_{g,k,\mathbf {e}}$
has a component of the expected codimension
![]() $\max \{0,-\widetilde {\rho }\}$
in
$\max \{0,-\widetilde {\rho }\}$
in
![]() ${\mathcal M}_{g,n}$
whose general member
${\mathcal M}_{g,n}$
whose general member
![]() $(C,x_1,\ldots ,x_n)$
satisfies
$(C,x_1,\ldots ,x_n)$
satisfies
Remark 2.2. Since the general member in any component of
![]() ${\mathcal G}^1_{g,k,\mathbf {e}}$
is base point free, has simple ramification elsewhere and all ramification points lie in distinct fibres, the same properties are true for the general member in any component of
${\mathcal G}^1_{g,k,\mathbf {e}}$
is base point free, has simple ramification elsewhere and all ramification points lie in distinct fibres, the same properties are true for the general member in any component of
![]() $G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
as in the theorem.
$G^1_k(C,(x_1,e_1),\ldots ,(x_n,e_n))$
as in the theorem.
As a consequence, we also solve the classical problem regarding the dominance or generic finiteness of the forgetful map from the Hurwitz scheme
![]() ${\mathcal H}_{g,k,\mathbf {e}}$
to
${\mathcal H}_{g,k,\mathbf {e}}$
to
![]() ${\mathcal M}_g$
:
${\mathcal M}_g$
:
(where
![]() $\lambda _{g,k,\mathbf {e}}$
and
$\lambda _{g,k,\mathbf {e}}$
and
![]() $\kappa _{g,k,\mathbf {e}}$
are as in (2.5) and (2.4), respectively, and
$\kappa _{g,k,\mathbf {e}}$
are as in (2.5) and (2.4), respectively, and
![]() $\phi _{g,k,\mathbf {e}}$
is the forgetful map). Since
$\phi _{g,k,\mathbf {e}}$
is the forgetful map). Since
![]() $\dim {\mathcal H}_{g,k,\mathbf {e}}= \dim {\mathcal G}^1_{g,k,\mathbf {e}} =\dim {\mathcal M}_g+(n+\widetilde {\rho })$
one may expect, as best case scenario, this map to be dominant if
$\dim {\mathcal H}_{g,k,\mathbf {e}}= \dim {\mathcal G}^1_{g,k,\mathbf {e}} =\dim {\mathcal M}_g+(n+\widetilde {\rho })$
one may expect, as best case scenario, this map to be dominant if
![]() $n+\widetilde {\rho } \geq 0$
and generically finite (on some component) if
$n+\widetilde {\rho } \geq 0$
and generically finite (on some component) if
![]() $n+\widetilde {\rho } < 0$
, so that, in the latter case, the codimension of its image is
$n+\widetilde {\rho } < 0$
, so that, in the latter case, the codimension of its image is
![]() $-(n+\widetilde {\rho })$
. We prove that, under the assumption
$-(n+\widetilde {\rho })$
. We prove that, under the assumption
![]() $\widetilde {\rho } \geq -g$
, this best case scenario actually happens:
$\widetilde {\rho } \geq -g$
, this best case scenario actually happens:
Theorem 2.3. In the setting (2.1)-(2.2), assume that
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
. Then the forgetful map
$\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
. Then the forgetful map
![]() ${\mathcal H}_{g,k,\mathbf {e}} \to {\mathcal M}_g$
is dominant if
${\mathcal H}_{g,k,\mathbf {e}} \to {\mathcal M}_g$
is dominant if
![]() $n+\widetilde {\rho } \geq 0$
and generically finite on at least one component if
$n+\widetilde {\rho } \geq 0$
and generically finite on at least one component if
![]() $n+\widetilde {\rho } < 0$
.
$n+\widetilde {\rho } < 0$
.
2.2 Gonality loci on
 $K3$
surfaces
$K3$
surfaces
Let
![]() $(S,H)$
be a primitively polarized complex
$(S,H)$
be a primitively polarized complex
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $p \geq 2$
. Let
$p \geq 2$
. Let
![]() $V_{|H|,\delta }\subseteq \vert H\vert $
be the Severi variety of curves with
$V_{|H|,\delta }\subseteq \vert H\vert $
be the Severi variety of curves with
![]() $0 \leq \delta \leq p$
nodes, which is known to be nonempty of dimension
$0 \leq \delta \leq p$
nodes, which is known to be nonempty of dimension
![]() $g:=p-\delta $
, if
$g:=p-\delta $
, if
![]() $(S,H)$
is general in moduli. It has recently been proved in [Reference Bruno and Lelli-Chiesa4] that
$(S,H)$
is general in moduli. It has recently been proved in [Reference Bruno and Lelli-Chiesa4] that
![]() $V_{|H|,\delta }$
is irreducible for general
$V_{|H|,\delta }$
is irreducible for general
![]() $(S,H)$
whenever
$(S,H)$
whenever
![]() $g \geq 4$
and connected whenever
$g \geq 4$
and connected whenever
![]() $g\in \{1,2,3\}$
, but we will not make use of this.
$g\in \{1,2,3\}$
, but we will not make use of this.
For
![]() $C \in V_{|H|,\delta }$
, denote by
$C \in V_{|H|,\delta }$
, denote by
![]() $\nu :C^{\nu } \to C$
its normalization map. Then
$\nu :C^{\nu } \to C$
its normalization map. Then
![]() $C^{\nu }$
has genus g. We have a moduli map
$C^{\nu }$
has genus g. We have a moduli map
mapping
![]() $[C]$
to
$[C]$
to
![]() $[C^{\nu }]$
. We let
$[C^{\nu }]$
. We let
![]() ${\mathcal M}^1_{g,k}$
denote the locus of curves carrying a
${\mathcal M}^1_{g,k}$
denote the locus of curves carrying a
![]() $g^1_k$
, which is known to be irreducible of codimension
$g^1_k$
, which is known to be irreducible of codimension
![]() $\max \{0,\rho (g,1,k)\}$
. We set
$\max \{0,\rho (g,1,k)\}$
. We set
that is,
![]() $V^k_{|H|,\delta }\subseteq V_{|H|,\delta }$
is the subvariety of curves whose normalizations carry a
$V^k_{|H|,\delta }\subseteq V_{|H|,\delta }$
is the subvariety of curves whose normalizations carry a
![]() $g^1_k$
. If
$g^1_k$
. If
![]() $(S,H)$
is general, then every smooth curve in
$(S,H)$
is general, then every smooth curve in
![]() $|H|$
is Brill-Noether general by Lazarsfeld’s famous result [Reference Lazarsfeld28, Lem. 1.1], whence
$|H|$
is Brill-Noether general by Lazarsfeld’s famous result [Reference Lazarsfeld28, Lem. 1.1], whence
![]() $V^k_{|H|,0} \neq \emptyset $
if and only if
$V^k_{|H|,0} \neq \emptyset $
if and only if
![]() $\rho (p,1,k) \geq 0$
, that is,
$\rho (p,1,k) \geq 0$
, that is,
![]() $p \leq 2k-2$
; in fact
$p \leq 2k-2$
; in fact
![]() $V^k_{|H|,0} = V_{|H|,0}$
when
$V^k_{|H|,0} = V_{|H|,0}$
when
![]() $p \leq 2k-2$
. In [Reference Ciliberto and Knutsen12, Thm. 0.1] a complete description is given in the case
$p \leq 2k-2$
. In [Reference Ciliberto and Knutsen12, Thm. 0.1] a complete description is given in the case
![]() $\delta>0$
: if
$\delta>0$
: if
![]() $(S,H)$
is general, then
$(S,H)$
is general, then
![]() $V^k_{|H|,\delta } \neq \emptyset $
if and only if
$V^k_{|H|,\delta } \neq \emptyset $
if and only if
equivalently
In particular, this provides, quite surprisingly, the existence of curves in
![]() $|H|$
whose normalizations carry pencils with negative Brill-Noether number, in contrast to the smooth case. More precisely, it is proved that
$|H|$
whose normalizations carry pencils with negative Brill-Noether number, in contrast to the smooth case. More precisely, it is proved that
![]() $V^k_{|H|,\delta }$
is equidimensional of dimension
$V^k_{|H|,\delta }$
is equidimensional of dimension
![]() $\min \{2(k-1),g\}$
under this condition [Reference Knutsen, Lelli-Chiesa and Mongardi27, Rem. 5.6], and has an irreducible component whose general element is an irreducible curve C such that
$\min \{2(k-1),g\}$
under this condition [Reference Knutsen, Lelli-Chiesa and Mongardi27, Rem. 5.6], and has an irreducible component whose general element is an irreducible curve C such that
![]() $G^1_k(C^{\nu })$
is again as ‘nice’ as possible, that is,
$G^1_k(C^{\nu })$
is again as ‘nice’ as possible, that is,
![]() $\dim G^1_k(C^{\nu })=\max \{0,\rho (g,1,k)\}$
, and when
$\dim G^1_k(C^{\nu })=\max \{0,\rho (g,1,k)\}$
, and when
![]() $\rho (g,1,k) \leq 0$
(resp.
$\rho (g,1,k) \leq 0$
(resp.
![]() $\rho> 0$
), any (resp. the general)
$\rho> 0$
), any (resp. the general)
![]() $g^1_k$
on
$g^1_k$
on
![]() $C^{\nu }$
has simple ramification and all nodes of C are non-neutral with respect to itFootnote 5.
$C^{\nu }$
has simple ramification and all nodes of C are non-neutral with respect to itFootnote 5.
We will study the loci of pointed curves in
![]() $V^k_{|H|,\delta }$
with prescribed ramification:
$V^k_{|H|,\delta }$
with prescribed ramification:
Definition 2.4. We define
![]() $V_{|H|,\delta ,n}$
to be the
$V_{|H|,\delta ,n}$
to be the
![]() $(g+n)$
-dimensional scheme parametrizing pointed curves
$(g+n)$
-dimensional scheme parametrizing pointed curves
![]() $(C,x_1,\ldots ,x_n)$
such that
$(C,x_1,\ldots ,x_n)$
such that
![]() $C \in V_{|H|,\delta }$
and
$C \in V_{|H|,\delta }$
and
![]() $x_1,\ldots ,x_n$
are distinct points different from the nodes of C.
$x_1,\ldots ,x_n$
are distinct points different from the nodes of C.
Recalling (2.1)-(2.2), we define
to be the sublocus of
![]() $V_{|H|,\delta ,n}$
such that
$V_{|H|,\delta ,n}$
such that
![]() $G^1_k(C^{\nu },(x_1,e_1),\ldots ,(x_n,e_n)) \neq \emptyset $
.
$G^1_k(C^{\nu },(x_1,e_1),\ldots ,(x_n,e_n)) \neq \emptyset $
.
In the definition we identify
![]() $x_i \in C$
with
$x_i \in C$
with
![]() $\nu ^{-1}(x_i) \in C^{\nu }$
. Note that we have a moduli map
$\nu ^{-1}(x_i) \in C^{\nu }$
. Note that we have a moduli map
mapping
![]() $(C,x_1,\ldots ,x_n)$
to
$(C,x_1,\ldots ,x_n)$
to
![]() $(C^{\nu },x_1,\ldots ,x_n)$
, and we then see that
$(C^{\nu },x_1,\ldots ,x_n)$
, and we then see that
By (2.8) and what we said in the previous subsection, the expected codimension of
![]() $V^k_{|H|,\delta ,\mathbf {e}}$
in
$V^k_{|H|,\delta ,\mathbf {e}}$
in
![]() $V_{|H|,\delta ,n}$
is
$V_{|H|,\delta ,n}$
is
![]() $\max \{0,-\widetilde {\rho }\}$
.
$\max \{0,-\widetilde {\rho }\}$
.
A necessary condition for the nonemptiness of
![]() $V^k_{|H|,\delta ,\mathbf {e}}$
is the nonemptiness of
$V^k_{|H|,\delta ,\mathbf {e}}$
is the nonemptiness of
![]() $V^k_{|H|,\delta }$
, which as recalled above requires (2.7) to hold. Under the assumption
$V^k_{|H|,\delta }$
, which as recalled above requires (2.7) to hold. Under the assumption
![]() $\widetilde {\rho } \geq -g$
, we will prove that the latter is also a sufficient condition. More precisely, we will prove the following version of Theorems 2.1 and 2.3 on
$\widetilde {\rho } \geq -g$
, we will prove that the latter is also a sufficient condition. More precisely, we will prove the following version of Theorems 2.1 and 2.3 on
![]() $K3$
surfaces. Since the properties in Remark 2.2 are not automatic in this case, we will make use of the following:
$K3$
surfaces. Since the properties in Remark 2.2 are not automatic in this case, we will make use of the following:
Notation 2.5. A
![]() $g^1_k$
on a marked curve satisfies
$g^1_k$
on a marked curve satisfies
![]() $(\star )$
if it is base point free, has simple ramification outside the marked points, and all ramification points lie in distinct fibres.
$(\star )$
if it is base point free, has simple ramification outside the marked points, and all ramification points lie in distinct fibres.
Theorem 2.6. Let
![]() $(S,H)$
be a general primitively polarized
$(S,H)$
be a general primitively polarized
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $p \geq 2$
, let
$p \geq 2$
, let
![]() $0 \leq \delta < p$
and set
$0 \leq \delta < p$
and set
![]() $g=p-\delta $
. In the setting (2.1)-(2.2), assume that
$g=p-\delta $
. In the setting (2.1)-(2.2), assume that
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
holds.
$\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
holds.
Then
![]() $V^k_{|H|,\delta ,\mathbf {e}} \neq \emptyset $
if and only if (2.7) holds, and whenever nonempty, it has an irreducible component
$V^k_{|H|,\delta ,\mathbf {e}} \neq \emptyset $
if and only if (2.7) holds, and whenever nonempty, it has an irreducible component
![]() $V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
of the expected codimension
$V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
of the expected codimension
![]() $\max \{0,-\widetilde {\rho }\}$
in
$\max \{0,-\widetilde {\rho }\}$
in
![]() $V_{|H|,\delta ,n}$
. More precisely, the following hold:
$V_{|H|,\delta ,n}$
. More precisely, the following hold:
-
(i) If
 $\widetilde {\rho } \geq 0$
, then
$\widetilde {\rho } \geq 0$
, then
 $V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
is a component of
$V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
is a component of
 $V_{|H|,\delta ,n}$
, and for a general
$V_{|H|,\delta ,n}$
, and for a general
 $(C,x_1,\ldots ,x_n) \in V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
the variety
$(C,x_1,\ldots ,x_n) \in V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
the variety
 $G^1_k(C^{\nu },(x_1,e_1),\ldots ,(x_n,e_n))$
has dimension
$G^1_k(C^{\nu },(x_1,e_1),\ldots ,(x_n,e_n))$
has dimension
 $\widetilde {\rho }$
, and the general member in any component satisfies
$\widetilde {\rho }$
, and the general member in any component satisfies
 $(\star )$
and all nodes of C are non-neutral with respect to it;
$(\star )$
and all nodes of C are non-neutral with respect to it; -
(ii) If
 $\widetilde {\rho } < 0$
, then for a general
$\widetilde {\rho } < 0$
, then for a general
 $(C,x_1,\ldots ,x_n) \in V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
the variety
$(C,x_1,\ldots ,x_n) \in V^{k,\star }_{|H|,\delta ,\mathbf {e}}$
the variety
 $G^1_k(C^{\nu },(x_1,e_1),\ldots ,(x_n,e_n))$
is finite, and each member satisfies
$G^1_k(C^{\nu },(x_1,e_1),\ldots ,(x_n,e_n))$
is finite, and each member satisfies
 $(\star )$
and all nodes of C are non-neutral with respect to it. Moreover,
$(\star )$
and all nodes of C are non-neutral with respect to it. Moreover,-
(ii-a) if
 $n+\widetilde {\rho }\geq 0$
, then the forgetful map
$n+\widetilde {\rho }\geq 0$
, then the forgetful map
 $V^{k,\star }_{|H|,\delta ,\mathbf {e}} \to V_{|H|,\delta }$
is dominant onto a component, and
$V^{k,\star }_{|H|,\delta ,\mathbf {e}} \to V_{|H|,\delta }$
is dominant onto a component, and -
(ii-b) if
 $n+\widetilde {\rho }<0$
, then the forgetful map is generically finite.
$n+\widetilde {\rho }<0$
, then the forgetful map is generically finite.
-
Theorem 2.6 will be proved in §5.
The special case of
![]() $V^k_{|H|,\delta ,k,k}$
, that is, of curves carrying pencils with two points of total ramification, will find a special application in the study of cycles on
$V^k_{|H|,\delta ,k,k}$
, that is, of curves carrying pencils with two points of total ramification, will find a special application in the study of cycles on
![]() $K3$
surfaces, as we will explain in the next subsection. In this case,
$K3$
surfaces, as we will explain in the next subsection. In this case,
![]() $n=2$
and
$n=2$
and
![]() $e_1=e_2=k$
, and one checks that the condition
$e_1=e_2=k$
, and one checks that the condition
![]() $\widetilde {\rho } \geq -g$
is automatically satisfied; we will actually prove that
$\widetilde {\rho } \geq -g$
is automatically satisfied; we will actually prove that
![]() $V^k_{|H|,\delta ,k,k}$
is equidimensional of dimension
$V^k_{|H|,\delta ,k,k}$
is equidimensional of dimension
![]() $2$
, cf. (2.9) and Theorem 2.8 below.
$2$
, cf. (2.9) and Theorem 2.8 below.
2.3 Cycles of torsion differences of points on curves on
 $K3$
surfaces, Beauville-Voisin points and tautological points in
$K3$
surfaces, Beauville-Voisin points and tautological points in
 ${\mathcal M}_{g,2}$
${\mathcal M}_{g,2}$
Let
![]() $(S,H)$
be a primitively polarized complex
$(S,H)$
be a primitively polarized complex
![]() $K3$
surface of genus
$K3$
surface of genus
![]() $p \geq 2$
and
$p \geq 2$
and
![]() $0 \leq \delta \leq p$
. As above, for any irreducible curve
$0 \leq \delta \leq p$
. As above, for any irreducible curve
![]() $C \in |H|$
, we denote by
$C \in |H|$
, we denote by
![]() $C^{\nu }$
its normalization and
$C^{\nu }$
its normalization and
![]() $\nu :C^{\nu }\to C$
its normalization map.
$\nu :C^{\nu }\to C$
its normalization map.
The next definition generalizes [Reference Torelli39, Def. 3.1 and 3.4] to the case of nodal curves:
Definition 2.7. Fix an integer
![]() $k \geq 1$
. We define the loci
$k \geq 1$
. We define the loci
and
![]() $Z^{\circ }_{k,\delta }(S,H)$
its image in
$Z^{\circ }_{k,\delta }(S,H)$
its image in
![]() $S \times S$
by the forgetful map. We denote their closures by
$S \times S$
by the forgetful map. We denote their closures by
![]() $Z^{\prime }_{k,\delta }(S,H)$
and
$Z^{\prime }_{k,\delta }(S,H)$
and
![]() $Z_{k,\delta }(S,H)$
.
$Z_{k,\delta }(S,H)$
.
With this notation, the cases studied in [Reference Torelli39, Def. 3.1 and 3.4] are
![]() $Z^{\prime }_{k,0}(S,H)$
and
$Z^{\prime }_{k,0}(S,H)$
and
![]() $Z_{k,0}(S,H)$
.
$Z_{k,0}(S,H)$
.
It is immediate to see that
Since one may check that the condition
![]() $\widetilde {\rho } \geq -g$
is satisfied in this case, Theorem 2.6 yields that
$\widetilde {\rho } \geq -g$
is satisfied in this case, Theorem 2.6 yields that
![]() $Z^{\prime }_{k,\delta }(S,H)$
has a component of dimension
$Z^{\prime }_{k,\delta }(S,H)$
has a component of dimension
![]() $2$
whenever (2.7) is satisfied, and is otherwise empty. We can improve this result to give equidimensionality and show that the dimension does not drop when forgetting the curves:
$2$
whenever (2.7) is satisfied, and is otherwise empty. We can improve this result to give equidimensionality and show that the dimension does not drop when forgetting the curves:
Theorem 2.8. Let
![]() $(S,H)$
be a general primitively polarized K3 surface of genus
$(S,H)$
be a general primitively polarized K3 surface of genus
![]() $p\geq 2$
. Let
$p\geq 2$
. Let
![]() $0 \leq \delta < p$
and
$0 \leq \delta < p$
and
![]() $k \geq 2$
. Then
$k \geq 2$
. Then
![]() $Z^{\prime }_{k,\delta }(S,H)$
and
$Z^{\prime }_{k,\delta }(S,H)$
and
![]() $Z_{k,\delta }(S,H)$
are equidimensional of dimension
$Z_{k,\delta }(S,H)$
are equidimensional of dimension
![]() $2$
whenever (2.7) is satisfied, and are otherwise empty.
$2$
whenever (2.7) is satisfied, and are otherwise empty.
If
![]() $\delta =0$
, this says that
$\delta =0$
, this says that
![]() $Z^{\prime }_{k,0}(S,H)$
and
$Z^{\prime }_{k,0}(S,H)$
and
![]() $Z_{k,0}(S,H)$
are nonempty with a
$Z_{k,0}(S,H)$
are nonempty with a
![]() $2$
-dimensional component for
$2$
-dimensional component for
![]() $p\leq 2(k-1)$
and are otherwise empty, which proves Conjecture [Reference Torelli39, Conj. 1]. On the other hand, for any
$p\leq 2(k-1)$
and are otherwise empty, which proves Conjecture [Reference Torelli39, Conj. 1]. On the other hand, for any
![]() $k\geq 2$
there is a
$k\geq 2$
there is a
![]() $\delta _0(p,k)\geq 0$
computed by (2.7) such that for any
$\delta _0(p,k)\geq 0$
computed by (2.7) such that for any
![]() $\delta _0(p,k)\leq \delta < p$
, the varieties
$\delta _0(p,k)\leq \delta < p$
, the varieties
![]() $Z^{\prime }_{k,\delta }(S,H)$
and
$Z^{\prime }_{k,\delta }(S,H)$
and
![]() $Z_{k,\delta }(S,H)$
are nonempty (and
$Z_{k,\delta }(S,H)$
are nonempty (and
![]() $2$
-dimensional). In other words, one can decrease k by adding nodes, as depicted in the following example for low genus p:
$2$
-dimensional). In other words, one can decrease k by adding nodes, as depicted in the following example for low genus p:
Example 2.9. If
![]() $p=3$
, Theorem 2.8 says that
$p=3$
, Theorem 2.8 says that
![]() $Z^{\prime }_{k,0}(S,H)$
is nonempty if and only if
$Z^{\prime }_{k,0}(S,H)$
is nonempty if and only if
![]() $k \geq 3$
and that
$k \geq 3$
and that
![]() $Z^{\prime }_{2,1}(S,H)$
and
$Z^{\prime }_{2,1}(S,H)$
and
![]() $Z^{\prime }_{2,2}(S,H)$
are nonempty, since one computes
$Z^{\prime }_{2,2}(S,H)$
are nonempty, since one computes
![]() $\delta _0(3,2)=1$
from (2.7).
$\delta _0(3,2)=1$
from (2.7).
If
![]() $p=4$
, Theorem 2.8 says that
$p=4$
, Theorem 2.8 says that
![]() $Z^{\prime }_{k,0}(S,H)$
is nonempty if and only if
$Z^{\prime }_{k,0}(S,H)$
is nonempty if and only if
![]() $k \geq 3$
and that
$k \geq 3$
and that
![]() $Z^{\prime }_{2,1}(S,H)$
,
$Z^{\prime }_{2,1}(S,H)$
,
![]() $Z^{\prime }_{2,2}(S,H)$
and
$Z^{\prime }_{2,2}(S,H)$
and
![]() $Z^{\prime }_{2,3}(S,H)$
are nonempty, since one again computes
$Z^{\prime }_{2,3}(S,H)$
are nonempty, since one again computes
![]() $\delta _0(4,2)=1$
from (2.7).
$\delta _0(4,2)=1$
from (2.7).
If
![]() $p=5$
, Theorem 2.8 says that
$p=5$
, Theorem 2.8 says that
![]() $Z^{\prime }_{k,0}(S,H)$
is nonempty if and only if
$Z^{\prime }_{k,0}(S,H)$
is nonempty if and only if
![]() $k\geq 4$
. One computes
$k\geq 4$
. One computes
![]() $\delta _0(5,3)=1$
from (2.7), so the theorem says that
$\delta _0(5,3)=1$
from (2.7), so the theorem says that
![]() $Z^{\prime }_{3,\delta }(S,H)$
is nonempty for all
$Z^{\prime }_{3,\delta }(S,H)$
is nonempty for all
![]() $\delta \in \{1,2,3,4\}$
. Similarly, one computes
$\delta \in \{1,2,3,4\}$
. Similarly, one computes
![]() $\delta _0(5,2)=2$
, so the theorem says that
$\delta _0(5,2)=2$
, so the theorem says that
![]() $Z^{\prime }_{2,\delta }(S,H)$
is nonempty for all
$Z^{\prime }_{2,\delta }(S,H)$
is nonempty for all
![]() $\delta \in \{2,3,4\}$
, while
$\delta \in \{2,3,4\}$
, while
![]() $Z^{\prime }_{2,1}(S,H)=\emptyset $
.
$Z^{\prime }_{2,1}(S,H)=\emptyset $
.
We next relate the loci
![]() $Z_{k,\delta }(S,H)\subset S \times S$
provided by Theorem 2.8 to the theory of Beauville-Voisin points and constant cycle curves. Recall that, by a classical result of Mumford [Reference Mumford33], the Chow group
$Z_{k,\delta }(S,H)\subset S \times S$
provided by Theorem 2.8 to the theory of Beauville-Voisin points and constant cycle curves. Recall that, by a classical result of Mumford [Reference Mumford33], the Chow group
![]() $CH_0(S)$
of
$CH_0(S)$
of
![]() $0$
-cycles on S is huge. Nonetheless, it contains a distinguished class
$0$
-cycles on S is huge. Nonetheless, it contains a distinguished class
![]() $c_S$
of degree
$c_S$
of degree
![]() $1$
, called the Beauville-Voisin class, which is defined as the class of a point on a rational curve (cf. [Reference Beauville and Voisin3, Thm. 1]). A Beauville-Voisin point (BV-point in short)
$1$
, called the Beauville-Voisin class, which is defined as the class of a point on a rational curve (cf. [Reference Beauville and Voisin3, Thm. 1]). A Beauville-Voisin point (BV-point in short)
![]() $p\in S$
is a point with class
$p\in S$
is a point with class
![]() $c_S$
. By [Reference Maclean29, Thm. 1.2] BV-points are dense in S and the set is expected to be a union of curves. A curve whose points all define the class
$c_S$
. By [Reference Maclean29, Thm. 1.2] BV-points are dense in S and the set is expected to be a union of curves. A curve whose points all define the class
![]() $c_S$
is called constant cycle curve (cf. [Reference Huybrechts25, Def. 3.1] and [Reference Voisin40]). By [Reference Huybrechts25, Thm. 11.1] and [Reference Chen and Gounelas9, Introd.], constant cycle curves are dense.
$c_S$
is called constant cycle curve (cf. [Reference Huybrechts25, Def. 3.1] and [Reference Voisin40]). By [Reference Huybrechts25, Thm. 11.1] and [Reference Chen and Gounelas9, Introd.], constant cycle curves are dense.
In [Reference Torelli39]
![]() $2$
-cycles Z such that
$2$
-cycles Z such that
![]() $Z_*$
preserves BV-points and constant cycle curves are introduced, a notion we rephrase as:
$Z_*$
preserves BV-points and constant cycle curves are introduced, a notion we rephrase as:
Definition 2.10. Let S be a
![]() $K3$
surface. A 2-cycle
$K3$
surface. A 2-cycle
![]() $Z\subset S\times S$
is said to preserve BV-points (respectively, constant cycle curves) if
$Z\subset S\times S$
is said to preserve BV-points (respectively, constant cycle curves) if
-
(i) there is a lifting
 $Z_*:Z_i(S)\to Z_i(S)$
to the group
$Z_*:Z_i(S)\to Z_i(S)$
to the group
 $Z_i(S)$
of i-cycles of the natural morphism
$Z_i(S)$
of i-cycles of the natural morphism
 $Z_*:CH_i(S)\to CH_i(S)$
, defined on irreducible subvarieties
$Z_*:CH_i(S)\to CH_i(S)$
, defined on irreducible subvarieties
 $W\subset S$
as
$W\subset S$
as
 $Z_*W={p_2}_*p_1^*W$
, where
$Z_*W={p_2}_*p_1^*W$
, where
 $p_1,p_2:Z\to S$
are the two projections;
$p_1,p_2:Z\to S$
are the two projections; -
(ii) for any BV-point
 $p \in S$
(resp., constant cycle curve
$p \in S$
(resp., constant cycle curve
 $Y \subset S$
), each point (resp. integral curve) in the support of the
$Y \subset S$
), each point (resp. integral curve) in the support of the
 $0$
-cycle
$0$
-cycle
 $Z_*p$
(resp., in the
$Z_*p$
(resp., in the
 $1$
-cycle
$1$
-cycle
 $Z_*Y$
) is a BV-point (resp. a constant cycle curve).
$Z_*Y$
) is a BV-point (resp. a constant cycle curve).
In [Reference Torelli39] it is shown that
![]() $Z_{k,0}(S,H)_*$
preserves constant cycle curves. We can now extend this study to
$Z_{k,0}(S,H)_*$
preserves constant cycle curves. We can now extend this study to
![]() $\delta>0$
. Indeed, as a consequence of Theorem 2.8, we obtain:
$\delta>0$
. Indeed, as a consequence of Theorem 2.8, we obtain:
Corollary 2.11. In the setting of Theorem 2.8, assume that (2.7) is satisfied. Then
![]() $Z_{k,\delta }(S,H)_*$
preserves BV-points and constant cycle curves (cf. Definition 2.10).
$Z_{k,\delta }(S,H)_*$
preserves BV-points and constant cycle curves (cf. Definition 2.10).
Moreover, the points
![]() $(p,q)\in Z_{k,\delta }(S,H)$
defining the class
$(p,q)\in Z_{k,\delta }(S,H)$
defining the class
![]() $(c_S,c_S)$
are dense in every component.
$(c_S,c_S)$
are dense in every component.
The latter property in the corollary allows us to give an application to tautological points in
![]() ${\mathcal M}_{g,2}$
, in view of [Reference Pandharipande and Schmitt36, Thm. 1.5] relating them to BV-points on curves on
${\mathcal M}_{g,2}$
, in view of [Reference Pandharipande and Schmitt36, Thm. 1.5] relating them to BV-points on curves on
![]() $K3$
surfaces. Recall that, by [Reference Graber and Vakil22, Thm. 1.1], the degree-
$K3$
surfaces. Recall that, by [Reference Graber and Vakil22, Thm. 1.1], the degree-
![]() $0$
tautological group
$0$
tautological group
![]() $R_0(\overline {\mathcal {M}_{g,n}}) \subseteq CH_0(\overline {\mathcal {M}_{g,n}})$
is always isomorphic to
$R_0(\overline {\mathcal {M}_{g,n}}) \subseteq CH_0(\overline {\mathcal {M}_{g,n}})$
is always isomorphic to
![]() $\mathbb {Q}$
, even though
$\mathbb {Q}$
, even though
![]() $CH_0(\overline {\mathcal {M}_{g,n}})$
is expected to be huge except for finitely many
$CH_0(\overline {\mathcal {M}_{g,n}})$
is expected to be huge except for finitely many
![]() $(g,n)$
(cf. [Reference Pandharipande and Schmitt36, Spec. 1.1]). This setting is similar to the one on K3 surfaces. In [Reference Pandharipande and Schmitt36, Thm. 1.5] it is proved that
$(g,n)$
(cf. [Reference Pandharipande and Schmitt36, Spec. 1.1]). This setting is similar to the one on K3 surfaces. In [Reference Pandharipande and Schmitt36, Thm. 1.5] it is proved that
![]() $(C,x_1,..,x_n)\in \overline {{\mathcal M}_{g,n}}$
is tautological if C is a smooth curve of genus g sitting in a K3 surface S,
$(C,x_1,..,x_n)\in \overline {{\mathcal M}_{g,n}}$
is tautological if C is a smooth curve of genus g sitting in a K3 surface S,
![]() $x_i\in C$
is a BV-point for
$x_i\in C$
is a BV-point for
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $n\leq g$
. As an application of this relation and Corollary 2.11 we obtain:
$n\leq g$
. As an application of this relation and Corollary 2.11 we obtain:
Corollary 2.12. In the setting of Theorem 2.8, assume that
![]() $\rho (g,1,k) \geq 0$
. Then the set of tautological points in
$\rho (g,1,k) \geq 0$
. Then the set of tautological points in
![]() $m_{g,2}(Z^{\prime \circ }_{k,0}(S,H))=m_{g,2}(V^k_{|H|,0,k,k})\subset {\mathcal M}_{g,2}$
(cf. (2.8)) is dense in every component, for
$m_{g,2}(Z^{\prime \circ }_{k,0}(S,H))=m_{g,2}(V^k_{|H|,0,k,k})\subset {\mathcal M}_{g,2}$
(cf. (2.8)) is dense in every component, for
![]() $g\geq 2$
.
$g\geq 2$
.
Theorem 2.8 and Corollaries 2.11 and 2.12 will be proved in §6.
3 Proofs of Theorems 2.1 and 2.3
Let
![]() $\overline {{\mathcal M}_{g,n}}$
be the Deligne-Mumford compactification of
$\overline {{\mathcal M}_{g,n}}$
be the Deligne-Mumford compactification of
![]() ${\mathcal M}_{g,n}$
. We denote by
${\mathcal M}_{g,n}$
. We denote by
![]() $\overline {{\mathcal M}_{g,k,\mathbf {e}}} \subset \overline {{\mathcal M}_{g,n}}$
the compactification of
$\overline {{\mathcal M}_{g,k,\mathbf {e}}} \subset \overline {{\mathcal M}_{g,n}}$
the compactification of
![]() ${\mathcal M}_{g,k,\mathbf {e}}$
in
${\mathcal M}_{g,k,\mathbf {e}}$
in
![]() $\overline {{\mathcal M}_{g,n}}$
.
$\overline {{\mathcal M}_{g,n}}$
.
Let
![]() $\overline {{\mathcal H}_{g,k,\mathbf {e}}}$
be the (Deligne-Mumford) compactification of the Hurwitz space
$\overline {{\mathcal H}_{g,k,\mathbf {e}}}$
be the (Deligne-Mumford) compactification of the Hurwitz space
![]() ${\mathcal H}_{g,k,\mathbf {e}}$
, which is given by a generalization of the classical theory of admissible covers, see, for example, [Reference Harris and Mumford24, Reference Faber and Pandharipande15, Reference Abramovich, Corti and Vistoli1, Reference Cavalieri, Markwig and Ranganathan5]. We denote by
${\mathcal H}_{g,k,\mathbf {e}}$
, which is given by a generalization of the classical theory of admissible covers, see, for example, [Reference Harris and Mumford24, Reference Faber and Pandharipande15, Reference Abramovich, Corti and Vistoli1, Reference Cavalieri, Markwig and Ranganathan5]. We denote by
the forgetful map sending the domain of a cover to its stable reduction, which is an extension of
![]() $\mu _{g,k,\mathbf {e}}:=\kappa _{g,k,\mathbf {e}}\circ \lambda _{g,k,\mathbf {e}}$
(cf. (2.4) and (2.5)). We recall that by the theory of admissible covers,
$\mu _{g,k,\mathbf {e}}:=\kappa _{g,k,\mathbf {e}}\circ \lambda _{g,k,\mathbf {e}}$
(cf. (2.4) and (2.5)). We recall that by the theory of admissible covers,
![]() $(X,P_1,\ldots ,P_n)$
with X irreducible lies in
$(X,P_1,\ldots ,P_n)$
with X irreducible lies in
![]() $\overline {{\mathcal M}_{g,k,\mathbf {e}}}$
if and only if the normalization
$\overline {{\mathcal M}_{g,k,\mathbf {e}}}$
if and only if the normalization
![]() $\nu :X^{\nu } \to X$
has the property that
$\nu :X^{\nu } \to X$
has the property that
![]() $X^{\nu }$
carries a
$X^{\nu }$
carries a
![]() $g^1_k$
in
$g^1_k$
in
![]() $G^1_k(X^{\nu },(P_1,e_1),\ldots ,(P_n,e_n))$
such that each pair of points on
$G^1_k(X^{\nu },(P_1,e_1),\ldots ,(P_n,e_n))$
such that each pair of points on
![]() $X^{\nu }$
lying above a node of X lies in the same fibre of the
$X^{\nu }$
lying above a node of X lies in the same fibre of the
![]() $g^1_k$
. In other words, the morphism
$g^1_k$
. In other words, the morphism
![]() $X^{\nu } \to {\mathbb P}^1$
defined by the
$X^{\nu } \to {\mathbb P}^1$
defined by the
![]() $g^1_k$
factors through the normalization
$g^1_k$
factors through the normalization
![]() $X^{\nu }\to X \to {\mathbb P}^1$
. We call such a
$X^{\nu }\to X \to {\mathbb P}^1$
. We call such a
![]() $g^1_k$
on
$g^1_k$
on
![]() $X^{\nu }$
a descending
$X^{\nu }$
a descending
![]() $g^1_k$
and denote by
$g^1_k$
and denote by
![]() $G^1_k(X, (P_1,e_1),\ldots , (P_n,e_n))$
the locus of such descending
$G^1_k(X, (P_1,e_1),\ldots , (P_n,e_n))$
the locus of such descending
![]() $g^1_k$
s. Then the theory of admissible covers yields
$g^1_k$
s. Then the theory of admissible covers yields
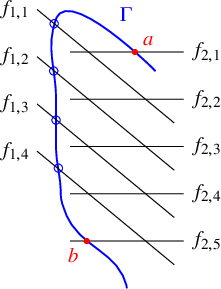
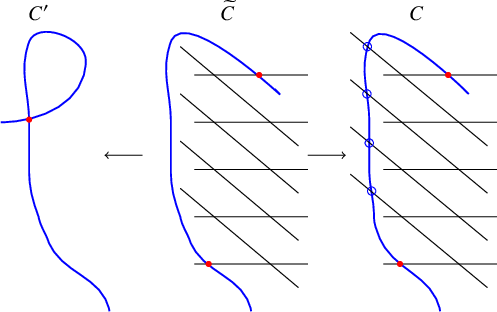
To prove Theorem 2.1 we will find an n-pointed g-nodal rational curve
![]() $(X,P_1,\ldots ,P_n)$
in
$(X,P_1,\ldots ,P_n)$
in
![]() $\overline {{\mathcal M}_{g,k,\mathbf {e}}}$
such that
$\overline {{\mathcal M}_{g,k,\mathbf {e}}}$
such that
![]() $G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
has dimension
$G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
has dimension
![]() $\max \{0,\widetilde {\rho }\}$
.
$\max \{0,\widetilde {\rho }\}$
.
To construct
![]() $g^1_k$
s on
$g^1_k$
s on
![]() ${\mathbb P}^1$
s descending to nodal models, we will work on
${\mathbb P}^1$
s descending to nodal models, we will work on
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
. As customary, we identify
$\operatorname {Sym}^2({\mathbb P}^1)$
. As customary, we identify
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
with
$\operatorname {Sym}^2({\mathbb P}^1)$
with
![]() ${\mathbb P}^2$
, in such a way that the diagonal
${\mathbb P}^2$
, in such a way that the diagonal
![]() $\Delta $
is a conic and each coordinate curve
$\Delta $
is a conic and each coordinate curve
![]() $\{x+y\;|\; y\in {\mathbb P}^ 1\}$
is the tangent line
$\{x+y\;|\; y\in {\mathbb P}^ 1\}$
is the tangent line
![]() $\ell _x$
to
$\ell _x$
to
![]() $\Delta $
at
$\Delta $
at
![]() $2x$
.
$2x$
.
Consider
![]() ${\mathbb Q}={\mathbb P}^ 1\times {\mathbb P}^ 1$
with the two projections
${\mathbb Q}={\mathbb P}^ 1\times {\mathbb P}^ 1$
with the two projections
![]() $\pi _i: {\mathbb Q}\to {\mathbb P}^ 1$
,
$\pi _i: {\mathbb Q}\to {\mathbb P}^ 1$
,
![]() $i=1,2$
and the line bundle
$i=1,2$
and the line bundle
![]() ${\mathcal O}_{{\mathbb Q}}(k,k):=\pi _1^ *({\mathcal O}_{{\mathbb P}^ 1}(k))\otimes \pi _2^ *({\mathcal O}_{{\mathbb P}^ 1}(k))$
, for any
${\mathcal O}_{{\mathbb Q}}(k,k):=\pi _1^ *({\mathcal O}_{{\mathbb P}^ 1}(k))\otimes \pi _2^ *({\mathcal O}_{{\mathbb P}^ 1}(k))$
, for any
![]() $k \in {\mathbb Z}^+$
. Then
$k \in {\mathbb Z}^+$
. Then
![]() $H^0({\mathcal O}_{{\mathbb Q}}(k,k))=H^ 0({\mathbb P}^1, {\mathcal O}_{{\mathbb P}^ 1}(k))^ {\otimes 2}$
. The two subspaces
$H^0({\mathcal O}_{{\mathbb Q}}(k,k))=H^ 0({\mathbb P}^1, {\mathcal O}_{{\mathbb P}^ 1}(k))^ {\otimes 2}$
. The two subspaces
![]() $\operatorname {Sym}^ 2(H^ 0({\mathbb P}^ 1, {\mathcal O}_{{\mathbb P}^ 1}(k)))$
and
$\operatorname {Sym}^ 2(H^ 0({\mathbb P}^ 1, {\mathcal O}_{{\mathbb P}^ 1}(k)))$
and
![]() $\wedge ^ 2 H^ 0({\mathbb P}^ 1, {\mathcal O}_{{\mathbb P}^ 1}(k))$
are invariant (resp. anti-invariant) under the natural involution that exchanges the coordinates. Hence they are pull-backs of sections of line bundles on
$\wedge ^ 2 H^ 0({\mathbb P}^ 1, {\mathcal O}_{{\mathbb P}^ 1}(k))$
are invariant (resp. anti-invariant) under the natural involution that exchanges the coordinates. Hence they are pull-backs of sections of line bundles on
![]() $\operatorname {Sym}^ 2({\mathbb P}^ 1)$
, say
$\operatorname {Sym}^ 2({\mathbb P}^ 1)$
, say
![]() ${\mathcal O}_k^+$
and
${\mathcal O}_k^+$
and
![]() ${\mathcal O}_k^-$
, respectively. For instance, one has
${\mathcal O}_k^-$
, respectively. For instance, one has
Let
![]() $\mathfrak {g}$
be any
$\mathfrak {g}$
be any
![]() $g^1_k$
on
$g^1_k$
on
![]() ${\mathbb P}^1$
. Then it can be identified with a point of the Grassmannian
${\mathbb P}^1$
. Then it can be identified with a point of the Grassmannian
![]() $\mathbb G(1,k)\subset {\mathbb P}( \wedge ^ 2 H^ 0({\mathbb P}^ 1, {\mathcal O}_{{\mathbb P}^ 1}(k)))$
, which by (3.3) can again be identified with the degree
$\mathbb G(1,k)\subset {\mathbb P}( \wedge ^ 2 H^ 0({\mathbb P}^ 1, {\mathcal O}_{{\mathbb P}^ 1}(k)))$
, which by (3.3) can again be identified with the degree
![]() $k-1$
curve in
$k-1$
curve in
![]() ${\mathbb P}^ 2$
${\mathbb P}^ 2$
Definition 3.1. We denote the family of curves
![]() $\{C_{\mathfrak {g}}\}_{\mathfrak {g} \in G^1_k({\mathbb P}^1)}$
by
$\{C_{\mathfrak {g}}\}_{\mathfrak {g} \in G^1_k({\mathbb P}^1)}$
by
![]() ${\mathcal F}_k$
.
${\mathcal F}_k$
.
Note that
![]() ${\mathcal F}_k$
is irreducible of dimension
${\mathcal F}_k$
is irreducible of dimension
![]() $2(k-1)=\dim (\mathbb {G}(1,k))$
.
$2(k-1)=\dim (\mathbb {G}(1,k))$
.
Lemma 3.2. The curve
![]() $C_{\mathfrak {g}}$
is reduced if and only if
$C_{\mathfrak {g}}$
is reduced if and only if
![]() $\mathfrak {g}$
does not have multiple base points.
$\mathfrak {g}$
does not have multiple base points.
Proof. If
![]() $P \in {\mathbb P}^1$
is a base point of multiplicity
$P \in {\mathbb P}^1$
is a base point of multiplicity
![]() $n \geq 2$
of
$n \geq 2$
of
![]() $\mathfrak {g}$
, then
$\mathfrak {g}$
, then
![]() $C_{\mathfrak {g}}$
contains the line
$C_{\mathfrak {g}}$
contains the line
![]() $\ell _P:=\{P+Q \; | \; Q \in {\mathbb P}^1\} \subset \operatorname {Sym}^2({\mathbb P}^1)$
as a component, and the residual curve is
$\ell _P:=\{P+Q \; | \; Q \in {\mathbb P}^1\} \subset \operatorname {Sym}^2({\mathbb P}^1)$
as a component, and the residual curve is
![]() $C_{\mathfrak {g}(-nP)}$
. As the latter has degree
$C_{\mathfrak {g}(-nP)}$
. As the latter has degree
![]() $k-1-n$
, the line
$k-1-n$
, the line
![]() $\ell _P$
has multiplicity n, whence
$\ell _P$
has multiplicity n, whence
![]() $C_{\mathfrak {g}}$
is not reduced.
$C_{\mathfrak {g}}$
is not reduced.
If
![]() $\mathfrak {g}$
does not have multiple base points, then its general member consists of k distinct points. Then
$\mathfrak {g}$
does not have multiple base points, then its general member consists of k distinct points. Then
![]() $C_{\mathfrak {g}}$
intersects the line
$C_{\mathfrak {g}}$
intersects the line
![]() $\ell _P$
in
$\ell _P$
in
![]() $k-1$
distinct points. As
$k-1$
distinct points. As
![]() $C_{\mathfrak {g}}$
has degree
$C_{\mathfrak {g}}$
has degree
![]() $k-1$
, this shows that it is reduced.
$k-1$
, this shows that it is reduced.
We will need the following:
Lemma 3.3. If
![]() $e_1,\ldots ,e_n,k$
are integers such that
$e_1,\ldots ,e_n,k$
are integers such that
![]() $2 \leq e_i \leq k$
,
$2 \leq e_i \leq k$
,
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $\widetilde {\rho }(0,1,k;\mathbf {e}) \geq 0$
, then
$\widetilde {\rho }(0,1,k;\mathbf {e}) \geq 0$
, then
![]() $G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n)) \neq \emptyset $
for any distinct points
$G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n)) \neq \emptyset $
for any distinct points
![]() $P_1,\ldots ,P_n \in {\mathbb P}^1$
. Moreover, every component has dimension at least
$P_1,\ldots ,P_n \in {\mathbb P}^1$
. Moreover, every component has dimension at least
![]() $\widetilde {\rho }(0,1,k;\mathbf {e})$
and equality holds if
$\widetilde {\rho }(0,1,k;\mathbf {e})$
and equality holds if
![]() $P_1,\ldots ,P_n$
are general.
$P_1,\ldots ,P_n$
are general.
Proof. By the classical result [Reference Eisenbud and Harris13, Thm. 4.5] of Eisenbud and Harris, it suffices to prove nonemptiness. Moreover, it suffices to prove it in the case
![]() $\widetilde {\rho }(0,1,k;\mathbf {e}) =0$
, that is,
$\widetilde {\rho }(0,1,k;\mathbf {e}) =0$
, that is,
![]() $e=\sum e_i=2(k-1)+n$
, by adding further simple ramification points if necessary to complete the ramification profile. The latter has been proved by Osserman [Reference Osserman35, Thms. 2.4]. We provide a proof independent of Schubert calculus.
$e=\sum e_i=2(k-1)+n$
, by adding further simple ramification points if necessary to complete the ramification profile. The latter has been proved by Osserman [Reference Osserman35, Thms. 2.4]. We provide a proof independent of Schubert calculus.
By Riemann’s Existence Theorem (cf., e.g., [Reference Miranda30, III, Cor. 4.10]) it suffices to prove that there are cycles
![]() $\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
of orders
$\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
of orders
![]() $e_1,\ldots ,e_n$
generating a transitive subgroup and such that
$e_1,\ldots ,e_n$
generating a transitive subgroup and such that
![]() $\sigma _1\cdots \sigma _n=\operatorname {id}_k$
(the identity in
$\sigma _1\cdots \sigma _n=\operatorname {id}_k$
(the identity in
![]() $\operatorname {Sym}(k)$
). We will do this by proving the following claim by induction on k:
$\operatorname {Sym}(k)$
). We will do this by proving the following claim by induction on k:
Claim 3.4. There exist cycles
![]() $\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
of orders
$\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
of orders
![]() $e_1,\ldots ,e_n$
such that
$e_1,\ldots ,e_n$
such that
-
(i)
 $\sigma _1\cdots \sigma _n=\operatorname {id}_k$
,
$\sigma _1\cdots \sigma _n=\operatorname {id}_k$
, -
(ii) the subgroup generated by
 $\sigma _1,\ldots ,\sigma _n$
is transitive,
$\sigma _1,\ldots ,\sigma _n$
is transitive, -
(iii) for all
 $i \in \{1,\ldots ,n-1\}$
,
$i \in \{1,\ldots ,n-1\}$
,
 $\sigma _i$
and
$\sigma _i$
and
 $\sigma _{i+1}$
are not disjoint.
$\sigma _{i+1}$
are not disjoint.
Proof of claim
We first treat the case
![]() $e_1=\cdots =e_n=2$
, in which case
$e_1=\cdots =e_n=2$
, in which case
![]() $n=2k-2$
. Then
$n=2k-2$
. Then
will do.
We then prove the claim by induction on k. In the case
![]() $k=2$
, we only have the case
$k=2$
, we only have the case
![]() $e_1=e_2=2$
, which falls into the case treated above.
$e_1=e_2=2$
, which falls into the case treated above.
Assume now that
![]() $k>2$
. We may also assume that
$k>2$
. We may also assume that
![]() $\max \{e_j\} \geq 3$
, and we note that at most one
$\max \{e_j\} \geq 3$
, and we note that at most one
![]() $e_i$
equals k. To ease notation we will assume that
$e_i$
equals k. To ease notation we will assume that
![]() $\max \{e_j\}=e_1$
, since the other cases are treated similarly. Note that
$\max \{e_j\}=e_1$
, since the other cases are treated similarly. Note that
![]() $n \geq 2$
. We set
$n \geq 2$
. We set
 $$\begin{align*}e^{\prime}_i =\begin{cases} e_i-1, & \; \; \text{for} \;\; i=1,2, \\ e_i, & \; \; \text{for} \;\; i>2. \end{cases} \end{align*}$$
$$\begin{align*}e^{\prime}_i =\begin{cases} e_i-1, & \; \; \text{for} \;\; i=1,2, \\ e_i, & \; \; \text{for} \;\; i>2. \end{cases} \end{align*}$$
We have
![]() $\sum (e^{\prime }_i-1)=2(k-2)$
and
$\sum (e^{\prime }_i-1)=2(k-2)$
and
![]() $e^{\prime }_i \leq k-1$
for all i. If also
$e^{\prime }_i \leq k-1$
for all i. If also
![]() $e_2 \geq 3$
, then all
$e_2 \geq 3$
, then all
![]() $e^{\prime }_i \geq 2$
, and we may apply the induction hypothesis to find
$e^{\prime }_i \geq 2$
, and we may apply the induction hypothesis to find
![]() $\sigma ^{\prime }_1,\ldots ,\sigma ^{\prime }_n \in \operatorname {Sym}(k-1)$
of orders
$\sigma ^{\prime }_1,\ldots ,\sigma ^{\prime }_n \in \operatorname {Sym}(k-1)$
of orders
![]() $e^{\prime }_1,\ldots ,e^{\prime }_n$
such that
$e^{\prime }_1,\ldots ,e^{\prime }_n$
such that
-
(i)’
 $\sigma ^{\prime }_1\cdots \sigma ^{\prime }_n=\operatorname {id}_{k-1}$
,
$\sigma ^{\prime }_1\cdots \sigma ^{\prime }_n=\operatorname {id}_{k-1}$
, -
(ii)’ the subgroup generated by
 $\sigma ^{\prime }_1,\ldots ,\sigma ^{\prime }_n$
is transitive,
$\sigma ^{\prime }_1,\ldots ,\sigma ^{\prime }_n$
is transitive, -
(iii)’ for all
 $i \in \{1,\ldots ,n-1\}$
,
$i \in \{1,\ldots ,n-1\}$
,
 $\sigma ^{\prime }_i$
and
$\sigma ^{\prime }_i$
and
 $\sigma ^{\prime }_{i+1}$
are not disjoint.
$\sigma ^{\prime }_{i+1}$
are not disjoint.
Since
![]() $\sigma ^{\prime }_1$
and
$\sigma ^{\prime }_1$
and
![]() $\sigma ^{\prime }_2$
are not disjoint, there is one integer, say
$\sigma ^{\prime }_2$
are not disjoint, there is one integer, say
![]() $x \in \{1,\ldots ,k-1\}$
, appearing in them both. We may write
$x \in \{1,\ldots ,k-1\}$
, appearing in them both. We may write
Set
Then, viewing
![]() $\sigma ^{\prime }_1$
and
$\sigma ^{\prime }_1$
and
![]() $\sigma ^{\prime }_2$
as elements of
$\sigma ^{\prime }_2$
as elements of
![]() $\operatorname {Sym}(k)$
, one may check that
$\operatorname {Sym}(k)$
, one may check that
Set now
![]() $\sigma _j:=\sigma ^{\prime }_j$
for all
$\sigma _j:=\sigma ^{\prime }_j$
for all
![]() $j \in \{3,\ldots ,n\}$
and view them as elements of
$j \in \{3,\ldots ,n\}$
and view them as elements of
![]() $\operatorname {Sym}(k)$
. Then, because of (i)’-(iii)’ and (3.4), the cycles
$\operatorname {Sym}(k)$
. Then, because of (i)’-(iii)’ and (3.4), the cycles
![]() $\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
satisfy (i)-(iii) in the claim.
$\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
satisfy (i)-(iii) in the claim.
Assume now that
![]() $e_2=2$
, so that
$e_2=2$
, so that
![]() $e^{\prime }_2=1$
. We remark that
$e^{\prime }_2=1$
. We remark that
![]() $n>2$
; indeed, if
$n>2$
; indeed, if
![]() $n=2$
, then
$n=2$
, then
![]() $e_1=e-e_2=[2(k-1)+2]-2=2k-2$
, which is incompatible with
$e_1=e-e_2=[2(k-1)+2]-2=2k-2$
, which is incompatible with
![]() $e_1\leq k$
and
$e_1\leq k$
and
![]() $k>2$
. We have
$k>2$
. We have
![]() $2 \leq e^{\prime }_i \leq k-1$
for all
$2 \leq e^{\prime }_i \leq k-1$
for all
![]() $i \neq 2$
. Then we apply the induction hypothesis to find
$i \neq 2$
. Then we apply the induction hypothesis to find
![]() $\sigma ^{\prime }_1,\sigma ^{\prime }_3,\ldots ,\sigma ^{\prime }_n \in \operatorname {Sym}(k-1)$
of orders
$\sigma ^{\prime }_1,\sigma ^{\prime }_3,\ldots ,\sigma ^{\prime }_n \in \operatorname {Sym}(k-1)$
of orders
![]() $e^{\prime }_1,e^{\prime }_3\ldots ,e^{\prime }_n$
such that
$e^{\prime }_1,e^{\prime }_3\ldots ,e^{\prime }_n$
such that
-
(i)”
 $\sigma ^{\prime }_1\sigma ^{\prime }_3\cdots \sigma ^{\prime }_n=\operatorname {id}_{k-1}$
,
$\sigma ^{\prime }_1\sigma ^{\prime }_3\cdots \sigma ^{\prime }_n=\operatorname {id}_{k-1}$
, -
(ii)” the subgroup generated by
 $\sigma ^{\prime }_1,\sigma ^{\prime }_3,\ldots ,\sigma ^{\prime }_n$
is transitive,
$\sigma ^{\prime }_1,\sigma ^{\prime }_3,\ldots ,\sigma ^{\prime }_n$
is transitive, -
(iii)”
 $\sigma ^{\prime }_1$
and
$\sigma ^{\prime }_1$
and
 $\sigma ^{\prime }_3$
are not disjoint, and for all
$\sigma ^{\prime }_3$
are not disjoint, and for all
 $i \in \{3,\ldots ,n-1\}$
,
$i \in \{3,\ldots ,n-1\}$
,
 $\sigma ^{\prime }_i$
and
$\sigma ^{\prime }_i$
and
 $\sigma ^{\prime }_{i+1}$
are not disjoint.
$\sigma ^{\prime }_{i+1}$
are not disjoint.
Since
![]() $\sigma ^{\prime }_1$
and
$\sigma ^{\prime }_1$
and
![]() $\sigma ^{\prime }_3$
are not disjoint, there is one integer, say
$\sigma ^{\prime }_3$
are not disjoint, there is one integer, say
![]() $x \in \{1,\ldots ,k-1\}$
, appearing in them both. We may write
$x \in \{1,\ldots ,k-1\}$
, appearing in them both. We may write
Set
Then, viewing
![]() $\sigma ^{\prime }_1$
as element of
$\sigma ^{\prime }_1$
as element of
![]() $\operatorname {Sym}(k)$
, one may check that
$\operatorname {Sym}(k)$
, one may check that
Set now
![]() $\sigma _j:=\sigma ^{\prime }_j$
for all
$\sigma _j:=\sigma ^{\prime }_j$
for all
![]() $j \in \{3,\ldots ,n\}$
and view them as elements of
$j \in \{3,\ldots ,n\}$
and view them as elements of
![]() $\operatorname {Sym}(k)$
. Then, because of (i)”-(iii)” and (3.5), the cycles
$\operatorname {Sym}(k)$
. Then, because of (i)”-(iii)” and (3.5), the cycles
![]() $\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
satisfy (i)-(iii) in the claim.
$\sigma _1,\ldots ,\sigma _n \in \operatorname {Sym}(k)$
satisfy (i)-(iii) in the claim.
Having proved the claim, the lemma follows.
Proof of Theorem 2.1
Since
![]() $\widetilde {\rho }(0,1,k;\mathbf {e})=\widetilde {\rho }(g,1,k;\mathbf {e})+g$
, our assumption
$\widetilde {\rho }(0,1,k;\mathbf {e})=\widetilde {\rho }(g,1,k;\mathbf {e})+g$
, our assumption
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
, together with Lemma 3.3, yields that the locus
$\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
, together with Lemma 3.3, yields that the locus
![]() $G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n))$
is nonempty and equidimensional of dimension
$G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n))$
is nonempty and equidimensional of dimension
![]() $\widetilde {\rho }(g,1,k;\mathbf {e})+g$
for general
$\widetilde {\rho }(g,1,k;\mathbf {e})+g$
for general
![]() $P_1,\ldots ,P_n \in {\mathbb P}^1$
. This defines a subfamily
$P_1,\ldots ,P_n \in {\mathbb P}^1$
. This defines a subfamily
![]() ${\mathcal F}_{k,(P_1,\ldots\, ,P_n),\mathbf {e}}$
of
${\mathcal F}_{k,(P_1,\ldots\, ,P_n),\mathbf {e}}$
of
![]() ${\mathcal F}_k$
(cf. Definition 3.1) of dimension
${\mathcal F}_k$
(cf. Definition 3.1) of dimension
The case
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) \geq 0$
. For a general set of g points
$\widetilde {\rho }(g,1,k;\mathbf {e}) \geq 0$
. For a general set of g points
![]() $\{\xi _i=y_i+z_i\}_{1 \leq i \leq g}$
in
$\{\xi _i=y_i+z_i\}_{1 \leq i \leq g}$
in
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
the family of curves in
$\operatorname {Sym}^2({\mathbb P}^1)$
the family of curves in
![]() ${\mathcal F}_{k,(P_1,\ldots\, ,P_n),\mathbf {e}}$
passing through
${\mathcal F}_{k,(P_1,\ldots\, ,P_n),\mathbf {e}}$
passing through
![]() $\xi _1,\ldots ,\xi _g$
has dimension
$\xi _1,\ldots ,\xi _g$
has dimension
![]() $\widetilde {\rho }(g,1,k;\mathbf {e})$
by (3.6). This family yields the variety
$\widetilde {\rho }(g,1,k;\mathbf {e})$
by (3.6). This family yields the variety
![]() $G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
on the g-nodal curve X obtained by identifying the g pairs
$G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
on the g-nodal curve X obtained by identifying the g pairs
![]() $(y_i,z_i)$
of points on
$(y_i,z_i)$
of points on
![]() ${\mathbb P}^1$
. Thus, we have proved that
${\mathbb P}^1$
. Thus, we have proved that
![]() $G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
has dimension
$G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
has dimension
![]() $\widetilde {\rho }(g,1,k;\mathbf {e})$
.
$\widetilde {\rho }(g,1,k;\mathbf {e})$
.
The case
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) < 0$
. Set
$\widetilde {\rho }(g,1,k;\mathbf {e}) < 0$
. Set
![]() $g':=\widetilde {\rho }(g,1,k;\mathbf {e})+g <g$
. For a general set of
$g':=\widetilde {\rho }(g,1,k;\mathbf {e})+g <g$
. For a general set of
![]() $g'$
points
$g'$
points
![]() $\{\xi _i=y_i+z_i\}_{1 \leq i \leq g'}$
in
$\{\xi _i=y_i+z_i\}_{1 \leq i \leq g'}$
in
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
the family of curves in
$\operatorname {Sym}^2({\mathbb P}^1)$
the family of curves in
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
passing through
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
passing through
![]() $\xi _1,\ldots ,\xi _{g'}$
has dimension
$\xi _1,\ldots ,\xi _{g'}$
has dimension
![]() $0$
by (3.6). Choose any set of distinct
$0$
by (3.6). Choose any set of distinct
![]() $g-g'$
points
$g-g'$
points
![]() $\{\xi _i=y_i+z_i\}_{g'+1 \leq i \leq g}$
on any of the finitely many curves in
$\{\xi _i=y_i+z_i\}_{g'+1 \leq i \leq g}$
on any of the finitely many curves in
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
so obtained. Then, on the g-nodal curve X obtained by identifying the g pairs
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
so obtained. Then, on the g-nodal curve X obtained by identifying the g pairs
![]() $(y_i,z_i)$
of points on
$(y_i,z_i)$
of points on
![]() ${\mathbb P}^1$
, the variety
${\mathbb P}^1$
, the variety
![]() $G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
is
$G^1_k(X,(P_1,e_1),\ldots ,(P_n,e_n))$
is
![]() $0$
-dimensional.
$0$
-dimensional.
Theorem 2.1 now follows by semicontinuity, in view of (3.2), (2.5) and what we explained right after (2.6).
Proof of Theorem 2.3
To prove the theorem we will prove that the general fibres of
![]() ${\mathcal H}_{g,k,\mathbf {e}} \to {\mathcal M}_g$
have dimension
${\mathcal H}_{g,k,\mathbf {e}} \to {\mathcal M}_g$
have dimension
![]() $\max \{0,n+\widetilde {\rho }(g,1,k;\mathbf {e})\}$
on some component. We will prove this by degeneration to a g-nodal rational curve in
$\max \{0,n+\widetilde {\rho }(g,1,k;\mathbf {e})\}$
on some component. We will prove this by degeneration to a g-nodal rational curve in
![]() $\overline {{\mathcal M}_g}$
as in the previous proof.
$\overline {{\mathcal M}_g}$
as in the previous proof.
With the notation therein, we set
![]() ${\mathcal F}_{k,\mathbf {e}}$
to be the variety parametrizing
${\mathcal F}_{k,\mathbf {e}}$
to be the variety parametrizing
for varying distinct general
![]() $P_1,\ldots ,P_n$
. Then
$P_1,\ldots ,P_n$
. Then
![]() ${\mathcal F}_{k,\mathbf {e}}$
is equidimensional of dimension
${\mathcal F}_{k,\mathbf {e}}$
is equidimensional of dimension
The case
![]() $n+\widetilde {\rho }(g,1,k;\mathbf {e}) \geq 0$
. The same argument as in the previous proof starting with
$n+\widetilde {\rho }(g,1,k;\mathbf {e}) \geq 0$
. The same argument as in the previous proof starting with
![]() ${\mathcal F}_{k,\mathbf {e}}$
shows that for a general set of g points in
${\mathcal F}_{k,\mathbf {e}}$
shows that for a general set of g points in
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
, the family of curves in
$\operatorname {Sym}^2({\mathbb P}^1)$
, the family of curves in
![]() ${\mathcal F}_{k,\mathbf {e}}$
passing through these points has dimension
${\mathcal F}_{k,\mathbf {e}}$
passing through these points has dimension
![]() $\widetilde {\rho }(g,1,k;\mathbf {e})+n \geq 0$
by (3.7). This produces, as in the previous proof, a g-nodal rational curve X having a
$\widetilde {\rho }(g,1,k;\mathbf {e})+n \geq 0$
by (3.7). This produces, as in the previous proof, a g-nodal rational curve X having a
![]() $(\widetilde {\rho }(g,1,k;\mathbf {e})+n)$
-dimensional family of
$(\widetilde {\rho }(g,1,k;\mathbf {e})+n)$
-dimensional family of
![]() $g^1_k$
s with the given ramification order at some n points. Recalling (3.2), this proves that the fibre over X of
$g^1_k$
s with the given ramification order at some n points. Recalling (3.2), this proves that the fibre over X of
![]() $\overline {{\mathcal H}_{g,k,\mathbf {e}}} \to \overline {{\mathcal M}_g}$
has dimension
$\overline {{\mathcal H}_{g,k,\mathbf {e}}} \to \overline {{\mathcal M}_g}$
has dimension
![]() $n+\widetilde {\rho }(g,1,k;\mathbf {e})$
. The theorem follows by semicontinuity.
$n+\widetilde {\rho }(g,1,k;\mathbf {e})$
. The theorem follows by semicontinuity.
The case
![]() $n+\widetilde {\rho }(g,1,k;\mathbf {e}) < 0$
. Set
$n+\widetilde {\rho }(g,1,k;\mathbf {e}) < 0$
. Set
![]() $g':=\widetilde {\rho }(g,1,k;\mathbf {e})+g+n <g$
. Then, for a general set of
$g':=\widetilde {\rho }(g,1,k;\mathbf {e})+g+n <g$
. Then, for a general set of
![]() $g'$
points in
$g'$
points in
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
, the family of curves in
$\operatorname {Sym}^2({\mathbb P}^1)$
, the family of curves in
![]() ${\mathcal F}_{k,\mathbf {e}}$
passing through these points is zero-dimensional by (3.7). Then, on the g-nodal curve X obtained by identifying the
${\mathcal F}_{k,\mathbf {e}}$
passing through these points is zero-dimensional by (3.7). Then, on the g-nodal curve X obtained by identifying the
![]() $g'$
pairs of points on
$g'$
pairs of points on
![]() ${\mathbb P}^1$
corresponding to the
${\mathbb P}^1$
corresponding to the
![]() $g'$
points in
$g'$
points in
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
, plus an arbitrary set of
$\operatorname {Sym}^2({\mathbb P}^1)$
, plus an arbitrary set of
![]() $g-g'$
points, we have obtained a finite family of
$g-g'$
points, we have obtained a finite family of
![]() $g^1_k$
s with the given ramification order at some n points. Recalling (3.2), this proves that the fibre over X of
$g^1_k$
s with the given ramification order at some n points. Recalling (3.2), this proves that the fibre over X of
![]() $\overline {{\mathcal H}_{g,k,\mathbf {e}}} \to \overline {{\mathcal M}_g}$
has dimension
$\overline {{\mathcal H}_{g,k,\mathbf {e}}} \to \overline {{\mathcal M}_g}$
has dimension
![]() $0$
. The theorem follows by semicontinuity.
$0$
. The theorem follows by semicontinuity.
4 Building on the construction and results in [Reference Ciliberto and Knutsen12]
To prove Theorem 2.6, we will use a degeneration argument developed in [Reference Ciliberto and Knutsen12].
Let
![]() $p\geq 3$
. We denote by
$p\geq 3$
. We denote by
![]() ${\mathcal K}_p$
the moduli space of primitively polarized
${\mathcal K}_p$
the moduli space of primitively polarized
![]() $K3$
surfaces of genus p, which is irreducible of dimension
$K3$
surfaces of genus p, which is irreducible of dimension
![]() $19$
. The following result is central in our investigation:
$19$
. The following result is central in our investigation:
Theorem 4.1. If
![]() $(S,H)$
is a general primitive
$(S,H)$
is a general primitive
![]() $K3$
surface of genus p, then
$K3$
surface of genus p, then
![]() $V^k_{|H|,\delta } \neq \emptyset $
if and only if (2.7) is satisfied. When nonempty,
$V^k_{|H|,\delta } \neq \emptyset $
if and only if (2.7) is satisfied. When nonempty,
![]() $V^k_{|H|,\delta }$
is equidimensional of dimension
$V^k_{|H|,\delta }$
is equidimensional of dimension
![]() $\min \{2(k-1),g\}$
.
$\min \{2(k-1),g\}$
.
The nonemptiness part of the theorem is [Reference Ciliberto and Knutsen12, Thm. 0.1], whereas the assertion about equidimensionality follows from [Reference Knutsen, Lelli-Chiesa and Mongardi27, Rem. 5.6]. In this section we review and build on the proof of the assertion concerning nonemptiness in order to approach the refined ramified version in §5. The general strategy consists in degenerating the polarized K3 surface
![]() $(S,H)$
to a pair
$(S,H)$
to a pair
![]() $(S_0,H_0)$
(§4.1) so that the Severi variety
$(S_0,H_0)$
(§4.1) so that the Severi variety
![]() $V_{|H|,\delta }$
degenerates to a locus containing an irreducible component
$V_{|H|,\delta }$
degenerates to a locus containing an irreducible component
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
(cf. Definition 4.2), whose curves all contain a special component isomorphic to
$V(\alpha _{1}, \ldots , \alpha _{p})$
(cf. Definition 4.2), whose curves all contain a special component isomorphic to
![]() ${\mathbb P}^1$
with a collection of pairs of distinguished points (§4.2). The computation of the dimension of
${\mathbb P}^1$
with a collection of pairs of distinguished points (§4.2). The computation of the dimension of
![]() $V^k_{|H|,\delta }$
reduces in this way to computing the dimension of families of
$V^k_{|H|,\delta }$
reduces in this way to computing the dimension of families of
![]() $g^1_k$
s on
$g^1_k$
s on
![]() ${\mathbb P}^1$
satisfying certain compatibility conditions. More precisely, each pair of distinguished points must belong to a divisor of the given
${\mathbb P}^1$
satisfying certain compatibility conditions. More precisely, each pair of distinguished points must belong to a divisor of the given
![]() $g^1_k$
. Such a computation is obtained by intersecting appropriate curves in
$g^1_k$
. Such a computation is obtained by intersecting appropriate curves in
![]() ${\mathbb P}^2$
(§4.3).
${\mathbb P}^2$
(§4.3).
4.1 Limit K3 surface
We describe now the degeneration of
![]() $(S,H)\in {\mathcal K}_p$
to a pair
$(S,H)\in {\mathcal K}_p$
to a pair
![]() $(S_0,H_0)$
(cf. [Reference Ciliberto and Knutsen12, §4]).
$(S_0,H_0)$
(cf. [Reference Ciliberto and Knutsen12, §4]).
Let E be a smooth elliptic curve with two distinct general line bundles
![]() $L_1,L_2 \in \operatorname {Pic}^2(E)$
. Consider the embedding of
$L_1,L_2 \in \operatorname {Pic}^2(E)$
. Consider the embedding of
![]() $E \subset {\mathbb P}^{2p-1}$
as a smooth elliptic normal curve of degree
$E \subset {\mathbb P}^{2p-1}$
as a smooth elliptic normal curve of degree
![]() $2p$
given by
$2p$
given by
![]() $L_2^ {\otimes p}$
. Let
$L_2^ {\otimes p}$
. Let
![]() $R_1$
and
$R_1$
and
![]() $R_2$
be the rational normal scrolls of degree
$R_2$
be the rational normal scrolls of degree
![]() $2p-2$
in
$2p-2$
in
![]() ${\mathbb P}^{2p-1}$
defined by
${\mathbb P}^{2p-1}$
defined by
![]() $L_1$
and
$L_1$
and
![]() $L_2$
, respectively, that is,
$L_2$
, respectively, that is,
![]() $R_i$
is the union of lines spanned by the divisors of
$R_i$
is the union of lines spanned by the divisors of
![]() $\vert L_i\vert $
. Then
$\vert L_i\vert $
. Then
-
○
 $R_1 \cong {\mathbb P}^1 \times {\mathbb P}^1$
and
$R_1 \cong {\mathbb P}^1 \times {\mathbb P}^1$
and
 $R_2 \cong \mathbb {F}_2$
,
$R_2 \cong \mathbb {F}_2$
, -
○
 $R_1 \cap R_2 =E$
transversally,
$R_1 \cap R_2 =E$
transversally, -
○ E is anticanonical on each
 $R_i$
.
$R_i$
.
Set
![]() $R:=R_1 \cup R_2$
.
$R:=R_1 \cup R_2$
.
We will denote by
![]() $f:{\mathbb P}^1 \times {\mathbb P}^1 \to {\mathbb P}^1$
the projection to
$f:{\mathbb P}^1 \times {\mathbb P}^1 \to {\mathbb P}^1$
the projection to
![]() ${\mathbb P}^1$
defined by the pencil
${\mathbb P}^1$
defined by the pencil
![]() $|L_1|$
. Let
$|L_1|$
. Let
![]() $\mathfrak {s}_i$
and
$\mathfrak {s}_i$
and
![]() $\mathfrak {f}_i$
denote the classes of the nonpositive section and fibre, respectively, of
$\mathfrak {f}_i$
denote the classes of the nonpositive section and fibre, respectively, of
![]() $R_i$
, for
$R_i$
, for
![]() $1\le i\le 2$
. Thus, the members of
$1\le i\le 2$
. Thus, the members of
![]() $|\mathfrak {f}_1|$
are the fibres of f. Then
$|\mathfrak {f}_1|$
are the fibres of f. Then
![]() ${\mathcal O}_{R_1}(1) \cong {\mathcal O}_{R_1}(\mathfrak {s}_1 +(p-1)\mathfrak {f}_1)$
and
${\mathcal O}_{R_1}(1) \cong {\mathcal O}_{R_1}(\mathfrak {s}_1 +(p-1)\mathfrak {f}_1)$
and
![]() ${\mathcal O}_{R_2}(1) \cong {\mathcal O}_{R_2}(\mathfrak {s}_2 +p\mathfrak {f}_2)$
. The section
${\mathcal O}_{R_2}(1) \cong {\mathcal O}_{R_2}(\mathfrak {s}_2 +p\mathfrak {f}_2)$
. The section
![]() $\mathfrak {s}_2$
does not intersect E, hence lies in the smooth locus of R. In particular,
$\mathfrak {s}_2$
does not intersect E, hence lies in the smooth locus of R. In particular,
![]() $\mathfrak {s}_2$
is a Cartier divisor on R, so that
$\mathfrak {s}_2$
is a Cartier divisor on R, so that
is also Cartier, with
![]() $H_0^2=2p-2$
and
$H_0^2=2p-2$
and
![]() $\mathfrak {s}_2 \cdot H_0=p$
. By [Reference Ciliberto and Knutsen12, Lem. 4.1] the pair
$\mathfrak {s}_2 \cdot H_0=p$
. By [Reference Ciliberto and Knutsen12, Lem. 4.1] the pair
![]() $(S_0:=R,H_0)$
can be flatly deformed to a member of
$(S_0:=R,H_0)$
can be flatly deformed to a member of
![]() ${\mathcal K}_p$
. More precisely, there is a flat family
${\mathcal K}_p$
. More precisely, there is a flat family
![]() $\pi :{\mathcal X}\to {\mathbb D}$
, where
$\pi :{\mathcal X}\to {\mathbb D}$
, where
![]() ${\mathbb D}$
is the disc, such that the special fibre
${\mathbb D}$
is the disc, such that the special fibre
![]() $\pi ^{-1}(0)\simeq R$
and the fibres
$\pi ^{-1}(0)\simeq R$
and the fibres
![]() $S_t:=\pi ^{-1}(t)$
for
$S_t:=\pi ^{-1}(t)$
for
![]() $t \neq 0$
are smooth
$t \neq 0$
are smooth
![]() $K3$
surfaces, and a line bundle
$K3$
surfaces, and a line bundle
![]() ${\mathcal H}$
on
${\mathcal H}$
on
![]() ${\mathcal X}$
such that
${\mathcal X}$
such that
![]() ${\mathcal H}|_{S_0}=H_0$
and, setting
${\mathcal H}|_{S_0}=H_0$
and, setting
![]() $H_t:={\mathcal H}|_{S_t}$
also for
$H_t:={\mathcal H}|_{S_t}$
also for
![]() $t \neq 0$
, we have that
$t \neq 0$
, we have that
![]() $(S_t,H_t) \in {\mathcal K}_p$
is general.
$(S_t,H_t) \in {\mathcal K}_p$
is general.
Note that the total space
![]() ${\mathcal X}$
has
${\mathcal X}$
has
![]() $16$
double points on E in the central fibre, and is otherwise smooth. One may perform a small resolution of the singularities of
$16$
double points on E in the central fibre, and is otherwise smooth. One may perform a small resolution of the singularities of
![]() ${\mathcal X}$
, obtaining a new family with unchanged fibres for
${\mathcal X}$
, obtaining a new family with unchanged fibres for
![]() $t \neq 0$
, but whose new central fibre is a birational modification of R. Precisely one can make sure that the new central fibre is
$t \neq 0$
, but whose new central fibre is a birational modification of R. Precisely one can make sure that the new central fibre is
![]() $R_1\cup \widetilde R_2$
, where
$R_1\cup \widetilde R_2$
, where
![]() $\widetilde R_2$
is the blow-up of
$\widetilde R_2$
is the blow-up of
![]() $R_2$
at the
$R_2$
at the
![]() $16$
singular points of
$16$
singular points of
![]() ${\mathcal X}$
, and
${\mathcal X}$
, and
![]() $R_1$
and
$R_1$
and
![]() $\widetilde R_2$
meet transversally along
$\widetilde R_2$
meet transversally along
![]() $E\subset R_1$
and its strict transform on
$E\subset R_1$
and its strict transform on
![]() $\widetilde R_2$
. Since we can make sure that the interesting curves we work with on R will lie off the singular points of
$\widetilde R_2$
. Since we can make sure that the interesting curves we work with on R will lie off the singular points of
![]() ${\mathcal X}$
, we can choose to work with
${\mathcal X}$
, we can choose to work with
![]() ${\mathcal X}$
without caring about the singularities.
${\mathcal X}$
without caring about the singularities.
4.2 Limit Severi varieties
We now describe limit curves of
![]() $V_{|H_t|,\delta }$
, following [Reference Ciliberto and Knutsen12, §6].
$V_{|H_t|,\delta }$
, following [Reference Ciliberto and Knutsen12, §6].
Let m be a positive integer satisfying
![]() $m \leq p$
. A chain of length
$m \leq p$
. A chain of length
![]() $2m-1$
is a sum of
$2m-1$
is a sum of
![]() $2m-1$
distinct lines
$2m-1$
distinct lines
where
![]() $f_{1,j}$
intersects only
$f_{1,j}$
intersects only
![]() $f_{2,j}$
and
$f_{2,j}$
and
![]() $f_{2,j+1}$
, for
$f_{2,j+1}$
, for
![]() $j=1, \ldots , m-1$
. The chain intersects E in
$j=1, \ldots , m-1$
. The chain intersects E in
![]() $2m$
points, consisting of m divisors of
$2m$
points, consisting of m divisors of
![]() $|L_2|$
, and
$|L_2|$
, and
![]() $2m-2$
of them lie on the intersections between two lines, whereas the remaining two are on
$2m-2$
of them lie on the intersections between two lines, whereas the remaining two are on
![]() $f_{2,1}$
and
$f_{2,1}$
and
![]() $f_{2,m}$
and will be denoted by a and b, respectively. This pair of points will be called the distinguished pair of points of the chain. Figure 1 shows a chain of length
$f_{2,m}$
and will be denoted by a and b, respectively. This pair of points will be called the distinguished pair of points of the chain. Figure 1 shows a chain of length
![]() $9$
and its distinguished pair of points. If the chain is contained in a member C of
$9$
and its distinguished pair of points. If the chain is contained in a member C of
![]() $|H_0|$
, and we denote by
$|H_0|$
, and we denote by
![]() $\Gamma $
the section of the ruling on
$\Gamma $
the section of the ruling on
![]() $R_1$
contained in C, the distinguished points are
$R_1$
contained in C, the distinguished points are
![]() $a=\Gamma \cap f_{2,1}$
and
$a=\Gamma \cap f_{2,1}$
and
![]() $b=\Gamma \cap f_{2,m}$
. Denoting the restriction of f to E still by f (so that
$b=\Gamma \cap f_{2,m}$
. Denoting the restriction of f to E still by f (so that
![]() $f:E \to \Gamma \cong {\mathbb P}^1$
is the morphism determined by the linear series
$f:E \to \Gamma \cong {\mathbb P}^1$
is the morphism determined by the linear series
![]() $|L_1|$
), we note that
$|L_1|$
), we note that
![]() $a+b \in f_*\left (|mL_2-(m-1)L_1|\right )$
.
$a+b \in f_*\left (|mL_2-(m-1)L_1|\right )$
.

Figure 1 A chain of length
![]() $9$
contained in a member of
$9$
contained in a member of
![]() $|H_0|$
.
$|H_0|$
.
We denote by
![]() ${\mathcal C}_{m}$
the family of chains of length
${\mathcal C}_{m}$
the family of chains of length
![]() $2m-1$
, which is a locally closed subvariety of a Hilbert scheme of curves on R. In [Reference Ciliberto and Knutsen12, Lem. 4.2] it is proved that the map
$2m-1$
, which is a locally closed subvariety of a Hilbert scheme of curves on R. In [Reference Ciliberto and Knutsen12, Lem. 4.2] it is proved that the map
sending a chain of length
![]() $2m-1$
to its pair of distinguished points on E is birational and injective.
$2m-1$
to its pair of distinguished points on E is birational and injective.
Definition 4.2. For each tuple
![]() $(\alpha _1,\ldots , \alpha _p)$
of nonnegative integers satisfying
$(\alpha _1,\ldots , \alpha _p)$
of nonnegative integers satisfying
 $$ \begin{align} p=\displaystyle\sum_{j=1}^p j\alpha_j \end{align} $$
$$ \begin{align} p=\displaystyle\sum_{j=1}^p j\alpha_j \end{align} $$
one defines
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
to be the locally closed subset of reduced curves in
$V(\alpha _{1}, \ldots , \alpha _{p})$
to be the locally closed subset of reduced curves in
![]() $|H_0|$
not passing through the singular locus of
$|H_0|$
not passing through the singular locus of
![]() ${\mathcal X}$
and containing exactly
${\mathcal X}$
and containing exactly
![]() $\alpha _{j}$
chains of length
$\alpha _{j}$
chains of length
![]() $2j-1$
, for
$2j-1$
, for
![]() $j=1,\ldots ,p$
.
$j=1,\ldots ,p$
.
By (4.2) we have a morphism

which is proved to be bijective in [Reference Ciliberto and Knutsen12, Proof of Prop. 5.2]. Indeed, its inverse is given in the following way: the coordinates of any member of the target uniquely define a chain, and the intersection between the union of the lines in
![]() $|\mathfrak {f}_2|$
of these chains and E is an effective divisor lying in
$|\mathfrak {f}_2|$
of these chains and E is an effective divisor lying in
![]() $|(\sum j \alpha _j)L_2|=|pL_2|=|{\mathcal O}_E(1)|$
, by (4.3). This can be extended to a unique hyperplane section of R, which necessarily contains
$|(\sum j \alpha _j)L_2|=|pL_2|=|{\mathcal O}_E(1)|$
, by (4.3). This can be extended to a unique hyperplane section of R, which necessarily contains
![]() $\mathfrak {s}_2$
, so it gives a curve in
$\mathfrak {s}_2$
, so it gives a curve in
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
. As the dimension of the target in (4.4) is
$V(\alpha _{1}, \ldots , \alpha _{p})$
. As the dimension of the target in (4.4) is
 $$ \begin{align} g:=\sum_{j=1}^p\alpha_j, \end{align} $$
$$ \begin{align} g:=\sum_{j=1}^p\alpha_j, \end{align} $$
we see that
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
is g-dimensional.
$V(\alpha _{1}, \ldots , \alpha _{p})$
is g-dimensional.
Any curve C in
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
is nodal, and we denote as above by
$V(\alpha _{1}, \ldots , \alpha _{p})$
is nodal, and we denote as above by
![]() $\Gamma $
the section of the ruling on
$\Gamma $
the section of the ruling on
![]() $R_1$
contained in C (i.e., C is the union of
$R_1$
contained in C (i.e., C is the union of
![]() $\Gamma $
and of chains). We will call
$\Gamma $
and of chains). We will call
![]() $\Gamma $
the sectional component of C. The curve C has
$\Gamma $
the sectional component of C. The curve C has
 $$ \begin{align} \delta=\delta(\alpha_{1}, \ldots, \alpha_{p}):= \displaystyle\sum_{j=1}^p (j-1) \alpha_{j} \end{align} $$
$$ \begin{align} \delta=\delta(\alpha_{1}, \ldots, \alpha_{p}):= \displaystyle\sum_{j=1}^p (j-1) \alpha_{j} \end{align} $$
nodes lying off E, which we call the marked nodes of C, and they all lie on its sectional component
![]() $\Gamma $
. In Figure 1 they are marked with circles. We note that (4.3), (4.5) and (4.6) yield
$\Gamma $
. In Figure 1 they are marked with circles. We note that (4.3), (4.5) and (4.6) yield
It is proved in [Reference Ciliberto and Knutsen12, Prop. 5.2] that
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
is a component of the flat limit of
$V(\alpha _{1}, \ldots , \alpha _{p})$
is a component of the flat limit of
![]() $V_{| H_t|,\delta }$
.
$V_{| H_t|,\delta }$
.
4.3 Limit Severi varieties of curves whose normalization carry a
 $g^1_k$
$g^1_k$
We now describe limit curves of
![]() $V^k_{|H_t|,\delta }$
and compute the dimension of the component they define, following [Reference Ciliberto and Knutsen12, §6].
$V^k_{|H_t|,\delta }$
and compute the dimension of the component they define, following [Reference Ciliberto and Knutsen12, §6].
As in Figure 2, we denote by
![]() $\widetilde {C}$
the partial normalization of C at its
$\widetilde {C}$
the partial normalization of C at its
![]() $\delta $
marked nodes and by
$\delta $
marked nodes and by
![]() $C'$
the stable model of
$C'$
the stable model of
![]() $\widetilde {C}$
, obtained by contracting all chains of C. We already noted that the distinguished pair of points of each chain contained in C lies on
$\widetilde {C}$
, obtained by contracting all chains of C. We already noted that the distinguished pair of points of each chain contained in C lies on
![]() $\Gamma $
. There are g such pairs. Thus,
$\Gamma $
. There are g such pairs. Thus,
![]() $C'$
is equivalently the g-nodal curve obtained by identifying each distinguished pair of points on
$C'$
is equivalently the g-nodal curve obtained by identifying each distinguished pair of points on
![]() $\Gamma $
, as shown in Figure 2. We note that the natural map
$\Gamma $
, as shown in Figure 2. We note that the natural map
![]() $\Gamma \to C'$
is the normalization, and that a degree k cover
$\Gamma \to C'$
is the normalization, and that a degree k cover
![]() $\Gamma \to {\mathbb P}^1$
factors through
$\Gamma \to {\mathbb P}^1$
factors through
![]() $C'$
if and only if all distinguished pairs of points lie in the same fibres of
$C'$
if and only if all distinguished pairs of points lie in the same fibres of
![]() $\Gamma \to {\mathbb P}^1$
. This motivates the following definition.
$\Gamma \to {\mathbb P}^1$
. This motivates the following definition.

Figure 2 The partial normalization
![]() $\widetilde {C}$
of C and its stable model
$\widetilde {C}$
of C and its stable model
![]() $C'$
, around a chain.
$C'$
, around a chain.
Definition 4.3. Let
![]() $C \in V(\alpha _1,\ldots ,\alpha _p)$
. We say that a
$C \in V(\alpha _1,\ldots ,\alpha _p)$
. We say that a
![]() $g^1_k$
on the sectional component
$g^1_k$
on the sectional component
![]() $\Gamma $
of C is a descending
$\Gamma $
of C is a descending
![]() $g^1_k$
if all distinguished pairs of points of each chain contained in C belong to divisors of the
$g^1_k$
if all distinguished pairs of points of each chain contained in C belong to divisors of the
![]() $g^1_{k}$
.
$g^1_{k}$
.
We denote by
![]() $G^1_k(C')$
the variety of all descending
$G^1_k(C')$
the variety of all descending
![]() $g^1_k$
s on
$g^1_k$
s on
![]() $\Gamma $
and by
$\Gamma $
and by
![]() ${\mathcal G}^k(\alpha _1,\ldots ,\alpha _p)$
the variety parametrizing pairs
${\mathcal G}^k(\alpha _1,\ldots ,\alpha _p)$
the variety parametrizing pairs
![]() $(C,\mathfrak {g})$
such that
$(C,\mathfrak {g})$
such that
![]() $C \in V(\alpha _1,\ldots ,\alpha _p)$
and
$C \in V(\alpha _1,\ldots ,\alpha _p)$
and
![]() $\mathfrak {g} \in G^1_k(C')$
.
$\mathfrak {g} \in G^1_k(C')$
.
We denote by
![]() $V^k(\alpha _1,\ldots ,\alpha _p)$
the image of the forgetful map
$V^k(\alpha _1,\ldots ,\alpha _p)$
the image of the forgetful map
(which has fibres
![]() $G^1_k(C')$
).
$G^1_k(C')$
).
By what we said prior to the definition, C lies in
![]() $V^k(\alpha _1,\ldots ,\alpha _p)$
if and only if
$V^k(\alpha _1,\ldots ,\alpha _p)$
if and only if
![]() $C'$
lies in
$C'$
lies in
![]() $\overline {{\mathcal M}^1_{g,k}}$
(see [Reference Ciliberto and Knutsen12, Lem. 5.3]).
$\overline {{\mathcal M}^1_{g,k}}$
(see [Reference Ciliberto and Knutsen12, Lem. 5.3]).
In [Reference Ciliberto and Knutsen12, Prop. 6.5 and Cor. 6.6] the following is proved:
Proposition 4.4. If (4.3) and
hold, the variety
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
is nonempty and irreducible of dimension
$V^k( \alpha _1,\ldots ,\alpha _p)$
is nonempty and irreducible of dimension
![]() $\min \{2(k-1),g\}$
, and is contained in the limit of
$\min \{2(k-1),g\}$
, and is contained in the limit of
![]() $V^k_{|H_t|,\delta }$
as t tends to
$V^k_{|H_t|,\delta }$
as t tends to
![]() $0$
.
$0$
.
It is also proved in [Reference Ciliberto and Knutsen12] that there are
![]() $(\alpha _1,\ldots ,\alpha _p)$
satisfying conditions (4.3) and (4.8) whenever (2.7) is satisfied (cf. [Reference Ciliberto and Knutsen12, Prop. 7.1]).
$(\alpha _1,\ldots ,\alpha _p)$
satisfying conditions (4.3) and (4.8) whenever (2.7) is satisfied (cf. [Reference Ciliberto and Knutsen12, Prop. 7.1]).
To prove Proposition 4.4, the variety
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
is explicitly constructed in the following way. Let
$V^k( \alpha _1,\ldots ,\alpha _p)$
is explicitly constructed in the following way. Let
![]() $f: E \rightarrow {\mathbb P}^1$
be the morphism determined by
$f: E \rightarrow {\mathbb P}^1$
be the morphism determined by
![]() $\vert L_1\vert $
and
$\vert L_1\vert $
and
![]() $f^{(2)}: \operatorname {Sym}^2(E) \rightarrow \operatorname {Sym}^2({\mathbb P}^1)$
the induced map. We identify
$f^{(2)}: \operatorname {Sym}^2(E) \rightarrow \operatorname {Sym}^2({\mathbb P}^1)$
the induced map. We identify
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
with
$\operatorname {Sym}^2({\mathbb P}^1)$
with
![]() ${\mathbb P}^2$
as in the previous section. We denote by
${\mathbb P}^2$
as in the previous section. We denote by
![]() $\mathfrak {c}_{j}$
, for
$\mathfrak {c}_{j}$
, for
![]() $1\le j \le n$
, the image via
$1\le j \le n$
, the image via
![]() $f^{(2)}$
of the smooth rational curves in
$f^{(2)}$
of the smooth rational curves in
![]() $\operatorname {Sym}^2(E)$
defined by the pencils
$\operatorname {Sym}^2(E)$
defined by the pencils
![]() $|jL_{2}-(j-1)L_{1}|$
. These are distinct conics, each intersecting the diagonal
$|jL_{2}-(j-1)L_{1}|$
. These are distinct conics, each intersecting the diagonal
![]() $\Delta $
in four distinct points corresponding to the ramification points of the pencils. Recall from the previous section that to each
$\Delta $
in four distinct points corresponding to the ramification points of the pencils. Recall from the previous section that to each
![]() $\mathfrak {g} \in G^1_k({\mathbb P}^1)$
we associate the degree
$\mathfrak {g} \in G^1_k({\mathbb P}^1)$
we associate the degree
![]() $k-1$
curve in
$k-1$
curve in
![]() ${\mathbb P}^ 2=\operatorname {Sym}^2({\mathbb P}^1)$
given by
${\mathbb P}^ 2=\operatorname {Sym}^2({\mathbb P}^1)$
given by
![]() $ C_{\mathfrak {g}}= \{ W \in \operatorname {Sym}^2({\mathbb P}^1) \; | \; \mathfrak {g}(-W) \geq 0\}$
and that we denote the family of such curves by
$ C_{\mathfrak {g}}= \{ W \in \operatorname {Sym}^2({\mathbb P}^1) \; | \; \mathfrak {g}(-W) \geq 0\}$
and that we denote the family of such curves by
![]() ${\mathcal F}_k$
(cf. Definition 3.1).
${\mathcal F}_k$
(cf. Definition 3.1).
We state here a stronger version of [Reference Ciliberto and Knutsen12, Lem. 6.3], as we will need it later to prove our main results:
Lemma 4.5. Fix a reduced curve
![]() $C_{\mathfrak {g}}$
in
$C_{\mathfrak {g}}$
in
![]() ${\mathcal F}_k$
. Then, for general
${\mathcal F}_k$
. Then, for general
![]() $L_2 \in \operatorname {Pic}^2(E)$
, the curve
$L_2 \in \operatorname {Pic}^2(E)$
, the curve
![]() $C_{\mathfrak {g}}$
intersects each
$C_{\mathfrak {g}}$
intersects each
![]() $\mathfrak {c}_{j}$
transversally in
$\mathfrak {c}_{j}$
transversally in
![]() $2(k-1)$
distinct points. Moreover, varying
$2(k-1)$
distinct points. Moreover, varying
![]() $C_{\mathfrak {g}}$
in
$C_{\mathfrak {g}}$
in
![]() ${\mathcal F}_k$
, none of these points is fixed.
${\mathcal F}_k$
, none of these points is fixed.
Proof. The fibres of the Albanese (summation) map
![]() $ \text {alb}:\operatorname {Sym}^2(E) \to E$
are the one-dimensional family of
$ \text {alb}:\operatorname {Sym}^2(E) \to E$
are the one-dimensional family of
![]() $g^1_2$
s on E, and each curve
$g^1_2$
s on E, and each curve
![]() $\mathfrak {c}_{j}$
is the image of one such fibre. Varying
$\mathfrak {c}_{j}$
is the image of one such fibre. Varying
![]() $L_2 \in \operatorname {Pic}^2(E)$
the fibres sent to
$L_2 \in \operatorname {Pic}^2(E)$
the fibres sent to
![]() $\mathfrak {c}_{j}$
cover all fibres of
$\mathfrak {c}_{j}$
cover all fibres of
![]() $\text {alb}$
, so that
$\text {alb}$
, so that
![]() $\mathfrak {c}_{j}$
becomes the image of a general fibre. Each pair of fibres of a moves in a base point free linear system, whence
$\mathfrak {c}_{j}$
becomes the image of a general fibre. Each pair of fibres of a moves in a base point free linear system, whence
![]() $(f^{(2)})^{-1}C_{\mathfrak {g}}$
has transversal intersection with the general fibre of
$(f^{(2)})^{-1}C_{\mathfrak {g}}$
has transversal intersection with the general fibre of
![]() $\text {alb}$
and the intersection occurs outside of the ramification locus of
$\text {alb}$
and the intersection occurs outside of the ramification locus of
![]() $f^{(2)}$
. This proves that also the intersection
$f^{(2)}$
. This proves that also the intersection
![]() $C_{\mathfrak {g}} \cap \mathfrak {c}_{j}$
is transversal.
$C_{\mathfrak {g}} \cap \mathfrak {c}_{j}$
is transversal.
The case
![]() $L_2=L_1$
yields
$L_2=L_1$
yields
![]() $\mathfrak {c}_j=\Delta $
for all j. Varying
$\mathfrak {c}_j=\Delta $
for all j. Varying
![]() $\mathfrak {g}$
, none of the points in
$\mathfrak {g}$
, none of the points in
![]() $C_{\mathfrak {g}} \cap \Delta $
is fixed, proving the last assertion also for general
$C_{\mathfrak {g}} \cap \Delta $
is fixed, proving the last assertion also for general
![]() $L_2$
.
$L_2$
.
By (4.8) we can pick
![]() $\alpha _{j}$
of the intersection points
$\alpha _{j}$
of the intersection points
![]() $C_{\mathfrak {g}} \cap \mathfrak {c}_{j}$
. Each of these
$C_{\mathfrak {g}} \cap \mathfrak {c}_{j}$
. Each of these
![]() $\alpha _{j}$
intersection points gives rise to a chain of length
$\alpha _{j}$
intersection points gives rise to a chain of length
![]() $2j-1$
with distinguished pair given by the
$2j-1$
with distinguished pair given by the
![]() $2$
-cycle corresponding to the point itself (recall (4.2)) and the one-to-one correspondence (4.4) yields the existence of curves in
$2$
-cycle corresponding to the point itself (recall (4.2)) and the one-to-one correspondence (4.4) yields the existence of curves in
![]() $V( \alpha _1,\ldots ,\alpha _p)$
containing all the above chains, which lie in
$V( \alpha _1,\ldots ,\alpha _p)$
containing all the above chains, which lie in
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
by construction. In other words, we have natural surjective maps
$V^k( \alpha _1,\ldots ,\alpha _p)$
by construction. In other words, we have natural surjective maps

where
![]() $\sigma _k$
is the forgetful map and
$\sigma _k$
is the forgetful map and
![]() $\gamma _k$
is finite. The fibre of
$\gamma _k$
is finite. The fibre of
![]() $\gamma _k$
over a curve
$\gamma _k$
over a curve
![]() $C_{\mathfrak {g}}$
is given by all the choices of
$C_{\mathfrak {g}}$
is given by all the choices of
![]() $\alpha _j$
of the intersection points in each
$\alpha _j$
of the intersection points in each
![]() $C_{\mathfrak {g}} \cap \mathfrak {c}_{j}$
.
$C_{\mathfrak {g}} \cap \mathfrak {c}_{j}$
.
When
![]() $g=\sum \alpha _i>2(k-1)$
, this is used in [Reference Ciliberto and Knutsen12] to prove that
$g=\sum \alpha _i>2(k-1)$
, this is used in [Reference Ciliberto and Knutsen12] to prove that
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
is irreducible (and nonempty) of dimension
$V^k( \alpha _1,\ldots ,\alpha _p)$
is irreducible (and nonempty) of dimension
![]() $2(k-1)$
and that its general element corresponds to finitely many of the curves
$2(k-1)$
and that its general element corresponds to finitely many of the curves
![]() $C_{\mathfrak {g}}$
. When
$C_{\mathfrak {g}}$
. When
![]() $g \leq 2(k-1)$
, one has
$g \leq 2(k-1)$
, one has
![]() $V^k( \alpha _1,\ldots ,\alpha _p)= V( \alpha _1,\ldots ,\alpha _p)$
and its general element corresponds to a family of dimension
$V^k( \alpha _1,\ldots ,\alpha _p)= V( \alpha _1,\ldots ,\alpha _p)$
and its general element corresponds to a family of dimension
![]() $2(k-1)-\sum \alpha _{j}=2(k-1)-g=\rho (g,1,k)$
of the curves
$2(k-1)-\sum \alpha _{j}=2(k-1)-g=\rho (g,1,k)$
of the curves
![]() $C_{\mathfrak {g}}$
. This also shows that the generic fibre dimension of
$C_{\mathfrak {g}}$
. This also shows that the generic fibre dimension of
![]() $\sigma _k$
is
$\sigma _k$
is
![]() $\max \{0,\rho (g,1,k)\}$
, in other words that
$\max \{0,\rho (g,1,k)\}$
, in other words that
![]() $\dim G^1_k(C')=\max \{0,\rho (g,1,k)\}$
for general C in
$\dim G^1_k(C')=\max \{0,\rho (g,1,k)\}$
for general C in
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
.
$V^k( \alpha _1,\ldots ,\alpha _p)$
.
We will also make use of the following observation, implicitly used in [Reference Ciliberto and Knutsen12, Proof of Cor. 6.6(iv)]:
Lemma 4.6. If
![]() $\mathfrak {g}$
is base point free, then any corresponding curve in
$\mathfrak {g}$
is base point free, then any corresponding curve in
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
has the property that the stable model of a partial normalization of C at fewer than its
$V^k( \alpha _1,\ldots ,\alpha _p)$
has the property that the stable model of a partial normalization of C at fewer than its
![]() $\delta $
marked nodes does not lie in
$\delta $
marked nodes does not lie in
![]() $\overline {{\mathcal M}^1_{g,k}}$
.
$\overline {{\mathcal M}^1_{g,k}}$
.
Proof. Such a partial normalization would need to have at least one more component other than
![]() $\Gamma $
, intersecting
$\Gamma $
, intersecting
![]() $\Gamma $
in three points. For the stable model of such a curve to lie in
$\Gamma $
in three points. For the stable model of such a curve to lie in
![]() $\overline {{\mathcal M}^1_{g,k}}$
, the pencil
$\overline {{\mathcal M}^1_{g,k}}$
, the pencil
![]() $\mathfrak {g}$
on
$\mathfrak {g}$
on
![]() $\Gamma $
would need to have base points, since it would have to induce a map from
$\Gamma $
would need to have base points, since it would have to induce a map from
![]() $\Gamma $
to
$\Gamma $
to
![]() ${\mathbb P}^1$
of degree
${\mathbb P}^1$
of degree
![]() $<k$
.
$<k$
.
Under conditions (4.3) and (4.8) we thus have a relative scheme
![]() $\pi _{\delta }: {\mathcal V}_{\delta } \to {\mathbb D}$
of dimension
$\pi _{\delta }: {\mathcal V}_{\delta } \to {\mathbb D}$
of dimension
![]() $\dim {\mathcal V}_{\delta }=g+1$
such that the fibre over
$\dim {\mathcal V}_{\delta }=g+1$
such that the fibre over
![]() $t \neq 0$
is a component of
$t \neq 0$
is a component of
![]() $V_{|H_t|,\delta }$
(of dimension
$V_{|H_t|,\delta }$
(of dimension
![]() $g:=p-\delta $
) and a subscheme
$g:=p-\delta $
) and a subscheme
![]() ${\mathcal V}^k_{\delta } \subset {\mathcal V}_{\delta }$
such that the fibre over
${\mathcal V}^k_{\delta } \subset {\mathcal V}_{\delta }$
such that the fibre over
![]() $t \neq 0$
is a component of
$t \neq 0$
is a component of
![]() $V^k_{|H_t|,\delta }$
of dimension
$V^k_{|H_t|,\delta }$
of dimension
![]() $\min \{2(k-1),g\}$
and the special fibre contains a dense open subset of
$\min \{2(k-1),g\}$
and the special fibre contains a dense open subset of
![]() $V^k( \alpha _1,\ldots ,\alpha _p)$
. By construction, the map from
$V^k( \alpha _1,\ldots ,\alpha _p)$
. By construction, the map from
![]() ${\mathcal V}^k_{\delta }$
sending a curve to the stable model of its normalization at the
${\mathcal V}^k_{\delta }$
sending a curve to the stable model of its normalization at the
![]() $\delta $
marked nodes lands in
$\delta $
marked nodes lands in
![]() $\overline {{\mathcal M}^1_{g,k}}$
, the compactification of
$\overline {{\mathcal M}^1_{g,k}}$
, the compactification of
![]() ${\mathcal M}^1_{g,k}$
in the Deligne-Mumford compactification
${\mathcal M}^1_{g,k}$
in the Deligne-Mumford compactification
![]() $\overline {{\mathcal M}_g}$
of
$\overline {{\mathcal M}_g}$
of
![]() ${\mathcal M}_g$
; in other words, we have moduli maps
${\mathcal M}_g$
; in other words, we have moduli maps

5 Proof of Theorem 2.6
The theorem is trivial in the case
![]() $p=2$
, so we will assume that
$p=2$
, so we will assume that
![]() $p\geq 3$
.
$p\geq 3$
.
We will prove Theorem 2.6 by degeneration, following the structure of the proof of Theorem 4.1 as reviewed in §4. We will use the same degeneration of the K3 surface
![]() $(S,H)$
to
$(S,H)$
to
![]() $(S_0,H_0)$
, and of the Severi variety
$(S_0,H_0)$
, and of the Severi variety
![]() $V_{|H|,\delta }$
to a locus containing an irreducible component
$V_{|H|,\delta }$
to a locus containing an irreducible component
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
. We will introduce a pointed version
$V(\alpha _{1}, \ldots , \alpha _{p})$
. We will introduce a pointed version
![]() $V_n(\alpha _1,\ldots ,\alpha _p)$
of
$V_n(\alpha _1,\ldots ,\alpha _p)$
of
![]() $V(\alpha _{1}, \ldots , \alpha _{p})$
, in order to cut out subloci
$V(\alpha _{1}, \ldots , \alpha _{p})$
, in order to cut out subloci
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
by imposing fixed ramification at the marked points. We will study these subloci by reducing the problem to the study of
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
by imposing fixed ramification at the marked points. We will study these subloci by reducing the problem to the study of
![]() $g^1_k$
s on
$g^1_k$
s on
![]() ${\mathbb P}^1$
with prescribed ramification and with the same compatibility conditions as in §4, that is, distinguished pairs of points must belong to a divisor of the
${\mathbb P}^1$
with prescribed ramification and with the same compatibility conditions as in §4, that is, distinguished pairs of points must belong to a divisor of the
![]() $g^1_k$
.
$g^1_k$
.
Recall (4.10). Denoting by
![]() ${\mathcal V}_{\delta ,n}$
the locus of n-pointed curves
${\mathcal V}_{\delta ,n}$
the locus of n-pointed curves
![]() $(C,x_1,\ldots , x_n)$
, with
$(C,x_1,\ldots , x_n)$
, with
![]() $[C] \in {\mathcal V}_{\delta }$
, where the marked points are disjoint from the nodes of the curves, we have
$[C] \in {\mathcal V}_{\delta }$
, where the marked points are disjoint from the nodes of the curves, we have
![]() $\dim {\mathcal V}_{\delta ,n}=g+n+1$
and a relative scheme
$\dim {\mathcal V}_{\delta ,n}=g+n+1$
and a relative scheme
and moduli map
We define
![]() ${\mathcal V}^k_{\delta ,\mathbf {e}}:=\sigma _{\delta ,n}^{-1}(\overline {{\mathcal M}_{g,k,\mathbf {e}}})$
.
${\mathcal V}^k_{\delta ,\mathbf {e}}:=\sigma _{\delta ,n}^{-1}(\overline {{\mathcal M}_{g,k,\mathbf {e}}})$
.
To prove the first assertion in Theorem 2.6, we would like to prove that
![]() ${\mathcal V}^k_{\delta ,\mathbf {e}} \cap \pi _{\delta ,n}^{-1}(t)$
is nonempty and has a component of the expected codimension for general t. Since
${\mathcal V}^k_{\delta ,\mathbf {e}} \cap \pi _{\delta ,n}^{-1}(t)$
is nonempty and has a component of the expected codimension for general t. Since
![]() ${\mathcal M}_{g,k,\mathbf {e}}$
has a component of the expected codimension by Theorem 2.1, it suffices to prove that
${\mathcal M}_{g,k,\mathbf {e}}$
has a component of the expected codimension by Theorem 2.1, it suffices to prove that
![]() ${\mathcal V}^k_{\delta ,\mathbf {e}} \cap \pi _{\delta ,n}^{-1}(0)$
is nonempty and has a component of the expected codimension. We will find such a component in Proposition 5.2 below.
${\mathcal V}^k_{\delta ,\mathbf {e}} \cap \pi _{\delta ,n}^{-1}(0)$
is nonempty and has a component of the expected codimension. We will find such a component in Proposition 5.2 below.
Definition 5.1. We define
![]() $V_n(\alpha _1,\ldots ,\alpha _p)$
to be the variety parametrizing
$V_n(\alpha _1,\ldots ,\alpha _p)$
to be the variety parametrizing
![]() $(C,x_1,\ldots ,x_n)$
such that
$(C,x_1,\ldots ,x_n)$
such that
![]() $C \in V( \alpha _1,\ldots ,\alpha _p)$
and
$C \in V( \alpha _1,\ldots ,\alpha _p)$
and
![]() $x_1,\ldots , x_n$
are distinct points on the sectional component
$x_1,\ldots , x_n$
are distinct points on the sectional component
![]() $\Gamma $
of C different from the nodes of C.
$\Gamma $
of C different from the nodes of C.
We denote by
![]() $G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
the variety parametrizing
$G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
the variety parametrizing
![]() $\mathfrak {g} \in G^1_k(C')$
(i.e.,
$\mathfrak {g} \in G^1_k(C')$
(i.e.,
![]() $\mathfrak {g}$
is a descending
$\mathfrak {g}$
is a descending
![]() $g^1_k$
on
$g^1_k$
on
![]() $\Gamma $
) with ramification of order
$\Gamma $
) with ramification of order
![]() $e_i \geq 2$
at each
$e_i \geq 2$
at each
![]() $x_i$
.
$x_i$
.
We define
![]() ${\mathcal G}^k_{n,\mathbf {e}}( \alpha _1,\ldots ,\alpha _p)$
to be the variety parametrizing pairs
${\mathcal G}^k_{n,\mathbf {e}}( \alpha _1,\ldots ,\alpha _p)$
to be the variety parametrizing pairs
![]() $\Big (\left (C,x_1,\ldots ,x_n\right ),\mathfrak {g}\Big )$
such that
$\Big (\left (C,x_1,\ldots ,x_n\right ),\mathfrak {g}\Big )$
such that
![]() $(C,x_1,\ldots ,x_n) \in V_{n,\mathbf {e}}( \alpha _1,\ldots ,\alpha _p)$
and
$(C,x_1,\ldots ,x_n) \in V_{n,\mathbf {e}}( \alpha _1,\ldots ,\alpha _p)$
and
![]() $\mathfrak {g} \in G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
.
$\mathfrak {g} \in G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
.
We define
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
to be the image of the forgetful map
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
to be the image of the forgetful map
which has fibres
![]() $G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
.
$G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
.
Proposition 5.2. Assume that (4.3) and (4.8) hold, as well as
![]() $\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
. Then
$\widetilde {\rho }(g,1,k;\mathbf {e}) \geq -g$
. Then
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
is equidimensional of codimension
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
is equidimensional of codimension
![]() $\max \{0,-\widetilde {\rho }\}$
.
$\max \{0,-\widetilde {\rho }\}$
.
More precisely,
-
(i) if
 $\widetilde {\rho }\geq 0$
, then
$\widetilde {\rho }\geq 0$
, then
 $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)=V_{n}(\alpha _1,\ldots ,\alpha _p)$
and for the general element
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)=V_{n}(\alpha _1,\ldots ,\alpha _p)$
and for the general element
 $(C,x_1,\ldots ,x_n) \in V_{n}(\alpha _1,\ldots ,\alpha _p)$
the variety
$(C,x_1,\ldots ,x_n) \in V_{n}(\alpha _1,\ldots ,\alpha _p)$
the variety
 $G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
has dimension
$G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
has dimension
 $\widetilde {\rho }$
and the general member in any component satisfies
$\widetilde {\rho }$
and the general member in any component satisfies
 $(\star )$
(cf. Notation 2.5);
$(\star )$
(cf. Notation 2.5); -
(ii) if
 $\widetilde {\rho }< 0$
, then
$\widetilde {\rho }< 0$
, then
 $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
is a proper subvariety of
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
is a proper subvariety of
 $V_{n}(\alpha _1,\ldots ,\alpha _p)$
of dimension
$V_{n}(\alpha _1,\ldots ,\alpha _p)$
of dimension
 $g+n+\widetilde {\rho }$
, and for general
$g+n+\widetilde {\rho }$
, and for general
 $(C,x_1,\ldots ,x_n)$
in any component of
$(C,x_1,\ldots ,x_n)$
in any component of
 $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
the variety
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
the variety
 $G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
is
$G^1_k(C',(x_1,e_1),\ldots ,(x_n,e_n))$
is
 $0$
-dimensional and any member satisfies
$0$
-dimensional and any member satisfies
 $(\star )$
; moreover,
$(\star )$
; moreover,-
(ii-a) if
 $n+\widetilde {\rho }\geq 0$
, then
$n+\widetilde {\rho }\geq 0$
, then
 $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
dominates
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
dominates
 $V(\alpha _1,\ldots ,\alpha _p)$
via the forgetful map, and
$V(\alpha _1,\ldots ,\alpha _p)$
via the forgetful map, and -
(ii-b) if
 $n+\widetilde {\rho }< 0$
, then the forgetful map is generically finite.
$n+\widetilde {\rho }< 0$
, then the forgetful map is generically finite.
-
Proof. We follow the lines of the proofs of Theorems 2.1 and 2.3. In particular, we let
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
and
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
and
![]() ${\mathcal F}_{k,\mathbf {e}}$
be the subfamilies of
${\mathcal F}_{k,\mathbf {e}}$
be the subfamilies of
![]() ${\mathcal F}_k$
as defined therein. In those proofs, we considered the subfamilies of curves passing through sets of general points
${\mathcal F}_k$
as defined therein. In those proofs, we considered the subfamilies of curves passing through sets of general points
![]() $\xi _i$
in
$\xi _i$
in
![]() $\operatorname {Sym}^2({\mathbb P}^1)$
. Now we will need those points to lie in
$\operatorname {Sym}^2({\mathbb P}^1)$
. Now we will need those points to lie in
![]() $\mathfrak {c}_1 \cup \cdots \cup \mathfrak {c}_p$
.
$\mathfrak {c}_1 \cup \cdots \cup \mathfrak {c}_p$
.
We recall that the assumption
![]() $\widetilde {\rho } \geq -g$
along with Lemma 3.3 yields that the locus
$\widetilde {\rho } \geq -g$
along with Lemma 3.3 yields that the locus
![]() $G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n))$
is nonempty and equidimensional of dimension
$G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n))$
is nonempty and equidimensional of dimension
![]() $\widetilde {\rho }+g$
for general
$\widetilde {\rho }+g$
for general
![]() $P_1,\ldots ,P_n \in {\mathbb P}^1$
. We also need to remark that the general member in any component of the variety
$P_1,\ldots ,P_n \in {\mathbb P}^1$
. We also need to remark that the general member in any component of the variety
![]() $G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n))$
satisfies
$G^1_k({\mathbb P}^1,(P_1,e_1),\ldots ,(P_n,e_n))$
satisfies
![]() $(\star )$
(cf. Notation 2.5 and Remark 2.2). In particular, the general member in any component of
$(\star )$
(cf. Notation 2.5 and Remark 2.2). In particular, the general member in any component of
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
and
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
and
![]() ${\mathcal F}_{k,\mathbf {e}}$
corresponds to a
${\mathcal F}_{k,\mathbf {e}}$
corresponds to a
![]() $g^1_k$
satisfying
$g^1_k$
satisfying
![]() $(\star )$
.
$(\star )$
.
Since none of the curves
![]() $\mathfrak {c}_{j}$
is contained in a
$\mathfrak {c}_{j}$
is contained in a
![]() $C_{\mathfrak g}$
by Lemmas 3.2 and 4.5, passing through any set of general points on
$C_{\mathfrak g}$
by Lemmas 3.2 and 4.5, passing through any set of general points on
![]() $\mathfrak {c}_1 \cup \cdots \cup \mathfrak {c}_p$
imposes independent conditions on the families
$\mathfrak {c}_1 \cup \cdots \cup \mathfrak {c}_p$
imposes independent conditions on the families
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
and
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
and
![]() ${\mathcal F}_{k,\mathbf {e}}$
and the general members in each component of the resulting families intersect each
${\mathcal F}_{k,\mathbf {e}}$
and the general members in each component of the resulting families intersect each
![]() $\mathfrak {c}_j$
transversally in
$\mathfrak {c}_j$
transversally in
![]() $2(k-1)$
distinct points.
$2(k-1)$
distinct points.
We have surjective maps that are the marked versions of the ones in (4.9):

where, again,
![]() $\sigma _{k,n,\mathbf {e}}$
is the forgetful map (forgetting the
$\sigma _{k,n,\mathbf {e}}$
is the forgetful map (forgetting the
![]() $g^1_k$
) and
$g^1_k$
) and
![]() $\gamma _{k,n,\mathbf {e}}$
is finite.
$\gamma _{k,n,\mathbf {e}}$
is finite.
The case
![]() $\widetilde {\rho } \geq 0$
. For a general set of
$\widetilde {\rho } \geq 0$
. For a general set of
![]() $\alpha _j$
points on each
$\alpha _j$
points on each
![]() $\mathfrak {c}_j$
, the family of curves in
$\mathfrak {c}_j$
, the family of curves in
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
passing through these points has dimension
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
passing through these points has dimension
and the general member in any component corresponds to a
![]() $g^1_k$
satisfying
$g^1_k$
satisfying
![]() $(\star )$
. This family produces, by the bijection (4.4), the same curve C in
$(\star )$
. This family produces, by the bijection (4.4), the same curve C in
![]() $V(\alpha _1,\ldots ,\alpha _p)$
, which lies in
$V(\alpha _1,\ldots ,\alpha _p)$
, which lies in
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, with the marked points of ramification being
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, with the marked points of ramification being
![]() $P_1,\ldots ,P_n \in \Gamma \subset C$
. This means that the fibre dimension of
$P_1,\ldots ,P_n \in \Gamma \subset C$
. This means that the fibre dimension of
![]() $\sigma _{k,n,\mathbf {e}}$
is
$\sigma _{k,n,\mathbf {e}}$
is
![]() $\widetilde {\rho }$
. The total family of pointed curves produced is therefore of dimension
$\widetilde {\rho }$
. The total family of pointed curves produced is therefore of dimension
whence it covers all of
![]() $V_n(\alpha _1,\ldots ,\alpha _p)$
. This proves (i).
$V_n(\alpha _1,\ldots ,\alpha _p)$
. This proves (i).
The case
![]() $\widetilde {\rho } < 0$
. For any p-tuple of nonnegative integers
$\widetilde {\rho } < 0$
. For any p-tuple of nonnegative integers
![]() $(\alpha ^{\prime }_1,\ldots ,\alpha ^{\prime }_p)$
such that
$(\alpha ^{\prime }_1,\ldots ,\alpha ^{\prime }_p)$
such that
![]() $\alpha ^{\prime }_i \leq \alpha _i$
for all i and
$\alpha ^{\prime }_i \leq \alpha _i$
for all i and
![]() $\sum \alpha ^{\prime }_i=\widetilde {\rho }+g$
, and any general choice of
$\sum \alpha ^{\prime }_i=\widetilde {\rho }+g$
, and any general choice of
![]() $\alpha ^{\prime }_j$
points on each
$\alpha ^{\prime }_j$
points on each
![]() $\mathfrak {c}_j$
, the family of curves in
$\mathfrak {c}_j$
, the family of curves in
![]() ${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
passing through these points is zero-dimensional by (3.6), and the curves correspond to
${\mathcal F}_{k,(P_1,\ldots ,P_n),\mathbf {e}}$
passing through these points is zero-dimensional by (3.6), and the curves correspond to
![]() $g^1_k$
s satisfying
$g^1_k$
s satisfying
![]() $(\star )$
. Hence, as above, this finite family produces, by the bijection (4.4), the same curve C in
$(\star )$
. Hence, as above, this finite family produces, by the bijection (4.4), the same curve C in
![]() $V(\alpha _1,\ldots ,\alpha _p)$
, which lies in
$V(\alpha _1,\ldots ,\alpha _p)$
, which lies in
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, having finitely many
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, having finitely many
![]() $g^1_k$
s with the marked points of ramification being
$g^1_k$
s with the marked points of ramification being
![]() $P_1,\ldots ,P_n \in \Gamma \subset C$
. This means that
$P_1,\ldots ,P_n \in \Gamma \subset C$
. This means that
![]() $\sigma _{k,n,\mathbf {e}}$
is generically finite. Varying
$\sigma _{k,n,\mathbf {e}}$
is generically finite. Varying
![]() $P_1,\ldots , P_n$
, the total family of pointed curves produced is now
$P_1,\ldots , P_n$
, the total family of pointed curves produced is now
and equals
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
. This proves the first assertion in (ii).
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
. This proves the first assertion in (ii).
The subcase
![]() $n+\widetilde {\rho } \geq 0$
. The same argument starting with
$n+\widetilde {\rho } \geq 0$
. The same argument starting with
![]() ${\mathcal F}_{k,\mathbf {e}}$
shows that for a general set of
${\mathcal F}_{k,\mathbf {e}}$
shows that for a general set of
![]() $\alpha _j$
points on each
$\alpha _j$
points on each
![]() $\mathfrak {c}_j$
, the family of curves in
$\mathfrak {c}_j$
, the family of curves in
![]() ${\mathcal F}_{k,\mathbf {e}}$
passing through these points has dimension
${\mathcal F}_{k,\mathbf {e}}$
passing through these points has dimension
Hence, as above, we get a family of curves in
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, having a
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, having a
![]() $(\widetilde {\rho }+n)$
-dimensional family of
$(\widetilde {\rho }+n)$
-dimensional family of
![]() $g^1_k$
s with the given ramification order at some (varying) points. The total family of (unpointed) curves produced is therefore
$g^1_k$
s with the given ramification order at some (varying) points. The total family of (unpointed) curves produced is therefore
and lies in
![]() $V(\alpha _1,\ldots ,\alpha _p)$
, so it has to cover the whole of it. This finishes the proof of case (ii-a).
$V(\alpha _1,\ldots ,\alpha _p)$
, so it has to cover the whole of it. This finishes the proof of case (ii-a).
The subcase
![]() $n+\widetilde {\rho } < 0$
. The same argument starting with
$n+\widetilde {\rho } < 0$
. The same argument starting with
![]() ${\mathcal F}_{k,\mathbf {e}}$
shows that we get a family of curves in
${\mathcal F}_{k,\mathbf {e}}$
shows that we get a family of curves in
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, having finitely many
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p)$
, having finitely many
![]() $g^1_k$
s with the given ramification order at some (varying) points. Thus, the forgetful map
$g^1_k$
s with the given ramification order at some (varying) points. Thus, the forgetful map
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p) \to V(\alpha _1,\ldots ,\alpha _p)$
is generically finite. Its image lies in
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p) \to V(\alpha _1,\ldots ,\alpha _p)$
is generically finite. Its image lies in
![]() $V^k(\alpha _1,\ldots ,\alpha _p)$
.
$V^k(\alpha _1,\ldots ,\alpha _p)$
.
Proof of Theorem 2.6
As mentioned above, we may assume
![]() $p \geq 3$
. First of all we note that since
$p \geq 3$
. First of all we note that since
![]() $V^k_{|H|,\delta }=\emptyset $
if (2.7) is not satisfied, we also have that
$V^k_{|H|,\delta }=\emptyset $
if (2.7) is not satisfied, we also have that
![]() $V^k_{|H|,\delta ,\mathbf {e}}=\emptyset $
if (2.7) is not satisfied.
$V^k_{|H|,\delta ,\mathbf {e}}=\emptyset $
if (2.7) is not satisfied.
Now assume that the condition (2.7) holds. Proposition 5.2 implies that
![]() $V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p) \subset V^k_{\delta ,\mathbf {e}} \cap \pi _{\delta ,n}^{-1}(0)$
has a component of the expected dimension, for some
$V^k_{n,\mathbf {e}}(\alpha _1,\ldots ,\alpha _p) \subset V^k_{\delta ,\mathbf {e}} \cap \pi _{\delta ,n}^{-1}(0)$
has a component of the expected dimension, for some
![]() $\alpha _i$
fulfilling (4.3) and (4.8). Such
$\alpha _i$
fulfilling (4.3) and (4.8). Such
![]() $\alpha _i$
s exist whenever (2.7) is satisfied, as shown in [Reference Ciliberto and Knutsen12]. The theorem now follows by semicontinuity and Proposition 5.2. To be more precise, one uses Lemma 4.6 to show non-neutrality of the nodes. Moreover, to prove the assertion about simple ramification, note that the limit ramification points of a general pencil are the ones of
$\alpha _i$
s exist whenever (2.7) is satisfied, as shown in [Reference Ciliberto and Knutsen12]. The theorem now follows by semicontinuity and Proposition 5.2. To be more precise, one uses Lemma 4.6 to show non-neutrality of the nodes. Moreover, to prove the assertion about simple ramification, note that the limit ramification points of a general pencil are the ones of
![]() $\mathfrak g$
on the sectional component
$\mathfrak g$
on the sectional component
![]() $\Gamma $
plus the ones tending to the nodes of
$\Gamma $
plus the ones tending to the nodes of
![]() $\overline C$
. The former ramification is simple by Proposition 5.2 and the latter is simple because, in the admissible cover setting, each node is replaced by a
$\overline C$
. The former ramification is simple by Proposition 5.2 and the latter is simple because, in the admissible cover setting, each node is replaced by a
![]() ${\mathbb P}^ 1$
joining the two branches and mapping
${\mathbb P}^ 1$
joining the two branches and mapping
![]() $2:1$
to a
$2:1$
to a
![]() ${\mathbb P}^ 1$
, hence the ramification is simple there.
${\mathbb P}^ 1$
, hence the ramification is simple there.
6 Proofs of Theorem 2.8 and of Corollaries 2.11 and 2.12
Let
![]() $(S,H)$
be a primitively polarized
$(S,H)$
be a primitively polarized
![]() $K3$
surface of genus p and
$K3$
surface of genus p and
![]() $0 \leq \delta <p$
. Let
$0 \leq \delta <p$
. Let
![]() $CH_0(S)$
be the Chow group of
$CH_0(S)$
be the Chow group of
![]() $0$
-cycles on S. We note that
$0$
-cycles on S. We note that
Indeed, for any
![]() $(p,q) \in Z_{k,\delta }^{\circ }(S,H)$
the image of
$(p,q) \in Z_{k,\delta }^{\circ }(S,H)$
the image of
![]() $k[p-q]=0\in Jac(C^{\nu })$
via the map
$k[p-q]=0\in Jac(C^{\nu })$
via the map
![]() $Jac(C^{\nu }) \to CH_0(S)$
must be 0. As
$Jac(C^{\nu }) \to CH_0(S)$
must be 0. As
![]() $CH_0(S)$
is torsion free, we conclude that
$CH_0(S)$
is torsion free, we conclude that
![]() $[p-q]=0\in CH_0(S)$
. By specialization, it also holds for all
$[p-q]=0\in CH_0(S)$
. By specialization, it also holds for all
![]() $(p,q) \in Z_{k,\delta }(S,H)$
, proving (6.1). Consequently,
$(p,q) \in Z_{k,\delta }(S,H)$
, proving (6.1). Consequently,
![]() $Z_{k,\delta }(S,H)$
is a subvariety of the fibre over
$Z_{k,\delta }(S,H)$
is a subvariety of the fibre over
![]() $0$
of the difference map
$0$
of the difference map
![]() $S \times S\to CH_0(S)$
. Now (6.2) follows from Mumford’s proof of the bound on the fibre dimension [Reference Mumford33], which says that the fibre is a countable union of varieties of dimension at most two.
$S \times S\to CH_0(S)$
. Now (6.2) follows from Mumford’s proof of the bound on the fibre dimension [Reference Mumford33], which says that the fibre is a countable union of varieties of dimension at most two.
Lemma 6.1. All components of
![]() $Z^{\prime }_{k,\delta }(S,H)=V^k_{|H|,\delta ,k,k}$
have dimension at least
$Z^{\prime }_{k,\delta }(S,H)=V^k_{|H|,\delta ,k,k}$
have dimension at least
![]() $2$
.
$2$
.
Proof. Set
![]() $\mathbf {e}=(k,k)$
. The forgetful morphism
$\mathbf {e}=(k,k)$
. The forgetful morphism
![]() $\kappa _{g,k, \mathbf {e}}$
from (2.4) is bijective since the fibre over any
$\kappa _{g,k, \mathbf {e}}$
from (2.4) is bijective since the fibre over any
![]() $(C,p,q)$
is the unique
$(C,p,q)$
is the unique
![]() $g^1_k$
generated by
$g^1_k$
generated by
![]() $kp$
and
$kp$
and
![]() $kq$
. It follows by (2.6) that
$kq$
. It follows by (2.6) that
![]() ${\mathcal M}_{g,k,\mathbf {e}}$
is equidimensional of codimension
${\mathcal M}_{g,k,\mathbf {e}}$
is equidimensional of codimension
![]() $-\widetilde {\rho }(g,1,k;k,k)=g$
in
$-\widetilde {\rho }(g,1,k;k,k)=g$
in
![]() ${\mathcal M}_{g,2}$
. Via the moduli map (2.8) we conclude that all components of
${\mathcal M}_{g,2}$
. Via the moduli map (2.8) we conclude that all components of
![]() $V^k_{|H|,\delta , \mathbf {e}}$
have codimension at most g in
$V^k_{|H|,\delta , \mathbf {e}}$
have codimension at most g in
![]() $V^k_{|H|,\delta ,2}$
.
$V^k_{|H|,\delta ,2}$
.
Lemma 6.2. The forgetful map
![]() $Z^{\prime \circ }_{k,\delta }(S,H) \to Z^{\circ }_{k,\delta }(S,H)$
is finite.
$Z^{\prime \circ }_{k,\delta }(S,H) \to Z^{\circ }_{k,\delta }(S,H)$
is finite.
Proof. Assume the map is not finite. Then there would exist
![]() $p,q\in S$
and a one dimensional family of curves
$p,q\in S$
and a one dimensional family of curves
![]() $\{(C_t,p,q)\}\in V^k_{|H|,\delta , \mathbf {e}}$
with total ramification at the same points
$\{(C_t,p,q)\}\in V^k_{|H|,\delta , \mathbf {e}}$
with total ramification at the same points
![]() $p,q$
. Via the incidence variety in
$p,q$
. Via the incidence variety in
![]() $Z\times \operatorname {Sym}^k(S)$
, this yields a one dimensional family of rational curves in
$Z\times \operatorname {Sym}^k(S)$
, this yields a one dimensional family of rational curves in
![]() $\operatorname {Sym}^k(S)$
all containing the points
$\operatorname {Sym}^k(S)$
all containing the points
![]() $kp$
and
$kp$
and
![]() $kq$
. By bend-and-break the closure of this family contains a reducible member. Pulling back via the incidence variety, this produces a reducible curve in the limit of the family
$kq$
. By bend-and-break the closure of this family contains a reducible member. Pulling back via the incidence variety, this produces a reducible curve in the limit of the family
![]() $\{C_t\}$
on S (see, e.g., the proofs of [Reference Flamini, Knutsen and Pacienza20, Lem. 2.1 and Prop. 4.3]). This is not possible for a general
$\{C_t\}$
on S (see, e.g., the proofs of [Reference Flamini, Knutsen and Pacienza20, Lem. 2.1 and Prop. 4.3]). This is not possible for a general
![]() $(S,H)\in {\mathcal K}_p$
.
$(S,H)\in {\mathcal K}_p$
.
Proof of Theorem 2.8
We note that the condition
![]() $\widetilde {\rho } \geq -g $
is automatically satisfied when
$\widetilde {\rho } \geq -g $
is automatically satisfied when
![]() $n=2$
and
$n=2$
and
![]() $e_1=e_2=k$
, whence Theorem 2.6 shows that
$e_1=e_2=k$
, whence Theorem 2.6 shows that
![]() $V^k_{|H|,\delta ,k,k}=Z^{\prime }_{k,\delta }(S,H)$
is nonempty if and only if (2.7) is satisfied. Lemmas 6.1 and 6.2 together with (6.2) show that both
$V^k_{|H|,\delta ,k,k}=Z^{\prime }_{k,\delta }(S,H)$
is nonempty if and only if (2.7) is satisfied. Lemmas 6.1 and 6.2 together with (6.2) show that both
![]() $Z^{\prime }_{k,\delta }(S,H)$
and
$Z^{\prime }_{k,\delta }(S,H)$
and
![]() $Z_{k,\delta }(S,H)$
have dimension
$Z_{k,\delta }(S,H)$
have dimension
![]() $2$
when nonempty.
$2$
when nonempty.
Proof of Corollary 2.11
Since
![]() $Z_{k,\delta }(S,H)$
is equidimensional of dimension
$Z_{k,\delta }(S,H)$
is equidimensional of dimension
![]() $2$
in
$2$
in
![]() $S\times S$
, on each of its components either one of the projections is dominant or both projections map to curves. Hence, the assumptions of [Reference Torelli39, Lem. 2.1] are satisfied and therefore
$S\times S$
, on each of its components either one of the projections is dominant or both projections map to curves. Hence, the assumptions of [Reference Torelli39, Lem. 2.1] are satisfied and therefore
![]() $Z_{k,\delta }(S,H)_*$
admits a lifting to
$Z_{k,\delta }(S,H)_*$
admits a lifting to
![]() $Z_1(S)$
. One can proceed analogously to check that the same holds for
$Z_1(S)$
. One can proceed analogously to check that the same holds for
![]() $Z_0(S)$
. The properties (i) and (ii) in Definition 2.10 are now direct consequences of (6.1).
$Z_0(S)$
. The properties (i) and (ii) in Definition 2.10 are now direct consequences of (6.1).
We finally prove the last assertion. If one of the projections to S is dominant, we conclude by (6.1). Otherwise, both projections map to curves, say to
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, respectively. For any
$C_2$
, respectively. For any
![]() $x \in C_1$
, the fibre
$x \in C_1$
, the fibre
![]() $p_1^{-1}(x)$
is a curve, mapping birationally to
$p_1^{-1}(x)$
is a curve, mapping birationally to
![]() $C_2$
via
$C_2$
via
![]() $p_2$
. By (6.1), any point
$p_2$
. By (6.1), any point
![]() $y \in C_2$
is rationally equivalent to x. As
$y \in C_2$
is rationally equivalent to x. As
![]() $C_2$
intersects any rational curve in
$C_2$
intersects any rational curve in
![]() $|H|$
, all points y have class
$|H|$
, all points y have class
![]() $c_S$
, whence also x has class
$c_S$
, whence also x has class
![]() $c_S$
.
$c_S$
.
Proof of Corollary 2.12
As every component of
![]() $Z_{k,0}(S,H)$
contains a dense set of points
$Z_{k,0}(S,H)$
contains a dense set of points
![]() $(p,q)$
defining the class
$(p,q)$
defining the class
![]() $(c_S,c_S)$
by Corollary 2.11, the same holds for the marked points of
$(c_S,c_S)$
by Corollary 2.11, the same holds for the marked points of
![]() $(C,p,q)$
in every component of
$(C,p,q)$
in every component of
![]() ${Z'}_{k,0}(S,H)$
. As
${Z'}_{k,0}(S,H)$
. As
![]() $2\leq g$
, by [Reference Pandharipande and Schmitt36, Thm. 1.5] this constructs a dense set of tautological points
$2\leq g$
, by [Reference Pandharipande and Schmitt36, Thm. 1.5] this constructs a dense set of tautological points
![]() $(C,p,q)$
in the image of
$(C,p,q)$
in the image of
![]() $m_{g,2}$
as wanted.
$m_{g,2}$
as wanted.
Corollary 2.12 constructs subvarieties of dimension
![]() $\leq 2$
of
$\leq 2$
of
![]() $\mathcal {M}_{g,2}$
containing a dense set of tautological points. One can find higher-dimensional cycles by considering the relative cycles obtained by moving the polarized K3 surface
$\mathcal {M}_{g,2}$
containing a dense set of tautological points. One can find higher-dimensional cycles by considering the relative cycles obtained by moving the polarized K3 surface
![]() $(S,H)$
in
$(S,H)$
in
![]() $\mathcal {K}_p$
and considering the universal pointed Severi variety
$\mathcal {K}_p$
and considering the universal pointed Severi variety
![]() ${\mathcal {V}_{p,\delta ,n}} \to {\mathcal K}_p$
. Let
${\mathcal {V}_{p,\delta ,n}} \to {\mathcal K}_p$
. Let
![]() $M_{p,\delta ,n}:\mathcal {V}_{p,\delta ,n}\to \mathcal {M}_{g,n}$
be the map fibrewise defined as
$M_{p,\delta ,n}:\mathcal {V}_{p,\delta ,n}\to \mathcal {M}_{g,n}$
be the map fibrewise defined as
![]() $m_{g,n}$
(cf. (2.8)). Let
$m_{g,n}$
(cf. (2.8)). Let
![]() $\mathcal {Z}^{\prime }_{k,\delta }\subset {\mathcal {V}_{p,\delta ,n}}$
be the cycle defined fibrewise as
$\mathcal {Z}^{\prime }_{k,\delta }\subset {\mathcal {V}_{p,\delta ,n}}$
be the cycle defined fibrewise as
![]() ${Z'}_{k,\delta }(S,H)$
. From Corollary 2.12 we conclude that the set of tautological points in
${Z'}_{k,\delta }(S,H)$
. From Corollary 2.12 we conclude that the set of tautological points in
![]() $M_{p,0,2}(\mathcal {Z}^{\prime }_{k,0})$
is dense. Moreover, we remark that this cycle has dimension exactly
$M_{p,0,2}(\mathcal {Z}^{\prime }_{k,0})$
is dense. Moreover, we remark that this cycle has dimension exactly
![]() $21$
for
$21$
for
![]() $p=g=11$
or
$p=g=11$
or
![]() $g \geq 13$
. To explain this latter fact, denote by
$g \geq 13$
. To explain this latter fact, denote by
![]() $\mathcal {V}_{p,\delta } \to {\mathcal K}_p$
the universal (unpointed) Severi variety, with fibre over
$\mathcal {V}_{p,\delta } \to {\mathcal K}_p$
the universal (unpointed) Severi variety, with fibre over
![]() $(S,H)$
being
$(S,H)$
being
![]() $V_{|H|,\delta }$
, and by
$V_{|H|,\delta }$
, and by
![]() ${M}_{p,\delta }:\mathcal {V}_{p,\delta }\to \mathcal {M}_{g}$
the map sending an element
${M}_{p,\delta }:\mathcal {V}_{p,\delta }\to \mathcal {M}_{g}$
the map sending an element
![]() $(S,H,C) \in \mathcal {V}_{p,\delta }$
to the class of
$(S,H,C) \in \mathcal {V}_{p,\delta }$
to the class of
![]() $C^{\nu }$
. Then we have a commutative diagram
$C^{\nu }$
. Then we have a commutative diagram

with the vertical maps being the finite maps forgetting the points. When
![]() $\delta =0$
, the kernel of the differential of
$\delta =0$
, the kernel of the differential of
![]() $M_{p,0}$
at a point
$M_{p,0}$
at a point
![]() $(S,H,C)$
is
$(S,H,C)$
is
![]() $H^1({\mathcal T}_S(-C))=H^1({\mathcal T}_S(-H))$
(cf. [Reference Beauville2]), which is independent of the curve
$H^1({\mathcal T}_S(-C))=H^1({\mathcal T}_S(-H))$
(cf. [Reference Beauville2]), which is independent of the curve
![]() $C \in V_{|H|,0}$
for fixed
$C \in V_{|H|,0}$
for fixed
![]() $(S,H) \in {\mathcal K}_p$
. As
$(S,H) \in {\mathcal K}_p$
. As
![]() ${M}_{p,0}$
is known to be generically finite for
${M}_{p,0}$
is known to be generically finite for
![]() $p=11$
and
$p=11$
and
![]() $p \geq 13$
, it follows that
$p \geq 13$
, it follows that
![]() $H^1({\mathcal T}_S(-H))=0$
for general
$H^1({\mathcal T}_S(-H))=0$
for general
![]() $(S,H)$
. Thus, the differential of
$(S,H)$
. Thus, the differential of
![]() $M_{p,\delta }$
is injective at any point
$M_{p,\delta }$
is injective at any point
![]() $(S,C) \in V_{|H|,0}$
for general
$(S,C) \in V_{|H|,0}$
for general
![]() $(S,H)$
, whence
$(S,H)$
, whence
![]() $M_{p,\delta }$
is finite at these points. In particular, the map
$M_{p,\delta }$
is finite at these points. In particular, the map
![]() $M_{p,0,2}$
restricted to
$M_{p,0,2}$
restricted to
![]() $\mathcal {Z}^{\prime }_{k,0}$
is generically finite.
$\mathcal {Z}^{\prime }_{k,0}$
is generically finite.
Acknowledgements
This collaboration started during the conference Algebraic Geometry in L’Aquila in July 2023. We warmly thank the organizers for the wonderful conference. We also thank the referee for the careful reading of the paper and useful suggestions.
Competing interests
The authors have no competing interests to declare.
Financial support
The conference Algebraic Geometry in L’Aquila was funded by PRIN 2017 - 2017SSNZAW: ‘Moduli Theory and Birational Classification’. A.L. Knutsen was partially supported by the Trond Mohn Foundation project ‘Pure Mathematics in Norway’. S. Torelli was partially supported by PRIN 2022 ‘Moduli spaces and Birational Geometry’ and by INdAM-GNSAGA.