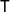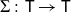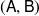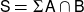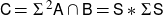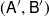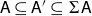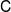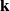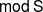Introduction
Happel–Reiten–Smalø (HRS) tilting was introduced in [
Reference Happel, Reiten and Smalø13
] as a method to construct new t-structures from torsion pairs in the heart of a given t-structure. Suppose
![]() $\textsf{T}$
is a triangulated category with shift functor
$\textsf{T}$
is a triangulated category with shift functor
![]() $\Sigma \colon \textsf{T} \to \textsf{T}$
, and
$\Sigma \colon \textsf{T} \to \textsf{T}$
, and
![]() $(\textsf{U},\textsf{V})$
is a t-structure in
$(\textsf{U},\textsf{V})$
is a t-structure in
![]() $\textsf{T}$
with the heart
$\textsf{T}$
with the heart
![]() $\textsf{H} = \textsf{U} \cap \Sigma \textsf{V}$
. Given a torsion pair
$\textsf{H} = \textsf{U} \cap \Sigma \textsf{V}$
. Given a torsion pair
![]() $(\mathcal{T},\mathcal{F})$
in
$(\mathcal{T},\mathcal{F})$
in
![]() $\textsf{H}$
, the HRS tilt of
$\textsf{H}$
, the HRS tilt of
![]() $(\textsf{U},\textsf{V})$
at
$(\textsf{U},\textsf{V})$
at
![]() $(\mathcal{T},\mathcal{F})$
is the t-structure
$(\mathcal{T},\mathcal{F})$
is the t-structure
In addition to providing a method for constructing new t-structures from old, HRS tilting gives all t-structures that are ‘sufficiently close’ to the initial one; see [ Reference Beligiannis and Reiten7 , Reference Polishchuk28 , Reference Woolf32 ]. Explicitly, there is a bijection:
Such t-structures
![]() $ (\textsf{U}^{\prime},\textsf{V}^{\prime})$
are often called intermediate with respect to
$ (\textsf{U}^{\prime},\textsf{V}^{\prime})$
are often called intermediate with respect to
![]() $ (\textsf{U},\textsf{V})$
.
$ (\textsf{U},\textsf{V})$
.
HRS tilting has many applications in representation theory and algebraic geometry. For example, it provides a method for constructing derived equivalences between abelian categories in cases where explicit tilting objects are not available. In this context, HRS tilting was used to study derived equivalences for smooth compact analytic surfaces with no curves [ Reference Bondal and Van den Bergh8 ] or for K3 surfaces [ Reference Bridgeland10 , Reference Huybrechts15 ]. Recently, HRS tilting has been extensively used in the study of Bridgeland stability conditions [ Reference Bridgeland10 , Reference Pauksztello, Saorín and Zvonareva27 , Reference Qiu and Woolf29 , Reference Woolf32 ].
A co-t-structure in
![]() $\textsf{T}$
consists of a pair of full subcategories
$\textsf{T}$
consists of a pair of full subcategories
![]() $(\textsf{A},\textsf{B})$
of
$(\textsf{A},\textsf{B})$
of
![]() $\textsf{T}$
, which are closed under direct summands, such that
$\textsf{T}$
, which are closed under direct summands, such that
![]() $\Sigma^{-1} \textsf{A} \subseteq \textsf{A}$
,
$\Sigma^{-1} \textsf{A} \subseteq \textsf{A}$
,
![]() $\textsf{T}(\textsf{A},\textsf{B}) = 0$
, and
$\textsf{T}(\textsf{A},\textsf{B}) = 0$
, and
![]() $\textsf{T} = \textsf{A} * \textsf{B}$
[
Reference Bondarko9
,
Reference Pauksztello26
]; note that in [
Reference Bondarko9
] co-t-structures are called weight structures. The subcategory
$\textsf{T} = \textsf{A} * \textsf{B}$
[
Reference Bondarko9
,
Reference Pauksztello26
]; note that in [
Reference Bondarko9
] co-t-structures are called weight structures. The subcategory
![]() $\textsf{S} = \Sigma \textsf{A} \cap \textsf{B}$
is called the coheart; it is a presilting subcategory of
$\textsf{S} = \Sigma \textsf{A} \cap \textsf{B}$
is called the coheart; it is a presilting subcategory of
![]() $\textsf{T}$
, see Section 1. Since their introduction, co-t-structures have acquired an important role in representation theory in connection with silting theory and
$\textsf{T}$
, see Section 1. Since their introduction, co-t-structures have acquired an important role in representation theory in connection with silting theory and
![]() $\tau$
-tilting theory [
Reference Adachi, Iyama and Reiten1
,
Reference Aihara and Iyama2
,
Reference Iyama16
,
Reference Keller and Vossieck20
,
Reference Koenig and Yang21
,
Reference Mendoza Hernández, Sáenz Valadez, Santiago Vargas and Souto Salorio23
]; for surveys of recent results see [
Reference Angeleri–Hügel4
,
Reference Jørgensen19
]. At first sight, the definitions of t-structure and co-t-structure appear very similar and there are, indeed, a number of parallels between the two theories. However, t-structures and co-t-structures are not dual to each other in a mathematical sense and there are notable differences between them, with the most basic being the failure of abelianness of the coheart.
$\tau$
-tilting theory [
Reference Adachi, Iyama and Reiten1
,
Reference Aihara and Iyama2
,
Reference Iyama16
,
Reference Keller and Vossieck20
,
Reference Koenig and Yang21
,
Reference Mendoza Hernández, Sáenz Valadez, Santiago Vargas and Souto Salorio23
]; for surveys of recent results see [
Reference Angeleri–Hügel4
,
Reference Jørgensen19
]. At first sight, the definitions of t-structure and co-t-structure appear very similar and there are, indeed, a number of parallels between the two theories. However, t-structures and co-t-structures are not dual to each other in a mathematical sense and there are notable differences between them, with the most basic being the failure of abelianness of the coheart.
The main result of this paper is an analogue of bijection (0·1) for co-t-structures. A priori it is not clear what are the co-t-structure counterparts of the HRS tilting procedure and the torsion pair in the heart. The recent introduction of extriangulated categories in [
Reference Nakaoka and Palu24
] provides the right context. If
![]() $(\textsf{A},\textsf{B})$
is a co-t-structure in
$(\textsf{A},\textsf{B})$
is a co-t-structure in
![]() $\textsf{T}$
with coheart
$\textsf{T}$
with coheart
![]() $\textsf{S}$
, then
$\textsf{S}$
, then
![]() $\textsf{C} = \Sigma^2\textsf{A} \cap \textsf{B} =\textsf{S} * \Sigma \textsf{S}$
, which we call the extended coheart, is an extriangulated category, in which there is a notion of a complete cotorsion pair [
Reference Hovey14
,
Reference Nakaoka and Palu24
,
Reference Salce30
]. A particular example of the extended coheart appears in the context of Amiot cluster categories in the guise of the fundamental domain of the cluster category [
Reference Amiot3
].
$\textsf{C} = \Sigma^2\textsf{A} \cap \textsf{B} =\textsf{S} * \Sigma \textsf{S}$
, which we call the extended coheart, is an extriangulated category, in which there is a notion of a complete cotorsion pair [
Reference Hovey14
,
Reference Nakaoka and Palu24
,
Reference Salce30
]. A particular example of the extended coheart appears in the context of Amiot cluster categories in the guise of the fundamental domain of the cluster category [
Reference Amiot3
].
Theorem A (Theorem 2·2). Suppose
![]() $\textsf{T}$
is a triangulated category,
$\textsf{T}$
is a triangulated category,
![]() $(\textsf{A},\textsf{B})$
is a co-t-structure in
$(\textsf{A},\textsf{B})$
is a co-t-structure in
![]() $\textsf{T}$
, and
$\textsf{T}$
, and
![]() $\textsf{C}$
is its extended coheart. There is a bijection
$\textsf{C}$
is its extended coheart. There is a bijection
Let A be a finite-dimensional
![]() $\textbf{k}$
-algebra. From [
Reference Koenig and Yang21
], there are bijections between the following objects:
$\textbf{k}$
-algebra. From [
Reference Koenig and Yang21
], there are bijections between the following objects:
-
(i) silting subcategories,
 $\textsf{S}$
, in
$\textsf{S}$
, in
 $\textsf{K}^b(\textsf{proj}(A))$
;
$\textsf{K}^b(\textsf{proj}(A))$
; -
(ii) bounded co-t-structures,
 $(\textsf{A}_\textsf{S},\textsf{B}_\textsf{S})$
, in
$(\textsf{A}_\textsf{S},\textsf{B}_\textsf{S})$
, in
 $\textsf{K}^b(\textsf{proj}(A))$
;
$\textsf{K}^b(\textsf{proj}(A))$
; -
(iii) algebraic t-structures, that is, bounded t-structures,
 $(\textsf{U}_\textsf{S},\textsf{V}_\textsf{S})$
, in
$(\textsf{U}_\textsf{S},\textsf{V}_\textsf{S})$
, in
 $\textsf{D}^b(A)$
with length heart.
$\textsf{D}^b(A)$
with length heart.
Fixing a silting subcategory
![]() $\textsf{S} = \textsf{add}(s)$
for a silting object s, by [
Reference Iyama16
] these bijections restrict to bijections between:
$\textsf{S} = \textsf{add}(s)$
for a silting object s, by [
Reference Iyama16
] these bijections restrict to bijections between:
-
(i) algebraic t-structures intermediate with respect to
 $(\textsf{U}_\textsf{S},\textsf{V}_\textsf{S})$
;
$(\textsf{U}_\textsf{S},\textsf{V}_\textsf{S})$
; -
(ii) bounded co-t-structures intermediate with respect to
 $(\textsf{A}_\textsf{S},\textsf{B}_\textsf{S})$
;
$(\textsf{A}_\textsf{S},\textsf{B}_\textsf{S})$
; -
(iii) silting subcategories
 $\textsf{S}^{\prime}$
with
$\textsf{S}^{\prime}$
with
 $\textsf{S}^{\prime} \subseteq \textsf{S} * \Sigma \textsf{S}$
.
$\textsf{S}^{\prime} \subseteq \textsf{S} * \Sigma \textsf{S}$
.
Finally, HRS tilting and support
![]() $\tau$
-tilting theory [
Reference Adachi, Iyama and Reiten1
,
Reference Iyama16
] adds a bijection with:
$\tau$
-tilting theory [
Reference Adachi, Iyama and Reiten1
,
Reference Iyama16
] adds a bijection with:
-
(iv) functorially finite torsion pairs in
 $\textsf{mod}\, \text{End}(s) \simeq \textsf{mod}\, \textsf{S}$
$\textsf{mod}\, \text{End}(s) \simeq \textsf{mod}\, \textsf{S}$
into the mix. Theorem A completes the picture with the co-t-structure version of torsion pairs: cotorsion pairs in
![]() $\textsf{S}*\Sigma \textsf{S}$
. Moreover, working with co-t-structures and cotorsion pairs seems to provide a more convenient context for representation theory: one does not have to care about the additional condition on the t-structure that it has a length heart, which may be difficult to check in practice, cf. [
Reference Coelho Simões, Pauksztello and Ploog11
].
$\textsf{S}*\Sigma \textsf{S}$
. Moreover, working with co-t-structures and cotorsion pairs seems to provide a more convenient context for representation theory: one does not have to care about the additional condition on the t-structure that it has a length heart, which may be difficult to check in practice, cf. [
Reference Coelho Simões, Pauksztello and Ploog11
].
Our second result provides a direct and explicit connection between cotorsion pairs in
![]() $\textsf{S} * \Sigma \textsf{S}$
and torsion pairs in
$\textsf{S} * \Sigma \textsf{S}$
and torsion pairs in
![]() $ \textsf{mod}\, \textsf{S}$
.
$ \textsf{mod}\, \textsf{S}$
.
Theorem B (see Theorem 3·7). Suppose
![]() $\textsf{T}$
is an essentially small, Hom-finite,
$\textsf{T}$
is an essentially small, Hom-finite,
![]() $\textbf{k}$
-linear, Krull–Schmidt triangulated category. If
$\textbf{k}$
-linear, Krull–Schmidt triangulated category. If
![]() $\textsf{S} = \textsf{add}(s)$
is a presilting subcategory of
$\textsf{S} = \textsf{add}(s)$
is a presilting subcategory of
![]() $\textsf{T}$
and
$\textsf{T}$
and
![]() $\textsf{C} = \textsf{S} * \Sigma \textsf{S}$
, then the restricted Yoneda functor,
$\textsf{C} = \textsf{S} * \Sigma \textsf{S}$
, then the restricted Yoneda functor,
![]() $F \colon \textsf{C} \to \textsf{mod}\, \textsf{S}$
, induces a bijection
$F \colon \textsf{C} \to \textsf{mod}\, \textsf{S}$
, induces a bijection
In particular, F sends cotorsionfree classes to torsion classes. Moreover, if in addition
![]() $\textsf{mod}\, \textsf{S}\simeq\textsf{mod}\, A$
for an artin algebra A, there is a bijection between complete cotorsion pairs in
$\textsf{mod}\, \textsf{S}\simeq\textsf{mod}\, A$
for an artin algebra A, there is a bijection between complete cotorsion pairs in
![]() $\textsf{C}$
and functorially finite torsion pairs in
$\textsf{C}$
and functorially finite torsion pairs in
![]() $\textsf{mod}\, \textsf{S}$
.
$\textsf{mod}\, \textsf{S}$
.
We note that the connections between torsion and cotorsion pairs have been studied before in a different setting [ Reference Beligiannis and Reiten7 ]. In particular, Beligiannis and Reiten consider cotorsion pairs in abelian categories and the corresponding cotorsion pairs in pretriangulated categories.
1. Background
Let
![]() $\textsf{A}$
be an additive category and
$\textsf{A}$
be an additive category and
![]() $\textsf{B} \subset \textsf{A}$
a subcategory. For objects
$\textsf{B} \subset \textsf{A}$
a subcategory. For objects
![]() $a_1$
,
$a_1$
,
![]() $a_2$
of
$a_2$
of
![]() $\textsf{A}$
we will write
$\textsf{A}$
we will write
![]() $\textsf{A}(a_1,a_2) = {\text{Hom}}_\textsf{A}(a_1,a_2)$
. We define the left and right orthogonal categories of
$\textsf{A}(a_1,a_2) = {\text{Hom}}_\textsf{A}(a_1,a_2)$
. We define the left and right orthogonal categories of
![]() $\textsf{B}$
as follows:
$\textsf{B}$
as follows:
We will often use the shorthand
![]() $\textsf{A}(a,\textsf{B}) = 0$
to mean
$\textsf{A}(a,\textsf{B}) = 0$
to mean
![]() $\textsf{A}(a,b) = 0$
for all
$\textsf{A}(a,b) = 0$
for all
![]() $b \in \textsf{B}$
; similarly for the shorthand
$b \in \textsf{B}$
; similarly for the shorthand
![]() $\textsf{A}(\textsf{B},a) = 0$
.
$\textsf{A}(\textsf{B},a) = 0$
.
Throughout this paper
![]() $\textsf{T}$
will be a triangulated category with shift functor
$\textsf{T}$
will be a triangulated category with shift functor
![]() $\Sigma \colon \textsf{T} \to \textsf{T}$
. For two subcategories
$\Sigma \colon \textsf{T} \to \textsf{T}$
. For two subcategories
![]() $\textsf{A}$
,
$\textsf{A}$
,
![]() $\textsf{B}$
of
$\textsf{B}$
of
![]() $\textsf{T}$
, the full subcategory with objects
$\textsf{T}$
, the full subcategory with objects
![]() $\{t\mid $
there exists a triangle
$\{t\mid $
there exists a triangle
![]() $a \to t \to b \to \Sigma a$
with
$a \to t \to b \to \Sigma a$
with
![]() $a \in \textsf{A}$
and
$a \in \textsf{A}$
and
![]() $b \in \textsf{B}\}$
will be denoted by
$b \in \textsf{B}\}$
will be denoted by
![]() $\textsf{A} * \textsf{B}$
. A full additive subcategory
$\textsf{A} * \textsf{B}$
. A full additive subcategory
![]() $\textsf{C}$
of
$\textsf{C}$
of
![]() $\textsf{T}$
is extension-closed if
$\textsf{T}$
is extension-closed if
![]() $\textsf{C} * \textsf{C} = \textsf{C}$
.
$\textsf{C} * \textsf{C} = \textsf{C}$
.
1·1. Approximations
Let
![]() $\textsf{A}$
be a subcategory of
$\textsf{A}$
be a subcategory of
![]() $\textsf{T}$
and let t be an object of
$\textsf{T}$
and let t be an object of
![]() $\textsf{T}$
. A morphism
$\textsf{T}$
. A morphism
![]() $f \colon t \to a$
with
$f \colon t \to a$
with
![]() $a \in \textsf{A}$
is called:
$a \in \textsf{A}$
is called:
-
(i) a left
 $\textsf{A}$
-approximation of t if
$\textsf{A}$
-approximation of t if
 $\textsf{T}(f,\textsf{A}) \colon \textsf{T}(a,\textsf{A}) \to \textsf{T}(t,\textsf{A})$
is surjective;
$\textsf{T}(f,\textsf{A}) \colon \textsf{T}(a,\textsf{A}) \to \textsf{T}(t,\textsf{A})$
is surjective; -
(ii) left minimal if any
 $g \colon a \to a$
such that
$g \colon a \to a$
such that
 $gf = f$
is an automorphism;
$gf = f$
is an automorphism; -
(iii) a minimal left
 $\textsf{A}$
-approximation of t if it is both left minimal and a left
$\textsf{A}$
-approximation of t if it is both left minimal and a left
 $\textsf{A}$
-approximation of t.
$\textsf{A}$
-approximation of t.
Left
![]() $\textsf{A}$
-approximations are sometimes called
$\textsf{A}$
-approximations are sometimes called
![]() $\textsf{A}$
-pre-envelopes. If every object of
$\textsf{A}$
-pre-envelopes. If every object of
![]() $\textsf{T}$
admits a left
$\textsf{T}$
admits a left
![]() $\textsf{A}$
-approximation then
$\textsf{A}$
-approximation then
![]() $\textsf{A}$
is said to be covariantly finite in
$\textsf{A}$
is said to be covariantly finite in
![]() $\textsf{T}$
. There is a dual notion of a (minimal) right
$\textsf{T}$
. There is a dual notion of a (minimal) right
![]() $\textsf{A}$
-approximation (or an
$\textsf{A}$
-approximation (or an
![]() $\textsf{A}$
-precover); if every object of
$\textsf{A}$
-precover); if every object of
![]() $\textsf{T}$
admits a right
$\textsf{T}$
admits a right
![]() $\textsf{A}$
-approximation, then
$\textsf{A}$
-approximation, then
![]() $\textsf{A}$
is said to be contravariantly finite in
$\textsf{A}$
is said to be contravariantly finite in
![]() $\textsf{T}$
. The subcategory
$\textsf{T}$
. The subcategory
![]() $\textsf{A}$
is said to be functorially finite if it is both covariantly finite and contravariantly finite.
$\textsf{A}$
is said to be functorially finite if it is both covariantly finite and contravariantly finite.
Minimal approximations admit the following important property; see, for example, [ Reference Jørgensen18 ] for a triangulated version. We give the statement for left approximations; there is a dual statement for right approximations.
Lemma 1·1 (Wakamatsu lemma for triangulated categories). Let
![]() $\textsf{A}$
be an extension closed subcategory of
$\textsf{A}$
be an extension closed subcategory of
![]() $\textsf{T}$
and suppose
$\textsf{T}$
and suppose
![]() $f \colon t \to a$
is a minimal left
$f \colon t \to a$
is a minimal left
![]() $\textsf{A}$
-approximation of t. Then in the triangle
$\textsf{A}$
-approximation of t. Then in the triangle
we have
![]() $b \in {}{}^\perp\textsf{A}$
.
$b \in {}{}^\perp\textsf{A}$
.
1·2. Co-t-structures, silting subcategories and the extended coheart
We recall the following definitions from [ Reference Aihara and Iyama2 , Reference Bondarko9 , Reference Keller and Vossieck20 , Reference Pauksztello26 ], respectively.
Definition 1·2. A subcategory
![]() $\textsf{S}$
of a triangulated category
$\textsf{S}$
of a triangulated category
![]() $\textsf{T}$
is presilting if
$\textsf{T}$
is presilting if
![]() $\textsf{T}(\textsf{S},$
$\textsf{T}(\textsf{S},$
![]() $\Sigma^i \textsf{S}) = 0$
for all
$\Sigma^i \textsf{S}) = 0$
for all
![]() $i \gt 0$
; it is called silting if, in addition
$i \gt 0$
; it is called silting if, in addition
![]() $\textsf{thick}\ \textsf{S} = \textsf{T}$
, where
$\textsf{thick}\ \textsf{S} = \textsf{T}$
, where
![]() $\textsf{thick}\ \textsf{S}$
is the smallest triangulated subcategory of
$\textsf{thick}\ \textsf{S}$
is the smallest triangulated subcategory of
![]() $\textsf{T}$
containing
$\textsf{T}$
containing
![]() $\textsf{S}$
that is closed under direct summands. An object s of
$\textsf{S}$
that is closed under direct summands. An object s of
![]() $\textsf{T}$
is a (pre)silting object if
$\textsf{T}$
is a (pre)silting object if
![]() $\textsf{add}(s)$
is a (pre)silting subcategory, where
$\textsf{add}(s)$
is a (pre)silting subcategory, where
![]() $\textsf{add}(s)$
consists of the direct summands of finite direct sums of copies of s.
$\textsf{add}(s)$
consists of the direct summands of finite direct sums of copies of s.
Definition 1·3. A co-t-structure in
![]() $\textsf{T}$
consists of a pair of full subcategories
$\textsf{T}$
consists of a pair of full subcategories
![]() $(\textsf{A},\textsf{B})$
of
$(\textsf{A},\textsf{B})$
of
![]() $\textsf{T}$
, which are closed under direct summands, such that
$\textsf{T}$
, which are closed under direct summands, such that
![]() $\Sigma^{-1} \textsf{A} \subseteq \textsf{A}$
,
$\Sigma^{-1} \textsf{A} \subseteq \textsf{A}$
,
![]() $\textsf{T}(\textsf{A},\textsf{B}) = 0$
, and
$\textsf{T}(\textsf{A},\textsf{B}) = 0$
, and
![]() $\textsf{T} = \textsf{A} * \textsf{B}$
. A co-t-structure
$\textsf{T} = \textsf{A} * \textsf{B}$
. A co-t-structure
![]() $(\textsf{A},\textsf{B})$
in
$(\textsf{A},\textsf{B})$
in
![]() $\textsf{T}$
is bounded if
$\textsf{T}$
is bounded if
![]() $\bigcup_{i\in \mathbb{Z}}\Sigma^i\textsf{A}=\textsf{T}=\bigcup_{i\in \mathbb{Z}}\Sigma^i\textsf{B}$
.
$\bigcup_{i\in \mathbb{Z}}\Sigma^i\textsf{A}=\textsf{T}=\bigcup_{i\in \mathbb{Z}}\Sigma^i\textsf{B}$
.
The coheart
![]() $\textsf{S} = \Sigma \textsf{A} \cap \textsf{B}$
of a co-t-structure
$\textsf{S} = \Sigma \textsf{A} \cap \textsf{B}$
of a co-t-structure
![]() $(\textsf{A},\textsf{B})$
is always a presilting subcategory. It is silting precisely when the co-t-structure is bounded [
Reference Mendoza Hernández, Sáenz Valadez, Santiago Vargas and Souto Salorio23
, corollary 5·9].
$(\textsf{A},\textsf{B})$
is always a presilting subcategory. It is silting precisely when the co-t-structure is bounded [
Reference Mendoza Hernández, Sáenz Valadez, Santiago Vargas and Souto Salorio23
, corollary 5·9].
Definition 1·4. Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
. The subcategory
$\textsf{T}$
. The subcategory
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
will be called the extended coheart of the co-t-structure.
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
will be called the extended coheart of the co-t-structure.
The following lemma shows that the extended coheart of
![]() $(\textsf{A},\textsf{B})$
consists of precisely the objects of
$(\textsf{A},\textsf{B})$
consists of precisely the objects of
![]() $\textsf{T}$
which are ‘two-term’ with respect to the coheart
$\textsf{T}$
which are ‘two-term’ with respect to the coheart
![]() $\textsf{S}$
.
$\textsf{S}$
.
Lemma 1·5 ([
Reference Iyama16
, lemma 2·1]). Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
with coheart
$\textsf{T}$
with coheart
![]() $\textsf{S}$
. Then the extended coheart
$\textsf{S}$
. Then the extended coheart
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{S} * \Sigma \textsf{S}$
.
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{S} * \Sigma \textsf{S}$
.
1·3. Extriangulated categories and complete cotorsion pairs
We will use the notion of an extriangulated category from [ Reference Nakaoka and Palu24 ] without recalling the complete definition.
An extriangulated category consists of a triple
![]() $(\textsf{C}, \mathbb{E}, \mathfrak{s})$
, where
$(\textsf{C}, \mathbb{E}, \mathfrak{s})$
, where
![]() $\textsf{C}$
is an additive category,
$\textsf{C}$
is an additive category,
![]() $\mathbb{E}(-,{-}) \colon \textsf{C}^{op} \times \textsf{C} \to \textsf{Ab}$
is a biadditive functor and
$\mathbb{E}(-,{-}) \colon \textsf{C}^{op} \times \textsf{C} \to \textsf{Ab}$
is a biadditive functor and
![]() $\mathfrak{s}$
assigns to any element of
$\mathfrak{s}$
assigns to any element of
![]() $\mathbb{E}(c,a)$
an equivalence class of pairs of morphisms
$\mathbb{E}(c,a)$
an equivalence class of pairs of morphisms
![]() $[a\to b\to c]$
, called an
$[a\to b\to c]$
, called an
![]() $\mathbb{E}$
-triangle. In addition the triple
$\mathbb{E}$
-triangle. In addition the triple
![]() $(\textsf{C}, \mathbb{E}, \mathfrak{s})$
should satisfy a number of axioms reminiscent of the axioms of a triangulated category (without rotation of triangles).
$(\textsf{C}, \mathbb{E}, \mathfrak{s})$
should satisfy a number of axioms reminiscent of the axioms of a triangulated category (without rotation of triangles).
If
![]() $\textsf{C}$
is an additive category,
$\textsf{C}$
is an additive category,
![]() $\Sigma$
is an equivalence on
$\Sigma$
is an equivalence on
![]() $\textsf{C}$
and
$\textsf{C}$
and
![]() $\mathbb{E}\,:\!=\,\textsf{C}(-,\Sigma {-})$
, then by [
Reference Nakaoka and Palu24
, proposition 3·22] fixing a triangulated structure on
$\mathbb{E}\,:\!=\,\textsf{C}(-,\Sigma {-})$
, then by [
Reference Nakaoka and Palu24
, proposition 3·22] fixing a triangulated structure on
![]() $\textsf{C}$
with the shift functor
$\textsf{C}$
with the shift functor
![]() $\Sigma$
is equivalent to fixing an extriangulated structure on
$\Sigma$
is equivalent to fixing an extriangulated structure on
![]() $\textsf{C}$
with the additive bifunctor
$\textsf{C}$
with the additive bifunctor
![]() $\mathbb{E}$
, where
$\mathbb{E}$
, where
![]() $\mathfrak{s}$
assigns to an element
$\mathfrak{s}$
assigns to an element
![]() $\delta\in\textsf{C}(c,\Sigma a)$
the isomorphism class of distinguished triangles
$\delta\in\textsf{C}(c,\Sigma a)$
the isomorphism class of distinguished triangles
![]() $a\to b \to c \xrightarrow{\delta} \Sigma a$
.
$a\to b \to c \xrightarrow{\delta} \Sigma a$
.
All extriangulated categories
![]() $\textsf{C}$
used in this paper will be subcategories of some triangulated category
$\textsf{C}$
used in this paper will be subcategories of some triangulated category
![]() $\textsf{T}$
with the induced extriangulated structure, that is,
$\textsf{T}$
with the induced extriangulated structure, that is,
![]() $\mathbb{E}(-,{-})$
is the restriction of
$\mathbb{E}(-,{-})$
is the restriction of
![]() $\textsf{T}(-,\Sigma {-})$
and
$\textsf{T}(-,\Sigma {-})$
and
![]() $\mathbb{E}$
-triangles are distinguished triangles
$\mathbb{E}$
-triangles are distinguished triangles
![]() $a\to b \to c \xrightarrow{\delta} \Sigma a$
with a, b, c in the subcategory
$a\to b \to c \xrightarrow{\delta} \Sigma a$
with a, b, c in the subcategory
![]() $\textsf{C}$
. Analogously to triangulated and exact categories, a subcategory
$\textsf{C}$
. Analogously to triangulated and exact categories, a subcategory
![]() $\mathcal{X}$
of an extriangulated category
$\mathcal{X}$
of an extriangulated category
![]() $\textsf{C}$
is called extension-closed if for any
$\textsf{C}$
is called extension-closed if for any
![]() $\mathbb{E}$
-triangle
$\mathbb{E}$
-triangle
![]() $x^{\prime} \to x \to x^{\prime\prime}$
with
$x^{\prime} \to x \to x^{\prime\prime}$
with
![]() $x^{\prime},x^{\prime\prime}\in \mathcal{X}$
, the object x is also in
$x^{\prime},x^{\prime\prime}\in \mathcal{X}$
, the object x is also in
![]() $\mathcal{X}$
.
$\mathcal{X}$
.
Lemma 1·6.
Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
. Then the triangulated structure of
$\textsf{T}$
. Then the triangulated structure of
![]() $\textsf{T}$
induces an extriangulated structure on
$\textsf{T}$
induces an extriangulated structure on
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
.
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
.
Proof. Since both
![]() $\textsf{A}$
and
$\textsf{A}$
and
![]() $\textsf{B}$
are extension-closed subcategories of
$\textsf{B}$
are extension-closed subcategories of
![]() $\textsf{T}$
, we have that
$\textsf{T}$
, we have that
![]() $\textsf{C}$
is an extension-closed subcategory of
$\textsf{C}$
is an extension-closed subcategory of
![]() $\textsf{T}$
. The triangulated structure on
$\textsf{T}$
. The triangulated structure on
![]() $\textsf{T}$
also provides an extriangulated structure on
$\textsf{T}$
also provides an extriangulated structure on
![]() $\textsf{T}$
, see [
Reference Nakaoka and Palu24
, example 2·13]. Hence, by [
Reference Nakaoka and Palu24
, remark 2·18], the triangulated structure on
$\textsf{T}$
, see [
Reference Nakaoka and Palu24
, example 2·13]. Hence, by [
Reference Nakaoka and Palu24
, remark 2·18], the triangulated structure on
![]() $\textsf{T}$
restricted to
$\textsf{T}$
restricted to
![]() $\textsf{C}$
induces an extriangulated structure on
$\textsf{C}$
induces an extriangulated structure on
![]() $\textsf{C}$
.
$\textsf{C}$
.
We adopt the following definitions from the exact and abelian settings (see [ Reference Hovey14 , Reference Salce30 ]) to the extriangulated setting.
Definition 1·7. Let
![]() $(\textsf{C},\mathbb{E},\mathfrak{s})$
be an extriangulated category. A cotorsion pair in
$(\textsf{C},\mathbb{E},\mathfrak{s})$
be an extriangulated category. A cotorsion pair in
![]() $\textsf{C}$
consists of a pair of full additive subcategories
$\textsf{C}$
consists of a pair of full additive subcategories
![]() $(\mathcal{X},\mathcal{Y})$
closed under direct summands and such that for each
$(\mathcal{X},\mathcal{Y})$
closed under direct summands and such that for each
![]() $c \in \textsf{C}$
the following holds:
$c \in \textsf{C}$
the following holds:
-
(i)
 $c \in \mathcal{X}$
if and only if
$c \in \mathcal{X}$
if and only if
 $\mathbb{E}(c,\mathcal{Y}) = 0$
;
$\mathbb{E}(c,\mathcal{Y}) = 0$
; -
(ii)
 $c \in \mathcal{Y}$
if and only if
$c \in \mathcal{Y}$
if and only if
 $\mathbb{E}(\mathcal{X},c) = 0$
.
$\mathbb{E}(\mathcal{X},c) = 0$
.
If
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in an extriangulated category
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in an extriangulated category
![]() $\textsf{C}$
, we will refer to
$\textsf{C}$
, we will refer to
![]() $\mathcal{X}$
as the cotorsion class and to
$\mathcal{X}$
as the cotorsion class and to
![]() $\mathcal{Y}$
as the cotorsionfree class. Since
$\mathcal{Y}$
as the cotorsionfree class. Since
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
are each realised as orthogonal subcategories, they are closed under extensions. Indeed, by [
Reference Nakaoka and Palu24
, proposition 3·3] any
$\mathcal{Y}$
are each realised as orthogonal subcategories, they are closed under extensions. Indeed, by [
Reference Nakaoka and Palu24
, proposition 3·3] any
![]() $\mathbb{E}$
-triangle
$\mathbb{E}$
-triangle
![]() $a\to b\to c$
gives rise to an exact sequence
$a\to b\to c$
gives rise to an exact sequence
![]() $\textsf{C}(-,a) \to \textsf{C}(-,b) \to \textsf{C}(-,c) \to \mathbb{E}(-,a) \to \mathbb{E}(-,b) \to \mathbb{E}(-,c)$
and its dual.
$\textsf{C}(-,a) \to \textsf{C}(-,b) \to \textsf{C}(-,c) \to \mathbb{E}(-,a) \to \mathbb{E}(-,b) \to \mathbb{E}(-,c)$
and its dual.
Remark 1·8. Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
with coheart
$\textsf{T}$
with coheart
![]() $\textsf{S}$
and extended coheart
$\textsf{S}$
and extended coheart
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{S} * \Sigma \textsf{S}$
, considered with the extriangulated structure induced from
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{S} * \Sigma \textsf{S}$
, considered with the extriangulated structure induced from
![]() $\textsf{T}$
. Let
$\textsf{T}$
. Let
![]() $(\mathcal{X},\mathcal{Y})$
be an arbitrary cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
be an arbitrary cotorsion pair in
![]() $\textsf{C}$
. From the definition above one immediately sees that
$\textsf{C}$
. From the definition above one immediately sees that
![]() $\textsf{S}\subseteq \mathcal{X}$
and
$\textsf{S}\subseteq \mathcal{X}$
and
![]() $\Sigma \textsf{S} \subseteq \mathcal{Y}$
.
$\Sigma \textsf{S} \subseteq \mathcal{Y}$
.
Definition 1·9 ([
Reference Nakaoka and Palu24
, definition 4·1]) Let
![]() $(\textsf{C},\mathbb{E},\mathfrak{s})$
be an extriangulated category. A complete cotorsion pair in
$(\textsf{C},\mathbb{E},\mathfrak{s})$
be an extriangulated category. A complete cotorsion pair in
![]() $\textsf{C}$
consists of a pair of full additive subcategories
$\textsf{C}$
consists of a pair of full additive subcategories
![]() $(\mathcal{X},\mathcal{Y})$
closed under direct summands and such that the following hold:
$(\mathcal{X},\mathcal{Y})$
closed under direct summands and such that the following hold:
-
(i) for each
 $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
 $y \in \mathcal{Y}$
, we have
$y \in \mathcal{Y}$
, we have
 $\mathbb{E}(x,y) = 0$
;
$\mathbb{E}(x,y) = 0$
; -
(ii) for each
 $c \in \textsf{C}$
, there is an
$c \in \textsf{C}$
, there is an
 $\mathbb{E}$
-triangle
$\mathbb{E}$
-triangle
 $c \to y \to x$
with
$c \to y \to x$
with
 $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
 $y \in \mathcal{Y}$
;
$y \in \mathcal{Y}$
; -
(iii) for each
 $c \in \textsf{C}$
, there is an
$c \in \textsf{C}$
, there is an
 $\mathbb{E}$
-triangle
$\mathbb{E}$
-triangle
 $y \to x \to c$
with
$y \to x \to c$
with
 $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
 $y \in \mathcal{Y}$
.
$y \in \mathcal{Y}$
.
A pair of full subcategories
![]() $(\mathcal{X},\mathcal{Y})$
satisfying only condition (i) will be called an Ext-orthogonal pair.
$(\mathcal{X},\mathcal{Y})$
satisfying only condition (i) will be called an Ext-orthogonal pair.
For each object c of
![]() $\textsf{C}$
, the morphism
$\textsf{C}$
, the morphism
![]() $c \to y$
occurring in the
$c \to y$
occurring in the
![]() $\mathbb{E}$
-triangle above is always a left
$\mathbb{E}$
-triangle above is always a left
![]() $\mathcal{Y}$
-approximation of c. Similarly, the morphism
$\mathcal{Y}$
-approximation of c. Similarly, the morphism
![]() $x \to c$
in the
$x \to c$
in the
![]() $\mathbb{E}$
-triangle above is a right
$\mathbb{E}$
-triangle above is a right
![]() $\mathcal{X}$
-approximation of c.
$\mathcal{X}$
-approximation of c.
Remark 1·10. In this paper we revert to the classical distinction between complete cotorsion pairs and cotorsion pairs in [
Reference Hovey14
,
Reference Salce30
]. Therefore what is called a cotorsion pair in [
Reference Nakaoka and Palu24
] will be called a complete cotorsion pair here. By [
Reference Nakaoka and Palu24
, remark 4·4], any complete cotorsion pair is a cotorsion pair, since the 0 element of
![]() $\mathbb{E}(c,a)$
is represented, up to equivalence, by a split
$\mathbb{E}(c,a)$
is represented, up to equivalence, by a split
![]() $\mathbb{E}$
-triangle
$\mathbb{E}$
-triangle
![]() $a\to a\oplus c\to c$
.
$a\to a\oplus c\to c$
.
1·4. The restricted Yoneda functor
Assume now that
![]() $\textsf{T}$
is essentially small, idempotent complete, Hom-finite,
$\textsf{T}$
is essentially small, idempotent complete, Hom-finite,
![]() $\textbf{k}$
-linear and Krull-Schmidt, where
$\textbf{k}$
-linear and Krull-Schmidt, where
![]() $\textbf{k}$
is a commutative noetherian ring. In this situation, Hom-finiteness means that
$\textbf{k}$
is a commutative noetherian ring. In this situation, Hom-finiteness means that
![]() $\textsf{T}(a,b)$
is a finitely-generated
$\textsf{T}(a,b)$
is a finitely-generated
![]() $\textbf{k}$
-module for any
$\textbf{k}$
-module for any
![]() $a,b\in \textsf{T}$
. In particular, the endomorphism ring of an object
$a,b\in \textsf{T}$
. In particular, the endomorphism ring of an object
![]() $\textsf{T}(s,s)$
is a noetherian ring. Suppose
$\textsf{T}(s,s)$
is a noetherian ring. Suppose
![]() $\textsf{S}$
is a presilting subcategory of
$\textsf{S}$
is a presilting subcategory of
![]() $\textsf{T}$
and let
$\textsf{T}$
and let
![]() $\textsf{C} \,:\!=\, \textsf{S} * \Sigma \textsf{S}$
. We write
$\textsf{C} \,:\!=\, \textsf{S} * \Sigma \textsf{S}$
. We write
![]() $\textsf{Mod}\ \textsf{S}$
for the category of contravariant additive functors from
$\textsf{Mod}\ \textsf{S}$
for the category of contravariant additive functors from
![]() $\textsf{S}$
to the category
$\textsf{S}$
to the category
![]() $\textsf{Mod}\ \textbf{k}$
and
$\textsf{Mod}\ \textbf{k}$
and
![]() $\textsf{mod}\ \textsf{S}$
for the full subcategory of finitely presented functors; see [
Reference Auslander6
]. Consider the restricted Yoneda functor
$\textsf{mod}\ \textsf{S}$
for the full subcategory of finitely presented functors; see [
Reference Auslander6
]. Consider the restricted Yoneda functor
By [ Reference Iyama and Yoshino17 , proposition 6·2], [ Reference Iyama16 , remark 3·1] the restricted Yoneda functor induces an equivalence of categories,
where
![]() $(\textsf{S} * \Sigma \textsf{S})/\Sigma \textsf{S}$
denotes the subfactor category in which morphisms factoring through an object of
$(\textsf{S} * \Sigma \textsf{S})/\Sigma \textsf{S}$
denotes the subfactor category in which morphisms factoring through an object of
![]() $\Sigma \textsf{S}$
are sent to zero. We will usually use this equivalence in case
$\Sigma \textsf{S}$
are sent to zero. We will usually use this equivalence in case
![]() $\textsf{mod}\, \textsf{S}$
is an abelian category or, equivalently, when
$\textsf{mod}\, \textsf{S}$
is an abelian category or, equivalently, when
![]() $\textsf{S}$
has weak kernels [
Reference Freyd12
]. If
$\textsf{S}$
has weak kernels [
Reference Freyd12
]. If
![]() $\textsf{S} = \textsf{add}(s)$
for some object
$\textsf{S} = \textsf{add}(s)$
for some object
![]() $s\in \textsf{T}$
there is an equivalence
$s\in \textsf{T}$
there is an equivalence
![]() $\textsf{mod}\, \textsf{S} \simeq \textsf{mod}\, E$
, where
$\textsf{mod}\, \textsf{S} \simeq \textsf{mod}\, E$
, where
![]() $E = \textsf{T}(s,s)$
; see [
Reference Iyama16
, remark 4·1], and
$E = \textsf{T}(s,s)$
; see [
Reference Iyama16
, remark 4·1], and
![]() $\textsf{mod}\, \textsf{S}$
is automatically abelian.
$\textsf{mod}\, \textsf{S}$
is automatically abelian.
1·5. Torsion pairs
A torsion pair in an abelian category
![]() $\textsf{H}$
consists of a pair of full subcategories
$\textsf{H}$
consists of a pair of full subcategories
![]() $(\mathcal{T},\mathcal{F})$
of
$(\mathcal{T},\mathcal{F})$
of
![]() $\textsf{H}$
such that
$\textsf{H}$
such that
![]() $\mathcal{T}{}^\perp = \mathcal{F}$
,
$\mathcal{T}{}^\perp = \mathcal{F}$
,
![]() ${}{}^\perp \mathcal{F} = \mathcal{T}$
, and for each object h of
${}{}^\perp \mathcal{F} = \mathcal{T}$
, and for each object h of
![]() $\textsf{H}$
, there is a short exact sequence
$\textsf{H}$
, there is a short exact sequence
with
![]() $t \in \mathcal{T}$
and
$t \in \mathcal{T}$
and
![]() $f \in \mathcal{F}$
. The subcategory
$f \in \mathcal{F}$
. The subcategory
![]() $\mathcal{T}$
is called the torsion class and the subcategory
$\mathcal{T}$
is called the torsion class and the subcategory
![]() $\mathcal{F}$
is called the torsionfree class.
$\mathcal{F}$
is called the torsionfree class.
By virtue of the short exact sequence (1·1), it follows that
![]() $\mathcal{T}$
is contravariantly finite in
$\mathcal{T}$
is contravariantly finite in
![]() $\textsf{H}$
and
$\textsf{H}$
and
![]() $\mathcal{F}$
is covariantly finite in
$\mathcal{F}$
is covariantly finite in
![]() $\textsf{H}$
. If, in addition,
$\textsf{H}$
. If, in addition,
![]() $\mathcal{T}$
is covariantly finite in
$\mathcal{T}$
is covariantly finite in
![]() $\textsf{H}$
, we say that
$\textsf{H}$
, we say that
![]() $\mathcal{T}$
is a functorially finite torsion class. Note that, if
$\mathcal{T}$
is a functorially finite torsion class. Note that, if
![]() $\textsf{H}\simeq\textsf{mod}\, A$
for an artin algebra A and
$\textsf{H}\simeq\textsf{mod}\, A$
for an artin algebra A and
![]() $(\mathcal{T},\mathcal{F})$
is a torsion pair in
$(\mathcal{T},\mathcal{F})$
is a torsion pair in
![]() $\textsf{H}$
, then
$\textsf{H}$
, then
![]() $\mathcal{T}$
is covariantly finite in
$\mathcal{T}$
is covariantly finite in
![]() $\textsf{H}$
if and only if
$\textsf{H}$
if and only if
![]() $\mathcal{F}$
is contravariantly finite in
$\mathcal{F}$
is contravariantly finite in
![]() $\textsf{H}$
[
Reference Smalø31
, theorem]. Torsion pairs
$\textsf{H}$
[
Reference Smalø31
, theorem]. Torsion pairs
![]() $(\mathcal{T},\mathcal{F})$
with functorially finite torsion class
$(\mathcal{T},\mathcal{F})$
with functorially finite torsion class
![]() $\mathcal{T}$
and functorially finite torsionfree class
$\mathcal{T}$
and functorially finite torsionfree class
![]() $\mathcal{F}$
are called functorially finite; see e.g. [
Reference Adachi, Iyama and Reiten1
].
$\mathcal{F}$
are called functorially finite; see e.g. [
Reference Adachi, Iyama and Reiten1
].
If
![]() $\textsf{H}$
is noetherian, for example
$\textsf{H}$
is noetherian, for example
![]() $\textsf{H} \simeq \textsf{mod}\, E$
for a noetherian ring E, then any subcategory closed under extensions and quotients is a torsion class of a torsion pair; see, e.g. [
Reference Assem, Simson and Skowroński5
, chapter VI] or [
Reference Liu and Stanley22
, proposition 3·5]. When
$\textsf{H} \simeq \textsf{mod}\, E$
for a noetherian ring E, then any subcategory closed under extensions and quotients is a torsion class of a torsion pair; see, e.g. [
Reference Assem, Simson and Skowroński5
, chapter VI] or [
Reference Liu and Stanley22
, proposition 3·5]. When
![]() $\textsf{H}$
is artinian, the dual statement holds for torsionfree classes.
$\textsf{H}$
is artinian, the dual statement holds for torsionfree classes.
2. HRS tilting of co-t-structures at complete cotorsion pairs
In this section
![]() $\textsf{T}$
will be an arbitrary triangulated category. The aim of this section is to prove Theorem A. We will need the following technical lemma.
$\textsf{T}$
will be an arbitrary triangulated category. The aim of this section is to prove Theorem A. We will need the following technical lemma.
Lemma 2·1.
Suppose
![]() $\textsf{T}$
is a triangulated category,
$\textsf{T}$
is a triangulated category,
![]() $(\textsf{A},\textsf{B})$
is a co-t-structure in
$(\textsf{A},\textsf{B})$
is a co-t-structure in
![]() $\textsf{T}$
, and
$\textsf{T}$
, and
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
is the extended coheart of
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
is the extended coheart of
![]() $(\textsf{A},\textsf{B})$
. If
$(\textsf{A},\textsf{B})$
. If
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in
![]() $\textsf{C}$
then:
$\textsf{C}$
then:
-
(i)
 $\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X} = \textsf{A} * \Sigma^{-1} \mathcal{X}$
, and
$\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X} = \textsf{A} * \Sigma^{-1} \mathcal{X}$
, and
-
(ii)
 $\mathcal{Y} * \Sigma^2 \textsf{B} = \mathcal{Y} * \Sigma \textsf{B}$
.
$\mathcal{Y} * \Sigma^2 \textsf{B} = \mathcal{Y} * \Sigma \textsf{B}$
.
Proof. We show the first equality holds; the second equality is analogous. The inclusion
![]() $\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X} \subseteq \textsf{A} * \Sigma^{-1} \mathcal{X}$
is immediate because
$\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X} \subseteq \textsf{A} * \Sigma^{-1} \mathcal{X}$
is immediate because
![]() $\Sigma^{-1} \textsf{A} \subseteq \textsf{A}$
. For the other inclusion, consider a decomposition of
$\Sigma^{-1} \textsf{A} \subseteq \textsf{A}$
. For the other inclusion, consider a decomposition of
![]() $t \in \textsf{A} * \Sigma^{-1} \mathcal{X}$
,
$t \in \textsf{A} * \Sigma^{-1} \mathcal{X}$
,
with
![]() $a \in \textsf{A}$
and
$a \in \textsf{A}$
and
![]() $x \in \mathcal{X}$
. Decompose a with respect to the co-t-structure
$x \in \mathcal{X}$
. Decompose a with respect to the co-t-structure
![]() $(\Sigma^{-1} \textsf{A},\Sigma^{-1} \textsf{B})$
to get a triangle
$(\Sigma^{-1} \textsf{A},\Sigma^{-1} \textsf{B})$
to get a triangle
![]() $\Sigma^{-1} a^{\prime} \to a \to \Sigma^{-1} s \to a^{\prime}$
with
$\Sigma^{-1} a^{\prime} \to a \to \Sigma^{-1} s \to a^{\prime}$
with
![]() $s \in \textsf{S} = \Sigma \textsf{A} \cap \textsf{B}$
. Since
$s \in \textsf{S} = \Sigma \textsf{A} \cap \textsf{B}$
. Since
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair, by Remark 1·8, we have
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair, by Remark 1·8, we have
![]() $\textsf{S} \subseteq \mathcal{X}$
. Applying the octahedral axiom to the two triangles gives
$\textsf{S} \subseteq \mathcal{X}$
. Applying the octahedral axiom to the two triangles gives
in which
![]() $x^{\prime} \in \mathcal{X}$
, giving a decomposition of
$x^{\prime} \in \mathcal{X}$
, giving a decomposition of
![]() $t \in \Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}$
. Hence
$t \in \Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}$
. Hence
![]() .
.
Theorem 2·2.
Suppose
![]() $\textsf{T}$
is a triangulated category,
$\textsf{T}$
is a triangulated category,
![]() $(\textsf{A},\textsf{B})$
is a co-t-structure in
$(\textsf{A},\textsf{B})$
is a co-t-structure in
![]() $\textsf{T}$
, and
$\textsf{T}$
, and
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
is the extended coheart of
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
is the extended coheart of
![]() $(\textsf{A},\textsf{B})$
. Then there is a bijection
$(\textsf{A},\textsf{B})$
. Then there is a bijection
 \begin{align*}\{{co\mbox{-}t\mbox{-}structures }\ (\textsf{A}^{\prime},\textsf{B}^{\prime}) \ { with }\ \textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}\}& \stackrel{1-1}{\longleftrightarrow}\{{complete\ cotorsion\ pairs }\ (\mathcal{X},\mathcal{Y})\ { in }\ \textsf{C}\}. \\(\textsf{A}^{\prime},\textsf{B}^{\prime})& \shortmid\!\longrightarrow(\textsf{B}\cap \Sigma \textsf{A}^{\prime},\textsf{B}^{\prime}\cap \Sigma^2 \textsf{A}) \\(\textsf{add}(\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}), \textsf{add}(\mathcal{Y} * \Sigma^2 \textsf{B}))& \longleftarrow\!\shortmid(\mathcal{X},\mathcal{Y}).\end{align*}
\begin{align*}\{{co\mbox{-}t\mbox{-}structures }\ (\textsf{A}^{\prime},\textsf{B}^{\prime}) \ { with }\ \textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}\}& \stackrel{1-1}{\longleftrightarrow}\{{complete\ cotorsion\ pairs }\ (\mathcal{X},\mathcal{Y})\ { in }\ \textsf{C}\}. \\(\textsf{A}^{\prime},\textsf{B}^{\prime})& \shortmid\!\longrightarrow(\textsf{B}\cap \Sigma \textsf{A}^{\prime},\textsf{B}^{\prime}\cap \Sigma^2 \textsf{A}) \\(\textsf{add}(\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}), \textsf{add}(\mathcal{Y} * \Sigma^2 \textsf{B}))& \longleftarrow\!\shortmid(\mathcal{X},\mathcal{Y}).\end{align*}
Remark 2·3. Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
. A co-t-structure
$\textsf{T}$
. A co-t-structure
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
![]() $\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
(or, equivalently,
$\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
(or, equivalently,
![]() $\textsf{B} \supseteq \textsf{B}^{\prime} \supseteq \Sigma \textsf{B}$
) is often said to be intermediate with respect to
$\textsf{B} \supseteq \textsf{B}^{\prime} \supseteq \Sigma \textsf{B}$
) is often said to be intermediate with respect to
![]() $(\textsf{A},\textsf{B})$
, cf. [
Reference Angeleri–Hügel4
] or [
Reference Iyama16
]; in the former case ‘intermediate’ means with respect to the ‘standard co-t-structure’ and the interval may be larger.
$(\textsf{A},\textsf{B})$
, cf. [
Reference Angeleri–Hügel4
] or [
Reference Iyama16
]; in the former case ‘intermediate’ means with respect to the ‘standard co-t-structure’ and the interval may be larger.
Proof. The proof of this theorem consists of three steps: first we construct the map
then we construct the map
![]() $\psi$
in the opposite direction; then we prove that
$\psi$
in the opposite direction; then we prove that
![]() $\varphi\psi=\text{id}$
and
$\varphi\psi=\text{id}$
and
![]() $\psi\varphi=\text{id}$
.
$\psi\varphi=\text{id}$
.
Step 1: Let
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
be a co-t-structure in
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
be a co-t-structure in
![]() $\textsf{T}$
such that
$\textsf{T}$
such that
![]() $\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
(equivalently
$\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
(equivalently
![]() $\Sigma \textsf{B} \subseteq \textsf{B}^{\prime} \subseteq \textsf{B}$
) and consider the following subcategories of the extended coheart
$\Sigma \textsf{B} \subseteq \textsf{B}^{\prime} \subseteq \textsf{B}$
) and consider the following subcategories of the extended coheart
![]() $\textsf{C}$
:
$\textsf{C}$
:
Note that
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
are closed under summands, since so are
$\mathcal{Y}$
are closed under summands, since so are
![]() $\textsf{A}, \textsf{A}^{\prime}, \textsf{B}$
and
$\textsf{A}, \textsf{A}^{\prime}, \textsf{B}$
and
![]() $\textsf{B}^{\prime}$
. We claim that
$\textsf{B}^{\prime}$
. We claim that
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
![]() $\textsf{C}$
. Since
$\textsf{C}$
. Since
![]() $\mathcal{X} \subseteq \Sigma \textsf{A}^{\prime}$
and
$\mathcal{X} \subseteq \Sigma \textsf{A}^{\prime}$
and
![]() $\Sigma \mathcal{Y} \subseteq \Sigma \textsf{B}^{\prime}$
, we have
$\Sigma \mathcal{Y} \subseteq \Sigma \textsf{B}^{\prime}$
, we have
![]() $\mathbb{E}(\mathcal{X},\mathcal{Y})=\textsf{T}(\mathcal{X},\Sigma \mathcal{Y})=0$
and condition (i) of Definition 1·9 holds.
$\mathbb{E}(\mathcal{X},\mathcal{Y})=\textsf{T}(\mathcal{X},\Sigma \mathcal{Y})=0$
and condition (i) of Definition 1·9 holds.
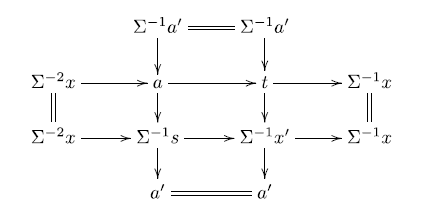
To find the
![]() $\mathbb{E}$
-triangle required for condition (ii), consider the following triangles for
$\mathbb{E}$
-triangle required for condition (ii), consider the following triangles for
![]() $c\in \textsf{C}$
given by taking approximation triangles coming from the co-t-structures
$c\in \textsf{C}$
given by taking approximation triangles coming from the co-t-structures
![]() $(\Sigma \textsf{A}, \Sigma \textsf{B})$
and
$(\Sigma \textsf{A}, \Sigma \textsf{B})$
and
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
, respectively,
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
, respectively,
where
![]() $a\in\textsf{A}$
,
$a\in\textsf{A}$
,
![]() $b\in\textsf{B}$
,
$b\in\textsf{B}$
,
![]() $a^{\prime}\in\textsf{A}^{\prime}$
and
$a^{\prime}\in\textsf{A}^{\prime}$
and
![]() $b^{\prime}\in\textsf{B}^{\prime}$
. Applying the octahedral axiom, we get:
$b^{\prime}\in\textsf{B}^{\prime}$
. Applying the octahedral axiom, we get:
We first observe that
![]() $y \in \mathcal{Y}$
. In the triangle
$y \in \mathcal{Y}$
. In the triangle
![]() $b^{\prime}\to y \to \Sigma b\to \Sigma b^{\prime}$
the outer terms
$b^{\prime}\to y \to \Sigma b\to \Sigma b^{\prime}$
the outer terms
![]() $b^{\prime}\in \textsf{B}^{\prime}$
and
$b^{\prime}\in \textsf{B}^{\prime}$
and
![]() $\Sigma b\in \Sigma \textsf{B} \subseteq \textsf{B}^{\prime}$
, so
$\Sigma b\in \Sigma \textsf{B} \subseteq \textsf{B}^{\prime}$
, so
![]() $y\in \textsf{B}^{\prime}$
. In the triangle
$y\in \textsf{B}^{\prime}$
. In the triangle
![]() $c\to y \to \Sigma a^{\prime}\to \Sigma c$
the outer terms
$c\to y \to \Sigma a^{\prime}\to \Sigma c$
the outer terms
![]() $c\in \Sigma^2 \textsf{A}$
and
$c\in \Sigma^2 \textsf{A}$
and
![]() $\Sigma a^{\prime}\in \Sigma \textsf{A}^{\prime} \subseteq \Sigma^2 \textsf{A}$
, so
$\Sigma a^{\prime}\in \Sigma \textsf{A}^{\prime} \subseteq \Sigma^2 \textsf{A}$
, so
![]() $y\in \Sigma^2 \textsf{A}$
and thus
$y\in \Sigma^2 \textsf{A}$
and thus
![]() $y\in \mathcal{Y}$
.
$y\in \mathcal{Y}$
.
Since
![]() $\Sigma b\in \textsf{B}$
and
$\Sigma b\in \textsf{B}$
and
![]() $\Sigma c \in \textsf{B}$
, we get that
$\Sigma c \in \textsf{B}$
, we get that
![]() $\Sigma^2 a \in \textsf{B}$
. In the triangle
$\Sigma^2 a \in \textsf{B}$
. In the triangle
![]() $b^{\prime}\to \Sigma a^{\prime} \to \Sigma^2 a\to \Sigma b^{\prime}$
the outer terms
$b^{\prime}\to \Sigma a^{\prime} \to \Sigma^2 a\to \Sigma b^{\prime}$
the outer terms
![]() $b^{\prime}\in \textsf{B}^{\prime} \subseteq \textsf{B}$
and
$b^{\prime}\in \textsf{B}^{\prime} \subseteq \textsf{B}$
and
![]() $\Sigma^2 a\in \textsf{B}$
, so
$\Sigma^2 a\in \textsf{B}$
, so
![]() $\Sigma a^{\prime}\in \Sigma \textsf{A}^{\prime} \cap \textsf{B} = \mathcal{X}$
. Thus, the triangle
$\Sigma a^{\prime}\in \Sigma \textsf{A}^{\prime} \cap \textsf{B} = \mathcal{X}$
. Thus, the triangle
gives the
![]() $\mathbb{E}$
-triangle required for condition (ii) of Definition 1·9.
$\mathbb{E}$
-triangle required for condition (ii) of Definition 1·9.
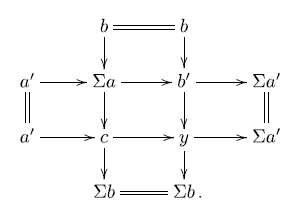
To find the
![]() $\mathbb{E}$
-triangle required for condition (iii), consider
$\mathbb{E}$
-triangle required for condition (iii), consider
![]() $c \in \textsf{C}$
as above and a triangle
$c \in \textsf{C}$
as above and a triangle
where b is the object in the triangle in (2·1),
![]() $a^{\prime\prime}\in\textsf{A}^{\prime}$
and
$a^{\prime\prime}\in\textsf{A}^{\prime}$
and
![]() $b^{\prime\prime}\in\textsf{B}^{\prime}$
. Observe that
$b^{\prime\prime}\in\textsf{B}^{\prime}$
. Observe that
![]() $\Sigma^{-1}c\in \Sigma \textsf{A}$
and
$\Sigma^{-1}c\in \Sigma \textsf{A}$
and
![]() $\Sigma a\in \Sigma \textsf{A}$
, so
$\Sigma a\in \Sigma \textsf{A}$
, so
![]() $b\in \Sigma \textsf{A} \subseteq \Sigma^2 \textsf{A}$
. Since
$b\in \Sigma \textsf{A} \subseteq \Sigma^2 \textsf{A}$
. Since
![]() $\Sigma a^{\prime\prime} \in \Sigma \textsf{A}^{\prime} \subseteq \Sigma^2 \textsf{A}$
, we get
$\Sigma a^{\prime\prime} \in \Sigma \textsf{A}^{\prime} \subseteq \Sigma^2 \textsf{A}$
, we get
![]() $b^{\prime\prime}\in \Sigma^2 \textsf{A}$
. Applying the octahedral axiom again, we get:
$b^{\prime\prime}\in \Sigma^2 \textsf{A}$
. Applying the octahedral axiom again, we get:
Clearly
![]() $x\in \mathcal{X}$
and
$x\in \mathcal{X}$
and
![]() $b^{\prime\prime}\in \mathcal{Y}$
, so the triangle
$b^{\prime\prime}\in \mathcal{Y}$
, so the triangle
gives the
![]() $\mathbb{E}$
-triangle required for condition (iii) of Definition 1·9. Thus the assignment
$\mathbb{E}$
-triangle required for condition (iii) of Definition 1·9. Thus the assignment
![]() $\varphi \colon (\textsf{A}^{\prime},\textsf{B}^{\prime}) \mapsto (\mathcal{X},\mathcal{Y})$
defines a map from co-t-structures
$\varphi \colon (\textsf{A}^{\prime},\textsf{B}^{\prime}) \mapsto (\mathcal{X},\mathcal{Y})$
defines a map from co-t-structures
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
![]() $\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
to complete cotorsion pairs in
$\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
to complete cotorsion pairs in
![]() $\textsf{C}$
.
$\textsf{C}$
.
Step 2: We now construct the map in the other direction. Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
and let
$\textsf{T}$
and let
![]() $(\mathcal{X},\mathcal{Y})$
be a complete cotorsion pair in the extended coheart
$(\mathcal{X},\mathcal{Y})$
be a complete cotorsion pair in the extended coheart
![]() $\textsf{C}=\Sigma^2 \textsf{A} \cap \textsf{B}$
. Consider the following pair of subcategories of
$\textsf{C}=\Sigma^2 \textsf{A} \cap \textsf{B}$
. Consider the following pair of subcategories of
![]() $\textsf{T}$
:
$\textsf{T}$
:
Note that
![]() $\textsf{T}(\Sigma^{-1} \mathcal{X}, \Sigma^2 \textsf{B}) = 0$
since
$\textsf{T}(\Sigma^{-1} \mathcal{X}, \Sigma^2 \textsf{B}) = 0$
since
![]() $\Sigma^{-1} \mathcal{X} \subseteq \Sigma \textsf{A} \subseteq \Sigma^2 \textsf{A}$
and
$\Sigma^{-1} \mathcal{X} \subseteq \Sigma \textsf{A} \subseteq \Sigma^2 \textsf{A}$
and
![]() $\textsf{T}(\Sigma^2 \textsf{A}, \Sigma^2 \textsf{B}) = 0$
because
$\textsf{T}(\Sigma^2 \textsf{A}, \Sigma^2 \textsf{B}) = 0$
because
![]() $(\textsf{A},\textsf{B})$
is a co-t-structure. Hence,
$(\textsf{A},\textsf{B})$
is a co-t-structure. Hence,
![]() $\textsf{T}(\textsf{A}^{\prime},\textsf{B}^{\prime}) = 0$
, verifying the orthogonality condition of the definition of a co-t-structure.
$\textsf{T}(\textsf{A}^{\prime},\textsf{B}^{\prime}) = 0$
, verifying the orthogonality condition of the definition of a co-t-structure.
We claim that
![]() $\textsf{A} \subseteq \textsf{A}^{\prime}\subseteq \Sigma \textsf{A}$
, from which it follows that
$\textsf{A} \subseteq \textsf{A}^{\prime}\subseteq \Sigma \textsf{A}$
, from which it follows that
![]() $\Sigma^{-1} \textsf{A}^{\prime} \subseteq \textsf{A}^{\prime}$
. By Lemma 2·1(i), we have
$\Sigma^{-1} \textsf{A}^{\prime} \subseteq \textsf{A}^{\prime}$
. By Lemma 2·1(i), we have
![]() $\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X} = \textsf{A} * \Sigma^{-1} \mathcal{X}$
, and therefore
$\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X} = \textsf{A} * \Sigma^{-1} \mathcal{X}$
, and therefore
![]() $\textsf{A} \subseteq \textsf{A} * \Sigma^{-1} \mathcal{X} \subseteq \textsf{A}^{\prime}$
. As
$\textsf{A} \subseteq \textsf{A} * \Sigma^{-1} \mathcal{X} \subseteq \textsf{A}^{\prime}$
. As
![]() $\mathcal{X} \subseteq \Sigma^2 \textsf{A}$
, again using Lemma 2·1(i), we have
$\mathcal{X} \subseteq \Sigma^2 \textsf{A}$
, again using Lemma 2·1(i), we have
![]() $\textsf{A}^{\prime} = \textsf{add}(\textsf{A} * \Sigma^{-1} \mathcal{X}) \subseteq \textsf{add}(\textsf{A} * \Sigma \textsf{A}) \subseteq \Sigma \textsf{A}$
since
$\textsf{A}^{\prime} = \textsf{add}(\textsf{A} * \Sigma^{-1} \mathcal{X}) \subseteq \textsf{add}(\textsf{A} * \Sigma \textsf{A}) \subseteq \Sigma \textsf{A}$
since
![]() $\textsf{A} \subseteq \Sigma \textsf{A}$
and
$\textsf{A} \subseteq \Sigma \textsf{A}$
and
![]() $\Sigma \textsf{A}$
is closed under extensions and summands. Similarly, using Lemma 2·1(ii), one can check that
$\Sigma \textsf{A}$
is closed under extensions and summands. Similarly, using Lemma 2·1(ii), one can check that
![]() $\Sigma \textsf{B} \subseteq \textsf{B}^{\prime} \subseteq \textsf{B}$
, from which it follows that
$\Sigma \textsf{B} \subseteq \textsf{B}^{\prime} \subseteq \textsf{B}$
, from which it follows that
![]() $\Sigma \textsf{B}^{\prime} \subseteq \textsf{B}^{\prime}$
.
$\Sigma \textsf{B}^{\prime} \subseteq \textsf{B}^{\prime}$
.
It remains for us to construct the approximation triangle from the definition of the co-t-structure. Consider the following triangles for
![]() $t\in \textsf{T}$
:
$t\in \textsf{T}$
:
where
![]() $a_t, a \in\textsf{A}$
and
$a_t, a \in\textsf{A}$
and
![]() $b,b_t \in \textsf{B}$
. Since
$b,b_t \in \textsf{B}$
. Since
![]() $\Sigma^2 a \in \Sigma^2 \textsf{A} \cap \textsf{B}=\textsf{C}$
, there is a triangle
$\Sigma^2 a \in \Sigma^2 \textsf{A} \cap \textsf{B}=\textsf{C}$
, there is a triangle
with
![]() $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
![]() $y \in \mathcal{Y}$
coming from the
$y \in \mathcal{Y}$
coming from the
![]() $\mathbb{E}$
-triangle occurring in condition (ii) of the definition of complete cotorsion pair. Applying the octahedral axiom twice, we get:
$\mathbb{E}$
-triangle occurring in condition (ii) of the definition of complete cotorsion pair. Applying the octahedral axiom twice, we get:
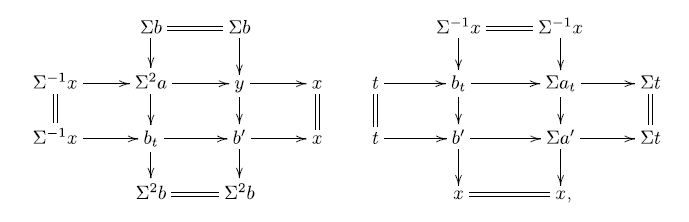
where, in the left-hand diagram, we see
![]() $b^{\prime}\in \mathcal{Y} * \Sigma^{2} \textsf{B} \subseteq \textsf{B}^{\prime}$
, and in the right-hand diagram, we have
$b^{\prime}\in \mathcal{Y} * \Sigma^{2} \textsf{B} \subseteq \textsf{B}^{\prime}$
, and in the right-hand diagram, we have
![]() $a^{\prime}\in \textsf{A} * \Sigma^{-1} \mathcal{X} \subseteq \textsf{A}^{\prime}$
. Thus the triangle
$a^{\prime}\in \textsf{A} * \Sigma^{-1} \mathcal{X} \subseteq \textsf{A}^{\prime}$
. Thus the triangle
is an approximation triangle for t with respect to the co-t-structure
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
. Thus the assignment
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
. Thus the assignment
![]() $\psi \colon (\mathcal{X},\mathcal{Y}) \mapsto (\textsf{A}^{\prime}= \textsf{add}(\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}),\textsf{B}^{\prime} = \textsf{add}(\mathcal{Y} * \Sigma^2 \textsf{B}))$
defines a map from complete cotorsion pairs in
$\psi \colon (\mathcal{X},\mathcal{Y}) \mapsto (\textsf{A}^{\prime}= \textsf{add}(\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}),\textsf{B}^{\prime} = \textsf{add}(\mathcal{Y} * \Sigma^2 \textsf{B}))$
defines a map from complete cotorsion pairs in
![]() $\textsf{C}$
to co-t-structures
$\textsf{C}$
to co-t-structures
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
![]() $\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
.
$\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
.
Step 3: We now show that the maps
![]() $\varphi$
and
$\varphi$
and
![]() $\psi$
defined in Steps 1 and 2 are mutually inverse. Let
$\psi$
defined in Steps 1 and 2 are mutually inverse. Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
, let
$\textsf{T}$
, let
![]() $(\mathcal{X},\mathcal{Y})$
be a complete cotorsion pair in the extended coheart
$(\mathcal{X},\mathcal{Y})$
be a complete cotorsion pair in the extended coheart
![]() $\textsf{C}=\Sigma^2 \textsf{A} \cap \textsf{B}$
and let
$\textsf{C}=\Sigma^2 \textsf{A} \cap \textsf{B}$
and let
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime}) = \psi\big( (\mathcal{X},\mathcal{Y}) \big)$
be the co-t-structure constructed in Step 2. Let
$(\textsf{A}^{\prime},\textsf{B}^{\prime}) = \psi\big( (\mathcal{X},\mathcal{Y}) \big)$
be the co-t-structure constructed in Step 2. Let
![]() $(\mathcal{X}^{\prime},\mathcal{Y}^{\prime}) = \varphi \big( (\textsf{A}^{\prime},\textsf{B}^{\prime}) \big)$
be the complete cotorsion pair constructed from
$(\mathcal{X}^{\prime},\mathcal{Y}^{\prime}) = \varphi \big( (\textsf{A}^{\prime},\textsf{B}^{\prime}) \big)$
be the complete cotorsion pair constructed from
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
in Step 1. That is,
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
in Step 1. That is,
Since
![]() $\Sigma \mathcal{Y}^{\prime}\subseteq \textsf{add}(\Sigma \mathcal{Y} * \Sigma^3 \textsf{B}) $
and
$\Sigma \mathcal{Y}^{\prime}\subseteq \textsf{add}(\Sigma \mathcal{Y} * \Sigma^3 \textsf{B}) $
and
![]() $\mathcal{X}\subseteq \Sigma^2 \textsf{A}$
, we get that
$\mathcal{X}\subseteq \Sigma^2 \textsf{A}$
, we get that
![]() $\textsf{T}(\mathcal{X},\Sigma\mathcal{Y}^{\prime})=0$
. For an object
$\textsf{T}(\mathcal{X},\Sigma\mathcal{Y}^{\prime})=0$
. For an object
![]() $y^{\prime}\in \mathcal{Y}^{\prime}$
, we can consider the triangle
$y^{\prime}\in \mathcal{Y}^{\prime}$
, we can consider the triangle
![]() $y^{\prime}\to y \to x \to \Sigma y^{\prime}$
, where
$y^{\prime}\to y \to x \to \Sigma y^{\prime}$
, where
![]() $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
![]() $y \in \mathcal{Y}$
, coming from the complete cotorsion pair
$y \in \mathcal{Y}$
, coming from the complete cotorsion pair
![]() $(\mathcal{X},\mathcal{Y})$
. Since the map
$(\mathcal{X},\mathcal{Y})$
. Since the map
![]() $x \to \Sigma y^{\prime}$
is zero, the triangle splits and y
′ is a summand of y. Since
$x \to \Sigma y^{\prime}$
is zero, the triangle splits and y
′ is a summand of y. Since
![]() $\mathcal{Y}$
is closed under summands, we get
$\mathcal{Y}$
is closed under summands, we get
![]() $\mathcal{Y}^{\prime}\subseteq \mathcal{Y}$
. Similarly,
$\mathcal{Y}^{\prime}\subseteq \mathcal{Y}$
. Similarly,
![]() $\textsf{T}(\mathcal{X}^{\prime},\Sigma\mathcal{Y})=0$
, and so the splitting of the triangle
$\textsf{T}(\mathcal{X}^{\prime},\Sigma\mathcal{Y})=0$
, and so the splitting of the triangle
![]() $y\to y^{\prime} \to x^{\prime} \to \Sigma y$
, where
$y\to y^{\prime} \to x^{\prime} \to \Sigma y$
, where
![]() $x^{\prime}\in \mathcal{X}^{\prime}$
and
$x^{\prime}\in \mathcal{X}^{\prime}$
and
![]() $y^{\prime} \in \mathcal{Y}^{\prime}$
, coming from the complete cotorsion pair
$y^{\prime} \in \mathcal{Y}^{\prime}$
, coming from the complete cotorsion pair
![]() $(\mathcal{X}^{\prime},\mathcal{Y}^{\prime})$
gives that
$(\mathcal{X}^{\prime},\mathcal{Y}^{\prime})$
gives that
![]() $\mathcal{Y}\subseteq \mathcal{Y}^{\prime}$
. Since
$\mathcal{Y}\subseteq \mathcal{Y}^{\prime}$
. Since
![]() $\mathcal{X}=\textsf{C}\cap(^{\perp}\Sigma\mathcal{Y})=\textsf{C}\cap(^{\perp}\Sigma\mathcal{Y}^{\prime})=\mathcal{X}^{\prime}$
, the cotorsion pairs coincide and
$\mathcal{X}=\textsf{C}\cap(^{\perp}\Sigma\mathcal{Y})=\textsf{C}\cap(^{\perp}\Sigma\mathcal{Y}^{\prime})=\mathcal{X}^{\prime}$
, the cotorsion pairs coincide and
![]() $\varphi\psi=\text{id}$
.
$\varphi\psi=\text{id}$
.
Let
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
be a co-t-structure such that
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
be a co-t-structure such that
![]() $\textsf{A}\subseteq \textsf{A}^{\prime}\subseteq \Sigma \textsf{A}$
(equivalently,
$\textsf{A}\subseteq \textsf{A}^{\prime}\subseteq \Sigma \textsf{A}$
(equivalently,
![]() $\Sigma \textsf{B}\subseteq \textsf{B}^{\prime}\subseteq \textsf{B}$
). Consider the co-t-structure
$\Sigma \textsf{B}\subseteq \textsf{B}^{\prime}\subseteq \textsf{B}$
). Consider the co-t-structure
Clearly,
![]() $\textsf{A}^{\prime\prime}\subseteq \textsf{A}^{\prime}$
and
$\textsf{A}^{\prime\prime}\subseteq \textsf{A}^{\prime}$
and
![]() $\textsf{B}^{\prime\prime}\subseteq \textsf{B}^{\prime}$
and, since both pairs of subcategories are co-t-structures, we get
$\textsf{B}^{\prime\prime}\subseteq \textsf{B}^{\prime}$
and, since both pairs of subcategories are co-t-structures, we get
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})=(\textsf{A}^{\prime\prime},\textsf{B}^{\prime\prime})$
and
$(\textsf{A}^{\prime},\textsf{B}^{\prime})=(\textsf{A}^{\prime\prime},\textsf{B}^{\prime\prime})$
and
![]() $\psi\varphi=\text{id}$
. Thus we get the desired bijection.
$\psi\varphi=\text{id}$
. Thus we get the desired bijection.
Remark 2·4. Let
![]() $(\textsf{A},\textsf{B})$
be a co-t-structure in
$(\textsf{A},\textsf{B})$
be a co-t-structure in
![]() $\textsf{T}$
with coheart
$\textsf{T}$
with coheart
![]() $\textsf{S}$
and extended coheart
$\textsf{S}$
and extended coheart
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{S} * \Sigma \textsf{S}$
. Suppose
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{S} * \Sigma \textsf{S}$
. Suppose
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
![]() $\textsf{C}$
.
$\textsf{C}$
.
-
(i) In the definition of the intermediate co-t-structure
 $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
obtained from
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
obtained from
 $(\mathcal{X},\mathcal{Y})$
in Theorem 2·2 it is not obvious that
$(\mathcal{X},\mathcal{Y})$
in Theorem 2·2 it is not obvious that
 $\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}$
and
$\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}$
and
 $\mathcal{Y} * \Sigma^2 \textsf{B}$
are closed under summands, hence we are required to take the additive closure. However, one can check that
$\mathcal{Y} * \Sigma^2 \textsf{B}$
are closed under summands, hence we are required to take the additive closure. However, one can check that
 $\textsf{T}(\textsf{A},\mathcal{X}) = 0$
and
$\textsf{T}(\textsf{A},\mathcal{X}) = 0$
and
 $\textsf{T}(\mathcal{Y},\Sigma^2 \textsf{B}) = 0$
, so that in the case that
$\textsf{T}(\mathcal{Y},\Sigma^2 \textsf{B}) = 0$
, so that in the case that
 $\textsf{T}$
is Krull-Schmidt, applying [
Reference Iyama and Yoshino17
, proposition 2·1], we see that
$\textsf{T}$
is Krull-Schmidt, applying [
Reference Iyama and Yoshino17
, proposition 2·1], we see that
 $\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}=\textsf{A} * \Sigma^{-1} \mathcal{X}$
and
$\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}=\textsf{A} * \Sigma^{-1} \mathcal{X}$
and
 $\mathcal{Y} * \Sigma^2 \textsf{B}$
are closed under direct summands.
$\mathcal{Y} * \Sigma^2 \textsf{B}$
are closed under direct summands. -
(ii) We have
 $\Sigma^{-1} \mathcal{X} * \mathcal{Y} = \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
. The inclusion
$\Sigma^{-1} \mathcal{X} * \mathcal{Y} = \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
. The inclusion
 $\Sigma^{-1} \mathcal{X} * \mathcal{Y} \subseteq \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
is clear since
$\Sigma^{-1} \mathcal{X} * \mathcal{Y} \subseteq \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
is clear since
 $\mathcal{X}, \mathcal{Y} \subseteq \textsf{S} * \Sigma \textsf{S}$
. The inclusion
$\mathcal{X}, \mathcal{Y} \subseteq \textsf{S} * \Sigma \textsf{S}$
. The inclusion
 $\Sigma^{-1} \mathcal{X} * \mathcal{Y} \supseteq \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
follows from the inclusions
$\Sigma^{-1} \mathcal{X} * \mathcal{Y} \supseteq \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
follows from the inclusions
 $\textsf{S} * \Sigma \textsf{S} \subseteq \Sigma^{-1} \mathcal{X} * \mathcal{Y}$
and
$\textsf{S} * \Sigma \textsf{S} \subseteq \Sigma^{-1} \mathcal{X} * \mathcal{Y}$
and
 $\Sigma^{-1} \textsf{S} * \textsf{S} \subseteq \Sigma^{-1} \mathcal{X} * \mathcal{Y}$
coming from the two
$\Sigma^{-1} \textsf{S} * \textsf{S} \subseteq \Sigma^{-1} \mathcal{X} * \mathcal{Y}$
coming from the two
 $\mathbb{E}$
-triangles in Definition 1·9, and the fact that
$\mathbb{E}$
-triangles in Definition 1·9, and the fact that
 $\Sigma^{-1} \mathcal{X} * \mathcal{Y}$
is extension closed by [
Reference Nicolás, Saorín and Zvonareva25
, lemma 8] since
$\Sigma^{-1} \mathcal{X} * \mathcal{Y}$
is extension closed by [
Reference Nicolás, Saorín and Zvonareva25
, lemma 8] since
 $\textsf{T}(\Sigma^{-1} \mathcal{X} ,\Sigma \mathcal{Y}) =0$
.
$\textsf{T}(\Sigma^{-1} \mathcal{X} ,\Sigma \mathcal{Y}) =0$
. -
(iii) In light of Lemma 2·1, there are two descriptions of
 $\textsf{A}^{\prime}$
and
$\textsf{A}^{\prime}$
and
 $\textsf{B}^{\prime}$
. Namely,The description we have chosen to present in the statement of Theorem 2·2 has two advantages: it is the closest parallel to classic HRS tilting for t-structures using torsion pairs in that it is written in terms of non-overlapping classes, and it makes the equality
$\textsf{B}^{\prime}$
. Namely,The description we have chosen to present in the statement of Theorem 2·2 has two advantages: it is the closest parallel to classic HRS tilting for t-structures using torsion pairs in that it is written in terms of non-overlapping classes, and it makes the equality \begin{align*}\textsf{A}^{\prime} & = \textsf{add}(\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}) = \textsf{add}(\textsf{A} * \Sigma^{-1} \mathcal{X}) \\\textsf{B}^{\prime} & = \textsf{add}(\mathcal{Y} * \Sigma^2 \textsf{B}) = \textsf{add}(\mathcal{Y} * \Sigma \textsf{B}).\end{align*}
\begin{align*}\textsf{A}^{\prime} & = \textsf{add}(\Sigma^{-1} \textsf{A} * \Sigma^{-1} \mathcal{X}) = \textsf{add}(\textsf{A} * \Sigma^{-1} \mathcal{X}) \\\textsf{B}^{\prime} & = \textsf{add}(\mathcal{Y} * \Sigma^2 \textsf{B}) = \textsf{add}(\mathcal{Y} * \Sigma \textsf{B}).\end{align*}
 $\Sigma^{-1} \mathcal{X} * \mathcal{Y} = \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
in (ii) above intuitive; see Figure 1 for a schematic.
$\Sigma^{-1} \mathcal{X} * \mathcal{Y} = \Sigma^{-1} \textsf{S} * \textsf{S} * \Sigma \textsf{S}$
in (ii) above intuitive; see Figure 1 for a schematic.

Fig. 1. Schematic showing the construction of the intermediate co-t-structure
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
in Theorem 2·2 from a complete cotorsion pair
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
in Theorem 2·2 from a complete cotorsion pair
![]() $(\mathcal{X},\mathcal{Y})$
in the extended coheart
$(\mathcal{X},\mathcal{Y})$
in the extended coheart
![]() $\textsf{C}= \textsf{S}* \Sigma \textsf{S}$
of the co-t-structure
$\textsf{C}= \textsf{S}* \Sigma \textsf{S}$
of the co-t-structure
![]() $(\textsf{A},\textsf{B})$
.
$(\textsf{A},\textsf{B})$
.
The corollary below shows that Theorem 2·2 recovers the bijection between co-t-structures intermediate with respect to
![]() $(\textsf{A},\textsf{B})$
and silting subcategories
$(\textsf{A},\textsf{B})$
and silting subcategories
![]() $\textsf{S}^{\prime} \subseteq \textsf{S} * \Sigma \textsf{S}$
in [
Reference Iyama16
, theorem 2·3].
$\textsf{S}^{\prime} \subseteq \textsf{S} * \Sigma \textsf{S}$
in [
Reference Iyama16
, theorem 2·3].
Corollary 2·5.
Suppose
![]() $(\textsf{A},\textsf{B})$
is a co-t-structure in
$(\textsf{A},\textsf{B})$
is a co-t-structure in
![]() $\textsf{T}$
, and
$\textsf{T}$
, and
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
is the extended coheart of
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
is the extended coheart of
![]() $(\textsf{A},\textsf{B})$
. If
$(\textsf{A},\textsf{B})$
. If
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
![]() $\textsf{C}$
, then its core
$\textsf{C}$
, then its core
![]() $\mathcal{W} = \mathcal{X} \cap \mathcal{Y}$
is the coheart of the corresponding intermediate co-t-structure
$\mathcal{W} = \mathcal{X} \cap \mathcal{Y}$
is the coheart of the corresponding intermediate co-t-structure
![]() .
.
Proof. Let
![]() $\textsf{S}^{\prime} = \Sigma \textsf{A}^{\prime} \cap \textsf{B}^{\prime}$
be the coheart of the co-t-structure
$\textsf{S}^{\prime} = \Sigma \textsf{A}^{\prime} \cap \textsf{B}^{\prime}$
be the coheart of the co-t-structure
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
. By Theorem 2·2,
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
. By Theorem 2·2,
![]() $\mathcal{X} = \textsf{B} \cap \Sigma \textsf{A}^{\prime}$
and
$\mathcal{X} = \textsf{B} \cap \Sigma \textsf{A}^{\prime}$
and
![]() $\mathcal{Y} = \textsf{B}^{\prime} \cap \Sigma^2 \textsf{A}$
. Hence
$\mathcal{Y} = \textsf{B}^{\prime} \cap \Sigma^2 \textsf{A}$
. Hence
![]() $\mathcal{W} = \mathcal{X} \cap \mathcal{Y} = \textsf{S}^{\prime} \cap \textsf{C}$
. But since
$\mathcal{W} = \mathcal{X} \cap \mathcal{Y} = \textsf{S}^{\prime} \cap \textsf{C}$
. But since
![]() $\textsf{S}^{\prime} = \Sigma \textsf{A}^{\prime} \cap \textsf{B}^{\prime} \subseteq \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{C}$
, we have
$\textsf{S}^{\prime} = \Sigma \textsf{A}^{\prime} \cap \textsf{B}^{\prime} \subseteq \Sigma^2 \textsf{A} \cap \textsf{B} = \textsf{C}$
, we have
![]() $\mathcal{W} = \textsf{S}^{\prime}$
.
$\mathcal{W} = \textsf{S}^{\prime}$
.
We finish this section with a straightforward example illustrating Theorem 2·2.
Example 2·6. Let
![]() $\textbf{k}$
be a field and let
$\textbf{k}$
be a field and let
![]() $A_3$
be the equi-oriented Dynkin diagram of type
$A_3$
be the equi-oriented Dynkin diagram of type
![]() $A_3$
. In the diagram below we show the indecomposable objects in the Auslander–Reiten quiver of
$A_3$
. In the diagram below we show the indecomposable objects in the Auslander–Reiten quiver of
![]() $\textsf{T} = \textsf{D}^b(\textbf{k} A_3)$
; note that we suppress the arrows in the AR quiver. The diagram depicts a co-t-structure
$\textsf{T} = \textsf{D}^b(\textbf{k} A_3)$
; note that we suppress the arrows in the AR quiver. The diagram depicts a co-t-structure
![]() $(\textsf{A},\textsf{B})$
, its extended coheart
$(\textsf{A},\textsf{B})$
, its extended coheart
![]() $\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
, an intermediate co-t-structure
$\textsf{C} = \Sigma^2 \textsf{A} \cap \textsf{B}$
, an intermediate co-t-structure
![]() $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
such that
![]() $\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
, and a complete cotorsion pair
$\textsf{A} \subseteq \textsf{A}^{\prime} \subseteq \Sigma \textsf{A}$
, and a complete cotorsion pair
![]() $(\mathcal{X},\mathcal{Y}) = (\textsf{B} \cap \Sigma \textsf{A}^{\prime}, \textsf{B}^{\prime} \cap \Sigma^2 \textsf{A})$
. We highlight these objects in the diagram as follows:
$(\mathcal{X},\mathcal{Y}) = (\textsf{B} \cap \Sigma \textsf{A}^{\prime}, \textsf{B}^{\prime} \cap \Sigma^2 \textsf{A})$
. We highlight these objects in the diagram as follows:
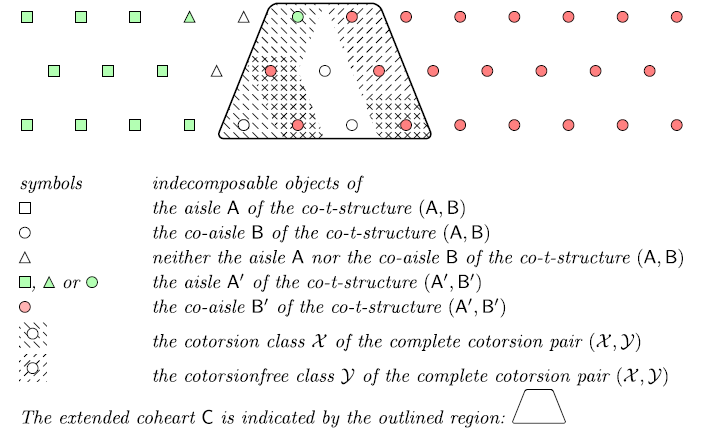
3. Cotorsion pairs versus torsion pairs
The aim of this section is to provide a direct proof of Theorem B. We restrict to the following setup so that we can apply the setup of Section 1·4.
Setup 3·1. From now on we will assume that
![]() $\textsf{T}$
is essentially small, Hom-finite,
$\textsf{T}$
is essentially small, Hom-finite,
![]() $\textbf{k}$
-linear and Krull–Schmidt, where
$\textbf{k}$
-linear and Krull–Schmidt, where
![]() $\textbf{k}$
is a commutative noetherian ring. Note that in that case
$\textbf{k}$
is a commutative noetherian ring. Note that in that case
![]() $\textsf{T}$
is automatically idempotent complete. Let
$\textsf{T}$
is automatically idempotent complete. Let
![]() $\textsf{S}$
be a presilting subcategory of
$\textsf{S}$
be a presilting subcategory of
![]() $\textsf{T}$
such that
$\textsf{T}$
such that
![]() $\textsf{mod}\, \textsf{S}$
is abelian and noetherian and set
$\textsf{mod}\, \textsf{S}$
is abelian and noetherian and set
![]() $\textsf{C} = \textsf{S}* \Sigma \textsf{S}$
. Note that, since
$\textsf{C} = \textsf{S}* \Sigma \textsf{S}$
. Note that, since
![]() $\textsf{S}$
is silting in
$\textsf{S}$
is silting in
![]() $\textsf{thick}\ \textsf{S}$
, the subcategory
$\textsf{thick}\ \textsf{S}$
, the subcategory
![]() $ \textsf{S} * \Sigma \textsf{S}$
is closed under summands and extensions.
$ \textsf{S} * \Sigma \textsf{S}$
is closed under summands and extensions.
Under the assumptions of Setup 3·1, if
![]() $\textsf{S} = \textsf{add}(s)$
, then
$\textsf{S} = \textsf{add}(s)$
, then
![]() $\textsf{mod}\, \textsf{S} \simeq \textsf{mod}\, E$
, where
$\textsf{mod}\, \textsf{S} \simeq \textsf{mod}\, E$
, where
![]() $E = \textsf{T}(s,s)$
is a noetherian ring, making
$E = \textsf{T}(s,s)$
is a noetherian ring, making
![]() $\textsf{mod}\, \textsf{S}$
abelian and noetherian.
$\textsf{mod}\, \textsf{S}$
abelian and noetherian.
Proposition 3·2.
Suppose that the hypotheses of Setup 3·1 hold. Then the equivalence
![]() $F \colon \textsf{C}/\Sigma \textsf{S} \to \textsf{mod}\, \textsf{S}$
induces a well-defined map
$F \colon \textsf{C}/\Sigma \textsf{S} \to \textsf{mod}\, \textsf{S}$
induces a well-defined map
which restricts to a well-defined map
Proof. Let
![]() $(\mathcal{X},\mathcal{Y})$
be a cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
be a cotorsion pair in
![]() $\textsf{C}$
. We claim that the essential image
$\textsf{C}$
. We claim that the essential image
![]() $\mathcal{T} = F\mathcal{Y}$
is a torsion class in
$\mathcal{T} = F\mathcal{Y}$
is a torsion class in
![]() $\textsf{mod}\, \textsf{S}$
. Since
$\textsf{mod}\, \textsf{S}$
. Since
![]() $\textsf{mod}\, \textsf{S}$
is noetherian, by [
Reference Liu and Stanley22
, proposition 3·5] it is enough to show that
$\textsf{mod}\, \textsf{S}$
is noetherian, by [
Reference Liu and Stanley22
, proposition 3·5] it is enough to show that
![]() $\mathcal{T}$
is closed under quotients and extensions.
$\mathcal{T}$
is closed under quotients and extensions.
We start by showing that
![]() $\mathcal{T} = F \mathcal{Y}$
is closed under quotients. Consider an exact sequence
$\mathcal{T} = F \mathcal{Y}$
is closed under quotients. Consider an exact sequence
![]() $t \stackrel{\varphi}{\longrightarrow} u \to 0$
in
$t \stackrel{\varphi}{\longrightarrow} u \to 0$
in
![]() $\textsf{mod}\, \textsf{S}$
with
$\textsf{mod}\, \textsf{S}$
with
![]() $t \in \mathcal{T}$
. Lifting this to
$t \in \mathcal{T}$
. Lifting this to
![]() $\textsf{C}$
via F, there are objects
$\textsf{C}$
via F, there are objects
![]() $y\in \mathcal{Y}$
and
$y\in \mathcal{Y}$
and
![]() $v\in \textsf{C}$
and a morphism
$v\in \textsf{C}$
and a morphism
![]() $f \colon y \to v$
such that
$f \colon y \to v$
such that
![]() $Fy \simeq t$
,
$Fy \simeq t$
,
![]() $Fv \simeq u$
and
$Fv \simeq u$
and
![]() $Ff \simeq \varphi$
. Completing the morphism f to a distinguished triangle in
$Ff \simeq \varphi$
. Completing the morphism f to a distinguished triangle in
![]() $\textsf{T}$
gives
$\textsf{T}$
gives
Applying F to this triangle, we get the exact sequence
Since
![]() $\textsf{T}(-,f)|_\textsf{S} \simeq \varphi$
is an epimorphism, we have
$\textsf{T}(-,f)|_\textsf{S} \simeq \varphi$
is an epimorphism, we have
![]() $\textsf{T}(-,g)|_\textsf{S} = 0$
. Moreover,
$\textsf{T}(-,g)|_\textsf{S} = 0$
. Moreover,
![]() $\Sigma y \in \Sigma \textsf{S} * \Sigma^2 \textsf{S}$
so that
$\Sigma y \in \Sigma \textsf{S} * \Sigma^2 \textsf{S}$
so that
![]() $\textsf{S}$
presilting implies that
$\textsf{S}$
presilting implies that
![]() $\textsf{T}(-,\Sigma y)|_\textsf{S}=0$
. Hence,
$\textsf{T}(-,\Sigma y)|_\textsf{S}=0$
. Hence,
![]() $\textsf{T}(-,\Sigma c)|_\textsf{S} = 0$
. In particular, it follows that
$\textsf{T}(-,\Sigma c)|_\textsf{S} = 0$
. In particular, it follows that
![]() $\Sigma c \in (\textsf{S} * \Sigma \textsf{S} * \Sigma^2 \textsf{S}) \cap \textsf{S}{}^\perp$
, in which case we get that
$\Sigma c \in (\textsf{S} * \Sigma \textsf{S} * \Sigma^2 \textsf{S}) \cap \textsf{S}{}^\perp$
, in which case we get that
![]() $c \in \textsf{S} * \Sigma \textsf{S}$
. Now applying
$c \in \textsf{S} * \Sigma \textsf{S}$
. Now applying
![]() $\textsf{T}(\mathcal{X},{-})$
to the triangle above gives
$\textsf{T}(\mathcal{X},{-})$
to the triangle above gives
![]() $\textsf{T}(\mathcal{X},\Sigma v) = 0$
, which means
$\textsf{T}(\mathcal{X},\Sigma v) = 0$
, which means
![]() $v \in \mathcal{Y}$
because
$v \in \mathcal{Y}$
because
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair. Hence,
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair. Hence,
![]() $u \simeq Fv \in \mathcal{T}$
and
$u \simeq Fv \in \mathcal{T}$
and
![]() $\mathcal{T}$
is closed under quotients.
$\mathcal{T}$
is closed under quotients.
Next we show that
![]() $\mathcal{T}$
is closed under extensions. Consider a short exact sequence
$\mathcal{T}$
is closed under extensions. Consider a short exact sequence
in
![]() $\textsf{mod}\, \textsf{S}$
with
$\textsf{mod}\, \textsf{S}$
with
![]() $t^{\prime},t^{\prime\prime} \in \mathcal{T}$
. Lift the morphism
$t^{\prime},t^{\prime\prime} \in \mathcal{T}$
. Lift the morphism
![]() $\varphi \colon t^{\prime} \to t$
to
$\varphi \colon t^{\prime} \to t$
to
![]() $\textsf{C}$
to obtain a morphism
$\textsf{C}$
to obtain a morphism
![]() $f \colon y^{\prime} \to y$
such that
$f \colon y^{\prime} \to y$
such that
![]() $y^{\prime}\in\mathcal{Y}$
,
$y^{\prime}\in\mathcal{Y}$
,
![]() $Ff \simeq \varphi$
,
$Ff \simeq \varphi$
,
![]() $Fy^{\prime} \simeq t^{\prime}$
and
$Fy^{\prime} \simeq t^{\prime}$
and
![]() $Fy \simeq t$
. Extend f to a distinguished triangle to get
$Fy \simeq t$
. Extend f to a distinguished triangle to get
Applying the restricted Yoneda functor to this triangle and noting that
![]() $\textsf{T}(-,\Sigma y^{\prime})|_\textsf{S} = 0$
gives a commutative diagram,
$\textsf{T}(-,\Sigma y^{\prime})|_\textsf{S} = 0$
gives a commutative diagram,
whence
![]() $Fc \simeq t^{\prime\prime}\simeq Fy^{\prime\prime}$
for some
$Fc \simeq t^{\prime\prime}\simeq Fy^{\prime\prime}$
for some
![]() $y^{\prime\prime}\in \mathcal{Y}$
.
$y^{\prime\prime}\in \mathcal{Y}$
.
If
![]() $c \in \mathcal{Y} \subseteq \textsf{C}$
, then we are done. However, we do not know this to be the case. Reading off from the triangle above,
$c \in \mathcal{Y} \subseteq \textsf{C}$
, then we are done. However, we do not know this to be the case. Reading off from the triangle above,
![]() $c \in \textsf{S} * \Sigma \textsf{S} * \Sigma^2 \textsf{S}$
, so we can consider a decomposition
$c \in \textsf{S} * \Sigma \textsf{S} * \Sigma^2 \textsf{S}$
, so we can consider a decomposition
![]() $m \to c \to n \to \Sigma m$
in which
$m \to c \to n \to \Sigma m$
in which
![]() $m \in \textsf{S} * \Sigma \textsf{S}$
and
$m \in \textsf{S} * \Sigma \textsf{S}$
and
![]() $n \in \Sigma^2 \textsf{S}$
. Consider the octahedral diagram obtained from the two triangles below.
$n \in \Sigma^2 \textsf{S}$
. Consider the octahedral diagram obtained from the two triangles below.
Applying the restricted Yoneda functor to a rotation of the lower horizontal triangle gives an isomorphism
![]() $Fe \stackrel{\sim}{\longrightarrow} Fy$
. Rotating the right-hand vertical triangle gives
$Fe \stackrel{\sim}{\longrightarrow} Fy$
. Rotating the right-hand vertical triangle gives
showing that
![]() $e \in \textsf{C}$
. Consider the octahedral diagram obtained using this triangle together with the triangle
$e \in \textsf{C}$
. Consider the octahedral diagram obtained using this triangle together with the triangle
![]() $e \to y \to n \to \Sigma e$
.
$e \to y \to n \to \Sigma e$
.
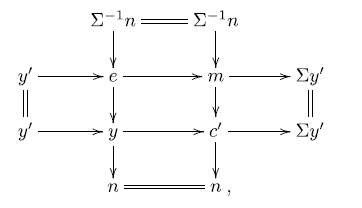
Note that from the previous diagram c
′ is isomorphic to the cone of the map
![]() $y^{\prime}\xrightarrow{f} y$
, so
$y^{\prime}\xrightarrow{f} y$
, so
![]() $c^{\prime}\simeq c$
and
$c^{\prime}\simeq c$
and
![]() $Fc^{\prime}\simeq Fc$
. Applying the restricted Yoneda functor to the two horizontal triangles gives,
$Fc^{\prime}\simeq Fc$
. Applying the restricted Yoneda functor to the two horizontal triangles gives,
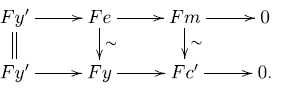
In particular, there is an isomorphism
![]() $Fy^{\prime\prime} \stackrel{\sim}{\longrightarrow} Fm$
, so by the argument showing
$Fy^{\prime\prime} \stackrel{\sim}{\longrightarrow} Fm$
, so by the argument showing
![]() $\mathcal{T}$
is closed under quotients, we see that m lies in
$\mathcal{T}$
is closed under quotients, we see that m lies in
![]() $\mathcal{Y}$
. Since
$\mathcal{Y}$
. Since
![]() $\mathcal{Y}$
is closed under extensions, it follows that
$\mathcal{Y}$
is closed under extensions, it follows that
![]() $e \in \mathcal{Y}$
. Hence
$e \in \mathcal{Y}$
. Hence
![]() $Fe \simeq Fy \simeq t$
, showing that
$Fe \simeq Fy \simeq t$
, showing that
![]() $t \in \mathcal{T}$
, as required.
$t \in \mathcal{T}$
, as required.
Finally, we check that the map induced by the restricted Yoneda functor restricts as claimed. We need to show that
![]() $\mathcal{T} = F\mathcal{Y}$
is covariantly finite when
$\mathcal{T} = F\mathcal{Y}$
is covariantly finite when
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair. Let
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair. Let
![]() $m \in \textsf{mod}\, \textsf{S}$
. Suppose
$m \in \textsf{mod}\, \textsf{S}$
. Suppose
![]() $c \in \textsf{C}$
is such that
$c \in \textsf{C}$
is such that
![]() $Fc \simeq m$
. Without loss of generality we can assume
$Fc \simeq m$
. Without loss of generality we can assume
![]() $Fc = m$
. Consider a decomposition triangle of c with respect to the complete cotorsion pair
$Fc = m$
. Consider a decomposition triangle of c with respect to the complete cotorsion pair
![]() $(\mathcal{X},\mathcal{Y})$
,
$(\mathcal{X},\mathcal{Y})$
,
Note that
![]() $f \colon c \to y$
is a left
$f \colon c \to y$
is a left
![]() $\mathcal{Y}$
-approximation of c in
$\mathcal{Y}$
-approximation of c in
![]() $\textsf{C}$
. We claim that
$\textsf{C}$
. We claim that
![]() $Ff \colon m \to Fy$
is a left
$Ff \colon m \to Fy$
is a left
![]() $\mathcal{T}$
-approximation of m in
$\mathcal{T}$
-approximation of m in
![]() $\textsf{mod}\, \textsf{S}$
. Suppose
$\textsf{mod}\, \textsf{S}$
. Suppose
![]() $\varphi \colon m \to t$
is a morphism in
$\varphi \colon m \to t$
is a morphism in
![]() $\textsf{mod}\, \textsf{S}$
with
$\textsf{mod}\, \textsf{S}$
with
![]() $t \in \mathcal{T}$
. Then there exist
$t \in \mathcal{T}$
. Then there exist
![]() $y^{\prime} \in \mathcal{Y}$
together with an isomorphism
$y^{\prime} \in \mathcal{Y}$
together with an isomorphism
![]() $e \colon Fy^{\prime} \stackrel{\sim}{\longrightarrow} t$
and
$e \colon Fy^{\prime} \stackrel{\sim}{\longrightarrow} t$
and
![]() $g \colon c \to y^{\prime}$
such that
$g \colon c \to y^{\prime}$
such that
![]() $ \varphi=eFg$
. Since f is a left
$ \varphi=eFg$
. Since f is a left
![]() $\mathcal{Y}$
-approximation of c in
$\mathcal{Y}$
-approximation of c in
![]() $\textsf{C}$
, there exists
$\textsf{C}$
, there exists
![]() $h \colon y \to y^{\prime}$
such that
$h \colon y \to y^{\prime}$
such that
![]() $g = hf$
. Applying F to this composition gives
$g = hf$
. Applying F to this composition gives
![]() $\varphi = eFg = eFh Ff$
, that is, Ff is a left
$\varphi = eFg = eFh Ff$
, that is, Ff is a left
![]() $\mathcal{T}$
-approximation, as required.
$\mathcal{T}$
-approximation, as required.
Remark 3·3. If we relax the assumption of
![]() $\textsf{mod}\, \textsf{S}$
being noetherian and require simply that
$\textsf{mod}\, \textsf{S}$
being noetherian and require simply that
![]() $\textsf{mod}\, \textsf{S}$
is abelian, then each instance of the term ‘torsion class’ appearing in Proposition 3·2 can be replaced by ‘nullity class’ in the sense of [
Reference Liu and Stanley22
].
$\textsf{mod}\, \textsf{S}$
is abelian, then each instance of the term ‘torsion class’ appearing in Proposition 3·2 can be replaced by ‘nullity class’ in the sense of [
Reference Liu and Stanley22
].
The next lemma provides a useful criterion to detect when a cotorsion pair is complete.
Lemma 3·4.
Let
![]() $\textsf{S}$
be a presilting subcategory of a triangulated category
$\textsf{S}$
be a presilting subcategory of a triangulated category
![]() $\textsf{T}$
and
$\textsf{T}$
and
![]() $\textsf{C} = \textsf{S} * \Sigma \textsf{S}$
. Suppose
$\textsf{C} = \textsf{S} * \Sigma \textsf{S}$
. Suppose
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in
![]() $\textsf{C}$
, then
$\textsf{C}$
, then
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
![]() $\textsf{C}$
if and only if for each object s of
$\textsf{C}$
if and only if for each object s of
![]() $\textsf{S}$
there exists a triangle
$\textsf{S}$
there exists a triangle
![]() $s \to y \to x \to \Sigma s$
with
$s \to y \to x \to \Sigma s$
with
![]() $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
![]() $y \in \mathcal{Y}$
.
$y \in \mathcal{Y}$
.
Proof. If
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
![]() $\textsf{C}$
then by definition such a triangle exists for
$\textsf{C}$
then by definition such a triangle exists for
![]() $s \in \textsf{S}$
because such a triangle exists for each
$s \in \textsf{S}$
because such a triangle exists for each
![]() $c \in \textsf{C}$
.
$c \in \textsf{C}$
.
Conversely, suppose
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair in
![]() $\textsf{C}$
and that for each
$\textsf{C}$
and that for each
![]() $s \in \textsf{S}$
, there is a triangle
$s \in \textsf{S}$
, there is a triangle
![]() $s \to y \to x \to \Sigma s$
with
$s \to y \to x \to \Sigma s$
with
![]() $x \in \mathcal{X}$
and
$x \in \mathcal{X}$
and
![]() $y \in \mathcal{Y}$
. Let
$y \in \mathcal{Y}$
. Let
![]() $c \in \textsf{C}$
and take a decomposition triangle,
$c \in \textsf{C}$
and take a decomposition triangle,
![]() $s_2 \to s_1 \to c \to \Sigma s_2$
, and the triangle
$s_2 \to s_1 \to c \to \Sigma s_2$
, and the triangle
![]() $s_2 \to y_2 \to x_2 \to \Sigma s_2$
given by the assumption. Applying the octahedral axiom to these triangles gives the following diagram.
$s_2 \to y_2 \to x_2 \to \Sigma s_2$
given by the assumption. Applying the octahedral axiom to these triangles gives the following diagram.
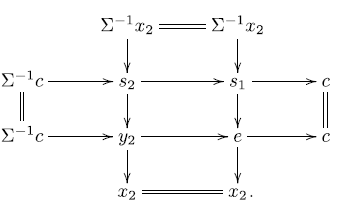
We have
![]() $e \in \mathcal{X}$
since
$e \in \mathcal{X}$
since
![]() $\textsf{S} \subseteq \mathcal{X}$
, because
$\textsf{S} \subseteq \mathcal{X}$
, because
![]() $(\mathcal{X},\mathcal{Y})$
is a cotorsion pair. Thus, the triangle
$(\mathcal{X},\mathcal{Y})$
is a cotorsion pair. Thus, the triangle
![]() $y_2 \to e \to c \to \Sigma y_2$
provides the second triangle required for completeness in Definition 1·9.
$y_2 \to e \to c \to \Sigma y_2$
provides the second triangle required for completeness in Definition 1·9.
To obtain the first triangle in Definition 1·9, we use the octahedral axiom again together with the triangle
![]() $s_1 \to y_1 \to x_1 \to \Sigma s_1$
given by the assumption:
$s_1 \to y_1 \to x_1 \to \Sigma s_1$
given by the assumption:
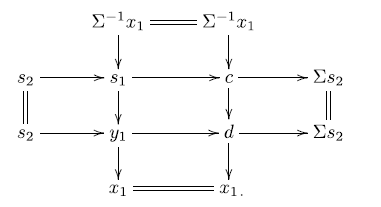
Analogously, we have
![]() $d \in \mathcal{Y}$
because
$d \in \mathcal{Y}$
because
![]() $\Sigma \textsf{S} \subseteq \mathcal{Y}$
, making
$\Sigma \textsf{S} \subseteq \mathcal{Y}$
, making
![]() $c \to d \to x_1 \to \Sigma c$
the required triangle.
$c \to d \to x_1 \to \Sigma c$
the required triangle.
Remark 3·5. We make two observations regarding Lemma 3·4.
-
(i) Lemma 3·4, in fact, holds in the case that
 $(\mathcal{X},\mathcal{Y})$
is an Ext-orthogonal pair of subcategories of
$(\mathcal{X},\mathcal{Y})$
is an Ext-orthogonal pair of subcategories of
 $\textsf{C}$
closed under extensions and direct summands and such that
$\textsf{C}$
closed under extensions and direct summands and such that
 $\textsf{S} \subseteq \mathcal{X}$
and
$\textsf{S} \subseteq \mathcal{X}$
and
 $\Sigma \textsf{S} \subseteq \mathcal{Y}$
.
$\Sigma \textsf{S} \subseteq \mathcal{Y}$
. -
(ii) Let
 $\textsf{S}$
,
$\textsf{S}$
,
 $\textsf{C}$
and
$\textsf{C}$
and
 $(\mathcal{X},\mathcal{Y})$
be as in the statement of Lemma 3·4. In the triangle
$(\mathcal{X},\mathcal{Y})$
be as in the statement of Lemma 3·4. In the triangle
 $s \to y \to x \to \Sigma s$
we observe that since
$s \to y \to x \to \Sigma s$
we observe that since
 $\textsf{S} \subseteq \mathcal{X}$
and
$\textsf{S} \subseteq \mathcal{X}$
and
 $\Sigma \textsf{S} \subseteq \mathcal{Y}$
, we have
$\Sigma \textsf{S} \subseteq \mathcal{Y}$
, we have
 $x,y \in \mathcal{X} \cap \mathcal{Y}$
. In the context of Section 2 this provides a decomposition of
$x,y \in \mathcal{X} \cap \mathcal{Y}$
. In the context of Section 2 this provides a decomposition of
 $\textsf{S}$
in
$\textsf{S}$
in
 $\Sigma^{-1}\textsf{S}^{\prime} * \textsf{S}^{\prime}$
, where
$\Sigma^{-1}\textsf{S}^{\prime} * \textsf{S}^{\prime}$
, where
 $\textsf{S}^{\prime}=\mathcal{X} \cap \mathcal{Y}$
is the coheart of the co-t-structure
$\textsf{S}^{\prime}=\mathcal{X} \cap \mathcal{Y}$
is the coheart of the co-t-structure
 $(\textsf{A}^{\prime},\textsf{B}^{\prime})$
.
$(\textsf{A}^{\prime},\textsf{B}^{\prime})$
.
We now define an inverse to the restricted map in Proposition 3·2. For a subcategory
![]() $\mathcal{T}$
of
$\mathcal{T}$
of
![]() $\textsf{mod}\, \textsf{S}$
, denote by
$\textsf{mod}\, \textsf{S}$
, denote by
![]() $F^{-1}(\mathcal{T})$
the full subcategory of
$F^{-1}(\mathcal{T})$
the full subcategory of
![]() $\textsf{C}$
whose objects are
$\textsf{C}$
whose objects are
![]() $\{c \in \textsf{C} \mid Fc \in \mathcal{T}\}$
.
$\{c \in \textsf{C} \mid Fc \in \mathcal{T}\}$
.
Proposition 3·6.
Let
![]() $\textsf{S}$
be a presilting subcategory of
$\textsf{S}$
be a presilting subcategory of
![]() $\textsf{T}$
and
$\textsf{T}$
and
![]() $\textsf{C} = \textsf{S} * \Sigma \textsf{S}$
. There is a well-defined map
$\textsf{C} = \textsf{S} * \Sigma \textsf{S}$
. There is a well-defined map

Proof. Let
![]() $(\mathcal{T},\mathcal{F})$
be a torsion pair in
$(\mathcal{T},\mathcal{F})$
be a torsion pair in
![]() $\textsf{mod}\, \textsf{S}$
whose torsion class is functorially finite,
$\textsf{mod}\, \textsf{S}$
whose torsion class is functorially finite,
![]() $\mathcal{Y} = \{c \in \textsf{C} \mid Fc \in \mathcal{T}\}$
and
$\mathcal{Y} = \{c \in \textsf{C} \mid Fc \in \mathcal{T}\}$
and
![]() $\mathcal{X} = {}{}^\perp (\Sigma \mathcal{Y})\cap \textsf{C}$
. The subcategories
$\mathcal{X} = {}{}^\perp (\Sigma \mathcal{Y})\cap \textsf{C}$
. The subcategories
![]() $\mathcal{Y}$
and
$\mathcal{Y}$
and
![]() $\mathcal{X}$
are closed under direct summands, since
$\mathcal{X}$
are closed under direct summands, since
![]() $\mathcal{T}$
is closed under direct summands and
$\mathcal{T}$
is closed under direct summands and
![]() $\mathcal{X}$
is defined as an orthogonal subcategory. We set
$\mathcal{X}$
is defined as an orthogonal subcategory. We set
![]() $\Theta\big( (\mathcal{T},\mathcal{F}) \big) = (\mathcal{X},\mathcal{Y})$
. We claim that
$\Theta\big( (\mathcal{T},\mathcal{F}) \big) = (\mathcal{X},\mathcal{Y})$
. We claim that
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair. We start by showing that
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair. We start by showing that
![]() $\mathcal{Y}$
is closed under extensions (in
$\mathcal{Y}$
is closed under extensions (in
![]() $\textsf{C}$
).
$\textsf{C}$
).
Let
![]() $y^{\prime} \stackrel{f}{\longrightarrow} y \longrightarrow y^{\prime\prime} \longrightarrow \Sigma y^{\prime}$
be an extension with
$y^{\prime} \stackrel{f}{\longrightarrow} y \longrightarrow y^{\prime\prime} \longrightarrow \Sigma y^{\prime}$
be an extension with
![]() $y^{\prime}, y^{\prime\prime} \in \mathcal{Y}$
. Applying F to this
$y^{\prime}, y^{\prime\prime} \in \mathcal{Y}$
. Applying F to this
![]() $\mathbb{E}$
-triangle in
$\mathbb{E}$
-triangle in
![]() $\textsf{C}$
gives an exact sequence
$\textsf{C}$
gives an exact sequence
![]() $Fy^{\prime} \stackrel{Ff}{\longrightarrow} Fy \longrightarrow Fy^{\prime\prime} \longrightarrow 0$
in
$Fy^{\prime} \stackrel{Ff}{\longrightarrow} Fy \longrightarrow Fy^{\prime\prime} \longrightarrow 0$
in
![]() $\textsf{mod}\, \textsf{S}$
since
$\textsf{mod}\, \textsf{S}$
since
![]() . We thus obtain a short exact sequence
. We thus obtain a short exact sequence
![]() $0 \to \text{im}\ Ff \to Fy \to Fy^{\prime\prime} \to 0$
. Since
$0 \to \text{im}\ Ff \to Fy \to Fy^{\prime\prime} \to 0$
. Since
![]() $\mathcal{T}$
is a torsion class, it follows that
$\mathcal{T}$
is a torsion class, it follows that
![]() $\text{im}\ Ff \in \mathcal{T}$
and
$\text{im}\ Ff \in \mathcal{T}$
and
![]() $Fy \in \mathcal{T}$
. Hence, we conclude that
$Fy \in \mathcal{T}$
. Hence, we conclude that
![]() $y \in \mathcal{Y}$
.
$y \in \mathcal{Y}$
.
For
![]() $s \in \textsf{S}$
, we will construct a triangle
$s \in \textsf{S}$
, we will construct a triangle
![]() $s \to y \to x \to \Sigma s$
in which
$s \to y \to x \to \Sigma s$
in which
![]() $y \in \mathcal{Y}$
and
$y \in \mathcal{Y}$
and
![]() $x \in \mathcal{X}$
, which will allow us to apply Lemma 3·4 to conclude that
$x \in \mathcal{X}$
, which will allow us to apply Lemma 3·4 to conclude that
![]() $(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
is a complete cotorsion pair in
![]() $\textsf{C}$
. First, we need to check that Lemma 3·4 applies. Since
$\textsf{C}$
. First, we need to check that Lemma 3·4 applies. Since
![]() $\mathcal{Y} \subseteq \textsf{C}$
, we have that
$\mathcal{Y} \subseteq \textsf{C}$
, we have that
![]() $\textsf{T}(\textsf{S},\Sigma \mathcal{Y}) = 0$
so that
$\textsf{T}(\textsf{S},\Sigma \mathcal{Y}) = 0$
so that
![]() $\textsf{S} \subseteq \mathcal{X}$
. Furthermore, if
$\textsf{S} \subseteq \mathcal{X}$
. Furthermore, if
![]() $s \in \textsf{S}$
then
$s \in \textsf{S}$
then
![]() $F(\Sigma s) = 0 \in \mathcal{T}$
so that
$F(\Sigma s) = 0 \in \mathcal{T}$
so that
![]() $\Sigma s \in \mathcal{Y}$
. By Remark 3·5(i), Lemma 3·4 applies.
$\Sigma s \in \mathcal{Y}$
. By Remark 3·5(i), Lemma 3·4 applies.
Now let
![]() $s \in \textsf{S}$
. Consider a left
$s \in \textsf{S}$
. Consider a left
![]() $\mathcal{T}$
-approximation
$\mathcal{T}$
-approximation
![]() $\varphi \colon Fs \to t$
of Fs in
$\varphi \colon Fs \to t$
of Fs in
![]() $\textsf{mod}\, \textsf{S}$
. Replacing t by an isomorphic object we can assume without loss of generality that
$\textsf{mod}\, \textsf{S}$
. Replacing t by an isomorphic object we can assume without loss of generality that
![]() $t= Fy$
for some
$t= Fy$
for some
![]() $y\in \mathcal{Y}$
. Let
$y\in \mathcal{Y}$
. Let
![]() $f \colon s \to y$
be such that
$f \colon s \to y$
be such that
![]() $Ff = \varphi$
. We claim that
$Ff = \varphi$
. We claim that
![]() $f \colon s \to y$
is a left
$f \colon s \to y$
is a left
![]() $\mathcal{Y}$
-approximation of s. Consider a morphism
$\mathcal{Y}$
-approximation of s. Consider a morphism
![]() $g \colon s \to y^{\prime}$
with
$g \colon s \to y^{\prime}$
with
![]() $y^{\prime} \in \mathcal{Y}$
. Applying F to f and g gives a diagram,
$y^{\prime} \in \mathcal{Y}$
. Applying F to f and g gives a diagram,
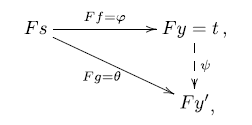
where the morphism
![]() $\psi \colon t \to Fy^{\prime}$
exists because
$\psi \colon t \to Fy^{\prime}$
exists because
![]() $\varphi$
is a left
$\varphi$
is a left
![]() $\mathcal{T}$
-approximation. Since the functor F is full, there exists
$\mathcal{T}$
-approximation. Since the functor F is full, there exists
![]() $h \colon y \to y^{\prime}$
such that
$h \colon y \to y^{\prime}$
such that
![]() $Fh = \psi$
. We claim that
$Fh = \psi$
. We claim that
![]() $g = hf$
.
$g = hf$
.
Applying F to
![]() $g - hf$
shows that
$g - hf$
shows that
![]() $g - hf = 0$
in
$g - hf = 0$
in
![]() $\textsf{C}/\Sigma \textsf{S}$
. Hence,
$\textsf{C}/\Sigma \textsf{S}$
. Hence,
![]() $g-hf$
factors through
$g-hf$
factors through
![]() $\Sigma \textsf{S}$
.
$\Sigma \textsf{S}$
.
Hence,
![]() $g - hf = 0$
in
$g - hf = 0$
in
![]() $\textsf{C}$
since
$\textsf{C}$
since
![]() $\textsf{S}$
is presilting. It follows that
$\textsf{S}$
is presilting. It follows that
![]() $f \colon s \to y$
is a left
$f \colon s \to y$
is a left
![]() $\mathcal{Y}$
-approximation of
$\mathcal{Y}$
-approximation of
![]() $\textsf{S}$
. As
$\textsf{S}$
. As
![]() $\textsf{T}$
is Krull–Schmidt, without loss of generality, we may assume that
$\textsf{T}$
is Krull–Schmidt, without loss of generality, we may assume that
![]() $f \colon s \to y$
is a minimal left
$f \colon s \to y$
is a minimal left
![]() $\mathcal{Y}$
-approximation and extend it to a distinguished triangle,
$\mathcal{Y}$
-approximation and extend it to a distinguished triangle,
![]() $s \stackrel{f}{\longrightarrow} y \longrightarrow x \longrightarrow \Sigma s$
. By the Wakamatsu lemma for triangulated categories, Lemma 1·1, we see that
$s \stackrel{f}{\longrightarrow} y \longrightarrow x \longrightarrow \Sigma s$
. By the Wakamatsu lemma for triangulated categories, Lemma 1·1, we see that
![]() $x \in {}{}^\perp (\Sigma \mathcal{Y})$
. Since y and
$x \in {}{}^\perp (\Sigma \mathcal{Y})$
. Since y and
![]() $\Sigma s$
are in
$\Sigma s$
are in
![]() $\textsf{C}$
, we get that
$\textsf{C}$
, we get that
![]() $x \in \textsf{C}$
, and so
$x \in \textsf{C}$
, and so
![]() $x\in \mathcal{X}$
.
$x\in \mathcal{X}$
.
Theorem 3·7. Suppose the hypotheses of Setup 3·1 hold. Then, there is a bijection
Moreover, if in addition
![]() $\textsf{mod}\, \textsf{S}\simeq\textsf{mod}\, A$
for an artin algebra A, there is a bijection between complete cotorsion pairs in
$\textsf{mod}\, \textsf{S}\simeq\textsf{mod}\, A$
for an artin algebra A, there is a bijection between complete cotorsion pairs in
![]() $\textsf{C}$
and functorially finite torsion pairs in
$\textsf{C}$
and functorially finite torsion pairs in
![]() $\textsf{mod}\, \textsf{S}$
.
$\textsf{mod}\, \textsf{S}$
.
Proof. We show that the maps
![]() $\Phi$
and
$\Phi$
and
![]() $\Theta$
defined in Propositions 3·2 and 3·6 are mutually inverse. Let
$\Theta$
defined in Propositions 3·2 and 3·6 are mutually inverse. Let
![]() $(\mathcal{X},\mathcal{Y})$
be a complete cotorsion pair in
$(\mathcal{X},\mathcal{Y})$
be a complete cotorsion pair in
![]() $\textsf{C}$
. By Proposition 3·2 we have
$\textsf{C}$
. By Proposition 3·2 we have
![]() $\Phi \big( (\mathcal{X},\mathcal{Y}) \big) = (\mathcal{T},\mathcal{F})$
, where
$\Phi \big( (\mathcal{X},\mathcal{Y}) \big) = (\mathcal{T},\mathcal{F})$
, where
![]() $\mathcal{T} = F\mathcal{Y}$
and
$\mathcal{T} = F\mathcal{Y}$
and
![]() $\mathcal{F} = \mathcal{T}{}^\perp$
in
$\mathcal{F} = \mathcal{T}{}^\perp$
in
![]() $\textsf{mod}\, \textsf{S}$
. Applying
$\textsf{mod}\, \textsf{S}$
. Applying
![]() $\Theta$
to
$\Theta$
to
![]() $(\mathcal{T},\mathcal{F})$
produces a complete cotorsion pair
$(\mathcal{T},\mathcal{F})$
produces a complete cotorsion pair
![]() $(\mathcal{X}^{\prime},\mathcal{Y}^{\prime})$
in which
$(\mathcal{X}^{\prime},\mathcal{Y}^{\prime})$
in which
![]() $\mathcal{Y}^{\prime} = \{ c \in \textsf{C} \mid Fc \in \mathcal{T}\}$
. Clearly,
$\mathcal{Y}^{\prime} = \{ c \in \textsf{C} \mid Fc \in \mathcal{T}\}$
. Clearly,
![]() $\mathcal{Y} \subseteq \mathcal{Y}^{\prime}$
. To see that
$\mathcal{Y} \subseteq \mathcal{Y}^{\prime}$
. To see that
![]() $\mathcal{Y}^{\prime} \subseteq \mathcal{Y}$
take
$\mathcal{Y}^{\prime} \subseteq \mathcal{Y}$
take
![]() $y^{\prime} \in \mathcal{Y}^{\prime}$
and observe that there is an isomorphism
$y^{\prime} \in \mathcal{Y}^{\prime}$
and observe that there is an isomorphism
![]() $\varphi \colon Fy \to Fy^{\prime}$
in
$\varphi \colon Fy \to Fy^{\prime}$
in
![]() $\textsf{mod}\, \textsf{S}$
for some
$\textsf{mod}\, \textsf{S}$
for some
![]() $y\in \mathcal{Y}$
by the definition of
$y\in \mathcal{Y}$
by the definition of
![]() $\mathcal{T}$
. Now, applying the same argument used to show that
$\mathcal{T}$
. Now, applying the same argument used to show that
![]() $F\mathcal{Y}$
is closed under quotients in the proof of Proposition 3·2 shows that
$F\mathcal{Y}$
is closed under quotients in the proof of Proposition 3·2 shows that
![]() $\textsf{T}(\mathcal{X},\Sigma y^{\prime}) = 0$
, whence by completeness of the cotorsion pair
$\textsf{T}(\mathcal{X},\Sigma y^{\prime}) = 0$
, whence by completeness of the cotorsion pair
![]() $(\mathcal{X},\mathcal{Y})$
and the fact that any complete cotorsion pair is a cotorsion pair, we get
$(\mathcal{X},\mathcal{Y})$
and the fact that any complete cotorsion pair is a cotorsion pair, we get
![]() $y^{\prime} \in \mathcal{Y}$
. As a cotorsionfree class determines a cotorsion pair uniquely, we get
$y^{\prime} \in \mathcal{Y}$
. As a cotorsionfree class determines a cotorsion pair uniquely, we get
![]() $(\mathcal{X}^{\prime},\mathcal{Y}^{\prime})=(\mathcal{X},\mathcal{Y})$
. The equality
$(\mathcal{X}^{\prime},\mathcal{Y}^{\prime})=(\mathcal{X},\mathcal{Y})$
. The equality
![]() $\Phi \Theta = 1$
follows from
$\Phi \Theta = 1$
follows from
![]() $F(F^{-1}(\mathcal{T}))=\mathcal{T}$
. The last statement follows from [
Reference Smalø31
, theorem].
$F(F^{-1}(\mathcal{T}))=\mathcal{T}$
. The last statement follows from [
Reference Smalø31
, theorem].
Acknowledgements
The authors would like to thank Steffen König for reading a preliminary version of this paper and two anonymous referees for their careful reading and valuable comments which have improved the exposition in the paper. The authors gratefully acknowledge support from the Representation Theory Group at Universität Stuttgart and the Lancaster University Department of Mathematics and Statistics’ Visitor Fund. The first named author was partially supported by EPSRC grant no. EP/V050524/1.