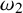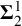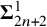1 Introduction
A central theme in descriptive set theory is the study of the complexity of various natural processes in terms of their ordinal lengths. In this line of thought, it is often shown that some ordinal is unreachable via processes of certain complexity. For example, there is no analytic well-founded relation of length
![]() $\omega _1$
, and so
$\omega _1$
, and so
![]() $\omega _1$
is inaccessible with respect to analytic surjections with domain
$\omega _1$
is inaccessible with respect to analytic surjections with domain
![]() ${\mathbb {R}}$
.
${\mathbb {R}}$
.
One way to study the complexity of a definability class
![]() $\boldsymbol {\Gamma }$
is to seek definable ways of assigning sets from
$\boldsymbol {\Gamma }$
is to seek definable ways of assigning sets from
![]() $\boldsymbol {\Gamma }$
to ordinals in such a way that no two ordinals are assigned to the same set. For example, if
$\boldsymbol {\Gamma }$
to ordinals in such a way that no two ordinals are assigned to the same set. For example, if
![]() ${\alpha }$
is a countable ordinal then we can assign to
${\alpha }$
is a countable ordinal then we can assign to
![]() ${\alpha }$
the set
${\alpha }$
the set
![]() $A_{\alpha }\subseteq {\mathbb {R}}$
consisting of those reals that code
$A_{\alpha }\subseteq {\mathbb {R}}$
consisting of those reals that code
![]() ${\alpha }$
in some natural way. Each
${\alpha }$
in some natural way. Each
![]() $A_{\alpha }$
is Borel and clearly the assignment
$A_{\alpha }$
is Borel and clearly the assignment
![]() ${\alpha }\mapsto A_{\alpha }$
is definable. However, a remarkable theorem of Harrington (see [Reference Harrington5, Theorem 4.5]) says that such an assignment cannot exist if we further demand that each set comes from a specific Borel class.
${\alpha }\mapsto A_{\alpha }$
is definable. However, a remarkable theorem of Harrington (see [Reference Harrington5, Theorem 4.5]) says that such an assignment cannot exist if we further demand that each set comes from a specific Borel class.
Below
![]() $\mathsf {{AD}}$
is the
$\mathsf {{AD}}$
is the
![]() $\mathsf {{Axiom\ of\ Determinacy}}$
,
$\mathsf {{Axiom\ of\ Determinacy}}$
,
![]() $\mathsf {{ZF}}$
are the axioms of the Zermelo-Fraenkel set theory (which does not include the
$\mathsf {{ZF}}$
are the axioms of the Zermelo-Fraenkel set theory (which does not include the
![]() $\mathsf {{Axiom\ of\ Choice}})$
and
$\mathsf {{Axiom\ of\ Choice}})$
and
![]() $\mathsf {{DC}}$
is the axiom of dependent choice.
$\mathsf {{DC}}$
is the axiom of dependent choice.
Theorem 1.1 (Harrington).
Assume
![]() $\mathsf {{AD+ZF+DC}}$
. If
$\mathsf {{AD+ZF+DC}}$
. If
![]() ${\beta }<\omega _1$
then there is no injection
${\beta }<\omega _1$
then there is no injection
![]() $f:\omega _1\rightarrow \boldsymbol {\Pi }^0_{\beta }$
.
$f:\omega _1\rightarrow \boldsymbol {\Pi }^0_{\beta }$
.
Notice that the content of Harrington’s theorem isn’t that
![]() ${\vert \boldsymbol {\Pi }^0_{\beta } \vert } <\omega _1$
, which is in fact not true as
${\vert \boldsymbol {\Pi }^0_{\beta } \vert } <\omega _1$
, which is in fact not true as
![]() $\boldsymbol {\Pi }^0_{\beta }$
has continuum many distinct sets. The content of Harrington’s theorem is that if we fix
$\boldsymbol {\Pi }^0_{\beta }$
has continuum many distinct sets. The content of Harrington’s theorem is that if we fix
![]() ${\beta }<\omega _1$
and devise an algorithm that picks a new set from the Borel class
${\beta }<\omega _1$
and devise an algorithm that picks a new set from the Borel class
![]() $\boldsymbol {\Pi }^0_{\beta }$
then at some stage less than
$\boldsymbol {\Pi }^0_{\beta }$
then at some stage less than
![]() $\omega _1$
our algorithm will stop outputting anythingFootnote
1
.
$\omega _1$
our algorithm will stop outputting anythingFootnote
1
.
Harrington’s theorem was recently used by Marks and Day to prove the decomposability conjecture (see [Reference Day and Marks4]).
Definition 1.2. Suppose
![]() $\boldsymbol {\Gamma }\subseteq {\wp }({\mathbb {R}})$
. We say
$\boldsymbol {\Gamma }\subseteq {\wp }({\mathbb {R}})$
. We say
![]() ${\kappa }$
is
${\kappa }$
is
![]() $\boldsymbol {\Gamma }$
-reachable if there is an injection
$\boldsymbol {\Gamma }$
-reachable if there is an injection
![]() $f:\kappa \rightarrow \boldsymbol {\Gamma }$
, and that
$f:\kappa \rightarrow \boldsymbol {\Gamma }$
, and that
![]() ${\kappa }$
is
${\kappa }$
is
![]() $\boldsymbol {\Gamma }$
-unreachable if it is not
$\boldsymbol {\Gamma }$
-unreachable if it is not
![]() $\boldsymbol {\Gamma }$
-reachable.
$\boldsymbol {\Gamma }$
-reachable.
Let
![]() $\Theta $
be the least ordinal that is not a surjective image of
$\Theta $
be the least ordinal that is not a surjective image of
![]() ${\mathbb {R}}$
. Then in
${\mathbb {R}}$
. Then in
![]() $L({\mathbb {R}})$
,
$L({\mathbb {R}})$
,
![]() $\Theta $
is
$\Theta $
is
![]() ${\wp }({\mathbb {R}})$
-reachable. Indeed, in
${\wp }({\mathbb {R}})$
-reachable. Indeed, in
![]() $L({\mathbb {R}})$
, if
$L({\mathbb {R}})$
, if
![]() ${\alpha }<\Theta $
then there is a pre-well-ordering (pwoFootnote
2
)
${\alpha }<\Theta $
then there is a pre-well-ordering (pwoFootnote
2
)
![]() $\leq ^*$
of
$\leq ^*$
of
![]() ${\mathbb {R}}$
that is ordinal definable and has length
${\mathbb {R}}$
that is ordinal definable and has length
![]() ${\alpha }$
. We can then let
${\alpha }$
. We can then let
![]() $\leq ^*_{\alpha }$
be the least ordinal definable pwo of
$\leq ^*_{\alpha }$
be the least ordinal definable pwo of
![]() ${\mathbb {R}}$
that has length
${\mathbb {R}}$
that has length
![]() ${\alpha }$
. Thus we have assigned an ordinal definable pwo of length
${\alpha }$
. Thus we have assigned an ordinal definable pwo of length
![]() ${\alpha }$
to each
${\alpha }$
to each
![]() ${\alpha }$
in an ordinal definable manner.
${\alpha }$
in an ordinal definable manner.
The above construction has a well-known Harrington-type analogue. Assume
![]() $\mathsf {{AD}}$
. If
$\mathsf {{AD}}$
. If
![]() ${\beta }<\Theta $
and
${\beta }<\Theta $
and
![]() $\boldsymbol {\Gamma }$
consists of those sets of reals whose Wadge rankFootnote
3
is
$\boldsymbol {\Gamma }$
consists of those sets of reals whose Wadge rankFootnote
3
is
![]() $\leq {\beta }$
then
$\leq {\beta }$
then
![]() $\Theta $
is
$\Theta $
is
![]() $\boldsymbol {\Gamma }$
-unreachable. This is because Wadge’s lemmaFootnote
4
implies that there is a surjection
$\boldsymbol {\Gamma }$
-unreachable. This is because Wadge’s lemmaFootnote
4
implies that there is a surjection
![]() $f:{\mathbb {R}}\rightarrow \boldsymbol {\Gamma }$
, so if
$f:{\mathbb {R}}\rightarrow \boldsymbol {\Gamma }$
, so if
![]() $\Theta $
was
$\Theta $
was
![]() $\boldsymbol {\Gamma }$
-reachable then we could find a surjection
$\boldsymbol {\Gamma }$
-reachable then we could find a surjection
![]() $g:{\mathbb {R}}\rightarrow \Theta $
.
$g:{\mathbb {R}}\rightarrow \Theta $
.
Perhaps the most natural way of showing that
![]() ${\kappa }$
is
${\kappa }$
is
![]() $\boldsymbol {\Gamma }$
-reachable is to find a surjection
$\boldsymbol {\Gamma }$
-reachable is to find a surjection
![]() $f: {\mathbb {R}}\rightarrow {\kappa }$
such that for each
$f: {\mathbb {R}}\rightarrow {\kappa }$
such that for each
![]() ${\alpha }<{\kappa }$
,
${\alpha }<{\kappa }$
,
![]() $A_{\alpha }=\{ x\in {\mathbb {R}}: f(x)<{\alpha }\}\in \boldsymbol {\Gamma }$
. In this case, the sets
$A_{\alpha }=\{ x\in {\mathbb {R}}: f(x)<{\alpha }\}\in \boldsymbol {\Gamma }$
. In this case, the sets
![]() $(A_{\alpha }: {\alpha }<{\kappa })$
form a strictly
$(A_{\alpha }: {\alpha }<{\kappa })$
form a strictly
![]() $\subset $
-increasing sequence. Thus, the fact that
$\subset $
-increasing sequence. Thus, the fact that
![]() ${\kappa }$
is not
${\kappa }$
is not
![]() $\boldsymbol {\Gamma }$
-reachable via a strictly
$\boldsymbol {\Gamma }$
-reachable via a strictly
![]() $\subset $
-increasing sequence implies that
$\subset $
-increasing sequence implies that
![]() $\kappa $
is inaccessible with respect to
$\kappa $
is inaccessible with respect to
![]() $\boldsymbol {\Gamma }$
-surjections.
$\boldsymbol {\Gamma }$
-surjections.
An equivalence relation on
![]() ${\mathbb {R}}$
is called thin if it does not have a perfect set of inequivalent elements. Assuming
${\mathbb {R}}$
is called thin if it does not have a perfect set of inequivalent elements. Assuming
![]() $\mathsf {{AD}}$
holds in
$\mathsf {{AD}}$
holds in
![]() $L({\mathbb {R}})$
, or in fact just
$L({\mathbb {R}})$
, or in fact just
![]() $\mathsf {{AD^+}}$
, Woodin (see [Reference Caicedo and Ketchersid2], [Reference Chan3] and [Reference Hjorth6, Theorem 0.3]), generalizing Harrington’s earlier result on
$\mathsf {{AD^+}}$
, Woodin (see [Reference Caicedo and Ketchersid2], [Reference Chan3] and [Reference Hjorth6, Theorem 0.3]), generalizing Harrington’s earlier result on
![]() $\Pi ^1_2$
-equivalence relations, showed that if
$\Pi ^1_2$
-equivalence relations, showed that if
![]() $E\subseteq {\mathbb {R}}^2$
is a thin equivalence relation then the set
$E\subseteq {\mathbb {R}}^2$
is a thin equivalence relation then the set
![]() $\{[x]_E: x\in {\mathbb {R}}\}$
is well-orderable. Thus, assuming
$\{[x]_E: x\in {\mathbb {R}}\}$
is well-orderable. Thus, assuming
![]() $\mathsf {{AD^+}}$
, if
$\mathsf {{AD^+}}$
, if
![]() ${\kappa }$
is
${\kappa }$
is
![]() $\boldsymbol {\Gamma }$
-unreachable then any thin equivalence relation
$\boldsymbol {\Gamma }$
-unreachable then any thin equivalence relation
![]() $E\in {\wp }({\mathbb {R}}^2)\cap \boldsymbol {\Gamma }$
has
$E\in {\wp }({\mathbb {R}}^2)\cap \boldsymbol {\Gamma }$
has
![]() $<{\kappa }$
many equivalence classes.
$<{\kappa }$
many equivalence classes.
Below
![]() $\boldsymbol {\delta }^1_{n}$
is the supremum of the lengths of
$\boldsymbol {\delta }^1_{n}$
is the supremum of the lengths of
![]() $\boldsymbol {\Delta }^1_n$
pre-well-orderings of
$\boldsymbol {\Delta }^1_n$
pre-well-orderings of
![]() ${\mathbb {R}}$
. In a seminal work, Jackson, building on an early work of Kechris, Kunen, Martin, Moschovakis and Solovay computed
${\mathbb {R}}$
. In a seminal work, Jackson, building on an early work of Kechris, Kunen, Martin, Moschovakis and Solovay computed
![]() $\boldsymbol {\delta }^1_n$
. Before Jackson’s work, it was known that assuming
$\boldsymbol {\delta }^1_n$
. Before Jackson’s work, it was known that assuming
![]() $\mathsf {{AD}}^{L({\mathbb {R}})}$
,
$\mathsf {{AD}}^{L({\mathbb {R}})}$
,
![]() $\delta ^1_1=\aleph _1$
,
$\delta ^1_1=\aleph _1$
,
![]() $\delta ^1_2=\aleph _2^{L({\mathbb {R}})}$
,
$\delta ^1_2=\aleph _2^{L({\mathbb {R}})}$
,
![]() $\delta ^1_3=\aleph _{\omega +1}^{L({\mathbb {R}})}$
,
$\delta ^1_3=\aleph _{\omega +1}^{L({\mathbb {R}})}$
,
![]() $\delta ^1_4=\aleph _{\omega +2}^{L({\mathbb {R}})}$
, for every n,
$\delta ^1_4=\aleph _{\omega +2}^{L({\mathbb {R}})}$
, for every n,
![]() $\delta ^1_{2n+2}=((\delta ^1_{2n+1})^+)^{L({\mathbb {R}})}$
, for every n,
$\delta ^1_{2n+2}=((\delta ^1_{2n+1})^+)^{L({\mathbb {R}})}$
, for every n,
![]() $\delta ^1_{2n+1}$
is itself a successor cardinal of
$\delta ^1_{2n+1}$
is itself a successor cardinal of
![]() $L({\mathbb {R}})$
and
$L({\mathbb {R}})$
and
![]() $\boldsymbol {\Sigma }^1_{2n+2}$
is exactly the collection of
$\boldsymbol {\Sigma }^1_{2n+2}$
is exactly the collection of
![]() ${\delta }^1_{2n+1}$
-Suslin setsFootnote
5
. In [Reference Jackson12], Jackson computed the remaining
${\delta }^1_{2n+1}$
-Suslin setsFootnote
5
. In [Reference Jackson12], Jackson computed the remaining
![]() $\delta ^1_n$
’s and in particular, showed that
$\delta ^1_n$
’s and in particular, showed that
![]() $\delta ^1_5=\aleph _{\omega ^{\omega ^\omega }+1}^{L({\mathbb {R}})}$
.
$\delta ^1_5=\aleph _{\omega ^{\omega ^\omega }+1}^{L({\mathbb {R}})}$
.
In [Reference Kechris17], Kechris proved a partial generalization of Harrington’s theoremFootnote 6 .
Theorem 1.3 (Kechris).
Assume
![]() $\mathsf {{ZF+AD+DC}}$
. Then
$\mathsf {{ZF+AD+DC}}$
. Then
![]() $\delta ^1_{2n+2}$
is
$\delta ^1_{2n+2}$
is
![]() $\boldsymbol {\Delta }^1_{2n+1}$
-unreachable.
$\boldsymbol {\Delta }^1_{2n+1}$
-unreachable.
Moreover, in [Reference Kechris17], Kechris showed that there is no
![]() $f:\boldsymbol {\delta }^1_{2n+2}\rightarrow \boldsymbol {\Sigma }^1_{2n+2}$
such that for all
$f:\boldsymbol {\delta }^1_{2n+2}\rightarrow \boldsymbol {\Sigma }^1_{2n+2}$
such that for all
![]() ${\alpha }, {\beta }<{\delta }^1_{2n+2}$
, if
${\alpha }, {\beta }<{\delta }^1_{2n+2}$
, if
![]() ${\alpha }\not ={\beta }$
then
${\alpha }\not ={\beta }$
then
![]() $f({\alpha })\cap f({\beta })=\emptyset $
. In Chapter 4 of [Reference Kechris17], Kechris conjectured that in fact a general form of Harrington-type theorem is true for projective pointclasses.
$f({\alpha })\cap f({\beta })=\emptyset $
. In Chapter 4 of [Reference Kechris17], Kechris conjectured that in fact a general form of Harrington-type theorem is true for projective pointclasses.
Conjecture 1.4 (Kechris 1st Conjecture).
Assume
![]() $\mathsf {{ZF+AD+DC}}$
. Then
$\mathsf {{ZF+AD+DC}}$
. Then
![]() $\boldsymbol {\delta }^1_{2n+2}$
is
$\boldsymbol {\delta }^1_{2n+2}$
is
![]() $\boldsymbol {\Delta }^1_{2n+2}$
-unreachable.
$\boldsymbol {\Delta }^1_{2n+2}$
-unreachable.
In [Reference Jackson11], Jackson proved Kechris’ 1st Conjecture by establishing the following remarkable theorem (see [Reference Jackson11, Corollary 4.5]).
Theorem 1.5 (Jackson).
Assume
![]() $\mathsf {{ZF+AD+DC}}$
. Then
$\mathsf {{ZF+AD+DC}}$
. Then
![]() ${\delta }^1_{2n+2}$
is
${\delta }^1_{2n+2}$
is
![]() $\boldsymbol {\Delta }^1_{2n+2}$
-unreachable.
$\boldsymbol {\Delta }^1_{2n+2}$
-unreachable.
Jackson’s proof used his computation of the projective ordinals. In particular, that
![]() $\boldsymbol {\delta }^1_{2n+1}$
has the strong partition property. In the last paragraph of [Reference Kechris17, Chapter 4], Kechris made the following stronger conjecture.
$\boldsymbol {\delta }^1_{2n+1}$
has the strong partition property. In the last paragraph of [Reference Kechris17, Chapter 4], Kechris made the following stronger conjecture.
Conjecture 1.6 (Kechris 2nd Conjecture).
Assume
![]() $\mathsf {{ZF+AD+DC}}$
. Then
$\mathsf {{ZF+AD+DC}}$
. Then
![]() $\boldsymbol {\delta }^1_{2n+2}$
is
$\boldsymbol {\delta }^1_{2n+2}$
is
![]() $\boldsymbol {\Sigma }^1_{2n+2}$
-unreachable.
$\boldsymbol {\Sigma }^1_{2n+2}$
-unreachable.
This was partially resolved by Jackson and Martin who showed the following (see the Theorem on Page 84 of [Reference Jackson11]).
Theorem 1.7 (Jackson-Martin).
Assume
![]() $\mathsf {{ZF+AD+DC}}$
. Then there is no strictly
$\mathsf {{ZF+AD+DC}}$
. Then there is no strictly
![]() $\subset $
-increasing or
$\subset $
-increasing or
![]() $\subset $
-decreasing sequence
$\subset $
-decreasing sequence
![]() $(A_{\alpha }:{\alpha }<\boldsymbol {\delta }^1_{2n+2})\subseteq \boldsymbol {\Sigma }^1_{2n+2}$
.
$(A_{\alpha }:{\alpha }<\boldsymbol {\delta }^1_{2n+2})\subseteq \boldsymbol {\Sigma }^1_{2n+2}$
.
Chuang then generalized Theorem 1.7 by showing that in fact there are no strictly
![]() $\subset $
-increasing or
$\subset $
-increasing or
![]() $\subset $
-decreasing sequences of
$\subset $
-decreasing sequences of
![]() ${\boldsymbol {\Gamma }}$
sets of length
${\boldsymbol {\Gamma }}$
sets of length
![]() ${\delta }_{\boldsymbol {\Gamma }}^+$
provided
${\delta }_{\boldsymbol {\Gamma }}^+$
provided
![]() $\boldsymbol {\Gamma }$
is closed under
$\boldsymbol {\Gamma }$
is closed under
![]() $\forall ^{\mathbb {R}}$
,
$\forall ^{\mathbb {R}}$
,
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
and that
$\vee $
and that
![]() $\boldsymbol {\Gamma }$
has the pre-well-ordering property (see [Reference Jackson13, Theorem 3.5]). Here
$\boldsymbol {\Gamma }$
has the pre-well-ordering property (see [Reference Jackson13, Theorem 3.5]). Here
![]() ${\delta }_{\boldsymbol {\Gamma }}$
is the supremum of the lengths of
${\delta }_{\boldsymbol {\Gamma }}$
is the supremum of the lengths of
![]() $\boldsymbol {\Delta }_{\boldsymbol {\Gamma }}$
-pwosFootnote
7
.
$\boldsymbol {\Delta }_{\boldsymbol {\Gamma }}$
-pwosFootnote
7
.
Kechris’ 2nd Conjecture also appears in Kanamori’s book where it appears as [Reference Kanamori16, Question 30.21]. In [Reference Hjorth7], Hjorth verified Kechris’ 2nd Conjecture for
![]() $n=0$
using techniques from inner model theory. In this paper, we prove Kechris’ 2nd Conjecture.
$n=0$
using techniques from inner model theory. In this paper, we prove Kechris’ 2nd Conjecture.
Theorem 1.8 (Hjorth-S.).
Assume
![]() $\mathsf {{ZF+AD+DC}}$
. Then
$\mathsf {{ZF+AD+DC}}$
. Then
![]() $\boldsymbol {\delta }^1_{2n+2}$
is
$\boldsymbol {\delta }^1_{2n+2}$
is
![]() $\boldsymbol {\Sigma }^1_{2n+2}$
-unreachable.
$\boldsymbol {\Sigma }^1_{2n+2}$
-unreachable.
The following is an immediate corollary of Theorem 1.8 and Woodin’s result mentioned aboveFootnote
8
. The case
![]() $n=0$
is due to Hjorth ([Reference Hjorth7]).
$n=0$
is due to Hjorth ([Reference Hjorth7]).
Corollary 1.9. Assume
![]() $\mathsf {{ZFC}}+\mathsf {{AD}}^{L({\mathbb {R}})}$
. If E is a thin
$\mathsf {{ZFC}}+\mathsf {{AD}}^{L({\mathbb {R}})}$
. If E is a thin
![]() $\boldsymbol {\Pi }^1_{2n+2}$
-equivalence relation then it has
$\boldsymbol {\Pi }^1_{2n+2}$
-equivalence relation then it has
![]() $\leq \boldsymbol {\delta }^1_{2n+1}$
-many equivalence classes. In particular, any thin
$\leq \boldsymbol {\delta }^1_{2n+1}$
-many equivalence classes. In particular, any thin
![]() $\boldsymbol {\Pi }^1_2$
equivalence relation has
$\boldsymbol {\Pi }^1_2$
equivalence relation has
![]() $\leq \omega _1$
-equivalence classes and any thin
$\leq \omega _1$
-equivalence classes and any thin
![]() $\boldsymbol {\Pi }^1_4$
equivalence relation has
$\boldsymbol {\Pi }^1_4$
equivalence relation has
![]() $\leq \aleph _{\omega +1}^{L({\mathbb {R}})}$
-equivalence classes.
$\leq \aleph _{\omega +1}^{L({\mathbb {R}})}$
-equivalence classes.
Our proof of Theorem 1.8 uses inner model theory and directly builds on [Reference Hjorth7] and [Reference Sargsyan29]. From [Reference Hjorth7], we will mainly use the reflection argument
Footnote
9
used by Hjorth which appears on page 104 of [Reference Hjorth7]. We state it as Lemma 4.7. According to Page 95 of [Reference Hjorth7], Hjorth’s reflection argument is inspired by Woodin’s unpublished proof of the pre-well-ordering property for
![]() $\Pi ^1_3$
. We strongly believe that it can have many other applications.
$\Pi ^1_3$
. We strongly believe that it can have many other applications.
The reason that Theorem 1.8 has been open since [Reference Sargsyan29] is that the proof in [Reference Hjorth7] uses the well-known Kechris-Martin theorem (see (i) and (ii) on page 105 of [Reference Hjorth7], see [Reference Kechris and Martin19] for the Kechris-Martin theorem). It has been quite challenging to extend Kechris-Martin result in a way that could be useful to us. However, as it turns out, the use of Kechris-Martin theorem can be removed from [Reference Hjorth7], and this is our main new idea (see Section 4.5). Clearly Theorem 1.5 is a corollary of Theorem 1.8, and so the inner model proof of Theorem 1.5 avoids the sophisticated machinery developed by Jackson in [Reference Jackson12], though it uses inner model theory.
The main technical ingredient of our argument is the directed systems of mice. This is the system that Steel used in his calculation of
![]() $(\mathrm {{HOD}}|\Theta )^{L({\mathbb {R}})}$
([Reference Steel38]) and Woodin used in his calculation of the
$(\mathrm {{HOD}}|\Theta )^{L({\mathbb {R}})}$
([Reference Steel38]) and Woodin used in his calculation of the
![]() $\mathrm {{HOD}}^{L({\mathbb {R}})}$
. The theory of these directed systems of mice has appeared in [Reference Steel and Woodin40]. We will use the material developed in [Reference Steel and Woodin40, Chapter 6]. [Reference Neeman26] has a nice introduction to the subject.
$\mathrm {{HOD}}^{L({\mathbb {R}})}$
. The theory of these directed systems of mice has appeared in [Reference Steel and Woodin40]. We will use the material developed in [Reference Steel and Woodin40, Chapter 6]. [Reference Neeman26] has a nice introduction to the subject.
We expect that our methods will generalize and settle the following conjecture.
![]() $\mathsf {{AD}}^+$
is an extension of
$\mathsf {{AD}}^+$
is an extension of
![]() $\mathsf {{AD}}$
introduced by Woodin ([Reference Larson21]).
$\mathsf {{AD}}$
introduced by Woodin ([Reference Larson21]).
Conjecture 1.10. Assume
![]() $\mathsf {{AD}}^+$
. Suppose
$\mathsf {{AD}}^+$
. Suppose
![]() ${\kappa }$
is a regular Suslin cardinal and
${\kappa }$
is a regular Suslin cardinal and
![]() $\boldsymbol {\Gamma }$
is the pointclass of
$\boldsymbol {\Gamma }$
is the pointclass of
![]() ${\kappa }$
-Suslin sets. Then
${\kappa }$
-Suslin sets. Then
![]() ${\kappa }^+$
is
${\kappa }^+$
is
![]() $\boldsymbol {\Gamma }$
-unreachable.
$\boldsymbol {\Gamma }$
-unreachable.
Conjecture 1.10 is a global conjecture like those made by Jackson (see [Reference Jackson13, Conjecture 6.4], the conjectures in [Reference Jackson10] and [41, Problem 19]) though perhaps given the result of this paper Conjecture 1.10 is somewhat easier than those made by Jackson. Such global conjectures test our understanding of projective sets. It is one of the deepest mysteries of descriptive set theory that, assuming
![]() $\mathsf {{AD}}$
, the complete theory of analytic and co-analytic sets doesn’t immediately generalize to projective hierarchy. Perhaps the most well-known example of this phenomenon is that
$\mathsf {{AD}}$
, the complete theory of analytic and co-analytic sets doesn’t immediately generalize to projective hierarchy. Perhaps the most well-known example of this phenomenon is that
![]() $\Delta ^1_3$
to
$\Delta ^1_3$
to
![]() $(\Pi ^1_3, \Sigma ^1_3)$
is not the same as
$(\Pi ^1_3, \Sigma ^1_3)$
is not the same as
![]() $\Delta ^1_1$
to
$\Delta ^1_1$
to
![]() $(\Pi ^1_1, \Sigma ^1_1)$
(see [Reference Kechris, Martin and Solovay20]). From a current point of view, it seems that the function
$(\Pi ^1_1, \Sigma ^1_1)$
(see [Reference Kechris, Martin and Solovay20]). From a current point of view, it seems that the function
![]() $x\mapsto x^\#$
provides singularly magical coding of subsets of
$x\mapsto x^\#$
provides singularly magical coding of subsets of
![]() $\omega _1$
, and that coding – which was used by Martin to establish the strong partition property for
$\omega _1$
, and that coding – which was used by Martin to establish the strong partition property for
![]() $\omega _1$
(see [Reference Kanamori16, Theorem 28.12]) and by Kechris-Martin to establish their celebrated Kechris-Martin theorem (see [Reference Kechris and Martin19]) – doesn’t yet have a proper inner model theoretic generalization to higher levels of the projective hierarchy and beyond. Our current understanding is based on Jackson’s deep analysis of measures (see [Reference Jackson13]). The fact that global conjectures such as Conjecture 1.10 and Jackson’s conjectures are still open seems to suggest that our current understanding of the projective hierarchy, just like it was with our understanding of
$\omega _1$
(see [Reference Kanamori16, Theorem 28.12]) and by Kechris-Martin to establish their celebrated Kechris-Martin theorem (see [Reference Kechris and Martin19]) – doesn’t yet have a proper inner model theoretic generalization to higher levels of the projective hierarchy and beyond. Our current understanding is based on Jackson’s deep analysis of measures (see [Reference Jackson13]). The fact that global conjectures such as Conjecture 1.10 and Jackson’s conjectures are still open seems to suggest that our current understanding of the projective hierarchy, just like it was with our understanding of
![]() $(\Pi ^1_1, \Sigma ^1_1)$
, may not be the final one, as whatever methods we discover to settle these global conjectures, the projective case will have to be the special case of these conjectures, and so these yet-to-be-discovered ideas will come with new insight into the projective hierarchy.
$(\Pi ^1_1, \Sigma ^1_1)$
, may not be the final one, as whatever methods we discover to settle these global conjectures, the projective case will have to be the special case of these conjectures, and so these yet-to-be-discovered ideas will come with new insight into the projective hierarchy.
2 Remarks, notations and terminology
Experts can skip this and the following sections and directly go to Section 4. The results in Section 3 are not fundamentally new and go back to [Reference Steel37]. However, [Reference Steel37] doesn’t state them in the exact form that we need. Below we make some remarks, and set up our notation and terminology.
Review 2.1. Basic concepts from inner model theory:
The reader unfamiliar with basic concepts of inner model theory might find it helpful to consult [Reference Steel39]. Also, the introduction of [Reference Neeman26] is accessible and introduces many of the concepts that we need. Extenders were treated both in [Reference Jech14] and [Reference Kanamori16].
-
1. Suppose
 $x\in \mathsf {{HC}}$
Footnote
10
is such that there is a wellordering of x in
$x\in \mathsf {{HC}}$
Footnote
10
is such that there is a wellordering of x in
 $L_1[x]$
which can be defined without parameters over
$L_1[x]$
which can be defined without parameters over
 $L_0[x]$
Footnote
11
. We say
$L_0[x]$
Footnote
11
. We say
 $({\mathcal {M}}, \Phi )$
is an x-mouse pair if
$({\mathcal {M}}, \Phi )$
is an x-mouse pair if
 ${\mathcal {M}}$
is an x-premouse and
${\mathcal {M}}$
is an x-premouse and
 $\Phi $
is an
$\Phi $
is an
 $(\omega _1, \omega _1)$
-iteration strategy for
$(\omega _1, \omega _1)$
-iteration strategy for
 ${\mathcal {M}}$
(e.g., see [Reference Steel39, Definition 2.19, 3.9 and 4.4]Footnote
12
)Footnote
13
. We say
${\mathcal {M}}$
(e.g., see [Reference Steel39, Definition 2.19, 3.9 and 4.4]Footnote
12
)Footnote
13
. We say
 $({\mathcal {M}}, \Phi )$
is a countable mouse pair if
$({\mathcal {M}}, \Phi )$
is a countable mouse pair if
 ${\mathcal {M}}$
is countable. We will often say that
${\mathcal {M}}$
is countable. We will often say that
 ${\mathcal {M}}$
is a premouse or
${\mathcal {M}}$
is a premouse or
 $({\mathcal {M}}, \Phi )$
is a mouse pair without mentioning the x.
$({\mathcal {M}}, \Phi )$
is a mouse pair without mentioning the x. -
2. Suppose
 ${\mathcal {M}}=\mathcal {J}_{\beta }^{\vec {E}}$
is a premouse and
${\mathcal {M}}=\mathcal {J}_{\beta }^{\vec {E}}$
is a premouse and
 ${\alpha }\leq \mathsf {{Ord}}\cap {\mathcal {M}}$
. We let
${\alpha }\leq \mathsf {{Ord}}\cap {\mathcal {M}}$
. We let
 $\vec {E}^{\mathcal {M}}$
be the extender sequence of
$\vec {E}^{\mathcal {M}}$
be the extender sequence of
 ${\mathcal {M}}$
. Because we will allow padded iterations, we let
${\mathcal {M}}$
. Because we will allow padded iterations, we let
 $\mathrm { dom}(\vec {E})^{\mathcal {M}}={\beta }$
and for those
$\mathrm { dom}(\vec {E})^{\mathcal {M}}={\beta }$
and for those
 ${\gamma} $
such that
${\gamma} $
such that
 ${\mathcal {M}}$
doesn’t have an extender indexed at
${\mathcal {M}}$
doesn’t have an extender indexed at
 ${\gamma} $
, we set
${\gamma} $
, we set
 $\vec {E}^{\mathcal {M}}({\gamma} )=\emptyset $
. We then let
$\vec {E}^{\mathcal {M}}({\gamma} )=\emptyset $
. We then let
 ${\mathcal {M}}|{\alpha }=(\mathcal {J}_{\omega {\alpha }}^{\vec {E}\restriction \omega {\alpha }}, \vec {E}\restriction \omega {\alpha }, \in )$
and
${\mathcal {M}}|{\alpha }=(\mathcal {J}_{\omega {\alpha }}^{\vec {E}\restriction \omega {\alpha }}, \vec {E}\restriction \omega {\alpha }, \in )$
and
 ${\mathcal {M}}||{\alpha }=(\mathcal {J}_{\omega {\alpha }}^{\vec {E}\restriction \omega {\alpha }}, \vec {E}\restriction \omega {\alpha }, \vec {E}(\omega {\alpha }), \in )$
.
${\mathcal {M}}||{\alpha }=(\mathcal {J}_{\omega {\alpha }}^{\vec {E}\restriction \omega {\alpha }}, \vec {E}\restriction \omega {\alpha }, \vec {E}(\omega {\alpha }), \in )$
. -
3. Suppose
 ${\mathcal {M}}$
is a premouse. We say
${\mathcal {M}}$
is a premouse. We say
 $\eta $
is a cutpoint of
$\eta $
is a cutpoint of
 ${\mathcal {M}}$
if for all
${\mathcal {M}}$
if for all
 $E\in \vec {E}^{\mathcal {M}}$
with the property that
$E\in \vec {E}^{\mathcal {M}}$
with the property that
 $\mathrm {crit }(E)<\eta $
,
$\mathrm {crit }(E)<\eta $
,
 $\mathrm {lh}(E)\leq \eta $
.
$\mathrm {lh}(E)\leq \eta $
. -
4. Under
 $\mathsf {{AD}}$
, as
$\mathsf {{AD}}$
, as
 $\omega _1$
is measurable,
$\omega _1$
is measurable,
 $\omega _1$
-iterabilityFootnote
14
is what is needed to prove the
$\omega _1$
-iterabilityFootnote
14
is what is needed to prove the
 $\mathsf {{Comparison\ Theorem}}$
for countable mouse pairs (see [Reference Steel39, Theorem 3.11]).
$\mathsf {{Comparison\ Theorem}}$
for countable mouse pairs (see [Reference Steel39, Theorem 3.11]). -
5. For a definition of an iterationFootnote 15 and an iteration strategy see [Reference Steel39, Definition 3.3 and 3.9]. Given an iteration
 ${\mathcal {T}}$
of a premouse
${\mathcal {T}}$
of a premouse
 ${\mathcal {M}}$
, we write
${\mathcal {M}}$
, we write
 ${\mathcal {T}}=(({\mathcal {M}}_{\alpha }: {\alpha }<\mathrm {lh}({\mathcal {T}})), (E_{\alpha }: {\alpha }+1<\mathrm {lh}({\mathcal {T}})), \mathcal {D}, T)$
where
${\mathcal {T}}=(({\mathcal {M}}_{\alpha }: {\alpha }<\mathrm {lh}({\mathcal {T}})), (E_{\alpha }: {\alpha }+1<\mathrm {lh}({\mathcal {T}})), \mathcal {D}, T)$
where-
(a)
 $E_{\alpha }\in \vec {E}^{{\mathcal {M}}_{\alpha }}$
is the extender picked from
$E_{\alpha }\in \vec {E}^{{\mathcal {M}}_{\alpha }}$
is the extender picked from
 ${\mathcal {M}}_{\alpha }$
,
${\mathcal {M}}_{\alpha }$
, -
(b)
 $\mathcal {D}$
is the set of those
$\mathcal {D}$
is the set of those
 ${\alpha }$
where a drop occurs, and
${\alpha }$
where a drop occurs, and -
(c) T is the tree order of
 ${\mathcal {T}}$
.
${\mathcal {T}}$
.
We allow padded iterations, and so it is possible that
 $E_{\alpha }=\emptyset $
.
$E_{\alpha }=\emptyset $
. -
-
6. Suppose
 $({\mathcal {M}}, \Phi )$
is a mouse pair and
$({\mathcal {M}}, \Phi )$
is a mouse pair and
 ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
 $\Phi $
-iterate of
$\Phi $
-iterate of
 ${\mathcal {M}}$
via iteration
${\mathcal {M}}$
via iteration
 ${\mathcal {T}}$
. We then let
${\mathcal {T}}$
. We then let
 $\Phi _{{\mathcal {N}}, {\mathcal {T}}}$
be the strategy of
$\Phi _{{\mathcal {N}}, {\mathcal {T}}}$
be the strategy of
 ${\mathcal {N}}$
induced by the pair
${\mathcal {N}}$
induced by the pair
 $(\Phi , {\mathcal {T}})$
. More precisely,
$(\Phi , {\mathcal {T}})$
. More precisely,
 $\Phi _{{\mathcal {N}}, {\mathcal {T}}}({\mathcal {U}})=\Phi ({\mathcal {T}}^\frown {\mathcal {U}})$
.
$\Phi _{{\mathcal {N}}, {\mathcal {T}}}({\mathcal {U}})=\Phi ({\mathcal {T}}^\frown {\mathcal {U}})$
. -
7. Continuing with
 $({\mathcal {M}}, \Phi )$
,
$({\mathcal {M}}, \Phi )$
,
 ${\mathcal {N}}$
and
${\mathcal {N}}$
and
 ${\mathcal {T}}$
as above, we say
${\mathcal {T}}$
as above, we say
 ${\mathcal {N}}$
is a complete
${\mathcal {N}}$
is a complete
 $\Phi $
-iterate if the iteration embedding
$\Phi $
-iterate if the iteration embedding
 $\pi ^{\mathcal {T}}$
is defined, which happens if and only if there is no drop on the main branch of
$\pi ^{\mathcal {T}}$
is defined, which happens if and only if there is no drop on the main branch of
 ${\mathcal {T}}$
(see the paragraph after [Reference Steel39, Definition 3.3]).
${\mathcal {T}}$
(see the paragraph after [Reference Steel39, Definition 3.3]). -
8. We say
 ${\mathcal {M}}$
is an almost knowledgeable mouse if
${\mathcal {M}}$
is an almost knowledgeable mouse if
 ${\mathcal {M}}$
has a unique
${\mathcal {M}}$
has a unique
 $(\omega _1, \omega _1)$
-iteration strategy
$(\omega _1, \omega _1)$
-iteration strategy
 $\Phi $
such that whenever
$\Phi $
such that whenever
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
via
${\mathcal {M}}$
via
 $\Phi $
and
$\Phi $
and
 ${\mathcal {N}}$
is the last model of
${\mathcal {N}}$
is the last model of
 ${\mathcal {T}}$
then
${\mathcal {T}}$
then-
(a)
 $\Phi _{{\mathcal {N}}, {\mathcal {T}}}$
is independent of
$\Phi _{{\mathcal {N}}, {\mathcal {T}}}$
is independent of
 ${\mathcal {T}}$
, andFootnote
16
${\mathcal {T}}$
, andFootnote
16
-
(b) if
 ${\mathcal {N}}$
is a complete iterate of
${\mathcal {N}}$
is a complete iterate of
 ${\mathcal {M}}$
then
${\mathcal {M}}$
then
 $\pi ^{\mathcal {T}}$
is independent of
$\pi ^{\mathcal {T}}$
is independent of
 ${\mathcal {T}}$
Footnote
17
.
${\mathcal {T}}$
Footnote
17
.
-
-
9. We say
 ${\mathcal {M}}$
is knowledgeable if letting
${\mathcal {M}}$
is knowledgeable if letting
 $\Phi $
be the unique
$\Phi $
be the unique
 $(\omega _1, \omega _1)$
-iteration strategy of
$(\omega _1, \omega _1)$
-iteration strategy of
 ${\mathcal {M}}$
, whenever
${\mathcal {M}}$
, whenever
 ${\mathcal {N}}$
is a complete iterate of
${\mathcal {N}}$
is a complete iterate of
 ${\mathcal {M}}$
via
${\mathcal {M}}$
via
 $\Phi $
,
$\Phi $
,
 ${\mathcal {N}}$
is almost knowledgeable.
${\mathcal {N}}$
is almost knowledgeable. -
10. If
 ${\mathcal {M}}$
is knowledgeable then we let
${\mathcal {M}}$
is knowledgeable then we let
 $\Phi _{\mathcal {M}}$
be its unique
$\Phi _{\mathcal {M}}$
be its unique
 $(\omega _1, \omega _1)$
-iteration strategy and for each
$(\omega _1, \omega _1)$
-iteration strategy and for each
 $\Phi $
-iterate
$\Phi $
-iterate
 ${\mathcal {N}}$
of
${\mathcal {N}}$
of
 ${\mathcal {M}}$
, we let
${\mathcal {M}}$
, we let
 $\Phi _{\mathcal {N}}=\Phi _{{\mathcal {N}}, {\mathcal {T}}}$
where
$\Phi _{\mathcal {N}}=\Phi _{{\mathcal {N}}, {\mathcal {T}}}$
where
 ${\mathcal {T}}$
is some iteration of
${\mathcal {T}}$
is some iteration of
 ${\mathcal {M}}$
via
${\mathcal {M}}$
via
 $\Phi $
with last model
$\Phi $
with last model
 ${\mathcal {N}}$
. If
${\mathcal {N}}$
. If
 ${\mathcal {M}}$
is knowledgeable and
${\mathcal {M}}$
is knowledgeable and
 ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
 $\Phi _{\mathcal {M}}$
-iterate of
$\Phi _{\mathcal {M}}$
-iterate of
 ${\mathcal {M}}$
then we say that
${\mathcal {M}}$
then we say that
 ${\mathcal {N}}$
is an iterate of
${\mathcal {N}}$
is an iterate of
 ${\mathcal {M}}$
. If
${\mathcal {M}}$
. If
 ${\mathcal {N}}$
is a complete
${\mathcal {N}}$
is a complete
 $\Phi _{\mathcal {M}}$
-iterate of
$\Phi _{\mathcal {M}}$
-iterate of
 ${\mathcal {M}}$
then we say that
${\mathcal {M}}$
then we say that
 ${\mathcal {N}}$
is a complete iterate of
${\mathcal {N}}$
is a complete iterate of
 ${\mathcal {M}}$
.
${\mathcal {M}}$
. -
11. Suppose
 ${\mathcal {M}}$
is a knowledgeable mouse and
${\mathcal {M}}$
is a knowledgeable mouse and
 ${\mathcal {N}}$
is a normal iterateFootnote
18
of
${\mathcal {N}}$
is a normal iterateFootnote
18
of
 ${\mathcal {M}}$
. Then we let
${\mathcal {M}}$
. Then we let
 ${\mathcal {T}}_{{\mathcal {M}}, {\mathcal {N}}}$
be the unique normal iteration of
${\mathcal {T}}_{{\mathcal {M}}, {\mathcal {N}}}$
be the unique normal iteration of
 ${\mathcal {M}}$
according to
${\mathcal {M}}$
according to
 ${\mathcal {M}}$
’s unique iteration strategy whose last model is
${\mathcal {M}}$
’s unique iteration strategy whose last model is
 ${\mathcal {N}}$
Footnote
19
. In general, if
${\mathcal {N}}$
Footnote
19
. In general, if
 ${\mathcal {N}}$
is an iterate of
${\mathcal {N}}$
is an iterate of
 ${\mathcal {M}}$
then
${\mathcal {M}}$
then
 ${\mathcal {M}}$
-to-
${\mathcal {M}}$
-to-
 ${\mathcal {N}}$
iteration may not be uniqueFootnote
20
. If
${\mathcal {N}}$
iteration may not be uniqueFootnote
20
. If
 ${\mathcal {N}}$
is a complete iterate of
${\mathcal {N}}$
is a complete iterate of
 ${\mathcal {M}}$
, we let
${\mathcal {M}}$
, we let
 $\pi _{{\mathcal {M}}, {\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}$
be the iteration embedding.
$\pi _{{\mathcal {M}}, {\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}$
be the iteration embedding. -
12. Suppose
 ${\mathcal {M}}$
is an x-premouse and
${\mathcal {M}}$
is an x-premouse and
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
of limit length. We let
${\mathcal {M}}$
of limit length. We let
 ${\delta }({\mathcal {T}})=\sup \{\mathrm {lh}(E_{\alpha }^{\mathcal {T}}): {\alpha }<\mathrm {lh}({\mathcal {T}})\}$
and
${\delta }({\mathcal {T}})=\sup \{\mathrm {lh}(E_{\alpha }^{\mathcal {T}}): {\alpha }<\mathrm {lh}({\mathcal {T}})\}$
and
 $\mathsf {{cop}}({\mathcal {T}})=\cup _{{\alpha }<\mathrm {lh}({\mathcal {T}})}{\mathcal {M}}_{\alpha }^{\mathcal {T}}|\mathrm { lh}(E_{\alpha }^{\mathcal {T}})$
Footnote
21
. For more on these objects see [Reference Steel39, Definition 6.9].
$\mathsf {{cop}}({\mathcal {T}})=\cup _{{\alpha }<\mathrm {lh}({\mathcal {T}})}{\mathcal {M}}_{\alpha }^{\mathcal {T}}|\mathrm { lh}(E_{\alpha }^{\mathcal {T}})$
Footnote
21
. For more on these objects see [Reference Steel39, Definition 6.9]. -
13. Suppose
 $x\in {\mathbb {R}}$
.
$x\in {\mathbb {R}}$
.
 ${\mathcal {M}}_n(x)$
is the minimal class size x-mouse with n Woodin cardinals.
${\mathcal {M}}_n(x)$
is the minimal class size x-mouse with n Woodin cardinals.
 ${\mathcal {M}}_n^\#(x)$
is the minimal activeFootnote
22
x-mouse with n Woodin cardinals. We say
${\mathcal {M}}_n^\#(x)$
is the minimal activeFootnote
22
x-mouse with n Woodin cardinals. We say
 ${\mathcal {M}}_n^\#(x)$
exists if there is an
${\mathcal {M}}_n^\#(x)$
exists if there is an
 $\omega _1+1$
-iterable active x-premouse with n Woodin cardinals. Assuming
$\omega _1+1$
-iterable active x-premouse with n Woodin cardinals. Assuming
 $\mathsf {{AD}}$
,
$\mathsf {{AD}}$
,
 ${\mathcal {M}}_n^\#(x)$
exists (e.g., see [Reference Müller, Schindler and Woodin25] or [Reference Sargsyan31, Sublemma 3.2]). For each n,
${\mathcal {M}}_n^\#(x)$
exists (e.g., see [Reference Müller, Schindler and Woodin25] or [Reference Sargsyan31, Sublemma 3.2]). For each n,
 ${\mathcal {M}}_n^\#(x)$
is knowledgeable (assuming it exist). If every real has a sharp and
${\mathcal {M}}_n^\#(x)$
is knowledgeable (assuming it exist). If every real has a sharp and
 ${\mathcal {M}}_n(x)$
exists then
${\mathcal {M}}_n(x)$
exists then
 ${\mathcal {M}}_n(x)$
is knowledgeable. For the proof of these and relevant results see [Reference Steel and Woodin40, Chapter 2 and 3] and especially [Reference Steel and Woodin40, Theorem 3.23].
${\mathcal {M}}_n(x)$
is knowledgeable. For the proof of these and relevant results see [Reference Steel and Woodin40, Chapter 2 and 3] and especially [Reference Steel and Woodin40, Theorem 3.23]. -
14. Suppose
 ${\mathcal {M}}$
is an x-premouse,
${\mathcal {M}}$
is an x-premouse,
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
of limit length and b is a branch. We say
${\mathcal {M}}$
of limit length and b is a branch. We say
 ${\mathcal { Q}}(b, {\mathcal {T}})$
exists if there is
${\mathcal { Q}}(b, {\mathcal {T}})$
exists if there is
 ${\alpha }$
such that
${\alpha }$
such that
 ${\mathcal {M}}^{\mathcal {T}}_b||{\alpha }\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’ but
${\mathcal {M}}^{\mathcal {T}}_b||{\alpha }\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’ but
 $\mathcal {J}_1[{\mathcal {M}}^{\mathcal {T}}_b||{\alpha }]\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. If
$\mathcal {J}_1[{\mathcal {M}}^{\mathcal {T}}_b||{\alpha }]\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. If
 ${\mathcal { Q}}(b, {\mathcal {T}})$
exists we let it be
${\mathcal { Q}}(b, {\mathcal {T}})$
exists we let it be
 ${\mathcal {M}}^{\mathcal {T}}_b||{\alpha }$
where
${\mathcal {M}}^{\mathcal {T}}_b||{\alpha }$
where
 ${\alpha }$
is the largest such that
${\alpha }$
is the largest such that
 ${\mathcal {M}}^{\mathcal {T}}_b||{\alpha }\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’.
${\mathcal {M}}^{\mathcal {T}}_b||{\alpha }\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. -
15.
 ${\mathcal { Q}}(b, {\mathcal {T}})$
defined above is one of the most used objects in inner model theory. The reader may want to consult [Reference Steel39, Definition 6.11] and [Reference Steel37, Definition 2.11]. The reason that
${\mathcal { Q}}(b, {\mathcal {T}})$
defined above is one of the most used objects in inner model theory. The reader may want to consult [Reference Steel39, Definition 6.11] and [Reference Steel37, Definition 2.11]. The reason that
 ${\mathcal { Q}}(b, {\mathcal {T}})$
is important is that it uniquely identifies b. More precisely, if
${\mathcal { Q}}(b, {\mathcal {T}})$
is important is that it uniquely identifies b. More precisely, if
 $c\not =b$
is another cofinal branch of
$c\not =b$
is another cofinal branch of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 ${\mathcal { Q}}(c, {\mathcal {T}})$
exists then
${\mathcal { Q}}(c, {\mathcal {T}})$
exists then
 ${\mathcal { Q}}(c, {\mathcal {T}})\not ={\mathcal { Q}}(b, {\mathcal {T}})$
.
${\mathcal { Q}}(c, {\mathcal {T}})\not ={\mathcal { Q}}(b, {\mathcal {T}})$
. -
16. Suppose
 ${\mathcal {M}}$
is an x-premouse and
${\mathcal {M}}$
is an x-premouse and
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
. We say
${\mathcal {M}}$
. We say
 ${\mathcal {T}}$
is below
${\mathcal {T}}$
is below
 ${\delta }$
if for every
${\delta }$
if for every
 ${\alpha }<\mathrm {lh}({\mathcal {T}})$
either
${\alpha }<\mathrm {lh}({\mathcal {T}})$
either
 $\pi _{0, {\alpha }}^{\mathcal {T}}$
is not defined or
$\pi _{0, {\alpha }}^{\mathcal {T}}$
is not defined or
 $E_{\alpha }^{\mathcal {T}}\in \vec {E}^{{\mathcal {M}}_{\alpha }^{\mathcal {T}}|\pi _{0, {\alpha }}^{\mathcal {T}}({\delta })}$
. We say
$E_{\alpha }^{\mathcal {T}}\in \vec {E}^{{\mathcal {M}}_{\alpha }^{\mathcal {T}}|\pi _{0, {\alpha }}^{\mathcal {T}}({\delta })}$
. We say
 ${\mathcal {T}}$
is above
${\mathcal {T}}$
is above
 $\nu $
if for every
$\nu $
if for every
 ${\alpha }<\mathrm {lh}({\mathcal {T}})$
,
${\alpha }<\mathrm {lh}({\mathcal {T}})$
,
 $\mathrm {crit }(E_{\alpha }^{\mathcal {T}})\geq \nu $
.
$\mathrm {crit }(E_{\alpha }^{\mathcal {T}})\geq \nu $
. -
17. We remark that when we say that
 $`{\kappa }$
is a measurable cardinal in a premouse
$`{\kappa }$
is a measurable cardinal in a premouse
 ${\mathcal {M}}$
’ or
${\mathcal {M}}$
’ or
 $`{\kappa }$
is a strong cardinal in a premouse
$`{\kappa }$
is a strong cardinal in a premouse
 ${\mathcal {M}}$
’ or say other similar expressions we tacitly assume that these large cardinal properties are witnessed by the extenders on the extender sequence of
${\mathcal {M}}$
’ or say other similar expressions we tacitly assume that these large cardinal properties are witnessed by the extenders on the extender sequence of
 ${\mathcal {M}}$
. See [Reference Schlutzenberg36] for results showing that such a restriction is unnecessary.
${\mathcal {M}}$
. See [Reference Schlutzenberg36] for results showing that such a restriction is unnecessary.
Review 2.2. The directed system:
The theory of directed systems, by now, has a long history. It originates in Steel’s seminal paper [Reference Steel38]. Since then it has been used to establish a number of striking applications of inner model theory to descriptive set theory. To learn more about the subject the interested reader may consult [Reference Steel39, Chapter 8], [Reference Steel and Woodin40, Chapter 6], [Reference Mueller and Sargsyan24], [Reference Neeman26], [Reference Sargsyan28], [Reference Sargsyan30], [Reference Sargsyan and Schindler32] and many other sources.
-
1. Suppose
 ${\mathcal {P}}$
is a knowledgeable mouse. Let
${\mathcal {P}}$
is a knowledgeable mouse. Let
 $\mathcal {I}_{\mathcal {P}}$
be the set of complete iterates
$\mathcal {I}_{\mathcal {P}}$
be the set of complete iterates
 ${\mathcal {N}}$
of
${\mathcal {N}}$
of
 ${\mathcal {P}}$
such that
${\mathcal {P}}$
such that
 ${\mathcal {P}}$
-to-
${\mathcal {P}}$
-to-
 ${\mathcal {N}}$
iteration has a countable length.
${\mathcal {N}}$
iteration has a countable length. -
2. Suppose that either there is some
 $\nu <\omega _1$
such that
$\nu <\omega _1$
such that
 ${\mathcal {P}}=L[{\mathcal {P}}|\nu ]$
or
${\mathcal {P}}=L[{\mathcal {P}}|\nu ]$
or
 ${\mathcal {P}}$
itself is countable. Then comparison implies that if
${\mathcal {P}}$
itself is countable. Then comparison implies that if
 ${\mathcal R}, {\mathcal {S}}\in \mathcal {I}_{\mathcal {P}}$
then there is
${\mathcal R}, {\mathcal {S}}\in \mathcal {I}_{\mathcal {P}}$
then there is
 ${\mathcal {W} }\in \mathcal {I}_{\mathcal {P}}$
such that
${\mathcal {W} }\in \mathcal {I}_{\mathcal {P}}$
such that
 ${\mathcal {W} }$
is a complete iterate of both
${\mathcal {W} }$
is a complete iterate of both
 ${\mathcal R}$
and
${\mathcal R}$
and
 ${\mathcal {S}}$
. Define
${\mathcal {S}}$
. Define
 $\leq _{\mathcal {P}}$
on
$\leq _{\mathcal {P}}$
on
 $\mathcal {I}_{\mathcal {P}}$
by setting
$\mathcal {I}_{\mathcal {P}}$
by setting
 ${\mathcal R}\leq _{\mathcal {P}} {\mathcal {S}}$
if and only if
${\mathcal R}\leq _{\mathcal {P}} {\mathcal {S}}$
if and only if
 ${\mathcal {S}}$
is an iterate of
${\mathcal {S}}$
is an iterate of
 ${\mathcal R}$
. Assuming
${\mathcal R}$
. Assuming
 ${\mathcal {P}}$
is knowledgeable, we then get a directed system
${\mathcal {P}}$
is knowledgeable, we then get a directed system
 $\mathcal {F}_{\mathcal {P}}$
whose models consist of the models in
$\mathcal {F}_{\mathcal {P}}$
whose models consist of the models in
 $\mathcal {I}_{\mathcal {P}}$
, whose directed order is
$\mathcal {I}_{\mathcal {P}}$
, whose directed order is
 $\leq _{\mathcal {P}}$
and whose embeddings are the iteration embeddings
$\leq _{\mathcal {P}}$
and whose embeddings are the iteration embeddings
 $\pi _{{\mathcal R}, {\mathcal {S}}}$
.
$\pi _{{\mathcal R}, {\mathcal {S}}}$
. -
3. Assuming
 ${\mathcal {P}}$
is as above, we let
${\mathcal {P}}$
is as above, we let
 ${\mathcal {M}}_\infty ({\mathcal {P}})$
be the direct limit of
${\mathcal {M}}_\infty ({\mathcal {P}})$
be the direct limit of
 $\mathcal {F}_{\mathcal {P}}$
and given
$\mathcal {F}_{\mathcal {P}}$
and given
 ${\mathcal {N}}\in \mathcal {I}_{\mathcal {P}}$
, we let
${\mathcal {N}}\in \mathcal {I}_{\mathcal {P}}$
, we let
 $\pi _{{\mathcal {N}}, \infty }:{\mathcal {N}}\rightarrow {\mathcal {M}}_\infty ({\mathcal {P}})$
be the iteration embedding according to
$\pi _{{\mathcal {N}}, \infty }:{\mathcal {N}}\rightarrow {\mathcal {M}}_\infty ({\mathcal {P}})$
be the iteration embedding according to
 $\Phi _{\mathcal {N}}$
.
$\Phi _{\mathcal {N}}$
.
 $\mathsf {{Comparison\ Theorem}}$
(see [Reference Steel39, Theorem 3.11]) implies that
$\mathsf {{Comparison\ Theorem}}$
(see [Reference Steel39, Theorem 3.11]) implies that
 ${\mathcal {M}}_\infty ({\mathcal {P}})$
is well-founded (see, e.g., the remark after [Reference Steel39, Definition 8.15])).
${\mathcal {M}}_\infty ({\mathcal {P}})$
is well-founded (see, e.g., the remark after [Reference Steel39, Definition 8.15])).
Review 2.3. The extender algebra:
The extender algebra, which was discovered by Woodin, is the magic tool of inner model theory. The reader may consult [Reference Steel39, Chapter 7.2].
-
1. Suppose
 ${\mathcal {P}}$
is a premouse,
${\mathcal {P}}$
is a premouse,
 ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 $\nu <{\delta }$
.
$\nu <{\delta }$
.Definition 2.4. We say that
 $\mathcal {E}$
is weakly appropriate at
$\mathcal {E}$
is weakly appropriate at
 ${\delta }$
if
${\delta }$
if
 $\mathcal {E}$
is a set consisting of extenders
$\mathcal {E}$
is a set consisting of extenders
 $E\in \vec {E}^{{\mathcal {P}}|{\delta }}$
such that
$E\in \vec {E}^{{\mathcal {P}}|{\delta }}$
such that-
(a)
 $\nu (E)$
Footnote
23
is an inaccessible cardinal in
$\nu (E)$
Footnote
23
is an inaccessible cardinal in
 ${\mathcal {P}}$
,
${\mathcal {P}}$
, -
(b)
 $\mathcal {E}$
witnesses that
$\mathcal {E}$
witnesses that
 ${\delta }$
is a Woodin cardinalFootnote
24
.
${\delta }$
is a Woodin cardinalFootnote
24
.
If in addition
-
(c) for each
 $E\in \mathcal {E}$
,
$E\in \mathcal {E}$
,
 $\pi _E(\mathcal {E})\cap ({\mathcal {P}}|\nu (E))=\mathcal {E}\cap ({\mathcal {P}}|\nu (E))$
,
$\pi _E(\mathcal {E})\cap ({\mathcal {P}}|\nu (E))=\mathcal {E}\cap ({\mathcal {P}}|\nu (E))$
,
then we say that
 $\mathcal {E}$
is appropriate.
$\mathcal {E}$
is appropriate.When
 ${\delta }$
is clear from the context we will omit the expression ‘at
${\delta }$
is clear from the context we will omit the expression ‘at
 ${\delta }$
’. Suppose now that
${\delta }$
’. Suppose now that
 $\mathcal {E}$
is weakly appropriate. We then let
$\mathcal {E}$
is weakly appropriate. We then let
 $\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
be the extender algebra of
$\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
be the extender algebra of
 ${\mathcal {P}}$
defined using extenders
${\mathcal {P}}$
defined using extenders
 $E\in \mathcal {E}$
such that
$E\in \mathcal {E}$
such that
 $\mathrm {crit }(E)>\nu $
. If
$\mathrm {crit }(E)>\nu $
. If
 $\nu =0$
then we omit it from our notation. If
$\nu =0$
then we omit it from our notation. If
 $\mathcal {E}$
consists of all extenders or if its role is irrelevant then we omit it from the notation.
$\mathcal {E}$
consists of all extenders or if its role is irrelevant then we omit it from the notation. $\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
is the basic extender algebra for adding a real: thus, it has only countably many predicate symbols. The conditions in
$\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
is the basic extender algebra for adding a real: thus, it has only countably many predicate symbols. The conditions in
 $\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
are formulas, and so given
$\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
are formulas, and so given
 $g\subseteq \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
and
$g\subseteq \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
and
 $r\in \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
, we will often write
$r\in \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
, we will often write
 $g\models r$
instead of
$g\models r$
instead of
 $r\in g$
.
$r\in g$
.Instead of making our notation endlessly complicated, we will abuse our terminology and notation in the following way. Suppose
 $a=L[b]$
where for some
$a=L[b]$
where for some
 ${\alpha }$
,
${\alpha }$
,
 $b\subseteq {\alpha }$
. Then we will say that a is generic for
$b\subseteq {\alpha }$
. Then we will say that a is generic for
 $\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
to mean that if
$\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
to mean that if
 ${\alpha }$
is the least such that there is
${\alpha }$
is the least such that there is
 $b\in a$
with the property that
$b\in a$
with the property that
 $b\subseteq {\alpha }$
and
$b\subseteq {\alpha }$
and
 $a=L[b]$
, then b is generic for the extender algebra at
$a=L[b]$
, then b is generic for the extender algebra at
 ${\delta }$
that uses
${\delta }$
that uses
 ${\alpha }$
many generators and extenders who critical points are strictly greater than
${\alpha }$
many generators and extenders who critical points are strictly greater than
 $\nu $
.
$\nu $
.A celebrated theorem of Woodin says that
 $\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
has the
$\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu , \mathcal {E}}$
has the
 ${\delta }$
-c.c. condition (assuming only that
${\delta }$
-c.c. condition (assuming only that
 $\mathcal {E}$
is weakly appropriate, see [Reference Steel39, Chapter 7.2]).
$\mathcal {E}$
is weakly appropriate, see [Reference Steel39, Chapter 7.2]). -
-
2. Suppose
 $({\mathcal {P}}, \Sigma )$
is a mouse pair,
$({\mathcal {P}}, \Sigma )$
is a mouse pair,
 ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
 ${\mathcal {P}}$
,
${\mathcal {P}}$
,
 $\nu <{\delta }$
,
$\nu <{\delta }$
,
 $\mathcal {E}$
is an appropriateFootnote
25
set of extenders and
$\mathcal {E}$
is an appropriateFootnote
25
set of extenders and
 $(x_1, ..., x_k)\in {\mathbb {R}}^k$
. We say
$(x_1, ..., x_k)\in {\mathbb {R}}^k$
. We say
 ${\mathcal {T}}$
is the
${\mathcal {T}}$
is the
 $(\vec {x}, {\delta }, \nu , \mathcal {E})$
-genericity iteration of
$(\vec {x}, {\delta }, \nu , \mathcal {E})$
-genericity iteration of
 ${\mathcal {P}}$
if
${\mathcal {P}}$
if
 ${\mathcal {T}}$
is according to
${\mathcal {T}}$
is according to
 $\Sigma $
and for each
$\Sigma $
and for each
 ${\alpha }<lh({\mathcal {T}})$
, setting
${\alpha }<lh({\mathcal {T}})$
, setting
 ${\mathcal {M}}_{\alpha }=_{def}{\mathcal {M}}_{\alpha }^{\mathcal {T}}$
and
${\mathcal {M}}_{\alpha }=_{def}{\mathcal {M}}_{\alpha }^{\mathcal {T}}$
and
 $E_{\alpha }=_{def}E_{\alpha }^{{\mathcal {T}}}\in \vec {E}^{{\mathcal {M}}_{\alpha }}$
,
$E_{\alpha }=_{def}E_{\alpha }^{{\mathcal {T}}}\in \vec {E}^{{\mathcal {M}}_{\alpha }}$
,
 $\mathrm {lh}(E_{\alpha })$
is the least
$\mathrm {lh}(E_{\alpha })$
is the least
 ${\gamma} \in \mathrm {dom}(\vec {E}^{{\mathcal {M}}_{\alpha }})$
such that setting
${\gamma} \in \mathrm {dom}(\vec {E}^{{\mathcal {M}}_{\alpha }})$
such that setting
 $E=\vec {E}^{{\mathcal {M}}_{\alpha }}({\gamma} )$
, the following clauses hold:
$E=\vec {E}^{{\mathcal {M}}_{\alpha }}({\gamma} )$
, the following clauses hold:-
(a)
 $\mathrm {crit }(E)>\nu $
and
$\mathrm {crit }(E)>\nu $
and
 $\mathrm {lh}(E)<\pi ^{\mathcal {T}}_{0, {\alpha }}({\delta })$
,
$\mathrm {lh}(E)<\pi ^{\mathcal {T}}_{0, {\alpha }}({\delta })$
, -
(b)
 $E\in \pi _{0, {\alpha }}^{\mathcal {T}}(\mathcal {E})$
(and hence, E measures all subsets of
$E\in \pi _{0, {\alpha }}^{\mathcal {T}}(\mathcal {E})$
(and hence, E measures all subsets of
 $\mathrm {crit }(E)$
in
$\mathrm {crit }(E)$
in
 ${\mathcal {M}}_{\alpha }$
),
${\mathcal {M}}_{\alpha }$
), -
(c) for some
 $i\leq k$
,
$i\leq k$
,
 $x_i$
doesn’t satisfy an axiom of
$x_i$
doesn’t satisfy an axiom of
 $\pi _{{\mathcal {P}}, {\mathcal {M}}_{\alpha }}(\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu. \mathcal {E}})$
that is generated by E. More precisely,
$\pi _{{\mathcal {P}}, {\mathcal {M}}_{\alpha }}(\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }, \nu. \mathcal {E}})$
that is generated by E. More precisely,
 $x_i\not \models A_{E, \vec {\phi }}$
where
$x_i\not \models A_{E, \vec {\phi }}$
where
 $\vec {\phi }\in {\mathcal {M}}_{\alpha }|(\mathrm {crit }(E)^+)^{{\mathcal {M}}_{\alpha }}$
and
$\vec {\phi }\in {\mathcal {M}}_{\alpha }|(\mathrm {crit }(E)^+)^{{\mathcal {M}}_{\alpha }}$
and
 $A_{E, \vec {\phi }}$
is the axiom
$A_{E, \vec {\phi }}$
is the axiom
 $\bigvee \vec {\phi }{\mathrel {\leftrightarrow }} \bigvee \pi _{E}^{{\mathcal {M}}_{\alpha }}(\vec {\phi })\restriction \nu (E)$
, and
$\bigvee \vec {\phi }{\mathrel {\leftrightarrow }} \bigvee \pi _{E}^{{\mathcal {M}}_{\alpha }}(\vec {\phi })\restriction \nu (E)$
, and -
(d) for all
 ${\gamma} '<{\gamma} $
, if
${\gamma} '<{\gamma} $
, if
 ${\gamma} '\in \mathrm {dom}(\vec {E}^{{\mathcal {M}}_{\alpha }})$
then
${\gamma} '\in \mathrm {dom}(\vec {E}^{{\mathcal {M}}_{\alpha }})$
then
 $E_{{\gamma} '}^{{\mathcal {M}}_{\alpha }}$
does not satisfy clauses (a)-(c) above.
$E_{{\gamma} '}^{{\mathcal {M}}_{\alpha }}$
does not satisfy clauses (a)-(c) above.
-
-
3. Suppose
 $\phi (v_0, ..., v_k)$
is a
$\phi (v_0, ..., v_k)$
is a
 $\Sigma ^1_{2n+2}$
formula,
$\Sigma ^1_{2n+2}$
formula,
 ${\mathcal {M}}$
is a premouse,
${\mathcal {M}}$
is a premouse,
 ${\delta }_0<...<{\delta }_{2n-1}$
are Woodin cardinals of
${\delta }_0<...<{\delta }_{2n-1}$
are Woodin cardinals of
 ${\mathcal {M}}$
,
${\mathcal {M}}$
,
 ${\kappa }<{\delta }_0$
,
${\kappa }<{\delta }_0$
,
 $d=({\kappa }, {\delta }_0, ..., {\delta }_{2n-1})$
and
$d=({\kappa }, {\delta }_0, ..., {\delta }_{2n-1})$
and
 $\vec {a}\in [{\mathbb {R}}^{{\mathcal {M}}}]^{<\omega }$
. By induction, we define
$\vec {a}\in [{\mathbb {R}}^{{\mathcal {M}}}]^{<\omega }$
. By induction, we define
 $\phi _{{\mathcal {M}}, d}$
and the meaning of
$\phi _{{\mathcal {M}}, d}$
and the meaning of
 ${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
. If
${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
. If
 $n=0$
then
$n=0$
then
 $\phi _{{\mathcal {M}}, d}=\phi $
and
$\phi _{{\mathcal {M}}, d}=\phi $
and
 ${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
if and only if
${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
if and only if
 ${\mathcal {M}}\models \phi [\vec {a}]$
. Next let
${\mathcal {M}}\models \phi [\vec {a}]$
. Next let
 $\psi $
be a
$\psi $
be a
 $\Sigma ^1_{2n}$
formula such that
$\Sigma ^1_{2n}$
formula such that
 $\phi (v_0, ..., v_k){\mathrel {\leftrightarrow }} \exists u_0 \forall u_1 \psi (u_0, u_1, v_0, ..., v_k)$
. We then write
$\phi (v_0, ..., v_k){\mathrel {\leftrightarrow }} \exists u_0 \forall u_1 \psi (u_0, u_1, v_0, ..., v_k)$
. We then write
 ${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
if and only if there is
${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
if and only if there is
 $p\in \mathsf {{Ea}}_{{\delta }_0, {\kappa }}$
such that if g is the name of the generic for
$p\in \mathsf {{Ea}}_{{\delta }_0, {\kappa }}$
such that if g is the name of the generic for
 $\mathsf {{Ea}}_{{\delta }_0, {\kappa }}$
then p forces that there is
$\mathsf {{Ea}}_{{\delta }_0, {\kappa }}$
then p forces that there is
 $x\in {\mathbb {R}}$
such that every
$x\in {\mathbb {R}}$
such that every
 $q\in \mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0}$
forces that for all
$q\in \mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0}$
forces that for all
 $y\in {\mathbb {R}}$
,
$y\in {\mathbb {R}}$
,
 $\psi _{{\mathcal {M}}, d'}[ x, y, \vec {a}]$
where
$\psi _{{\mathcal {M}}, d'}[ x, y, \vec {a}]$
where
 $d'=({\delta }_1, {\delta }_2,..., {\delta }_{2n-1})$
.Footnote
26
Similarly we can define
$d'=({\delta }_1, {\delta }_2,..., {\delta }_{2n-1})$
.Footnote
26
Similarly we can define
 $\phi _{{\mathcal {M}}, d}$
for a
$\phi _{{\mathcal {M}}, d}$
for a
 $\Pi ^1_{2n+3}$
formula
$\Pi ^1_{2n+3}$
formula
 $\phi $
and
$\phi $
and
 $d=({\kappa }, {\delta }_0, {\delta }_1, ..., {\delta }_{2n})$
(assuming that
$d=({\kappa }, {\delta }_0, {\delta }_1, ..., {\delta }_{2n})$
(assuming that
 ${\delta }_0, {\delta }_1, ..., {\delta }_{2n}$
are Woodin cardinals of
${\delta }_0, {\delta }_1, ..., {\delta }_{2n}$
are Woodin cardinals of
 ${\mathcal {M}}$
).
${\mathcal {M}}$
). -
4. We will need the following basic applications of the extender algebra.
Proposition 2.5. Suppose
 $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
 ${\mathcal {M}}$
is countable
${\mathcal {M}}$
is countable
 $\omega _1+1$
-iterable mouse over x,
$\omega _1+1$
-iterable mouse over x,
 ${\mathcal {M}}\models \mathsf {{ZFC}}$
,
${\mathcal {M}}\models \mathsf {{ZFC}}$
,
 ${\mathcal {M}}$
has
${\mathcal {M}}$
has
 $2n$
Woodin cardinals, and
$2n$
Woodin cardinals, and
 $\phi (\vec {v})$
is a
$\phi (\vec {v})$
is a
 $\Sigma ^1_{2n+2}$
formula. Let
$\Sigma ^1_{2n+2}$
formula. Let
 ${\delta }_0<{\delta }_1<...<{\delta }_{2n-1}$
be the Woodin cardinals of
${\delta }_0<{\delta }_1<...<{\delta }_{2n-1}$
be the Woodin cardinals of
 ${\mathcal {M}}$
and let
${\mathcal {M}}$
and let
 ${\kappa }<{\delta }_0$
be any ordinal. Set
${\kappa }<{\delta }_0$
be any ordinal. Set
 $d=({\kappa }, {\delta }_0, ..., {\delta }_{2n-1})$
and suppose that for some
$d=({\kappa }, {\delta }_0, ..., {\delta }_{2n-1})$
and suppose that for some
 $\vec {a}\in {\mathcal {M}}\cap {\mathbb {R}}^k$
,
$\vec {a}\in {\mathcal {M}}\cap {\mathbb {R}}^k$
,
 ${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
. Then
${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
. Then
 $\phi [\vec {a}]$
.The same proof also gives the following.
$\phi [\vec {a}]$
.The same proof also gives the following.Proof. We give the proof of the prototypical case of
 $n=1$
. Suppose
$n=1$
. Suppose
 $\phi $
is
$\phi $
is
 $\exists u_0 \forall u_1 \psi [u_0, u_1, \vec {v}]$
where
$\exists u_0 \forall u_1 \psi [u_0, u_1, \vec {v}]$
where
 $\psi $
is
$\psi $
is
 $\Sigma ^1_2$
. Let
$\Sigma ^1_2$
. Let
 $p\in \mathsf {{Ea}}^{\mathcal {M}}_{{\delta }_0, {\kappa }}$
be a condition witnessing
$p\in \mathsf {{Ea}}^{\mathcal {M}}_{{\delta }_0, {\kappa }}$
be a condition witnessing
 $\phi _{{\mathcal {M}}, d}[\vec {a}]$
. Let
$\phi _{{\mathcal {M}}, d}[\vec {a}]$
. Let
 $g\subseteq \mathsf {{Ea}}^{\mathcal {M}}_{{\delta }_0, {\kappa }}$
be
$g\subseteq \mathsf {{Ea}}^{\mathcal {M}}_{{\delta }_0, {\kappa }}$
be
 ${\mathcal {M}}$
-generic such that
${\mathcal {M}}$
-generic such that
 $p\in g$
and
$p\in g$
and
 $g\in V$
. Let then
$g\in V$
. Let then
 $b_0$
be a real in
$b_0$
be a real in
 ${\mathcal {M}}[g]$
such that every
${\mathcal {M}}[g]$
such that every
 $q\in \mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0}$
forces that if u is a real then
$q\in \mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0}$
forces that if u is a real then
 $\psi [b_0, u, \vec {a}]$
.
$\psi [b_0, u, \vec {a}]$
.We now want to see that for all
 $b_1\in {\mathbb {R}}$
,
$b_1\in {\mathbb {R}}$
,
 $\psi [b_0, b_1, \vec {a}]$
holds. Fix
$\psi [b_0, b_1, \vec {a}]$
holds. Fix
 $b_1\in {\mathbb {R}}$
and an
$b_1\in {\mathbb {R}}$
and an
 $\omega _1+1$
-strategy
$\omega _1+1$
-strategy
 $\Sigma $
for
$\Sigma $
for
 ${\mathcal {M}}$
. Let
${\mathcal {M}}$
. Let
 ${\mathcal {N}}$
be a complete iterate of
${\mathcal {N}}$
be a complete iterate of
 ${\mathcal {M}}$
via iteration
${\mathcal {M}}$
via iteration
 ${\mathcal {T}}$
that is above
${\mathcal {T}}$
that is above
 ${\delta }_0$
and is such that
${\delta }_0$
and is such that
 $b_1$
is generic over
$b_1$
is generic over
 ${\mathcal {N}}$
for
${\mathcal {N}}$
for
 $\pi ^{\mathcal {T}}(\mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0})$
. Because
$\pi ^{\mathcal {T}}(\mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0})$
. Because
 $\mathrm {crit }(\pi ^{\mathcal {T}})>{\delta }_0$
, we have that in
$\mathrm {crit }(\pi ^{\mathcal {T}})>{\delta }_0$
, we have that in
 ${\mathcal {N}}[g]$
, every
${\mathcal {N}}[g]$
, every
 $q\in \pi ^{\mathcal {T}}(\mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0})$
forces that if u is a real then
$q\in \pi ^{\mathcal {T}}(\mathsf {{Ea}}^{{\mathcal {M}}[g]}_{{\delta }_1, {\delta }_0})$
forces that if u is a real then
 $\psi [b_0, u, \vec {a}]$
. Therefore, we have that
$\psi [b_0, u, \vec {a}]$
. Therefore, we have that
 ${\mathcal {N}}[g][b_1]\models \psi [b_0, b_1, \vec {a}]$
. But then it follows from the upward absoluteness of
${\mathcal {N}}[g][b_1]\models \psi [b_0, b_1, \vec {a}]$
. But then it follows from the upward absoluteness of
 $\Sigma ^1_2$
formulas that
$\Sigma ^1_2$
formulas that
 $\psi [b_0, b_1, \vec {a}]$
.
$\psi [b_0, b_1, \vec {a}]$
.Proposition 2.6. Suppose
 $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
 ${\mathcal {M}}$
is countable
${\mathcal {M}}$
is countable
 $\omega _1+1$
-iterable mouse over x,
$\omega _1+1$
-iterable mouse over x,
 ${\mathcal {M}}\models \mathsf {{ZFC}}$
,
${\mathcal {M}}\models \mathsf {{ZFC}}$
,
 ${\mathcal {M}}$
has
${\mathcal {M}}$
has
 $2n+1$
Woodin cardinals, and
$2n+1$
Woodin cardinals, and
 $\phi (\vec {v})$
is a
$\phi (\vec {v})$
is a
 $\Pi ^1_{2n+3}$
formula. Let
$\Pi ^1_{2n+3}$
formula. Let
 ${\delta }_0<{\delta }_1<...<{\delta }_{2n}$
be the Woodin cardinals of
${\delta }_0<{\delta }_1<...<{\delta }_{2n}$
be the Woodin cardinals of
 ${\mathcal {M}}$
and let
${\mathcal {M}}$
and let
 ${\kappa }<{\delta }_0$
be any ordinal. Set
${\kappa }<{\delta }_0$
be any ordinal. Set
 $d=({\kappa }, {\delta }_0, ..., {\delta }_{2n})$
and suppose that for some
$d=({\kappa }, {\delta }_0, ..., {\delta }_{2n})$
and suppose that for some
 $\vec {a}\in {\mathcal {M}}\cap {\mathbb {R}}^k$
,
$\vec {a}\in {\mathcal {M}}\cap {\mathbb {R}}^k$
,
 ${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
. Then
${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[\vec {a}]$
. Then
 $\phi [\vec {a}]$
.
$\phi [\vec {a}]$
. -
5. In [Reference Hjorth7], Hjorth showed that the product of the extender algebra with itself is still
 ${\delta }$
-c.c. More precisely, suppose M is a transitive model of
${\delta }$
-c.c. More precisely, suppose M is a transitive model of
 $\mathsf {{ZFC}}$
,
$\mathsf {{ZFC}}$
,
 ${\delta }$
is a Woodin cardinal of M,
${\delta }$
is a Woodin cardinal of M,
 $\mathcal {E}$
is a weakly appropriate set of extenders and
$\mathcal {E}$
is a weakly appropriate set of extenders and
 $\nu , \nu '<{\delta }$
. Then
$\nu , \nu '<{\delta }$
. Then
 $\mathsf {{Ea}}^M_{{\delta }, \nu , \mathcal {E}}\times \mathsf {{Ea}}^M_{{\delta }, \nu ', \mathcal {E}}$
is
$\mathsf {{Ea}}^M_{{\delta }, \nu , \mathcal {E}}\times \mathsf {{Ea}}^M_{{\delta }, \nu ', \mathcal {E}}$
is
 ${\delta }$
-c.c. For the proof see [Reference Hjorth7, Lemma 1.2].
${\delta }$
-c.c. For the proof see [Reference Hjorth7, Lemma 1.2]. -
6. Suppose M,
 ${\delta }$
and
${\delta }$
and
 $\nu , \nu '<{\delta }$
are as above. We then let
$\nu , \nu '<{\delta }$
are as above. We then let
 $\mathsf {{ea}}$
be the name for the generic object for
$\mathsf {{ea}}$
be the name for the generic object for
 $\mathsf {{Ea}}^M_{{\delta }, \nu }$
and let
$\mathsf {{Ea}}^M_{{\delta }, \nu }$
and let
 $(\mathsf {{ea}}_1, \mathsf {{ea}}_2,..., \mathsf {{ea}}_n)$
be the sequence of reals
$(\mathsf {{ea}}_1, \mathsf {{ea}}_2,..., \mathsf {{ea}}_n)$
be the sequence of reals
 $\mathsf {{ea}}$
codes. We let
$\mathsf {{ea}}$
codes. We let
 $(\mathsf {{ea}}^l, \mathsf {{ea}}^r)$
be the name for the generic of
$(\mathsf {{ea}}^l, \mathsf {{ea}}^r)$
be the name for the generic of
 $\mathsf {{Ea}}^M_{{\delta }, \nu }\times \mathsf {{Ea}}^M_{{\delta }, \nu '}$
. We then have that
$\mathsf {{Ea}}^M_{{\delta }, \nu }\times \mathsf {{Ea}}^M_{{\delta }, \nu '}$
. We then have that
 $(\mathsf {{ea}}^l_1,..., \mathsf {{ea}}^l_n)$
and
$(\mathsf {{ea}}^l_1,..., \mathsf {{ea}}^l_n)$
and
 $(\mathsf {ea}^r_1,..., \mathsf {{ea}}^r_m)$
are the finite sequences of reals coded by
$(\mathsf {ea}^r_1,..., \mathsf {{ea}}^r_m)$
are the finite sequences of reals coded by
 $\mathsf {{ea}}^l$
and
$\mathsf {{ea}}^l$
and
 $\mathsf {{ea}}^r$
.
$\mathsf {{ea}}^r$
.
Review 2.7. Backgrounded constructions and S -constructions:
S-construction is a method of translating the mouse structure to a similar structure over some inner model. The details of such a construction first appeared in [Reference Schindler and Steel33, Lemma 1.5] where it was called P-constructions. In [Reference Sargsyan29], the author renamed them S-constructionsFootnote 27 . In this paper, we will need a special instance of S-constructions. The reader is advised to review the notion of fully backgrounded constructions Footnote 28 as defined in [Reference Mitchell and Steel23, Chapter 11].
-
1. Suppose
 ${\mathcal {P}}$
is a premouse,
${\mathcal {P}}$
is a premouse,
 ${\delta }$
is a
${\delta }$
is a
 ${\mathcal {P}}$
-cardinal and
${\mathcal {P}}$
-cardinal and
 $z\in {\mathcal {P}}|{\delta }$
. We then let
$z\in {\mathcal {P}}|{\delta }$
. We then let
 $\mathsf {{Le}}(z)$
be the last modelFootnote
29
of the fully backgrounded construction of
$\mathsf {{Le}}(z)$
be the last modelFootnote
29
of the fully backgrounded construction of
 ${\mathcal {P}}|{\delta }$
over z as defined in [Reference Mitchell and Steel23, Chapter 11]. In this construction, all extenders used have critical points
${\mathcal {P}}|{\delta }$
over z as defined in [Reference Mitchell and Steel23, Chapter 11]. In this construction, all extenders used have critical points
 $>\eta $
where
$>\eta $
where
 $\eta $
is the least such that
$\eta $
is the least such that
 $z\in {\mathcal {P}}|\eta $
. If
$z\in {\mathcal {P}}|\eta $
. If
 $z=\emptyset $
then we omit it from our notation. We will only consider such fully backgrounded constructions over z that can be easily coded as a subset of ordinals. Typical examples of z’s that we will consider are reals and premice.
$z=\emptyset $
then we omit it from our notation. We will only consider such fully backgrounded constructions over z that can be easily coded as a subset of ordinals. Typical examples of z’s that we will consider are reals and premice.If
 ${\mathcal {P}}$
is
${\mathcal {P}}$
is
 $\omega _1+1$
-iterable then
$\omega _1+1$
-iterable then
 $\mathsf {{Ord}}\cap \mathsf {{Le}}(z)={\delta }$
, and if
$\mathsf {{Ord}}\cap \mathsf {{Le}}(z)={\delta }$
, and if
 ${\alpha }=\mathsf {{Ord}}\cap {\mathcal {P}}$
and
${\alpha }=\mathsf {{Ord}}\cap {\mathcal {P}}$
and
 ${\delta }$
is Woodin in
${\delta }$
is Woodin in
 ${\mathcal {P}}$
then
${\mathcal {P}}$
then
 $L_{\alpha }[\mathsf {{Le}}(z)]\models `{\delta }$
is a Woodin cardinal’ (see [Reference Mitchell and Steel23, Chapter 11]).
$L_{\alpha }[\mathsf {{Le}}(z)]\models `{\delta }$
is a Woodin cardinal’ (see [Reference Mitchell and Steel23, Chapter 11]).Below, in clauses 2-6,
 ${\mathcal {P}}$
,
${\mathcal {P}}$
,
 ${\delta }$
and z are as above,
${\delta }$
and z are as above,
 ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 $u\in {\mathbb {R}}\cap {\mathcal {P}}$
.
$u\in {\mathbb {R}}\cap {\mathcal {P}}$
. -
2. Suppose the z-premouse
 ${\mathcal {M}}\subseteq {\mathcal {P}}$
is such that
${\mathcal {M}}\subseteq {\mathcal {P}}$
is such that
 $\mathsf {{Le}}(z)\trianglelefteq {\mathcal {M}}$
and for every
$\mathsf {{Le}}(z)\trianglelefteq {\mathcal {M}}$
and for every
 ${\alpha }<\mathsf {{Ord}}\cap {\mathcal {M}}$
,
${\alpha }<\mathsf {{Ord}}\cap {\mathcal {M}}$
,
 ${\mathcal {M}}||{\alpha } \in {\mathcal {P}}$
. Then for any
${\mathcal {M}}||{\alpha } \in {\mathcal {P}}$
. Then for any
 $\nu <{\delta }$
, u is generic over
$\nu <{\delta }$
, u is generic over
 $\mathsf {{Ea}}^{\mathcal {M}}_{{\delta }, \nu }$
. This is because every extender
$\mathsf {{Ea}}^{\mathcal {M}}_{{\delta }, \nu }$
. This is because every extender
 $E\in \vec {E}^{\mathsf {{Le}}(z)}$
such that
$E\in \vec {E}^{\mathsf {{Le}}(z)}$
such that
 $\nu (E)$
is inaccessible in
$\nu (E)$
is inaccessible in
 $\mathsf {{Le}}(z)$
is backgrounded by an extender
$\mathsf {{Le}}(z)$
is backgrounded by an extender
 $F\in \vec {E}^{\mathcal {P}}$
such that there is a factor map
$F\in \vec {E}^{\mathcal {P}}$
such that there is a factor map
 $\tau : Ult(\mathsf {{Le}}(z), E)\rightarrow \pi ^{\mathcal {P}}_F(\mathsf {{Le}}(z))$
with the property that
$\tau : Ult(\mathsf {{Le}}(z), E)\rightarrow \pi ^{\mathcal {P}}_F(\mathsf {{Le}}(z))$
with the property that
 $\mathrm {crit }(\tau )\geq \nu (E)$
. Fixing now
$\mathrm {crit }(\tau )\geq \nu (E)$
. Fixing now
 $\vec {\phi }\in \mathsf {{Le}}(z)|(\mathrm {crit }(E)^+)^{\mathsf {{Le}}(z)}$
such that
$\vec {\phi }\in \mathsf {{Le}}(z)|(\mathrm {crit }(E)^+)^{\mathsf {{Le}}(z)}$
such that
 $u\models \bigvee \pi _E^{\mathsf {{Le}}(z)}(\vec {\phi })\restriction \nu (E)$
, we have that
$u\models \bigvee \pi _E^{\mathsf {{Le}}(z)}(\vec {\phi })\restriction \nu (E)$
, we have that
 $u\models \bigvee \pi ^{\mathcal {P}}_F(\vec {\phi })$
. But now because
$u\models \bigvee \pi ^{\mathcal {P}}_F(\vec {\phi })$
. But now because
 $u\in {\mathcal {P}}$
, we have that
$u\in {\mathcal {P}}$
, we have that
 $u\models \bigvee \vec {\phi }$
. Thus,
$u\models \bigvee \vec {\phi }$
. Thus,
 $u\models A_{E, \vee {\phi }}$
.
$u\models A_{E, \vee {\phi }}$
. -
3. We say
 ${\mathcal {P}}$
is translatable if for every
${\mathcal {P}}$
is translatable if for every
 $z\in {\mathcal {P}}\cap {\mathbb {R}}$
,
$z\in {\mathcal {P}}\cap {\mathbb {R}}$
,
 $\mathsf {{Ord}}\cap \mathsf {{Le}}(z)={\delta }$
Footnote
30
.
$\mathsf {{Ord}}\cap \mathsf {{Le}}(z)={\delta }$
Footnote
30
. -
4. Given a translatable
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 $z\in {\mathcal {P}}\cap {\mathbb {R}}$
, we let
$z\in {\mathcal {P}}\cap {\mathbb {R}}$
, we let
 $\mathsf {{StrLe}}({\mathcal {P}}, z)$
be the result of the S-construction over
$\mathsf {{StrLe}}({\mathcal {P}}, z)$
be the result of the S-construction over
 $\mathsf {{Le}}(z)$
that translates the extenders of
$\mathsf {{Le}}(z)$
that translates the extenders of
 ${\mathcal {P}}$
with critical points
${\mathcal {P}}$
with critical points
 $>{\delta }$
into extenders over
$>{\delta }$
into extenders over
 $\mathsf {{Le}}(z)$
.
$\mathsf {{Le}}(z)$
. -
5. It is shown in [Reference Schindler and Steel33, Lemma 1.5] that if
 $E\in \vec {E}^{\mathcal {P}}$
is such that
$E\in \vec {E}^{\mathcal {P}}$
is such that
 $\mathrm { crit }(E)>{\delta }$
then
$\mathrm { crit }(E)>{\delta }$
then
 $E\cap \mathsf {{StrLe}}({\mathcal {P}}, z)\in \vec {E}^{\mathsf {{StrLe}}({\mathcal {P}}, z)}$
.
$E\cap \mathsf {{StrLe}}({\mathcal {P}}, z)\in \vec {E}^{\mathsf {{StrLe}}({\mathcal {P}}, z)}$
. -
6. It follows that every Woodin cardinal of
 ${\mathcal {P}}$
greater than
${\mathcal {P}}$
greater than
 ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
 $\mathsf {{StrLe}}({\mathcal {P}}, z)$
, and also if
$\mathsf {{StrLe}}({\mathcal {P}}, z)$
, and also if
 ${\mathcal {P}}$
is
${\mathcal {P}}$
is
 $\omega _1$
-iterable then
$\omega _1$
-iterable then
 $\mathsf {{StrLe}}({\mathcal {P}}, z)$
is
$\mathsf {{StrLe}}({\mathcal {P}}, z)$
is
 $\omega _1$
-iterable.
$\omega _1$
-iterable. -
7. Suppose
 $x, z\in {\mathbb {R}}$
,
$x, z\in {\mathbb {R}}$
,
 ${\mathcal {N}}$
is a complete iterate of
${\mathcal {N}}$
is a complete iterate of
 ${\mathcal {M}}_n^\#(z)$
such that
${\mathcal {M}}_n^\#(z)$
such that
 ${\mathcal {T}}_{{\mathcal {M}}_n^\#(z), {\mathcal {N}}}$
is below the least Woodin cardinal of
${\mathcal {T}}_{{\mathcal {M}}_n^\#(z), {\mathcal {N}}}$
is below the least Woodin cardinal of
 ${\mathcal {M}}_n^\#(z)$
, and some real recursive in x codes
${\mathcal {M}}_n^\#(z)$
, and some real recursive in x codes
 ${\mathcal {N}}$
. Set
${\mathcal {N}}$
. Set
 ${\mathcal {P}}=\mathsf {{StrLe}}({\mathcal {M}}_n(x), z)$
. Then
${\mathcal {P}}=\mathsf {{StrLe}}({\mathcal {M}}_n(x), z)$
. Then
 ${\mathcal {P}}$
is a complete iterate of
${\mathcal {P}}$
is a complete iterate of
 ${\mathcal {N}}$
. The proof proceeds as follows. First it is shown that there is a normal iteration
${\mathcal {N}}$
. The proof proceeds as follows. First it is shown that there is a normal iteration
 ${\mathcal {T}}$
of
${\mathcal {T}}$
of
 ${\mathcal {N}}$
which is below the least Woodin cardinal of
${\mathcal {N}}$
which is below the least Woodin cardinal of
 ${\mathcal {N}}$
and if
${\mathcal {N}}$
and if
 ${\mathcal {P}}'$
is the last model of
${\mathcal {P}}'$
is the last model of
 ${\mathcal {T}}$
then
${\mathcal {T}}$
then
 $({\mathcal {N}}(z))^{{\mathcal {M}}_n(x)}={\mathcal {P}}'|{\delta }$
where
$({\mathcal {N}}(z))^{{\mathcal {M}}_n(x)}={\mathcal {P}}'|{\delta }$
where
 ${\delta }$
is the least Woodin cardinal of
${\delta }$
is the least Woodin cardinal of
 ${\mathcal {P}}'$
(and also
${\mathcal {P}}'$
(and also
 ${\mathcal {M}}_n(x)$
). To establish this result one uses the stationarity of the backgrounded constructions which says that in the comparison of
${\mathcal {M}}_n(x)$
). To establish this result one uses the stationarity of the backgrounded constructions which says that in the comparison of
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\mathcal {P}}'$
, the iteration of
${\mathcal {P}}'$
, the iteration of
 ${\mathcal {P}}$
is trivial. One then shows that
${\mathcal {P}}$
is trivial. One then shows that
 ${\mathcal {P}}'={\mathcal {P}}$
, and here, the important fact is that
${\mathcal {P}}'={\mathcal {P}}$
, and here, the important fact is that
 ${\mathcal {M}}_n(x)|{\delta }$
is generic over
${\mathcal {M}}_n(x)|{\delta }$
is generic over
 ${\mathcal {P}}$
. This in particular implies that
${\mathcal {P}}$
. This in particular implies that
 ${\mathcal {P}}[{\mathcal {M}}_n(x)|{\delta }]={\mathcal {M}}_n(x)$
. One then concludes that every set in
${\mathcal {P}}[{\mathcal {M}}_n(x)|{\delta }]={\mathcal {M}}_n(x)$
. One then concludes that every set in
 ${\mathcal {P}}$
is definable from a finite sequence
${\mathcal {P}}$
is definable from a finite sequence
 $s\in {\delta }^{<\omega }$
and a finite sequence of indiscernibles for
$s\in {\delta }^{<\omega }$
and a finite sequence of indiscernibles for
 ${\mathcal {M}}_n(x)$
. Since
${\mathcal {M}}_n(x)$
. Since
 ${\mathcal {P}}'|{\delta }={\mathcal {P}}|{\delta }$
and
${\mathcal {P}}'|{\delta }={\mathcal {P}}|{\delta }$
and
 ${\mathcal {P}}'$
has the same property (being a complete iterate of
${\mathcal {P}}'$
has the same property (being a complete iterate of
 ${\mathcal {N}}$
below its least Woodin cardinal), it follows that
${\mathcal {N}}$
below its least Woodin cardinal), it follows that
 ${\mathcal {P}}={\mathcal {P}}'$
. The details of what we have said have appeared in a number of places. The reader may find it useful to consult [Reference Mueller and Sargsyan24, Lemma 3.20], [Reference Sargsyan27, Definition 1.1], [Reference Sargsyan and Schindler32], [Reference Sargsyan30, Lemma 2.11], [Reference Schlutzenberg and Trang34, Lemma 3.23], [Reference Schindler and Steel33, Lemma 1.3] and the discussion after [Reference Schindler and Steel33, Lemma 1.4].
${\mathcal {P}}={\mathcal {P}}'$
. The details of what we have said have appeared in a number of places. The reader may find it useful to consult [Reference Mueller and Sargsyan24, Lemma 3.20], [Reference Sargsyan27, Definition 1.1], [Reference Sargsyan and Schindler32], [Reference Sargsyan30, Lemma 2.11], [Reference Schlutzenberg and Trang34, Lemma 3.23], [Reference Schindler and Steel33, Lemma 1.3] and the discussion after [Reference Schindler and Steel33, Lemma 1.4].The following objects will be used in clauses 8-10. Suppose
 ${\mathcal {P}}$
is a premouse,
${\mathcal {P}}$
is a premouse,
 ${\delta }$
is a Woodin cardinal of
${\delta }$
is a Woodin cardinal of
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 $a\in {\mathcal {P}}|{\delta }$
. Let
$a\in {\mathcal {P}}|{\delta }$
. Let
 ${\mathcal {N}}=(\mathsf {{Le}}(a))^{{\mathcal {P}}|{\delta }}$
and suppose
${\mathcal {N}}=(\mathsf {{Le}}(a))^{{\mathcal {P}}|{\delta }}$
and suppose
 $\mathsf {{Ord}}\cap {\mathcal {N}}={\delta }$
.Footnote
31
$\mathsf {{Ord}}\cap {\mathcal {N}}={\delta }$
.Footnote
31
-
8. Suppose
 ${\kappa }$
is a measurable cardinal of
${\kappa }$
is a measurable cardinal of
 ${\mathcal {N}}$
as witnessed by the extenders on the sequence of
${\mathcal {N}}$
as witnessed by the extenders on the sequence of
 ${\mathcal {N}}$
. Then
${\mathcal {N}}$
. Then
 ${\kappa }$
is a measurable cardinal in
${\kappa }$
is a measurable cardinal in
 ${\mathcal {P}}$
. This is essentially because in the fully backgrounded construction all extenders used for backgrounding purposes are total extenders.
${\mathcal {P}}$
. This is essentially because in the fully backgrounded construction all extenders used for backgrounding purposes are total extenders. -
9. Similarly, if
 ${\kappa }$
is a strong cardinal of
${\kappa }$
is a strong cardinal of
 ${\mathcal {N}}$
then
${\mathcal {N}}$
then
 $\kappa $
is a
$\kappa $
is a
 $<{\delta }$
-strong cardinal in
$<{\delta }$
-strong cardinal in
 ${\mathcal {P}}$
.
${\mathcal {P}}$
. -
10. Suppose
 ${\kappa }$
is a
${\kappa }$
is a
 $<{\delta }$
-strong cardinal in
$<{\delta }$
-strong cardinal in
 ${\mathcal {P}}$
. Then
${\mathcal {P}}$
. ThenLemma 2.8.
 ${\mathcal {N}}|{\kappa }=(\mathsf {{Le}}(a))^{{\mathcal {P}}|{\kappa }}$
.
${\mathcal {N}}|{\kappa }=(\mathsf {{Le}}(a))^{{\mathcal {P}}|{\kappa }}$
.Proof. To see this, suppose not. Set
 ${\mathcal {N}}'=(\mathsf {{Le}}(a))^{{\mathcal {P}}|{\kappa }}$
and let
${\mathcal {N}}'=(\mathsf {{Le}}(a))^{{\mathcal {P}}|{\kappa }}$
and let
 $\xi $
be the least such that the
$\xi $
be the least such that the
 $\xi $
th model of the fully backgrounded construction of
$\xi $
th model of the fully backgrounded construction of
 ${\mathcal {P}}|{\delta }$
over a projects across
${\mathcal {P}}|{\delta }$
over a projects across
 ${\kappa }$
. Let
${\kappa }$
. Let
 ${\mathcal { Q}}$
be the
${\mathcal { Q}}$
be the
 $\xi $
th model of the fully backgrounded construction of
$\xi $
th model of the fully backgrounded construction of
 ${\mathcal {P}}$
over a and let
${\mathcal {P}}$
over a and let
 $\nu <{\delta }$
be such that
$\nu <{\delta }$
be such that
 ${\mathcal { Q}}$
is constructed by the fully backgrounded construction of
${\mathcal { Q}}$
is constructed by the fully backgrounded construction of
 ${\mathcal {P}}|\nu $
over a. Let
${\mathcal {P}}|\nu $
over a. Let
 ${\mathcal { Q}}'$
be the core of
${\mathcal { Q}}'$
be the core of
 ${\mathcal { Q}}$
. Since
${\mathcal { Q}}$
. Since
 $\rho _\omega ({\mathcal { Q}})<{\kappa }$
, we must have that
$\rho _\omega ({\mathcal { Q}})<{\kappa }$
, we must have that
 ${\mathcal { Q}}'\in {\mathcal {P}}|{\kappa }$
. We now have that
${\mathcal { Q}}'\in {\mathcal {P}}|{\kappa }$
. We now have that
 ${\mathcal { Q}}'$
is not constructed by the fully backgrounded construction of
${\mathcal { Q}}'$
is not constructed by the fully backgrounded construction of
 ${\mathcal {P}}|{\kappa }$
over a
Footnote
32
. However, if
${\mathcal {P}}|{\kappa }$
over a
Footnote
32
. However, if
 $E\in \vec {E}^{{\mathcal {P}}|{\delta }}$
is any extender with
$E\in \vec {E}^{{\mathcal {P}}|{\delta }}$
is any extender with
 $lh(E)>\nu $
, then in
$lh(E)>\nu $
, then in
 $Ult({\mathcal {P}}, E)$
,
$Ult({\mathcal {P}}, E)$
,
 $\pi _E({\mathcal { Q}}')={\mathcal { Q}}'$
is constructed by the fully backgrounded construction of
$\pi _E({\mathcal { Q}}')={\mathcal { Q}}'$
is constructed by the fully backgrounded construction of
 $Ult({\mathcal {P}}, E)|\pi _E({\kappa })$
over a.
$Ult({\mathcal {P}}, E)|\pi _E({\kappa })$
over a.Definition 2.9. We say
 ${\kappa }$
is an
${\kappa }$
is an
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {P}}$
if letting
${\mathcal {P}}$
if letting
 ${\delta }_0$
be the least Woodin cardinal of
${\delta }_0$
be the least Woodin cardinal of
 ${\mathcal {P}}$
,
${\mathcal {P}}$
,
 ${\kappa }<{\delta }_0$
,
${\kappa }<{\delta }_0$
,
 ${\kappa }$
is a
${\kappa }$
is a
 ${\mathcal {P}}$
-cardinal and
${\mathcal {P}}$
-cardinal and  $$ \begin{align*} \mathsf{{Le}}^{{\mathcal{P}}|{\delta}_0}|{\kappa}=\mathsf{{Le}}^{{\mathcal{P}}|{\kappa}}. \end{align*} $$
$$ \begin{align*} \mathsf{{Le}}^{{\mathcal{P}}|{\delta}_0}|{\kappa}=\mathsf{{Le}}^{{\mathcal{P}}|{\kappa}}. \end{align*} $$
We say
 ${\kappa }$
is a weak
${\kappa }$
is a weak
 $fb$
-cut if whenever
$fb$
-cut if whenever
 ${\mathcal { Q}}$
is a mouse that appears in the fully backgrounded construction of
${\mathcal { Q}}$
is a mouse that appears in the fully backgrounded construction of
 ${\mathcal {P}}$
over
${\mathcal {P}}$
over
 $\mathsf {{Le}}^{{\mathcal {P}}|{\kappa }}$
(and hence uses extenders with critical points
$\mathsf {{Le}}^{{\mathcal {P}}|{\kappa }}$
(and hence uses extenders with critical points
 $>{\kappa }$
),
$>{\kappa }$
),
 $\rho _\omega ({\mathcal { Q}})\geq {\kappa }$
Footnote
33
.
$\rho _\omega ({\mathcal { Q}})\geq {\kappa }$
Footnote
33
. -
11. (Universality) Suppose
 ${\mathcal {P}}$
is a translatable premouse (see clause 3 above),
${\mathcal {P}}$
is a translatable premouse (see clause 3 above),
 ${\delta }$
is its least Woodin cardinal and
${\delta }$
is its least Woodin cardinal and
 $a\in {\mathcal {P}}|{\delta }$
. Suppose
$a\in {\mathcal {P}}|{\delta }$
. Suppose
 ${\mathcal { Q}}$
is a
${\mathcal { Q}}$
is a
 ${\delta }+1$
-iterable a-premouse in
${\delta }+1$
-iterable a-premouse in
 ${\mathcal {P}}$
. Then either
${\mathcal {P}}$
. Then either
 $\mathsf {{Le}}(a)$
has a superstrong cardinal or
$\mathsf {{Le}}(a)$
has a superstrong cardinal or
 ${\mathcal { Q}}\trianglelefteq \mathsf {{Le}}(a)$
. Moreover, if
${\mathcal { Q}}\trianglelefteq \mathsf {{Le}}(a)$
. Moreover, if
 ${\mathcal {N}}$
is some fully backgrounded construction of
${\mathcal {N}}$
is some fully backgrounded construction of
 ${\mathcal {P}}|{\delta }$
such that
${\mathcal {P}}|{\delta }$
such that
 $a\in {\mathcal {N}}$
and
$a\in {\mathcal {N}}$
and
 $\mathsf {{Ord}}\cap \mathsf {{Le}}(a)^{\mathcal {N}}={\delta }$
then either
$\mathsf {{Ord}}\cap \mathsf {{Le}}(a)^{\mathcal {N}}={\delta }$
then either
 $\mathsf {{Le}}(a)^{\mathcal {N}}$
has a superstrong cardinal or
$\mathsf {{Le}}(a)^{\mathcal {N}}$
has a superstrong cardinal or
 ${\mathcal { Q}}\trianglelefteq \mathsf {{Le}}(a)^{\mathcal {N}}$
. These results are due to Steel and are consequences of universality of the fully backgrounded constructions (e.g., see [Reference Sargsyan30, Lemma 2.12 and 2.13]).
${\mathcal { Q}}\trianglelefteq \mathsf {{Le}}(a)^{\mathcal {N}}$
. These results are due to Steel and are consequences of universality of the fully backgrounded constructions (e.g., see [Reference Sargsyan30, Lemma 2.12 and 2.13]). -
12. Let
 ${\mathcal {P}}={\mathcal {M}}_n(x)$
where
${\mathcal {P}}={\mathcal {M}}_n(x)$
where
 $n>0$
and
$n>0$
and
 $x\in {\mathbb {R}}$
, and let
$x\in {\mathbb {R}}$
, and let
 ${\delta }$
be the least Woodin cardinal of
${\delta }$
be the least Woodin cardinal of
 ${\mathcal {P}}$
. Let
${\mathcal {P}}$
. Let
 $\eta <{\delta }$
. Then
$\eta <{\delta }$
. Then
 ${\mathcal {P}}|\eta $
is
${\mathcal {P}}|\eta $
is
 ${\delta }+1$
-iterable inside
${\delta }+1$
-iterable inside
 ${\mathcal {P}}$
. This is because if
${\mathcal {P}}$
. This is because if
 ${\mathcal {T}}$
is a correct iteration of
${\mathcal {T}}$
is a correct iteration of
 ${\mathcal {P}}|\eta $
of length
${\mathcal {P}}|\eta $
of length
 $\leq {\delta }$
then
$\leq {\delta }$
then
 ${\mathcal { Q}}({\mathcal {T}})\trianglelefteq {\mathcal {M}}_{n-1}(\mathsf {{cop}}({\mathcal {T}}))$
implying that the correct branch of
${\mathcal { Q}}({\mathcal {T}})\trianglelefteq {\mathcal {M}}_{n-1}(\mathsf {{cop}}({\mathcal {T}}))$
implying that the correct branch of
 ${\mathcal {T}}$
is in
${\mathcal {T}}$
is in
 ${\mathcal {P}}$
.
${\mathcal {P}}$
. -
13. We will need the following lemma. We continue with the
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\delta }$
of clause 12, but the results we state are more general.
${\delta }$
of clause 12, but the results we state are more general.Lemma 2.10. Suppose
 ${\kappa }$
is an
${\kappa }$
is an
 $fb$
-cut. Then
$fb$
-cut. Then
 ${\kappa }$
is a weak
${\kappa }$
is a weak
 $fb$
-cut.
$fb$
-cut.Proof. If
 ${\mathcal { Q}}$
is an
${\mathcal { Q}}$
is an
 $\mathsf {{Le}}^{{\mathcal {P}}|{\kappa }}$
-premouse which is constructed by the fully backgrounded construction of
$\mathsf {{Le}}^{{\mathcal {P}}|{\kappa }}$
-premouse which is constructed by the fully backgrounded construction of
 ${\mathcal {P}}|{\delta }$
done over
${\mathcal {P}}|{\delta }$
done over
 $\mathsf {{Le}}^{{\mathcal {P}}|{\kappa }}$
then by universality
$\mathsf {{Le}}^{{\mathcal {P}}|{\kappa }}$
then by universality
 ${\mathcal { Q}}\trianglelefteq \mathsf {{Le}}^{{\mathcal {P}}|{\delta }}$
(see clause 11 above). Since
${\mathcal { Q}}\trianglelefteq \mathsf {{Le}}^{{\mathcal {P}}|{\delta }}$
(see clause 11 above). Since
 ${\kappa }$
is an
${\kappa }$
is an
 $fb$
-cut, we have that
$fb$
-cut, we have that
 $\rho _{\omega }({\mathcal { Q}})\geq {\kappa }$
. Hence,
$\rho _{\omega }({\mathcal { Q}})\geq {\kappa }$
. Hence,
 ${\kappa }$
is a weak
${\kappa }$
is a weak
 $fb$
-cut.
$fb$
-cut. -
14. We will need the following lemma. We continue with the
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\delta }$
as in clause 12.
${\delta }$
as in clause 12.Lemma 2.11. Let
 $E\in \vec {E}^{{\mathcal {P}}|{\delta }}$
be a total extender such that
$E\in \vec {E}^{{\mathcal {P}}|{\delta }}$
be a total extender such that
 $\nu (E)$
is an inaccessible cardinal of
$\nu (E)$
is an inaccessible cardinal of
 ${\mathcal {P}}$
. Then for any
${\mathcal {P}}$
. Then for any
 $\tau <\nu (E)$
,
$\tau <\nu (E)$
,
 $\tau $
is a weak
$\tau $
is a weak
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {P}}$
if and only if
${\mathcal {P}}$
if and only if
 $\tau $
is a weak
$\tau $
is a weak
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {P}}, E)$
.
$Ult({\mathcal {P}}, E)$
.Proof. Assume first that
 $\tau $
is an inaccessible weak
$\tau $
is an inaccessible weak
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {P}}$
. Let
${\mathcal {P}}$
. Let
 ${\mathcal { K}}=\mathsf {{Le}}^{{\mathcal {P}}|\tau }$
. Suppose
${\mathcal { K}}=\mathsf {{Le}}^{{\mathcal {P}}|\tau }$
. Suppose
 ${\mathcal { Q}}$
is a
${\mathcal { Q}}$
is a
 ${\mathcal { K}}$
-premouse constructed by the fully backgrounded construction of
${\mathcal { K}}$
-premouse constructed by the fully backgrounded construction of
 $Ult({\mathcal {P}}, E)|{\delta }$
done over
$Ult({\mathcal {P}}, E)|{\delta }$
done over
 ${\mathcal { K}}$
and
${\mathcal { K}}$
and
 $\rho _\omega ({\mathcal { Q}})=\tau $
Footnote
34
. Since
$\rho _\omega ({\mathcal { Q}})=\tau $
Footnote
34
. Since
 ${\mathcal { Q}}$
is
${\mathcal { Q}}$
is
 ${\delta }+1$
-iterable, universality implies that
${\delta }+1$
-iterable, universality implies that
 ${\mathcal { Q}}$
is constructed by the fully backgrounded construction of
${\mathcal { Q}}$
is constructed by the fully backgrounded construction of
 ${\mathcal {P}}|{\delta }$
done over
${\mathcal {P}}|{\delta }$
done over
 ${\mathcal { K}}$
. Hence, considering
${\mathcal { K}}$
. Hence, considering
 ${\mathcal { Q}}$
as a premouse,
${\mathcal { Q}}$
as a premouse,
 $\rho _\omega ({\mathcal { Q}})\geq \tau $
. Thus,
$\rho _\omega ({\mathcal { Q}})\geq \tau $
. Thus,
 $\tau $
is a weak
$\tau $
is a weak
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {P}}, E)$
.
$Ult({\mathcal {P}}, E)$
.Conversely, suppose
 $\tau $
is an inaccessible weak
$\tau $
is an inaccessible weak
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {P}}, E)$
. Again, let
$Ult({\mathcal {P}}, E)$
. Again, let
 ${\mathcal { K}}=\mathsf {{Le}}^{{\mathcal {P}}|\tau }$
. Suppose
${\mathcal { K}}=\mathsf {{Le}}^{{\mathcal {P}}|\tau }$
. Suppose
 ${\mathcal { Q}}$
is a
${\mathcal { Q}}$
is a
 ${\mathcal { K}}$
-premouse constructed by the fully backgrounded construction of
${\mathcal { K}}$
-premouse constructed by the fully backgrounded construction of
 ${\mathcal {P}}|{\delta }$
done over
${\mathcal {P}}|{\delta }$
done over
 ${\mathcal { K}}$
and
${\mathcal { K}}$
and
 $\rho _\omega ({\mathcal { Q}})=\tau $
. Then
$\rho _\omega ({\mathcal { Q}})=\tau $
. Then
 ${\mathcal { Q}}$
is
${\mathcal { Q}}$
is
 ${\delta }+1$
-iterable in
${\delta }+1$
-iterable in
 $Ult({\mathcal {P}}, E)$
Footnote
35
. Hence, again universality implies that, considering
$Ult({\mathcal {P}}, E)$
Footnote
35
. Hence, again universality implies that, considering
 ${\mathcal { Q}}$
as just a premouse,
${\mathcal { Q}}$
as just a premouse,
 $\rho _\omega ({\mathcal { Q}})\geq \tau $
.
$\rho _\omega ({\mathcal { Q}})\geq \tau $
. -
15.
 $\mathsf {Cond}$
is the following statement in the language of premice.
$\mathsf {Cond}$
is the following statement in the language of premice.
 $\dot {{\mathcal {V}}}$
is used for the universe.
$\dot {{\mathcal {V}}}$
is used for the universe. $\mathsf {{Cond:}}$
Suppose
$\mathsf {{Cond:}}$
Suppose
 ${\delta }$
is the least Woodin cardinal,
${\delta }$
is the least Woodin cardinal,
 ${\kappa }<{\delta }$
is the least
${\kappa }<{\delta }$
is the least
 $<{\delta }$
-strong cardinal (as witnessed by the extender sequence),
$<{\delta }$
-strong cardinal (as witnessed by the extender sequence),
 ${\gamma}>{\delta }$
is an inaccessible cardinal,
${\gamma}>{\delta }$
is an inaccessible cardinal,
 $\phi $
is a formula and
$\phi $
is a formula and
 $\dot {{\mathcal {V}}}|{\gamma} \models \phi [{\delta }, \vec {a}]$
where
$\dot {{\mathcal {V}}}|{\gamma} \models \phi [{\delta }, \vec {a}]$
where
 $\vec {a}\in [\dot {{\mathcal {V}}}|{\delta }]^{<\omega }$
. There is then
$\vec {a}\in [\dot {{\mathcal {V}}}|{\delta }]^{<\omega }$
. There is then
 ${\alpha }<{\beta }<{\kappa }$
and
${\alpha }<{\beta }<{\kappa }$
and
 $\vec {b}\in [\dot {{\mathcal {V}}}|{\alpha }]^{<\omega }$
such that
$\vec {b}\in [\dot {{\mathcal {V}}}|{\alpha }]^{<\omega }$
such that-
(a)
 $\dot {{\mathcal {V}}}|{\beta }\models `{\alpha }$
is the least Woodin cardinal’,
$\dot {{\mathcal {V}}}|{\beta }\models `{\alpha }$
is the least Woodin cardinal’, -
(b)
 $\vec {b}\in [\dot {{\mathcal {V}}}|{\alpha }]^{<\omega }$
,
$\vec {b}\in [\dot {{\mathcal {V}}}|{\alpha }]^{<\omega }$
, -
(c)
 $\dot {{\mathcal {V}}}|{\beta }\models \phi [{\alpha }, \vec {b}]$
, and
$\dot {{\mathcal {V}}}|{\beta }\models \phi [{\alpha }, \vec {b}]$
, and -
(d)
 ${\alpha }$
is an inaccessible cardinal of
${\alpha }$
is an inaccessible cardinal of
 $\dot {{\mathcal {V}}}$
,
$\dot {{\mathcal {V}}}$
, -
(e)
 ${\alpha }$
is an
${\alpha }$
is an
 $fb$
-cut of
$fb$
-cut of
 $\dot {{\mathcal {V}}}$
.
$\dot {{\mathcal {V}}}$
.
We will need the following lemma.
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\delta }$
are as in clause 12 above. Thus,
${\delta }$
are as in clause 12 above. Thus,
 ${\mathcal {P}}={\mathcal {M}}_n(x)$
where
${\mathcal {P}}={\mathcal {M}}_n(x)$
where
 $n>0$
,
$n>0$
,
 $x\in {\mathbb {R}}$
and
$x\in {\mathbb {R}}$
and
 ${\delta }$
is the least Woodin cardinal of
${\delta }$
is the least Woodin cardinal of
 ${\mathcal {P}}$
.
${\mathcal {P}}$
.Lemma 2.12.
 ${\mathcal {P}}\models \mathsf {{Cond}}$
.
${\mathcal {P}}\models \mathsf {{Cond}}$
.Proof. Let
 ${\mathcal {N}}=\mathsf {{Le}}^{{\mathcal {P}}|{\delta }}$
. Let
${\mathcal {N}}=\mathsf {{Le}}^{{\mathcal {P}}|{\delta }}$
. Let
 ${\delta }$
be the least Woodin cardinal of
${\delta }$
be the least Woodin cardinal of
 ${\mathcal {P}}$
. Suppose
${\mathcal {P}}$
. Suppose
 ${\gamma} $
,
${\gamma} $
,
 $\phi $
and
$\phi $
and
 $a\in {\mathcal {P}}|{\delta }$
are such that
$a\in {\mathcal {P}}|{\delta }$
are such that
 ${\gamma}>{\delta }$
is inaccessible and
${\gamma}>{\delta }$
is inaccessible and
 ${\mathcal {P}}|{\gamma} \models \phi [{\delta }, a]$
. We can find
${\mathcal {P}}|{\gamma} \models \phi [{\delta }, a]$
. We can find
 ${\mathcal { Q}}\trianglelefteq {\mathcal {P}}|{\delta }$
and an elementary
${\mathcal { Q}}\trianglelefteq {\mathcal {P}}|{\delta }$
and an elementary
 $\pi :{\mathcal { Q}}\rightarrow {\mathcal {P}}|{\gamma} $
such that if
$\pi :{\mathcal { Q}}\rightarrow {\mathcal {P}}|{\gamma} $
such that if
 $\tau =\pi ^{-1}({\delta })$
then
$\tau =\pi ^{-1}({\delta })$
then
 $\tau $
is an inaccessible cardinal of
$\tau $
is an inaccessible cardinal of
 ${\mathcal {P}}$
,
${\mathcal {P}}$
,
 $\pi \restriction \tau =id$
and
$\pi \restriction \tau =id$
and
 $a\in {\mathcal {P}}|\tau $
. We then have that
$a\in {\mathcal {P}}|\tau $
. We then have that
 $\tau $
is an
$\tau $
is an
 $fb$
-cut of
$fb$
-cut of
 ${\mathcal {P}}$
. However, we do not know that
${\mathcal {P}}$
. However, we do not know that
 $\tau <{\kappa }$
where
$\tau <{\kappa }$
where
 ${\kappa }$
is the least
${\kappa }$
is the least
 $<{\delta }$
-strong cardinal of
$<{\delta }$
-strong cardinal of
 ${\mathcal {P}}$
.We now want to show that there is
${\mathcal {P}}$
.We now want to show that there is
 ${\mathcal R}\trianglelefteq {\mathcal {P}}|{\kappa }$
such that
${\mathcal R}\trianglelefteq {\mathcal {P}}|{\kappa }$
such that-
(a)
 ${\mathcal R}$
has a Woodin cardinal and if
${\mathcal R}$
has a Woodin cardinal and if
 $\nu $
is its least Woodin cardinal then
$\nu $
is its least Woodin cardinal then
 $\nu $
is an inaccessible cardinal of
$\nu $
is an inaccessible cardinal of
 ${\mathcal {P}}|{\kappa }$
,
${\mathcal {P}}|{\kappa }$
, -
(b)
 ${\mathcal R}|\nu ={\mathcal {P}}|\nu $
and
${\mathcal R}|\nu ={\mathcal {P}}|\nu $
and
 $\nu $
is an
$\nu $
is an
 $fb$
-cut,
$fb$
-cut, -
(c) for some
 $b\in {\mathcal R}|\nu $
,
$b\in {\mathcal R}|\nu $
,
 ${\mathcal R}\models \phi [\nu , b]$
.
${\mathcal R}\models \phi [\nu , b]$
.
To get such an
 ${\mathcal R}\trianglelefteq {\mathcal {P}}|{\lambda }$
, let
${\mathcal R}\trianglelefteq {\mathcal {P}}|{\lambda }$
, let
 $E\in \vec {E}^{\mathcal {P}}$
be such that
$E\in \vec {E}^{\mathcal {P}}$
be such that
 ${\mathcal { Q}}\trianglelefteq {\mathcal {P}}|\mathrm {lh}(E)$
,
${\mathcal { Q}}\trianglelefteq {\mathcal {P}}|\mathrm {lh}(E)$
,
 $\mathrm {crit }(E)={\kappa }$
and
$\mathrm {crit }(E)={\kappa }$
and
 $\tau $
is a cutpoint in
$\tau $
is a cutpoint in
 $Ult({\mathcal {P}}, E)$
. Then in
$Ult({\mathcal {P}}, E)$
. Then in
 $Ult({\mathcal {P}}, E)$
,
$Ult({\mathcal {P}}, E)$
,
 ${\mathcal { Q}}$
has the properties that we look for except that we do not know that
${\mathcal { Q}}$
has the properties that we look for except that we do not know that
 $\tau $
is an
$\tau $
is an
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {P}}, E)$
. We now prove that in fact
$Ult({\mathcal {P}}, E)$
. We now prove that in fact
 $\tau $
is an
$\tau $
is an
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {P}}, E)$
.
$Ult({\mathcal {P}}, E)$
.It follows from Lemma 2.11 that
 $\tau $
is a weak
$\tau $
is a weak
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {P}}, E)$
. To see that
$Ult({\mathcal {P}}, E)$
. To see that
 $\tau $
is an
$\tau $
is an
 $fb$
-cut notice that the fully backgrounded construction of
$fb$
-cut notice that the fully backgrounded construction of
 $Ult({\mathcal {P}}, E)$
never adds extenders overlapping
$Ult({\mathcal {P}}, E)$
never adds extenders overlapping
 $\tau $
, and so in fact this construction is the fully backgrounded construction of
$\tau $
, and so in fact this construction is the fully backgrounded construction of
 $Ult({\mathcal {P}}, E)$
done over
$Ult({\mathcal {P}}, E)$
done over
 ${\mathcal {N}}|\tau $
.
${\mathcal {N}}|\tau $
. -
-
16. We will need the following two extender sequences.
Definition 2.13. Suppose
 ${\mathcal {S}}$
is a translatable premouse (see clause 3 above) and
${\mathcal {S}}$
is a translatable premouse (see clause 3 above) and
 $\tau $
is its least Woodin cardinal. Let
$\tau $
is its least Woodin cardinal. Let
 ${\mathcal {N}}=\mathsf {{Le}}^{{\mathcal {S}}|\tau }$
. We then let
${\mathcal {N}}=\mathsf {{Le}}^{{\mathcal {S}}|\tau }$
. We then let
 $\mathcal {E}^{\mathcal {S}}_{le}$
be the set of all extenders
$\mathcal {E}^{\mathcal {S}}_{le}$
be the set of all extenders
 $E\in \vec {E}^{{\mathcal {S}}|\tau }$
such that
$E\in \vec {E}^{{\mathcal {S}}|\tau }$
such that-
(a)
 $\nu (E)$
is an inaccessible cardinal of
$\nu (E)$
is an inaccessible cardinal of
 ${\mathcal {S}}$
,
${\mathcal {S}}$
, -
(b)
 $\pi _E({\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
,
$\pi _E({\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
, -
(c)
 $\mathrm {crit }(E)$
is an
$\mathrm {crit }(E)$
is an
 $fb$
-cut.
$fb$
-cut.
We let
 $\mathcal {E}_{sm}^{\mathcal {S}}$
be the set of
$\mathcal {E}_{sm}^{\mathcal {S}}$
be the set of
 $E\in \vec {E}^{{\mathcal {S}}|\tau }$
such that
$E\in \vec {E}^{{\mathcal {S}}|\tau }$
such that
 $\nu (E)$
is a measurable cardinal of
$\nu (E)$
is a measurable cardinal of
 ${\mathcal {S}}$
and
${\mathcal {S}}$
and
 $\mathrm {crit }(E)$
is a
$\mathrm {crit }(E)$
is a
 $<\tau $
-strong cardinal of
$<\tau $
-strong cardinal of
 ${\mathcal {S}}$
.
${\mathcal {S}}$
.Lemma 2.14. Continuing with
 ${\mathcal {S}}$
and
${\mathcal {S}}$
and
 $\tau $
as above,
$\tau $
as above,
 $\mathcal {E}_{ms}^{\mathcal {S}}$
is weakly appropriate and
$\mathcal {E}_{ms}^{\mathcal {S}}$
is weakly appropriate and
 $\mathcal {E}^{\mathcal {S}}_{le}$
is appropriate (see Definition 2.4 and Definition 2.13).The same proof can be used to show that the following also holds.
$\mathcal {E}^{\mathcal {S}}_{le}$
is appropriate (see Definition 2.4 and Definition 2.13).The same proof can be used to show that the following also holds.Proof. It is easy to show that
 $\mathcal {E}_{sm}^{\mathcal {S}}$
is weakly appropriate. Suppose then
$\mathcal {E}_{sm}^{\mathcal {S}}$
is weakly appropriate. Suppose then
 $E\in \mathcal {E}^{\mathcal {S}}_{le}$
. Let
$E\in \mathcal {E}^{\mathcal {S}}_{le}$
. Let
 ${\mathcal {N}}$
be the fully backgrounded construction of
${\mathcal {N}}$
be the fully backgrounded construction of
 ${\mathcal {S}}|\tau $
and set
${\mathcal {S}}|\tau $
and set
 $\mathcal {E}=\mathcal {E}^{\mathcal {S}}_{le}$
. We want to see that
$\mathcal {E}=\mathcal {E}^{\mathcal {S}}_{le}$
. We want to see that
 $\pi _E(\mathcal {E})\cap ({\mathcal {S}}|\nu (E))=\mathcal {E}\cap ({\mathcal {S}}|\nu (E))$
. We have that
$\pi _E(\mathcal {E})\cap ({\mathcal {S}}|\nu (E))=\mathcal {E}\cap ({\mathcal {S}}|\nu (E))$
. We have that
 $\pi _E({\mathcal {N}})$
is the fully backgrounded construction of
$\pi _E({\mathcal {N}})$
is the fully backgrounded construction of
 $Ult({\mathcal {S}}, E)|\tau $
and
$Ult({\mathcal {S}}, E)|\tau $
and
 $\pi _E({\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
.
$\pi _E({\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
.Suppose now that
 $F\in \pi _E(\mathcal {E})\cap ({\mathcal {S}}|\nu (E))$
. It follows that
$F\in \pi _E(\mathcal {E})\cap ({\mathcal {S}}|\nu (E))$
. It follows that(1)
 $\nu (F)$
is an inaccessible cardinal in
$\nu (F)$
is an inaccessible cardinal in
 $Ult({\mathcal {S}}, E)$
,
$Ult({\mathcal {S}}, E)$
,(2)
 $\pi ^{Ult({\mathcal {S}}, E)}_F(\pi _E({\mathcal {N}}))|\nu (F)=\pi _E({\mathcal {N}})|\nu (F)$
,
$\pi ^{Ult({\mathcal {S}}, E)}_F(\pi _E({\mathcal {N}}))|\nu (F)=\pi _E({\mathcal {N}})|\nu (F)$
,(3)
 $\mathrm {crit }(F)$
is an
$\mathrm {crit }(F)$
is an
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {S}}, E)$
.
$Ult({\mathcal {S}}, E)$
.We want to see that
(4)
 $\nu (F)$
is an inaccessible cardinal in
$\nu (F)$
is an inaccessible cardinal in
 ${\mathcal {S}}$
,
${\mathcal {S}}$
,(5)
 $\pi _F({\mathcal {N}})|\nu (F)={\mathcal {N}}|\nu (F)$
,
$\pi _F({\mathcal {N}})|\nu (F)={\mathcal {N}}|\nu (F)$
,(6)
 $\mathrm {crit }(F)$
is an
$\mathrm {crit }(F)$
is an
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {S}}$
.
${\mathcal {S}}$
.(4) is easy as
 $\nu (E)>\nu (F)$
and
$\nu (E)>\nu (F)$
and
 $\nu (E)$
is inaccessible in both
$\nu (E)$
is inaccessible in both
 ${\mathcal {S}}$
and
${\mathcal {S}}$
and
 $Ult({\mathcal {S}}, E)$
. To see (5) notice that because
$Ult({\mathcal {S}}, E)$
. To see (5) notice that because  $$ \begin{align*}\pi_F\restriction ({\mathcal{S}}|(\mathrm{crit }(F)^+)^{\mathcal{S}})=\pi_F^{Ult({\mathcal{S}}, F)}\restriction (Ult({\mathcal{S}}, F)|(\mathrm{crit }(F)^+)^{\mathcal{S}})\end{align*} $$
$$ \begin{align*}\pi_F\restriction ({\mathcal{S}}|(\mathrm{crit }(F)^+)^{\mathcal{S}})=\pi_F^{Ult({\mathcal{S}}, F)}\restriction (Ult({\mathcal{S}}, F)|(\mathrm{crit }(F)^+)^{\mathcal{S}})\end{align*} $$
and because of (2) we have that
 ${\mathcal {N}}|\nu (F)=\pi _F({\mathcal {N}})|\nu (F)$
.
${\mathcal {N}}|\nu (F)=\pi _F({\mathcal {N}})|\nu (F)$
.We now want to show (6) and we have that
 $\mathrm {crit }(F)$
is an
$\mathrm {crit }(F)$
is an
 $fb$
-cut in
$fb$
-cut in
 $Ult({\mathcal {S}}, F)$
. It follows that
$Ult({\mathcal {S}}, F)$
. It follows that
 $\pi _E({\mathcal {N}})|\mathrm {crit }(F)$
is the fully backgrounded construction of
$\pi _E({\mathcal {N}})|\mathrm {crit }(F)$
is the fully backgrounded construction of
 $Ult({\mathcal {S}}, F)|\mathrm {crit }(F)$
. But
$Ult({\mathcal {S}}, F)|\mathrm {crit }(F)$
. But
 $\pi _E({\mathcal {N}})|\mathrm {crit }(F)={\mathcal {N}}|\mathrm {crit }(F)$
and
$\pi _E({\mathcal {N}})|\mathrm {crit }(F)={\mathcal {N}}|\mathrm {crit }(F)$
and
 $Ult({\mathcal {S}}, F)|\mathrm {crit }(F)={\mathcal {S}}|\mathrm {crit }(F)$
. Therefore,
$Ult({\mathcal {S}}, F)|\mathrm {crit }(F)={\mathcal {S}}|\mathrm {crit }(F)$
. Therefore,  $$ \begin{align*}{\mathcal{N}}|\mathrm{crit }(F) \text{ is the fully backgrounded construction of } {\mathcal{S}}|\mathrm{crit }(F). \end{align*} $$
$$ \begin{align*}{\mathcal{N}}|\mathrm{crit }(F) \text{ is the fully backgrounded construction of } {\mathcal{S}}|\mathrm{crit }(F). \end{align*} $$
The proof that
 $\mathcal {E}\cap ({\mathcal {S}}|\nu (E))\subseteq \pi _E(\mathcal {E})\cap ({\mathcal {S}}|\nu (E))$
is very similar.
$\mathcal {E}\cap ({\mathcal {S}}|\nu (E))\subseteq \pi _E(\mathcal {E})\cap ({\mathcal {S}}|\nu (E))$
is very similar.Lemma 2.15. Continuing with
 ${\mathcal {S}}$
and
${\mathcal {S}}$
and
 $\tau $
as above, if
$\tau $
as above, if
 $E\in \mathcal {E}^{\mathcal {S}}_{le}$
then for all
$E\in \mathcal {E}^{\mathcal {S}}_{le}$
then for all
 $\xi <\nu (E)$
,
$\xi <\nu (E)$
,
 ${\mathcal {S}}\models `\xi $
is an
${\mathcal {S}}\models `\xi $
is an
 $fb$
-cut’ if and only if
$fb$
-cut’ if and only if
 $Ult({\mathcal {S}}, E)\models `\xi $
is an
$Ult({\mathcal {S}}, E)\models `\xi $
is an
 $fb$
-cut’.The following corollary can now easily be proven by induction on the length of the iteration.
$fb$
-cut’.The following corollary can now easily be proven by induction on the length of the iteration.Proof. Let
 ${\mathcal {N}}$
be as in the above proof. We have that
${\mathcal {N}}$
be as in the above proof. We have that
 $\pi _E({\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
. Set
$\pi _E({\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
. Set
 ${\mathcal { K}}=\mathsf {Le}^{{\mathcal {S}}|\xi }$
. We have that
${\mathcal { K}}=\mathsf {Le}^{{\mathcal {S}}|\xi }$
. We have that
 ${\mathcal { K}}=\mathsf {Le}^{Ult({\mathcal {S}}, E)|\xi }$
. Thus, the following equivalence holds.
${\mathcal { K}}=\mathsf {Le}^{Ult({\mathcal {S}}, E)|\xi }$
. Thus, the following equivalence holds.  $$ \begin{align*} {\mathcal{S}}\models `\xi\ \text{is an} fb\text{-cut}\text' &{\mathrel{\leftrightarrow}} {\mathcal{ K}}={\mathcal{N}}|\xi \\ &{\mathrel{\leftrightarrow}} {\mathcal{ K}}=\pi_E({\mathcal{N}})|\xi \\ &{\mathrel{\leftrightarrow}} Ult({\mathcal{S}}, E)\models `\xi\ \text{is an} fb\text{-cut}\text'.\\[-37pt] \end{align*} $$
$$ \begin{align*} {\mathcal{S}}\models `\xi\ \text{is an} fb\text{-cut}\text' &{\mathrel{\leftrightarrow}} {\mathcal{ K}}={\mathcal{N}}|\xi \\ &{\mathrel{\leftrightarrow}} {\mathcal{ K}}=\pi_E({\mathcal{N}})|\xi \\ &{\mathrel{\leftrightarrow}} Ult({\mathcal{S}}, E)\models `\xi\ \text{is an} fb\text{-cut}\text'.\\[-37pt] \end{align*} $$
Corollary 2.16. Continuing with
 ${\mathcal {S}}$
and
${\mathcal {S}}$
and
 $\tau $
as above, suppose
$\tau $
as above, suppose
 ${\mathcal {T}}$
is a normal nondropping (i.e.,
${\mathcal {T}}$
is a normal nondropping (i.e.,
 $\mathcal {D}^{\mathcal {T}}=\emptyset $
) iteration of
$\mathcal {D}^{\mathcal {T}}=\emptyset $
) iteration of
 ${\mathcal {S}}$
such that for every
${\mathcal {S}}$
such that for every
 ${\alpha }<\mathrm { lh}({\mathcal {T}})$
,
${\alpha }<\mathrm { lh}({\mathcal {T}})$
,
 $E_{\alpha }^{\mathcal {T}}\in \pi _{0, {\alpha }}^{\mathcal {T}}(\mathcal {E}^{\mathcal {S}}_{le})$
. Then for any
$E_{\alpha }^{\mathcal {T}}\in \pi _{0, {\alpha }}^{\mathcal {T}}(\mathcal {E}^{\mathcal {S}}_{le})$
. Then for any
 ${\alpha }<{\beta }<\mathrm {lh}({\mathcal {T}})$
,
${\alpha }<{\beta }<\mathrm {lh}({\mathcal {T}})$
,
 ${\mathcal {M}}^{\mathcal {T}}_{\beta }\models `\mathrm {crit }(E_{\alpha }^{\mathcal {T}})$
is an
${\mathcal {M}}^{\mathcal {T}}_{\beta }\models `\mathrm {crit }(E_{\alpha }^{\mathcal {T}})$
is an
 $fb$
-cut’.
$fb$
-cut’. -
-
17. We will need the following lemma.
Lemma 2.17. Suppose
 ${\mathcal {S}}$
is a premouse and
${\mathcal {S}}$
is a premouse and
 $\tau $
is its least Woodin cardinal. Let
$\tau $
is its least Woodin cardinal. Let
 ${\mathcal {N}}=\mathsf {{Le}}^{{\mathcal {S}}|\tau }$
and assume that
${\mathcal {N}}=\mathsf {{Le}}^{{\mathcal {S}}|\tau }$
and assume that
 $\mathsf {{Ord}}\cap {\mathcal {N}}=\tau $
. Suppose
$\mathsf {{Ord}}\cap {\mathcal {N}}=\tau $
. Suppose
 ${\alpha }<{\beta }$
are such that
${\alpha }<{\beta }$
are such that-
(a)
 ${\alpha }$
is an
${\alpha }$
is an
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {S}}$
and
${\mathcal {S}}$
and -
(b)
 ${\mathcal {S}}|{\beta }\models \mathsf {{ZFC}}+`{\alpha }$
is a Woodin cardinal’.
${\mathcal {S}}|{\beta }\models \mathsf {{ZFC}}+`{\alpha }$
is a Woodin cardinal’.
Suppose t is a real which satisfies all the axioms of
 $\mathsf {{Ea}}^{\mathcal {S}}_{\tau , \mathcal {E}^{\mathcal {S}}_{le}}$
that are generated by the extenders in
$\mathsf {{Ea}}^{\mathcal {S}}_{\tau , \mathcal {E}^{\mathcal {S}}_{le}}$
that are generated by the extenders in
 ${\mathcal {S}}|{\alpha }$
. Let
${\mathcal {S}}|{\alpha }$
. Let
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {S}}|{\beta })$
. Then t is generic for
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {S}}|{\beta })$
. Then t is generic for
 $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }, \mathcal {E}^{\mathcal { K}}_{sm}}$
.
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }, \mathcal {E}^{\mathcal { K}}_{sm}}$
.Proof. Suppose
 $E\in \vec {E}^{{\mathcal { K}}|{\alpha }}$
such that
$E\in \vec {E}^{{\mathcal { K}}|{\alpha }}$
such that
 $\nu (E)$
is a measurable cardinal of
$\nu (E)$
is a measurable cardinal of
 ${\mathcal { K}}$
and
${\mathcal { K}}$
and
 $\mathrm {crit }(E)$
is a
$\mathrm {crit }(E)$
is a
 $<{\alpha }$
-strong cardinal of
$<{\alpha }$
-strong cardinal of
 ${\mathcal { K}}$
. Let F be the background extender of E. It follows that
${\mathcal { K}}$
. Let F be the background extender of E. It follows that
 $E=F\cap {\mathcal { K}}$
. Moreover, since
$E=F\cap {\mathcal { K}}$
. Moreover, since
 $\mathrm {crit }(E)$
is a strong cardinal in
$\mathrm {crit }(E)$
is a strong cardinal in
 ${\mathcal { K}}|{\alpha }$
,
${\mathcal { K}}|{\alpha }$
,
 $\mathrm {crit }(E)$
is an
$\mathrm {crit }(E)$
is an
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {S}}|{\alpha }$
, and since
${\mathcal {S}}|{\alpha }$
, and since
 ${\alpha }$
itself is an
${\alpha }$
itself is an
 $fb$
-cut,
$fb$
-cut,
 $\mathrm {crit }(E)$
is an
$\mathrm {crit }(E)$
is an
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal {S}}$
. Also, F, since it coheres
${\mathcal {S}}$
. Also, F, since it coheres
 ${\mathcal {N}}$
, is in
${\mathcal {N}}$
, is in
 $\mathcal {E}^{\mathcal {S}}_{le}$
. Therefore, since there is a factor map
$\mathcal {E}^{\mathcal {S}}_{le}$
. Therefore, since there is a factor map
 $k:\pi _E^{\mathcal {N}}({\mathcal {N}}|(\mathrm {crit }(E)^+)^{\mathcal {N}})\rightarrow \pi _F^{\mathcal {S}}({\mathcal {N}}|(\mathrm {crit }(E)^+)^{\mathcal {N}})$
with
$k:\pi _E^{\mathcal {N}}({\mathcal {N}}|(\mathrm {crit }(E)^+)^{\mathcal {N}})\rightarrow \pi _F^{\mathcal {S}}({\mathcal {N}}|(\mathrm {crit }(E)^+)^{\mathcal {N}})$
with
 $\mathrm {crit }(k)\geq \nu (E)$
and since
$\mathrm {crit }(k)\geq \nu (E)$
and since
 $\pi _E^{\mathcal {N}}({\mathcal {N}}|(\mathrm {crit }(E)^+)^{\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
, any axiom generated by E in
$\pi _E^{\mathcal {N}}({\mathcal {N}}|(\mathrm {crit }(E)^+)^{\mathcal {N}})|\nu (E)={\mathcal {N}}|\nu (E)$
, any axiom generated by E in
 ${\mathcal { K}}$
is satisfied by z as it is also an axiom generated by F (see clause 2 of Review 2.7).
${\mathcal { K}}$
is satisfied by z as it is also an axiom generated by F (see clause 2 of Review 2.7). -
Review 2.18. Review of [Reference Sargsyan29]:
Unless otherwise specified, we assume
![]() $\mathsf {{AD}}^{L({\mathbb {R}})}$
. The material reviewed below appears in [Reference Sargsyan29] and in [Reference Steel and Woodin40]. Other treatments of similar concepts appear in [Reference Sargsyan and Schindler32] and [Reference Mueller and Sargsyan24].
$\mathsf {{AD}}^{L({\mathbb {R}})}$
. The material reviewed below appears in [Reference Sargsyan29] and in [Reference Steel and Woodin40]. Other treatments of similar concepts appear in [Reference Sargsyan and Schindler32] and [Reference Mueller and Sargsyan24].
-
1.
 $(u_i: i\in \mathsf {{Ord}})$
is the sequence of uniform indiscernibles for reals (assuming they exist).Footnote
36
Set
$(u_i: i\in \mathsf {{Ord}})$
is the sequence of uniform indiscernibles for reals (assuming they exist).Footnote
36
Set
 $s_{0}=\emptyset $
and for
$s_{0}=\emptyset $
and for
 $m\geq 1$
,
$m\geq 1$
,
 $s_m=(u_0, ..., u_{m-1})$
$s_m=(u_0, ..., u_{m-1})$
-
2. Fix
 $n\in \omega $
and
$n\in \omega $
and
 $x\in {\mathbb {R}}$
and suppose
$x\in {\mathbb {R}}$
and suppose
 ${\mathcal {P}}$
is a complete iterate of
${\mathcal {P}}$
is a complete iterate of
 ${\mathcal {M}}_{n}(x)$
. For
${\mathcal {M}}_{n}(x)$
. For
 $i\leq n$
,
$i\leq n$
,
 ${\delta }_i^{\mathcal {P}}$
is the
${\delta }_i^{\mathcal {P}}$
is the
 $i+1$
st Woodin of
$i+1$
st Woodin of
 ${\mathcal {P}}$
. Let Then
${\mathcal {P}}$
. Let Then $$ \begin{align*} {\gamma}_m^{\mathcal{P}}=\sup(Hull_1^{{\mathcal{P}}|u_{m}}(s_m)\cap {\delta}_0^{\mathcal{P}}). \end{align*} $$
$$ \begin{align*} {\gamma}_m^{\mathcal{P}}=\sup(Hull_1^{{\mathcal{P}}|u_{m}}(s_m)\cap {\delta}_0^{\mathcal{P}}). \end{align*} $$
 $\sup _{m<\omega }{\gamma} _m^{\mathcal {P}}={\delta }_0^{\mathcal {P}}$
. Given two pairs
$\sup _{m<\omega }{\gamma} _m^{\mathcal {P}}={\delta }_0^{\mathcal {P}}$
. Given two pairs
 $({\mathcal {P}}, {\alpha })$
and
$({\mathcal {P}}, {\alpha })$
and
 $({\mathcal { Q}}, {\beta })$
such that
$({\mathcal { Q}}, {\beta })$
such that
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\mathcal { Q}}$
are complete iterates of
${\mathcal { Q}}$
are complete iterates of
 ${\mathcal {M}}_n(x)$
,
${\mathcal {M}}_n(x)$
,
 ${\alpha }<{\gamma} _m^{\mathcal {P}}$
and
${\alpha }<{\gamma} _m^{\mathcal {P}}$
and
 ${\beta }<{\gamma} ^{\mathcal { Q}}_m$
, we write
${\beta }<{\gamma} ^{\mathcal { Q}}_m$
, we write
 $({\mathcal {P}}, {\alpha })\leq ^{n}_m ({\mathcal { Q}}, {\beta })$
if and only if letting
$({\mathcal {P}}, {\alpha })\leq ^{n}_m ({\mathcal { Q}}, {\beta })$
if and only if letting
 ${\mathcal R}$
be the common iterate of
${\mathcal R}$
be the common iterate of
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\mathcal { Q}}$
,
${\mathcal { Q}}$
,
 $\pi _{{\mathcal {P}}, {\mathcal R}}({\alpha })\leq \pi _{{\mathcal { Q}}, {\mathcal R}}({\beta })$
. Clearly,
$\pi _{{\mathcal {P}}, {\mathcal R}}({\alpha })\leq \pi _{{\mathcal { Q}}, {\mathcal R}}({\beta })$
. Clearly,
 $\leq ^n_m$
depends on x, but not mentioning x makes the notation simplerFootnote
37
. We then have that there is a formula
$\leq ^n_m$
depends on x, but not mentioning x makes the notation simplerFootnote
37
. We then have that there is a formula
 $\phi $
such that for all
$\phi $
such that for all
 $({\mathcal {P}}, {\alpha })$
and
$({\mathcal {P}}, {\alpha })$
and
 $({\mathcal { Q}}, {\beta })$
,
$({\mathcal { Q}}, {\beta })$
,
 $({\mathcal {P}}, {\alpha })\leq ^{n}_m ({\mathcal { Q}}, {\beta })$
if and only if The formula
$({\mathcal {P}}, {\alpha })\leq ^{n}_m ({\mathcal { Q}}, {\beta })$
if and only if The formula $$ \begin{align*} {\mathcal{M}}_{n-1}({\mathcal{M}}_n(x)^\#, ({\mathcal{P}}, {\alpha}), ({\mathcal{ Q}}, {\beta}))\models \phi[{\mathcal{M}}_n(x)^\#, ({\mathcal{P}}, {\alpha}), ({\mathcal{ Q}}, {\beta}), s_m]. \end{align*} $$
$$ \begin{align*} {\mathcal{M}}_{n-1}({\mathcal{M}}_n(x)^\#, ({\mathcal{P}}, {\alpha}), ({\mathcal{ Q}}, {\beta}))\models \phi[{\mathcal{M}}_n(x)^\#, ({\mathcal{P}}, {\alpha}), ({\mathcal{ Q}}, {\beta}), s_m]. \end{align*} $$
 $\phi $
essentially records what was said above. It is the conjunction of the following statements:
$\phi $
essentially records what was said above. It is the conjunction of the following statements:
-
(a)
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\mathcal { Q}}$
are complete iterates of
${\mathcal { Q}}$
are complete iterates of
 ${\mathcal {M}}_n(x)$
.
${\mathcal {M}}_n(x)$
. -
(b) There is
 ${\mathcal R}$
, which is a common iterate of
${\mathcal R}$
, which is a common iterate of
 ${\mathcal {P}}$
and
${\mathcal {P}}$
and
 ${\mathcal { Q}}$
and
${\mathcal { Q}}$
and
 $\pi _{{\mathcal {P}}, {\mathcal R}}({\alpha })\leq \pi _{{\mathcal { Q}}, {\mathcal R}}({\beta })$
.
$\pi _{{\mathcal {P}}, {\mathcal R}}({\alpha })\leq \pi _{{\mathcal { Q}}, {\mathcal R}}({\beta })$
.
Explaining the above equivalence is beyond the scope of this paper. The reader can consult [Reference Sargsyan29], [Reference Steel and Woodin40], [Reference Sargsyan and Schindler32] and [Reference Mueller and Sargsyan24]. Essentially, the following happens.Suppose
 ${\mathcal {P}}$
is a complete iterate of
${\mathcal {P}}$
is a complete iterate of
 ${\mathcal {M}}_n(x)$
. Then, there is an iteration tree
${\mathcal {M}}_n(x)$
. Then, there is an iteration tree
 ${\mathcal {T}}\in {\mathcal {M}}_{n-1}({\mathcal {M}}_n(x)^\#, ({\mathcal {P}}, {\alpha }), ({\mathcal { Q}}, {\beta }))$
such that
${\mathcal {T}}\in {\mathcal {M}}_{n-1}({\mathcal {M}}_n(x)^\#, ({\mathcal {P}}, {\alpha }), ({\mathcal { Q}}, {\beta }))$
such that
 ${\mathcal {T}}$
is an iteration tree on
${\mathcal {T}}$
is an iteration tree on
 ${\mathcal {M}}_{n}(x)^\#$
according to its unique
${\mathcal {M}}_{n}(x)^\#$
according to its unique
 $(\omega _1+1)$
-iteration strategy and such that either
$(\omega _1+1)$
-iteration strategy and such that either
 ${\mathcal {T}}$
has a last model which is
${\mathcal {T}}$
has a last model which is
 ${\mathcal {P}}$
or
${\mathcal {P}}$
or
 ${\mathcal {P}}=L(\mathsf {{cop}}({\mathcal {T}}))$
and
${\mathcal {P}}=L(\mathsf {{cop}}({\mathcal {T}}))$
and
 ${\delta }({\mathcal {T}})$
is the largest Woodin cardinal of
${\delta }({\mathcal {T}})$
is the largest Woodin cardinal of
 ${\mathcal {P}}$
(such iteration trees are called maximal). This is the fact used to identify complete iterates of
${\mathcal {P}}$
(such iteration trees are called maximal). This is the fact used to identify complete iterates of
 ${\mathcal {M}}_n(x)^\#$
inside models of the form
${\mathcal {M}}_n(x)^\#$
inside models of the form
 ${\mathcal {M}}_{n-1}({\mathcal {M}}_n(x)^\#, d)$
.Suppose next that there is
${\mathcal {M}}_{n-1}({\mathcal {M}}_n(x)^\#, d)$
.Suppose next that there is
 ${\mathcal R}$
such that
${\mathcal R}$
such that
 $\pi _{{\mathcal {P}}, {\mathcal R}}({\alpha })\leq \pi _{{\mathcal { Q}}, {\mathcal R}}({\beta })$
. We can assume that
$\pi _{{\mathcal {P}}, {\mathcal R}}({\alpha })\leq \pi _{{\mathcal { Q}}, {\mathcal R}}({\beta })$
. We can assume that
 ${\mathcal R}$
is obtained via the usual comparison procedure of [Reference Steel39], which means that
${\mathcal R}$
is obtained via the usual comparison procedure of [Reference Steel39], which means that
 ${\mathcal R}\in {\mathcal {M}}_{n-1}({\mathcal {M}}_n(x)^\#, ({\mathcal {P}}, {\alpha }), ({\mathcal { Q}}, {\beta }))$
. One then shows that can correctly compute
${\mathcal R}\in {\mathcal {M}}_{n-1}({\mathcal {M}}_n(x)^\#, ({\mathcal {P}}, {\alpha }), ({\mathcal { Q}}, {\beta }))$
. One then shows that can correctly compute $$ \begin{align*}{\mathcal{M}}_{n-1}({\mathcal{M}}_n(x)^\#, ({\mathcal{P}}, {\alpha}), ({\mathcal{ Q}}, {\beta}))\end{align*} $$
$$ \begin{align*}{\mathcal{M}}_{n-1}({\mathcal{M}}_n(x)^\#, ({\mathcal{P}}, {\alpha}), ({\mathcal{ Q}}, {\beta}))\end{align*} $$
 $\pi _{{\mathcal {P}}, {\mathcal R}}\restriction \gamma ^{\mathcal {P}}_m$
and
$\pi _{{\mathcal {P}}, {\mathcal R}}\restriction \gamma ^{\mathcal {P}}_m$
and
 $\pi _{{\mathcal { Q}}, {\mathcal R}}\restriction \gamma _m^{\mathcal { Q}}$
, even though it cannot in general compute
$\pi _{{\mathcal { Q}}, {\mathcal R}}\restriction \gamma _m^{\mathcal { Q}}$
, even though it cannot in general compute
 $\pi _{{\mathcal {P}}, {\mathcal R}}$
and
$\pi _{{\mathcal {P}}, {\mathcal R}}$
and
 $\pi _{{\mathcal { Q}}, {\mathcal R}}$
.
$\pi _{{\mathcal { Q}}, {\mathcal R}}$
.
-
-
3. For
 $x\in {\mathbb {R}}$
and
$x\in {\mathbb {R}}$
and
 $n\in \omega $
, set
$n\in \omega $
, set
 ${\gamma} ^{2n+1}_{m, x, \infty }=\pi _{{\mathcal {M}}_{2n+1}(x), \infty }({\gamma} _m^{{\mathcal {M}}_{2n+1}(x)})$
.
${\gamma} ^{2n+1}_{m, x, \infty }=\pi _{{\mathcal {M}}_{2n+1}(x), \infty }({\gamma} _m^{{\mathcal {M}}_{2n+1}(x)})$
. -
4. For
 $x\in {\mathbb {R}}$
and
$x\in {\mathbb {R}}$
and
 $n\in \omega $
, set
$n\in \omega $
, set
 $b_{2n+1, m}=\sup _{x\in {\mathbb {R}}}{\gamma} _{m, x, \infty }^{2n+1}$
.
$b_{2n+1, m}=\sup _{x\in {\mathbb {R}}}{\gamma} _{m, x, \infty }^{2n+1}$
. -
5. Let
 ${\kappa }^1_{2n+1}$
be the predecessor of
${\kappa }^1_{2n+1}$
be the predecessor of
 ${\delta }^1_{2n+1}$
(e.g., see [Reference Jackson13, Theorem 2.18]). It follows from [Reference Sargsyan29] that for each n,
${\delta }^1_{2n+1}$
(e.g., see [Reference Jackson13, Theorem 2.18]). It follows from [Reference Sargsyan29] that for each n,
 $\sup _{m\in \omega }b_{2n+1, m}={\kappa }^1_{2n+3}$
. In fact, for each
$\sup _{m\in \omega }b_{2n+1, m}={\kappa }^1_{2n+3}$
. In fact, for each
 $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
 $\sup _{m<\omega }{\gamma} _{m, x, \infty }^{2n+1}={\kappa }^1_{2n+3}$
. Moreover, for each
$\sup _{m<\omega }{\gamma} _{m, x, \infty }^{2n+1}={\kappa }^1_{2n+3}$
. Moreover, for each
 $n, m\in \omega $
,
$n, m\in \omega $
,
 $b_{2n+1, m}$
is a cardinal and
$b_{2n+1, m}$
is a cardinal and
 $b_{2n+1, 0}>{\delta }^1_{2n+1}$
. Thus,
$b_{2n+1, 0}>{\delta }^1_{2n+1}$
. Thus,
 $b_{2n+1, 0}\geq {\delta }^1_{2n+2}$
. For the proofs of these results see [Reference Sargsyan29, Theorem 4.1, Corollary 5.23, Lemma 6.1].
$b_{2n+1, 0}\geq {\delta }^1_{2n+2}$
. For the proofs of these results see [Reference Sargsyan29, Theorem 4.1, Corollary 5.23, Lemma 6.1]. -
6. It is conjectured in [Reference Sargsyan29] that for all n,
 $b_{2n+1, 0}={\delta }^1_{2n+2}$
. For
$b_{2n+1, 0}={\delta }^1_{2n+2}$
. For
 $n=0$
this is shown in [Reference Hjorth8]. The case
$n=0$
this is shown in [Reference Hjorth8]. The case
 $n\geq 1$
is still open.
$n\geq 1$
is still open.
Review 2.19.
![]() ${\gamma} $
-stability:
${\gamma} $
-stability:
The main technical fact from [Reference Sargsyan29] that we will need in this paper appears in the bottom of page 760 of [Reference Sargsyan29]. It claims that for each
![]() $x\in {\mathbb {R}}$
, each
$x\in {\mathbb {R}}$
, each
![]() $n\in \omega $
and for each
$n\in \omega $
and for each
![]() ${\gamma} <{\kappa }^1_{2n+3}$
, there is a
${\gamma} <{\kappa }^1_{2n+3}$
, there is a
![]() ${\gamma} $
-stable complete iterate
${\gamma} $
-stable complete iterate
![]() ${\mathcal {P}}$
of
${\mathcal {P}}$
of
![]() ${\mathcal {M}}_{2n+1}(x)$
. Because our situation is just a little bit different we outline how to obtain
${\mathcal {M}}_{2n+1}(x)$
. Because our situation is just a little bit different we outline how to obtain
![]() ${\gamma} $
-stable iterates. The reader may find it useful as well.
${\gamma} $
-stable iterates. The reader may find it useful as well.
![]() ${\gamma} $
-stable iterates:
${\gamma} $
-stable iterates:
-
1. Fix
 $n\in \omega $
and
$n\in \omega $
and
 $x\in {\mathbb {R}}$
. Let
$x\in {\mathbb {R}}$
. Let
 ${\mathcal {M}}={\mathcal {M}}_{2n+1}(x)$
and suppose that
${\mathcal {M}}={\mathcal {M}}_{2n+1}(x)$
and suppose that
 ${\mathcal {M}}^\#_{2n+1}\in {\mathcal {M}}$
Footnote
38
. Suppose
${\mathcal {M}}^\#_{2n+1}\in {\mathcal {M}}$
Footnote
38
. Suppose
 ${\gamma} $
is an ordinal such that for some
${\gamma} $
is an ordinal such that for some
 $m_0$
,
$m_0$
,
 ${\gamma} <{\gamma} ^{2n+1}_{m_0, \infty }$
. Let
${\gamma} <{\gamma} ^{2n+1}_{m_0, \infty }$
. Let
 ${\mathcal {P}}$
be a complete iterate of
${\mathcal {P}}$
be a complete iterate of
 ${\mathcal {M}}$
.
${\mathcal {M}}$
. -
2. Let
 $\nu $
be the least inaccessible of
$\nu $
be the least inaccessible of
 ${\mathcal {P}}$
above
${\mathcal {P}}$
above
 ${\delta }_0^{\mathcal {P}}$
and let
${\delta }_0^{\mathcal {P}}$
and let
 ${\mathcal { H}}^{\mathcal {P}}$
be the direct limit of all iterates of
${\mathcal { H}}^{\mathcal {P}}$
be the direct limit of all iterates of
 ${\mathcal {M}}_{2n+1}$
that are in
${\mathcal {M}}_{2n+1}$
that are in
 ${\mathcal {P}}|\nu $
Footnote
39
. The construction of such limits has been carried out in [Reference Sargsyan29], [Reference Mueller and Sargsyan24], [Reference Sargsyan and Schindler32]. For example see [Reference Sargsyan29, Section 5.1].
${\mathcal {P}}|\nu $
Footnote
39
. The construction of such limits has been carried out in [Reference Sargsyan29], [Reference Mueller and Sargsyan24], [Reference Sargsyan and Schindler32]. For example see [Reference Sargsyan29, Section 5.1]. -
3. The results of [Reference Sargsyan29] and other similar calculations done, for example, in [Reference Steel and Woodin40] show that
 ${\mathcal { H}}^{\mathcal {P}}$
is a complete iterate of
${\mathcal { H}}^{\mathcal {P}}$
is a complete iterate of
 ${\mathcal {M}}_{2n+1}$
.
${\mathcal {M}}_{2n+1}$
. -
4. We say
 ${\mathcal {P}}$
is locally
${\mathcal {P}}$
is locally
 ${\gamma} $
-stable if
${\gamma} $
-stable if
 ${\gamma} \in \mathrm {rge}(\pi _{{\mathcal { H}}^{\mathcal {P}}, \infty })$
.
${\gamma} \in \mathrm {rge}(\pi _{{\mathcal { H}}^{\mathcal {P}}, \infty })$
. -
5. We say
 ${\mathcal {P}}$
is
${\mathcal {P}}$
is
 ${\gamma} $
-stable if
${\gamma} $
-stable if
 ${\mathcal {P}}$
is locally
${\mathcal {P}}$
is locally
 ${\gamma} $
-stable and if
${\gamma} $
-stable and if
 $\xi =\pi _{{\mathcal { H}}^{\mathcal {P}}, \infty }^{-1}({\gamma} )$
then whenever
$\xi =\pi _{{\mathcal { H}}^{\mathcal {P}}, \infty }^{-1}({\gamma} )$
then whenever
 ${\mathcal { Q}}$
is a complete iterate of
${\mathcal { Q}}$
is a complete iterate of
 ${\mathcal {P}}$
,
${\mathcal {P}}$
,  $$ \begin{align*} \pi_{{\mathcal{ H}}^{\mathcal{ Q}}, \infty}(\pi_{{\mathcal{P}}, {\mathcal{ Q}}}(\xi))={\gamma}. \end{align*} $$
$$ \begin{align*} \pi_{{\mathcal{ H}}^{\mathcal{ Q}}, \infty}(\pi_{{\mathcal{P}}, {\mathcal{ Q}}}(\xi))={\gamma}. \end{align*} $$
-
6. The argument on page 760 of [Reference Sargsyan29] can be used to show the following lemma.
Lemma 2.20. There is a complete
 ${\gamma} $
-stable iterate
${\gamma} $
-stable iterate
 ${\mathcal {P}}$
of
${\mathcal {P}}$
of
 ${\mathcal {M}}_{2n+1}(x)$
.
${\mathcal {M}}_{2n+1}(x)$
.Proof. (Outline) Towards a contradiction assume not. The key observation is that whenever
 ${\mathcal {P}}$
is a complete iterate of
${\mathcal {P}}$
is a complete iterate of
 ${\mathcal {M}}_{2n+1}(x)$
and
${\mathcal {M}}_{2n+1}(x)$
and
 ${\mathcal { Q}}$
is a complete iterate of
${\mathcal { Q}}$
is a complete iterate of
 ${\mathcal {P}}$
, the Dodd-Jensen argument (see [Reference Steel39, Chapter 4.2]) implies that for all
${\mathcal {P}}$
, the Dodd-Jensen argument (see [Reference Steel39, Chapter 4.2]) implies that for all
 $\xi \in {\mathcal { H}}^{\mathcal {P}}$
,
$\xi \in {\mathcal { H}}^{\mathcal {P}}$
,
 $\pi _{{\mathcal { H}}^{\mathcal {P}}, \infty }(\xi )\leq \pi _{{\mathcal { H}}^{\mathcal { Q}}, \infty }(\pi _{{\mathcal {P}}, {\mathcal { Q}}}(\xi ))$
.
$\pi _{{\mathcal { H}}^{\mathcal {P}}, \infty }(\xi )\leq \pi _{{\mathcal { H}}^{\mathcal { Q}}, \infty }(\pi _{{\mathcal {P}}, {\mathcal { Q}}}(\xi ))$
.Suppose now that
 ${\mathcal R}$
is a complete iterate of
${\mathcal R}$
is a complete iterate of
 ${\mathcal {M}}_{2n+1}$
such that
${\mathcal {M}}_{2n+1}$
such that
 ${\gamma} \in \mathrm {rge}(\pi _{{\mathcal R}, \infty })$
. We set
${\gamma} \in \mathrm {rge}(\pi _{{\mathcal R}, \infty })$
. We set
 ${\gamma} _{\mathcal R}=\pi ^{-1}_{{\mathcal R}, \infty }({\gamma} )$
.
${\gamma} _{\mathcal R}=\pi ^{-1}_{{\mathcal R}, \infty }({\gamma} )$
.Let now
 ${\mathcal {P}}$
be a compete iterate of
${\mathcal {P}}$
be a compete iterate of
 ${\mathcal {M}}_{2n+1}(x)$
and
${\mathcal {M}}_{2n+1}(x)$
and
 ${\mathcal { Q}}$
be a complete iterate of
${\mathcal { Q}}$
be a complete iterate of
 ${\mathcal {P}}$
. What we have observed implies that if
${\mathcal {P}}$
. What we have observed implies that if
 ${\gamma} _{{\mathcal { H}}^{\mathcal {P}}}$
and
${\gamma} _{{\mathcal { H}}^{\mathcal {P}}}$
and
 ${\gamma} _{{\mathcal { H}}^{\mathcal { Q}}}$
are defined then
${\gamma} _{{\mathcal { H}}^{\mathcal { Q}}}$
are defined then
 $\pi _{{\mathcal {P}}, {\mathcal { Q}}}({\gamma} _{{\mathcal { H}}^{\mathcal {P}}})\geq {\gamma} _{{\mathcal { H}}^{\mathcal { Q}}}$
. Moreover, if
$\pi _{{\mathcal {P}}, {\mathcal { Q}}}({\gamma} _{{\mathcal { H}}^{\mathcal {P}}})\geq {\gamma} _{{\mathcal { H}}^{\mathcal { Q}}}$
. Moreover, if
 ${\mathcal { Q}}$
witnesses that
${\mathcal { Q}}$
witnesses that
 ${\mathcal {P}}$
is not
${\mathcal {P}}$
is not
 ${\gamma} $
-stable then we in fact have that
${\gamma} $
-stable then we in fact have that
 $\pi _{{\mathcal {P}}, {\mathcal { Q}}}({\gamma} _{{\mathcal { H}}^{\mathcal {P}}})>{\gamma} _{{\mathcal { H}}^{\mathcal { Q}}}$
.
$\pi _{{\mathcal {P}}, {\mathcal { Q}}}({\gamma} _{{\mathcal { H}}^{\mathcal {P}}})>{\gamma} _{{\mathcal { H}}^{\mathcal { Q}}}$
.Observe further that given any
 $({\mathcal {P}}, {\mathcal { Q}})$
we can iterate
$({\mathcal {P}}, {\mathcal { Q}})$
we can iterate
 ${\mathcal { Q}}$
to obtain a complete iterate
${\mathcal { Q}}$
to obtain a complete iterate
 ${\mathcal R}$
of
${\mathcal R}$
of
 ${\mathcal { Q}}$
such that
${\mathcal { Q}}$
such that
 ${\gamma} _{{\mathcal { H}}^{\mathcal R}}$
is defined. To do this, it is enough to fix some complete iterate
${\gamma} _{{\mathcal { H}}^{\mathcal R}}$
is defined. To do this, it is enough to fix some complete iterate
 ${\mathcal {S}}$
of
${\mathcal {S}}$
of
 ${\mathcal {M}}_{2n+1}$
for which
${\mathcal {M}}_{2n+1}$
for which
 ${\gamma} _{\mathcal {S}}$
is defined and iterate
${\gamma} _{\mathcal {S}}$
is defined and iterate
 ${\mathcal { Q}}$
to obtain a complete iterate
${\mathcal { Q}}$
to obtain a complete iterate
 ${\mathcal R}$
of
${\mathcal R}$
of
 ${\mathcal { Q}}$
such that
${\mathcal { Q}}$
such that
 ${\mathcal {S}}$
is generic for
${\mathcal {S}}$
is generic for
 $\mathsf {Ea}^{{\mathcal R}}_{{\delta }_0^{\mathcal R}}$
.Footnote
40
It then follows that
$\mathsf {Ea}^{{\mathcal R}}_{{\delta }_0^{\mathcal R}}$
.Footnote
40
It then follows that
 ${\mathcal {S}}$
is a point in the directed system of
${\mathcal {S}}$
is a point in the directed system of
 ${\mathcal R}[{\mathcal {S}}]$
that converges to
${\mathcal R}[{\mathcal {S}}]$
that converges to
 ${\mathcal { H}}^{\mathcal R}$
, and so
${\mathcal { H}}^{\mathcal R}$
, and so
 ${\gamma} _{{\mathcal { H}}^{\mathcal R}}$
is defined.
${\gamma} _{{\mathcal { H}}^{\mathcal R}}$
is defined.We now get that our assumption that there is no
 ${\gamma} $
-stable complete iterate of
${\gamma} $
-stable complete iterate of
 ${\mathcal {M}}$
implies that there is a sequence
${\mathcal {M}}$
implies that there is a sequence
 $({\mathcal {P}}_i: i<\omega )$
such that (a) for each i,
$({\mathcal {P}}_i: i<\omega )$
such that (a) for each i,
 ${\mathcal {P}}_{i+1}$
is a complete iterate of
${\mathcal {P}}_{i+1}$
is a complete iterate of
 ${\mathcal {P}}_i$
, (b) for each i,
${\mathcal {P}}_i$
, (b) for each i,
 ${\gamma} _{{\mathcal { H}}^{{\mathcal {P}}_i}}$
is defined (c)
${\gamma} _{{\mathcal { H}}^{{\mathcal {P}}_i}}$
is defined (c)
 ${\mathcal {P}}_0$
is a complete iterate of
${\mathcal {P}}_0$
is a complete iterate of
 ${\mathcal {M}}$
and finally (d) for each i,
${\mathcal {M}}$
and finally (d) for each i,  $$ \begin{align*} \pi_{{\mathcal{P}}_i, {\mathcal{P}}_{i+1}}({\gamma}_{{\mathcal{ H}}^{{\mathcal{P}}_i}})>{\gamma}_{{\mathcal{ H}}^{{\mathcal{P}}_{i+1}}}. \end{align*} $$
$$ \begin{align*} \pi_{{\mathcal{P}}_i, {\mathcal{P}}_{i+1}}({\gamma}_{{\mathcal{ H}}^{{\mathcal{P}}_i}})>{\gamma}_{{\mathcal{ H}}^{{\mathcal{P}}_{i+1}}}. \end{align*} $$
We thus have that the direct limit of
 $({\mathcal {P}}_i: i<\omega )$
is ill-founded, which is clearly a contradiction.
$({\mathcal {P}}_i: i<\omega )$
is ill-founded, which is clearly a contradiction. -
7. Suppose now that
 ${\mathcal {P}}$
is
${\mathcal {P}}$
is
 ${\gamma} $
-stable,
${\gamma} $
-stable,
 $\nu <{\delta }_0^{\mathcal {P}}$
and
$\nu <{\delta }_0^{\mathcal {P}}$
and
 $p\in \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }_0^{\mathcal {P}}, \nu }$
. Suppose
$p\in \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }_0^{\mathcal {P}}, \nu }$
. Suppose
 $m\leq k$
are natural numbers (so
$m\leq k$
are natural numbers (so
 $m\geq 1$
). We say p is
$m\geq 1$
). We say p is
 $({\gamma} , k, m)$
-good if p forces that when the generic is decoded as a k-tuple
$({\gamma} , k, m)$
-good if p forces that when the generic is decoded as a k-tuple
 $(u_1, ..., u_k)$
(via one of the standard ways of decoding a real into tuples)
$(u_1, ..., u_k)$
(via one of the standard ways of decoding a real into tuples)
 $u_m$
codes a complete iterate
$u_m$
codes a complete iterate
 ${\mathcal R}$
of
${\mathcal R}$
of
 ${\mathcal {M}}_{2n+1}$
with the property that
${\mathcal {M}}_{2n+1}$
with the property that
 ${\mathcal {T}}_{{\mathcal {M}}_{2n+1}, {\mathcal R}}$
is below the least Woodin cardinal of
${\mathcal {T}}_{{\mathcal {M}}_{2n+1}, {\mathcal R}}$
is below the least Woodin cardinal of
 ${\mathcal {M}}_{2n+1}$
and
${\mathcal {M}}_{2n+1}$
and
 ${\gamma} _{{\mathcal { H}}^{\mathcal {P}}}\in \mathrm {rge}(\pi _{{\mathcal R}, {\mathcal { H}}^{\mathcal {P}}})$
.
${\gamma} _{{\mathcal { H}}^{\mathcal {P}}}\in \mathrm {rge}(\pi _{{\mathcal R}, {\mathcal { H}}^{\mathcal {P}}})$
. -
8. It is not immediately clear that the definition of
 $({\gamma} , k, m)$
-good condition is first order over
$({\gamma} , k, m)$
-good condition is first order over
 ${\mathcal {P}}$
. This follows from the fact that the directed system can be internalized to
${\mathcal {P}}$
. This follows from the fact that the directed system can be internalized to
 ${\mathcal {P}}[g]$
where
${\mathcal {P}}[g]$
where
 $g\subseteq Coll(\omega , {\delta }_0^{\mathcal {P}})$
is
$g\subseteq Coll(\omega , {\delta }_0^{\mathcal {P}})$
is
 ${\mathcal {P}}$
-generic. To do this, one uses the concept of
${\mathcal {P}}$
-generic. To do this, one uses the concept of
 $s_n$
-iterability and the details of this were carried out in [Reference Sargsyan29]. For example, see [Reference Sargsyan29, Definition 5.4] and [Reference Sargsyan29, Chapter 5.1]. The basic ideas that are used in internalizing directed systems are due to Woodin who carried out such internalization in
$s_n$
-iterability and the details of this were carried out in [Reference Sargsyan29]. For example, see [Reference Sargsyan29, Definition 5.4] and [Reference Sargsyan29, Chapter 5.1]. The basic ideas that are used in internalizing directed systems are due to Woodin who carried out such internalization in
 $L[x]$
(see [Reference Steel and Woodin40]).
$L[x]$
(see [Reference Steel and Woodin40]). -
9. Because the statement ‘p is
 $({\gamma} , k,m)$
-good’ is first order over
$({\gamma} , k,m)$
-good’ is first order over
 ${\mathcal {P}}$
, there is a maximal antichain of
${\mathcal {P}}$
, there is a maximal antichain of
 $({\gamma} , k, m)$
-good conditions. As
$({\gamma} , k, m)$
-good conditions. As
 $\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }_0^{\mathcal {P}}, \nu }$
has
$\mathsf {{Ea}}^{\mathcal {P}}_{{\delta }_0^{\mathcal {P}}, \nu }$
has
 ${\delta }_0^{\mathcal {P}}$
-cc, we have a condition p such that p is the disjunction of the conditions of some maximal antichain consisting of
${\delta }_0^{\mathcal {P}}$
-cc, we have a condition p such that p is the disjunction of the conditions of some maximal antichain consisting of
 $({\gamma} , k, m)$
-good conditions, and as a consequence, p is
$({\gamma} , k, m)$
-good conditions, and as a consequence, p is
 $({\gamma} , k, m)$
-good and if
$({\gamma} , k, m)$
-good and if
 $g\subseteq \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }_0^{\mathcal {P}}, \nu }$
is generic such that g is a tuple
$g\subseteq \mathsf {{Ea}}^{\mathcal {P}}_{{\delta }_0^{\mathcal {P}}, \nu }$
is generic such that g is a tuple
 $(g_1, g_2,..., g_k)$
and some
$(g_1, g_2,..., g_k)$
and some
 $r\in g$
is
$r\in g$
is
 $({\gamma} , k, m)$
-good then
$({\gamma} , k, m)$
-good then
 $p\in g$
. We can then let
$p\in g$
. We can then let
 $p_{{\gamma} , \nu , k, m}^{\mathcal {P}}$
be the
$p_{{\gamma} , \nu , k, m}^{\mathcal {P}}$
be the
 ${\mathcal {P}}$
-least
${\mathcal {P}}$
-least
 $({\gamma} , k, m)$
-good condition with the property that any other
$({\gamma} , k, m)$
-good condition with the property that any other
 $({\gamma} , k, m)$
-good condition is compatible with it. We call
$({\gamma} , k, m)$
-good condition is compatible with it. We call
 $p_{{\gamma} , \nu , k, m}^{\mathcal {P}}$
the
$p_{{\gamma} , \nu , k, m}^{\mathcal {P}}$
the
 $({\gamma} , \nu , k, m)$
-master condition.
$({\gamma} , \nu , k, m)$
-master condition.
3
 $\Pi ^1_n$
-iterability
$\Pi ^1_n$
-iterability
We will use the concept of
![]() $\Pi ^1_n$
-iterability introduced in [Reference Steel37, Definition 1.4]. Following [Reference Steel37, Definition], we say that a premouse
$\Pi ^1_n$
-iterability introduced in [Reference Steel37, Definition 1.4]. Following [Reference Steel37, Definition], we say that a premouse
![]() ${\mathcal {M}}$
is n-small if for every
${\mathcal {M}}$
is n-small if for every
![]() ${\alpha }\in \mathrm { dom}(\vec {E})$
,Footnote
41
${\alpha }\in \mathrm { dom}(\vec {E})$
,Footnote
41
![]() ${\mathcal {M}}|{\alpha }\models `$
there does not exist n Woodin cardinals’. Thus,
${\mathcal {M}}|{\alpha }\models `$
there does not exist n Woodin cardinals’. Thus,
![]() ${\mathcal {M}}_1^\#$
is 2-small and
${\mathcal {M}}_1^\#$
is 2-small and
![]() ${\mathcal {M}}_1$
is 1-small while
${\mathcal {M}}_1$
is 1-small while
![]() ${\mathcal {M}}_2^\#$
is 3-small and
${\mathcal {M}}_2^\#$
is 3-small and
![]() ${\mathcal {M}}_2$
is 2-small. Notice however that all proper initial segments of
${\mathcal {M}}_2$
is 2-small. Notice however that all proper initial segments of
![]() ${\mathcal {M}}_1^\#$
are 1-small. We then say that
${\mathcal {M}}_1^\#$
are 1-small. We then say that
![]() ${\mathcal {M}}$
is properly n-small if
${\mathcal {M}}$
is properly n-small if
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() $n+1$
-small and all of its proper initial segments are n-small.
$n+1$
-small and all of its proper initial segments are n-small.
We will use
![]() $\Pi ^1_{2n+2}$
-iterability in conjunction with properly
$\Pi ^1_{2n+2}$
-iterability in conjunction with properly
![]() $2n+1$
-small premice as well as
$2n+1$
-small premice as well as
![]() $2n+1$
-small premice. There is a lot to review here, but the details are technical and we suggest that the reader consult [Reference Steel37]. The following is a list of facts that we will need.
$2n+1$
-small premice. There is a lot to review here, but the details are technical and we suggest that the reader consult [Reference Steel37]. The following is a list of facts that we will need.
-
1. We say
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 ${\mathcal {M}}_n$
-like premouse over x if
${\mathcal {M}}_n$
-like premouse over x if
 ${\mathcal {M}}$
is n-small premouse over x with n Woodin cardinals and such that
${\mathcal {M}}$
is n-small premouse over x with n Woodin cardinals and such that
 $\mathsf {{Ord}}\subseteq {\mathcal {M}}$
. Similarly, we say
$\mathsf {{Ord}}\subseteq {\mathcal {M}}$
. Similarly, we say
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 ${\mathcal {M}}_n^\#$
-like premouse over x (or just x-premouse) if
${\mathcal {M}}_n^\#$
-like premouse over x (or just x-premouse) if
 ${\mathcal {M}}$
is active, sound, properly n-small premouse over x with n Woodin cardinals.
${\mathcal {M}}$
is active, sound, properly n-small premouse over x with n Woodin cardinals. -
2. Given two premice
 ${\mathcal {M}}$
and
${\mathcal {M}}$
and
 ${\mathcal {M}}'$
we say
${\mathcal {M}}'$
we say
 $({\mathcal {T}}, {\mathcal {T}}')$
is a coiteration of
$({\mathcal {T}}, {\mathcal {T}}')$
is a coiteration of
 $({\mathcal {M}}, {\mathcal {M}}')$
if the extenders of
$({\mathcal {M}}, {\mathcal {M}}')$
if the extenders of
 ${\mathcal {T}}$
and
${\mathcal {T}}$
and
 ${\mathcal {T}}'$
are chosen to be the least ones causing disagreement. More precisely,
${\mathcal {T}}'$
are chosen to be the least ones causing disagreement. More precisely,
 $\mathrm {lh}({\mathcal {T}})=\mathrm {lh}({\mathcal {T}}')$
and for every
$\mathrm {lh}({\mathcal {T}})=\mathrm {lh}({\mathcal {T}}')$
and for every
 ${\alpha }<\mathrm { lh}({\mathcal {T}})$
,
${\alpha }<\mathrm { lh}({\mathcal {T}})$
,
 $\mathrm {lh}(E_{\alpha }^{\mathcal {T}})$
is the least
$\mathrm {lh}(E_{\alpha }^{\mathcal {T}})$
is the least
 ${\beta }$
such that
${\beta }$
such that
 ${\mathcal {M}}_{\alpha }^{\mathcal {T}}|{\beta }={\mathcal {M}}_{\alpha }^{{\mathcal {T}}'}|{\beta }$
but
${\mathcal {M}}_{\alpha }^{\mathcal {T}}|{\beta }={\mathcal {M}}_{\alpha }^{{\mathcal {T}}'}|{\beta }$
but
 ${\mathcal {M}}_{\alpha }^{\mathcal {T}}||{\beta }\not ={\mathcal {M}}_{\alpha }^{{\mathcal {T}}'}||{\beta }$
, and similarly for
${\mathcal {M}}_{\alpha }^{\mathcal {T}}||{\beta }\not ={\mathcal {M}}_{\alpha }^{{\mathcal {T}}'}||{\beta }$
, and similarly for
 $E_{\alpha }^{{\mathcal {T}}'}$
. We then must have that
$E_{\alpha }^{{\mathcal {T}}'}$
. We then must have that
 $\mathrm {lh}(E_{\alpha }^{\mathcal {T}})=\mathrm { lh}(E_{\alpha }^{{\mathcal {T}}'})$
. It is possible that only one of
$\mathrm {lh}(E_{\alpha }^{\mathcal {T}})=\mathrm { lh}(E_{\alpha }^{{\mathcal {T}}'})$
. It is possible that only one of
 $E_{\alpha }^{\mathcal {T}}$
and
$E_{\alpha }^{\mathcal {T}}$
and
 $E_{\alpha }^{{\mathcal {T}}'}$
is defined, in which case we allow paddingFootnote
42
.
$E_{\alpha }^{{\mathcal {T}}'}$
is defined, in which case we allow paddingFootnote
42
. -
3. We say that the coiteration
 $({\mathcal {T}}, {\mathcal {T}}')$
of
$({\mathcal {T}}, {\mathcal {T}}')$
of
 $({\mathcal {M}}, {\mathcal {M}}')$
is successful if
$({\mathcal {M}}, {\mathcal {M}}')$
is successful if
 $\mathrm { lh}({\mathcal {T}})$
is a successor ordinal and if
$\mathrm { lh}({\mathcal {T}})$
is a successor ordinal and if
 ${\mathcal {N}}$
is the last model of
${\mathcal {N}}$
is the last model of
 ${\mathcal {T}}$
and
${\mathcal {T}}$
and
 ${\mathcal {N}}'$
is the last model of
${\mathcal {N}}'$
is the last model of
 ${\mathcal {T}}'$
then either
${\mathcal {T}}'$
then either
 ${\mathcal {N}}\trianglelefteq {\mathcal {N}}'$
or
${\mathcal {N}}\trianglelefteq {\mathcal {N}}'$
or
 ${\mathcal {N}}'\trianglelefteq {\mathcal {N}}$
.
${\mathcal {N}}'\trianglelefteq {\mathcal {N}}$
. -
4. Suppose
 ${\mathcal {M}}$
is a premouse,
${\mathcal {M}}$
is a premouse,
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
of limit length,
${\mathcal {M}}$
of limit length,
 ${\alpha }<\omega _1$
and b is a maximal branch of
${\alpha }<\omega _1$
and b is a maximal branch of
 ${\mathcal {T}}$
. We say
${\mathcal {T}}$
. We say
 ${\mathcal {N}}$
is
${\mathcal {N}}$
is
 $({\alpha }, b)$
-relevant if either
$({\alpha }, b)$
-relevant if either
 ${\mathcal {N}}={\mathcal {M}}^{\mathcal {T}}_b$
or for some
${\mathcal {N}}={\mathcal {M}}^{\mathcal {T}}_b$
or for some
 ${\mathcal {P}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
and for some
${\mathcal {P}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
and for some
 $E\in \vec {E}^{\mathcal {P}}$
,
$E\in \vec {E}^{\mathcal {P}}$
,
 ${\mathcal {N}}$
is the
${\mathcal {N}}$
is the
 ${\alpha }$
th linear iterate of
${\alpha }$
th linear iterate of
 ${\mathcal {P}}$
via E. We say that b is
${\mathcal {P}}$
via E. We say that b is
 ${\alpha }$
-good if whenever
${\alpha }$
-good if whenever
 ${\mathcal {N}}$
is
${\mathcal {N}}$
is
 $({\alpha }, b)$
-relevant, either
$({\alpha }, b)$
-relevant, either
 ${\mathcal {N}}$
is well-founded or
${\mathcal {N}}$
is well-founded or
 ${\alpha }$
is in the well-founded part of
${\alpha }$
is in the well-founded part of
 ${\mathcal {N}}$
. We say
${\mathcal {N}}$
. We say
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 $\Pi ^1_2$
-iterable if for every iteration
$\Pi ^1_2$
-iterable if for every iteration
 ${\mathcal {T}}$
of
${\mathcal {T}}$
of
 ${\mathcal {M}}$
of countable limit length and for every ordinal
${\mathcal {M}}$
of countable limit length and for every ordinal
 ${\alpha }$
there is an
${\alpha }$
there is an
 ${\alpha }$
-good maximal branch b of
${\alpha }$
-good maximal branch b of
 ${\mathcal {T}}$
.
${\mathcal {T}}$
. -
5. Recall
 $\mathcal {G}({\mathcal {M}}, 0, 2n+1)$
, which is the iteration game introduced on page 83 of [Reference Steel37].
$\mathcal {G}({\mathcal {M}}, 0, 2n+1)$
, which is the iteration game introduced on page 83 of [Reference Steel37].
 $\mathcal {G}({\mathcal {M}}, 0, 1)$
defines
$\mathcal {G}({\mathcal {M}}, 0, 1)$
defines
 $\Pi ^1_2$
-iterability. In
$\Pi ^1_2$
-iterability. In
 $\mathcal {G}({\mathcal {M}}, 0, 1)$
, Player I plays a pair
$\mathcal {G}({\mathcal {M}}, 0, 1)$
, Player I plays a pair
 $({\mathcal {T}}, {\beta })$
such that
$({\mathcal {T}}, {\beta })$
such that
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
and
${\mathcal {M}}$
and
 ${\beta }<\omega _1$
. Player II must either accept
${\beta }<\omega _1$
. Player II must either accept
 ${\mathcal {T}}$
or play a
${\mathcal {T}}$
or play a
 ${\beta }$
-good branch of
${\beta }$
-good branch of
 ${\mathcal {T}}$
. If
${\mathcal {T}}$
. If
 $\mathrm {lh}({\mathcal {T}})$
is a limit ordinal or
$\mathrm {lh}({\mathcal {T}})$
is a limit ordinal or
 ${\mathcal {T}}$
has an ill-founded last model then Player II is not allowed to accept
${\mathcal {T}}$
has an ill-founded last model then Player II is not allowed to accept
 ${\mathcal {T}}$
. If Player II doesn’t violate any of the rules of the game then Player II wins the game. We thus have that
${\mathcal {T}}$
. If Player II doesn’t violate any of the rules of the game then Player II wins the game. We thus have that
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 $\Pi ^1_2$
-iterable if and only if Player II has a winning strategy in
$\Pi ^1_2$
-iterable if and only if Player II has a winning strategy in
 $\mathcal {G}({\mathcal {M}}, 0, 1)$
.
$\mathcal {G}({\mathcal {M}}, 0, 1)$
. -
6. Suppose
 ${\mathcal {M}}$
is as above. We say that
${\mathcal {M}}$
is as above. We say that
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 $\Pi ^1_{2n+2}$
-iterable if player
$\Pi ^1_{2n+2}$
-iterable if player
 $II$
has a winning strategy in
$II$
has a winning strategy in
 $\mathcal {G}({\mathcal {M}}, 0, 2n+1)$
. The game has
$\mathcal {G}({\mathcal {M}}, 0, 2n+1)$
. The game has
 $2n+1$
many rounds. We describe the game for
$2n+1$
many rounds. We describe the game for
 $n>0$
. We modify the game very slightly and present it as a game that has only two rounds. We start by assuming that
$n>0$
. We modify the game very slightly and present it as a game that has only two rounds. We start by assuming that
 ${\mathcal {M}}$
is a
${\mathcal {M}}$
is a
 ${\delta }$
-mouse in the sense of [Reference Steel37, Definition 1.3]Footnote
43
.
${\delta }$
-mouse in the sense of [Reference Steel37, Definition 1.3]Footnote
43
.-
(a) In the first round, Player I plays a pair
 $({\mathcal {T}}_0, x_0)$
such that
$({\mathcal {T}}_0, x_0)$
such that
 ${\mathcal {T}}_0$
is an iteration of
${\mathcal {T}}_0$
is an iteration of
 ${\mathcal {M}}$
that is above
${\mathcal {M}}$
that is above
 ${\delta }+1$
Footnote
44
and
${\delta }+1$
Footnote
44
and
 $x_0\in {\mathbb {R}}$
. Player II must either accept
$x_0\in {\mathbb {R}}$
. Player II must either accept
 ${\mathcal {T}}_0$
or play a maximal well-founded branch
${\mathcal {T}}_0$
or play a maximal well-founded branch
 $b_0$
of
$b_0$
of
 ${\mathcal {T}}_0$
. If
${\mathcal {T}}_0$
. If
 $\mathrm {lh}({\mathcal {T}}_0)$
is a limit ordinal or
$\mathrm {lh}({\mathcal {T}}_0)$
is a limit ordinal or
 ${\mathcal {T}}_0$
has an ill-founded last model then Player II is not allowed to accept
${\mathcal {T}}_0$
has an ill-founded last model then Player II is not allowed to accept
 ${\mathcal {T}}_0$
. If Player II accepts
${\mathcal {T}}_0$
. If Player II accepts
 ${\mathcal {T}}_0$
then we set
${\mathcal {T}}_0$
then we set
 ${\delta }_1=\sup \{\nu (E_{\alpha }^{{\mathcal {T}}_0}): {\alpha }+1<\mathrm {lh}({\mathcal {T}}_0)\}$
and
${\delta }_1=\sup \{\nu (E_{\alpha }^{{\mathcal {T}}_0}): {\alpha }+1<\mathrm {lh}({\mathcal {T}}_0)\}$
and
 ${\mathcal {N}}_1={\mathcal {M}}_{\mathrm {lh}({\mathcal {T}}_0)-1}^{{\mathcal {T}}_0}$
. If Player II plays b then we set
${\mathcal {N}}_1={\mathcal {M}}_{\mathrm {lh}({\mathcal {T}}_0)-1}^{{\mathcal {T}}_0}$
. If Player II plays b then we set
 ${\delta }_1={\delta }({\mathcal {T}}_0)$
and
${\delta }_1={\delta }({\mathcal {T}}_0)$
and
 ${\mathcal {N}}_1={\mathcal {M}}^{{\mathcal {T}}_0}_{b_0}$
.
${\mathcal {N}}_1={\mathcal {M}}^{{\mathcal {T}}_0}_{b_0}$
. -
(b) The second round is played on
 ${\mathcal {N}}_1$
, which is now a
${\mathcal {N}}_1$
, which is now a
 ${\delta }_1$
-mouse. In this round, Player I plays an iteration
${\delta }_1$
-mouse. In this round, Player I plays an iteration
 ${\mathcal {T}}_1$
of
${\mathcal {T}}_1$
of
 ${\mathcal {N}}_1$
above
${\mathcal {N}}_1$
above
 ${\delta }_1$
such that for some
${\delta }_1$
such that for some
 $\Pi ^1_{2n}$
-iterable
$\Pi ^1_{2n}$
-iterable
 ${\mathcal {M}}_{2n-1}^\#$
-like
${\mathcal {M}}_{2n-1}^\#$
-like
 $({\mathcal {T}}_0, b_0, x_0)$
-premouse
$({\mathcal {T}}_0, b_0, x_0)$
-premouse
 ${\mathcal {M}}'$
,
${\mathcal {M}}'$
,
 ${\mathcal {T}}_1\in {\mathcal {M}}'|\omega _1^{{\mathcal {M}}'}$
Footnote
45
. Once again Player II must either accept
${\mathcal {T}}_1\in {\mathcal {M}}'|\omega _1^{{\mathcal {M}}'}$
Footnote
45
. Once again Player II must either accept
 ${\mathcal {T}}_1$
or play a maximal well-founded branch
${\mathcal {T}}_1$
or play a maximal well-founded branch
 $b_1$
of
$b_1$
of
 ${\mathcal {T}}_1$
. If
${\mathcal {T}}_1$
. If
 $\mathrm {lh}({\mathcal {T}}_1)$
is a limit ordinal or
$\mathrm {lh}({\mathcal {T}}_1)$
is a limit ordinal or
 ${\mathcal {T}}_1$
has an ill-founded last model then Player II is not allowed to accept
${\mathcal {T}}_1$
has an ill-founded last model then Player II is not allowed to accept
 ${\mathcal {T}}_1$
. If Player II accepts
${\mathcal {T}}_1$
. If Player II accepts
 ${\mathcal {T}}_1$
then we set
${\mathcal {T}}_1$
then we set
 ${\delta }_2=\sup \{\nu (E_{\alpha }^{{\mathcal {T}}_1}): {\alpha }+1<\mathrm {lh}({\mathcal {T}}_1)\}$
and
${\delta }_2=\sup \{\nu (E_{\alpha }^{{\mathcal {T}}_1}): {\alpha }+1<\mathrm {lh}({\mathcal {T}}_1)\}$
and
 ${\mathcal {N}}_2={\mathcal {M}}_{\mathrm {lh}({\mathcal {T}}_1)-1}^{{\mathcal {T}}_1}$
. If Player II plays
${\mathcal {N}}_2={\mathcal {M}}_{\mathrm {lh}({\mathcal {T}}_1)-1}^{{\mathcal {T}}_1}$
. If Player II plays
 $b_1$
then we set
$b_1$
then we set
 ${\delta }_2={\delta }({\mathcal {T}}_1)$
and
${\delta }_2={\delta }({\mathcal {T}}_1)$
and
 ${\mathcal {N}}_2={\mathcal {M}}^{{\mathcal {T}}_1}_{b_1}$
.
${\mathcal {N}}_2={\mathcal {M}}^{{\mathcal {T}}_1}_{b_1}$
.
Now, Player II wins if Player II doesn’t violate any of the rules of the game and
 ${\mathcal {N}}_2$
is
${\mathcal {N}}_2$
is
 $\Pi ^1_{2n}$
-iterable as a
$\Pi ^1_{2n}$
-iterable as a
 ${\delta }_2$
-mouse.
${\delta }_2$
-mouse. -
-
7. For
 $n>1$
, the statement
$n>1$
, the statement
 $`$
the real x codes a
$`$
the real x codes a
 $\Pi ^1_n$
-iterable premouse’ is
$\Pi ^1_n$
-iterable premouse’ is
 $\Pi ^1_n$
.
$\Pi ^1_n$
. -
8. Assuming that
 $\Pi ^1_{2n}$
-iterability is a
$\Pi ^1_{2n}$
-iterability is a
 $\Pi ^1_{2n}$
-condition, it is not hard to see that
$\Pi ^1_{2n}$
-condition, it is not hard to see that
 $\Pi ^1_{2n+2}$
-iterability is a
$\Pi ^1_{2n+2}$
-iterability is a
 $\Pi ^1_{2n+2}$
-condition.Footnote
46
$\Pi ^1_{2n+2}$
-condition.Footnote
46
-
9. Suppose
 $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
 $n\in \omega $
and
$n\in \omega $
and
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 ${\mathcal {M}}_{2n+1}^\#$
-like
${\mathcal {M}}_{2n+1}^\#$
-like
 $\Pi ^1_{2n+2}$
-iterable x-premouse. Let
$\Pi ^1_{2n+2}$
-iterable x-premouse. Let
 ${\delta }$
be the least Woodin cardinal of
${\delta }$
be the least Woodin cardinal of
 ${\mathcal {M}}$
and suppose
${\mathcal {M}}$
and suppose
 ${\mathcal {T}}$
is an iteration of
${\mathcal {T}}$
is an iteration of
 ${\mathcal {M}}$
that is below
${\mathcal {M}}$
that is below
 ${\delta }$
. We say
${\delta }$
. We say
 ${\mathcal {T}}$
is correct if
${\mathcal {T}}$
is correct if
 $\mathrm {lh}({\mathcal {T}})\leq \omega _1$
and for each limit
$\mathrm {lh}({\mathcal {T}})\leq \omega _1$
and for each limit
 ${\alpha }<\mathrm {lh}({\mathcal {T}})$
if
${\alpha }<\mathrm {lh}({\mathcal {T}})$
if
 $b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
then
$b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
then
 ${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
exists and
${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
exists and
 ${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })\trianglelefteq {\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
.
${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })\trianglelefteq {\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
. -
10. [Reference Steel37] shows that for
 $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
 ${\mathcal {M}}_n^\#(x)$
is the unique
${\mathcal {M}}_n^\#(x)$
is the unique
 $\Pi ^1_{n+2}$
-iterable, active, properly n-small, sound premouse over x. For example see clause 3 of [Reference Steel37, Lemma 2.2], and also the remark after [Reference Steel37, Corollary 4.11].
$\Pi ^1_{n+2}$
-iterable, active, properly n-small, sound premouse over x. For example see clause 3 of [Reference Steel37, Lemma 2.2], and also the remark after [Reference Steel37, Corollary 4.11]. -
11. It follows from [Reference Steel37] that if
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 $2n$
-small,
$2n$
-small,
 $\Pi ^1_{2n+2}$
-iterable, sound
$\Pi ^1_{2n+2}$
-iterable, sound
 ${\delta }$
-mouse (in the sense of [Reference Steel37, Definition 1.3]) over a real x then
${\delta }$
-mouse (in the sense of [Reference Steel37, Definition 1.3]) over a real x then
 ${\mathcal {M}}$
is
${\mathcal {M}}$
is
 $\omega _1$
-iterable above
$\omega _1$
-iterable above
 ${\delta }$
. For example, see [Reference Steel37, Lemma 3.3].
${\delta }$
. For example, see [Reference Steel37, Lemma 3.3]. -
12. [Reference Steel37, Corollary 4.7] implies that for all
 $n\in \omega $
and
$n\in \omega $
and
 $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
 ${\mathcal {M}}_{2n}(x)$
is
${\mathcal {M}}_{2n}(x)$
is
 $\Sigma ^1_{2n+2}$
-correct. More precisely, if
$\Sigma ^1_{2n+2}$
-correct. More precisely, if
 $\vec {a}\in {\mathbb {R}}^{<\omega }\cap {\mathcal {M}}_{2n}(x)$
and
$\vec {a}\in {\mathbb {R}}^{<\omega }\cap {\mathcal {M}}_{2n}(x)$
and
 $\phi $
is a
$\phi $
is a
 $\Sigma ^1_{2n+2}$
formula then
$\Sigma ^1_{2n+2}$
formula then
 ${\mathcal {M}}_{2n}(x)\models \phi [\vec {a}]$
if and only if
${\mathcal {M}}_{2n}(x)\models \phi [\vec {a}]$
if and only if
 $V\models \phi [\vec {a}]$
.
$V\models \phi [\vec {a}]$
. -
13. The following is a consequence of clause 12 above and the proof of Lemma 2.5.
Proposition 3.1. Suppose
 $x\in {\mathbb {R}}$
and
$x\in {\mathbb {R}}$
and
 ${\mathcal {M}}$
is a complete iterate of
${\mathcal {M}}$
is a complete iterate of
 ${\mathcal {M}}_{2n}(x)$
such that
${\mathcal {M}}_{2n}(x)$
such that
 ${\mathcal {T}}_{{\mathcal {M}}_{2n}(x), {\mathcal {M}}}$
has a countable length. Let
${\mathcal {T}}_{{\mathcal {M}}_{2n}(x), {\mathcal {M}}}$
has a countable length. Let
 $\exists u \phi (\vec {v})$
be a
$\exists u \phi (\vec {v})$
be a
 $\Sigma ^1_{2n+2}$
formula. Let
$\Sigma ^1_{2n+2}$
formula. Let
 ${\delta }_0<{\delta }_1<...<{\delta }_{2n-1}$
be the Woodin cardinals of
${\delta }_0<{\delta }_1<...<{\delta }_{2n-1}$
be the Woodin cardinals of
 ${\mathcal {M}}$
. Set
${\mathcal {M}}$
. Set
 $d=({\delta }_0, ..., {\delta }_{2n-1})$
. Suppose
$d=({\delta }_0, ..., {\delta }_{2n-1})$
. Suppose
 $\vec {a}\in {\mathcal {M}}\cap {\mathbb {R}}^k$
is such that
$\vec {a}\in {\mathcal {M}}\cap {\mathbb {R}}^k$
is such that
 $V\models \exists u \phi [\vec {a}]$
. There is then
$V\models \exists u \phi [\vec {a}]$
. There is then
 $b\in {\mathbb {R}}\cap {\mathcal {M}}_{2n}(x)$
such that
$b\in {\mathbb {R}}\cap {\mathcal {M}}_{2n}(x)$
such that
 ${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[b, \vec {a}]$
.
${\mathcal {M}}\models \phi _{{\mathcal {M}}, d}[b, \vec {a}]$
.
The following are consequences of [Reference Steel37] that we will need. The proofs of these facts are implicitly present in [Reference Steel37], but [Reference Steel37] doesn’t isolate these facts.
Lemma 3.2. Suppose
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() $\Pi ^1_2$
-iterable and
$\Pi ^1_2$
-iterable and
![]() ${\mathcal {M}}_1^\#$
-like, and suppose
${\mathcal {M}}_1^\#$
-like, and suppose
![]() ${\mathcal {T}}$
is a correct iteration of
${\mathcal {T}}$
is a correct iteration of
![]() ${\mathcal {M}}$
of countable limit length. Let
${\mathcal {M}}$
of countable limit length. Let
![]() ${\beta }$
be such that for each limit
${\beta }$
be such that for each limit
![]() ${\alpha }<\mathrm {lh}({\mathcal {T}})$
, if
${\alpha }<\mathrm {lh}({\mathcal {T}})$
, if
![]() $b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
then
$b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
then
![]() ${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
exists and
${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
exists and
![]() ${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha }){\triangleleft } \mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
. Suppose I plays
${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha }){\triangleleft } \mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
. Suppose I plays
![]() $({\mathcal {T}}, {\beta })$
in
$({\mathcal {T}}, {\beta })$
in
![]() $\mathcal {G}({\mathcal {M}}, 0, 1)$
and
$\mathcal {G}({\mathcal {M}}, 0, 1)$
and
![]() $II$
responds, using her winning strategy in
$II$
responds, using her winning strategy in
![]() $\mathcal {G}({\mathcal {M}}, 0, 1)$
, with a branch b. Then b is a cofinal branch of
$\mathcal {G}({\mathcal {M}}, 0, 1)$
, with a branch b. Then b is a cofinal branch of
![]() ${\mathcal {T}}$
.
${\mathcal {T}}$
.
Proof. Towards a contradiction suppose that b is not a cofinal branch, and set
![]() ${\alpha }=\sup (b)$
.
${\alpha }=\sup (b)$
.
Suppose for a moment that
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists. We claim that then
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists. We claim that then
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\trianglelefteq \mathcal {J}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
. To see this, suppose not. Because
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\trianglelefteq \mathcal {J}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
. To see this, suppose not. Because
![]() $\mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))\models `{\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal’, we have that
$\mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))\models `{\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal’, we have that
![]() ${\beta }$
is not in the well-founded part of
${\beta }$
is not in the well-founded part of
![]() ${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
. This implies that
${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
. This implies that
![]() ${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
is well-founded and has ordinal height less than
${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
is well-founded and has ordinal height less than
![]() ${\beta }$
. But since
${\beta }$
. But since
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\not \trianglelefteq \mathcal {J}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
,
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\not \trianglelefteq \mathcal {J}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
,
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
must have an active level above
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
must have an active level above
![]() ${\delta }({\mathcal {T}} \restriction {\alpha })$
. Let
${\delta }({\mathcal {T}} \restriction {\alpha })$
. Let
![]() $E\in \vec {E}^{{\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })}$
be such that
$E\in \vec {E}^{{\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })}$
be such that
![]() $\mathrm {crit }(E)>{\delta }({\mathcal {T}})$
. Let
$\mathrm {crit }(E)>{\delta }({\mathcal {T}})$
. Let
![]() ${\mathcal {N}}$
be the
${\mathcal {N}}$
be the
![]() ${\beta }$
th iterate of
${\beta }$
th iterate of
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
via E. It follows that
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
via E. It follows that
![]() ${\beta }$
is in the well-founded part of
${\beta }$
is in the well-founded part of
![]() ${\mathcal {N}}$
, and so
${\mathcal {N}}$
, and so
![]() ${\mathcal {N}}|{\beta }\models `{\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal’. Hence,
${\mathcal {N}}|{\beta }\models `{\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal’. Hence,
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\trianglelefteq {\mathcal {N}}|{\beta }$
, which is a contradiction as no mouse is an initial segment of its own iterate.
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\trianglelefteq {\mathcal {N}}|{\beta }$
, which is a contradiction as no mouse is an initial segment of its own iterate.
Now, because the existence of
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
implies that
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
implies that
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\trianglelefteq \mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
, we must have that if
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })\trianglelefteq \mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
, we must have that if
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists then
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists then
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })={\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
which then implies that
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })={\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
which then implies that
![]() $b=b_{\alpha }$
. Thus, because
$b=b_{\alpha }$
. Thus, because
![]() $b\not =b_{\alpha }$
,
$b\not =b_{\alpha }$
,
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
does not exist.
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
does not exist.
It now immediately follows that
![]() ${\beta }$
cannot be in the well-founded part of
${\beta }$
cannot be in the well-founded part of
![]() ${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
. Thus,
${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
. Thus,
![]() ${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
must be well-founded and
${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
must be well-founded and
![]() $\sup (\mathsf {{Ord}}\cap {\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b)< {\beta }$
. Because
$\sup (\mathsf {{Ord}}\cap {\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b)< {\beta }$
. Because
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
does not exist,
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
does not exist,
![]() $\pi ^{{\mathcal {T}}\restriction {\alpha }}_b$
is defined. If now
$\pi ^{{\mathcal {T}}\restriction {\alpha }}_b$
is defined. If now
![]() ${\mathcal {N}}$
is the
${\mathcal {N}}$
is the
![]() ${\beta }$
th iterate of
${\beta }$
th iterate of
![]() ${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
via the last extender of
${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
via the last extender of
![]() ${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
,
${\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
,
![]() ${\mathcal {N}}\models `{\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal’. This contradicts the fact that
${\mathcal {N}}\models `{\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal’. This contradicts the fact that
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
does not exist.
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
does not exist.
Proposition 3.3. Assume V is closed under the sharp function
![]() $x\mapsto x^\#$
. Suppose
$x\mapsto x^\#$
. Suppose
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() $\Pi ^1_2$
-iterable and
$\Pi ^1_2$
-iterable and
![]() ${\mathcal {M}}_1^\#$
-like, and suppose
${\mathcal {M}}_1^\#$
-like, and suppose
![]() ${\mathcal {T}}$
is a correct iteration of
${\mathcal {T}}$
is a correct iteration of
![]() ${\mathcal {M}}$
of countable limit length. Let
${\mathcal {M}}$
of countable limit length. Let
![]() ${\beta }$
be such that for each
${\beta }$
be such that for each
![]() ${\alpha }<\mathrm {lh}({\mathcal {T}})$
, if
${\alpha }<\mathrm {lh}({\mathcal {T}})$
, if
![]() $b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
then
$b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
then
![]() ${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
exists and
${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
exists and
![]() ${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha }){\triangleleft } \mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}))$
. Suppose that there is an
${\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha }){\triangleleft } \mathcal {J}_{\beta }(\mathsf {{cop}}({\mathcal {T}}))$
. Suppose that there is an
![]() ${\alpha }$
such that
${\alpha }$
such that
![]() $\mathcal {J}_{\alpha }(\mathsf {{cop}}({\mathcal {T}}))\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’ and
$\mathcal {J}_{\alpha }(\mathsf {{cop}}({\mathcal {T}}))\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’ and
![]() $\mathcal {J}_{{\alpha }+1}(\mathsf {{cop}}({\mathcal {T}}))\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’, and finally, suppose I plays
$\mathcal {J}_{{\alpha }+1}(\mathsf {{cop}}({\mathcal {T}}))\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’, and finally, suppose I plays
![]() $({\mathcal {T}}, \max ({\alpha }+1, {\beta }))$
in
$({\mathcal {T}}, \max ({\alpha }+1, {\beta }))$
in
![]() $\mathcal {G}({\mathcal {M}}, 0, 1)$
and
$\mathcal {G}({\mathcal {M}}, 0, 1)$
and
![]() $II$
responds with a branch b (according to her winning strategy). Then b is the unique cofinal well-founded branch of
$II$
responds with a branch b (according to her winning strategy). Then b is the unique cofinal well-founded branch of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() $\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
.
$\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
.
Proof. We have that Lemma 3.2 implies that b is cofinal. Also, there can be at most one such well-founded cofinal branch. Towards a contradiction assume that either b is ill-founded or
![]() $\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))\not \trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
. Suppose for a moment that b is well-founded. Then we must have that
$\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))\not \trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
. Suppose for a moment that b is well-founded. Then we must have that
![]() $\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))\not \trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
, which implies that
$\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))\not \trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
, which implies that
![]() $\pi ^{\mathcal {T}}_b$
is defined. But now if
$\pi ^{\mathcal {T}}_b$
is defined. But now if
![]() ${\mathcal {N}}$
is the
${\mathcal {N}}$
is the
![]() $\max ({\alpha }+1, {\beta })$
th iterate of
$\max ({\alpha }+1, {\beta })$
th iterate of
![]() ${\mathcal {M}}^{\mathcal {T}}_b$
via its last extender then
${\mathcal {M}}^{\mathcal {T}}_b$
via its last extender then
![]() $\mathcal {J}_{{\alpha }+1}(\mathsf {{cop}}({\mathcal {T}}))\trianglelefteq {\mathcal {N}}$
. Hence,
$\mathcal {J}_{{\alpha }+1}(\mathsf {{cop}}({\mathcal {T}}))\trianglelefteq {\mathcal {N}}$
. Hence,
![]() ${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’ implying that
${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’ implying that
![]() $\mathcal {J}_{{\alpha }+1}(\mathsf {{cop}}({\mathcal {T}})) \trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
.
$\mathcal {J}_{{\alpha }+1}(\mathsf {{cop}}({\mathcal {T}})) \trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
.
We thus have that b is an ill-founded branch, and this implies that
![]() $\max ({\alpha }+1, {\beta })$
is in the well-founded part of
$\max ({\alpha }+1, {\beta })$
is in the well-founded part of
![]() ${\mathcal {M}}^{\mathcal {T}}_b$
, which then implies that
${\mathcal {M}}^{\mathcal {T}}_b$
, which then implies that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
exists and
${\mathcal { Q}}(b, {\mathcal {T}})$
exists and
![]() ${\mathcal { Q}}(b, {\mathcal {T}})=\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))$
. Thus, we have that
${\mathcal { Q}}(b, {\mathcal {T}})=\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))$
. Thus, we have that
(*) there is a cofinal branch b of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
exists,
${\mathcal { Q}}(b, {\mathcal {T}})$
exists,
![]() ${\mathcal { Q}}(b, {\mathcal {T}})=\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))$
and this branch is ill-founded.
${\mathcal { Q}}(b, {\mathcal {T}})=\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {T}}))$
and this branch is ill-founded.
Let
![]() ${\mathcal {M}}'$
be the result of iterating the last extender of
${\mathcal {M}}'$
be the result of iterating the last extender of
![]() ${\mathcal {M}}$
out of the universe and let
${\mathcal {M}}$
out of the universe and let
![]() ${\gamma}>\max ({\alpha }, {\beta })$
be such that the ill-foundedness of b can be witnessed by functions in
${\gamma}>\max ({\alpha }, {\beta })$
be such that the ill-foundedness of b can be witnessed by functions in
![]() ${\mathcal {M}}'|{\gamma} $
Footnote
47
. We can now express (*) by the following formula:
${\mathcal {M}}'|{\gamma} $
Footnote
47
. We can now express (*) by the following formula:
(**) there are reals
![]() $x, y$
and z such that
$x, y$
and z such that
-
1. x codes an iteration
 ${\mathcal {U}}$
of
${\mathcal {U}}$
of
 ${\mathcal {M}}'|{\gamma} $
${\mathcal {M}}'|{\gamma} $
-
2. y codes a well-founded model
 ${\mathcal {N}}=\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {U}}))$
such that
${\mathcal {N}}=\mathcal {J}_{{\alpha }}(\mathsf {{cop}}({\mathcal {U}}))$
such that
 $J_{1}[{\mathcal {N}}]\models `{\delta }({\mathcal {U}})$
is not a Woodin cardinal’,
$J_{1}[{\mathcal {N}}]\models `{\delta }({\mathcal {U}})$
is not a Woodin cardinal’, -
3. z codes a cofinal ill-founded branch c of
 ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
 ${\mathcal {N}}\trianglelefteq {\mathcal {M}}^{\mathcal {U}}_c$
.
${\mathcal {N}}\trianglelefteq {\mathcal {M}}^{\mathcal {U}}_c$
.
(**) is a
![]() $\Sigma ^1_2$
statement in any code of
$\Sigma ^1_2$
statement in any code of
![]() $({\mathcal {M}}'|{\gamma} , {\alpha })$
, and so we get such a
$({\mathcal {M}}'|{\gamma} , {\alpha })$
, and so we get such a
![]() ${\mathcal {U}}$
in
${\mathcal {U}}$
in
![]() ${\mathcal {M}}[g]$
where
${\mathcal {M}}[g]$
where
![]() $g\subseteq Coll(\omega , {\beta })$
is generic. But then we can use the proof of [Reference Steel and Woodin40, Corollary 4.17] to get a contradictionFootnote
48
.
$g\subseteq Coll(\omega , {\beta })$
is generic. But then we can use the proof of [Reference Steel and Woodin40, Corollary 4.17] to get a contradictionFootnote
48
.
Proposition 3.4. Suppose
![]() $n\in \omega $
and
$n\in \omega $
and
![]() ${\mathcal {M}}$
is
${\mathcal {M}}$
is
![]() ${\mathcal {M}}^\#_{2n+1}$
-like
${\mathcal {M}}^\#_{2n+1}$
-like
![]() $\Pi ^1_{2n+2}$
-iterable x-premouse. Let
$\Pi ^1_{2n+2}$
-iterable x-premouse. Let
![]() $\Sigma $
be a strategy for player
$\Sigma $
be a strategy for player
![]() $II$
in
$II$
in
![]() $\mathcal {G}({\mathcal {M}}, 0, 2n+1)$
. Let
$\mathcal {G}({\mathcal {M}}, 0, 2n+1)$
. Let
![]() ${\delta }$
be the least Woodin cardinal of
${\delta }$
be the least Woodin cardinal of
![]() ${\mathcal {M}}$
and suppose
${\mathcal {M}}$
and suppose
![]() ${\mathcal {T}}$
is a correct iteration of
${\mathcal {T}}$
is a correct iteration of
![]() ${\mathcal {M}}$
below
${\mathcal {M}}$
below
![]() ${\delta }$
such that
${\delta }$
such that
![]() $\mathrm {lh}({\mathcal {T}})$
is a limit ordinal. For a limit
$\mathrm {lh}({\mathcal {T}})$
is a limit ordinal. For a limit
![]() ${\alpha }<\mathrm {lh}({\mathcal {T}})$
let
${\alpha }<\mathrm {lh}({\mathcal {T}})$
let
![]() $b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
. Let
$b_{\alpha }=[0, {\alpha })_{\mathcal {T}}$
. Let
![]() $y_0$
be a real that codes the sequence
$y_0$
be a real that codes the sequence
![]() $({\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha }): {\alpha }<\mathrm {lh}({\mathcal {T}})\wedge {\alpha }\in Lim)$
and
$({\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha }): {\alpha }<\mathrm {lh}({\mathcal {T}})\wedge {\alpha }\in Lim)$
and
![]() ${\mathcal {M}}_{2n}^\#(\mathsf {{cop}}({\mathcal {T}}))$
. Finally set
${\mathcal {M}}_{2n}^\#(\mathsf {{cop}}({\mathcal {T}}))$
. Finally set
![]() $b=\Sigma ({\mathcal {T}}, y)$
where y is any real that is Turing above
$b=\Sigma ({\mathcal {T}}, y)$
where y is any real that is Turing above
![]() $y_0$
and also set
$y_0$
and also set
![]() ${\mathcal {N}}={\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}))$
. Then the following hold.
${\mathcal {N}}={\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}))$
. Then the following hold.
-
1. b is a cofinal branch.
-
2. Suppose further that
 ${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. Then
${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. Then
 ${\mathcal { Q}}(b, {\mathcal {T}})$
exists and
${\mathcal { Q}}(b, {\mathcal {T}})$
exists and
 ${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {N}}$
.
${\mathcal { Q}}(b, {\mathcal {T}})\trianglelefteq {\mathcal {N}}$
. -
3. Suppose that
 ${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Then
${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Then
 ${\mathcal {N}}|({\delta }({\mathcal {T}})^+)^{{\mathcal {N}}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
.
${\mathcal {N}}|({\delta }({\mathcal {T}})^+)^{{\mathcal {N}}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
.
Proof. Set
![]() ${\alpha }=\sup (b)$
. We do the proof for the prototypical case
${\alpha }=\sup (b)$
. We do the proof for the prototypical case
![]() $n=1$
.
$n=1$
.
Lemma 3.5. b is cofinal.
Proof. Towards a contradiction suppose that
![]() ${\alpha }<\mathrm {lh}({\mathcal {T}})$
.
${\alpha }<\mathrm {lh}({\mathcal {T}})$
.
Case 1.
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists.
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists.
Set
![]() ${\mathcal R}={\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
and
${\mathcal R}={\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
and
![]() ${\mathcal {S}}={\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
. Note that
${\mathcal {S}}={\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
. Note that
![]() ${\delta }({\mathcal {T}}\restriction {\alpha })$
is a Woodin cardinal in both
${\delta }({\mathcal {T}}\restriction {\alpha })$
is a Woodin cardinal in both
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() ${\mathcal {S}}$
. We claim that
${\mathcal {S}}$
. We claim that
![]() ${\mathcal R}={\mathcal {S}}$
. To see this, we compare them inside
${\mathcal R}={\mathcal {S}}$
. To see this, we compare them inside
![]() ${\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})$
. If there is a successful coiteration of
${\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})$
. If there is a successful coiteration of
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() ${\mathcal {S}}$
then we indeed have that
${\mathcal {S}}$
then we indeed have that
![]() ${\mathcal R}={\mathcal {S}}$
(e.g., see [[Reference Steel37], Lemma 1.11]), and so any attempt to coiterate them is doomed to failure.
${\mathcal R}={\mathcal {S}}$
(e.g., see [[Reference Steel37], Lemma 1.11]), and so any attempt to coiterate them is doomed to failure.
We attempt to coiterate
![]() $({\mathcal R}, {\mathcal {S}})$
in
$({\mathcal R}, {\mathcal {S}})$
in
![]() ${\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})$
by building a coiteration
${\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})$
by building a coiteration
![]() $({\mathcal {U}}, {\mathcal {W} })$
in which the branches are picked as follows. Suppose
$({\mathcal {U}}, {\mathcal {W} })$
in which the branches are picked as follows. Suppose
![]() ${\lambda }$
is a limit ordinal and we have defined
${\lambda }$
is a limit ordinal and we have defined
![]() ${\mathcal {U}}\restriction {\lambda }$
and
${\mathcal {U}}\restriction {\lambda }$
and
![]() ${\mathcal {W} }\restriction {\lambda }$
. We want to describe our procedure for picking a branch of
${\mathcal {W} }\restriction {\lambda }$
. We want to describe our procedure for picking a branch of
![]() ${\mathcal {U}}\restriction {\lambda }$
and
${\mathcal {U}}\restriction {\lambda }$
and
![]() ${\mathcal {W} }\restriction {\lambda }$
. As
${\mathcal {W} }\restriction {\lambda }$
. As
![]() ${\mathcal {S}}$
is
${\mathcal {S}}$
is
![]() $\omega _1+1$
-iterable inside
$\omega _1+1$
-iterable inside
![]() ${\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})$
, we have a branch d of
${\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})$
, we have a branch d of
![]() ${\mathcal {W} }\restriction {\lambda }$
that is according to the unique strategy of
${\mathcal {W} }\restriction {\lambda }$
that is according to the unique strategy of
![]() ${\mathcal {S}}$
. Also, we must have that
${\mathcal {S}}$
. Also, we must have that
![]() ${\mathcal { Q}}(d, {\mathcal {W} }\restriction {\lambda })$
exists as
${\mathcal { Q}}(d, {\mathcal {W} }\restriction {\lambda })$
exists as
![]() ${\mathcal {S}}$
is a
${\mathcal {S}}$
is a
![]() ${\delta }({\mathcal {T}}\restriction {\alpha })$
-mouse (in the sense of [[Reference Steel37], Definition 1.3])Footnote
49
. We now seek a branch c of
${\delta }({\mathcal {T}}\restriction {\alpha })$
-mouse (in the sense of [[Reference Steel37], Definition 1.3])Footnote
49
. We now seek a branch c of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\lambda })$
exists and
${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\lambda })$
exists and
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\lambda })={\mathcal { Q}}(d, {\mathcal {W} }\restriction {\lambda })$
. If there is such a branch then we choose it and continue the coiteration. Otherwise we stop the coiteration. As we cannot successfully coiterate
${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\lambda })={\mathcal { Q}}(d, {\mathcal {W} }\restriction {\lambda })$
. If there is such a branch then we choose it and continue the coiteration. Otherwise we stop the coiteration. As we cannot successfully coiterate
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() ${\mathcal {S}}$
, we must end up with a coiteration
${\mathcal {S}}$
, we must end up with a coiteration
![]() $({\mathcal {U}}, {\mathcal {W} })$
such that
$({\mathcal {U}}, {\mathcal {W} })$
such that
![]() $\mathrm {lh}({\mathcal {U}})=\mathrm { lh}({\mathcal {W} })$
is a limit ordinal
$\mathrm {lh}({\mathcal {U}})=\mathrm { lh}({\mathcal {W} })$
is a limit ordinal
![]() $< \omega _1^{{\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})}$
Footnote
50
and if d is the branch of
$< \omega _1^{{\mathcal {M}}_1({\mathcal R}, {\mathcal {S}})}$
Footnote
50
and if d is the branch of
![]() ${\mathcal {W} }$
according to
${\mathcal {W} }$
according to
![]() ${\mathcal {S}}$
’s unique strategy then there is no branch c of
${\mathcal {S}}$
’s unique strategy then there is no branch c of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() ${\mathcal { Q}}(c, {\mathcal {U}})$
exists and
${\mathcal { Q}}(c, {\mathcal {U}})$
exists and
![]() ${\mathcal { Q}}(c, {\mathcal {U}})={\mathcal { Q}}(d, {\mathcal {W} })$
.
${\mathcal { Q}}(c, {\mathcal {U}})={\mathcal { Q}}(d, {\mathcal {W} })$
.
We are now in the lucky situation that
![]() ${\mathcal {U}}$
is an allowed move for I in the second round of
${\mathcal {U}}$
is an allowed move for I in the second round of
![]() $\mathcal {G}({\mathcal {M}}, 0, 3)$
. Indeed, some real recursive in y codes
$\mathcal {G}({\mathcal {M}}, 0, 3)$
. Indeed, some real recursive in y codes
![]() ${\mathcal {S}}$
, and therefore,
${\mathcal {S}}$
, and therefore,
![]() ${\mathcal {U}}\in {\mathcal {M}}_1(y, {\mathcal {T}}, b)|\omega _1^{{\mathcal {M}}_1(y, {\mathcal {T}}, b)}$
Footnote
51
. Let then I play
${\mathcal {U}}\in {\mathcal {M}}_1(y, {\mathcal {T}}, b)|\omega _1^{{\mathcal {M}}_1(y, {\mathcal {T}}, b)}$
Footnote
51
. Let then I play
![]() ${\mathcal {U}}$
and
${\mathcal {U}}$
and
![]() $II$
play a branch c such that
$II$
play a branch c such that
![]() ${\mathcal {M}}^{\mathcal {U}}_c$
is well-founded. Once again, we only know that c is maximal. But now
${\mathcal {M}}^{\mathcal {U}}_c$
is well-founded. Once again, we only know that c is maximal. But now
![]() ${\mathcal {M}}^{\mathcal {U}}_c$
is
${\mathcal {M}}^{\mathcal {U}}_c$
is
![]() $\Pi ^1_2$
-iterable above
$\Pi ^1_2$
-iterable above
![]() ${\delta }({\mathcal {U}})$
. Let
${\delta }({\mathcal {U}})$
. Let
![]() ${\gamma} =\sup (c)$
,
${\gamma} =\sup (c)$
,
![]() $\nu ={\delta }({\mathcal {U}}\restriction {\gamma} )$
and set
$\nu ={\delta }({\mathcal {U}}\restriction {\gamma} )$
and set
![]() ${\mathcal R}'={\mathcal { Q}}(c, {\mathcal {U}}\restriction {\gamma} )$
if it exists and otherwise set
${\mathcal R}'={\mathcal { Q}}(c, {\mathcal {U}}\restriction {\gamma} )$
if it exists and otherwise set
![]() ${\mathcal R}'={\mathcal {M}}^{{\mathcal {U}}\restriction {\gamma} }_c$
. If
${\mathcal R}'={\mathcal {M}}^{{\mathcal {U}}\restriction {\gamma} }_c$
. If
![]() ${\gamma} <\mathrm {lh}({\mathcal {U}})$
we set
${\gamma} <\mathrm {lh}({\mathcal {U}})$
we set
![]() ${\mathcal {S}}'={\mathcal { Q}}(c', {\mathcal {U}}\restriction {\gamma} )$
where
${\mathcal {S}}'={\mathcal { Q}}(c', {\mathcal {U}}\restriction {\gamma} )$
where
![]() $c'=[0, {\gamma} )_{{\mathcal {U}}}$
. Otherwise let
$c'=[0, {\gamma} )_{{\mathcal {U}}}$
. Otherwise let
![]() ${\mathcal {S}}'={\mathcal { Q}}(d, {\mathcal {W} })$
. In either of the cases, we have that
${\mathcal {S}}'={\mathcal { Q}}(d, {\mathcal {W} })$
. In either of the cases, we have that
![]() ${\mathcal {S}}'$
is
${\mathcal {S}}'$
is
![]() $\omega _1$
-iterable, 1-small,
$\omega _1$
-iterable, 1-small,
![]() ${\delta }({\mathcal {U}})$
-mouse and neither
${\delta }({\mathcal {U}})$
-mouse and neither
![]() ${\mathcal R}'\not \trianglelefteq {\mathcal {S}}'$
nor
${\mathcal R}'\not \trianglelefteq {\mathcal {S}}'$
nor
![]() ${\mathcal {S}}'\not \trianglelefteq {\mathcal R}'$
. Moreover,
${\mathcal {S}}'\not \trianglelefteq {\mathcal R}'$
. Moreover,
![]() $\nu $
is a Woodin cardinal in both
$\nu $
is a Woodin cardinal in both
![]() ${\mathcal R}'$
and
${\mathcal R}'$
and
![]() ${\mathcal {S}}'$
. Thus,
${\mathcal {S}}'$
. Thus,
![]() ${\mathcal R}'$
and
${\mathcal R}'$
and
![]() ${\mathcal {S}}'$
have at least 2 Woodin cardinals,
${\mathcal {S}}'$
have at least 2 Woodin cardinals,
![]() ${\delta }({\mathcal {T}}\restriction {\alpha })$
and
${\delta }({\mathcal {T}}\restriction {\alpha })$
and
![]() $\nu $
.
$\nu $
.
Because
![]() ${\mathcal R}'$
is
${\mathcal R}'$
is
![]() $\Pi ^1_2$
-iterable above
$\Pi ^1_2$
-iterable above
![]() $\nu $
and
$\nu $
and
![]() ${\mathcal {S}}'$
is iterable, if
${\mathcal {S}}'$
is iterable, if
![]() ${\mathcal R}'={\mathcal { Q}}(c, {\mathcal {U}}\restriction {\gamma} )$
then clause 3 of [[Reference Steel37], Lemma 2.2] implies that
${\mathcal R}'={\mathcal { Q}}(c, {\mathcal {U}}\restriction {\gamma} )$
then clause 3 of [[Reference Steel37], Lemma 2.2] implies that
![]() ${\mathcal R}'={\mathcal {S}}'$
, which is a contradiction. Thus,
${\mathcal R}'={\mathcal {S}}'$
, which is a contradiction. Thus,
![]() ${\mathcal R}'={\mathcal {M}}^{{\mathcal {U}}\restriction {\gamma} }_c$
and
${\mathcal R}'={\mathcal {M}}^{{\mathcal {U}}\restriction {\gamma} }_c$
and
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\gamma} )$
doesn’t exist. It follows that
${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\gamma} )$
doesn’t exist. It follows that
![]() $\pi ^{{\mathcal {T}}^\frown {\mathcal {U}}}$
is defined, and hence,
$\pi ^{{\mathcal {T}}^\frown {\mathcal {U}}}$
is defined, and hence,
![]() ${\mathcal R}'$
is not 1-small. But now [[Reference Steel37], Lemma 3.1] implies that
${\mathcal R}'$
is not 1-small. But now [[Reference Steel37], Lemma 3.1] implies that
![]() ${\mathcal {S}}'\trianglelefteq {\mathcal R}'$
. Hence, after all,
${\mathcal {S}}'\trianglelefteq {\mathcal R}'$
. Hence, after all,
![]() ${\delta }({\mathcal {U}})$
is not a Woodin cardinal in
${\delta }({\mathcal {U}})$
is not a Woodin cardinal in
![]() ${\mathcal R}'$
, contradiction.
${\mathcal R}'$
, contradiction.
Case 2.
![]() ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
doesn’t exist.
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
doesn’t exist.
Set now
![]() ${\mathcal R}={\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
and
${\mathcal R}={\mathcal {M}}^{{\mathcal {T}}\restriction {\alpha }}_b$
and
![]() ${\mathcal {S}}={\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
. Let
${\mathcal {S}}={\mathcal { Q}}(b_{\alpha }, {\mathcal {T}}\restriction {\alpha })$
. Let
![]() $\nu $
be the second least Woodin cardinal of
$\nu $
be the second least Woodin cardinal of
![]() ${\mathcal R}$
. We now coiterate
${\mathcal R}$
. We now coiterate
![]() ${\mathcal R}_0={\mathcal R}|(\nu ^+)^{\mathcal R}$
and
${\mathcal R}_0={\mathcal R}|(\nu ^+)^{\mathcal R}$
and
![]() ${\mathcal {S}}$
inside
${\mathcal {S}}$
inside
![]() ${\mathcal {M}}_1({\mathcal R}_0, {\mathcal {S}})$
using the same procedure as before, that is, if
${\mathcal {M}}_1({\mathcal R}_0, {\mathcal {S}})$
using the same procedure as before, that is, if
![]() $({\mathcal {U}}_0, {\mathcal {W} })$
is the coiteration that we build then at each limit stage
$({\mathcal {U}}_0, {\mathcal {W} })$
is the coiteration that we build then at each limit stage
![]() ${\lambda }<\mathrm {lh}({\mathcal {U}}_0)=\mathrm {lh}({\mathcal {W} })$
,
${\lambda }<\mathrm {lh}({\mathcal {U}}_0)=\mathrm {lh}({\mathcal {W} })$
,
![]() $d=[0, {\lambda })_{\mathcal {W} }$
is the branch of
$d=[0, {\lambda })_{\mathcal {W} }$
is the branch of
![]() ${\mathcal {W} }\restriction {\lambda }$
according to the unique strategy of
${\mathcal {W} }\restriction {\lambda }$
according to the unique strategy of
![]() ${\mathcal {S}}$
as a
${\mathcal {S}}$
as a
![]() ${\delta }({\mathcal {T}}\restriction {\alpha })$
-mouse, and
${\delta }({\mathcal {T}}\restriction {\alpha })$
-mouse, and
![]() $c=[0,{\lambda })_{{\mathcal {U}}_0}$
is the unique well-founded cofinal branch of
$c=[0,{\lambda })_{{\mathcal {U}}_0}$
is the unique well-founded cofinal branch of
![]() ${\mathcal {U}}\restriction {\lambda }$
such that
${\mathcal {U}}\restriction {\lambda }$
such that
![]() ${\mathcal { Q}}(c, {\mathcal {U}}_0\restriction {\lambda })$
exists and
${\mathcal { Q}}(c, {\mathcal {U}}_0\restriction {\lambda })$
exists and
![]() ${\mathcal { Q}}(c, {\mathcal {U}}_0\restriction {\lambda })={\mathcal { Q}}(d, {\mathcal {W} }\restriction {\lambda })$
.
${\mathcal { Q}}(c, {\mathcal {U}}_0\restriction {\lambda })={\mathcal { Q}}(d, {\mathcal {W} }\restriction {\lambda })$
.
Assume for a moment that the coiteration is successful. Thus
![]() ${\mathcal {U}}_0$
and
${\mathcal {U}}_0$
and
![]() ${\mathcal {W} }$
have last models, say
${\mathcal {W} }$
have last models, say
![]() ${\mathcal R}^{\prime }_0$
and
${\mathcal R}^{\prime }_0$
and
![]() ${\mathcal {S}}'$
. If
${\mathcal {S}}'$
. If
![]() ${\mathcal {S}}'\trianglelefteq {\mathcal R}^{\prime }_0$
then we in fact have that
${\mathcal {S}}'\trianglelefteq {\mathcal R}^{\prime }_0$
then we in fact have that
![]() ${\mathcal {S}}{\triangleleft } {\mathcal R}_0$
and so
${\mathcal {S}}{\triangleleft } {\mathcal R}_0$
and so
![]() ${\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal in
${\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal in
![]() ${\mathcal R}$
. Thus, it must be the case that
${\mathcal R}$
. Thus, it must be the case that
![]() ${\mathcal R}^{\prime }_0\trianglelefteq {\mathcal {S}}'$
. This means that
${\mathcal R}^{\prime }_0\trianglelefteq {\mathcal {S}}'$
. This means that
![]() $\pi ^{{\mathcal {U}}_0}$
exists. Let now
$\pi ^{{\mathcal {U}}_0}$
exists. Let now
![]() ${\mathcal {U}}$
be the copy of
${\mathcal {U}}$
be the copy of
![]() ${\mathcal {U}}_0$
on
${\mathcal {U}}_0$
on
![]() ${\mathcal R}$
using the identity map. The extenders of
${\mathcal R}$
using the identity map. The extenders of
![]() ${\mathcal {U}}$
and the tree structure of
${\mathcal {U}}$
and the tree structure of
![]() ${\mathcal {U}}$
are the same as the extenders of
${\mathcal {U}}$
are the same as the extenders of
![]() ${\mathcal {U}}_0$
and the tree structure of
${\mathcal {U}}_0$
and the tree structure of
![]() ${\mathcal {U}}_0$
. Let
${\mathcal {U}}_0$
. Let
![]() ${\mathcal R}'$
be the last model of
${\mathcal R}'$
be the last model of
![]() ${\mathcal {U}}$
.
${\mathcal {U}}$
.
Now
![]() ${\mathcal {U}}$
again is a valid move for I in
${\mathcal {U}}$
again is a valid move for I in
![]() $\mathcal {G}({\mathcal {M}}, 0, 3)$
, and so we let I play it.
$\mathcal {G}({\mathcal {M}}, 0, 3)$
, and so we let I play it.
![]() $II$
has to now either accept
$II$
has to now either accept
![]() ${\mathcal {U}}$
or play a maximal branch of
${\mathcal {U}}$
or play a maximal branch of
![]() ${\mathcal {U}}$
. If
${\mathcal {U}}$
. If
![]() $II$
plays a maximal non-cofinal branch then we have two different branches
$II$
plays a maximal non-cofinal branch then we have two different branches
![]() $c_0, c_1$
of some
$c_0, c_1$
of some
![]() ${\mathcal {U}}\restriction {\lambda }$
such that both
${\mathcal {U}}\restriction {\lambda }$
such that both
![]() ${\mathcal { Q}}(c_0, {\mathcal {U}}\restriction {\lambda })$
and
${\mathcal { Q}}(c_0, {\mathcal {U}}\restriction {\lambda })$
and
![]() ${\mathcal { Q}}(c_1, {\mathcal {U}}\restriction {\lambda })$
exist, one of them is
${\mathcal { Q}}(c_1, {\mathcal {U}}\restriction {\lambda })$
exist, one of them is
![]() $\omega _1+1$
iterable and the other is
$\omega _1+1$
iterable and the other is
![]() $\Pi ^1_2$
-iterable. It then follows from clause 3 of [[Reference Steel37], Lemma 2.2] that
$\Pi ^1_2$
-iterable. It then follows from clause 3 of [[Reference Steel37], Lemma 2.2] that
![]() ${\mathcal { Q}}(c_0, {\mathcal {U}}\restriction {\lambda })={\mathcal { Q}}(c_1, {\mathcal {U}}\restriction {\lambda })$
implying that
${\mathcal { Q}}(c_0, {\mathcal {U}}\restriction {\lambda })={\mathcal { Q}}(c_1, {\mathcal {U}}\restriction {\lambda })$
implying that
![]() $c_0=c_1$
, contradiction. Thus,
$c_0=c_1$
, contradiction. Thus,
![]() $II$
must accept it. But now we are in the second scenario of this repetitive argument, namely if
$II$
must accept it. But now we are in the second scenario of this repetitive argument, namely if
![]() $\nu '$
is the second Woodin cardinal of
$\nu '$
is the second Woodin cardinal of
![]() ${\mathcal R}'$
then
${\mathcal R}'$
then
![]() ${\mathcal R}'$
as a
${\mathcal R}'$
as a
![]() $\nu '$
-mouse is
$\nu '$
-mouse is
![]() $\Pi ^1_2$
-iterable and not 1-small while
$\Pi ^1_2$
-iterable and not 1-small while
![]() ${\mathcal {S}}'$
as
${\mathcal {S}}'$
as
![]() $\nu '$
-mouse is
$\nu '$
-mouse is
![]() $\omega _1+1$
-iterable and is 1-small. Thus, [[Reference Steel37], Lemma 3.1] implies that
$\omega _1+1$
-iterable and is 1-small. Thus, [[Reference Steel37], Lemma 3.1] implies that
![]() ${\mathcal {S}}'\trianglelefteq {\mathcal R}'$
, which in fact implies that
${\mathcal {S}}'\trianglelefteq {\mathcal R}'$
, which in fact implies that
![]() ${\mathcal {S}}\trianglelefteq {\mathcal R}$
and hence,
${\mathcal {S}}\trianglelefteq {\mathcal R}$
and hence,
![]() ${\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal in
${\delta }({\mathcal {T}}\restriction {\alpha })$
is not a Woodin cardinal in
![]() ${\mathcal R}$
.
${\mathcal R}$
.
We thus have that the coiteration
![]() $({\mathcal {U}}_0, {\mathcal {W} })$
of
$({\mathcal {U}}_0, {\mathcal {W} })$
of
![]() $({\mathcal R}_0, {\mathcal {S}})$
that we described above is not successful, which can only happen if we fail to find a branch c of
$({\mathcal R}_0, {\mathcal {S}})$
that we described above is not successful, which can only happen if we fail to find a branch c of
![]() ${\mathcal {U}}_0$
such that
${\mathcal {U}}_0$
such that
![]() ${\mathcal { Q}}(c, {\mathcal {U}}_0)$
exists and
${\mathcal { Q}}(c, {\mathcal {U}}_0)$
exists and
![]() ${\mathcal { Q}}(c, {\mathcal {U}}_0)={\mathcal { Q}}(d, {\mathcal {W} })$
, where once again d is the unique branch of
${\mathcal { Q}}(c, {\mathcal {U}}_0)={\mathcal { Q}}(d, {\mathcal {W} })$
, where once again d is the unique branch of
![]() ${\mathcal {W} }$
that is according to the unique strategy of
${\mathcal {W} }$
that is according to the unique strategy of
![]() ${\mathcal {S}}$
. We again let
${\mathcal {S}}$
. We again let
![]() ${\mathcal {U}}$
be the copy of
${\mathcal {U}}$
be the copy of
![]() ${\mathcal {U}}_0$
onto
${\mathcal {U}}_0$
onto
![]() ${\mathcal R}$
via identity and let I play it in the second round of
${\mathcal R}$
via identity and let I play it in the second round of
![]() $\mathcal {G}({\mathcal {M}}, 0, 3)$
. Clause 3 of [[Reference Steel37], Lemma 2.2] implies that
$\mathcal {G}({\mathcal {M}}, 0, 3)$
. Clause 3 of [[Reference Steel37], Lemma 2.2] implies that
![]() $II$
must play a cofinal branch c of
$II$
must play a cofinal branch c of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() ${\mathcal {M}}^{\mathcal {U}}_c$
is well-founded. Clause 3 of [[Reference Steel37], Lemma 2.2] implies that
${\mathcal {M}}^{\mathcal {U}}_c$
is well-founded. Clause 3 of [[Reference Steel37], Lemma 2.2] implies that
![]() ${\mathcal { Q}}(c, {\mathcal {U}})$
cannot exists while [[Reference Steel37], Lemma 3.1] implies that
${\mathcal { Q}}(c, {\mathcal {U}})$
cannot exists while [[Reference Steel37], Lemma 3.1] implies that
![]() ${\mathcal { Q}}(d, {\mathcal {W} })\trianglelefteq {\mathcal {M}}^{\mathcal {U}}_c$
.
${\mathcal { Q}}(d, {\mathcal {W} })\trianglelefteq {\mathcal {M}}^{\mathcal {U}}_c$
.
We thus have that b is a cofinal branch. Assume then
![]() ${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. Let
${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is not a Woodin cardinal’. Let
![]() ${\mathcal {S}}\trianglelefteq {\mathcal {N}}$
be the longest such that
${\mathcal {S}}\trianglelefteq {\mathcal {N}}$
be the longest such that
![]() ${\mathcal {S}}\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Assume first that
${\mathcal {S}}\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Assume first that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
exists and set
${\mathcal { Q}}(b, {\mathcal {T}})$
exists and set
![]() ${\mathcal R}={\mathcal { Q}}(b, {\mathcal {T}})$
. We want to see that
${\mathcal R}={\mathcal { Q}}(b, {\mathcal {T}})$
. We want to see that
![]() ${\mathcal R}={\mathcal {S}}$
, and this can be achieved by repeating the proof of Case 1 of the Lemma above. Assume then
${\mathcal R}={\mathcal {S}}$
, and this can be achieved by repeating the proof of Case 1 of the Lemma above. Assume then
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
doesn’t exist. We then let
${\mathcal { Q}}(b, {\mathcal {T}})$
doesn’t exist. We then let
![]() ${\mathcal R}={\mathcal {M}}^{\mathcal {T}}_b$
and argue as in Case 2 of the Lemma above to conclude that
${\mathcal R}={\mathcal {M}}^{\mathcal {T}}_b$
and argue as in Case 2 of the Lemma above to conclude that
![]() ${\mathcal {S}}\trianglelefteq {\mathcal R}$
, contradicting the fact that
${\mathcal {S}}\trianglelefteq {\mathcal R}$
, contradicting the fact that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
doesn’t exist.
${\mathcal { Q}}(b, {\mathcal {T}})$
doesn’t exist.
Assume next that
![]() ${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Let
${\mathcal {N}}\models `{\delta }({\mathcal {T}})$
is a Woodin cardinal’. Let
![]() ${\mathcal {S}}\trianglelefteq {\mathcal {N}}$
be such that
${\mathcal {S}}\trianglelefteq {\mathcal {N}}$
be such that
![]() ${\mathcal {S}}$
is a
${\mathcal {S}}$
is a
![]() ${\delta }({\mathcal {T}})$
-mouse. We want to see that
${\delta }({\mathcal {T}})$
-mouse. We want to see that
![]() ${\mathcal {S}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
. Assume first that
${\mathcal {S}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
. Assume first that
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
exists and set
${\mathcal { Q}}(b, {\mathcal {T}})$
exists and set
![]() ${\mathcal R}={\mathcal { Q}}(b, {\mathcal {T}})$
. We then compare
${\mathcal R}={\mathcal { Q}}(b, {\mathcal {T}})$
. We then compare
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() ${\mathcal {S}}$
as in Case 1 of the Lemma and conclude that
${\mathcal {S}}$
as in Case 1 of the Lemma and conclude that
![]() ${\mathcal {S}}\trianglelefteq {\mathcal R}$
as
${\mathcal {S}}\trianglelefteq {\mathcal R}$
as
![]() ${\mathcal R}$
witnesses that
${\mathcal R}$
witnesses that
![]() ${\delta }({\mathcal {T}})$
is not a Woodin cardinal while
${\delta }({\mathcal {T}})$
is not a Woodin cardinal while
![]() ${\mathcal {S}}$
does not. Suppose then
${\mathcal {S}}$
does not. Suppose then
![]() ${\mathcal { Q}}(b, {\mathcal {T}})$
doesn’t exist and set
${\mathcal { Q}}(b, {\mathcal {T}})$
doesn’t exist and set
![]() ${\mathcal R}={\mathcal {M}}^{\mathcal {T}}_b$
. We then compare
${\mathcal R}={\mathcal {M}}^{\mathcal {T}}_b$
. We then compare
![]() ${\mathcal R}$
with
${\mathcal R}$
with
![]() ${\mathcal {S}}$
as in Case 2 of the Lemma above. Just like in that proof, the conclusion once again is that
${\mathcal {S}}$
as in Case 2 of the Lemma above. Just like in that proof, the conclusion once again is that
![]() ${\mathcal {S}}\trianglelefteq {\mathcal R}$
.
${\mathcal {S}}\trianglelefteq {\mathcal R}$
.
4 The proof of Theorem 1.8
After setting up some notation, we will present the main ideas of the proof in Section 4.1.
Fix n. Below we prove Theorem 1.8 for n. As [Reference Hjorth7] proves Theorem 1.8 for
![]() $n=0$
, we might just as well assume that
$n=0$
, we might just as well assume that
![]() $n\geq 1$
. As was already mentioned in clause 5 of Review 2.18, we have that
$n\geq 1$
. As was already mentioned in clause 5 of Review 2.18, we have that
Fix then
![]() $m<\omega $
such that
$m<\omega $
such that
![]() ${\gamma} ^{2n+1}_{m, \infty }\geq {\delta }^1_{2n+2}$
. We then let
${\gamma} ^{2n+1}_{m, \infty }\geq {\delta }^1_{2n+2}$
. We then let
![]() $({\mathcal {S}}_0, \xi _0)$
be such that
$({\mathcal {S}}_0, \xi _0)$
be such that
-
1.
 ${\mathcal {S}}_0$
is a complete iterate of
${\mathcal {S}}_0$
is a complete iterate of
 ${\mathcal {M}}^\#_{2n+1}$
such that
${\mathcal {M}}^\#_{2n+1}$
such that
 ${\mathcal {T}}_{{\mathcal {M}}^\#_{2n+1}, {\mathcal {S}}_0}$
is below the least Woodin cardinal of
${\mathcal {T}}_{{\mathcal {M}}^\#_{2n+1}, {\mathcal {S}}_0}$
is below the least Woodin cardinal of
 ${\mathcal {M}}^\#_{2n+1}$
,
${\mathcal {M}}^\#_{2n+1}$
, -
2.
 $\xi _0\leq {\gamma} _{m}^{{\mathcal {S}}_0}$
,
$\xi _0\leq {\gamma} _{m}^{{\mathcal {S}}_0}$
, -
3.
 $\pi _{{\mathcal {S}}_0, \infty }(\xi _0)={\delta }^1_{2n+2}$
.
$\pi _{{\mathcal {S}}_0, \infty }(\xi _0)={\delta }^1_{2n+2}$
.
Let
![]() $x_0$
be a real coding
$x_0$
be a real coding
![]() $({\mathcal {S}}_0, \xi _0)$
and let
$({\mathcal {S}}_0, \xi _0)$
and let
![]() $\mathsf {{Code}}$
be the set of reals y such that y codes a pair
$\mathsf {{Code}}$
be the set of reals y such that y codes a pair
![]() $({\mathcal R}_y, \tau _y)$
with a property that
$({\mathcal R}_y, \tau _y)$
with a property that
-
1.
 ${\mathcal R}_y$
is a complete iterate of
${\mathcal R}_y$
is a complete iterate of
 ${\mathcal {S}}_0$
such that
${\mathcal {S}}_0$
such that
 ${\mathcal {T}}_{{\mathcal {S}}_0, {\mathcal R}_y}$
is below the least Woodin cardinal of
${\mathcal {T}}_{{\mathcal {S}}_0, {\mathcal R}_y}$
is below the least Woodin cardinal of
 ${\mathcal {S}}_0$
,
${\mathcal {S}}_0$
, -
2.
 $\tau _y<\pi _{{\mathcal {S}}_0, {\mathcal R}_y}(\xi _0)$
.
$\tau _y<\pi _{{\mathcal {S}}_0, {\mathcal R}_y}(\xi _0)$
.
For
![]() $x, y\in \mathsf {{Code}}$
set
$x, y\in \mathsf {{Code}}$
set
![]() $x\leq ^* y$
if and only if letting
$x\leq ^* y$
if and only if letting
![]() ${\mathcal { Q}}$
be the common complete iterate of
${\mathcal { Q}}$
be the common complete iterate of
![]() ${\mathcal R}_x$
and
${\mathcal R}_x$
and
![]() ${\mathcal R}_y$
,
${\mathcal R}_y$
,
![]() $\pi _{{\mathcal R}_x, {\mathcal { Q}}}(\tau _x)\leq \pi _{{\mathcal R}_y, {\mathcal { Q}}}(\tau _y)$
. We have that there is a formula
$\pi _{{\mathcal R}_x, {\mathcal { Q}}}(\tau _x)\leq \pi _{{\mathcal R}_y, {\mathcal { Q}}}(\tau _y)$
. We have that there is a formula
![]() $\phi $
such that for all
$\phi $
such that for all
![]() $(x, y)\in {\mathbb {R}}^2$
,
$(x, y)\in {\mathbb {R}}^2$
,
It follows that
![]() $\leq ^*$
is
$\leq ^*$
is
![]() $\Delta ^1_{2n+3}(x_0)$
(see clause 10 of Section 3). For
$\Delta ^1_{2n+3}(x_0)$
(see clause 10 of Section 3). For
![]() $x\in \mathrm {dom}(\leq ^*)$
, let
$x\in \mathrm {dom}(\leq ^*)$
, let
![]() ${\gamma} _x=\pi _{{\mathcal R}_x, \infty }(\tau _x)$
. We have that the length of
${\gamma} _x=\pi _{{\mathcal R}_x, \infty }(\tau _x)$
. We have that the length of
![]() $\leq ^*$
is
$\leq ^*$
is
![]() ${\delta }^1_{2n+2}$
, and for each ordinal
${\delta }^1_{2n+2}$
, and for each ordinal
![]() ${\alpha }<{\delta }^1_{2n+2}$
, there is
${\alpha }<{\delta }^1_{2n+2}$
, there is
![]() $x\in \mathrm {dom}(\leq ^*)$
such that
$x\in \mathrm {dom}(\leq ^*)$
such that
![]() ${\gamma} _x={\alpha }$
.
${\gamma} _x={\alpha }$
.
Towards a contradiction, suppose
![]() $(A_{\alpha }: {\alpha }<{\delta }^1_{2n+2})$
is a sequence consisting of distinct
$(A_{\alpha }: {\alpha }<{\delta }^1_{2n+2})$
is a sequence consisting of distinct
![]() $\boldsymbol {\Sigma }^1_{2n+2}$
-sets. Let
$\boldsymbol {\Sigma }^1_{2n+2}$
-sets. Let
![]() $U\subseteq {\mathbb {R}}^2$
be a universal
$U\subseteq {\mathbb {R}}^2$
be a universal
![]() $\Sigma ^1_{2n+2}$
formulaFootnote
52
and let for
$\Sigma ^1_{2n+2}$
formulaFootnote
52
and let for
![]() ${\alpha }<{\delta }^1_{2n+2}$
,
${\alpha }<{\delta }^1_{2n+2}$
,
![]() $B_{\alpha }=\{ y: \{ z: U(y, z)\}=A_{\alpha }\}$
. Using the
$B_{\alpha }=\{ y: \{ z: U(y, z)\}=A_{\alpha }\}$
. Using the
![]() $\mathsf {{Coding\ Lemma}}$
(see [Reference Jackson13, Theorem 2.12]) we can find a real z Turing above
$\mathsf {{Coding\ Lemma}}$
(see [Reference Jackson13, Theorem 2.12]) we can find a real z Turing above
![]() $x_0$
and a
$x_0$
and a
![]() $\Sigma ^1_{2n+3}(z)$
set
$\Sigma ^1_{2n+3}(z)$
set
![]() $D^*\subseteq \mathrm {dom}(\leq ^*)\times {\mathbb {R}}$
such that
$D^*\subseteq \mathrm {dom}(\leq ^*)\times {\mathbb {R}}$
such that
-
1. for each
 $x\in \mathrm {dom}(\leq ^*)$
,
$x\in \mathrm {dom}(\leq ^*)$
,
 $D^*_x\not =\emptyset $
,
$D^*_x\not =\emptyset $
, -
2. for each
 $(x, y)\in D^*$
,
$(x, y)\in D^*$
,
 $y\in B_{{\gamma} _x}$
(therefore,
$y\in B_{{\gamma} _x}$
(therefore,
 $U_y=A_{{\gamma} _x}$
).
$U_y=A_{{\gamma} _x}$
).
Let
![]() $D\in \Pi ^1_{2n+2}(z)$
be such that
$D\in \Pi ^1_{2n+2}(z)$
be such that
![]() $D\subseteq {\mathbb {R}}^3$
and
$D\subseteq {\mathbb {R}}^3$
and
![]() $(x, y)\in D^*{\mathrel {\leftrightarrow }} \exists u (x, y, u)\in D$
. To get that
$(x, y)\in D^*{\mathrel {\leftrightarrow }} \exists u (x, y, u)\in D$
. To get that
![]() $\mathrm {dom}(D^*)=\mathrm {dom}(\leq ^*)$
we use the fact that
$\mathrm {dom}(D^*)=\mathrm {dom}(\leq ^*)$
we use the fact that
![]() $\Sigma ^1_{2n+3}(z)$
is closed under
$\Sigma ^1_{2n+3}(z)$
is closed under
![]() $\exists ^{\mathbb {R}}$
. For details, see the discussion above [Reference Jackson13, Lemma 2.13].
$\exists ^{\mathbb {R}}$
. For details, see the discussion above [Reference Jackson13, Lemma 2.13].
We now set
![]() ${\mathcal {M}}=_{def}{\mathcal {M}}_{2n+1}(z)$
. Given a complete iterate
${\mathcal {M}}=_{def}{\mathcal {M}}_{2n+1}(z)$
. Given a complete iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
, let
${\mathcal {M}}$
, let
![]() ${\delta }_{\mathcal {N}}$
be the least Woodin cardinal of
${\delta }_{\mathcal {N}}$
be the least Woodin cardinal of
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\kappa }_{\mathcal {N}}$
be the least
${\kappa }_{\mathcal {N}}$
be the least
![]() $<{\delta }_{\mathcal {N}}$
-strong cardinal of
$<{\delta }_{\mathcal {N}}$
-strong cardinal of
![]() ${\mathcal {N}}$
.
${\mathcal {N}}$
.
If
![]() $x\in {\mathbb {R}}$
codes a countable premouse then we let
$x\in {\mathbb {R}}$
codes a countable premouse then we let
![]() ${\mathcal R}_x$
be this premouse and let
${\mathcal R}_x$
be this premouse and let
![]() $\mathsf {{C}}'$
be the set of reals that code a countable
$\mathsf {{C}}'$
be the set of reals that code a countable
![]() $\Pi ^1_{2n+2}$
-iterable
$\Pi ^1_{2n+2}$
-iterable
![]() ${\mathcal {M}}_{2n+1}^\#$
-like premouse over some real. For
${\mathcal {M}}_{2n+1}^\#$
-like premouse over some real. For
![]() $x\in \mathsf {{C}}'$
we let
$x\in \mathsf {{C}}'$
we let
![]() $\nu _x$
be the least Woodin of
$\nu _x$
be the least Woodin of
![]() ${\mathcal R}_x$
and
${\mathcal R}_x$
and
![]() $\mu _x$
be the least
$\mu _x$
be the least
![]() $<\nu _x$
-strong of
$<\nu _x$
-strong of
![]() ${\mathcal R}_x$
. Because
${\mathcal R}_x$
. Because
![]() ${\mathcal R}_x$
may not be iterable,
${\mathcal R}_x$
may not be iterable,
![]() ${\mathcal R}_x$
may not satisfy condensation (see [Reference Steel39, Theorem 5.1]). Because for
${\mathcal R}_x$
may not satisfy condensation (see [Reference Steel39, Theorem 5.1]). Because for
![]() $u\in {\mathbb {R}}$
,
$u\in {\mathbb {R}}$
,
![]() ${\mathcal {M}}_{2n+1}^\#(u)$
is iterable it does have condensation, and in particular, it follows from Lemma 2.12 that
${\mathcal {M}}_{2n+1}^\#(u)$
is iterable it does have condensation, and in particular, it follows from Lemma 2.12 that
![]() ${\mathcal {M}}_{2n+1}(u)\models \mathsf {{Cond}}$
. Let now
${\mathcal {M}}_{2n+1}(u)\models \mathsf {{Cond}}$
. Let now
![]() $\mathsf {{C}}$
be the set of
$\mathsf {{C}}$
be the set of
![]() $x\in \mathsf {{C}}'$
such that
$x\in \mathsf {{C}}'$
such that
-
1.
 ${\mathcal R}_x\models \mathsf {{Cond}}$
,
${\mathcal R}_x\models \mathsf {{Cond}}$
, -
2.
 ${\mathcal R}_x$
is translatable (see clause 3 of Review 2.7),
${\mathcal R}_x$
is translatable (see clause 3 of Review 2.7), -
3. for all
 $\eta <{\delta }$
,
$\eta <{\delta }$
,
 ${\mathcal R}_x|\eta $
is
${\mathcal R}_x|\eta $
is
 $\eta +1$
-iterable in
$\eta +1$
-iterable in
 ${\mathcal R}_x$
(see clause 11 of Review 2.7).
${\mathcal R}_x$
(see clause 11 of Review 2.7).
It follows from clause 1, 3 and 11 of Review 2.7 that if x codes
![]() ${\mathcal {M}}_{2n+1}^\#(u)$
then
${\mathcal {M}}_{2n+1}^\#(u)$
then
![]() $x\in \mathsf {{C}}$
.
$x\in \mathsf {{C}}$
.
We now work towards applying Hjorth’s reflection argument to produce a code of each
![]() $A_{\gamma} $
below
$A_{\gamma} $
below
![]() ${\kappa }_{\mathcal {M}}$
. Let
${\kappa }_{\mathcal {M}}$
. Let
![]() $w\subseteq \omega $
be a
$w\subseteq \omega $
be a
![]() $\Pi ^1_{2n+3}(z)$
real that is not
$\Pi ^1_{2n+3}(z)$
real that is not
![]() $\Sigma ^1_{2n+3}(z)$
. Let
$\Sigma ^1_{2n+3}(z)$
. Let
![]() $\psi $
be a
$\psi $
be a
![]() $\Sigma ^1_{2n+2}$
formula such that
$\Sigma ^1_{2n+2}$
formula such that
4.1 The main ideas of the proof
Before we go on, we give an outline of the proof that follows. The main idea of the proof is that each
![]() $A_{\alpha }=U_{w_0}$
for some
$A_{\alpha }=U_{w_0}$
for some
![]() $w_0$
that can be obtained ‘below
$w_0$
that can be obtained ‘below
![]() ${\kappa }_{\mathcal {M}}$
’. We say
${\kappa }_{\mathcal {M}}$
’. We say
![]() $w_0$
is a U code for
$w_0$
is a U code for
![]() $A_{\alpha }$
. This means that for each
$A_{\alpha }$
. This means that for each
![]() ${\alpha }<{\delta }^1_{2n+2}$
we would like to find some complete iterate
${\alpha }<{\delta }^1_{2n+2}$
we would like to find some complete iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
,
${\mathcal {M}}$
,
![]() $\xi <{\kappa }_{\mathcal {N}}$
and a
$\xi <{\kappa }_{\mathcal {N}}$
and a
![]() $g\subseteq Coll(\omega , \xi )$
such that there is a U-code for
$g\subseteq Coll(\omega , \xi )$
such that there is a U-code for
![]() $A_{\alpha }$
in
$A_{\alpha }$
in
![]() ${\mathcal {N}}[g]$
.
${\mathcal {N}}[g]$
.
Notice that, using genericity iterations, for each
![]() ${\alpha }<{\delta }^1_{2n+2}$
, we can find a complete iterate
${\alpha }<{\delta }^1_{2n+2}$
, we can find a complete iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() $A_{\alpha }$
has a U-code that is
$A_{\alpha }$
has a U-code that is
![]() ${\mathcal {N}}$
-generic for the extender algebra at
${\mathcal {N}}$
-generic for the extender algebra at
![]() ${\delta }_{\mathcal {N}}$
. Because
${\delta }_{\mathcal {N}}$
. Because
![]() ${\mathcal {N}}\models \mathsf {{Cond}}$
, this allows us to obtain a
${\mathcal {N}}\models \mathsf {{Cond}}$
, this allows us to obtain a
![]() $\xi <{\kappa }_{\mathcal {N}}$
such that
$\xi <{\kappa }_{\mathcal {N}}$
such that
![]() $A_{\alpha }$
has a U-code that is generic over the extender algebra of
$A_{\alpha }$
has a U-code that is generic over the extender algebra of
![]() ${\mathcal {N}}|\xi $
. To make this work, we need to make sure that the U-code of
${\mathcal {N}}|\xi $
. To make this work, we need to make sure that the U-code of
![]() $A_{\alpha }$
can be identified in a first order way over
$A_{\alpha }$
can be identified in a first order way over
![]() ${\mathcal {N}}$
, and this is achieved by the formula
${\mathcal {N}}$
, and this is achieved by the formula
![]() $\theta _0$
introduced below.
$\theta _0$
introduced below.
However, the above is not enough. We need to find
![]() ${\mathcal {N}}$
as above which is
${\mathcal {N}}$
as above which is
![]() ${\alpha }$
-stable in the sense that for any complete iterate
${\alpha }$
-stable in the sense that for any complete iterate
![]() ${\mathcal { Q}}$
of
${\mathcal { Q}}$
of
![]() ${\mathcal {N}}$
there is such a
${\mathcal {N}}$
there is such a
![]() $w_0$
in
$w_0$
in
![]() ${\mathcal { Q}}^{Coll(\omega , \pi _{{\mathcal {N}}, {\mathcal { Q}}}(\xi ))}$
. Such a uniformity is not easy to achieve, and here, we use our reals w and
${\mathcal { Q}}^{Coll(\omega , \pi _{{\mathcal {N}}, {\mathcal { Q}}}(\xi ))}$
. Such a uniformity is not easy to achieve, and here, we use our reals w and
![]() $w'$
introduced below. w is a
$w'$
introduced below. w is a
![]() $\Pi ^1_{2n+3}(z)$
real which is not
$\Pi ^1_{2n+3}(z)$
real which is not
![]() $\Sigma ^1_{2n+3}(z)$
while
$\Sigma ^1_{2n+3}(z)$
while
![]() $w'$
is a
$w'$
is a
![]() $\Sigma ^1_{2n+3}(z)$
subset of w.
$\Sigma ^1_{2n+3}(z)$
subset of w.
The
![]() $\Pi ^1_{2n+2}(z)$
-formula
$\Pi ^1_{2n+2}(z)$
-formula
![]() $\theta $
is the key.
$\theta $
is the key.
![]() $w'$
is the real defined by
$w'$
is the real defined by
![]() $\exists \vec {y}\theta (x, \vec {y})$
. The formulas are defined in a way that assures the following. If
$\exists \vec {y}\theta (x, \vec {y})$
. The formulas are defined in a way that assures the following. If
![]() $k\in w'$
then the least initial segment of
$k\in w'$
then the least initial segment of
![]() ${\mathcal {M}}$
that ‘proves’ that
${\mathcal {M}}$
that ‘proves’ that
![]() $k\in w$
is below the least initial segment of
$k\in w$
is below the least initial segment of
![]() ${\mathcal {M}}$
that has a U-code for
${\mathcal {M}}$
that has a U-code for
![]() $A_{\alpha }$
. Thus, if
$A_{\alpha }$
. Thus, if
![]() $k\in w-w'$
then for any
$k\in w-w'$
then for any
![]() ${\alpha }$
(roughly speaking), the least initial segment of
${\alpha }$
(roughly speaking), the least initial segment of
![]() ${\mathcal {M}}$
that has a U-code for
${\mathcal {M}}$
that has a U-code for
![]() $A_{\alpha }$
is below the least initial segment that proves that
$A_{\alpha }$
is below the least initial segment that proves that
![]() $k\in w$
. This means that if we pick
$k\in w$
. This means that if we pick
![]() $\zeta $
to be the least such that
$\zeta $
to be the least such that
![]() ${\mathcal {M}}|\zeta $
proves that
${\mathcal {M}}|\zeta $
proves that
![]() $k\in w$
then each
$k\in w$
then each
![]() $A_{\alpha }$
will have a U-code below
$A_{\alpha }$
will have a U-code below
![]() $\zeta $
.
$\zeta $
.
Above by ‘the least initial segment of
![]() ${\mathcal {M}}$
that proves
${\mathcal {M}}$
that proves
![]() $k\in w$
’ we mean that the formula
$k\in w$
’ we mean that the formula
![]() $`k\in w$
’ is first order over
$`k\in w$
’ is first order over
![]() ${\mathcal {M}}$
as explained in Proposition 2.6, and therefore, because
${\mathcal {M}}$
as explained in Proposition 2.6, and therefore, because
![]() ${\mathcal {M}}\models \mathsf {{Cond}}$
, we have some
${\mathcal {M}}\models \mathsf {{Cond}}$
, we have some
![]() $\xi <{\kappa }_{\mathcal {M}}$
such that
$\xi <{\kappa }_{\mathcal {M}}$
such that
![]() $`k\in w$
’ is first order over
$`k\in w$
’ is first order over
![]() ${\mathcal {M}}|\xi $
. The least such
${\mathcal {M}}|\xi $
. The least such
![]() $\xi $
, which we call
$\xi $
, which we call
![]() $\zeta $
, determines the least level of
$\zeta $
, determines the least level of
![]() ${\mathcal {M}}$
that proves that
${\mathcal {M}}$
that proves that
![]() $k\in w$
.
$k\in w$
.
Because of
![]() $\mathsf {{Cond}}$
, we can assume that
$\mathsf {{Cond}}$
, we can assume that
![]() $\zeta $
is a cutpoint of
$\zeta $
is a cutpoint of
![]() ${\mathcal {M}}$
. We then finish the proof by showing that if
${\mathcal {M}}$
. We then finish the proof by showing that if
![]() ${\mathcal { Q}}={\mathcal {M}}|\zeta $
then (roughly) each
${\mathcal { Q}}={\mathcal {M}}|\zeta $
then (roughly) each
![]() $A_{\alpha }$
has a U-code in a generic extension of a complete iterate of
$A_{\alpha }$
has a U-code in a generic extension of a complete iterate of
![]() ${\mathcal { Q}}$
. But the set of complete iterates of
${\mathcal { Q}}$
. But the set of complete iterates of
![]() ${\mathcal { Q}}$
is too simple (this follows from calculations presented in Lemma 4.5), and one could not define
${\mathcal { Q}}$
is too simple (this follows from calculations presented in Lemma 4.5), and one could not define
![]() ${\delta }^1_{2n+2}$
many distinct
${\delta }^1_{2n+2}$
many distinct
![]() $\boldsymbol {\Sigma }^1_{2n+2}$
sets whose U-codes can be obtained in generic extensions of complete iterates of
$\boldsymbol {\Sigma }^1_{2n+2}$
sets whose U-codes can be obtained in generic extensions of complete iterates of
![]() ${\mathcal { Q}}$
. This then gives a contradiction as
${\mathcal { Q}}$
. This then gives a contradiction as
![]() $(A_{\alpha }: {\alpha }<{\delta }^1_{2n+2})$
consists of distinct
$(A_{\alpha }: {\alpha }<{\delta }^1_{2n+2})$
consists of distinct
![]() $\boldsymbol {\Sigma }^1_{2n+2}$
sets whose U-codes can be obtained in generic extensions of complete iterates of
$\boldsymbol {\Sigma }^1_{2n+2}$
sets whose U-codes can be obtained in generic extensions of complete iterates of
![]() ${\mathcal { Q}}$
.
${\mathcal { Q}}$
.
4.2 The formula
 $\theta $
$\theta $
We will need the following lemma. Recall that U is our fixed universal
![]() $\Sigma ^1_{2n+2}$
set.
$\Sigma ^1_{2n+2}$
set.
Lemma 4.1. Suppose
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() ${\mathcal {M}}_{2n+1}^\#$
-like
${\mathcal {M}}_{2n+1}^\#$
-like
![]() $\Pi ^1_{2n+2}$
-iterable z-premouse,
$\Pi ^1_{2n+2}$
-iterable z-premouse,
![]() $(\nu _0, \nu _1,..., \nu _{2n})$
are the Woodin cardinals of
$(\nu _0, \nu _1,..., \nu _{2n})$
are the Woodin cardinals of
![]() ${\mathcal {N}}$
enumerated in increasing order,
${\mathcal {N}}$
enumerated in increasing order,
![]() $\mathcal {E}$
is a weakly appropriate set of extenders (relative to
$\mathcal {E}$
is a weakly appropriate set of extenders (relative to
![]() $\nu _0$
),
$\nu _0$
),
![]() $\nu <\nu _0$
and suppose
$\nu <\nu _0$
and suppose
![]() $(w_0,( w_1, w_2, w_3))$
is a sequence of reals such that
$(w_0,( w_1, w_2, w_3))$
is a sequence of reals such that
-
1.
 $D(w_1, w_2, w_3)$
and
$D(w_1, w_2, w_3)$
and
 $U(w_2, w_0)$
,
$U(w_2, w_0)$
, -
2.
 $w_0$
and
$w_0$
and
 $(w_1, w_2, w_3)$
are generic over
$(w_1, w_2, w_3)$
are generic over
 ${\mathcal {N}}$
for
${\mathcal {N}}$
for
 $\mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
.
$\mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
.
There is then a condition
![]() $(p, q)\in \mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
such that
$(p, q)\in \mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
such that
-
1.
 $w_0\models p$
and
$w_0\models p$
and
 $(w_1, w_2, w_3)\models q$
,
$(w_1, w_2, w_3)\models q$
, -
2.
 ${\mathcal {N}}\models (p, q)\Vdash `D(\mathsf {{ea}}^r_1, \mathsf {{ea}}^r_2, \mathsf {{ea}}^r_3) \wedge U( \mathsf {{ea}}^r_2, \mathsf {{ea}}^l)$
’.
${\mathcal {N}}\models (p, q)\Vdash `D(\mathsf {{ea}}^r_1, \mathsf {{ea}}^r_2, \mathsf {{ea}}^r_3) \wedge U( \mathsf {{ea}}^r_2, \mathsf {{ea}}^l)$
’.
Proof. First of all, notice that
![]() ${\mathcal {N}}={\mathcal {M}}_{2n}^\#({\mathcal {N}}|\nu _0)$
(see clause 11 of Section 3). Suppose
${\mathcal {N}}={\mathcal {M}}_{2n}^\#({\mathcal {N}}|\nu _0)$
(see clause 11 of Section 3). Suppose
![]() $w_1$
codes a pair
$w_1$
codes a pair
![]() $({\mathcal R}, \xi )$
. Working in
$({\mathcal R}, \xi )$
. Working in
![]() ${\mathcal {N}}[w_1, w_2, w_3]$
, let
${\mathcal {N}}[w_1, w_2, w_3]$
, let
![]() ${\gamma} =\pi _{{\mathcal R}, {\mathcal { H}}^{\mathcal {N}}}(\xi )$
. We then have that there is a condition
${\gamma} =\pi _{{\mathcal R}, {\mathcal { H}}^{\mathcal {N}}}(\xi )$
. We then have that there is a condition
![]() $q_0\in \mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
such that
$q_0\in \mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
such that
![]() $(w_1, w_2, w_3)\models q_0$
and
$(w_1, w_2, w_3)\models q_0$
and
![]() $q_0\Vdash `$
if
$q_0\Vdash `$
if
![]() $({\mathcal {S}}, {\beta })$
is the pair coded by
$({\mathcal {S}}, {\beta })$
is the pair coded by
![]() $\mathsf {ea}_1$
then
$\mathsf {ea}_1$
then
![]() $\pi _{{\mathcal {S}}, {\mathcal { H}}}({\beta })=\check {{\gamma} }$
’Footnote
53
and also,
$\pi _{{\mathcal {S}}, {\mathcal { H}}}({\beta })=\check {{\gamma} }$
’Footnote
53
and also,
![]() $q_0\Vdash D(\mathsf {{ea}}_1, \mathsf {{ea}}_2, \mathsf {{ea}}_3)$
. Let now
$q_0\Vdash D(\mathsf {{ea}}_1, \mathsf {{ea}}_2, \mathsf {{ea}}_3)$
. Let now
![]() $(g_1, g_2, g_3)$
be
$(g_1, g_2, g_3)$
be
![]() ${\mathcal {N}}[w_0]$
-generic for
${\mathcal {N}}[w_0]$
-generic for
![]() $\mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
such that
$\mathsf {{Ea}}^{\mathcal {N}}_{\nu _0, \nu , \mathcal {E}}$
such that
![]() $(g_1, g_2, g_3)\models q_0$
. Because
$(g_1, g_2, g_3)\models q_0$
. Because
![]() ${\mathcal {N}}={\mathcal {M}}_{2n}^\#({\mathcal {N}}|\nu _0)$
(implying that
${\mathcal {N}}={\mathcal {M}}_{2n}^\#({\mathcal {N}}|\nu _0)$
(implying that
![]() ${\mathcal {N}}$
is
${\mathcal {N}}$
is
![]() $\Sigma ^1_{2n+2}$
-correct), it follows that
$\Sigma ^1_{2n+2}$
-correct), it follows that
![]() $g_1\in \mathsf {{Code}}$
and that
$g_1\in \mathsf {{Code}}$
and that
![]() $w_0\in A_{{\gamma} _{g_1}}$
,Footnote
54
,Footnote
55
. Then we must have that
$w_0\in A_{{\gamma} _{g_1}}$
,Footnote
54
,Footnote
55
. Then we must have that
![]() ${\mathcal {N}}[w_0][(g_1, g_2, g_3)]\models U(g_2, w_0)$
. The desired
${\mathcal {N}}[w_0][(g_1, g_2, g_3)]\models U(g_2, w_0)$
. The desired
![]() $(p, q)$
can now be found using the forcing theorem.
$(p, q)$
can now be found using the forcing theorem.
The formula
![]() $\theta _0$
:
$\theta _0$
:
Let
![]() $\theta _0(u, w_0, w_1, w_2, w_3)$
be the
$\theta _0(u, w_0, w_1, w_2, w_3)$
be the
![]() $\Pi ^{1}_{2n+2}(z)$
-formula that is the conjunction of the following clauses:
$\Pi ^{1}_{2n+2}(z)$
-formula that is the conjunction of the following clauses:
-
1.
 $D(w_1, w_2, w_3)$
Footnote
56
,
$D(w_1, w_2, w_3)$
Footnote
56
, -
2.
 $u\in \mathsf {{C}}$
and
$u\in \mathsf {{C}}$
and
 ${\mathcal R}_u$
is
${\mathcal R}_u$
is
 $\Pi ^1_{2n+2}$
-iterable,
$\Pi ^1_{2n+2}$
-iterable, -
3.
 $(z, w_0, w_1, w_2, w_3)\in {\mathcal R}_u\cap {\mathbb {R}}^5$
,
$(z, w_0, w_1, w_2, w_3)\in {\mathcal R}_u\cap {\mathbb {R}}^5$
, -
4.
 $R_u\models U(w_2, w_0)$
.
$R_u\models U(w_2, w_0)$
.
At this point the reader may find it useful to review Proposition 3.1, clause 3 and 6 of Review 2.3, and clause 2 of Review 2.7.
Let
![]() $U'$
be a
$U'$
be a
![]() $\Pi ^1_{2n+1}$
set such that
$\Pi ^1_{2n+1}$
set such that
![]() $U(\vec {a}){\mathrel {\leftrightarrow }} \exists b U'(b,\vec {a})$
.
$U(\vec {a}){\mathrel {\leftrightarrow }} \exists b U'(b,\vec {a})$
.
Suppose now that
![]() $\theta _0(u, w_0, w_1, w_2, w_3)$
holds. Let
$\theta _0(u, w_0, w_1, w_2, w_3)$
holds. Let
![]() ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}_u, z)$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}_u, z)$
and
![]() $\mathcal {E}=\mathcal {E}_{sm}^{\mathcal { K}}$
(see Definition 2.13). It follows from Lemma 4.1 that there is a condition
$\mathcal {E}=\mathcal {E}_{sm}^{\mathcal { K}}$
(see Definition 2.13). It follows from Lemma 4.1 that there is a condition
![]() $(p, q)\in \mathsf {{Ea}}^{\mathcal { K}}_{\nu _u, \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal { K}}_{\nu _u, \mathcal {E}}$
such that
$(p, q)\in \mathsf {{Ea}}^{\mathcal { K}}_{\nu _u, \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal { K}}_{\nu _u, \mathcal {E}}$
such that
-
1.
 $w_0\models p$
,
$w_0\models p$
, -
2.
 $(w_1, w_2, w_3)\models q$
, and
$(w_1, w_2, w_3)\models q$
, and -
3.
 $(p, q)\Vdash \exists b( U^{\prime }_{{\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)], d}(b, \mathsf {{ea}}^r_2, \mathsf {{ea}}^l))$
where letting
$(p, q)\Vdash \exists b( U^{\prime }_{{\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)], d}(b, \mathsf {{ea}}^r_2, \mathsf {{ea}}^l))$
where letting
 $(\nu _u, \xi _1, ..., \xi _{2n})$
be the Woodin cardinals of
$(\nu _u, \xi _1, ..., \xi _{2n})$
be the Woodin cardinals of
 ${\mathcal { K}}$
enumerated in increasing order,
${\mathcal { K}}$
enumerated in increasing order,
 $d=(\xi _1, \xi _2,..., \xi _{2n})$
.Footnote
57
$d=(\xi _1, \xi _2,..., \xi _{2n})$
.Footnote
57
Clause 3 above is a consequence of Proposition 3.1 and the fact that because
![]() ${\mathcal R}_u$
is
${\mathcal R}_u$
is
![]() $\Pi ^1_{2n+2}$
-iterable, it is
$\Pi ^1_{2n+2}$
-iterable, it is
![]() $\omega _1+1$
-iterable above
$\omega _1+1$
-iterable above
![]() $\nu _u$
(see clause 11 of Section 3 and recall that under
$\nu _u$
(see clause 11 of Section 3 and recall that under
![]() $\mathsf {AD}$
,
$\mathsf {AD}$
,
![]() $\omega _1$
-iterability implies
$\omega _1$
-iterability implies
![]() $\omega _1+1$
-iterability). Notice that to verify
$\omega _1+1$
-iterability). Notice that to verify
![]() $U'$
we skip the extender algebra
$U'$
we skip the extender algebra
![]() $\mathsf {{Ea}}^{\mathcal { K}}_{\xi _1, \nu _u}$
. However,
$\mathsf {{Ea}}^{\mathcal { K}}_{\xi _1, \nu _u}$
. However,
![]() $\xi _1$
is not a lazy Woodin cardinal, it has a noble role of making sure that the witness b can be found inside
$\xi _1$
is not a lazy Woodin cardinal, it has a noble role of making sure that the witness b can be found inside
![]() ${\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)]$
. The fact that we have skipped
${\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)]$
. The fact that we have skipped
![]() $\xi _1$
will be used in the proof of Lemma 4.2.
$\xi _1$
will be used in the proof of Lemma 4.2.
Because
![]() ${\mathcal R}_u\models \mathsf {{Cond}}$
, we have that if
${\mathcal R}_u\models \mathsf {{Cond}}$
, we have that if
![]() $\theta _0(u, w_0, w_1, w_2, w_3)$
holds then in fact there are
$\theta _0(u, w_0, w_1, w_2, w_3)$
holds then in fact there are
![]() ${\alpha }<{\beta }<\nu _u$
such that
${\alpha }<{\beta }<\nu _u$
such that
-
1.
 ${\mathcal R}_u|{\beta }\models \mathsf {{ZFC}}+`$
there are
${\mathcal R}_u|{\beta }\models \mathsf {{ZFC}}+`$
there are
 $2n+1$
many Woodin cardinals’,
$2n+1$
many Woodin cardinals’, -
2.
 ${\mathcal R}_u|{\beta }\models `{\alpha }$
is the least Woodin cardinal’,
${\mathcal R}_u|{\beta }\models `{\alpha }$
is the least Woodin cardinal’, -
3.
 ${\alpha }$
is an
${\alpha }$
is an
 $fb$
-cut of
$fb$
-cut of
 ${\mathcal R}_u$
(see Definition 2.9, in particular,
${\mathcal R}_u$
(see Definition 2.9, in particular,
 ${\alpha }$
is an
${\alpha }$
is an
 ${\mathcal R}_u$
-cardinal),
${\mathcal R}_u$
-cardinal), -
4. setting
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}_u|{\beta }, z)$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}_u|{\beta }, z)$
and
 $\mathcal {E}=\mathcal {E}^{\mathcal { K}}_{sm}$
, there is a condition
$\mathcal {E}=\mathcal {E}^{\mathcal { K}}_{sm}$
, there is a condition
 $(p, q)\in \mathsf {{Ea}}^{\mathcal { K}}_{{\alpha }, \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal { K}}_{{\alpha }, \mathcal {E}}$
such that
$(p, q)\in \mathsf {{Ea}}^{\mathcal { K}}_{{\alpha }, \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal { K}}_{{\alpha }, \mathcal {E}}$
such that-
(a)
 $w_0\models p$
,
$w_0\models p$
, -
(b)
 $(w_1, w_2, w_3)\models q$
, and
$(w_1, w_2, w_3)\models q$
, and -
(c)
 $(p, q)\Vdash \exists b(U^{\prime }_{{\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l))$
where letting
$(p, q)\Vdash \exists b(U^{\prime }_{{\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l))$
where letting
 $({\alpha }, \xi _1, ..., \xi _{2n})$
be the Woodin cardinals of
$({\alpha }, \xi _1, ..., \xi _{2n})$
be the Woodin cardinals of
 ${\mathcal { K}}$
enumerated in increasing order,
${\mathcal { K}}$
enumerated in increasing order,
 $d=(\xi _1, \xi _2,..., \xi _{2n})$
.
$d=(\xi _1, \xi _2,..., \xi _{2n})$
.
-
If
![]() $s=(u, w_0, w_1, w_2, w_3)$
then we say that
$s=(u, w_0, w_1, w_2, w_3)$
then we say that
![]() $({\alpha }, {\beta })$
witnesses
$({\alpha }, {\beta })$
witnesses
![]() $\theta _0$
-reflection for s if
$\theta _0$
-reflection for s if
![]() $({\alpha }, {\beta })$
satisfies clause 1-4 above. Assuming
$({\alpha }, {\beta })$
satisfies clause 1-4 above. Assuming
![]() $\theta _0(u, w_0, w_1, w_2, w_3)$
holds with
$\theta _0(u, w_0, w_1, w_2, w_3)$
holds with
![]() $s=(u, w_0, w_1, w_2, w_3)$
, we let
$s=(u, w_0, w_1, w_2, w_3)$
, we let
![]() $({\alpha }_s, {\beta }_s)$
be the lexicographically least witnessing
$({\alpha }_s, {\beta }_s)$
be the lexicographically least witnessing
![]() $\theta _0$
-reflection for s. Because
$\theta _0$
-reflection for s. Because
![]() ${\mathcal R}_u\models \mathsf {{Cond}}$
we have that
${\mathcal R}_u\models \mathsf {{Cond}}$
we have that
![]() $({\alpha }_s, {\beta }_s)\in \mu _u^2$
. Notice that
$({\alpha }_s, {\beta }_s)\in \mu _u^2$
. Notice that
![]() $({\alpha }_s, {\beta }_s)$
is definable from
$({\alpha }_s, {\beta }_s)$
is definable from
![]() $(z, w_0, w_1, w_2, w_3)$
over
$(z, w_0, w_1, w_2, w_3)$
over
![]() ${\mathcal R}_u$
in the sense that there is a formula
${\mathcal R}_u$
in the sense that there is a formula
![]() $\theta '$
such that
$\theta '$
such that
![]() $({\alpha }_s, {\beta }_s)$
is the unique pair
$({\alpha }_s, {\beta }_s)$
is the unique pair
![]() $({\alpha }, {\beta })$
such that
$({\alpha }, {\beta })$
such that
The formula
![]() $\theta $
:
$\theta $
:
Let
![]() $\psi '$
be a
$\psi '$
be a
![]() $\Pi ^1_{2n+1}$
such that
$\Pi ^1_{2n+1}$
such that
![]() $\psi (...){\mathrel {\leftrightarrow }} \exists v\psi '(..., v)$
(
$\psi (...){\mathrel {\leftrightarrow }} \exists v\psi '(..., v)$
(
![]() $\psi $
is the formula used to define w, see just before Section 4.2). Let
$\psi $
is the formula used to define w, see just before Section 4.2). Let
![]() $\theta (k, u, w_0, w_1, w_2, w_3)$
be the
$\theta (k, u, w_0, w_1, w_2, w_3)$
be the
![]() $\Pi ^1_{2n+2}(z)$
-formula that is the conjunction of the following clauses:
$\Pi ^1_{2n+2}(z)$
-formula that is the conjunction of the following clauses:
-
1.
 $k\in \omega $
,
$k\in \omega $
, -
2.
 $\theta _0(u, w_0, w_1, w_2, w_3)$
,
$\theta _0(u, w_0, w_1, w_2, w_3)$
, -
3. letting
 $s=(u, w_0, w_1, w_2, w_3)$
, in
$s=(u, w_0, w_1, w_2, w_3)$
, in
 ${\mathcal R}_u$
,Footnote
58
there are ordinals
${\mathcal R}_u$
,Footnote
58
there are ordinals
 ${\alpha }'<{\beta }'<{\alpha }_s$
such that
${\alpha }'<{\beta }'<{\alpha }_s$
such that-
(a)
 ${\mathcal R}_u|{\beta }'\models "\mathsf {{ZFC}}+`$
there are
${\mathcal R}_u|{\beta }'\models "\mathsf {{ZFC}}+`$
there are
 $2n+1$
many Woodin cardinals’ +
$2n+1$
many Woodin cardinals’ +
 $`{\alpha }'$
is the least Woodin cardinal’,
$`{\alpha }'$
is the least Woodin cardinal’, -
(b)
 ${\alpha }'$
is an
${\alpha }'$
is an
 $fb$
-cut in
$fb$
-cut in
 ${\mathcal R}_u|{\alpha }_s$
(and hence, in
${\mathcal R}_u|{\alpha }_s$
(and hence, in
 ${\mathcal R}_u$
), and
${\mathcal R}_u$
), andsetting
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}_u|{\beta }')$
,
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}_u|{\beta }')$
,
 $\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
$\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
 $i\in [1, 2n]$
, letting
$i\in [1, 2n]$
, letting
 $\xi _i$
be the
$\xi _i$
be the
 $i+1$
st Woodin cardinal of
$i+1$
st Woodin cardinal of
 ${\mathcal { K}}$
and
${\mathcal { K}}$
and
 $d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:
$d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds: -
(c) If
 $p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
$p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
 ${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal { K}}[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal { K}}[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
-
4.3 The real
 $w'$
$w'$
Set
Clearly
![]() $w'$
is
$w'$
is
![]() $\Sigma ^1_{2n+3}(z)$
. The proof of the next lemma is similar to the proof of Claim 2 that appears in the proof of [Reference Hjorth7, Theorem 3.3].
$\Sigma ^1_{2n+3}(z)$
. The proof of the next lemma is similar to the proof of Claim 2 that appears in the proof of [Reference Hjorth7, Theorem 3.3].
Lemma 4.2.
![]() $w'\subseteq w$
.
$w'\subseteq w$
.
Proof. Suppose
![]() $k\in w'$
. Let
$k\in w'$
. Let
![]() $\Sigma $
be a winning strategy for
$\Sigma $
be a winning strategy for
![]() $II$
in
$II$
in
![]() $\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
. We want to argue that
$\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
. We want to argue that
![]() $k\in w$
. Fix
$k\in w$
. Fix
![]() $s=(u, w_0, w_1, w_2, w_3)$
such that
$s=(u, w_0, w_1, w_2, w_3)$
such that
![]() $\theta [k,u, z, w_0, w_1, w_2, w_3]$
holds. We want to show that for each
$\theta [k,u, z, w_0, w_1, w_2, w_3]$
holds. We want to show that for each
![]() $z'$
,
$z'$
,
![]() $\psi [k, z, z']$
holds. Fix then such a
$\psi [k, z, z']$
holds. Fix then such a
![]() $z'$
.
$z'$
.
We have that
![]() ${\mathcal R}_u$
is a properly
${\mathcal R}_u$
is a properly
![]() $2n+1$
-small
$2n+1$
-small
![]() $\Pi ^1_{2n+2}$
-iterable premouse such that
$\Pi ^1_{2n+2}$
-iterable premouse such that
![]() $(z, w_0, w_1, w_2, w_3)\in {\mathcal R}_u\cap {\mathbb {R}}^5$
. We now want to use
$(z, w_0, w_1, w_2, w_3)\in {\mathcal R}_u\cap {\mathbb {R}}^5$
. We now want to use
![]() $\Pi ^1_{2n+2}$
-iterability of
$\Pi ^1_{2n+2}$
-iterability of
![]() ${\mathcal R}_u$
to make
${\mathcal R}_u$
to make
![]() $z'$
generic over the image of
$z'$
generic over the image of
![]() $\mathsf {{Ea}}^{{\mathcal R}_u}_{\nu _u, \mathcal {E}^{{\mathcal R}_u}_{le}}$
Footnote
59
. We iterate
$\mathsf {{Ea}}^{{\mathcal R}_u}_{\nu _u, \mathcal {E}^{{\mathcal R}_u}_{le}}$
Footnote
59
. We iterate
![]() ${\mathcal R}_u$
producing iteration
${\mathcal R}_u$
producing iteration
![]() ${\mathcal {T}}$
of
${\mathcal {T}}$
of
![]() ${\mathcal R}_u$
by using the rules of
${\mathcal R}_u$
by using the rules of
![]() $(z', \nu _u, 0)$
-genericity iteration to pick extenders (see clause 2 of Review 2.3) and by picking branches so that the iteration stays correct. More precisely, if
$(z', \nu _u, 0)$
-genericity iteration to pick extenders (see clause 2 of Review 2.3) and by picking branches so that the iteration stays correct. More precisely, if
![]() ${\gamma} <\mathrm {lh}({\mathcal {T}})$
and
${\gamma} <\mathrm {lh}({\mathcal {T}})$
and
![]() $c=[0, {\gamma} )_{{\mathcal {T}}}$
then
$c=[0, {\gamma} )_{{\mathcal {T}}}$
then
![]() ${\mathcal { Q}}(c, {\mathcal {T}}\restriction {\gamma} )$
exists and
${\mathcal { Q}}(c, {\mathcal {T}}\restriction {\gamma} )$
exists and
![]() ${\mathcal { Q}}(c, {\mathcal {T}}\restriction {\gamma} )\trianglelefteq {\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}\restriction {\gamma} ))$
. Thus the resulting iteration
${\mathcal { Q}}(c, {\mathcal {T}}\restriction {\gamma} )\trianglelefteq {\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}\restriction {\gamma} ))$
. Thus the resulting iteration
![]() ${\mathcal {T}}$
of
${\mathcal {T}}$
of
![]() ${\mathcal R}_u$
is correct, has no drops and is below
${\mathcal R}_u$
is correct, has no drops and is below
![]() $\nu _u$
Footnote
60
. There are two possibilities: either
$\nu _u$
Footnote
60
. There are two possibilities: either
(Pos1)
![]() ${\mathcal {T}}$
has a last model
${\mathcal {T}}$
has a last model
![]() ${\mathcal R}'$
and
${\mathcal R}'$
and
![]() $z'$
is generic over
$z'$
is generic over
![]() ${\mathcal R}'$
for
${\mathcal R}'$
for
![]() $\mathsf {{Ea}}^{{\mathcal R}'}_{\mu , \mathcal {E}^{{\mathcal R}'}_{le}}$
where
$\mathsf {{Ea}}^{{\mathcal R}'}_{\mu , \mathcal {E}^{{\mathcal R}'}_{le}}$
where
![]() $\mu =\pi ^{{\mathcal {T}}}(\nu _u)$
or
$\mu =\pi ^{{\mathcal {T}}}(\nu _u)$
or
(Pos2)
![]() ${\mathcal {T}}$
does not have a last model and
${\mathcal {T}}$
does not have a last model and
![]() $\mathrm {lh}({\mathcal {T}})$
is a limit ordinal.
$\mathrm {lh}({\mathcal {T}})$
is a limit ordinal.
Sublemma 4.3. There is
![]() $\xi <\mathrm {lh}({\mathcal {T}})$
and
$\xi <\mathrm {lh}({\mathcal {T}})$
and
![]() ${\alpha }'<{\beta }'$
such that the following conditions hold:
${\alpha }'<{\beta }'$
such that the following conditions hold:
-
1. The generators of
 ${\mathcal {T}}\restriction \xi $
are contained in
${\mathcal {T}}\restriction \xi $
are contained in
 ${\alpha }'$
.
${\alpha }'$
. -
2.
 ${\mathcal {M}}^{\mathcal {T}}_\xi |{\beta }'\models \mathsf {{ZFC}}+`$
there are
${\mathcal {M}}^{\mathcal {T}}_\xi |{\beta }'\models \mathsf {{ZFC}}+`$
there are
 $2n+1$
many Woodin cardinals’ +
$2n+1$
many Woodin cardinals’ +
 $`{\alpha }'$
is the least Woodin cardinal’.
$`{\alpha }'$
is the least Woodin cardinal’. -
3. Setting
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {M}}^{\mathcal {T}}_\xi |{\beta }')$
,
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {M}}^{\mathcal {T}}_\xi |{\beta }')$
,
 $\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
$\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
 $i\in [1, 2n]$
, letting
$i\in [1, 2n]$
, letting
 $\xi _i$
be the
$\xi _i$
be the
 $i+1$
st Woodin cardinal of
$i+1$
st Woodin cardinal of
 ${\mathcal { K}}$
and
${\mathcal { K}}$
and
 $d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:
$d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:-
(a) If
 $p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
$p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
 ${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal R}_u[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal R}_u[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
. -
(b)
 $z'$
satisfies all the axioms of
$z'$
satisfies all the axioms of
 $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
. -
(c) If player I plays
 $({\mathcal {T}}\restriction \xi +1, y)$
where
$({\mathcal {T}}\restriction \xi +1, y)$
where
 $y\in {\mathbb {R}}$
is any real coding
$y\in {\mathbb {R}}$
is any real coding
 ${\mathcal {T}}\restriction \xi +1$
then
${\mathcal {T}}\restriction \xi +1$
then
 $\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
and the iterations of
$\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
and the iterations of
 ${\mathcal { K}}[z']$
that are above
${\mathcal { K}}[z']$
that are above
 ${\alpha }'$
are legal moves for player I in the second round of
${\alpha }'$
are legal moves for player I in the second round of
 $\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
.
$\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
.
-
Proof.
Suppose first that (Pos1) holds. Set
![]() $({\alpha }, {\beta })=\pi ^{\mathcal {T}}({\alpha }_s, {\beta }_s)$
. We have that
$({\alpha }, {\beta })=\pi ^{\mathcal {T}}({\alpha }_s, {\beta }_s)$
. We have that
![]() ${\alpha }<{\beta }<\mu $
and
${\alpha }<{\beta }<\mu $
and
![]() ${\alpha }$
is an
${\alpha }$
is an
![]() $fb$
-cut in
$fb$
-cut in
![]() ${\mathcal R}'$
. Because
${\mathcal R}'$
. Because
![]() $k\in w'$
we have
$k\in w'$
we have
![]() ${\alpha }'<{\beta }'<{\alpha }$
such that
${\alpha }'<{\beta }'<{\alpha }$
such that
(A1)
![]() ${\mathcal R}'|{\beta }'\models \mathsf {{ZFC}}+`$
there are
${\mathcal R}'|{\beta }'\models \mathsf {{ZFC}}+`$
there are
![]() $2n+1$
many Woodin cardinals’ +
$2n+1$
many Woodin cardinals’ +
![]() $`{\alpha }'$
is the least Woodin cardinal’,
$`{\alpha }'$
is the least Woodin cardinal’,
(B1)
![]() ${\alpha }'$
is an
${\alpha }'$
is an
![]() $fb$
-cut in
$fb$
-cut in
![]() ${\mathcal R}'$
, and
${\mathcal R}'$
, and
setting
![]() ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}'|{\beta }')$
,
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal R}'|{\beta }')$
,
![]() $\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
$\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
![]() $i\in [1, 2n]$
, letting
$i\in [1, 2n]$
, letting
![]() $\xi _i$
be the
$\xi _i$
be the
![]() $i+1$
st Woodin cardinal of
$i+1$
st Woodin cardinal of
![]() ${\mathcal { K}}$
and
${\mathcal { K}}$
and
![]() $d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:
$d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:
(C1) If
![]() $p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
$p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
![]() ${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal R}_u[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal R}_u[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
We also have that if
![]() $\mathcal {E}'=\mathcal {E}^{{\mathcal R}'|{\alpha }}_{le}$
then
$\mathcal {E}'=\mathcal {E}^{{\mathcal R}'|{\alpha }}_{le}$
then
![]() $z'$
satisfies all the axioms of
$z'$
satisfies all the axioms of
![]() $\mathsf {{Ea}}^{{\mathcal R}'|{\alpha }}_{{\alpha },\mathcal {E}'}$
, and hence,
$\mathsf {{Ea}}^{{\mathcal R}'|{\alpha }}_{{\alpha },\mathcal {E}'}$
, and hence,
(D1)
![]() $z'$
satisfies all the axioms of
$z'$
satisfies all the axioms of
![]() $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
To see (D1), we use Lemma 2.17 and the fact that both
![]() ${\alpha }$
and
${\alpha }$
and
![]() ${\alpha }'$
are
${\alpha }'$
are
![]() $fb$
-cuts of
$fb$
-cuts of
![]() ${\mathcal R}'$
.
${\mathcal R}'$
.
Let
![]() $\xi <\mathrm {lh}({\mathcal {T}})$
be the least such that
$\xi <\mathrm {lh}({\mathcal {T}})$
be the least such that
![]() ${\mathcal {M}}_\xi ^{\mathcal {T}}|{\alpha }'={\mathcal R}'|{\alpha }'$
. It follows that
${\mathcal {M}}_\xi ^{\mathcal {T}}|{\alpha }'={\mathcal R}'|{\alpha }'$
. It follows that
(E1) the generators of
![]() ${\mathcal {T}}\restriction \xi $
are contained in
${\mathcal {T}}\restriction \xi $
are contained in
![]() ${\alpha }'$
and
${\alpha }'$
and
(F1) if y is a real coding
![]() ${\mathcal {T}}\restriction \xi +1$
then
${\mathcal {T}}\restriction \xi +1$
then
![]() $\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
(see Proposition 3.4).
$\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
(see Proposition 3.4).
(E1) and (F1) then imply the following.
(G1) If player I plays
![]() $({\mathcal {T}}\restriction \xi +1, y)$
where
$({\mathcal {T}}\restriction \xi +1, y)$
where
![]() $y\in {\mathbb {R}}$
is any real coding
$y\in {\mathbb {R}}$
is any real coding
![]() ${\mathcal {T}}\restriction \xi +1$
,
${\mathcal {T}}\restriction \xi +1$
,
![]() $\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
and iterations of
$\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
and iterations of
![]() ${\mathcal { K}}[z']$
that are above
${\mathcal { K}}[z']$
that are above
![]() ${\alpha }'$
are legal moves for player I in the second round of
${\alpha }'$
are legal moves for player I in the second round of
![]() $\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
.
$\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
.
Because
![]() ${\mathcal {M}}_\xi ^{\mathcal {T}}|{\beta }'={\mathcal R}'|{\beta }'$
we have that (A1)-(G1) imply clauses (1)-(3) of Sublemma 4.3. Indeed, (1) is a consequence of (E1), (2) is a consequence of (A1), (3a) is a consequence of (C1), (3b) is a consequence of (D1) and (3c) is a consequence of (G1).
${\mathcal {M}}_\xi ^{\mathcal {T}}|{\beta }'={\mathcal R}'|{\beta }'$
we have that (A1)-(G1) imply clauses (1)-(3) of Sublemma 4.3. Indeed, (1) is a consequence of (E1), (2) is a consequence of (A1), (3a) is a consequence of (C1), (3b) is a consequence of (D1) and (3c) is a consequence of (G1).
Suppose next that (Pos2) holds. Set
![]() ${\mathcal {N}}={\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}))$
and
${\mathcal {N}}={\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}))$
and
![]() ${\kappa }={\delta }({\mathcal {T}})$
.
${\kappa }={\delta }({\mathcal {T}})$
.
Claim. Let
![]() $y\in {\mathbb {R}}$
code the pair
$y\in {\mathbb {R}}$
code the pair
![]() $({\mathcal {T}}, {\mathcal {N}}|({\kappa }^+)^{\mathcal {N}})$
and set
$({\mathcal {T}}, {\mathcal {N}}|({\kappa }^+)^{\mathcal {N}})$
and set
![]() $b=\Sigma ({\mathcal {T}}, y)$
. Then
$b=\Sigma ({\mathcal {T}}, y)$
. Then
-
1.
 ${\mathcal {N}}\models `{\kappa }$
is a Woodin cardinal’ and
${\mathcal {N}}\models `{\kappa }$
is a Woodin cardinal’ and
 ${\mathcal {N}}|({\kappa }^+)^{\mathcal {N}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
and
${\mathcal {N}}|({\kappa }^+)^{\mathcal {N}}\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
and -
2.
 ${\kappa }$
is an
${\kappa }$
is an
 $fb$
-cut of
$fb$
-cut of
 ${\mathcal {M}}^{\mathcal {T}}_b$
.
${\mathcal {M}}^{\mathcal {T}}_b$
.
Proof. Clause 1 is a consequence of Proposition 3.4. To see clause 2 let
![]() ${\mathcal {X}}$
be the fully backgrounded construction of
${\mathcal {X}}$
be the fully backgrounded construction of
![]() $\mathsf {{cop}}({\mathcal {T}})={\mathcal {M}}^{\mathcal {T}}_b|{\kappa }$
. Suppose there is
$\mathsf {{cop}}({\mathcal {T}})={\mathcal {M}}^{\mathcal {T}}_b|{\kappa }$
. Suppose there is
![]() ${\mathcal {Y}}$
which extends
${\mathcal {Y}}$
which extends
![]() ${\mathcal {X}}$
, is constructed by the fully backgrounded construction of
${\mathcal {X}}$
, is constructed by the fully backgrounded construction of
![]() ${\mathcal {M}}^{\mathcal {T}}_b|\pi ^{\mathcal {T}}_b(\nu _u)$
and
${\mathcal {M}}^{\mathcal {T}}_b|\pi ^{\mathcal {T}}_b(\nu _u)$
and
![]() $\rho _\omega ({\mathcal {Y}})<{\kappa }$
. Let F be an extender used in b such that
$\rho _\omega ({\mathcal {Y}})<{\kappa }$
. Let F be an extender used in b such that
![]() $\mathrm {crit }(F)>\rho _\omega ({\mathcal {Y}})$
Footnote
61
. Let
$\mathrm {crit }(F)>\rho _\omega ({\mathcal {Y}})$
Footnote
61
. Let
![]() $\xi $
be such that
$\xi $
be such that
![]() $E_\xi ^{\mathcal {T}}=F$
. Then
$E_\xi ^{\mathcal {T}}=F$
. Then
![]() $\mathrm {crit }(F)$
is an
$\mathrm {crit }(F)$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {M}}^{\mathcal {T}}_{\xi +1}$
and
${\mathcal {M}}^{\mathcal {T}}_{\xi +1}$
and
![]() $\mathrm {crit }(\pi _{\xi +1, b}^{\mathcal {T}})>\mathrm {crit }(F)$
implying that in fact
$\mathrm {crit }(\pi _{\xi +1, b}^{\mathcal {T}})>\mathrm {crit }(F)$
implying that in fact
![]() $\mathrm {crit }(F)$
is an
$\mathrm {crit }(F)$
is an
![]() $fb$
-cut in
$fb$
-cut in
![]() ${\mathcal {M}}^{\mathcal {T}}_b$
. Hence,
${\mathcal {M}}^{\mathcal {T}}_b$
. Hence,
![]() $\rho _\omega ({\mathcal {Y}})\geq \mathrm {crit }(F)$
, contradiction.
$\rho _\omega ({\mathcal {Y}})\geq \mathrm {crit }(F)$
, contradiction.
Using condensation (applied in
![]() ${\mathcal {N}}$
) and Lemma 4.1, we can find
${\mathcal {N}}$
) and Lemma 4.1, we can find
![]() ${\beta }\in ({\kappa }, ({\kappa }^+)^{\mathcal {N}})$
such that
${\beta }\in ({\kappa }, ({\kappa }^+)^{\mathcal {N}})$
such that
-
1.
 ${\mathcal {N}}|{\beta }\models \mathsf {{ZFC}}+`$
there are
${\mathcal {N}}|{\beta }\models \mathsf {{ZFC}}+`$
there are
 $2n+1$
many Woodin cardinals’,
$2n+1$
many Woodin cardinals’, -
2. setting
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {N}}|{\beta }, z)$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {N}}|{\beta }, z)$
and
 $\mathcal {E}=\mathcal {E}_{sm}^{\mathcal { K}}$
, there is a condition
$\mathcal {E}=\mathcal {E}_{sm}^{\mathcal { K}}$
, there is a condition
 $(p, q)\in \mathsf {{Ea}}^{\mathcal { K}}_{{\kappa }, \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal { K}}_{{\kappa }, \mathcal {E}}$
such that
$(p, q)\in \mathsf {{Ea}}^{\mathcal { K}}_{{\kappa }, \mathcal {E}}\times \mathsf {{Ea}}^{\mathcal { K}}_{{\kappa }, \mathcal {E}}$
such that-
(a)
 $w_0\models p$
,
$w_0\models p$
, -
(b)
 $(w_1, w_2, w_3)\models q$
, and
$(w_1, w_2, w_3)\models q$
, and -
(c)
 $(p, q)\Vdash \exists b(U^{\prime }_{{\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l))$
where letting
$(p, q)\Vdash \exists b(U^{\prime }_{{\mathcal { K}}[(\mathsf {{ea}}^l, \mathsf {{ea}}^r)], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l))$
where letting
 $({\kappa }, \xi _1, ..., \xi _{2n})$
be the Woodin cardinals of
$({\kappa }, \xi _1, ..., \xi _{2n})$
be the Woodin cardinals of
 ${\mathcal { K}}$
enumerated in increasing order,
${\mathcal { K}}$
enumerated in increasing order,
 $d=(\xi _1, \xi _2,..., \xi _{2n})$
.
$d=(\xi _1, \xi _2,..., \xi _{2n})$
.
-
Let now
![]() $y_0\in {\mathbb {R}}$
code the pair
$y_0\in {\mathbb {R}}$
code the pair
![]() $({\mathcal {T}}, {\mathcal {N}}|({\kappa }^+)^{\mathcal {N}})$
and set
$({\mathcal {T}}, {\mathcal {N}}|({\kappa }^+)^{\mathcal {N}})$
and set
![]() $b=\Sigma ({\mathcal {T}}, y_0)$
. We then have that
$b=\Sigma ({\mathcal {T}}, y_0)$
. We then have that
![]() ${\mathcal {N}}|{\beta }\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
(see clause 1 of the Claim). Notice that because
${\mathcal {N}}|{\beta }\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
(see clause 1 of the Claim). Notice that because
![]() ${\kappa }$
is an
${\kappa }$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {M}}^{\mathcal {T}}_b$
(see clause 2 of the Claim) and because
${\mathcal {M}}^{\mathcal {T}}_b$
(see clause 2 of the Claim) and because
![]() ${\mathcal {N}}|{\beta }\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
, the above clauses imply that
${\mathcal {N}}|{\beta }\trianglelefteq {\mathcal {M}}^{\mathcal {T}}_b$
, the above clauses imply that
![]() $\pi ^{\mathcal {T}}_b({\alpha }_s)\leq {\kappa }$
. Because
$\pi ^{\mathcal {T}}_b({\alpha }_s)\leq {\kappa }$
. Because
![]() $k\in w'$
, we must have
$k\in w'$
, we must have
![]() ${\alpha }'<{\beta }'<\pi ^{\mathcal {T}}_b({\alpha }_s)\leq {\kappa }$
such that
${\alpha }'<{\beta }'<\pi ^{\mathcal {T}}_b({\alpha }_s)\leq {\kappa }$
such that
(A2)
![]() ${\mathcal {M}}^{\mathcal {T}}_b|{\beta }'\models "\mathsf {{ZFC}}+`$
there are
${\mathcal {M}}^{\mathcal {T}}_b|{\beta }'\models "\mathsf {{ZFC}}+`$
there are
![]() $2n+1$
many Woodin cardinals’ +
$2n+1$
many Woodin cardinals’ +
![]() $`{\alpha }'$
is the least Woodin cardinal’,
$`{\alpha }'$
is the least Woodin cardinal’,
(B2)
![]() ${\alpha }'$
is an
${\alpha }'$
is an
![]() $fb$
-cut in
$fb$
-cut in
![]() ${\mathcal {M}}^{\mathcal {T}}_b$
, and
${\mathcal {M}}^{\mathcal {T}}_b$
, and
setting
![]() ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {M}}^{\mathcal {T}}_b|{\beta }')$
,
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {M}}^{\mathcal {T}}_b|{\beta }')$
,
![]() $\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
$\mathcal {E}=\mathcal {E}_{sm}^{{\mathcal { K}}|{\alpha }'}$
and for
![]() $i\in [1, 2n]$
, letting
$i\in [1, 2n]$
, letting
![]() $\xi _i$
be the
$\xi _i$
be the
![]() $i+1$
st Woodin cardinal of
$i+1$
st Woodin cardinal of
![]() ${\mathcal { K}}$
and
${\mathcal { K}}$
and
![]() $d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:
$d=(\xi _1, \xi _2, ..., \xi _{2n})$
the following holds:
(C2) If
![]() $p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
$p\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
then
![]() ${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal R}_u[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
${\mathcal { K}}\models p\Vdash \exists v(\psi ^{\prime }_{{\mathcal R}_u[\mathsf {{ea}}], d}[k, z, \mathsf {{ea}}, v])$
.
Let then
![]() ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {M}}^{\mathcal {T}}_b|{\beta }')$
. Because
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {M}}^{\mathcal {T}}_b|{\beta }')$
. Because
(a)
![]() $z'$
satisfies all the axioms of
$z'$
satisfies all the axioms of
![]() $\mathsf {{Ea}}^{\mathsf {{cop}}({\mathcal {T}})}_{{\delta }({\mathcal {T}}), \mathcal {E}'}$
where
$\mathsf {{Ea}}^{\mathsf {{cop}}({\mathcal {T}})}_{{\delta }({\mathcal {T}}), \mathcal {E}'}$
where
![]() $\mathcal {E'}=\mathcal {E}^{\mathsf {{cop}}({\mathcal {T}})}_{le}$
, and
$\mathcal {E'}=\mathcal {E}^{\mathsf {{cop}}({\mathcal {T}})}_{le}$
, and
(b)
![]() ${\alpha }'$
is an
${\alpha }'$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {M}}^{\mathcal {T}}_b$
${\mathcal {M}}^{\mathcal {T}}_b$
(D2)
![]() $z'$
satisfies all the axioms of
$z'$
satisfies all the axioms of
![]() $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
Let
![]() $\xi <\mathrm {lh}({\mathcal {T}})$
be the least such that
$\xi <\mathrm {lh}({\mathcal {T}})$
be the least such that
![]() ${\mathcal {M}}_\xi ^{\mathcal {T}}|{\alpha }'={\mathcal {M}}^{\mathcal {T}}_b|{\alpha }'$
(notice that because
${\mathcal {M}}_\xi ^{\mathcal {T}}|{\alpha }'={\mathcal {M}}^{\mathcal {T}}_b|{\alpha }'$
(notice that because
![]() ${\alpha }'<{\delta }({\mathcal {T}})$
, we really do have such a
${\alpha }'<{\delta }({\mathcal {T}})$
, we really do have such a
![]() $\xi <\mathrm {lh}({\mathcal {T}})$
). It follows that
$\xi <\mathrm {lh}({\mathcal {T}})$
). It follows that
(E2) the generators of
![]() ${\mathcal {T}}\restriction \xi $
are contained in
${\mathcal {T}}\restriction \xi $
are contained in
![]() ${\alpha }'$
.
${\alpha }'$
.
(F2) if y is a real coding
![]() ${\mathcal {T}}\restriction \xi +1$
then
${\mathcal {T}}\restriction \xi +1$
then
![]() $\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
(see Proposition 3.4).
$\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
(see Proposition 3.4).
(E2) and (F2) then imply the following.
(G2) If player I plays
![]() $({\mathcal {T}}\restriction \xi +1, y)$
where
$({\mathcal {T}}\restriction \xi +1, y)$
where
![]() $y\in {\mathbb {R}}$
is any real coding
$y\in {\mathbb {R}}$
is any real coding
![]() ${\mathcal {T}}\restriction \xi +1$
,
${\mathcal {T}}\restriction \xi +1$
,
![]() $\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
and iterations of
$\Sigma ({\mathcal {T}}\restriction \xi +1, y)=\mathsf {{accept}}$
and iterations of
![]() ${\mathcal { K}}[z']$
that are above
${\mathcal { K}}[z']$
that are above
![]() ${\alpha }'$
are legal moves for player I in the second round of
${\alpha }'$
are legal moves for player I in the second round of
![]() $\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
.
$\mathcal {G}({\mathcal R}_u, 0, 2n+1)$
.
As in the case of (Pos1), (A2)-(G2) imply that (1)-(3) of Sublemma 4.3 hold.
Let then
![]() $\xi $
,
$\xi $
,
![]() $d=(\xi _1, \xi _2, ..., \xi _{2n})$
and
$d=(\xi _1, \xi _2, ..., \xi _{2n})$
and
![]() ${\mathcal { K}}$
be as in the conclusion of Sublemma 4.3. We now want to conclude that
${\mathcal { K}}$
be as in the conclusion of Sublemma 4.3. We now want to conclude that
![]() $\psi [k, z, z']$
holds. Let
$\psi [k, z, z']$
holds. Let
![]() $v\in {\mathcal { K}}[z']$
be such that
$v\in {\mathcal { K}}[z']$
be such that
![]() ${\mathcal { K}}[z']\models \psi ^{\prime }_{{\mathcal { K}}[z'], d}[k, z, z', v]$
. It is then enough to show that
${\mathcal { K}}[z']\models \psi ^{\prime }_{{\mathcal { K}}[z'], d}[k, z, z', v]$
. It is then enough to show that
![]() $\psi '[k, z, z', v]$
holds, and this will be established by Sublemma 4.4.
$\psi '[k, z, z', v]$
holds, and this will be established by Sublemma 4.4.
Sublemma 4.4.
![]() $\psi '[k, z, z', v]$
holds.
$\psi '[k, z, z', v]$
holds.
Proof.
![]() $\psi '[k, z, z', v]$
is a
$\psi '[k, z, z', v]$
is a
![]() $\Pi ^1_{2n+1}$
-formula, so we can find a
$\Pi ^1_{2n+1}$
-formula, so we can find a
![]() $\Sigma ^1_{2n}$
formula
$\Sigma ^1_{2n}$
formula
![]() $\psi "$
such that
$\psi "$
such that
![]() $\psi '[k, z, z', v]{\mathrel {\leftrightarrow }} \forall t\psi "[k, z, z', v, t]$
. Fix
$\psi '[k, z, z', v]{\mathrel {\leftrightarrow }} \forall t\psi "[k, z, z', v, t]$
. Fix
![]() $t\in {\mathbb {R}}$
. We now want to argue that
$t\in {\mathbb {R}}$
. We now want to argue that
![]() $\psi "[k, z, z', v, t]$
holds. Let I’s first move in
$\psi "[k, z, z', v, t]$
holds. Let I’s first move in
![]() $\mathcal {G}({\mathcal R}, 0, 2n+1)$
be
$\mathcal {G}({\mathcal R}, 0, 2n+1)$
be
![]() $({\mathcal {T}}\restriction \xi +1, t')$
where
$({\mathcal {T}}\restriction \xi +1, t')$
where
![]() $t'$
is a real coding t and
$t'$
is a real coding t and
![]() ${\mathcal {T}}\restriction \xi +1$
. As discussed above,
${\mathcal {T}}\restriction \xi +1$
. As discussed above,
![]() $II$
must accept
$II$
must accept
![]() ${\mathcal {T}}\restriction \xi +1$
.
${\mathcal {T}}\restriction \xi +1$
.
Notice now that
![]() ${\mathcal { K}}$
as a
${\mathcal { K}}$
as a
![]() ${\mathcal { K}}|\xi _1$
-mouse is
${\mathcal { K}}|\xi _1$
-mouse is
![]() $2n-1$
-small. Working inside
$2n-1$
-small. Working inside
![]() ${\mathcal {M}}_{2n-1}(t')$
, let
${\mathcal {M}}_{2n-1}(t')$
, let
![]() ${\mathcal {U}}$
be an iteration of
${\mathcal {U}}$
be an iteration of
![]() ${\mathcal { K}}$
such that
${\mathcal { K}}$
such that
-
1.
 ${\mathcal {U}}$
is a
${\mathcal {U}}$
is a
 $(t, \xi _2, \xi _1)$
-genericity iteration,
$(t, \xi _2, \xi _1)$
-genericity iteration, -
2. for each limit ordinal
 ${\lambda }<\mathrm {lh}({\mathcal {U}})-1$
, if
${\lambda }<\mathrm {lh}({\mathcal {U}})-1$
, if
 $c=[0, {\lambda })_{{\mathcal {U}}}$
then
$c=[0, {\lambda })_{{\mathcal {U}}}$
then
 ${\mathcal { Q}}(c, {\mathcal {U}})$
exists and is
${\mathcal { Q}}(c, {\mathcal {U}})$
exists and is
 ${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\lambda })\trianglelefteq {\mathcal {M}}_{2n-2}(\mathsf {{cop}}({\mathcal {U}}\restriction {\lambda }))$
.
${\mathcal { Q}}(c, {\mathcal {U}}\restriction {\lambda })\trianglelefteq {\mathcal {M}}_{2n-2}(\mathsf {{cop}}({\mathcal {U}}\restriction {\lambda }))$
.
As always, we have two possibilities: either
(1)
![]() ${\mathcal {U}}$
has a last model
${\mathcal {U}}$
has a last model
![]() ${\mathcal { K}}_1$
such that t is generic over
${\mathcal { K}}_1$
such that t is generic over
![]() ${\mathcal { K}}_1$
for
${\mathcal { K}}_1$
for
![]() $\mathsf {{Ea}}^{{\mathcal { K}}_1}_{\pi ^{{\mathcal {U}}}(\xi _2), \xi _1}$
or
$\mathsf {{Ea}}^{{\mathcal { K}}_1}_{\pi ^{{\mathcal {U}}}(\xi _2), \xi _1}$
or
(2)
![]() ${\mathcal {U}}$
is of limit length and there is no branch c of
${\mathcal {U}}$
is of limit length and there is no branch c of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() ${\mathcal { Q}}(c, {\mathcal {U}})\trianglelefteq {\mathcal {M}}_{2n-2}(\mathsf {{cop}}({\mathcal {U}}))$
Footnote
62
.
${\mathcal { Q}}(c, {\mathcal {U}})\trianglelefteq {\mathcal {M}}_{2n-2}(\mathsf {{cop}}({\mathcal {U}}))$
Footnote
62
.
We now let I play
![]() ${\mathcal {U}}$
in the second round of
${\mathcal {U}}$
in the second round of
![]() $\mathcal {G}({\mathcal R}, 0, 2n+1)$
. If
$\mathcal {G}({\mathcal R}, 0, 2n+1)$
. If
![]() $II$
accepts it then let
$II$
accepts it then let
![]() ${\mathcal { K}}_1$
be the last model of
${\mathcal { K}}_1$
be the last model of
![]() ${\mathcal {U}}$
. If
${\mathcal {U}}$
. If
![]() $II$
plays a maximal well-founded branch c then let
$II$
plays a maximal well-founded branch c then let
![]() ${\mathcal { K}}_1={\mathcal {M}}^{{\mathcal {U}}\restriction \sup (c)}_c$
Footnote
63
.
${\mathcal { K}}_1={\mathcal {M}}^{{\mathcal {U}}\restriction \sup (c)}_c$
Footnote
63
.
Suppose for a moment that
![]() $II$
plays a branch c. Set
$II$
plays a branch c. Set
![]() $\iota =\sup (c)$
. We want to argue that
$\iota =\sup (c)$
. We want to argue that
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction \iota )$
doesn’t exists. If it does then it is
${\mathcal { Q}}(c, {\mathcal {U}}\restriction \iota )$
doesn’t exists. If it does then it is
![]() $2n-2$
-small
$2n-2$
-small
![]() ${\delta }({\mathcal {U}}\restriction \iota )$
-mouse which is
${\delta }({\mathcal {U}}\restriction \iota )$
-mouse which is
![]() $\Pi ^1_{2n}$
-iterable above
$\Pi ^1_{2n}$
-iterable above
![]() ${\delta }({\mathcal {U}}\restriction \iota )$
. It follows from clause 11 of Review 3 that
${\delta }({\mathcal {U}}\restriction \iota )$
. It follows from clause 11 of Review 3 that
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction \iota )$
is iterable and hence,
${\mathcal { Q}}(c, {\mathcal {U}}\restriction \iota )$
is iterable and hence,
![]() ${\mathcal { Q}}(c, {\mathcal {U}}\restriction \iota )\trianglelefteq {\mathcal {M}}_{2n-2}(\mathsf {{cop}}({\mathcal {U}}\restriction \iota ))$
, which is a contradiction.
${\mathcal { Q}}(c, {\mathcal {U}}\restriction \iota )\trianglelefteq {\mathcal {M}}_{2n-2}(\mathsf {{cop}}({\mathcal {U}}\restriction \iota ))$
, which is a contradiction.
Let now
![]() $j:{\mathcal { K}}\rightarrow {\mathcal { K}}_1$
be the iteration map given by
$j:{\mathcal { K}}\rightarrow {\mathcal { K}}_1$
be the iteration map given by
![]() $\pi ^{{\mathcal {U}}}$
or
$\pi ^{{\mathcal {U}}}$
or
![]() $\pi ^{{\mathcal {U}}\restriction \iota }_{c}$
depending on which case was used to define
$\pi ^{{\mathcal {U}}\restriction \iota }_{c}$
depending on which case was used to define
![]() ${\mathcal { K}}_1$
. In both of these cases we have that t is generic over
${\mathcal { K}}_1$
. In both of these cases we have that t is generic over
![]() ${\mathcal { K}}_1$
for
${\mathcal { K}}_1$
for
![]() $\mathsf {{Ea}}^{{\mathcal { K}}_1}_{j(\xi _2), \xi _1}$
. Let
$\mathsf {{Ea}}^{{\mathcal { K}}_1}_{j(\xi _2), \xi _1}$
. Let
![]() $d'=(j(\xi _2), j(\xi _3), ..., j(\xi _{2n}))$
. We have that
$d'=(j(\xi _2), j(\xi _3), ..., j(\xi _{2n}))$
. We have that
![]() ${\mathcal { K}}_1[z', t]\models \psi ^{\prime \prime }_{{\mathcal { K}}_1[z', t], d'}[k, z, z', v, t]$
. Moreover,
${\mathcal { K}}_1[z', t]\models \psi ^{\prime \prime }_{{\mathcal { K}}_1[z', t], d'}[k, z, z', v, t]$
. Moreover,
![]() ${\mathcal { K}}_1$
above
${\mathcal { K}}_1$
above
![]() $j(\xi _2)$
is
$j(\xi _2)$
is
![]() $2n-2$
-small and
$2n-2$
-small and
![]() $\Pi ^1_{2n}$
-iterable. It follows from clause 11 of Review 3 that
$\Pi ^1_{2n}$
-iterable. It follows from clause 11 of Review 3 that
![]() ${\mathcal { K}}_1$
is iterable above
${\mathcal { K}}_1$
is iterable above
![]() $j(\xi _2)$
and hence, applying Proposition 2.5 to
$j(\xi _2)$
and hence, applying Proposition 2.5 to
![]() ${\mathcal { K}}_1[z', t]$
, we get that
${\mathcal { K}}_1[z', t]$
, we get that
![]() $\psi "[k, z, z', v, t]$
holds.
$\psi "[k, z, z', v, t]$
holds.
4.4 Hjorth’s reflection
Recall that w is
![]() $\Pi ^1_{2n+3}(z)$
but not
$\Pi ^1_{2n+3}(z)$
but not
![]() $\Sigma ^1_{2n+3}(z)$
, and since
$\Sigma ^1_{2n+3}(z)$
, and since
![]() $w'$
is
$w'$
is
![]() $\Sigma ^1_{2n+3}(z)$
, we have that
$\Sigma ^1_{2n+3}(z)$
, we have that
![]() $w-w'$
is not empty. Fix now
$w-w'$
is not empty. Fix now
![]() $k\in w-w'$
and let
$k\in w-w'$
and let
![]() ${\alpha }<{\beta }<{\kappa }_{\mathcal {M}}$
be the least such that
${\alpha }<{\beta }<{\kappa }_{\mathcal {M}}$
be the least such that
-
1.
 ${\mathcal {M}}|{\beta }\models \mathsf {{ZFC}}$
+‘there are
${\mathcal {M}}|{\beta }\models \mathsf {{ZFC}}$
+‘there are
 $2n+1$
Woodin cardinals’,
$2n+1$
Woodin cardinals’, -
2.
 ${\mathcal {M}}|{\beta }\models `{\alpha }$
is a Woodin cardinal’,
${\mathcal {M}}|{\beta }\models `{\alpha }$
is a Woodin cardinal’, -
3.
 ${\alpha }$
is both an inaccessible
${\alpha }$
is both an inaccessible
 $fb$
-cut of
$fb$
-cut of
 ${\mathcal {M}}$
and a cutpoint of
${\mathcal {M}}$
and a cutpoint of
 ${\mathcal {M}}$
,
${\mathcal {M}}$
, -
4. letting
 $({\alpha }, \tau _1, ..., \tau _{2n})$
be the Woodin cardinals of
$({\alpha }, \tau _1, ..., \tau _{2n})$
be the Woodin cardinals of
 ${\mathcal {M}}|{\beta }$
enumerated in the increasing order,
${\mathcal {M}}|{\beta }$
enumerated in the increasing order,
 $d=(\tau _1, ..., \tau _{2n})$
and
$d=(\tau _1, ..., \tau _{2n})$
and
 ${\mathcal { K}}=\mathsf {StrLe}({\mathcal {M}}|{\beta })$
, whenever
${\mathcal { K}}=\mathsf {StrLe}({\mathcal {M}}|{\beta })$
, whenever
 $q\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }, sm}$
,
$q\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }, sm}$
,
 ${\mathcal { K}}\models q\Vdash \exists v\psi ^{\prime }_{{\mathcal {M}}|{\beta }, d}[k, z, \mathsf {{ea}}, v]$
.
${\mathcal { K}}\models q\Vdash \exists v\psi ^{\prime }_{{\mathcal {M}}|{\beta }, d}[k, z, \mathsf {{ea}}, v]$
.
Notice that to get
![]() ${\beta }<{\kappa }_{\mathcal {M}}$
we are using that
${\beta }<{\kappa }_{\mathcal {M}}$
we are using that
![]() ${\mathcal {M}}\models \mathsf {{Cond}}$
. Also, notice that if
${\mathcal {M}}\models \mathsf {{Cond}}$
. Also, notice that if
![]() ${\mathcal {N}}$
is a complete iterate of
${\mathcal {N}}$
is a complete iterate of
![]() ${\mathcal {M}}$
then setting
${\mathcal {M}}$
then setting
![]() $\pi _{{\mathcal {M}}, {\mathcal {N}}}({\alpha }, {\beta })=(\iota _{\mathcal {N}}, \zeta _{\mathcal {N}})$
, we have that
$\pi _{{\mathcal {M}}, {\mathcal {N}}}({\alpha }, {\beta })=(\iota _{\mathcal {N}}, \zeta _{\mathcal {N}})$
, we have that
![]() $(\iota _{\mathcal {N}}, \zeta _{\mathcal {N}})$
has the same definition over
$(\iota _{\mathcal {N}}, \zeta _{\mathcal {N}})$
has the same definition over
![]() ${\mathcal {N}}$
as
${\mathcal {N}}$
as
![]() $({\alpha }, {\beta })$
over
$({\alpha }, {\beta })$
over
![]() ${\mathcal {M}}$
. Set
${\mathcal {M}}$
. Set
![]() ${\mathcal { Q}}={\mathcal {M}}|(\zeta _{\mathcal {M}}^+)^{\mathcal {M}}$
Footnote
64
. Given a complete iterate
${\mathcal { Q}}={\mathcal {M}}|(\zeta _{\mathcal {M}}^+)^{\mathcal {M}}$
Footnote
64
. Given a complete iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
we let
${\mathcal {M}}$
we let
![]() ${\mathcal { Q}}_{\mathcal {N}}=\pi _{{\mathcal {M}}, {\mathcal {N}}}({\mathcal { Q}})$
. Recall that we set
${\mathcal { Q}}_{\mathcal {N}}=\pi _{{\mathcal {M}}, {\mathcal {N}}}({\mathcal { Q}})$
. Recall that we set
![]() $B_{\gamma} =\{ y: U_y=A_{\gamma} \}$
. To implement Hjorth’s reflection we will need the following general lemma which is based on [Reference Steel37].
$B_{\gamma} =\{ y: U_y=A_{\gamma} \}$
. To implement Hjorth’s reflection we will need the following general lemma which is based on [Reference Steel37].
Lemma 4.5. Suppose
![]() ${\mathcal R}$
is a complete iterate of
${\mathcal R}$
is a complete iterate of
![]() ${\mathcal {M}}_{2n+1}$
such that
${\mathcal {M}}_{2n+1}$
such that
![]() $\mathrm { lh}({\mathcal {T}}_{{\mathcal {M}}_{2n+1}, {\mathcal R}})<\omega _1$
. Let
$\mathrm { lh}({\mathcal {T}}_{{\mathcal {M}}_{2n+1}, {\mathcal R}})<\omega _1$
. Let
![]() ${\alpha }\leq {\kappa }_{\mathcal R}$
be a cutpoint of
${\alpha }\leq {\kappa }_{\mathcal R}$
be a cutpoint of
![]() ${\mathcal R}$
and set
${\mathcal R}$
and set
![]() ${\mathcal {S}}={\mathcal R}|({\alpha }^+)^{\mathcal R}$
. Let
${\mathcal {S}}={\mathcal R}|({\alpha }^+)^{\mathcal R}$
. Let
![]() $x\in {\mathbb {R}}$
code
$x\in {\mathbb {R}}$
code
![]() ${\mathcal {S}}$
. Then the following statements hold:
${\mathcal {S}}$
. Then the following statements hold:
-
1. The statement that
 $`y$
codes a complete iterate of S’ is
$`y$
codes a complete iterate of S’ is
 $\Sigma ^1_{2n+2}(x)$
.
$\Sigma ^1_{2n+2}(x)$
. -
2. The statement that
 $`y$
codes a pair
$`y$
codes a pair
 $({\mathcal {N}}, \xi )$
,
$({\mathcal {N}}, \xi )$
,
 $y'$
codes a pair
$y'$
codes a pair
 $({\mathcal {N}}', \xi ')$
,
$({\mathcal {N}}', \xi ')$
,
 ${\mathcal {N}}$
and
${\mathcal {N}}$
and
 ${\mathcal {N}}'$
are complete iterates of
${\mathcal {N}}'$
are complete iterates of
 ${\mathcal {S}}$
and if
${\mathcal {S}}$
and if
 ${\mathcal {N}}"$
is the common complete iterate of
${\mathcal {N}}"$
is the common complete iterate of
 ${\mathcal {N}}$
and
${\mathcal {N}}$
and
 ${\mathcal {N}}'$
then
${\mathcal {N}}'$
then
 $\pi _{{\mathcal {N}}, {\mathcal {N}}"}(\xi )\leq \pi _{{\mathcal {N}}', {\mathcal {N}}"}(\xi ')$
’ is
$\pi _{{\mathcal {N}}, {\mathcal {N}}"}(\xi )\leq \pi _{{\mathcal {N}}', {\mathcal {N}}"}(\xi ')$
’ is
 $\Sigma ^1_{2n+2}(x)$
.
$\Sigma ^1_{2n+2}(x)$
.
Proof. To say that
![]() $`y$
codes a complete iterate of
$`y$
codes a complete iterate of
![]() ${\mathcal {S}}$
’ it is enough to say the following:
${\mathcal {S}}$
’ it is enough to say the following:
-
1. y codes a premouse
 ${\mathcal {N}}$
,
${\mathcal {N}}$
, -
2. there is a real u such that u codes an iteration
 ${\mathcal {T}}$
of
${\mathcal {T}}$
of
 ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that-
(a)
 ${\mathcal {T}}$
has a last model
${\mathcal {T}}$
has a last model
 ${\mathcal {N}}$
,
${\mathcal {N}}$
, -
(b)
 $\pi ^{\mathcal {T}}$
is defined,
$\pi ^{\mathcal {T}}$
is defined, -
(c) for every limit
 ${\alpha }<\mathrm {lh}({\mathcal {T}})$
, letting
${\alpha }<\mathrm {lh}({\mathcal {T}})$
, letting
 $b=[0, {\alpha })_{\mathcal {T}}$
,
$b=[0, {\alpha })_{\mathcal {T}}$
,
 ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists and
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha })$
exists and
 ${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha }){\triangleleft } {\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
.
${\mathcal { Q}}(b, {\mathcal {T}}\restriction {\alpha }){\triangleleft } {\mathcal {M}}_{2n}(\mathsf {{cop}}({\mathcal {T}}\restriction {\alpha }))$
.
-
The complexity of the statement comes from clause 2.3, and [[Reference Steel37], Corollary 4.9] implies that it is
![]() $\Sigma ^1_{2n+2}(u)$
. The reason is that for any
$\Sigma ^1_{2n+2}(u)$
. The reason is that for any
![]() $v\in {\mathbb {R}}$
,
$v\in {\mathbb {R}}$
,
![]() ${\mathbb {R}}\cap {\mathcal {M}}_{2n+2}(v)$
is the largest countable
${\mathbb {R}}\cap {\mathcal {M}}_{2n+2}(v)$
is the largest countable
![]() $\Sigma ^1_{2n+2}(v)$
setFootnote
65
. It is then not hard to see that
$\Sigma ^1_{2n+2}(v)$
setFootnote
65
. It is then not hard to see that
![]() $`y$
codes a complete iterate of
$`y$
codes a complete iterate of
![]() ${\mathcal {S}}$
’ is indeed
${\mathcal {S}}$
’ is indeed
![]() $\Sigma ^1_{2n+2}(x)$
. A very similar calculation shows that the statement in clause 2 is also
$\Sigma ^1_{2n+2}(x)$
. A very similar calculation shows that the statement in clause 2 is also
![]() $\Sigma ^1_{2n+2}(x)$
.
$\Sigma ^1_{2n+2}(x)$
.
Recall that Lemma 2.20 says that for every
![]() ${\gamma} <{\delta }^1_{2n+2}$
there is a
${\gamma} <{\delta }^1_{2n+2}$
there is a
![]() ${\gamma} $
-stable complete iterate
${\gamma} $
-stable complete iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
. Before we state and prove Hjorth’s Reflection argument, we will need the following lemma.
${\mathcal {M}}$
. Before we state and prove Hjorth’s Reflection argument, we will need the following lemma.
Lemma 4.6. There is a complete
![]() ${\gamma} $
-stable iterate
${\gamma} $
-stable iterate
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
such that if
${\mathcal {M}}$
such that if
![]() ${\mathcal {P}}=\mathsf {{StrLe}}({\mathcal {N}})$
then
${\mathcal {P}}=\mathsf {{StrLe}}({\mathcal {N}})$
then
![]() ${\mathcal {P}}$
is a
${\mathcal {P}}$
is a
![]() ${\gamma} $
-stable complete iterate of
${\gamma} $
-stable complete iterate of
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
Proof. Let
![]() ${\mathcal {N}}'$
be any
${\mathcal {N}}'$
be any
![]() ${\gamma} $
-stable complete iterate of
${\gamma} $
-stable complete iterate of
![]() ${\mathcal {M}}$
and set
${\mathcal {M}}$
and set
![]() ${\mathcal R}={\mathcal {M}}_{2n+1}({\mathcal {M}}, {\mathcal {N}}')$
. Let
${\mathcal R}={\mathcal {M}}_{2n+1}({\mathcal {M}}, {\mathcal {N}}')$
. Let
![]() ${\mathcal {N}}=\mathsf {{StreLe}}({\mathcal R})$
and let
${\mathcal {N}}=\mathsf {{StreLe}}({\mathcal R})$
and let
![]() ${\mathcal {P}}=\mathsf {{StreLe}}({\mathcal {N}})$
. Then both
${\mathcal {P}}=\mathsf {{StreLe}}({\mathcal {N}})$
. Then both
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {P}}$
are complete iterates of both
${\mathcal {P}}$
are complete iterates of both
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() ${\mathcal {N}}'$
. Therefore, both
${\mathcal {N}}'$
. Therefore, both
![]() ${\mathcal {N}}$
and
${\mathcal {N}}$
and
![]() ${\mathcal {P}}$
are
${\mathcal {P}}$
are
![]() ${\gamma} $
-stable.
${\gamma} $
-stable.
Lemma 4.7 (Hjorth’s Reflection).
Suppose
![]() ${\gamma} <{\delta }^1_{2n+2}$
and
${\gamma} <{\delta }^1_{2n+2}$
and
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() ${\gamma} $
-stable complete iterate of
${\gamma} $
-stable complete iterate of
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() $\mathsf {{StrLe}}({\mathcal {N}})$
is also a complete
$\mathsf {{StrLe}}({\mathcal {N}})$
is also a complete
![]() ${\gamma} $
-stable iterate of
${\gamma} $
-stable iterate of
![]() ${\mathcal {M}}$
. Then whenever
${\mathcal {M}}$
. Then whenever
![]() $g\subseteq Coll(\omega , {\mathcal { Q}}_{\mathcal {N}})$
is
$g\subseteq Coll(\omega , {\mathcal { Q}}_{\mathcal {N}})$
is
![]() ${\mathcal {N}}$
-generic,
${\mathcal {N}}$
-generic,
![]() $B_{\gamma} \cap {\mathcal {N}}[g]\not =\emptyset $
.
$B_{\gamma} \cap {\mathcal {N}}[g]\not =\emptyset $
.
Proof. Set
![]() $p=p^{\mathsf {{StrLe}}({\mathcal {N}})}_{{\gamma} , 0, 3, 1}$
(see clause 9 of Review 2.19, here we define
$p=p^{\mathsf {{StrLe}}({\mathcal {N}})}_{{\gamma} , 0, 3, 1}$
(see clause 9 of Review 2.19, here we define
![]() $p^{\mathsf {{StrLe}}({\mathcal {N}})}_{{\gamma} , 0, 3, 1}$
relative to
$p^{\mathsf {{StrLe}}({\mathcal {N}})}_{{\gamma} , 0, 3, 1}$
relative to
![]() $\mathcal {E}^{\mathsf {{StrLe}}({\mathcal {N}})}_{sm}$
). Let
$\mathcal {E}^{\mathsf {{StrLe}}({\mathcal {N}})}_{sm}$
). Let
![]() $\mathcal {A}\in {\mathcal {N}}$
consist of quadruples
$\mathcal {A}\in {\mathcal {N}}$
consist of quadruples
![]() $({\alpha }', {\beta }', q, r)$
such that
$({\alpha }', {\beta }', q, r)$
such that
-
1.
 ${\alpha }'\leq \iota _{\mathcal {N}}$
,
${\alpha }'\leq \iota _{\mathcal {N}}$
,
 ${\mathcal {N}}|{\beta }'\models \mathsf {{ZFC}}+`{\alpha }'$
is the least Woodin cardinal’+‘there are
${\mathcal {N}}|{\beta }'\models \mathsf {{ZFC}}+`{\alpha }'$
is the least Woodin cardinal’+‘there are
 $2n+1$
many Woodin cardinals’,
$2n+1$
many Woodin cardinals’, -
2.
 ${\alpha }'$
is an
${\alpha }'$
is an
 $fb$
-cut of
$fb$
-cut of
 ${\mathcal {N}}$
, and
${\mathcal {N}}$
, andletting
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {N}}|{\beta }')$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {N}}|{\beta }')$
and
 $\mathcal {E}=\mathcal {E}^{{\mathcal { K}}}_{sm}$
, there is
$\mathcal {E}=\mathcal {E}^{{\mathcal { K}}}_{sm}$
, there is
 $(q, r)\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}\times \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
,
$(q, r)\in \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}\times \mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
, -
3. r is compatible with p,
-
4.
 $(q, r)\Vdash \exists b( U^{\prime }_{{\mathcal { K}}[\mathsf {{ea}}^l, \mathsf {{ea}}^r], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l, b))$
where letting
$(q, r)\Vdash \exists b( U^{\prime }_{{\mathcal { K}}[\mathsf {{ea}}^l, \mathsf {{ea}}^r], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l, b))$
where letting
 $({\alpha }', \xi _1, ...\xi _{2n})$
be the Woodin cardinals of
$({\alpha }', \xi _1, ...\xi _{2n})$
be the Woodin cardinals of
 ${\mathcal { K}}$
enumerated in increasing order,
${\mathcal { K}}$
enumerated in increasing order,
 $d=(\xi _1, \xi _2,..., \xi _{2n})$
.
$d=(\xi _1, \xi _2,..., \xi _{2n})$
.
Sublemma 4.8. Suppose
![]() $x\in {\mathbb {R}}$
. Then the following are equivalent.
$x\in {\mathbb {R}}$
. Then the following are equivalent.
-
1.
 $x\in A_{\gamma} $
.
$x\in A_{\gamma} $
. -
2. There is a complete iterate
 ${\mathcal {S}}$
of
${\mathcal {S}}$
of
 ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
 ${\mathcal {T}}_{{\mathcal {N}}, {\mathcal {S}}}$
is below
${\mathcal {T}}_{{\mathcal {N}}, {\mathcal {S}}}$
is below
 $\iota _{\mathcal {N}}$
and for some
$\iota _{\mathcal {N}}$
and for some
 $({\alpha }', {\beta }', q, r)\in \pi _{{\mathcal {N}}, {\mathcal {S}}}(\mathcal {A})$
,
$({\alpha }', {\beta }', q, r)\in \pi _{{\mathcal {N}}, {\mathcal {S}}}(\mathcal {A})$
,
 $x\models q$
and letting
$x\models q$
and letting
 ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {S}}|{\beta }')$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {S}}|{\beta }')$
and
 $\mathcal {E}=\mathcal {E}^{\mathcal { K}}_{sm}$
, x is generic over
$\mathcal {E}=\mathcal {E}^{\mathcal { K}}_{sm}$
, x is generic over
 $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
.
Proof. (Clause 1 implies Clause 2:) Suppose
![]() $x\in A_{\gamma} $
. Let
$x\in A_{\gamma} $
. Let
![]() $x_1\in \mathsf {{Code}}$
be such that
$x_1\in \mathsf {{Code}}$
be such that
![]() ${\gamma} _{x_1}={\gamma} $
,
${\gamma} _{x_1}={\gamma} $
,
![]() $x_2\in B_{\gamma} $
and
$x_2\in B_{\gamma} $
and
![]() $x_3$
be such that
$x_3$
be such that
![]() $D(x_1, x_2, x_3)$
. Let
$D(x_1, x_2, x_3)$
. Let
![]() ${\mathcal {P}}={\mathcal {M}}_{2n+1}(z, x, (x_1, x_2, x_3))$
. Notice that if u is a real coding
${\mathcal {P}}={\mathcal {M}}_{2n+1}(z, x, (x_1, x_2, x_3))$
. Notice that if u is a real coding
![]() ${\mathcal {P}}$
then we in fact have that
${\mathcal {P}}$
then we in fact have that
![]() $\theta _0(u, x, x_1, x_2, x_3)$
holds.
$\theta _0(u, x, x_1, x_2, x_3)$
holds.
We now compare
![]() ${\mathcal {P}}$
and
${\mathcal {P}}$
and
![]() ${\mathcal {N}}$
to obtain
${\mathcal {N}}$
to obtain
![]() ${\mathcal {P}}'$
and
${\mathcal {P}}'$
and
![]() ${\mathcal {N}}'$
such that
${\mathcal {N}}'$
such that
(a) the least Woodin cardinals of
![]() ${\mathcal {P}}'$
and
${\mathcal {P}}'$
and
![]() ${\mathcal {N}}'$
coincide,
${\mathcal {N}}'$
coincide,
(b) if
![]() ${\kappa }$
is the least Woodin cardinal of
${\kappa }$
is the least Woodin cardinal of
![]() ${\mathcal {P}}'$
and
${\mathcal {P}}'$
and
![]() ${\mathcal {N}}'$
then the fully backgrounded construction of
${\mathcal {N}}'$
then the fully backgrounded construction of
![]() ${\mathcal {P}}|{\kappa }$
coincides with the fully backgrounded construction of
${\mathcal {P}}|{\kappa }$
coincides with the fully backgrounded construction of
![]() ${\mathcal {N}}'|{\kappa }$
Footnote
66
${\mathcal {N}}'|{\kappa }$
Footnote
66
Let
![]() $i: {\mathcal {P}}\rightarrow {\mathcal {P}}'$
be the iteration embedding.
$i: {\mathcal {P}}\rightarrow {\mathcal {P}}'$
be the iteration embedding.
Claim.
![]() $ i({\alpha }_s)\leq \iota _{{\mathcal {N}}'}$
.
$ i({\alpha }_s)\leq \iota _{{\mathcal {N}}'}$
.
Proof. Suppose that
![]() $i({\alpha }_s)>\iota _{{\mathcal {N}}'}$
. Because the fully backgrounded constructions of
$i({\alpha }_s)>\iota _{{\mathcal {N}}'}$
. Because the fully backgrounded constructions of
![]() ${\mathcal {P}}'$
and
${\mathcal {P}}'$
and
![]() ${\mathcal {N}}'$
are the same and because
${\mathcal {N}}'$
are the same and because
![]() $\iota _{{\mathcal {N}}'}$
is an
$\iota _{{\mathcal {N}}'}$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {N}}'$
, we have that
${\mathcal {N}}'$
, we have that
![]() $\iota _{{\mathcal {N}}'}$
is an
$\iota _{{\mathcal {N}}'}$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {P}}'$
. It now follows that
${\mathcal {P}}'$
. It now follows that
![]() $\theta (k, u, x, x_1, x_2, x_3)$
holds, and therefore,
$\theta (k, u, x, x_1, x_2, x_3)$
holds, and therefore,
![]() $k\in w'$
.
$k\in w'$
.
Now, set
![]() ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {N}}'|i({\beta }_s))=\mathsf {{StrLe}}({\mathcal {P}}'|i({\beta }_s))$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {N}}'|i({\beta }_s))=\mathsf {{StrLe}}({\mathcal {P}}'|i({\beta }_s))$
and
![]() $\mathcal {E}=\mathcal {E}^{{\mathcal { K}}|i({\alpha }_s)}_{sm}$
. Let
$\mathcal {E}=\mathcal {E}^{{\mathcal { K}}|i({\alpha }_s)}_{sm}$
. Let
![]() $(q, r)\in \mathsf {{Ea}}^{{\mathcal { K}}}_{i({\alpha }_s), \mathcal {E}}\times \mathsf {{Ea}}^{{\mathcal { K}}}_{i({\alpha }_s), \mathcal {E}}$
be such that
$(q, r)\in \mathsf {{Ea}}^{{\mathcal { K}}}_{i({\alpha }_s), \mathcal {E}}\times \mathsf {{Ea}}^{{\mathcal { K}}}_{i({\alpha }_s), \mathcal {E}}$
be such that
-
1.
 $x\models q$
,
$x\models q$
, -
2.
 $(x_1, x_2, x_3)\models r$
,
$(x_1, x_2, x_3)\models r$
, -
3.
 $(q, r)\Vdash \exists b( U^{\prime }_{{\mathcal { K}}[\mathsf {{ea}}^l, \mathsf {{ea}}^r], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l, b))$
where letting
$(q, r)\Vdash \exists b( U^{\prime }_{{\mathcal { K}}[\mathsf {{ea}}^l, \mathsf {{ea}}^r], d}(\mathsf {{ea}}^r_2, \mathsf {{ea}}^l, b))$
where letting
 $({\alpha }_s, \xi _1,..., \xi _{2n})$
be the Woodin cardinals of
$({\alpha }_s, \xi _1,..., \xi _{2n})$
be the Woodin cardinals of
 ${\mathcal { K}}$
enumerated in increasing order,
${\mathcal { K}}$
enumerated in increasing order,
 $d=(\xi _1, \xi _2,..., \xi _{2n})$
.
$d=(\xi _1, \xi _2,..., \xi _{2n})$
.
Assuming that
![]() $\pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
is compatible with r, we get that
$\pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
is compatible with r, we get that
![]() $(i({\alpha }_s), i({\beta }_s), q, r)\in \pi _{{\mathcal {N}}, {\mathcal {N}}'}(\mathcal {A})$
. To finish we need to see that in fact
$(i({\alpha }_s), i({\beta }_s), q, r)\in \pi _{{\mathcal {N}}, {\mathcal {N}}'}(\mathcal {A})$
. To finish we need to see that in fact
![]() $\pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
is compatible with r. Notice now that because
$\pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
is compatible with r. Notice now that because
![]() ${\gamma} _{x_1}={\gamma} $
,
${\gamma} _{x_1}={\gamma} $
,
![]() $(x_1, x_2, x_3)\models \pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
Footnote
67
. Because
$(x_1, x_2, x_3)\models \pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
Footnote
67
. Because
![]() $(x_1, x_2, x_3)\models r$
, we must have that r is compatible with
$(x_1, x_2, x_3)\models r$
, we must have that r is compatible with
![]() $\pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
. Thus,
$\pi _{{\mathcal {N}}, {\mathcal {N}}'}(p)$
. Thus,
![]() $(i({\alpha }_s), i({\beta }_s), q, r)\in \pi _{{\mathcal {N}}, {\mathcal {N}}'}(\mathcal {A})$
.
$(i({\alpha }_s), i({\beta }_s), q, r)\in \pi _{{\mathcal {N}}, {\mathcal {N}}'}(\mathcal {A})$
.
Set now
![]() ${\mathcal {T}}={\mathcal {T}}_{{\mathcal {N}}, {\mathcal {N}}'}$
and
${\mathcal {T}}={\mathcal {T}}_{{\mathcal {N}}, {\mathcal {N}}'}$
and
![]() $\tau =\mathrm {lh}({\mathcal {T}})-1$
. Because
$\tau =\mathrm {lh}({\mathcal {T}})-1$
. Because
![]() $\iota _{\mathcal {N}}$
is a cutpoint of
$\iota _{\mathcal {N}}$
is a cutpoint of
![]() ${\mathcal {N}}$
, we can find
${\mathcal {N}}$
, we can find
![]() $\xi <\mathrm {lh}({\mathcal {T}})$
such that
$\xi <\mathrm {lh}({\mathcal {T}})$
such that
-
1.
 ${\mathcal {M}}_\xi ^{\mathcal {T}}|\iota _{{\mathcal {N}}'}={\mathcal {N}}'|\iota _{{\mathcal {N}}'}$
,
${\mathcal {M}}_\xi ^{\mathcal {T}}|\iota _{{\mathcal {N}}'}={\mathcal {N}}'|\iota _{{\mathcal {N}}'}$
, -
2. the generators of
 ${\mathcal {T}}\restriction \xi $
are contained in
${\mathcal {T}}\restriction \xi $
are contained in
 $\iota _{{\mathcal {N}}'}$
,
$\iota _{{\mathcal {N}}'}$
, -
3.
 $\xi \in [0, \tau ]_{{\mathcal {T}}}$
,
$\xi \in [0, \tau ]_{{\mathcal {T}}}$
, -
4. all the extenders used in
 $[0, \tau )_{\mathcal {T}}$
after stage
$[0, \tau )_{\mathcal {T}}$
after stage
 $\xi $
have critical points
$\xi $
have critical points
 $>\iota _{\mathcal {N}}$
.
$>\iota _{\mathcal {N}}$
.
Set
![]() ${\mathcal {S}}={\mathcal {M}}_\xi ^{\mathcal {T}}$
. We then have that
${\mathcal {S}}={\mathcal {M}}_\xi ^{\mathcal {T}}$
. We then have that
![]() $\pi _{{\mathcal {N}}, {\mathcal {N}}'}(\mathcal {A})=\pi _{{\mathcal {N}}, {\mathcal {S}}}(\mathcal {A})$
, and the pair
$\pi _{{\mathcal {N}}, {\mathcal {N}}'}(\mathcal {A})=\pi _{{\mathcal {N}}, {\mathcal {S}}}(\mathcal {A})$
, and the pair
![]() $({\mathcal {T}}\restriction \xi +1, (i({\alpha }_s), i({\beta }_s), q, r))$
witnesses clause 2 of Lemma 4.8.
$({\mathcal {T}}\restriction \xi +1, (i({\alpha }_s), i({\beta }_s), q, r))$
witnesses clause 2 of Lemma 4.8.
(Clause 2 implies Clause 1.) Conversely, suppose
![]() ${\mathcal {S}}$
is a complete iterate of
${\mathcal {S}}$
is a complete iterate of
![]() ${\mathcal {N}}$
such that
${\mathcal {N}}$
such that
![]() ${\mathcal {T}}_{{\mathcal {N}}, {\mathcal {S}}}$
is based on
${\mathcal {T}}_{{\mathcal {N}}, {\mathcal {S}}}$
is based on
![]() ${\mathcal { Q}}_{\mathcal {N}}$
and for some
${\mathcal { Q}}_{\mathcal {N}}$
and for some
![]() $({\alpha }', {\beta }', q, r)\in \pi _{{\mathcal {N}}, {\mathcal {S}}}(\mathcal {A})$
,
$({\alpha }', {\beta }', q, r)\in \pi _{{\mathcal {N}}, {\mathcal {S}}}(\mathcal {A})$
,
![]() $x\models q$
and setting
$x\models q$
and setting
![]() ${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {S}}|{\beta }')$
and
${\mathcal { K}}=\mathsf {{StrLe}}({\mathcal {S}}|{\beta }')$
and
![]() $\mathcal {E}=\mathcal {E}^{{\mathcal { K}}}_{sm}$
, x is generic over
$\mathcal {E}=\mathcal {E}^{{\mathcal { K}}}_{sm}$
, x is generic over
![]() $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
. We now further iterate
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
. We now further iterate
![]() ${\mathcal {S}}$
above
${\mathcal {S}}$
above
![]() ${\alpha }'$
to get
${\alpha }'$
to get
![]() ${\mathcal {S}}'$
such that x is generic over
${\mathcal {S}}'$
such that x is generic over
![]() $\mathsf {{Ea}}^{{\mathcal {S}}'}_{{\delta }_{{\mathcal {S}}'}, {\alpha }'}$
Footnote
68
. We then have that x is actually generic over
$\mathsf {{Ea}}^{{\mathcal {S}}'}_{{\delta }_{{\mathcal {S}}'}, {\alpha }'}$
Footnote
68
. We then have that x is actually generic over
![]() ${\mathcal {P}}=_{def}\mathsf {{StrLe}}({\mathcal {S}}')$
(see Clause 2 of Review 2.7). It follows that there is a
${\mathcal {P}}=_{def}\mathsf {{StrLe}}({\mathcal {S}}')$
(see Clause 2 of Review 2.7). It follows that there is a
![]() ${\mathcal {P}}[x]$
-generic
${\mathcal {P}}[x]$
-generic
![]() $(x_1, x_2, x_3)$
such that
$(x_1, x_2, x_3)$
such that
![]() $(x_1, x_2, x_3)\models r\wedge \pi _{{\mathcal {N}}, {\mathcal {S}}'}(p)$
. Therefore, we must have that
$(x_1, x_2, x_3)\models r\wedge \pi _{{\mathcal {N}}, {\mathcal {S}}'}(p)$
. Therefore, we must have that
![]() ${\gamma} _{x_1}={\gamma} $
and
${\gamma} _{x_1}={\gamma} $
and
![]() $x_2\in B_{\gamma} $
. If we now show that
$x_2\in B_{\gamma} $
. If we now show that
![]() $U(x_2, x)$
holds then we will get that
$U(x_2, x)$
holds then we will get that
![]() $x\in A_{\gamma} $
.
$x\in A_{\gamma} $
.
To show that
![]() $U(x_2, x)$
holds it is enough to show that
$U(x_2, x)$
holds it is enough to show that
![]() $(x_1, x_2, x_3)$
is generic over
$(x_1, x_2, x_3)$
is generic over
![]() ${\mathcal { K}}[x]$
for
${\mathcal { K}}[x]$
for
![]() $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
. Assuming this, we have that since
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
. Assuming this, we have that since
and
![]() ${\mathcal { K}}[x, (x_1, x_2, x_3)]$
is
${\mathcal { K}}[x, (x_1, x_2, x_3)]$
is
![]() $\Sigma ^1_{2n+2}$
correct, in fact
$\Sigma ^1_{2n+2}$
correct, in fact
![]() $\exists b U'(x_2, x, b)$
holds in V. Therefore,
$\exists b U'(x_2, x, b)$
holds in V. Therefore,
![]() $U(x_2, x)$
holds.
$U(x_2, x)$
holds.
The fact that
![]() $(x_1, x_2, x_3)$
is generic over
$(x_1, x_2, x_3)$
is generic over
![]() ${\mathcal { K}}[x]$
for
${\mathcal { K}}[x]$
for
![]() $\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
follows from the Claim in the proof of [Reference Hjorth7, Theorem 2.2]. To apply that Claim, set g to be
$\mathsf {{Ea}}^{{\mathcal { K}}}_{{\alpha }', \mathcal {E}}$
follows from the Claim in the proof of [Reference Hjorth7, Theorem 2.2]. To apply that Claim, set g to be
![]() $(x_1, x_2, x_3)$
,
$(x_1, x_2, x_3)$
,
![]() $\psi _0$
to be
$\psi _0$
to be
![]() $r\wedge \pi _{{\mathcal {N}}, {\mathcal {S}}}(p)$
and y to be x. Here we use the fact that
$r\wedge \pi _{{\mathcal {N}}, {\mathcal {S}}}(p)$
and y to be x. Here we use the fact that
![]() ${\alpha }'$
is an
${\alpha }'$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {S}}'|\iota _{{\mathcal {S}}'}$
and
${\mathcal {S}}'|\iota _{{\mathcal {S}}'}$
and
![]() $\iota _{{\mathcal {S}}'}$
is an
$\iota _{{\mathcal {S}}'}$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {S}}'$
, implying that in fact
${\mathcal {S}}'$
, implying that in fact
![]() ${\alpha }'$
is an
${\alpha }'$
is an
![]() $fb$
-cut of
$fb$
-cut of
![]() ${\mathcal {S}}'$
. Thus,
${\mathcal {S}}'$
. Thus,
![]() ${\mathcal { K}}|{\alpha }'{\triangleleft } {\mathcal {P}}$
and
${\mathcal { K}}|{\alpha }'{\triangleleft } {\mathcal {P}}$
and
![]() $\sigma '$
is a cardinal of
$\sigma '$
is a cardinal of
![]() ${\mathcal {P}}$
.
${\mathcal {P}}$
.
To finish the proof, notice that if
![]() $g\subseteq Coll(\omega , (\iota _{\mathcal {N}}^+)^{\mathcal {N}})$
is generic over
$g\subseteq Coll(\omega , (\iota _{\mathcal {N}}^+)^{\mathcal {N}})$
is generic over
![]() ${\mathcal {N}}$
,
${\mathcal {N}}$
,
![]() $y\in {\mathcal {N}}[g]$
codes
$y\in {\mathcal {N}}[g]$
codes
![]() ${\mathcal { Q}}_{\mathcal {N}}$
and
${\mathcal { Q}}_{\mathcal {N}}$
and
![]() $\sigma $
is the formula displayed in clause 2 of Sublemma 4.8 then in fact
$\sigma $
is the formula displayed in clause 2 of Sublemma 4.8 then in fact
![]() $A_{\gamma} \in \Sigma ^1_{2n+2}(y)$
as witnessed by
$A_{\gamma} \in \Sigma ^1_{2n+2}(y)$
as witnessed by
![]() $\sigma $
(here we use clause 1 of Lemma 4.5). Therefore, we can find
$\sigma $
(here we use clause 1 of Lemma 4.5). Therefore, we can find
![]() $y'$
that is Turing reducible to y and such that
$y'$
that is Turing reducible to y and such that
![]() $u\in A_{\gamma} {\mathrel {\leftrightarrow }} U(y', u)$
. Hence, we have that
$u\in A_{\gamma} {\mathrel {\leftrightarrow }} U(y', u)$
. Hence, we have that
![]() $y'\in B_{\gamma} \cap {\mathcal {N}}[g]$
.
$y'\in B_{\gamma} \cap {\mathcal {N}}[g]$
.
4.5 Removing the use of Kechris-Martin
Recall that
![]() ${\mathcal { Q}}={\mathcal {M}}|(\iota _{\mathcal {M}}^+)^{\mathcal {M}}$
(where
${\mathcal { Q}}={\mathcal {M}}|(\iota _{\mathcal {M}}^+)^{\mathcal {M}}$
(where
![]() $\iota _{\mathcal {M}}, \zeta _{\mathcal {M}}$
were introduced in the beginning of Section 4.4) and if
$\iota _{\mathcal {M}}, \zeta _{\mathcal {M}}$
were introduced in the beginning of Section 4.4) and if
![]() ${\mathcal {S}}$
is a complete iterate of
${\mathcal {S}}$
is a complete iterate of
![]() ${\mathcal {M}}$
then let
${\mathcal {M}}$
then let
![]() ${\mathcal { Q}}_{\mathcal {S}}=\pi _{{\mathcal {M}}, {\mathcal {S}}}({\mathcal { Q}})$
. We have that
${\mathcal { Q}}_{\mathcal {S}}=\pi _{{\mathcal {M}}, {\mathcal {S}}}({\mathcal { Q}})$
. We have that
![]() ${\mathcal { Q}}{\triangleleft } {\mathcal {M}}|{\kappa }_{\mathcal {M}}$
and for each
${\mathcal { Q}}{\triangleleft } {\mathcal {M}}|{\kappa }_{\mathcal {M}}$
and for each
![]() ${\gamma} $
there is a complete iterate
${\gamma} $
there is a complete iterate
![]() ${\mathcal {S}}$
of
${\mathcal {S}}$
of
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() ${\mathcal {T}}_{{\mathcal {M}}, {\mathcal {S}}}$
is below
${\mathcal {T}}_{{\mathcal {M}}, {\mathcal {S}}}$
is below
![]() $\iota _{\mathcal {M}}$
and if
$\iota _{\mathcal {M}}$
and if
![]() $g\subseteq Coll(\omega , \pi _{{\mathcal {M}}, {\mathcal {S}}}({\mathcal { Q}}))$
is generic over
$g\subseteq Coll(\omega , \pi _{{\mathcal {M}}, {\mathcal {S}}}({\mathcal { Q}}))$
is generic over
![]() ${\mathcal {S}}$
then
${\mathcal {S}}$
then
![]() ${\mathcal {S}}[g]\cap B_{\gamma} \not =\emptyset $
. Fix some recursive enumeration
${\mathcal {S}}[g]\cap B_{\gamma} \not =\emptyset $
. Fix some recursive enumeration
![]() $(\phi _e: e\in \omega )$
of recursive functions.
$(\phi _e: e\in \omega )$
of recursive functions.
Fix
![]() ${\gamma} <{\delta }^1_{2n+2}$
and let
${\gamma} <{\delta }^1_{2n+2}$
and let
![]() ${\mathcal {S}}$
be a complete
${\mathcal {S}}$
be a complete
![]() ${\gamma} $
-stable iterate of
${\gamma} $
-stable iterate of
![]() ${\mathcal {M}}$
. Let
${\mathcal {M}}$
. Let
![]() $g\subseteq Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
be
$g\subseteq Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
be
![]() ${\mathcal {S}}$
-generic,
${\mathcal {S}}$
-generic,
![]() $a_g=\{(i, j)\in \omega ^2: g(i)\in g(j)\}$
and e be such that if
$a_g=\{(i, j)\in \omega ^2: g(i)\in g(j)\}$
and e be such that if
![]() $v=\phi _e(a_g)$
then
$v=\phi _e(a_g)$
then
![]() $U_v=A_{\gamma} $
. Let
$U_v=A_{\gamma} $
. Let
![]() $\dot {\mathbb {P}}$
be a
$\dot {\mathbb {P}}$
be a
![]() $Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
-name for
$Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
-name for
![]() $\mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
and let
$\mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
and let
![]() $\dot {s}\in {\mathcal {S}}$
be a
$\dot {s}\in {\mathcal {S}}$
be a
![]() $Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
-name for
$Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
-name for
![]() $p_{{\gamma} , 0, 3, 1}^{{\mathcal {S}}[g]}$
, the
$p_{{\gamma} , 0, 3, 1}^{{\mathcal {S}}[g]}$
, the
![]() $({\gamma} , 0, 3, 1)$
-master condition in
$({\gamma} , 0, 3, 1)$
-master condition in
![]() ${\mathcal {S}}[g]$
(see clause 9 of Review 2.19). It follows from clause 12 of Section 3 that
${\mathcal {S}}[g]$
(see clause 9 of Review 2.19). It follows from clause 12 of Section 3 that
(*) if
![]() $(\dot {s}, \dot {q})\in \dot {\mathbb {P}}\times \dot {\mathbb {P}}$
then
$(\dot {s}, \dot {q})\in \dot {\mathbb {P}}\times \dot {\mathbb {P}}$
then
![]() ${\mathcal {S}}[g]\models (\dot {s}_g, \dot {q}_g)\Vdash `D(\mathsf {{ea}}^r_1, \mathsf {{ea}}^r_2,\mathsf {{ea}}^r_3) \rightarrow (U_v= U_{\mathsf {{ea}}^r_2})$
’.
${\mathcal {S}}[g]\models (\dot {s}_g, \dot {q}_g)\Vdash `D(\mathsf {{ea}}^r_1, \mathsf {{ea}}^r_2,\mathsf {{ea}}^r_3) \rightarrow (U_v= U_{\mathsf {{ea}}^r_2})$
’.
Let
![]() $\dot {a}$
be
$\dot {a}$
be
![]() $Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
-name for
$Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
-name for
![]() $a_g$
. It follows from (*) that there is a condition
$a_g$
. It follows from (*) that there is a condition
![]() $p\in Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
and
$p\in Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
and
![]() $e\in \omega $
such that
$e\in \omega $
such that
(**) whenever
![]() $\dot {q}\in \dot {\mathbb {P}}$
,
$\dot {q}\in \dot {\mathbb {P}}$
,
![]() ${\mathcal {S}}\models (p, \dot {s}, \dot {q})\Vdash `D(\mathsf {{ea}}^r_1, \mathsf {{ea}}^r_2,\mathsf {{ea}}^r_3) \rightarrow (U_{\phi _e(\dot {a})}= U_{\mathsf {{ea}}^r_2})$
’.
${\mathcal {S}}\models (p, \dot {s}, \dot {q})\Vdash `D(\mathsf {{ea}}^r_1, \mathsf {{ea}}^r_2,\mathsf {{ea}}^r_3) \rightarrow (U_{\phi _e(\dot {a})}= U_{\mathsf {{ea}}^r_2})$
’.
Let
![]() $( p_{\gamma} ^{\mathcal {S}}, e^{\mathcal {S}}_{\gamma} )$
be the lexicographically least pair
$( p_{\gamma} ^{\mathcal {S}}, e^{\mathcal {S}}_{\gamma} )$
be the lexicographically least pair
![]() $(p, e)$
satisfying (**).
$(p, e)$
satisfying (**).
Suppose now that
![]() ${\mathcal {S}}'$
is a complete iterate of
${\mathcal {S}}'$
is a complete iterate of
![]() ${\mathcal {S}}$
. Then because
${\mathcal {S}}$
. Then because
![]() ${\mathcal {S}}$
is
${\mathcal {S}}$
is
![]() ${\gamma} $
-stable we have that
${\gamma} $
-stable we have that
![]() $\pi _{{\mathcal {S}}, {\mathcal {S}}'}(p_{\gamma} ^{\mathcal {S}}, e^{\mathcal {S}}_{\gamma} )=(p_{\gamma} ^{{\mathcal {S}}'}, e^{{\mathcal {S}}'}_{{\gamma} })$
. Set then
$\pi _{{\mathcal {S}}, {\mathcal {S}}'}(p_{\gamma} ^{\mathcal {S}}, e^{\mathcal {S}}_{\gamma} )=(p_{\gamma} ^{{\mathcal {S}}'}, e^{{\mathcal {S}}'}_{{\gamma} })$
. Set then
![]() $(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })=\pi _{{\mathcal {S}}, \infty }(p_{\gamma} ^{\mathcal {S}}, e_{\gamma} ^{\mathcal {S}})$
.
$(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })=\pi _{{\mathcal {S}}, \infty }(p_{\gamma} ^{\mathcal {S}}, e_{\gamma} ^{\mathcal {S}})$
.
We now claim that if
![]() ${\gamma} \not ={\gamma} '$
then
${\gamma} \not ={\gamma} '$
then
![]() $(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })\not =(p_{{\gamma} ', \infty }, e_{{\gamma} ', \infty })$
. Suppose to the contrary that
$(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })\not =(p_{{\gamma} ', \infty }, e_{{\gamma} ', \infty })$
. Suppose to the contrary that
![]() $(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })=(p_{{\gamma} ', \infty }, e_{{\gamma} ', \infty })$
. Let
$(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })=(p_{{\gamma} ', \infty }, e_{{\gamma} ', \infty })$
. Let
![]() ${\mathcal {S}}$
be a complete iterate of
${\mathcal {S}}$
be a complete iterate of
![]() ${\mathcal {M}}$
which is both
${\mathcal {M}}$
which is both
![]() ${\gamma} $
and
${\gamma} $
and
![]() ${\gamma} '$
stable. It is enough to show that
${\gamma} '$
stable. It is enough to show that
![]() $(p^{{\mathcal {S}}}_{{\gamma} }, e_{\gamma} ^{\mathcal {S}})\not =(p_{{\gamma} '}^{\mathcal {S}}, e_{{\gamma} '}^{\mathcal {S}})$
. Suppose then that
$(p^{{\mathcal {S}}}_{{\gamma} }, e_{\gamma} ^{\mathcal {S}})\not =(p_{{\gamma} '}^{\mathcal {S}}, e_{{\gamma} '}^{\mathcal {S}})$
. Suppose then that
![]() $(p^{{\mathcal {S}}}_{{\gamma} }, e_{\gamma} ^{\mathcal {S}})=(p_{{\gamma} '}^{\mathcal {S}}, e_{{\gamma} '}^{\mathcal {S}})=_{def}(p, e)$
. Let
$(p^{{\mathcal {S}}}_{{\gamma} }, e_{\gamma} ^{\mathcal {S}})=(p_{{\gamma} '}^{\mathcal {S}}, e_{{\gamma} '}^{\mathcal {S}})=_{def}(p, e)$
. Let
![]() $g\subseteq Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
be
$g\subseteq Coll(\omega , {\mathcal { Q}}_{\mathcal {S}})$
be
![]() ${\mathcal {S}}$
-generic such that
${\mathcal {S}}$
-generic such that
![]() $p\in g$
and let
$p\in g$
and let
![]() $v=\phi _e(a_g)$
. Let
$v=\phi _e(a_g)$
. Let
![]() $s\in \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
be the
$s\in \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
be the
![]() $({\gamma} , 0 , 3, 1)$
-master condition and let
$({\gamma} , 0 , 3, 1)$
-master condition and let
![]() $s'\in \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
be the
$s'\in \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
be the
![]() $({\gamma} ', 0, 3, 1)$
-master condition.
$({\gamma} ', 0, 3, 1)$
-master condition.
Because
![]() $A_{\gamma} \not =A_{{\gamma} '}$
, we can, without losing generality, assume that there is
$A_{\gamma} \not =A_{{\gamma} '}$
, we can, without losing generality, assume that there is
![]() $x\in A_{\gamma} -A_{{\gamma} '}$
. Fix such an x.
$x\in A_{\gamma} -A_{{\gamma} '}$
. Fix such an x.
We now have that
(***) there is a condition
![]() $(r, r')\in \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}\times \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
such that
$(r, r')\in \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}\times \mathsf {{Ea}}^{{\mathcal {S}}[g]}_{{\delta }_{\mathcal {S}}}$
such that
![]() $(r, r')$
extends
$(r, r')$
extends
![]() $(s, s')$
and
$(s, s')$
and
(***) can be shown by iterating
![]() ${\mathcal {S}}[g]$
to make two triples
${\mathcal {S}}[g]$
to make two triples
![]() $(y_1, y_2, y_3)$
and
$(y_1, y_2, y_3)$
and
![]() $(y_1', y_2', y_3')$
generic where the triples are chosen so that
$(y_1', y_2', y_3')$
generic where the triples are chosen so that
-
1.
 $D(y_1, y_2, y_3)$
and
$D(y_1, y_2, y_3)$
and
 $D(y^{\prime }_1, y^{\prime }_2, y^{\prime }_3)$
,
$D(y^{\prime }_1, y^{\prime }_2, y^{\prime }_3)$
, -
2.
 ${\gamma} _{y_1}={\gamma} $
and
${\gamma} _{y_1}={\gamma} $
and
 ${\gamma} _{y_1'}={\gamma} '$
.
${\gamma} _{y_1'}={\gamma} '$
.
Then elementarity would imply (***). Fix such a condition
![]() $(r, r')$
.
$(r, r')$
.
Suppose
![]() ${\mathcal R}$
is a complete iterate of
${\mathcal R}$
is a complete iterate of
![]() ${\mathcal {S}}[g]$
such that x is generic for
${\mathcal {S}}[g]$
such that x is generic for
![]() $\mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
over
$\mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
over
![]() ${\mathcal R}[g]$
. Let
${\mathcal R}[g]$
. Let
![]() $(x_1, x_2, x_3)$
be any
$(x_1, x_2, x_3)$
be any
![]() ${\mathcal R}[g, x]$
-generic for
${\mathcal R}[g, x]$
-generic for
![]() $\mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
with the property that
$\mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
with the property that
![]() $(x_1, x_2, x_3)\models \pi _{{\mathcal {S}}[g], {\mathcal R}[g]}(r)$
and let
$(x_1, x_2, x_3)\models \pi _{{\mathcal {S}}[g], {\mathcal R}[g]}(r)$
and let
![]() $(x_1', x_2', x_3')$
be any
$(x_1', x_2', x_3')$
be any
![]() ${\mathcal R}[g, x]$
-generic for
${\mathcal R}[g, x]$
-generic for
![]() $\mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
with the property that
$\mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
with the property that
![]() $(x_1', x_2', x_3')\models \pi _{{\mathcal {S}}[g], {\mathcal R}[g]}(r')$
. It follows from (***) that
$(x_1', x_2', x_3')\models \pi _{{\mathcal {S}}[g], {\mathcal R}[g]}(r')$
. It follows from (***) that
-
1.
 $D(x_1, x_2, x_3)$
and
$D(x_1, x_2, x_3)$
and
 $D(x_1', x_2', x_3')$
,
$D(x_1', x_2', x_3')$
, -
2.
 ${\gamma} _{x_1}={\gamma} $
and
${\gamma} _{x_1}={\gamma} $
and
 ${\gamma} _{x_1'}={\gamma} '$
.
${\gamma} _{x_1'}={\gamma} '$
.
We now have that (**) implies that
(1) if
![]() $q\in \mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
then
$q\in \mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
then
![]() ${\mathcal R}[g, (x_1, x_2, x_3)]\models q\Vdash `U_v=U_{x_2}$
’,
${\mathcal R}[g, (x_1, x_2, x_3)]\models q\Vdash `U_v=U_{x_2}$
’,
(2) if
![]() $q\in \mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
then
$q\in \mathsf {{Ea}}^{{\mathcal R}[g]}_{{\delta }_{\mathcal R}}$
then
![]() ${\mathcal R}[g, (x_1', x_2', x_3')]\models q\Vdash `U_v=U_{x_2'}$
’,
${\mathcal R}[g, (x_1', x_2', x_3')]\models q\Vdash `U_v=U_{x_2'}$
’,
Therefore, we get that
(3)
![]() ${\mathcal R}[g, (x_1, x_2, x_3)][x]\models `U_v=U_{x_2}$
’ and
${\mathcal R}[g, (x_1, x_2, x_3)][x]\models `U_v=U_{x_2}$
’ and
![]() ${\mathcal R}[g, (x_1', x_2', x_3')][x]\models `U_v=U_{x_2'}$
’.
${\mathcal R}[g, (x_1', x_2', x_3')][x]\models `U_v=U_{x_2'}$
’.
We now use (3) and clause 12 of Section 3 to make the following implications showing that
![]() $x\in A_{{\gamma} '}$
(recall that we chose
$x\in A_{{\gamma} '}$
(recall that we chose
![]() $x\in A_{\gamma} -A_{{\gamma} '}$
):
$x\in A_{\gamma} -A_{{\gamma} '}$
):
 $$ \begin{align*} U_{x_2}=A_{\gamma} &\rightarrow x\in (U_{x_2})^{{\mathcal R}[g, x, (x_1, x_2, x_3)]}\\ &\rightarrow x\in (U_v)^{{\mathcal R}[g, x, (x_1, x_2, x_3)]}\\ & \rightarrow x\in U_v\\ & \rightarrow x\in (U_v)^{{\mathcal R}[g, x, (x_1', x_2', x_3')]}\\ & \rightarrow x \in (U_{x_2'})^{{\mathcal R}[g, x, (x_1', x_2', x_3')]}\\ &\rightarrow x\in U_{x_2'}\\ &\rightarrow x\in A_{{\gamma}'} \end{align*} $$
$$ \begin{align*} U_{x_2}=A_{\gamma} &\rightarrow x\in (U_{x_2})^{{\mathcal R}[g, x, (x_1, x_2, x_3)]}\\ &\rightarrow x\in (U_v)^{{\mathcal R}[g, x, (x_1, x_2, x_3)]}\\ & \rightarrow x\in U_v\\ & \rightarrow x\in (U_v)^{{\mathcal R}[g, x, (x_1', x_2', x_3')]}\\ & \rightarrow x \in (U_{x_2'})^{{\mathcal R}[g, x, (x_1', x_2', x_3')]}\\ &\rightarrow x\in U_{x_2'}\\ &\rightarrow x\in A_{{\gamma}'} \end{align*} $$
Since we now have that the function
![]() $f({\gamma} )=(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })$
is an injection,
$f({\gamma} )=(p_{{\gamma} , \infty }, e_{{\gamma} , \infty })$
is an injection,
![]() ${\vert \pi _{{\mathcal {M}}, \infty }({\mathcal { Q}}) \vert } ={\delta }^1_{2n+2}$
.
${\vert \pi _{{\mathcal {M}}, \infty }({\mathcal { Q}}) \vert } ={\delta }^1_{2n+2}$
.
However, because
![]() $\mathsf {{Ord}}\cap {\mathcal { Q}}$
is a cutpoint of
$\mathsf {{Ord}}\cap {\mathcal { Q}}$
is a cutpoint of
![]() ${\mathcal {M}}$
,
${\mathcal {M}}$
,
![]() $\pi _{{\mathcal {M}}, \infty }({\mathcal { Q}})$
is the direct limit of all countable iterates of
$\pi _{{\mathcal {M}}, \infty }({\mathcal { Q}})$
is the direct limit of all countable iterates of
![]() ${\mathcal { Q}}$
, which we denoted by
${\mathcal { Q}}$
, which we denoted by
![]() ${\mathcal {M}}_\infty ({\mathcal { Q}})$
(see clause 3 of Review 2.2). It then follows from clause 2 of Lemma 4.5 that
${\mathcal {M}}_\infty ({\mathcal { Q}})$
(see clause 3 of Review 2.2). It then follows from clause 2 of Lemma 4.5 that
![]() ${\vert {\mathcal {M}}_\infty ({\mathcal { Q}}) \vert } <\delta ^1_{2n+2}$
. Indeed, consider the set
${\vert {\mathcal {M}}_\infty ({\mathcal { Q}}) \vert } <\delta ^1_{2n+2}$
. Indeed, consider the set
![]() $E=\{ u\in {\mathbb {R}}: u$
codes a pair
$E=\{ u\in {\mathbb {R}}: u$
codes a pair
![]() $({\mathcal R}_u, \iota _u)$
such that
$({\mathcal R}_u, \iota _u)$
such that
![]() ${\mathcal R}_u$
is a complete iterate of
${\mathcal R}_u$
is a complete iterate of
![]() ${\mathcal { Q}}$
and
${\mathcal { Q}}$
and
![]() $\iota _u\in \mathsf {{Ord}}\cap {\mathcal R}_u\}$
and for
$\iota _u\in \mathsf {{Ord}}\cap {\mathcal R}_u\}$
and for
![]() $u, u'\in E$
, set
$u, u'\in E$
, set
![]() $u\leq ^*_0u'$
if and only if letting
$u\leq ^*_0u'$
if and only if letting
![]() ${\mathcal R}$
be the complete common iterate of
${\mathcal R}$
be the complete common iterate of
![]() ${\mathcal R}_u$
and
${\mathcal R}_u$
and
![]() ${\mathcal R}_{u'}$
,
${\mathcal R}_{u'}$
,
![]() $\pi _{{\mathcal R}_u, {\mathcal R}}(\iota _u)\leq \pi _{{\mathcal R}_{u'}, {\mathcal R}}(\iota _{u'})$
. It now follows from clause 2 of Lemma 4.5 that
$\pi _{{\mathcal R}_u, {\mathcal R}}(\iota _u)\leq \pi _{{\mathcal R}_{u'}, {\mathcal R}}(\iota _{u'})$
. It now follows from clause 2 of Lemma 4.5 that
![]() $\leq ^*_0$
is
$\leq ^*_0$
is
![]() $\Sigma ^1_{2n+2}(u_0)$
where
$\Sigma ^1_{2n+2}(u_0)$
where
![]() $u_0$
codes
$u_0$
codes
![]() ${\mathcal { Q}}$
. Hence, the ordinal length of
${\mathcal { Q}}$
. Hence, the ordinal length of
![]() $\leq ^*_0$
is
$\leq ^*_0$
is
![]() $<{\delta }^1_{2n+2}$
Footnote
69
, and therefore
$<{\delta }^1_{2n+2}$
Footnote
69
, and therefore
![]() ${\vert {\mathcal {M}}_\infty ({\mathcal { Q}}) \vert } <{\delta }^1_{2n+2}$
.
${\vert {\mathcal {M}}_\infty ({\mathcal { Q}}) \vert } <{\delta }^1_{2n+2}$
.
5 Conclusion
Acknowledgements
I wish to thank John Steel for introducing me to [Reference Hjorth8] so many years ago. The work carried out in [Reference Sargsyan29], which answers most of the questions raised in the addendum of [Reference Hjorth8], was done while I was Steel’s PhD student. The addendum of [Reference Hjorth8] appeared in the unpublished version of Hjorth’s paper by the same title available on his web site. I am grateful to Derek Levinson for a list of typos and corrections, and indebted to the referee for a long list of corrections.
This paper is about 10 years late. Sometime in 2010, while I was a postdoc at UCLA, Hjorth suggested that two of us work on improving the results of [Reference Sargsyan29], and in particular compute
![]() $b_{2n+1, 0}$
(which [Reference Sargsyan29] conjectures to be
$b_{2n+1, 0}$
(which [Reference Sargsyan29] conjectures to be
![]() ${\delta }^1_{2n+2}$
) and also prove Kechris’ 2nd Conjecture. In [Reference Hjorth8], Hjorth showed that
${\delta }^1_{2n+2}$
) and also prove Kechris’ 2nd Conjecture. In [Reference Hjorth8], Hjorth showed that
![]() $b_{1, 0}=\delta ^1_2=\omega _2$
. The issues we encountered were the familiar ones: proving Kechris-Martin for
$b_{1, 0}=\delta ^1_2=\omega _2$
. The issues we encountered were the familiar ones: proving Kechris-Martin for
![]() $\Pi ^1_5$
and beyond, and avoiding fine boundedness arguments involving
$\Pi ^1_5$
and beyond, and avoiding fine boundedness arguments involving
![]() $\Sigma ^1_1$
relations and admissible ordinals. Unfortunately, on January 13 of 2011, Greg Hjorth unexpectedly passed away, and the project has remained unfinished. In the Spring of 2021 it became apparent that the use of Kechris-Martin in [Reference Hjorth8] is unnecessary.
$\Sigma ^1_1$
relations and admissible ordinals. Unfortunately, on January 13 of 2011, Greg Hjorth unexpectedly passed away, and the project has remained unfinished. In the Spring of 2021 it became apparent that the use of Kechris-Martin in [Reference Hjorth8] is unnecessary.
Funding statement
The author’s work is funded by the National Science Center, Poland under the Maestro Call, registration number UMO-2023/50/A/ST1/00258.