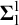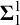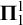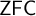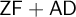1 Introduction
In [Reference Goldstern7], Goldstern showed the following theorem: let
![]() ${\langle A_x : x \in \omega ^\omega \rangle }$
be a family of Lebesgue measure zero sets. Assume that this family is increasing in the sense that if
${\langle A_x : x \in \omega ^\omega \rangle }$
be a family of Lebesgue measure zero sets. Assume that this family is increasing in the sense that if
![]() $x, x' \in \omega ^\omega $
satisfy
$x, x' \in \omega ^\omega $
satisfy
![]() $(\forall n\in \omega )(x(n) \le x'(n))$
then
$(\forall n\in \omega )(x(n) \le x'(n))$
then
![]() $A_x \subseteq A_{x'}$
. Also assume that
$A_x \subseteq A_{x'}$
. Also assume that
![]() $A = \{ (x, y) : y \in A_x \}$
is a
$A = \{ (x, y) : y \in A_x \}$
is a
![]() $\boldsymbol {\Sigma }^1_1$
set. Then
$\boldsymbol {\Sigma }^1_1$
set. Then
![]() $\bigcup _{x \in \omega ^\omega } A_x$
has also Lebesgue measure zero. Goldstern stated this theorem in terms of complements and applied it in the context of uniform distribution theory. Our main focus is to study to what extent we can remove this
$\bigcup _{x \in \omega ^\omega } A_x$
has also Lebesgue measure zero. Goldstern stated this theorem in terms of complements and applied it in the context of uniform distribution theory. Our main focus is to study to what extent we can remove this
![]() $\boldsymbol {\Sigma }^1_1$
assumption.
$\boldsymbol {\Sigma }^1_1$
assumption.
In Section 2, we will review Goldstern’s proof and define our principle
![]() $\mathsf {GP}(\Gamma )$
, which is the principle that replaces
$\mathsf {GP}(\Gamma )$
, which is the principle that replaces
![]() $\boldsymbol {\Sigma }^1_1$
in Goldstern’s theorem with a pointclass
$\boldsymbol {\Sigma }^1_1$
in Goldstern’s theorem with a pointclass
![]() $\Gamma $
. In Section 3, we will show
$\Gamma $
. In Section 3, we will show
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
. In Section 4, we will show the consistency of
$\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
. In Section 4, we will show the consistency of
![]() $\neg \mathsf {GP}(\mathsf {all})$
, where
$\neg \mathsf {GP}(\mathsf {all})$
, where
![]() $\mathsf {all}$
is the pointclass of all subsets of Polish spaces. In Section 5, we will prove that
$\mathsf {all}$
is the pointclass of all subsets of Polish spaces. In Section 5, we will prove that
![]() $\mathsf {GP}(\mathsf {all})$
is consistent with
$\mathsf {GP}(\mathsf {all})$
is consistent with
![]() $\mathsf {ZFC}$
. In Section 6, we will show that
$\mathsf {ZFC}$
. In Section 6, we will show that
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
implies a combinatorial hypothesis. In Section 7, we will show that
$\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
implies a combinatorial hypothesis. In Section 7, we will show that
![]() $\mathsf {GP}(\mathsf {all})$
holds under
$\mathsf {GP}(\mathsf {all})$
holds under
![]() $\mathsf {ZF}+\mathsf {AD}$
. In Section 8, we will prove under large cardinal hypotheses that
$\mathsf {ZF}+\mathsf {AD}$
. In Section 8, we will prove under large cardinal hypotheses that
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_n)$
and
$\mathsf {GP}(\boldsymbol {\Sigma }^1_n)$
and
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_{n+1})$
can be separated for each
$\mathsf {GP}(\boldsymbol {\Delta }^1_{n+1})$
can be separated for each
![]() $n \ge 2$
. In Section 9, we will show that
$n \ge 2$
. In Section 9, we will show that
![]() $\mathsf {GP}(\mathsf {all})$
holds in Solovay models. In Section 10, we will show
$\mathsf {GP}(\mathsf {all})$
holds in Solovay models. In Section 10, we will show
![]() $\neg \mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
, where
$\neg \mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
, where
![]() $\mathcal {E}$
is the
$\mathcal {E}$
is the
![]() $\sigma $
-ideal generated by closed null sets.
$\sigma $
-ideal generated by closed null sets.
In the rest of the section, we review basic terminology.
Definition 1.1. Define relations
![]() $\le $
and
$\le $
and
![]() $\le ^*$
on
$\le ^*$
on
![]() $\omega ^\omega $
as follows: for
$\omega ^\omega $
as follows: for
![]() $x, x' \in \omega ^\omega $
,
$x, x' \in \omega ^\omega $
,
 $$ \begin{align*} x \le x' &\iff (\forall n\in\omega)(x(n) \le x'(n))\text{, and} \\ x \le^* x' &\iff (\exists m \in \omega)(\forall n \ge m)(x(n) \le x'(n)). \end{align*} $$
$$ \begin{align*} x \le x' &\iff (\forall n\in\omega)(x(n) \le x'(n))\text{, and} \\ x \le^* x' &\iff (\exists m \in \omega)(\forall n \ge m)(x(n) \le x'(n)). \end{align*} $$
The cardinals defined below are typical examples of what are called cardinal invariants. For a detailed explanation of these cardinal invariants, see [Reference Bartoszynski and Judah3].
Definition 1.2.
-
(1) We say
 $F \subseteq \omega ^\omega $
is an unbounded family if
$F \subseteq \omega ^\omega $
is an unbounded family if
 $\neg (\exists g \in \omega ^\omega )(\forall f \in F)(f \le ^* g)$
. Put
$\neg (\exists g \in \omega ^\omega )(\forall f \in F)(f \le ^* g)$
. Put
 $\mathfrak {b} = \min \{ \left \lvert {F} \right \rvert : F \subseteq \omega ^\omega \text { unbounded family} \}$
.
$\mathfrak {b} = \min \{ \left \lvert {F} \right \rvert : F \subseteq \omega ^\omega \text { unbounded family} \}$
. -
(2) We say
 $F \subseteq \omega ^\omega $
is a dominating family if
$F \subseteq \omega ^\omega $
is a dominating family if
 $(\forall g \in \omega ^\omega )(\exists f \in F)(g \le ^* f)$
. Put
$(\forall g \in \omega ^\omega )(\exists f \in F)(g \le ^* f)$
. Put
 $\mathfrak {d} = \min \{ \left \lvert {F} \right \rvert : F \subseteq \omega ^\omega \text { dominating family} \}$
.
$\mathfrak {d} = \min \{ \left \lvert {F} \right \rvert : F \subseteq \omega ^\omega \text { dominating family} \}$
. -
(3)
 $\mathsf {null}$
and
$\mathsf {null}$
and
 $\mathsf {meager}$
denote the Lebesgue measure zero ideal and Baire first category ideal on
$\mathsf {meager}$
denote the Lebesgue measure zero ideal and Baire first category ideal on
 $2^\omega $
, respectively.
$2^\omega $
, respectively. -
(4) For an ideal
 $\mathcal {I}$
on a set X:
$\mathcal {I}$
on a set X:
 $\operatorname {add}(\mathcal {I})$
(the additivity number of
$\operatorname {add}(\mathcal {I})$
(the additivity number of
 $\mathcal {I}$
) is the smallest cardinality of a family F of sets in
$\mathcal {I}$
) is the smallest cardinality of a family F of sets in
 $\mathcal {I}$
such that the union of F is not in
$\mathcal {I}$
such that the union of F is not in
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(5) For an ideal
 $\mathcal {I}$
on a set X:
$\mathcal {I}$
on a set X:
 $\operatorname {cov}(\mathcal {I})$
(the covering number of
$\operatorname {cov}(\mathcal {I})$
(the covering number of
 $\mathcal {I}$
) is the smallest cardinality of a family F of sets in
$\mathcal {I}$
) is the smallest cardinality of a family F of sets in
 $\mathcal {I}$
such that the union of F is equal to X.
$\mathcal {I}$
such that the union of F is equal to X. -
(6) For an ideal
 $\mathcal {I}$
on a set X:
$\mathcal {I}$
on a set X:
 $\operatorname {non}(\mathcal {I})$
(the uniformity of
$\operatorname {non}(\mathcal {I})$
(the uniformity of
 $\mathcal {I}$
) is the smallest cardinality of a subset A of X such that A does not belong to
$\mathcal {I}$
) is the smallest cardinality of a subset A of X such that A does not belong to
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(7) For an ideal
 $\mathcal {I}$
on a set X:
$\mathcal {I}$
on a set X:
 $\operatorname {cof}(\mathcal {I})$
(the cofinality of
$\operatorname {cof}(\mathcal {I})$
(the cofinality of
 $\mathcal {I}$
) is the smallest cardinality of a family F of sets in
$\mathcal {I}$
) is the smallest cardinality of a family F of sets in
 $\mathcal {I}$
that satisfies the following condition: for every
$\mathcal {I}$
that satisfies the following condition: for every
 $A \in \mathcal {I}$
, there is
$A \in \mathcal {I}$
, there is
 $B \in F$
such that
$B \in F$
such that
 $A \subseteq B$
.
$A \subseteq B$
.
Notation 1.3. We denote interpretations of Borel codes by the hat symbol. So
![]() $\hat {c}$
is the interpretation of c if c is a Borel code.
$\hat {c}$
is the interpretation of c if c is a Borel code.
In this article we will often use pointclasses from the projective hierarchy, such as
![]() $\boldsymbol {\Sigma }^1_1$
,
$\boldsymbol {\Sigma }^1_1$
,
![]() $\boldsymbol {\Sigma }^1_2$
,
$\boldsymbol {\Sigma }^1_2$
,
![]() $\Sigma ^1_1(a)$
, etc. For a detailed explanation of projective hierarchy, see [Reference Moschovakis11].
$\Sigma ^1_1(a)$
, etc. For a detailed explanation of projective hierarchy, see [Reference Moschovakis11].
2 Review of Goldstern’s proof
In [Reference Goldstern7], Goldstern proved the following theorem. In the proof, he uses the Shoenfield absoluteness theorem and the random forcing. As for these, see [Reference Kanamori9, Chapter 3].
Theorem 2.1 (Goldstern)
Let
![]() $(Y, \mu )$
be a Polish probability space. Let
$(Y, \mu )$
be a Polish probability space. Let
![]() ${A \subseteq \omega ^\omega \times Y}$
be a
${A \subseteq \omega ^\omega \times Y}$
be a
![]() $\boldsymbol {\Sigma }^1_1$
set. Assume that for each
$\boldsymbol {\Sigma }^1_1$
set. Assume that for each
![]() $x \in \omega ^\omega $
,
$x \in \omega ^\omega $
,
has measure
![]() $0$
. Also, assume that
$0$
. Also, assume that
![]() $(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
. Then
$(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
. Then
![]() $\bigcup _{x \in \omega ^\omega } A_x$
also has measure
$\bigcup _{x \in \omega ^\omega } A_x$
also has measure
![]() $0$
.
$0$
.
Proof. We may assume that
![]() $Y = 2^\omega $
and
$Y = 2^\omega $
and
![]() $\mu $
is the usual measure of
$\mu $
is the usual measure of
![]() $2^\omega $
since for every Polish probability space Y, there is a Borel isomorphism between measure
$2^\omega $
since for every Polish probability space Y, there is a Borel isomorphism between measure
![]() $1$
subsets of Y and
$1$
subsets of Y and
![]() $2^\omega $
that preserves measure.
$2^\omega $
that preserves measure.
Fix a defining formula and a parameter of A. In generic extensions if we write A, we refer to the set defined by the formula and the parameter in the model.
Since A and
![]() $\bigcup _{x \in \omega ^\omega } A_x$
are
$\bigcup _{x \in \omega ^\omega } A_x$
are
![]() $\boldsymbol {\Sigma }^1_1$
sets, they are Lebesgue measurable. Toward a contradiction, assume that
$\boldsymbol {\Sigma }^1_1$
sets, they are Lebesgue measurable. Toward a contradiction, assume that
![]() $B := \bigcup _{x \in \omega ^\omega } A_x$
does not have measure 0. Then B has positive measure. By inner regularity of the measure, we can take a closed set
$B := \bigcup _{x \in \omega ^\omega } A_x$
does not have measure 0. Then B has positive measure. By inner regularity of the measure, we can take a closed set
![]() $K \subseteq B$
with positive measure. Take a Borel code k of K. We take a random real
$K \subseteq B$
with positive measure. Take a Borel code k of K. We take a random real
![]() $r \in 2^\omega $
over V such that
$r \in 2^\omega $
over V such that
![]() $r \in \hat {k}$
.
$r \in \hat {k}$
.
Now for each
![]() $x \in \omega ^\omega \cap V$
, we have
$x \in \omega ^\omega \cap V$
, we have
![]() $r \not \in A_x$
. In order to prove it, take a Borel code
$r \not \in A_x$
. In order to prove it, take a Borel code
![]() $d_x$
such that
$d_x$
such that
![]() $A_x \subseteq \hat {d_x}$
and
$A_x \subseteq \hat {d_x}$
and
![]() $\mu (\hat {d_x}) = 0$
. But the condition
$\mu (\hat {d_x}) = 0$
. But the condition
![]() $A_x \subseteq \hat {d_x}$
is
$A_x \subseteq \hat {d_x}$
is
![]() $\boldsymbol {\Pi }^1_1$
. Thus, since the random real avoids
$\boldsymbol {\Pi }^1_1$
. Thus, since the random real avoids
![]() $\hat {d_x}$
, we have
$\hat {d_x}$
, we have
![]() $r \not \in A_x$
.
$r \not \in A_x$
.
Therefore we have
But in
![]() $V[r]$
, it also holds that
$V[r]$
, it also holds that
since this formula is
![]() $\boldsymbol {\Pi }^1_2$
. Thus, by the assumption that
$\boldsymbol {\Pi }^1_2$
. Thus, by the assumption that
![]() $A_x$
is increasing and the fact that the random forcing is
$A_x$
is increasing and the fact that the random forcing is
![]() $\omega ^\omega $
-bounding, this implies
$\omega ^\omega $
-bounding, this implies
Therefore, in
![]() $V[r]$
, it holds that
$V[r]$
, it holds that
because
![]() $r' = r$
suffices. Recalling B is a
$r' = r$
suffices. Recalling B is a
![]() $\boldsymbol {\Sigma }^1_1$
set, this statement is written by a
$\boldsymbol {\Sigma }^1_1$
set, this statement is written by a
![]() $\boldsymbol {\Sigma }^1_2$
formula. Therefore, by Shoenfield’s absoluteness, it also holds in V. That is, there exists an
$\boldsymbol {\Sigma }^1_2$
formula. Therefore, by Shoenfield’s absoluteness, it also holds in V. That is, there exists an
![]() $r' \in 2^\omega $
in V such that
$r' \in 2^\omega $
in V such that
This contradicts the choice of K.
We define the principle
![]() $\mathsf {GP}(\Gamma )$
. We call the condition
$\mathsf {GP}(\Gamma )$
. We call the condition
![]() $(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
the monotonicity condition for A.
$(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
the monotonicity condition for A.
Definition 2.2. Let
![]() $\Gamma $
be a pointclass. Then
$\Gamma $
be a pointclass. Then
![]() $\mathsf {GP}(\Gamma )$
means the following statement: Let
$\mathsf {GP}(\Gamma )$
means the following statement: Let
![]() $(Y, \mu )$
be a Polish probability space and
$(Y, \mu )$
be a Polish probability space and
![]() $A \subseteq \omega ^\omega \times Y$
be in
$A \subseteq \omega ^\omega \times Y$
be in
![]() $\Gamma $
. Assume the monotonicity condition for A. Also suppose that
$\Gamma $
. Assume the monotonicity condition for A. Also suppose that
![]() $A_x$
has
$A_x$
has
![]() $\mu $
-measure
$\mu $
-measure
![]() $0$
for every
$0$
for every
![]() $x \in \omega ^\omega $
. Then
$x \in \omega ^\omega $
. Then
![]() $\bigcup _{x \in \omega ^\omega } A_x$
also has
$\bigcup _{x \in \omega ^\omega } A_x$
also has
![]() $\mu $
-measure
$\mu $
-measure
![]() $0$
.
$0$
.
We define
![]() $\mathsf {GP}^*(\Gamma )$
as the version of
$\mathsf {GP}^*(\Gamma )$
as the version of
![]() $\mathsf {GP}(\Gamma )$
where the order
$\mathsf {GP}(\Gamma )$
where the order
![]() $\le $
is replaced by
$\le $
is replaced by
![]() $\le ^*$
.
$\le ^*$
.
By Goldstern’s theorem, we have
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_1)$
.
$\mathsf {GP}(\boldsymbol {\Sigma }^1_1)$
.
For the reasons stated in the proof of Theorem 2.1, if the pointclass
![]() $\Gamma $
contains all Borel sets and closed under Borel functions, then we may assume that the space
$\Gamma $
contains all Borel sets and closed under Borel functions, then we may assume that the space
![]() $(Y, \mu )$
in the definition of
$(Y, \mu )$
in the definition of
![]() $\mathsf {GP}(\Gamma )$
is the Cantor space.
$\mathsf {GP}(\Gamma )$
is the Cantor space.
Recall that
![]() $\mathbb {B}$
denotes the random forcing.
$\mathbb {B}$
denotes the random forcing.
Theorem 2.3. For every natural number n, if
![]() $\boldsymbol {\Sigma }^1_{n+1}$
-
$\boldsymbol {\Sigma }^1_{n+1}$
-
![]() $\mathbb {B}$
-absoluteness holds and every
$\mathbb {B}$
-absoluteness holds and every
![]() $\boldsymbol {\Sigma }^1_n$
set is Lebesgue measurable, then
$\boldsymbol {\Sigma }^1_n$
set is Lebesgue measurable, then
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_n)$
holds. In particular, if every
$\mathsf {GP}(\boldsymbol {\Sigma }^1_n)$
holds. In particular, if every
![]() $\boldsymbol {\Sigma }^1_2$
set is Lebesgue measurable, then
$\boldsymbol {\Sigma }^1_2$
set is Lebesgue measurable, then
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_2)$
holds.
$\mathsf {GP}(\boldsymbol {\Sigma }^1_2)$
holds.
Proof. This is proved by the same argument as Theorem 2.1. Recall that
![]() $\boldsymbol {\Sigma }^1_3$
-
$\boldsymbol {\Sigma }^1_3$
-
![]() $\mathbb {B}$
-absoluteness follows from
$\mathbb {B}$
-absoluteness follows from
![]() $\boldsymbol {\Sigma }^1_2$
measurability (see [Reference Bartoszynski and Judah3, Theorems 9.2.12 and 9.3.8]).
$\boldsymbol {\Sigma }^1_2$
measurability (see [Reference Bartoszynski and Judah3, Theorems 9.2.12 and 9.3.8]).
Clearly
![]() $\mathsf {GP}(\Gamma )$
implies
$\mathsf {GP}(\Gamma )$
implies
![]() $\mathsf {GP}^*(\Gamma )$
. If we make a slight assumption on the pointclass
$\mathsf {GP}^*(\Gamma )$
. If we make a slight assumption on the pointclass
![]() $\Gamma $
, then the converse holds. We only consider such pointclasses.
$\Gamma $
, then the converse holds. We only consider such pointclasses.
Lemma 2.4. If a pointclass
![]() $\Gamma $
is closed under recursive substitution and projection along
$\Gamma $
is closed under recursive substitution and projection along
![]() $\omega $
, then
$\omega $
, then
![]() $\mathsf {GP}^*(\Gamma ) \Rightarrow \mathsf {GP}(\Gamma )$
.
$\mathsf {GP}^*(\Gamma ) \Rightarrow \mathsf {GP}(\Gamma )$
.
Proof. Assume
![]() $A \in \Gamma $
and for each
$A \in \Gamma $
and for each
![]() $x \in \omega ^\omega $
,
$x \in \omega ^\omega $
,
![]() $A_x$
has
$A_x$
has
![]() $\mu $
-measure
$\mu $
-measure
![]() $0$
and
$0$
and
![]() $(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
. Put
$(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
. Put
![]() $B_x = \bigcup \{ A_y : x \text { and } y \text { are almost equal} \}$
.
$B_x = \bigcup \{ A_y : x \text { and } y \text { are almost equal} \}$
.
Then by assumption,
![]() $B \in \Gamma $
and for each
$B \in \Gamma $
and for each
![]() $x \in \omega ^\omega $
,
$x \in \omega ^\omega $
,
![]() $B_x$
has
$B_x$
has
![]() $\mu $
-measure
$\mu $
-measure
![]() $0$
and that
$0$
and that
![]() $(\forall x, x' \in \omega ^\omega )(x \le ^* x' \Rightarrow B_{x} \subseteq B_{x'})$
. Therefore, by
$(\forall x, x' \in \omega ^\omega )(x \le ^* x' \Rightarrow B_{x} \subseteq B_{x'})$
. Therefore, by
![]() $\mathsf {GP}^*(\Gamma )$
,
$\mathsf {GP}^*(\Gamma )$
,
![]() $\bigcup _{x \in \omega ^\omega } B_x$
is a measure
$\bigcup _{x \in \omega ^\omega } B_x$
is a measure
![]() $0$
set. Thus
$0$
set. Thus
![]() $\bigcup _{x \in \omega ^\omega } A_x$
is a measure
$\bigcup _{x \in \omega ^\omega } A_x$
is a measure
![]() $0$
set.
$0$
set.
3
 $\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
$\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
In this section, we prove that
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
holds.
$\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
holds.
Fact 3.1 [Reference Kechris10, Reference Tanaka14]
Let
![]() $U \in \Sigma ^1_1$
,
$U \in \Sigma ^1_1$
,
![]() $U \subseteq \omega ^\omega \times 2^\omega $
be the universal for
$U \subseteq \omega ^\omega \times 2^\omega $
be the universal for
![]() $\boldsymbol {\Sigma }^1_1$
subset of
$\boldsymbol {\Sigma }^1_1$
subset of
![]() $2^\omega $
. Then the relation
$2^\omega $
. Then the relation
![]() $\mu (U_x)> r$
for
$\mu (U_x)> r$
for
![]() $x \in \omega ^\omega $
and
$x \in \omega ^\omega $
and
![]() $r \in \mathbb {R}$
is
$r \in \mathbb {R}$
is
![]() $\Sigma ^1_1$
.
$\Sigma ^1_1$
.
Corollary 3.2. Let
![]() $A \subseteq \omega ^\omega \times 2^\omega $
be a
$A \subseteq \omega ^\omega \times 2^\omega $
be a
![]() $\boldsymbol {\Sigma }^1_1$
set. Then the relation
$\boldsymbol {\Sigma }^1_1$
set. Then the relation
![]() $\mu (A_x)> r$
for
$\mu (A_x)> r$
for
![]() $x \in \omega ^\omega $
and
$x \in \omega ^\omega $
and
![]() $r \in \mathbb {R}$
is
$r \in \mathbb {R}$
is
![]() $\boldsymbol {\Sigma }^1_1$
.
$\boldsymbol {\Sigma }^1_1$
.
Proof. Take universal sets U and
![]() $U^{(2)}$
for
$U^{(2)}$
for
![]() $\boldsymbol {\Sigma }^1_1$
subsets of
$\boldsymbol {\Sigma }^1_1$
subsets of
![]() $2^\omega $
and
$2^\omega $
and
![]() $\omega ^\omega \times 2^\omega $
, respectively, with the following coherent property:
$\omega ^\omega \times 2^\omega $
, respectively, with the following coherent property:
![]() $U(S(e, x), y) \iff U^{(2)}(e, x, y)$
, where S is a recursively continuous function. As for the existence of such coherent universal sets, see [Reference Moschovakis11, Section 3.H]. Take
$U(S(e, x), y) \iff U^{(2)}(e, x, y)$
, where S is a recursively continuous function. As for the existence of such coherent universal sets, see [Reference Moschovakis11, Section 3.H]. Take
![]() $e \in \omega ^\omega $
such that
$e \in \omega ^\omega $
such that
![]() $A(x, y) \iff U^{(2)}(e, x, y)$
. Then we have
$A(x, y) \iff U^{(2)}(e, x, y)$
. Then we have
which is a
![]() $\boldsymbol {\Sigma }^1_1$
relation.
$\boldsymbol {\Sigma }^1_1$
relation.
Corollary 3.3. Let
![]() $A \subseteq \omega ^\omega \times 2^\omega $
be a
$A \subseteq \omega ^\omega \times 2^\omega $
be a
![]() $\boldsymbol {\Pi }^1_1$
set. Then the relation
$\boldsymbol {\Pi }^1_1$
set. Then the relation
![]() $\mu (A_x) = 0$
for
$\mu (A_x) = 0$
for
![]() $x \in \omega ^\omega $
is
$x \in \omega ^\omega $
is
![]() $\boldsymbol {\Sigma }^1_1$
.
$\boldsymbol {\Sigma }^1_1$
.
Proof. Let
![]() $B = (\omega ^\omega \times 2^\omega ) \smallsetminus A$
, which is
$B = (\omega ^\omega \times 2^\omega ) \smallsetminus A$
, which is
![]() $\boldsymbol {\Sigma }^1_1$
set. We have
$\boldsymbol {\Sigma }^1_1$
set. We have
which is a
![]() $\boldsymbol {\Sigma }^1_1$
relation.
$\boldsymbol {\Sigma }^1_1$
relation.
Theorem 3.4.
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
holds.
$\mathsf {GP}(\boldsymbol {\Pi }^1_1)$
holds.
Proof. Let
![]() $A \subseteq \omega ^\omega \times 2^\omega $
be a
$A \subseteq \omega ^\omega \times 2^\omega $
be a
![]() $\boldsymbol {\Pi }^1_1$
set. Assume
$\boldsymbol {\Pi }^1_1$
set. Assume
![]() ${\langle A_x : x \in \omega ^\omega \rangle }$
is monotone and each
${\langle A_x : x \in \omega ^\omega \rangle }$
is monotone and each
![]() $A_x$
is null. Take a Laver real d over V.
$A_x$
is null. Take a Laver real d over V.
![]() $(\forall x \in \omega ^\omega )(\mu (A_x) = 0)$
holds in V and this sentence is
$(\forall x \in \omega ^\omega )(\mu (A_x) = 0)$
holds in V and this sentence is
![]() $\boldsymbol {\Pi }^1_2$
using Corollary 3.3. So in
$\boldsymbol {\Pi }^1_2$
using Corollary 3.3. So in
![]() $V[d]$
,
$V[d]$
,
![]() $\mu (A_d) = 0$
holds. Also monotonicity of
$\mu (A_d) = 0$
holds. Also monotonicity of
![]() ${\langle A_x : x \in \omega ^\omega \rangle }$
can be written as a
${\langle A_x : x \in \omega ^\omega \rangle }$
can be written as a
![]() $\boldsymbol {\Pi }^1_2$
formula and holds in V, so it also holds in
$\boldsymbol {\Pi }^1_2$
formula and holds in V, so it also holds in
![]() $V[d]$
. Since d is a dominating real over V, we have
$V[d]$
. Since d is a dominating real over V, we have
![]() $(\bigcup _{x \in \omega ^\omega } A_x)^V \subseteq \bigcup _{x \in \omega ^\omega \cap V} A_x \subseteq A_d$
. Therefore
$(\bigcup _{x \in \omega ^\omega } A_x)^V \subseteq \bigcup _{x \in \omega ^\omega \cap V} A_x \subseteq A_d$
. Therefore
![]() $(\bigcup _{x \in \omega ^\omega } A_x)^V$
is null in
$(\bigcup _{x \in \omega ^\omega } A_x)^V$
is null in
![]() $V[d]$
. Since Laver forcing preserves Lebesgue outer measure, it holds that
$V[d]$
. Since Laver forcing preserves Lebesgue outer measure, it holds that
![]() $\bigcup _{x \in \omega ^\omega } A_x$
is null in V.
$\bigcup _{x \in \omega ^\omega } A_x$
is null in V.
4 Consistency of
 $\neg \mathsf {GP}(\mathsf {all})$
$\neg \mathsf {GP}(\mathsf {all})$
Definition 4.1. Let
![]() $\kappa $
be a cardinal. We call a sequence
$\kappa $
be a cardinal. We call a sequence
![]() ${\langle A_\alpha : \alpha < \kappa \rangle }$
a null tower of length
${\langle A_\alpha : \alpha < \kappa \rangle }$
a null tower of length
![]() $\kappa $
if it is an increasing sequence of measure
$\kappa $
if it is an increasing sequence of measure
![]() $0$
sets such that its union does not have measure
$0$
sets such that its union does not have measure
![]() $0$
.
$0$
.
Theorem 4.2. If there is a null tower of length either
![]() $\mathfrak {b}$
or
$\mathfrak {b}$
or
![]() $\mathfrak {d}$
, then
$\mathfrak {d}$
, then
![]() $\neg \mathsf {GP}(\mathsf {all})$
holds.
$\neg \mathsf {GP}(\mathsf {all})$
holds.
Proof. In the case of
![]() $\mathfrak {b}$
: By assumption, we take an increasing sequence
$\mathfrak {b}$
: By assumption, we take an increasing sequence
![]() ${\langle A_\alpha : \alpha < \mathfrak {b}\rangle }$
of measure-0 sets such that
${\langle A_\alpha : \alpha < \mathfrak {b}\rangle }$
of measure-0 sets such that
![]() $\bigcup _{\alpha < \mathfrak {b}} A_\alpha $
doesn’t have measure
$\bigcup _{\alpha < \mathfrak {b}} A_\alpha $
doesn’t have measure
![]() $0$
. We can take an increasing and unbounded sequence
$0$
. We can take an increasing and unbounded sequence
![]() ${\langle x_\alpha : \alpha < \mathfrak {b} \rangle }$
with respect to
${\langle x_\alpha : \alpha < \mathfrak {b} \rangle }$
with respect to
![]() $\le ^*$
(this sequence is not necessarily cofinal). For each
$\le ^*$
(this sequence is not necessarily cofinal). For each
![]() $x \in \omega ^\omega $
, put
$x \in \omega ^\omega $
, put
This is well-defined since
![]() ${\langle x_\alpha : \alpha < \mathfrak {b} \rangle }$
is unbounded. And then put
${\langle x_\alpha : \alpha < \mathfrak {b} \rangle }$
is unbounded. And then put
Now each
![]() $B_x$
has measure
$B_x$
has measure
![]() $0$
and we have
$0$
and we have
 $$ \begin{align*} x \le x' &\Rightarrow x \le^* x' \\ &\Rightarrow (\forall \alpha)(x_\alpha \le^* x \Rightarrow x_\alpha \le^* x') \\ &\Rightarrow \{ \alpha : x_\alpha \not \le^* x' \} \subseteq \{ \alpha : x_\alpha \not \le^* x \} \\ &\Rightarrow \alpha(x) \le \alpha(x') \\ &\Rightarrow B_x \subseteq B_{x'}. \end{align*} $$
$$ \begin{align*} x \le x' &\Rightarrow x \le^* x' \\ &\Rightarrow (\forall \alpha)(x_\alpha \le^* x \Rightarrow x_\alpha \le^* x') \\ &\Rightarrow \{ \alpha : x_\alpha \not \le^* x' \} \subseteq \{ \alpha : x_\alpha \not \le^* x \} \\ &\Rightarrow \alpha(x) \le \alpha(x') \\ &\Rightarrow B_x \subseteq B_{x'}. \end{align*} $$
Thus
![]() ${\langle B_x : x \in \omega ^\omega \rangle }$
is monotone. Also we have
${\langle B_x : x \in \omega ^\omega \rangle }$
is monotone. Also we have
![]() $\bigcup _{x \in \omega ^\omega } B_x = \bigcup _{\alpha < \mathfrak {b}} A_\alpha $
. Indeed, it is obvious that the left-hand side is contained in the right-hand side. To prove the reverse inclusion, it is sufficient to show that each
$\bigcup _{x \in \omega ^\omega } B_x = \bigcup _{\alpha < \mathfrak {b}} A_\alpha $
. Indeed, it is obvious that the left-hand side is contained in the right-hand side. To prove the reverse inclusion, it is sufficient to show that each
![]() $A_\alpha $
is contained in some
$A_\alpha $
is contained in some
![]() $B_x$
. So fix
$B_x$
. So fix
![]() $\alpha $
and consider
$\alpha $
and consider
![]() $x = x_{\alpha }$
. Since the sequence
$x = x_{\alpha }$
. Since the sequence
![]() ${\langle x_\alpha : \alpha < \mathfrak {b} \rangle }$
is increasing, we have
${\langle x_\alpha : \alpha < \mathfrak {b} \rangle }$
is increasing, we have
![]() $\alpha \le \alpha (x)$
. Thus
$\alpha \le \alpha (x)$
. Thus
![]() $A_\alpha \subseteq A_{\alpha (x)} = B_x$
.
$A_\alpha \subseteq A_{\alpha (x)} = B_x$
.
Therefore,
![]() $\bigcup _{x \in \omega ^\omega } B_x$
doesn’t have measure
$\bigcup _{x \in \omega ^\omega } B_x$
doesn’t have measure
![]() $0$
.
$0$
.
In the case of
![]() $\mathfrak {d}$
: As above, we can take an increasing sequence
$\mathfrak {d}$
: As above, we can take an increasing sequence
![]() ${\langle A_\alpha : \alpha < \mathfrak {d}\rangle }$
of measure-0 sets such that
${\langle A_\alpha : \alpha < \mathfrak {d}\rangle }$
of measure-0 sets such that
![]() $\bigcup _{\alpha < \mathfrak {d}} A_\alpha $
doesn’t have measure
$\bigcup _{\alpha < \mathfrak {d}} A_\alpha $
doesn’t have measure
![]() $0$
. By the definition of
$0$
. By the definition of
![]() $\mathfrak {d}$
, we can take a dominating sequence
$\mathfrak {d}$
, we can take a dominating sequence
![]() ${\langle x_\alpha : \alpha < \mathfrak {d} \rangle }$
with respect to
${\langle x_\alpha : \alpha < \mathfrak {d} \rangle }$
with respect to
![]() $\le ^*$
(this sequence is not necessarily increasing).
$\le ^*$
(this sequence is not necessarily increasing).
For each
![]() $x \in \omega ^\omega $
, put
$x \in \omega ^\omega $
, put
and put
One can easily show that
![]() ${\langle B_x : x \in \omega ^\omega \rangle }$
is monotone. Also we have
${\langle B_x : x \in \omega ^\omega \rangle }$
is monotone. Also we have
![]() $\bigcup _{x \in \omega ^\omega } B_x = \bigcup _{\alpha < \mathfrak {d}} A_\alpha $
. That the left-hand side is contained in the right-hand side is obvious. To show the reverse inclusion, fix
$\bigcup _{x \in \omega ^\omega } B_x = \bigcup _{\alpha < \mathfrak {d}} A_\alpha $
. That the left-hand side is contained in the right-hand side is obvious. To show the reverse inclusion, fix
![]() $\alpha $
. Since the sequence
$\alpha $
. Since the sequence
![]() ${\langle x_\beta : \beta < \alpha \rangle }$
is not a dominating family, we can find an
${\langle x_\beta : \beta < \alpha \rangle }$
is not a dominating family, we can find an
![]() $x \in \omega ^\omega $
such that for all
$x \in \omega ^\omega $
such that for all
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $x \not \le ^* x_\beta $
. Then
$x \not \le ^* x_\beta $
. Then
![]() $\alpha \le \alpha (x)$
. Thus we have
$\alpha \le \alpha (x)$
. Thus we have
![]() $A_\alpha \subseteq A_{\alpha (x)} = B_x$
.
$A_\alpha \subseteq A_{\alpha (x)} = B_x$
.
Corollary 4.3. Assume that at least one of the following three conditions holds:
-
(1)
 $\operatorname {add}(\mathsf {null}) = \mathfrak {b}$
,
$\operatorname {add}(\mathsf {null}) = \mathfrak {b}$
, -
(2)
 $\operatorname {non}(\mathsf {null}) = \mathfrak {b,}$
or
$\operatorname {non}(\mathsf {null}) = \mathfrak {b,}$
or -
(3)
 $\operatorname {non}(\mathsf {null}) = \mathfrak {d}$
.
$\operatorname {non}(\mathsf {null}) = \mathfrak {d}$
.
Then
![]() $\neg \mathsf {GP}(\mathsf {all})$
holds. In particular the continuum hypothesis implies
$\neg \mathsf {GP}(\mathsf {all})$
holds. In particular the continuum hypothesis implies
![]() $\neg \mathsf {GP}(\mathsf {all})$
.
$\neg \mathsf {GP}(\mathsf {all})$
.
Proof. Clearly there are null towers of length both
![]() $\operatorname {add}(\mathsf {null})$
and
$\operatorname {add}(\mathsf {null})$
and
![]() $\operatorname {non}(\mathsf {null})$
. So using Theorem 4.2, we have this corollary.
$\operatorname {non}(\mathsf {null})$
. So using Theorem 4.2, we have this corollary.
Proposition 4.4.
![]() $\mathsf {GP}(\mathsf {all})$
implies
$\mathsf {GP}(\mathsf {all})$
implies
![]() $\operatorname {add}(\mathsf {meager}) < \operatorname {cof}(\mathsf {meager})$
.
$\operatorname {add}(\mathsf {meager}) < \operatorname {cof}(\mathsf {meager})$
.
Proof. Assume
![]() $\operatorname {add}(\mathsf {meager}) = \operatorname {cof}(\mathsf {meager})$
. Let
$\operatorname {add}(\mathsf {meager}) = \operatorname {cof}(\mathsf {meager})$
. Let
![]() ${\langle M_\alpha : \alpha < \kappa \rangle }$
be a cofinal increasing sequence of meager sets. We can take such a sequence since
${\langle M_\alpha : \alpha < \kappa \rangle }$
be a cofinal increasing sequence of meager sets. We can take such a sequence since
![]() $\operatorname {add}(\mathsf {meager}) = \operatorname {cof}(\mathsf {meager}) = \kappa $
. For each
$\operatorname {add}(\mathsf {meager}) = \operatorname {cof}(\mathsf {meager}) = \kappa $
. For each
![]() $\alpha < \kappa $
, take
$\alpha < \kappa $
, take
![]() $x_\alpha \in M_{\alpha +1} \smallsetminus M_\alpha $
.
$x_\alpha \in M_{\alpha +1} \smallsetminus M_\alpha $
.
Now recall from Rothberger’s theorem (see, for example, Theorem 5.11 of [Reference Blass4]), there is a Tukey morphism
![]() $(\varphi , \psi ) \colon (2^\omega , \mathsf {null}, \in ) \to (\mathsf {meager}, 2^\omega , \not \ni )$
. That is, there are
$(\varphi , \psi ) \colon (2^\omega , \mathsf {null}, \in ) \to (\mathsf {meager}, 2^\omega , \not \ni )$
. That is, there are
![]() $\varphi \colon 2^\omega \to \mathsf {meager}$
and
$\varphi \colon 2^\omega \to \mathsf {meager}$
and
![]() $\psi \colon 2^\omega \to \mathsf {null}$
such that
$\psi \colon 2^\omega \to \mathsf {null}$
such that
![]() $\varphi (x) \not \ni y$
implies
$\varphi (x) \not \ni y$
implies
![]() $x \in \psi (y)$
for every
$x \in \psi (y)$
for every
![]() $x, y \in 2^\omega $
.
$x, y \in 2^\omega $
.
Using this theorem, we put
![]() $N_\alpha = \bigcap _{\beta \ge \alpha } \psi (x_\beta )$
for
$N_\alpha = \bigcap _{\beta \ge \alpha } \psi (x_\beta )$
for
![]() $\alpha < \kappa $
. Then
$\alpha < \kappa $
. Then
![]() ${\langle N_\alpha : \alpha < \kappa \rangle }$
is a sequence of null sets of length
${\langle N_\alpha : \alpha < \kappa \rangle }$
is a sequence of null sets of length
![]() $\kappa = \mathfrak {b}$
and its union is
$\kappa = \mathfrak {b}$
and its union is
![]() $2^\omega $
.
$2^\omega $
.
In the following proposition, we show that
![]() $\mathsf {GP}(\mathsf {all})$
cannot be forced by a finite support iteration of ccc forcings.
$\mathsf {GP}(\mathsf {all})$
cannot be forced by a finite support iteration of ccc forcings.
Proposition 4.5. For every finite support iteration of ccc forcings
![]() ${\langle P_\alpha : \alpha < \nu \rangle }$
with
${\langle P_\alpha : \alpha < \nu \rangle }$
with
![]() $\operatorname {cf}(\nu ) \ge \aleph _1$
, we have
$\operatorname {cf}(\nu ) \ge \aleph _1$
, we have
![]() $P_\nu \Vdash \neg \mathsf {GP}(\mathsf {all})$
.
$P_\nu \Vdash \neg \mathsf {GP}(\mathsf {all})$
.
Proof. Let G be a
![]() $(V, P_\nu )$
-generic filter and work in
$(V, P_\nu )$
-generic filter and work in
![]() $V[G]$
. Let
$V[G]$
. Let
![]() ${\langle c_\alpha : \alpha < \operatorname {cf}(\nu ) \rangle }$
be a sequence of Cohen reals added cofinally by
${\langle c_\alpha : \alpha < \operatorname {cf}(\nu ) \rangle }$
be a sequence of Cohen reals added cofinally by
![]() $P_\alpha $
.
$P_\alpha $
.
For a Cohen real c, let
![]() $\mathsf {nullset}(c)$
denote the standard null set constructed from c (for a detail, see Definition 3.15 of [Reference Wohofsky15]).
$\mathsf {nullset}(c)$
denote the standard null set constructed from c (for a detail, see Definition 3.15 of [Reference Wohofsky15]).
We have the following:
-
• For every
 $x \in \omega ^\omega $
, there is
$x \in \omega ^\omega $
, there is
 $\alpha < \operatorname {cf}(\nu )$
such that for every
$\alpha < \operatorname {cf}(\nu )$
such that for every
 $\beta> \alpha $
we have
$\beta> \alpha $
we have
 $c_\beta \not <^* x$
.
$c_\beta \not <^* x$
. -
• For every
 $z \in 2^\omega $
, there is
$z \in 2^\omega $
, there is
 $\alpha < \operatorname {cf}(\nu )$
such that for every
$\alpha < \operatorname {cf}(\nu )$
such that for every
 $\beta> \alpha $
we have
$\beta> \alpha $
we have
 $z \in \mathsf {nullset}(c_\beta )$
.
$z \in \mathsf {nullset}(c_\beta )$
.
For
![]() $x \in \omega ^\omega $
, we let
$x \in \omega ^\omega $
, we let
![]() $\alpha _x = \min \{ \alpha : (\forall \beta> \alpha ) (c_\beta \not <^* x) \}$
and let
$\alpha _x = \min \{ \alpha : (\forall \beta> \alpha ) (c_\beta \not <^* x) \}$
and let
![]() $A_x = \bigcap _{\beta> \alpha _x} \mathsf {nullset}(c_\beta )$
.
$A_x = \bigcap _{\beta> \alpha _x} \mathsf {nullset}(c_\beta )$
.
We can easily show that each
![]() $A_x$
is a null set, the sequence
$A_x$
is a null set, the sequence
![]() ${\langle A_x : x \in \omega ^\omega \rangle }$
is monotone and the union
${\langle A_x : x \in \omega ^\omega \rangle }$
is monotone and the union
![]() $\bigcup _{x \in \omega ^\omega } A_x$
is equal to
$\bigcup _{x \in \omega ^\omega } A_x$
is equal to
![]() $2^\omega $
. Therefore,
$2^\omega $
. Therefore,
![]() ${\langle A_x : x \in \omega ^\omega \rangle }$
is a witness of
${\langle A_x : x \in \omega ^\omega \rangle }$
is a witness of
![]() $\neg \mathsf {GP}(\mathsf {all})$
.
$\neg \mathsf {GP}(\mathsf {all})$
.
5 Consistency of
 $\mathsf {GP}(\mathsf {all})$
$\mathsf {GP}(\mathsf {all})$
In this section, as in the previous section, we assume
![]() $\mathsf {ZFC}$
. To obtain a model of
$\mathsf {ZFC}$
. To obtain a model of
![]() $\mathsf {GP}(\mathsf {all})$
,
$\mathsf {GP}(\mathsf {all})$
,
![]() $\operatorname {add}(\mathsf {null}) \ne \mathfrak {b}$
,
$\operatorname {add}(\mathsf {null}) \ne \mathfrak {b}$
,
![]() $\operatorname {non}(\mathsf {null}) \ne \mathfrak {b}$
,
$\operatorname {non}(\mathsf {null}) \ne \mathfrak {b}$
,
![]() $\operatorname {non}(\mathsf {null}) \ne \mathfrak {d,}$
and
$\operatorname {non}(\mathsf {null}) \ne \mathfrak {d,}$
and
![]() $\operatorname {add}(\mathsf {meager}) \ne \operatorname {cof}(\mathsf {meager})$
need to hold. A natural model in which they hold is the Laver model. In this section, we will see that
$\operatorname {add}(\mathsf {meager}) \ne \operatorname {cof}(\mathsf {meager})$
need to hold. A natural model in which they hold is the Laver model. In this section, we will see that
![]() $\mathsf {GP}(\mathsf {all})$
actually holds in the Laver model.
$\mathsf {GP}(\mathsf {all})$
actually holds in the Laver model.
Theorem 5.1. Assume that
![]() $\mathfrak {b} = \mathfrak {d}$
and let both of these be
$\mathfrak {b} = \mathfrak {d}$
and let both of these be
![]() $\kappa $
. Then the following are equivalent:
$\kappa $
. Then the following are equivalent:
-
(1) There is a null tower of length
 $\kappa $
.
$\kappa $
. -
(2)
 $\neg \mathsf {GP}(\mathsf {all})$
.
$\neg \mathsf {GP}(\mathsf {all})$
.
Proof. That (1) implies (2) is shown in Theorem 4.2.
We now prove the converse implication. Assume that
![]() $\neg \mathsf {GP}^*(\mathsf {all})$
. Then we can take
$\neg \mathsf {GP}^*(\mathsf {all})$
. Then we can take
![]() $A \subseteq \omega ^\omega \times 2^\omega $
such that each section
$A \subseteq \omega ^\omega \times 2^\omega $
such that each section
![]() $A_x$
has measure
$A_x$
has measure
![]() $0$
and
$0$
and
![]() $(\forall x, x' \in \omega ^\omega )(x \le ^* x' \Rightarrow A_{x} \subseteq A_{x'})$
holds and
$(\forall x, x' \in \omega ^\omega )(x \le ^* x' \Rightarrow A_{x} \subseteq A_{x'})$
holds and
![]() $B = \bigcup _{x \in \omega ^\omega } A_x$
does not have measure
$B = \bigcup _{x \in \omega ^\omega } A_x$
does not have measure
![]() $0$
. By
$0$
. By
![]() $\mathfrak {b} = \mathfrak {d} = \kappa $
, we can take a cofinal increasing sequence
$\mathfrak {b} = \mathfrak {d} = \kappa $
, we can take a cofinal increasing sequence
![]() ${\langle x_\alpha : \alpha < \kappa \rangle }$
with respect to
${\langle x_\alpha : \alpha < \kappa \rangle }$
with respect to
![]() $\le ^*$
. For each
$\le ^*$
. For each
![]() $\alpha < \kappa $
, put
$\alpha < \kappa $
, put
![]() $C_\alpha = A_{x_\alpha }$
. Then each
$C_\alpha = A_{x_\alpha }$
. Then each
![]() $C_\alpha $
has measure
$C_\alpha $
has measure
![]() $0$
. Since
$0$
. Since
![]() $\alpha \mapsto x_\alpha $
is increasing and
$\alpha \mapsto x_\alpha $
is increasing and
![]() $x \mapsto A_x$
is monotone,
$x \mapsto A_x$
is monotone,
![]() ${\langle C_\alpha : \alpha < \kappa \rangle }$
is also increasing. Also, since
${\langle C_\alpha : \alpha < \kappa \rangle }$
is also increasing. Also, since
![]() ${\langle x_\alpha : \alpha < \kappa \rangle }$
is cofinal, we have
${\langle x_\alpha : \alpha < \kappa \rangle }$
is cofinal, we have
![]() $B = \bigcup _{\alpha < \kappa } C_\alpha $
. So
$B = \bigcup _{\alpha < \kappa } C_\alpha $
. So
![]() $\bigcup _{\alpha < \kappa } C_\alpha $
does not have measure
$\bigcup _{\alpha < \kappa } C_\alpha $
does not have measure
![]() $0$
. Thus
$0$
. Thus
![]() ${\langle C_\alpha : \alpha < \kappa \rangle }$
is a null tower of length
${\langle C_\alpha : \alpha < \kappa \rangle }$
is a null tower of length
![]() $\kappa $
.
$\kappa $
.
The following lemma and theorem require knowledge of proper forcing (see [Reference Goldstern6]).
Lemma 5.2. Assume
![]() $\mathsf {CH}$
. Let
$\mathsf {CH}$
. Let
![]() ${\langle P_\alpha , \dot {Q}_\alpha : \alpha < \omega _2\rangle }$
be a countable support iteration of proper forcing notions such that
${\langle P_\alpha , \dot {Q}_\alpha : \alpha < \omega _2\rangle }$
be a countable support iteration of proper forcing notions such that
Let
![]() ${\langle \dot {X}_\alpha : \alpha < \omega _2\rangle }$
be a sequence of
${\langle \dot {X}_\alpha : \alpha < \omega _2\rangle }$
be a sequence of
![]() $P_{\omega _2}$
-names such that
$P_{\omega _2}$
-names such that
Then the set
 $$ \begin{align*} C &= \{ \alpha < \omega_2 : \operatorname{cf}(\alpha) = \omega_1 \,\mathbin{\text{and}}\Vdash_{\omega_2} ({\langle\dot{X}_\beta \cap V[\dot{G}_\alpha] : \beta < \alpha \rangle} \\& \qquad \in V[\dot{G}_\alpha] \mathbin{\text{and}} (\forall \beta < \alpha) (\dot{X}_\beta \cap V[\dot{G}_\alpha] \text{ has measure } 0)^{V[\dot{G}_\alpha]}) \}. \end{align*} $$
$$ \begin{align*} C &= \{ \alpha < \omega_2 : \operatorname{cf}(\alpha) = \omega_1 \,\mathbin{\text{and}}\Vdash_{\omega_2} ({\langle\dot{X}_\beta \cap V[\dot{G}_\alpha] : \beta < \alpha \rangle} \\& \qquad \in V[\dot{G}_\alpha] \mathbin{\text{and}} (\forall \beta < \alpha) (\dot{X}_\beta \cap V[\dot{G}_\alpha] \text{ has measure } 0)^{V[\dot{G}_\alpha]}) \}. \end{align*} $$
contains a
![]() $\omega _1$
-club set in
$\omega _1$
-club set in
![]() $\omega _2$
.
$\omega _2$
.
Proof. This is an example of a reflection argument (see also [Reference Halbeisen8, Chapter 26]).
Take a sequence
![]() ${\langle \dot {c}_\beta : \beta < \omega _2\rangle }$
of names of Borel codes such that
${\langle \dot {c}_\beta : \beta < \omega _2\rangle }$
of names of Borel codes such that
For each
![]() $\beta < \omega _2$
, take
$\beta < \omega _2$
, take
![]() $\gamma _\beta < \omega _2$
such that
$\gamma _\beta < \omega _2$
such that
![]() $\dot {c}_\beta $
is a
$\dot {c}_\beta $
is a
![]() $P_{\gamma _\beta }$
-name.
$P_{\gamma _\beta }$
-name.
Since for each
![]() $\alpha < \omega _2$
,
$\alpha < \omega _2$
,
![]() $\Vdash _\alpha \mathsf {CH}$
, we can take a sequence
$\Vdash _\alpha \mathsf {CH}$
, we can take a sequence
![]() ${\langle \dot {x}^\alpha _i : i < \omega _1\rangle }$
such that
${\langle \dot {x}^\alpha _i : i < \omega _1\rangle }$
such that
For each
![]() $\alpha , \beta < \omega _2$
and
$\alpha , \beta < \omega _2$
and
![]() $i < \omega _1$
, take a maximal antichain
$i < \omega _1$
, take a maximal antichain
![]() $A^{\alpha ,\beta }_i$
such that
$A^{\alpha ,\beta }_i$
such that
Since
![]() $P_{\omega _2}$
has
$P_{\omega _2}$
has
![]() $\omega _2$
-cc, we can take
$\omega _2$
-cc, we can take
![]() $\delta ^{\alpha ,\beta }_i < \omega _2$
such that
$\delta ^{\alpha ,\beta }_i < \omega _2$
such that
We define a function f from
![]() $\omega _2$
into
$\omega _2$
into
![]() $\omega _2$
as follows:
$\omega _2$
as follows:
Put
Then clearly
![]() $C'$
is
$C'$
is
![]() $\omega _1$
-club set. So it suffices to show that
$\omega _1$
-club set. So it suffices to show that
![]() $C' \subseteq C$
.
$C' \subseteq C$
.
Let
![]() $\alpha \in C'$
and we shall prove
$\alpha \in C'$
and we shall prove
![]() $\alpha \in C$
. Fix
$\alpha \in C$
. Fix
![]() $\beta < \alpha $
. Define a
$\beta < \alpha $
. Define a
![]() $P_\alpha $
-name
$P_\alpha $
-name
![]() $\dot {Y}$
by
$\dot {Y}$
by
 $$ \begin{align} \Vdash_\alpha "\dot{Y} = \bigcup_{\alpha' < \alpha} \{ \dot{x}^{\alpha'}_i : &(p \Vdash \dot{x}^{\alpha'}_i \in \dot{X}_\beta)^V \nonumber\\ & \text{for some } p \in A^{\alpha',\beta}_i \mathbin{\text{and}} p \upharpoonright \alpha \in \dot{G} \}". \end{align} $$
$$ \begin{align} \Vdash_\alpha "\dot{Y} = \bigcup_{\alpha' < \alpha} \{ \dot{x}^{\alpha'}_i : &(p \Vdash \dot{x}^{\alpha'}_i \in \dot{X}_\beta)^V \nonumber\\ & \text{for some } p \in A^{\alpha',\beta}_i \mathbin{\text{and}} p \upharpoonright \alpha \in \dot{G} \}". \end{align} $$
We claim that
![]() $\Vdash _{\omega _2} \dot {X}_\beta \cap V[\dot {G}_\alpha ] = \dot {Y}$
. In order to prove this, take a
$\Vdash _{\omega _2} \dot {X}_\beta \cap V[\dot {G}_\alpha ] = \dot {Y}$
. In order to prove this, take a
![]() $(V, P_{\omega _2})$
-generic filter G. In
$(V, P_{\omega _2})$
-generic filter G. In
![]() $V[G]$
, take
$V[G]$
, take
![]() $x \in \dot {X}^G_\beta \cap V[G_\alpha ]$
. Since no new real is added at stage
$x \in \dot {X}^G_\beta \cap V[G_\alpha ]$
. Since no new real is added at stage
![]() $\alpha $
, we can take
$\alpha $
, we can take
![]() $\alpha ' < \alpha $
such that
$\alpha ' < \alpha $
such that
![]() $x \in V[G_{\alpha '}]$
. Thus there is
$x \in V[G_{\alpha '}]$
. Thus there is
![]() $i < \omega _1$
such that
$i < \omega _1$
such that
![]() $x = (\dot {x}^{\alpha '}_i)^G$
. Since
$x = (\dot {x}^{\alpha '}_i)^G$
. Since
![]() $(\dot {x}^{\alpha '}_i)^G \in \dot {X}^G_\beta $
, in V, we can take a
$(\dot {x}^{\alpha '}_i)^G \in \dot {X}^G_\beta $
, in V, we can take a
![]() $p \in G \cap A^{\alpha ',\beta }_i$
such that
$p \in G \cap A^{\alpha ',\beta }_i$
such that
![]() $p \Vdash \dot {x}^{\alpha '}_i \in \dot {X}_\beta $
. We have
$p \Vdash \dot {x}^{\alpha '}_i \in \dot {X}_\beta $
. We have
![]() $p \in A^{\alpha ',\beta }_i$
. Thus x is an element of
$p \in A^{\alpha ',\beta }_i$
. Thus x is an element of
![]() $\dot {Y}^G$
.
$\dot {Y}^G$
.
Conversely, take an element x of
![]() $\dot {Y}^G$
. So we can take
$\dot {Y}^G$
. So we can take
![]() $\alpha ' < \alpha $
,
$\alpha ' < \alpha $
,
![]() $i < \omega _1$
and
$i < \omega _1$
and
![]() $p \in P_{\omega _2}$
such that
$p \in P_{\omega _2}$
such that
Clearly we have
![]() $x \in V[G_{\alpha '}] \subseteq V[G_\alpha ]$
. Suppose that
$x \in V[G_{\alpha '}] \subseteq V[G_\alpha ]$
. Suppose that
![]() $(\dot {x}^{\alpha '}_i)^G \not \in \dot {X}^G_\beta $
. Then we can take
$(\dot {x}^{\alpha '}_i)^G \not \in \dot {X}^G_\beta $
. Then we can take
![]() $q \in G$
such that
$q \in G$
such that
![]() $q \Vdash \dot {x}^{\alpha '}_i \not \in \dot {X}_\beta $
. By the maximality of
$q \Vdash \dot {x}^{\alpha '}_i \not \in \dot {X}_\beta $
. By the maximality of
![]() $A^{\alpha ',\beta }_i$
, we can take
$A^{\alpha ',\beta }_i$
, we can take
![]() ${r \in A^{\alpha ',\beta }_i \cap G}$
. Since both q and r are elements of G, q and r are compatible. So
${r \in A^{\alpha ',\beta }_i \cap G}$
. Since both q and r are elements of G, q and r are compatible. So
![]() $r \Vdash \dot {x}^{\alpha '}_i \not \in \dot {X}_\beta $
. Thus p and r are incompatible. But
$r \Vdash \dot {x}^{\alpha '}_i \not \in \dot {X}_\beta $
. Thus p and r are incompatible. But
![]() $\operatorname {supt}(p), \operatorname {supt}(r) \subseteq \alpha $
. So
$\operatorname {supt}(p), \operatorname {supt}(r) \subseteq \alpha $
. So
![]() $p \upharpoonright \alpha $
and
$p \upharpoonright \alpha $
and
![]() $r \upharpoonright \alpha $
are incompatible. But they are elements of
$r \upharpoonright \alpha $
are incompatible. But they are elements of
![]() $G_\alpha $
. It contradicts that
$G_\alpha $
. It contradicts that
![]() $G_\alpha $
is a
$G_\alpha $
is a
![]() $(V, P_\alpha )$
-generic filter.
$(V, P_\alpha )$
-generic filter.
Thus we have
![]() $\Vdash _{\omega _2} \dot {X}_\beta \cap V[G_\alpha ] \in V[G_\alpha ]$
.
$\Vdash _{\omega _2} \dot {X}_\beta \cap V[G_\alpha ] \in V[G_\alpha ]$
.
By performing the above operations simultaneously with respect to the
![]() $\beta $
, we have
$\beta $
, we have
Since we have
![]() $\Vdash _{\omega _2} \dot {X}_\beta \subseteq \hat {\dot {c}}_\beta $
, it holds that
$\Vdash _{\omega _2} \dot {X}_\beta \subseteq \hat {\dot {c}}_\beta $
, it holds that
Therefore, we have
![]() $\alpha \in C$
.
$\alpha \in C$
.
Recall that
![]() $\mathbf {LT}$
denotes the Laver forcing. As for basic properties of Laver forcing, see [Reference Bartoszynski and Judah3].
$\mathbf {LT}$
denotes the Laver forcing. As for basic properties of Laver forcing, see [Reference Bartoszynski and Judah3].
Theorem 5.3. Assume
![]() $\mathsf {CH}$
. Let
$\mathsf {CH}$
. Let
![]() ${\langle P_\alpha , \dot {Q}_\alpha : \alpha < \omega _2\rangle }$
be the countable support iteration such that
${\langle P_\alpha , \dot {Q}_\alpha : \alpha < \omega _2\rangle }$
be the countable support iteration such that
Then
In particular, if
![]() $\mathsf {ZFC}$
is consistent then so is
$\mathsf {ZFC}$
is consistent then so is
![]() $\mathsf {ZFC} + \mathsf {GP}(\mathsf {all})$
.
$\mathsf {ZFC} + \mathsf {GP}(\mathsf {all})$
.
Proof. By Theorem 5.1 and the fact that
![]() $ \Vdash _{\omega _2} \mathfrak {b} = \mathfrak {d} = \omega _2$
, it is sufficient to show that
$ \Vdash _{\omega _2} \mathfrak {b} = \mathfrak {d} = \omega _2$
, it is sufficient to show that
Let G be a
![]() $(V, P_{\omega _2})$
-generic filter. In
$(V, P_{\omega _2})$
-generic filter. In
![]() $V[G]$
, consider an increasing sequence
$V[G]$
, consider an increasing sequence
![]() ${\langle A_\alpha : \alpha < \omega _2\rangle }$
of measure
${\langle A_\alpha : \alpha < \omega _2\rangle }$
of measure
![]() $0$
sets. By Lemma 5.2, we can find a stationary set
$0$
sets. By Lemma 5.2, we can find a stationary set
![]() $S \subseteq \omega _2$
such that for all
$S \subseteq \omega _2$
such that for all
![]() $\alpha \in S$
,
$\alpha \in S$
,
![]() $\operatorname {cf}(\alpha ) = \omega _1$
and
$\operatorname {cf}(\alpha ) = \omega _1$
and
Fix
![]() $\alpha \in S$
. Put
$\alpha \in S$
. Put
![]() $B_\alpha := \bigcup _{\beta < \alpha } A_\beta \cap V[G_\alpha ]$
. Then we have
$B_\alpha := \bigcup _{\beta < \alpha } A_\beta \cap V[G_\alpha ]$
. Then we have
![]() $\bigcup _{\alpha < \omega _2} B_\alpha = \bigcup _{\alpha < \omega _2} A_\alpha $
. We now prove that
$\bigcup _{\alpha < \omega _2} B_\alpha = \bigcup _{\alpha < \omega _2} A_\alpha $
. We now prove that
![]() $B_\alpha $
is also a measure
$B_\alpha $
is also a measure
![]() $0$
set in
$0$
set in
![]() $V[G_\alpha ]$
. Let
$V[G_\alpha ]$
. Let
![]() $\alpha '$
be the successor of
$\alpha '$
be the successor of
![]() $\alpha $
in S. Then
$\alpha $
in S. Then
![]() $B_\alpha $
is a measure
$B_\alpha $
is a measure
![]() $0$
set in
$0$
set in
![]() $V[G_{\alpha '}]$
. Since the quotient forcing
$V[G_{\alpha '}]$
. Since the quotient forcing
![]() $P_{\alpha '} / G_\alpha $
is a countable support iteration of the Laver forcing, this forcing preserves positive outer measure. So
$P_{\alpha '} / G_\alpha $
is a countable support iteration of the Laver forcing, this forcing preserves positive outer measure. So
![]() $B_\alpha $
is also a measure
$B_\alpha $
is also a measure
![]() $0$
set in
$0$
set in
![]() $V[G_{\alpha }]$
.
$V[G_{\alpha }]$
.
For each
![]() $\alpha \in S$
, take a Borel code
$\alpha \in S$
, take a Borel code
![]() $c_\alpha \in \omega ^\omega $
of a measure
$c_\alpha \in \omega ^\omega $
of a measure
![]() $0$
set such that
$0$
set such that
![]() $B_\alpha \subseteq \hat {c}_\alpha $
in
$B_\alpha \subseteq \hat {c}_\alpha $
in
![]() $V[G_\alpha ]$
. Since
$V[G_\alpha ]$
. Since
![]() $\operatorname {cf}(\alpha ) = \omega _1$
, each
$\operatorname {cf}(\alpha ) = \omega _1$
, each
![]() $c_\alpha $
appears a prior stage. Then by Fodor’s lemma, we can take a stationary set
$c_\alpha $
appears a prior stage. Then by Fodor’s lemma, we can take a stationary set
![]() $S' \subseteq \omega _2$
that is contained in S and
$S' \subseteq \omega _2$
that is contained in S and
![]() $\beta < \omega _2$
such that
$\beta < \omega _2$
such that
![]() $(\forall \alpha \in S')(c_\alpha \in V[G_\beta ])$
. But the number of reals in
$(\forall \alpha \in S')(c_\alpha \in V[G_\beta ])$
. But the number of reals in
![]() $V[G_\beta ]$
is
$V[G_\beta ]$
is
![]() $\aleph _1$
, so we can take
$\aleph _1$
, so we can take
![]() ${T \subseteq S'}$
unbounded in
${T \subseteq S'}$
unbounded in
![]() $\omega _2$
and c such that
$\omega _2$
and c such that
![]() $(\forall \alpha \in T)(c_\alpha = c)$
. Then we have
$(\forall \alpha \in T)(c_\alpha = c)$
. Then we have
![]() $\bigcup _{\alpha < \omega _2} A_\alpha \subseteq \hat {c}$
in
$\bigcup _{\alpha < \omega _2} A_\alpha \subseteq \hat {c}$
in
![]() $V[G]$
. So
$V[G]$
. So
![]() $\bigcup _{\alpha < \omega _2} A_\alpha $
has measure
$\bigcup _{\alpha < \omega _2} A_\alpha $
has measure
![]() $0$
.
$0$
.
Corollary 5.4.
![]() $\operatorname {Con}(\mathsf {ZFC}) \rightarrow \operatorname {Con}(\mathsf {ZFC}+\mathsf {GP}(\mathsf {projective})+\neg \mathsf {GP}(\mathsf {all}))$
. Here,
$\operatorname {Con}(\mathsf {ZFC}) \rightarrow \operatorname {Con}(\mathsf {ZFC}+\mathsf {GP}(\mathsf {projective})+\neg \mathsf {GP}(\mathsf {all}))$
. Here,
![]() $\mathsf {projective} = \bigcup _{n \ge 1} \boldsymbol {\Sigma }^1_n$
.
$\mathsf {projective} = \bigcup _{n \ge 1} \boldsymbol {\Sigma }^1_n$
.
Proof. Assume
![]() $\mathsf {CH}$
and let P be the forcing poset from Theorem 5.3, that is, the countable support iteration of Laver forcing notions of length
$\mathsf {CH}$
and let P be the forcing poset from Theorem 5.3, that is, the countable support iteration of Laver forcing notions of length
![]() $\omega _2$
. Then we have
$\omega _2$
. Then we have
![]() $P \Vdash \mathsf {GP}(\mathsf {all})$
. In particular we have
$P \Vdash \mathsf {GP}(\mathsf {all})$
. In particular we have
![]() $P \Vdash \mathsf {GP}(\mathsf {projective})$
. Let
$P \Vdash \mathsf {GP}(\mathsf {projective})$
. Let
![]() $\dot {Q}$
be a P-name of the poset
$\dot {Q}$
be a P-name of the poset
with the reverse inclusion order. It is well-known that provably
![]() $\operatorname {Fn}(\omega _1, 2, \omega _1)$
adds no new reals and forces
$\operatorname {Fn}(\omega _1, 2, \omega _1)$
adds no new reals and forces
![]() $\mathsf {CH}$
. So we have
$\mathsf {CH}$
. So we have
![]() $P \ast \dot {Q} \Vdash \mathsf {CH}$
. Since
$P \ast \dot {Q} \Vdash \mathsf {CH}$
. Since
![]() $P \Vdash \mathsf {GP}(\mathsf {projective})$
and
$P \Vdash \mathsf {GP}(\mathsf {projective})$
and
![]() $P \Vdash "\dot {Q} \text { adds no new reals}$
,” we have
$P \Vdash "\dot {Q} \text { adds no new reals}$
,” we have
![]() $P \ast \dot {Q} \Vdash \mathsf {GP}(\mathsf {projective})$
.
$P \ast \dot {Q} \Vdash \mathsf {GP}(\mathsf {projective})$
.
6 A necessary condition for
 $\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
$\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
As mentioned in Section 2, a sufficient condition for
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_2)$
is every
$\mathsf {GP}(\boldsymbol {\Sigma }^1_2)$
is every
![]() $\boldsymbol {\Sigma }^1_2$
set is Lebesgue measurable, or equivalently for every real a, there is an amoeba real over
$\boldsymbol {\Sigma }^1_2$
set is Lebesgue measurable, or equivalently for every real a, there is an amoeba real over
![]() $L[a]$
. (This equivalence was proved by Solovay (see [Reference Bartoszynski and Judah3, Theorem 9.3.1]).) In this section we give a necessary condition for
$L[a]$
. (This equivalence was proved by Solovay (see [Reference Bartoszynski and Judah3, Theorem 9.3.1]).) In this section we give a necessary condition for
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
.
$\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
.
Fact 6.1 (Spector–Gandy, see [Reference Chong and Yu5, Proposition 4.4.3])
Let A be a set of reals. Then A is a
![]() $\Sigma ^1_2$
set iff there is a
$\Sigma ^1_2$
set iff there is a
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $\varphi $
such that
$\varphi $
such that
The following is well-known.
Lemma 6.2. Let M be a model of
![]() $\mathsf {ZFC}$
contained in V. And assume that the set
$\mathsf {ZFC}$
contained in V. And assume that the set
![]() $\{ y \in 2^\omega : y \text { is a random real over } M \}$
has measure
$\{ y \in 2^\omega : y \text { is a random real over } M \}$
has measure
![]() $1$
. Then there is a dominating real over M.
$1$
. Then there is a dominating real over M.
Proof. Let
![]() $\mathbf {nBC}$
denote the set of all Borel codes for measure
$\mathbf {nBC}$
denote the set of all Borel codes for measure
![]() $0$
Borel sets. There is an absolute Tukey morphism
$0$
Borel sets. There is an absolute Tukey morphism
![]() $(\varphi , \psi )$
that witnesses
$(\varphi , \psi )$
that witnesses
![]() $\operatorname {add}(\mathsf {null}) \le \mathfrak {b}$
. That is,
$\operatorname {add}(\mathsf {null}) \le \mathfrak {b}$
. That is,
![]() $(\varphi , \psi )$
satisfies
$(\varphi , \psi )$
satisfies
![]() $\varphi \colon \omega ^\omega \to \mathbf {nBC}$
,
$\varphi \colon \omega ^\omega \to \mathbf {nBC}$
,
![]() $\psi \colon \mathbf {nBC} \to \omega ^\omega $
, and
$\psi \colon \mathbf {nBC} \to \omega ^\omega $
, and
![]() $(\forall x \in \omega ^\omega )(\forall y \in \mathbf {nBC}) (\hat {\varphi (x)} \subseteq \hat {y} \rightarrow x \le ^* \psi (y))$
. By absoluteness, if
$(\forall x \in \omega ^\omega )(\forall y \in \mathbf {nBC}) (\hat {\varphi (x)} \subseteq \hat {y} \rightarrow x \le ^* \psi (y))$
. By absoluteness, if
![]() $x \in \omega ^\omega \cap M$
, then we have
$x \in \omega ^\omega \cap M$
, then we have
![]() $\varphi (x) \in M$
. Now
$\varphi (x) \in M$
. Now
has measure 0 since this is contained in
![]() $\{ y \in 2^\omega : y \text { is not a random real over } M \}$
by the definition of randomness. Take a
$\{ y \in 2^\omega : y \text { is not a random real over } M \}$
by the definition of randomness. Take a
![]() $z \in \mathbf {nBC}$
such that
$z \in \mathbf {nBC}$
such that
Now put
![]() $w = \psi (z)$
. Then using the fact that
$w = \psi (z)$
. Then using the fact that
![]() $(\varphi , \psi )$
is Tukey morphism, we have w is a dominating real over M.
$(\varphi , \psi )$
is Tukey morphism, we have w is a dominating real over M.
Theorem 6.3. For every real a,
![]() $\mathsf {GP}(\Delta ^1_2(a))$
implies there is a dominating real over
$\mathsf {GP}(\Delta ^1_2(a))$
implies there is a dominating real over
![]() $L[a]$
. Thus,
$L[a]$
. Thus,
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
implies for every real a, there is a dominating real over
$\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
implies for every real a, there is a dominating real over
![]() $L[a]$
. In particular
$L[a]$
. In particular
![]() $V=L$
implies
$V=L$
implies
![]() $\neg \mathsf {GP}(\Delta ^1_2)$
.
$\neg \mathsf {GP}(\Delta ^1_2)$
.
Proof. Fix a real a. Assume that
![]() $L[a] \cap \omega ^\omega $
is unbounded. Note that, in this situation, we have
$L[a] \cap \omega ^\omega $
is unbounded. Note that, in this situation, we have
![]() $\omega _1^{L[a]} = \omega _1$
. Let
$\omega _1^{L[a]} = \omega _1$
. Let
![]() ${\langle x_\alpha : \alpha < \omega _1\rangle }$
be a cofinal increasing sequence in
${\langle x_\alpha : \alpha < \omega _1\rangle }$
be a cofinal increasing sequence in
![]() $\omega ^\omega \cap L[a]$
. We can take this sequence with a
$\omega ^\omega \cap L[a]$
. We can take this sequence with a
![]() $\Delta _1(a)$
definition by using a
$\Delta _1(a)$
definition by using a
![]() $\Delta _1(a)$
canonical wellordering of
$\Delta _1(a)$
canonical wellordering of
![]() $L[a] \cap \omega ^\omega $
. Note that this sequence is unbounded in
$L[a] \cap \omega ^\omega $
. Note that this sequence is unbounded in
![]() $V \cap \omega ^\omega $
by assumption.
$V \cap \omega ^\omega $
by assumption.
Take a sequence
![]() ${\langle c_\alpha : \alpha < \omega _1\rangle }$
consisting of all Borel codes for measure
${\langle c_\alpha : \alpha < \omega _1\rangle }$
consisting of all Borel codes for measure
![]() $0$
Borel sets in
$0$
Borel sets in
![]() $L[a]$
. As above, we can take this sequence with a
$L[a]$
. As above, we can take this sequence with a
![]() $\Delta _1(a)$
definition.
$\Delta _1(a)$
definition.
For each
![]() $x \in \omega ^\omega $
, put
$x \in \omega ^\omega $
, put
This is well-defined since
![]() ${\langle x_\alpha : \alpha < \omega _1\rangle }$
is unbounded in
${\langle x_\alpha : \alpha < \omega _1\rangle }$
is unbounded in
![]() $V \cap \omega ^\omega $
. Also put
$V \cap \omega ^\omega $
. Also put
 $$\begin{align*}A_x = \bigcup_{\beta < \alpha(x)} \hat{c_\beta}. \end{align*}$$
$$\begin{align*}A_x = \bigcup_{\beta < \alpha(x)} \hat{c_\beta}. \end{align*}$$
Then the set A is
![]() $\Delta ^1_2(a)$
, by Spector–Gandy theorem and the following equations:
$\Delta ^1_2(a)$
, by Spector–Gandy theorem and the following equations:
 $$ \begin{align*} A &= \{ (x, y) \in \omega^\omega \times 2^\omega : (\exists \beta < \alpha(x))\ y \in \hat{c_\beta} \} \\ &= \{ (x, y) \in \omega^\omega \times 2^\omega : (\exists \alpha)(x_\alpha \not \le^* x \mathbin{\text{and}} (\forall \beta < \alpha)(x_\beta \le^* x) \mathbin{\text{and}} (\exists \beta < \alpha)(y \in \hat{c_\beta})) \} \\ &= \{ (x, y) \in \omega^\omega \times 2^\omega : (\forall \alpha)((x_\alpha \not \le^* x \mathbin{\text{and}} (\forall \beta < \alpha)(x_\beta \le^* x)) \rightarrow (\exists \beta < \alpha)(y \in \hat{c_\beta})) \}. \end{align*} $$
$$ \begin{align*} A &= \{ (x, y) \in \omega^\omega \times 2^\omega : (\exists \beta < \alpha(x))\ y \in \hat{c_\beta} \} \\ &= \{ (x, y) \in \omega^\omega \times 2^\omega : (\exists \alpha)(x_\alpha \not \le^* x \mathbin{\text{and}} (\forall \beta < \alpha)(x_\beta \le^* x) \mathbin{\text{and}} (\exists \beta < \alpha)(y \in \hat{c_\beta})) \} \\ &= \{ (x, y) \in \omega^\omega \times 2^\omega : (\forall \alpha)((x_\alpha \not \le^* x \mathbin{\text{and}} (\forall \beta < \alpha)(x_\beta \le^* x)) \rightarrow (\exists \beta < \alpha)(y \in \hat{c_\beta})) \}. \end{align*} $$
Note that each
![]() $A_x$
(
$A_x$
(
![]() $x \in \omega ^\omega $
) is a measure
$x \in \omega ^\omega $
) is a measure
![]() $0$
set since it is a countable union of measure
$0$
set since it is a countable union of measure
![]() $0$
sets. And we can easily observe that
$0$
sets. And we can easily observe that
![]() $x \le ^* x'$
implies
$x \le ^* x'$
implies
![]() $A_x \subseteq A_{x'}$
.
$A_x \subseteq A_{x'}$
.
Since
![]() $\alpha \le \alpha (x_\alpha )$
, we have
$\alpha \le \alpha (x_\alpha )$
, we have
![]() $\bigcup _{x \in \omega ^\omega } A_x = \bigcup _{\alpha < \omega _1} \hat {c_\alpha }$
. Thus it is sufficient to show that
$\bigcup _{x \in \omega ^\omega } A_x = \bigcup _{\alpha < \omega _1} \hat {c_\alpha }$
. Thus it is sufficient to show that
![]() $C := \bigcup _{\alpha < \omega _1} \hat {c_\alpha }$
is not a measure
$C := \bigcup _{\alpha < \omega _1} \hat {c_\alpha }$
is not a measure
![]() $0$
set. In order to show this, assume that C is a measure
$0$
set. In order to show this, assume that C is a measure
![]() $0$
set. Note that if a real
$0$
set. Note that if a real
![]() $y \in 2^\omega $
does not belong to C, then y is a random real over
$y \in 2^\omega $
does not belong to C, then y is a random real over
![]() $L[a]$
since the sequence
$L[a]$
since the sequence
![]() ${\langle c_\alpha : \alpha < \omega _1\rangle }$
enumerates all measure
${\langle c_\alpha : \alpha < \omega _1\rangle }$
enumerates all measure
![]() $0$
Borel codes in
$0$
Borel codes in
![]() $L[a]$
. So since we assumed C is measure
$L[a]$
. So since we assumed C is measure
![]() $0$
, the set
$0$
, the set
![]() $\{ y \in 2^\omega : y \text { is a random real over } L[a] \}$
has measure
$\{ y \in 2^\omega : y \text { is a random real over } L[a] \}$
has measure
![]() $1$
. Thus by Lemma 6.2, there is a dominating real over
$1$
. Thus by Lemma 6.2, there is a dominating real over
![]() $L[a]$
. This contradicts the assumption.
$L[a]$
. This contradicts the assumption.
So we constructed a set A that violates
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
. This finishes the proof.
$\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
. This finishes the proof.
Therefore, we obtain the following diagram of implications:

Here,
![]() $\boldsymbol {\Sigma }^1_2$
-LM means
$\boldsymbol {\Sigma }^1_2$
-LM means
![]() $\boldsymbol {\Sigma }^1_2$
-Lebesgue measurability and
$\boldsymbol {\Sigma }^1_2$
-Lebesgue measurability and
![]() $\boldsymbol {\Sigma }^1_2$
-BP means
$\boldsymbol {\Sigma }^1_2$
-BP means
![]() $\boldsymbol {\Sigma }^1_2$
-Baire property.
$\boldsymbol {\Sigma }^1_2$
-Baire property.
![]() $\boldsymbol {\Sigma }^1_2$
-LM and
$\boldsymbol {\Sigma }^1_2$
-LM and
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_2)$
can be separated since the Laver model over L satisfies
$\mathsf {GP}(\boldsymbol {\Sigma }^1_2)$
can be separated since the Laver model over L satisfies
![]() $\mathsf {GP}(\mathsf {all})$
but not
$\mathsf {GP}(\mathsf {all})$
but not
![]() $\boldsymbol {\Sigma }^1_2$
-LM.
$\boldsymbol {\Sigma }^1_2$
-LM.
7 Consequences of determinacy
In this section, we don’t assume the axiom of choice but assume the axiom of countable choice for the reals and we will discuss a consequence of determinacy for Goldstern’s principle.
For a pointclass
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $\operatorname {Det}(\Gamma )$
denote the axiom of determinacy for
$\operatorname {Det}(\Gamma )$
denote the axiom of determinacy for
![]() $\Gamma $
and
$\Gamma $
and
![]() $\mathsf {AD}$
denote
$\mathsf {AD}$
denote
![]() $\operatorname {Det}(\mathsf {all})$
.
$\operatorname {Det}(\mathsf {all})$
.
Theorem 7.1. Let
![]() $\Gamma $
be a pointclass that contains all Borel subsets and is closed under Borel substitution. Assume
$\Gamma $
be a pointclass that contains all Borel subsets and is closed under Borel substitution. Assume
![]() $\operatorname {Det}(\Gamma )$
. Then
$\operatorname {Det}(\Gamma )$
. Then
![]() $\mathsf {GP}(\operatorname {proj}(\Gamma ))$
holds, where
$\mathsf {GP}(\operatorname {proj}(\Gamma ))$
holds, where
![]() $\operatorname {proj}(\Gamma )$
is the pointclass of all projections along
$\operatorname {proj}(\Gamma )$
is the pointclass of all projections along
![]() $\omega ^\omega $
of a set in
$\omega ^\omega $
of a set in
![]() $\Gamma $
.
$\Gamma $
.
In particular,
![]() $\mathsf {AD}$
implies
$\mathsf {AD}$
implies
![]() $\mathsf {GP}(\mathsf {all})$
. Also
$\mathsf {GP}(\mathsf {all})$
. Also
![]() $\operatorname {Det}(\boldsymbol {\Pi }^1_n)$
implies
$\operatorname {Det}(\boldsymbol {\Pi }^1_n)$
implies
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
for every
$\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
for every
![]() $n \ge 1$
.
$n \ge 1$
.
Proof. This proof is based on Harrington’s covering game (see also [Reference Moschovakis11, Exercise 6A.17]). In this proof, we use the following notation: for
![]() $j < n < \omega $
,
$j < n < \omega $
,
Fix
![]() $B \subseteq \omega ^\omega \times \omega ^\omega \times 2^\omega $
and
$B \subseteq \omega ^\omega \times \omega ^\omega \times 2^\omega $
and
![]() $A = \operatorname {proj}^3_0(B)$
such that each section
$A = \operatorname {proj}^3_0(B)$
such that each section
![]() $A_x$
has measure
$A_x$
has measure
![]() $0$
,
$0$
,
![]() $(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
. Also let
$(\forall x, x' \in \omega ^\omega )(x \le x' \Rightarrow A_{x} \subseteq A_{x'})$
. Also let
![]() $\varepsilon> 0$
. We have to show that the outer measure
$\varepsilon> 0$
. We have to show that the outer measure
![]() $\mu ^*(\operatorname {proj}(A))$
is less than or equal to
$\mu ^*(\operatorname {proj}(A))$
is less than or equal to
![]() $\varepsilon $
.
$\varepsilon $
.
Fix a Borel isomorphism
![]() $\pi \colon 2^\omega \to \omega ^\omega $
. Consider the following game: At stage n, player I plays
$\pi \colon 2^\omega \to \omega ^\omega $
. Consider the following game: At stage n, player I plays
![]() $(s_n, t_n, u_n) \in \{0, 1\}^3$
. Player II then plays a finite union
$(s_n, t_n, u_n) \in \{0, 1\}^3$
. Player II then plays a finite union
![]() $G_n$
of basic open sets such that
$G_n$
of basic open sets such that
![]() $\mu (G_n) \le \varepsilon / 16^{n+1}$
. In this game, we define that player I wins if and only if
$\mu (G_n) \le \varepsilon / 16^{n+1}$
. In this game, we define that player I wins if and only if
![]() $(z, x, y) \in B$
and
$(z, x, y) \in B$
and
![]() $y \not \in \bigcup _{n \in \omega } G_n$
, where
$y \not \in \bigcup _{n \in \omega } G_n$
, where
![]() $x = \pi (s_0, s_1, \dots ), y = (t_0, t_1, \dots ),$
and
$x = \pi (s_0, s_1, \dots ), y = (t_0, t_1, \dots ),$
and
![]() $z = \pi (u_0, u_1, \dots )$
.
$z = \pi (u_0, u_1, \dots )$
.

Assume that player I has a winning strategy
![]() $\sigma $
. Put
$\sigma $
. Put
 $$\begin{align*}C &= \{ (z, x, y) \in \omega^\omega \times \omega^\omega \times 2^\omega : (\exists (G_0, G_1, \dots))((z, x, y)\\& \qquad \text{is the play of I along } \sigma \text{ against } (G_0, G_1, \dots)) \}. \end{align*}$$
$$\begin{align*}C &= \{ (z, x, y) \in \omega^\omega \times \omega^\omega \times 2^\omega : (\exists (G_0, G_1, \dots))((z, x, y)\\& \qquad \text{is the play of I along } \sigma \text{ against } (G_0, G_1, \dots)) \}. \end{align*}$$
Then clearly C is a
![]() $\boldsymbol {\Sigma }^1_1$
set. Since player I wins, we have
$\boldsymbol {\Sigma }^1_1$
set. Since player I wins, we have
![]() $C \subseteq B$
. So we have
$C \subseteq B$
. So we have
![]() $\operatorname {proj}^3_0(C) \subseteq \operatorname {proj}^3_0(B) = A$
. So each
$\operatorname {proj}^3_0(C) \subseteq \operatorname {proj}^3_0(B) = A$
. So each
![]() $(\operatorname {proj}^3_0(C))_x \subseteq A_x$
has measure
$(\operatorname {proj}^3_0(C))_x \subseteq A_x$
has measure
![]() $0$
. For
$0$
. For
![]() $x \in \omega ^\omega $
, put
$x \in \omega ^\omega $
, put
![]() $D_x = \bigcup _{x' \le x} (\operatorname {proj}^3_0(C))_{x'}$
, which is a
$D_x = \bigcup _{x' \le x} (\operatorname {proj}^3_0(C))_{x'}$
, which is a
![]() $\boldsymbol {\Sigma }^1_1$
set. Since
$\boldsymbol {\Sigma }^1_1$
set. Since
![]() $(\operatorname {proj}^3_0(C))_x \subseteq A_x$
, each
$(\operatorname {proj}^3_0(C))_x \subseteq A_x$
, each
![]() $D_x$
has measure
$D_x$
has measure
![]() $0$
. And we have
$0$
. And we have
![]() $x' \le x$
implies
$x' \le x$
implies
![]() $D_{x'} \subseteq D_x$
.
$D_{x'} \subseteq D_x$
.
Thus, by
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_1)$
,
$\mathsf {GP}(\boldsymbol {\Sigma }^1_1)$
,
![]() $\operatorname {proj}^2_0(D)$
has measure
$\operatorname {proj}^2_0(D)$
has measure
![]() $0$
. So
$0$
. So
![]() $\operatorname {proj}^2_0(\operatorname {proj}^3_0(C))$
has also measure
$\operatorname {proj}^2_0(\operatorname {proj}^3_0(C))$
has also measure
![]() $0$
. Therefore we can take
$0$
. Therefore we can take
![]() $(G_0, G_1, \dots )$
such that
$(G_0, G_1, \dots )$
such that
![]() $\operatorname {proj}^2_0(\operatorname {proj}^3_0(C)) \subseteq \bigcup _{n \in \omega } G_n$
and
$\operatorname {proj}^2_0(\operatorname {proj}^3_0(C)) \subseteq \bigcup _{n \in \omega } G_n$
and
![]() $\mu (G_n) \le \varepsilon / 16^{n+1}$
.
$\mu (G_n) \le \varepsilon / 16^{n+1}$
.
Let
![]() $(z, x, y)$
be the play along
$(z, x, y)$
be the play along
![]() $\sigma $
against
$\sigma $
against
![]() $(G_0, G_1, \dots )$
, then
$(G_0, G_1, \dots )$
, then
![]() $(z, x, y) \in C$
and
$(z, x, y) \in C$
and
![]() $y \not \in \bigcup _{n \in \omega } G_n$
. This contradicts to
$y \not \in \bigcup _{n \in \omega } G_n$
. This contradicts to
![]() $\operatorname {proj}^2_0(\operatorname {proj}^3_0(C)) \subseteq \bigcup _{n \in \omega } G_n$
.
$\operatorname {proj}^2_0(\operatorname {proj}^3_0(C)) \subseteq \bigcup _{n \in \omega } G_n$
.
So player I doesn’t have a winning strategy. Therefore, by
![]() $\operatorname {Det}(\Gamma )$
, player II has a winning strategy
$\operatorname {Det}(\Gamma )$
, player II has a winning strategy
![]() $\tau $
. Put
$\tau $
. Put
Then we have
![]() $\operatorname {proj}^2_0(\operatorname {proj}^3_0(B)) \subseteq E$
. In order to check this, let
$\operatorname {proj}^2_0(\operatorname {proj}^3_0(B)) \subseteq E$
. In order to check this, let
![]() $(z, x, y) \in B$
. Consider the player I’s play
$(z, x, y) \in B$
. Consider the player I’s play
![]() $(z, x, y)$
. Let
$(z, x, y)$
. Let
![]() $(G_0, G_1, \dots )$
be the play along
$(G_0, G_1, \dots )$
be the play along
![]() $\tau $
against
$\tau $
against
![]() $(z, x, y)$
. Since II wins,
$(z, x, y)$
. Since II wins,
![]() $y \in \bigcup _{n \in \omega } G_n \subseteq E$
.
$y \in \bigcup _{n \in \omega } G_n \subseteq E$
.
Also we have
Therefore we have
![]() $\mu ^*(\operatorname {proj}^2_0(A)) \le \mu (E) \le \varepsilon $
.
$\mu ^*(\operatorname {proj}^2_0(A)) \le \mu (E) \le \varepsilon $
.
8 Consequences of large cardinals
In this section, using large cardinals, we separate
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
and
$\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
and
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_n)$
for every
$\mathsf {GP}(\boldsymbol {\Sigma }^1_n)$
for every
![]() $n \ge 2$
.
$n \ge 2$
.
For a pointclass
![]() $\Gamma $
, recall that
$\Gamma $
, recall that
![]() $\triangleleft $
is a
$\triangleleft $
is a
![]() $\Gamma $
-good wellordering of the reals if it is a wellordering of the reals of order-type
$\Gamma $
-good wellordering of the reals if it is a wellordering of the reals of order-type
![]() $\omega _1$
, it is in
$\omega _1$
, it is in
![]() $\Gamma $
and the relation
$\Gamma $
and the relation
is in
![]() $\Gamma $
.
$\Gamma $
.
Fact 8.1.
-
(1) [Reference Bagaria and Woodin2] If
 $\mathsf {ZFC}$
is consistent, then so is
$\mathsf {ZFC}$
is consistent, then so is
 $\mathsf {ZFC}$
plus
$\mathsf {ZFC}$
plus
 $\boldsymbol {\Sigma }^1_2$
Lebesgue measurability plus “there is a
$\boldsymbol {\Sigma }^1_2$
Lebesgue measurability plus “there is a
 $\boldsymbol {\Sigma }^1_3$
good wellordering of the reals of length
$\boldsymbol {\Sigma }^1_3$
good wellordering of the reals of length
 $\omega _1$
.”
$\omega _1$
.” -
(2) [Reference Steel13] Assume that there are n many Woodin cardinals. Then there is an inner model
 $M_n$
of
$M_n$
of
 $\mathsf {ZFC}$
that models
$\mathsf {ZFC}$
that models
 $\operatorname {Det}(\boldsymbol {\Sigma }^1_n) $
and “
$\operatorname {Det}(\boldsymbol {\Sigma }^1_n) $
and “
 $\text {there is a}\ \boldsymbol {\Sigma }^1_{n+2} \text { good wellordering of the reals}$
.”
$\text {there is a}\ \boldsymbol {\Sigma }^1_{n+2} \text { good wellordering of the reals}$
.”
Lemma 8.2. Let
![]() $n \ge 2$
. If there is a
$n \ge 2$
. If there is a
![]() $\boldsymbol {\Sigma }^1_n$
good wellordering
$\boldsymbol {\Sigma }^1_n$
good wellordering
![]() $\trianglelefteq $
of the reals of length
$\trianglelefteq $
of the reals of length
![]() $\omega _1$
, then there is a cofinal increasing sequence of
$\omega _1$
, then there is a cofinal increasing sequence of
![]() $\omega ^\omega $
whose image is
$\omega ^\omega $
whose image is
![]() $\boldsymbol {\Delta }^1_n$
.
$\boldsymbol {\Delta }^1_n$
.
Proof. We define a function
![]() $G \colon [\omega ^\omega ]^{\le \aleph _0} \to \omega ^\omega $
by
$G \colon [\omega ^\omega ]^{\le \aleph _0} \to \omega ^\omega $
by
We define a sequence
![]() $(x_\alpha : \alpha < \omega _1)$
of reals in
$(x_\alpha : \alpha < \omega _1)$
of reals in
![]() $\omega ^\omega $
by
$\omega ^\omega $
by
Then we put
First we claim that D is
![]() $\boldsymbol {\Sigma }^1_n$
. Using the usual technique that writes a recursive construction in the way of the existence of an approximation, we have
$\boldsymbol {\Sigma }^1_n$
. Using the usual technique that writes a recursive construction in the way of the existence of an approximation, we have
 $$ \begin{align*} x \in D \iff & (\exists \alpha < \omega_1)(\exists F \colon \alpha + 1 \to \omega^\omega) \\ & [(\forall \beta < \alpha)(F(\beta) = G(F \upharpoonright \beta)) \mathbin{\text{and}} x = F(\alpha)]. \end{align*} $$
$$ \begin{align*} x \in D \iff & (\exists \alpha < \omega_1)(\exists F \colon \alpha + 1 \to \omega^\omega) \\ & [(\forall \beta < \alpha)(F(\beta) = G(F \upharpoonright \beta)) \mathbin{\text{and}} x = F(\alpha)]. \end{align*} $$
Eliminating ordinal variables, we have
 $$ \begin{align*} x \in D \iff &(\exists z)(\exists w)(\exists f \colon \omega \to \omega^\omega) \\ & \ [w \text{ codes the initial segment below } z \ \mathbin{\text{and}} \\ & \ \ (\forall k)(\exists w') [w' \text{ codes the initial segment below } w(k) \ \mathbin{\text{and}} \\ & \ \ f(k) = G(\{f(i) : \exists j\ ((w)_i = (w')_j) \})] \ \mathbin{\text{and}} \\ & \ x = G(\operatorname{ran} f)]. \end{align*} $$
$$ \begin{align*} x \in D \iff &(\exists z)(\exists w)(\exists f \colon \omega \to \omega^\omega) \\ & \ [w \text{ codes the initial segment below } z \ \mathbin{\text{and}} \\ & \ \ (\forall k)(\exists w') [w' \text{ codes the initial segment below } w(k) \ \mathbin{\text{and}} \\ & \ \ f(k) = G(\{f(i) : \exists j\ ((w)_i = (w')_j) \})] \ \mathbin{\text{and}} \\ & \ x = G(\operatorname{ran} f)]. \end{align*} $$
Therefore D is
![]() $\boldsymbol {\Sigma }^1_n$
.
$\boldsymbol {\Sigma }^1_n$
.
Next, we show that D is
![]() $\boldsymbol {\Pi }^1_n$
. As with the above claim, we have
$\boldsymbol {\Pi }^1_n$
. As with the above claim, we have
 $$ \begin{align*} x \not \in D \iff &(\exists \alpha < \omega_1)(\exists F \colon \alpha + 1 \to \omega^\omega) \\ & [(\forall \beta < \alpha)(F(\beta) = G(F \upharpoonright \beta)) \mathbin{\text{and}} x \le^* F(\alpha) \mathbin{\text{and}} (\forall \beta < \alpha)(x \ne F(\beta))]. \end{align*} $$
$$ \begin{align*} x \not \in D \iff &(\exists \alpha < \omega_1)(\exists F \colon \alpha + 1 \to \omega^\omega) \\ & [(\forall \beta < \alpha)(F(\beta) = G(F \upharpoonright \beta)) \mathbin{\text{and}} x \le^* F(\alpha) \mathbin{\text{and}} (\forall \beta < \alpha)(x \ne F(\beta))]. \end{align*} $$
By the same transform of formulas in the above claim, we have that
![]() $\omega ^\omega \smallsetminus D$
is
$\omega ^\omega \smallsetminus D$
is
![]() $\boldsymbol {\Sigma }^1_n$
.
$\boldsymbol {\Sigma }^1_n$
.
Using the above lemma, we can get the following.
Lemma 8.3. Let
![]() $n \ge 2$
. If there is a
$n \ge 2$
. If there is a
![]() $\boldsymbol {\Sigma }^1_n$
good wellordering
$\boldsymbol {\Sigma }^1_n$
good wellordering
![]() $\trianglelefteq $
of the reals of length
$\trianglelefteq $
of the reals of length
![]() $\omega _1$
, then
$\omega _1$
, then
![]() $\neg \mathsf {GP}(\boldsymbol {\Delta }^1_n)$
holds.
$\neg \mathsf {GP}(\boldsymbol {\Delta }^1_n)$
holds.
Proof. Let D denote the set defined in Lemma 8.2. We define a set A by
Then we have
 $$ \begin{align*} (x, y) \in A \iff & (\exists z)(\exists w) \\ &\ [w \text{ codes the initial segment below } z \mathbin{\text{and}} z \in D \ \mathbin{\text{and}} \\ &\ \ x \le^* z \ \mathbin{\text{and}} (\forall k)((w)_k \in D \rightarrow x \not \le^* (w)_k) \ \mathbin{\text{and}} \\ &\ \ y \trianglelefteq z]. \end{align*} $$
$$ \begin{align*} (x, y) \in A \iff & (\exists z)(\exists w) \\ &\ [w \text{ codes the initial segment below } z \mathbin{\text{and}} z \in D \ \mathbin{\text{and}} \\ &\ \ x \le^* z \ \mathbin{\text{and}} (\forall k)((w)_k \in D \rightarrow x \not \le^* (w)_k) \ \mathbin{\text{and}} \\ &\ \ y \trianglelefteq z]. \end{align*} $$
So A is
![]() $\boldsymbol {\Sigma }^1_n$
. Moreover, since we have
$\boldsymbol {\Sigma }^1_n$
. Moreover, since we have
 $$ \begin{align*} (x, y) \in A \iff & (\forall z)(\forall w) \\ &\ [[w \text{ codes the initial segment below } z \mathbin{\text{and}} z \in D \ \mathbin{\text{and}} \\ &\ \ x \le^* z \ \mathbin{\text{and}} (\forall k)((w)_k \in D \rightarrow x \not \le^* (w)_k)] \ \rightarrow \\ &\ \ y \trianglelefteq z], \end{align*} $$
$$ \begin{align*} (x, y) \in A \iff & (\forall z)(\forall w) \\ &\ [[w \text{ codes the initial segment below } z \mathbin{\text{and}} z \in D \ \mathbin{\text{and}} \\ &\ \ x \le^* z \ \mathbin{\text{and}} (\forall k)((w)_k \in D \rightarrow x \not \le^* (w)_k)] \ \rightarrow \\ &\ \ y \trianglelefteq z], \end{align*} $$
it is also true that A is
![]() $\boldsymbol {\Pi }^1_n$
. So A is
$\boldsymbol {\Pi }^1_n$
. So A is
![]() $\boldsymbol {\Delta }^1_n$
.
$\boldsymbol {\Delta }^1_n$
.
Since each
![]() $A_x$
is countable and
$A_x$
is countable and
![]() $\bigcup _{x \in \omega ^\omega } A_x = \omega ^\omega $
, this A witnesses
$\bigcup _{x \in \omega ^\omega } A_x = \omega ^\omega $
, this A witnesses
![]() $\neg \mathsf {GP}(\boldsymbol {\Delta }^1_n)$
.
$\neg \mathsf {GP}(\boldsymbol {\Delta }^1_n)$
.
Corollary 8.4.
-
(1) If
 $\mathsf {ZFC}$
is consistent, then so is
$\mathsf {ZFC}$
is consistent, then so is
 $\mathsf {ZFC}+\mathsf {GP}(\boldsymbol {\Sigma }^1_2)+\neg \mathsf {GP}(\boldsymbol {\Delta }^1_3)$
.
$\mathsf {ZFC}+\mathsf {GP}(\boldsymbol {\Sigma }^1_2)+\neg \mathsf {GP}(\boldsymbol {\Delta }^1_3)$
. -
(2) For every
 $n \ge 1$
, if
$n \ge 1$
, if
 $\mathsf {ZFC}+(\text {there are } n \text { many Woodin cardinals})$
is consistent, then so is
$\mathsf {ZFC}+(\text {there are } n \text { many Woodin cardinals})$
is consistent, then so is
 $\mathsf {ZFC}+\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})+\neg \mathsf {GP}(\boldsymbol {\Delta }^1_{n+2})$
.
$\mathsf {ZFC}+\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})+\neg \mathsf {GP}(\boldsymbol {\Delta }^1_{n+2})$
.
9
 $\mathsf {GP}(\mathsf {all})$
in Solovay models
$\mathsf {GP}(\mathsf {all})$
in Solovay models
Now that we know that
![]() $\mathsf {AD}$
implies
$\mathsf {AD}$
implies
![]() $\mathsf {GP}(\mathsf {all})$
, it is natural to ask whether
$\mathsf {GP}(\mathsf {all})$
, it is natural to ask whether
![]() $\mathsf {GP}(\mathsf {all})$
holds in Solovay models. In this section, we will solve this question affirmatively.
$\mathsf {GP}(\mathsf {all})$
holds in Solovay models. In this section, we will solve this question affirmatively.
Basic information about Solovay models can be found in [Reference Kanamori9, Chapter 3].
Let us recall that
![]() $\mathrm {Coll}_\kappa $
denotes the Levy collapse, where
$\mathrm {Coll}_\kappa $
denotes the Levy collapse, where
![]() $\kappa $
is an inaccessible cardinal.
$\kappa $
is an inaccessible cardinal.
Definition 9.1.
-
(1)
 $L(\mathbb {R})^M$
is a Solovay model over V (in the usual sense) if
$L(\mathbb {R})^M$
is a Solovay model over V (in the usual sense) if
 $M = V[G]$
for some inaccessible cardinal
$M = V[G]$
for some inaccessible cardinal
 $\kappa $
and
$\kappa $
and
 $(V, \mathrm {Coll}_\kappa )$
-generic filter G.
$(V, \mathrm {Coll}_\kappa )$
-generic filter G. -
(2)
 $L(\mathbb {R})^M$
is a Solovay model over V in the weak sense if the following two conditions hold in M:
$L(\mathbb {R})^M$
is a Solovay model over V in the weak sense if the following two conditions hold in M:-
(a) For every
 $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $\omega _1$
is an inaccessible cardinal in
$\omega _1$
is an inaccessible cardinal in
 $V[x]$
.
$V[x]$
. -
(b) For every
 $x \in \mathbb {R}$
,
$x \in \mathbb {R}$
,
 $V[x]$
is a generic extension of V by some poset in V, which is countable in M.
$V[x]$
is a generic extension of V by some poset in V, which is countable in M.
-
Fact 9.2 (Woodin, see [Reference Bagaria and Bosch1, Lemma 1.2])
If
![]() $L(\mathbb {R})^M$
is a Solovay model over V in the weak sense then there is a forcing poset
$L(\mathbb {R})^M$
is a Solovay model over V in the weak sense then there is a forcing poset
![]() $\mathbb {W}$
in M such that
$\mathbb {W}$
in M such that
![]() $\mathbb {W}$
adds no new reals and
$\mathbb {W}$
adds no new reals and
Fact 9.3 [Reference Bagaria and Bosch1, Theorem 2.4]
Suppose that
![]() $L(\mathbb {R})^M$
is a Solovay model over V in the weak sense and
$L(\mathbb {R})^M$
is a Solovay model over V in the weak sense and
![]() $\mathbb {P}$
is a strongly-
$\mathbb {P}$
is a strongly-
![]() $\boldsymbol {\Sigma }^1_3$
absolutely-ccc poset in M. Let G be an
$\boldsymbol {\Sigma }^1_3$
absolutely-ccc poset in M. Let G be an
![]() $(M, \mathbb {P})$
-generic filter. Then
$(M, \mathbb {P})$
-generic filter. Then
![]() $L(\mathbb {R})^{M[G]}$
is also a Solovay model in V in the weak sense.
$L(\mathbb {R})^{M[G]}$
is also a Solovay model in V in the weak sense.
We don’t define the terminology “strongly-
![]() $\boldsymbol {\Sigma }^1_3$
absolutely-ccc poset” here. But the random forcing is such a poset and we will use only the random forcing when applying Fact 9.3.
$\boldsymbol {\Sigma }^1_3$
absolutely-ccc poset” here. But the random forcing is such a poset and we will use only the random forcing when applying Fact 9.3.
Lemma 9.4. Let
![]() $M, N$
be models satisfying
$M, N$
be models satisfying
![]() $V \subseteq M \subseteq N$
. Assume that the
$V \subseteq M \subseteq N$
. Assume that the
![]() $L(\mathbb {R})$
of each of M and N are Solovay models over V in the weak sense. Then for every formula
$L(\mathbb {R})$
of each of M and N are Solovay models over V in the weak sense. Then for every formula
![]() $\varphi (v)$
in the language of set theory
$\varphi (v)$
in the language of set theory
![]() $\mathcal {L}_\in = \{\in \}$
and real r in M, the assertion
$\mathcal {L}_\in = \{\in \}$
and real r in M, the assertion
![]() $"L(\mathbb {R}) \models \varphi (r)"$
is absolute between M and N.
$"L(\mathbb {R}) \models \varphi (r)"$
is absolute between M and N.
Proof. By Fact 9.2, we may assume that
![]() $L(\mathbb {R})^M$
and
$L(\mathbb {R})^M$
and
![]() $L(\mathbb {R})^N$
are Solovay models over V in the usual sense. By universality and homogeneity of the Levy collapse, we have
$L(\mathbb {R})^N$
are Solovay models over V in the usual sense. By universality and homogeneity of the Levy collapse, we have
 $$ \begin{align*} M \models "L(\mathbb{R}) \models \varphi(r)" & \iff V[r] \models [\mathrm{Coll}_\kappa \Vdash "L(\mathbb{R}) \models \varphi(r)"] \\ & \iff N \models "L(\mathbb{R}) \models \varphi(r).\text{"}\\[-33pt] \end{align*} $$
$$ \begin{align*} M \models "L(\mathbb{R}) \models \varphi(r)" & \iff V[r] \models [\mathrm{Coll}_\kappa \Vdash "L(\mathbb{R}) \models \varphi(r)"] \\ & \iff N \models "L(\mathbb{R}) \models \varphi(r).\text{"}\\[-33pt] \end{align*} $$
Theorem 9.5. Let
![]() $\kappa $
be an inaccessible cardinal and G be a
$\kappa $
be an inaccessible cardinal and G be a
![]() $(V, \mathrm {Coll}_\kappa )$
-generic filter. Then
$(V, \mathrm {Coll}_\kappa )$
-generic filter. Then
![]() $L(\mathbb {R})^{V[G]}$
satisfies
$L(\mathbb {R})^{V[G]}$
satisfies
![]() $\mathsf {GP}(\mathsf {all})$
. That is, every Solovay model satisfies
$\mathsf {GP}(\mathsf {all})$
. That is, every Solovay model satisfies
![]() $\mathsf {GP}(\mathsf {all})$
.
$\mathsf {GP}(\mathsf {all})$
.
Proof. Let
![]() $A \subseteq \omega ^\omega \times 2^\omega $
in
$A \subseteq \omega ^\omega \times 2^\omega $
in
![]() $L(\mathbb {R})^{V[G]}$
. Take a formula
$L(\mathbb {R})^{V[G]}$
. Take a formula
![]() $\varphi $
and an ordinal
$\varphi $
and an ordinal
![]() $\alpha $
such that
$\alpha $
such that
In
![]() $L(\mathbb {R})^{V[G]}$
, assume that:
$L(\mathbb {R})^{V[G]}$
, assume that:
-
(1)
 $(\forall x \in \omega ^\omega ) (\exists c_x \in \omega ^\omega ) (c_x \text { is a Borel code for a measure 0 set} \mathbin {\text {and}} A_x \subseteq \hat {c_x}).$
$(\forall x \in \omega ^\omega ) (\exists c_x \in \omega ^\omega ) (c_x \text { is a Borel code for a measure 0 set} \mathbin {\text {and}} A_x \subseteq \hat {c_x}).$
-
(2)
 $(\forall x, x' \in \omega ^\omega ) (x \le x' \rightarrow A_x \subseteq A_{x'})$
.
$(\forall x, x' \in \omega ^\omega ) (x \le x' \rightarrow A_x \subseteq A_{x'})$
.
Using the axiom of choice in
![]() $V[G]$
we can choose such a family
$V[G]$
we can choose such a family
![]() $(c_x : x \in \omega ^\omega )$
. Note that this family is not necessarily in
$(c_x : x \in \omega ^\omega )$
. Note that this family is not necessarily in
![]() $L(\mathbb {R})^{V[G]}$
.
$L(\mathbb {R})^{V[G]}$
.
Since every set of reals is measurable in
![]() $L(\mathbb {R})^{V[G]}$
,
$L(\mathbb {R})^{V[G]}$
,
![]() $\bigcup _{x \in \omega ^\omega } A_x$
is measurable in
$\bigcup _{x \in \omega ^\omega } A_x$
is measurable in
![]() $L(\mathbb {R})^{V[G]}$
. In order to reach a contradiction, we assume that the measure is positive and take a closed code d in
$L(\mathbb {R})^{V[G]}$
. In order to reach a contradiction, we assume that the measure is positive and take a closed code d in
![]() $L(\mathbb {R})^{V[G]}$
such that
$L(\mathbb {R})^{V[G]}$
such that
![]() $\mu (\hat {d})> 0$
and
$\mu (\hat {d})> 0$
and
![]() $\hat {d} \subseteq \bigcup _{x \in \omega ^\omega } A_x$
in
$\hat {d} \subseteq \bigcup _{x \in \omega ^\omega } A_x$
in
![]() $L(\mathbb {R})^{V[G]}$
.
$L(\mathbb {R})^{V[G]}$
.
Take a random real r over
![]() $V[G]$
with
$V[G]$
with
![]() $r \in \hat {d}$
. Then by Lemma 9.4, we have in
$r \in \hat {d}$
. Then by Lemma 9.4, we have in
![]() $L(\mathbb {R})^{V[G][r]}$
:
$L(\mathbb {R})^{V[G][r]}$
:
-
(1’)
 $(\forall x \in \omega ^\omega \cap L(\mathbb {R})^{V[G]}) (A_x \subseteq \hat {c_x})$
, and
$(\forall x \in \omega ^\omega \cap L(\mathbb {R})^{V[G]}) (A_x \subseteq \hat {c_x})$
, and -
(2’)
 $(\forall x, x' \in \omega ^\omega ) (x \le x' \rightarrow A_x \subseteq A_{x'})$
.
$(\forall x, x' \in \omega ^\omega ) (x \le x' \rightarrow A_x \subseteq A_{x'})$
.
By randomness, we have
![]() $r \not \in \hat {c_x}$
for all
$r \not \in \hat {c_x}$
for all
![]() $x \in \omega ^\omega \cap L(\mathbb {R})^{V[G]}$
. But (2’) and the fact that the random forcing is
$x \in \omega ^\omega \cap L(\mathbb {R})^{V[G]}$
. But (2’) and the fact that the random forcing is
![]() $\omega ^\omega $
-bounding imply
$\omega ^\omega $
-bounding imply
![]() $r \not \in A_x$
for all
$r \not \in A_x$
for all
![]() $x \in \omega ^\omega $
in
$x \in \omega ^\omega $
in
![]() $V[G][r]$
. Thus we have
$V[G][r]$
. Thus we have
![]() $\hat {d} \smallsetminus \bigcup _{x \in \omega ^\omega } A_x \ne \varnothing $
in
$\hat {d} \smallsetminus \bigcup _{x \in \omega ^\omega } A_x \ne \varnothing $
in
![]() $L(\mathbb {R})^{V[G][r]}$
. Then using Lemma 9.4 again, we have
$L(\mathbb {R})^{V[G][r]}$
. Then using Lemma 9.4 again, we have
![]() $\hat {d} \smallsetminus \bigcup _{x \in \omega ^\omega } A_x \ne \varnothing $
in
$\hat {d} \smallsetminus \bigcup _{x \in \omega ^\omega } A_x \ne \varnothing $
in
![]() $L(\mathbb {R})^{V[G]}$
. It is a contradiction to the choice of d.
$L(\mathbb {R})^{V[G]}$
. It is a contradiction to the choice of d.
10 Other ideals than the Lebesgue measure zero ideal
In this section, we consider other ideals than the Lebesgue measure zero ideal.
Definition 10.1. Let
![]() $\Gamma $
be a pointclass and
$\Gamma $
be a pointclass and
![]() $\mathcal {I}$
be an ideal on a Polish space Y. Then
$\mathcal {I}$
be an ideal on a Polish space Y. Then
![]() $\mathsf {GP}(\Gamma , \mathcal {I})$
means the following statement: Let
$\mathsf {GP}(\Gamma , \mathcal {I})$
means the following statement: Let
![]() $A \subseteq \omega ^\omega \times Y$
be in
$A \subseteq \omega ^\omega \times Y$
be in
![]() $\Gamma $
. Assume the monotonicity condition for A. Assume also
$\Gamma $
. Assume the monotonicity condition for A. Assume also
![]() $A_x \in \mathcal {I}$
for every
$A_x \in \mathcal {I}$
for every
![]() $x \in \omega ^\omega $
. Then
$x \in \omega ^\omega $
. Then
![]() $\bigcup _{x \in \omega ^\omega } A_x$
is also in
$\bigcup _{x \in \omega ^\omega } A_x$
is also in
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Note that
![]() $\mathsf {GP}(\mathsf {Borel}, \mathsf {meager})$
does not hold by considering
$\mathsf {GP}(\mathsf {Borel}, \mathsf {meager})$
does not hold by considering
![]() $A_x = \{ y \in \omega ^\omega : y \le ^* x \}$
.
$A_x = \{ y \in \omega ^\omega : y \le ^* x \}$
.
In what follows,
![]() $\mathcal {E}$
means the
$\mathcal {E}$
means the
![]() $\sigma $
-ideal generated by closed null sets. We would like to prove
$\sigma $
-ideal generated by closed null sets. We would like to prove
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
does not hold.
$\mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
does not hold.
To prove it, we recall the basic notions of interval partitions. Let
![]() $\mathsf {IP}$
be the set of all interval partitions. Also
$\mathsf {IP}$
be the set of all interval partitions. Also
![]() $\sqsubset $
is the order on
$\sqsubset $
is the order on
![]() $\mathsf {IP}$
such that
$\mathsf {IP}$
such that
We use the following well-known fact.
Fact 10.2 [Reference Blass4, Theorem 2.10]
There is a Borel Tukey connection from
![]() $\mathsf {IP}$
to
$\mathsf {IP}$
to
![]() $\omega ^\omega $
. That is, there is Borel maps
$\omega ^\omega $
. That is, there is Borel maps
![]() $\phi \colon \mathsf {IP} \to \omega ^\omega $
and
$\phi \colon \mathsf {IP} \to \omega ^\omega $
and
![]() $\psi \colon \omega ^\omega \to \mathsf {IP}$
such that
$\psi \colon \omega ^\omega \to \mathsf {IP}$
such that
![]() $\phi (I) \le ^* y$
implies
$\phi (I) \le ^* y$
implies
![]() $I \sqsubset \psi (y)$
for every
$I \sqsubset \psi (y)$
for every
![]() $I \in \mathsf {IP}$
and
$I \in \mathsf {IP}$
and
![]() $y \in \omega ^\omega $
.
$y \in \omega ^\omega $
.
Theorem 10.3.
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
does not hold.
$\mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
does not hold.
Proof. Let
![]() ${\langle I_n : n \in \omega \rangle }$
be the interval partition with
${\langle I_n : n \in \omega \rangle }$
be the interval partition with
![]() $ \left \lvert {I_n} \right \rvert = n+1$
. Let
$ \left \lvert {I_n} \right \rvert = n+1$
. Let
![]() $A = \{ x \in 2^\omega : (\exists ^\infty n)(x \upharpoonright I_n \equiv 0) \}$
. It is well-known that A is null and comeager. In particular
$A = \{ x \in 2^\omega : (\exists ^\infty n)(x \upharpoonright I_n \equiv 0) \}$
. It is well-known that A is null and comeager. In particular
![]() $A \not \in \mathcal {E}$
. For an interval partition
$A \not \in \mathcal {E}$
. For an interval partition
![]() $J = {\langle J_k : k \in \omega \rangle }$
, let
$J = {\langle J_k : k \in \omega \rangle }$
, let
Each
![]() $A_J$
is
$A_J$
is
![]() $F_\sigma $
null set, so it holds that
$F_\sigma $
null set, so it holds that
![]() $A_J \in \mathcal {E}$
. And also we have
$A_J \in \mathcal {E}$
. And also we have
![]() $\bigcup _{J} A_J = A \not \in \mathcal {E}$
.
$\bigcup _{J} A_J = A \not \in \mathcal {E}$
.
Moreover,
![]() $\{ (J, y) : y \in A_J \}$
is Borel and the family is monotone.
$\{ (J, y) : y \in A_J \}$
is Borel and the family is monotone.
We now have to translate this family to the family indexed by
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Let
![]() $(\phi , \psi )$
be the Tukey connection in Fact 10.2. Let
$(\phi , \psi )$
be the Tukey connection in Fact 10.2. Let
![]() $B_x = \bigcap _{y \ge ^* x} A_{\psi (y)}$
for
$B_x = \bigcap _{y \ge ^* x} A_{\psi (y)}$
for
![]() $x \in \omega ^\omega $
.
$x \in \omega ^\omega $
.
![]() ${\langle B_x : x \in \omega ^\omega \rangle }$
is clearly monotone, each
${\langle B_x : x \in \omega ^\omega \rangle }$
is clearly monotone, each
![]() $B_x$
is in
$B_x$
is in
![]() $\mathcal {E}$
and the family B is
$\mathcal {E}$
and the family B is
![]() $\boldsymbol {\Pi }^1_1$
. On the other hand we have
$\boldsymbol {\Pi }^1_1$
. On the other hand we have
![]() $\bigcup _{J \in \mathsf {IP}} A_J \subseteq \bigcup _{x \in \omega } B_x$
. To see it, let
$\bigcup _{J \in \mathsf {IP}} A_J \subseteq \bigcup _{x \in \omega } B_x$
. To see it, let
![]() $J \in \mathsf {IP}$
and
$J \in \mathsf {IP}$
and
![]() $a \in A_J$
. Set
$a \in A_J$
. Set
![]() $x = \phi (J)$
. Then
$x = \phi (J)$
. Then
![]() $x \le ^* y$
implies
$x \le ^* y$
implies
![]() $J \sqsubset \psi (y)$
since
$J \sqsubset \psi (y)$
since
![]() $(\phi , \psi )$
is Tukey. So
$(\phi , \psi )$
is Tukey. So
![]() $a \in A_J \subseteq A_{\psi (y)}$
. Therefore we have
$a \in A_J \subseteq A_{\psi (y)}$
. Therefore we have
![]() $a \in B_x$
.
$a \in B_x$
.
Since
![]() $\bigcup _{J \in \mathsf {IP}} A_J \not \in \mathcal {E}$
, we have constructed a counterexample
$\bigcup _{J \in \mathsf {IP}} A_J \not \in \mathcal {E}$
, we have constructed a counterexample
![]() ${\langle B_x : x \in \omega ^\omega \rangle }$
of
${\langle B_x : x \in \omega ^\omega \rangle }$
of
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
.
$\mathsf {GP}(\boldsymbol {\Pi }^1_1, \mathcal {E})$
.
11 Open problems
In this section, we list the problems that remain.
Problem 11.1.
-
(1) Is
 $\mathsf {ZFC}+(\mathfrak {c}>\aleph _2)+\mathsf {GP}(\mathsf {all})$
consistent?
$\mathsf {ZFC}+(\mathfrak {c}>\aleph _2)+\mathsf {GP}(\mathsf {all})$
consistent? -
(2) Is
 $\mathsf {ZFC}+(\mathfrak {b}<\mathfrak {d})+\mathsf {GP}(\mathsf {all})$
consistent?
$\mathsf {ZFC}+(\mathfrak {b}<\mathfrak {d})+\mathsf {GP}(\mathsf {all})$
consistent?
We suspect that (1) of Problem 11.1 is proved by adding many random reals over the Laver model.
Problem 11.2. How much separation is possible between
![]() $\mathsf {GP}$
of pointclasses in the projective hierarchy? In particular how much is possible without large cardinals?
$\mathsf {GP}$
of pointclasses in the projective hierarchy? In particular how much is possible without large cardinals?
Note that we separated
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
and
$\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
and
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_{n+2})$
using n many Woodin cardinals. We are asking how about separation between
$\mathsf {GP}(\boldsymbol {\Delta }^1_{n+2})$
using n many Woodin cardinals. We are asking how about separation between
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
and
$\mathsf {GP}(\boldsymbol {\Sigma }^1_{n+1})$
and
![]() $\mathsf {GP}(\boldsymbol {\Pi }^1_{n+1})$
? Also, we are asking whether we can eliminate the use of Woodin cardinals.
$\mathsf {GP}(\boldsymbol {\Pi }^1_{n+1})$
? Also, we are asking whether we can eliminate the use of Woodin cardinals.
Problem 11.3. Can
![]() $\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
and
$\mathsf {GP}(\boldsymbol {\Delta }^1_2)$
and
![]() $(\forall a \in \mathbb {R})(\exists z \in \omega ^\omega ) (z \text {is a dominating real over } L[a])$
be separated?
$(\forall a \in \mathbb {R})(\exists z \in \omega ^\omega ) (z \text {is a dominating real over } L[a])$
be separated?
A nice candidate of this problem is Hechler model over L.
Problem 11.4. Is there a model of
![]() $\mathsf {ZF}$
satisfying that every set of reals is measurable and
$\mathsf {ZF}$
satisfying that every set of reals is measurable and
![]() $\neg \mathsf {GP}(\mathsf {all})$
?
$\neg \mathsf {GP}(\mathsf {all})$
?
Shelah [Reference Shelah12] constructed a model of
![]() $\mathsf {ZF}$
+(the dependent choice)+(every set of reals is Lebesgue measurable)+(there is a set of reals that does not have the Baire property). The idea of this construction might help Problem 11.4.
$\mathsf {ZF}$
+(the dependent choice)+(every set of reals is Lebesgue measurable)+(there is a set of reals that does not have the Baire property). The idea of this construction might help Problem 11.4.
Problem 11.5. Does
![]() $\mathsf {GP}(\mathsf {all})$
imply the Borel conjecture?
$\mathsf {GP}(\mathsf {all})$
imply the Borel conjecture?
Note that the Borel conjecture does not imply
![]() $\mathsf {GP}(\mathsf {all})$
, since the Mathias model satisfies the Borel conjecture and
$\mathsf {GP}(\mathsf {all})$
, since the Mathias model satisfies the Borel conjecture and
![]() $\operatorname {non}(\mathsf {null})=\mathfrak {b}$
, which implies
$\operatorname {non}(\mathsf {null})=\mathfrak {b}$
, which implies
![]() $\neg \mathsf {GP}(\mathsf {all})$
.
$\neg \mathsf {GP}(\mathsf {all})$
.
Finally, we ask the following question.
Problem 11.6. Does
![]() $\mathsf {GP}(\boldsymbol {\Sigma }^1_1, \mathcal {E})$
hold?
$\mathsf {GP}(\boldsymbol {\Sigma }^1_1, \mathcal {E})$
hold?
Acknowledgments
The author would like to thank Yasuo Yoshinobu, Takayuki Kihara, and Jörg Brendle, who gave him advices on this research. In particular, the idea of the proof of Theorem 5.3 is due to Brendle. The author would also like to thank Martin Goldstern, who read the preprint of this article and pointed out errors. The author would also like to thank Daisuke Ikegami, who gave him advice in proving Theorem 9.5.
Funding
This work was supported by JSPS KAKENHI Grant Number JP22J20021.