2.1 The oriented skein category

The framed HOMFLYPT skein category, or oriented skein category for short, , is the $\Bbbk $ -linear strict monoidal category generated by objects ${\mathord {\uparrow }}$ , ${\mathord {\downarrow }}$ and morphisms

subject to the relations

(2.1)

(2.2)

(2.3)

(2.4)

In (2.1), we have used the following morphisms:

(2.5)

This category was first introduced in [Reference TuraevTur89, §5.2], where it was called the Hecke category. In [Reference Queffelec and SartoriQS19, Definition 2.1] it is called the quantized oriented Brauer category. It was studied in depth in [Reference BrundanBru17]. Note that in [Reference BrundanBru17], the category is denoted , with the denominator $q-q^{-1}$ in (2.3) replaced by z. Since we will only be interested in the case $z=q-q^{-1}$ , we make this choice at the start and use the simpler notation instead of .

We define the following morphisms:

(2.6)

The category is strict pivotal. Furthermore, the following relations hold for any orientation of the strands:

(2.7)

(2.8)

We also have

(2.9)

It is straightforward to verify that there is a $\Bbbk $ -antilinear isomorphism of monoidal categories

(2.10)

acting on objects as ${\mathord {\uparrow }} \mapsto {\mathord {\downarrow }}$ , ${\mathord {\downarrow }} \mapsto {\mathord {\uparrow }}$ , and sending

(2.11)

Intuitively, $\Omega _{\updownarrow }$ reflects diagrams in the horizontal axis and inverts q and t. We also have an isomorphism of $\Bbbk $ -linear monoidal categories

(2.12)

that reverses the orientation of all strands. Finally, we have a $\Bbbk $ -antilinear isomorphism of monoidal categories

(2.13)

which we call the bar involution, acting as the identity on objects and given on morphisms by

Intuitively, the bar involution flips crossings in diagrams and inverts q and t.

Let $\langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ denote the set of objects for . Equivalently, writing the tensor product as juxtaposition, $\langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ is the set of words generated by ${\mathord {\uparrow }}$ and ${\mathord {\downarrow }}$ . It will be convenient to introduce thick strands:

The fact that is a braided monoidal category gives us a natural interpretation for crossings of such strands. For instance, if $\lambda = {\mathord {\downarrow }} {\mathord {\uparrow }}$ and $\mu = {\mathord {\uparrow }} {\mathord {\uparrow }} {\mathord {\downarrow }}$ , then

2.2 The disoriented skein category

Let be a $\Bbbk $ -linear strict monoidal category, and let $\mathcal {M}$ be a $\Bbbk $ -linear category. Let denote the strict monoidal category of $\Bbbk $ -linear endofunctors of $\mathcal {M}$ . A right action of $\mathcal {C}$ on $\mathcal {M}$ is a monoidal functor , where $\mathcal {D}^{\text {rev}}$ denotes the reverse of a monoidal category $\mathcal {D}$ , where we reverse the tensor product. Given such a right action, we also say that $\mathcal {M}$ is a right module category over $\mathcal {C}$ , or $\mathcal {C}$ -module for short; see [Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, §7.1]. For objects $C \in \mathcal {C}$ and $M \in \mathcal {M}$ , we set

(2.14) $$ \begin{align} M \otimes C := \mathbf{A}(C)(M). \end{align} $$

We say that the $\mathcal {C}$ -module $\mathcal {M}$ is strict if $\mathbf {A}$ is a strict monoidal functor. Equivalently, $\mathcal {M}$ is strict if

$$\begin{align*}M \otimes (C_1 \otimes C_2) = (M \otimes C_1) \otimes C_2,\qquad \text{for all } M \in \mathcal{M},\ C_1,C_2 \in \mathcal{C}, \end{align*}$$

and similarly for morphisms.

We now describe the notion of a presentation of $\mathcal {C}$ -modules by generators and relations. We restrict ourselves to the case where there are only generating morphisms (i.e., no nontrivial generating objects). Let $\mathtt {M}$ be the set of generating morphisms. These are formal morphisms whose domains and codomains are objects of $\mathcal {C}$ . Let $\mathcal {M}$ be the $\Bbbk $ -linear category whose objects are the objects of $\mathcal {C}$ and whose morphisms are generated (as a $\Bbbk $ -linear category) by morphisms of $\mathcal {C}$ and morphisms

$$\begin{align*}f \otimes g \colon \operatorname{\mathrm{dom}}(f) \otimes \operatorname{\mathrm{dom}}(g) \to \operatorname{\mathrm{codom}}(f) \otimes \operatorname{\mathrm{codom}}(g),\qquad f \in \mathtt{M},\ g \in \operatorname{\mathrm{Mor}}(\mathcal{C}), \end{align*}$$

modulo the relations

(2.15) $$ \begin{align} (1_Y \otimes g) \circ (f \otimes h) = f \otimes (g \circ h) = (f \otimes g) \circ (1_X \otimes h), \end{align} $$

for all $f \colon X \to Y$ in $\mathtt {M}$ and all composable morphisms $g,h$ in $\mathcal {C}$ . The category $\mathcal {M}$ has a natural structure of a strict $\mathcal {C}$ -module. Now, let $\mathtt {R}$ be a set of relations on the morphisms in $\mathcal {M}$ . Define $\hat {\mathtt {R}}$ to be the smallest subset of morphisms of $\mathcal {M}$ containing $\mathtt {R}$ and closed under composition, acting on the right by morphisms in $\mathcal {C}$ , and taking $\Bbbk $ -linear combinations. Then we define the $\mathcal {C}$ -module generated by the morphisms $\mathtt {M}$ subject to the relations $\mathtt {R}$ to be the quotient of $\mathcal {M}$ by $\hat {\mathtt {R}}$ . This has the structure of a strict $\mathcal {C}$ -module induced from the $\mathcal {C}$ -module structure on $\mathcal {M}$ .

Using the usual string diagram notation for module categories, the relations (2.15) become

(2.16)

Definition 2.1. The disoriented skein category is the -module generated by the morphisms

which we call toggles, subject to the relations

(2.17)

(2.18)

Lemma 2.2. The following relations hold in :

(2.19)

Proof. Composing on the top of the last relation in (2.17) with , then using the first relation in (2.17) gives

Multiplying both sides by t then yields the first relation in (2.19). The proof of the second relation in (2.19) is similar.

The next lemma shows that the relations (2.17) to (2.19) hold after flipping crossings and inverting q.

Lemma 2.3. The following relations hold in :

(2.20)

(2.21)

Proof. The first relation in (2.20) follows from the first relation in (2.18) after composing on the bottom with and using (2.1). The proofs of the second, third, and fourth relations in (2.20) are analogous.

Let $z=q-q^{-1}$ . We have

and

Subtracting and using the third relation in (2.17) then yields (2.21).

We note that a diagram representing a morphism in can only have or appearing on the leftmost strand. However, we define the following morphisms:

(2.22)

Using (2.22) and the module category structure of , we may now draw diagrams with and appearing on any strand and interpret them as morphisms in .

Lemma 2.4. The following relations hold in for any $\lambda ,\mu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ :

(2.23)

(2.24)

(2.25)

(2.26)

Proof. The equalities (2.23) and (2.25) follow easily from (2.17) and (2.22). To prove the first relation in (2.24), it suffices to prove that

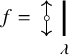where, in the braces, the strands in the cups and caps can have any orientation, and $\lambda ,\mu $ run over all objects of . For , we have

Composing on the top and bottom with

respectively, then using (2.17), yields the case 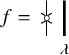. The remaining cases for f follow easily from (2.7), (2.8) and (2.16). This completes the proof of the first relation in (2.24). The proof of the second relation then follows by composing the first relation on the top and bottom with

respectively, then using (2.17).

To prove the first equality in (2.26), we have

The remaining relations in (2.26) are proved similarly. Note also that one can apply $\Omega _\updownarrow $ , defined in (2.27) below, to obtain the second and fourth equalities from the first and third, respectively.

In light of (2.24), we define toggles at the same height by

and similarly for the other toggles, or for more than two toggles at the same height.

Remark 2.5. We emphasize that is not a monoidal category. For example, the relations in (2.18) and (2.26) do not hold, in general, unless they are on the left side of a diagram. For instance, since

we cannot apply the last relation in (2.18) to the curl with a toggle directly in this situation.

We now describe three natural symmetries of the disoriented skein category. First, it follows from Lemma 2.3 that the isomorphism (2.10) induces a $\Bbbk $ -antilinear isomorphism of categories

(2.27)

such that the diagram

commutes.

Second, (2.12) induces an isomorphism of $\Bbbk $ -linear categories

(2.28)

such that the following diagram commutes:

Indeed, $\Theta $ respects the relations (2.18) by (2.19), and it respects the last relation in (2.17) by (2.22) and the case of the last relation in (2.24).

Finally, it follows from Lemma 2.3 that the bar involution (2.13) induces a $\Bbbk $ -antilinear isomorphism of categories

(2.29)

such that the following diagram commutes:

Note that, $\Omega _\updownarrow $ , $\Theta $ , and $\Xi $ do not behave well with respect to toggles on strands that are not on the left, due to the crossings in (2.22). However, the composites $\Theta \circ \Xi $ and $\Omega _\updownarrow \circ \Theta $ do behave well: they act as , on toggles in arbitrary position. Similarly, $\Omega _\updownarrow \circ \Xi $ acts as , on toggles in arbitrary position.

2.3 The iquantum Brauer category

We now recall the definition of the iquantum Brauer category. This category was defined in [Reference Sartori and TubbenhauerST19, Def. 7.9], where it was called the quantum or q-Brauer category. Its endomorphism algebras first appeared in [Reference MolevMol03, Def. 2.1]. The definition in [Reference Sartori and TubbenhauerST19, Def. 7.9] is as a module category over the subcategory of consisting of only upward-oriented strands. We start with a presentation as a $\Bbbk $ -linear category. Then, in Section 3, we endow the iquantum Brauer category with the structure of an -module category, extending the module category structure from [Reference Sartori and TubbenhauerST19, Def. 7.9]. Below and throughout the paper, we let $\mathbb {N}$ denote the set of nonnegative integers.

Definition 2.7. The iquantum Brauer category is the $\Bbbk $ -linear category with objects $\mathsf {B}_r$ , $r \in \mathbb {N}$ , and generating morphisms

(2.30)

(2.31)

subject to relations that we describe below. We denote the identity morphism of $\mathsf {B}_r$ by the thick strand . We define juxtaposition of thick strands by

(2.32)

We use (2.32) even when these strands are part of a larger diagram that involves cups, caps, or crossings.

We impose the following relations on morphisms, for all $r,s \in \mathbb {N}$ :

(2.33)

(2.34)

(2.35)

(2.36)

(2.37)

where, in (2.37), f runs over all generating morphisms, g runs over the generating morphisms (2.31), and we interpret the juxtaposition using (2.32). For example, when

then (2.37) becomes

This concludes the definition of .

We define cups and caps appearing at the same height by

(2.38)

Note that

(2.39)

A similar argument (or, alternatively, composing the second and third relations in (2.35) with the appropriate crossings, then using the first two relations in (2.33)) gives

(2.40)

Note that the third relation in (2.36) is obtained from the second by reflecting the diagrams in the horizontal axis. The next result shows that the diagrammatic relation obtained by reflecting the first relation in (2.36) also holds.

Lemma 2.8. In ,

(2.41)

Proof. We have

Since

and

the result follows.

Lemma 2.9. There is a $\Bbbk $ -antilinear isomorphism of categories

(2.42)

sending

Intuitively, $\Omega _\updownarrow $ reflects diagrams in a horizontal axis and inverts q and t.

The following proposition implies that the relations (2.36) continue to hold after all crossings are flipped.

Proposition 2.10. In ,

(2.43)

Proof. The second and third relations in (2.43) follow from applying the isomorphism $\Omega _{\updownarrow }$ to the third and second relations, respectively, in (2.36). Thus, it remains to prove the first relation in (2.43).

Let $z=q-q^{-1}$ . We repeatedly use the skein relation (2.34) to flip crossings:

Adding together all the extra terms that appeared above gives z times

Thus, the first relation in (2.43) is satisfied.

Lemma 2.11. There is a $\Bbbk $ -antilinear isomorphism of categories

which we call the bar involution, sending

4.1 Morphisms of module categories

Recall the definition of strict right module categories from Section 2.2. Let be a $\Bbbk $ -linear strict monoidal category, and let $\mathcal {M}$ , $\mathcal {N}$ be strict $\mathcal {C}$ -modules. A morphism of $\mathcal {C}$ -modules from $\mathcal {M}$ to $\mathcal {N}$ is a pair $(\mathbf {H},\omega )$ , where $\mathbf {H}$ is a $\Bbbk $ -linear functor from $\mathcal {M}$ to $\mathcal {N}$ and $\omega $ is a natural isomorphism with components

$$\begin{align*}\omega_{M,C} \colon \mathbf{H}(M \otimes C) \xrightarrow{\cong} \mathbf{H}(M) \otimes C,\qquad M \in \mathcal{M},\ C \in \mathcal{C}, \end{align*}$$

such that the diagram

(4.1)

commutes for all $M \in \mathcal {M}$ and $C,D \in \mathcal {C}$ . (See [Reference Etingof, Gelaki, Nikshych and OstrikEGNO15, Def. 7.2.1] for a more general definition, where the module categories are not required to be strict.) We say that a morphism of $\mathcal {C}$ -modules is strict if $\omega _{M,C}$ is the identity morphism for all $M \in \mathcal {M}$ and $C \in \mathcal {C}$ . An equivalence of $\mathcal {C}$ -modules is a morphism of $\mathcal {C}$ -modules that is also an equivalence of categories.

4.2 Functor from the disoriented skein category to the iquantum Brauer category

Proposition 4.1. There is a unique strict morphism of -modules given on objects by

and on morphisms by

Proof. Uniqueness is clear, since and generate as an -module. For existence, we verify that $\mathbf {F}$ respects the relations (2.17) and (2.18). We first compute

Similarly, using (3.5), (3.6), and (3.9), we have

Thus,

proving that $\mathbf {F}$ respects the first relation in (2.18). Similarly,

proving that $\mathbf {F}$ respects the last relation in (2.17). The remaining relations follow by analogous arguments and are omitted for brevity.

For $\lambda \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ , let $\ell (\lambda )$ denote the length of $\lambda $ . The following result allows us to easily compute the image under $\mathbf {F}$ of any morphism in .

Lemma 4.2. For all $\lambda ,\mu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ , we have

(4.2)

(4.3)

(4.4)

(4.5)

(4.6)

4.3 Functor from the iquantum Brauer category to the disoriented skein category

For $r \in \mathbb {N}$ , define the following morphisms in and :

Proposition 4.3. There is a unique $\Bbbk $ -linear functor given by

(4.7)

for all $r,s \in \mathbb {N}$ .

Proof. It suffices to check that relations (2.33) to (2.37) are preserved under $\mathbf {G}$ . The relations (2.33), (2.34), and (2.37) follow from (2.33), (2.2), and (2.16). The first and last relations in (2.35) follow from (2.3) and (2.17), while the second and third relations in (2.35) follow from (2.18).

For the first relation in (2.36), we compute

Hence, the first relation in (2.36) is preserved under $\mathbf {G}$ . The other relations in (2.36) follow similarly.

Remark 4.4. Note that $\mathbf {G}$ is not a strict morphism of -modules. For example,

$$\begin{align*}\mathbf{G}( \mathsf{B}_0 \otimes {\mathord{\downarrow}}) = \mathbf{G}(\mathsf{B}_1) = {\mathord{\uparrow}} \ne {\mathord{\downarrow}} = \mathbf{G}(\mathsf{B}_0) \otimes {\mathord{\downarrow}}. \end{align*}$$

Nevertheless, we will see in Corollary 4.6 that $\mathbf {G}$ can be made into a morphism of -modules.

4.4 Equivalence of categories

In this subsection, we show that the functors $\mathbf {G}$ and $\mathbf {F}$ are equivalences of module categories between and . We first observe that by definition. In the other direction, we construct a natural isomorphism .

Note that

$$\begin{align*}\mathbf{G} \mathbf{F}(\lambda) = {\mathord{\uparrow}}^{\ell(\lambda)},\qquad \lambda \in \langle {\mathord{\uparrow}},{\mathord{\downarrow}} \rangle. \end{align*}$$

For any $\lambda \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ , we construct an isomorphism $\eta _\lambda \colon \lambda \to \mathbf {G} \mathbf {F}(\lambda )$ in recursively by

(4.8)

For example, we have and .

Proof. To see that $\eta $ is indeed a natural transformation, we must show that

(4.9)

for all morphisms $f \colon \lambda \to \mu $ in . It suffices to check this for

since these generate as a $\Bbbk $ -linear category.

For , we have , and so (4.9) follows immediately from the definition of $\eta $ . The case is similar, using (2.17).

For , we have

The case is analogous.

When ,

The remaining cases are analogous.

Since the components of $\eta $ are isomorphisms by (2.23), it follows that is a natural isomorphism. Since , we conclude that $\mathbf {G}$ and $\mathbf {F}$ are equivalences of categories.

Corollary 4.6. We have an equivalence of -modules $(\mathbf {G},\omega )$ from to , where $\omega $ has components

$$\begin{align*}\omega_{\mathsf{B}_r,\lambda} \colon \mathbf{G}(\mathsf{B}_r \otimes \lambda) \xrightarrow{\eta_{\mathbf{G}(\mathsf{B}_r) \otimes \lambda}^{-1}} \mathbf{G}(\mathsf{B}_r) \otimes \lambda. \end{align*}$$

for $r \in \mathbb {N}$ , $\lambda \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ .

Proof. The fact that $\omega $ is a natural isomorphism follows from the fact that $\eta $ is. It remains to show that the analogue of diagram (4.1) commutes. To verify this, we compute that

$$\begin{align*}(\omega_{\mathsf{B}_r,\lambda} \otimes 1_\mu) \circ \omega_{\mathsf{B}_r \otimes \lambda, \mu} = (\eta_{\mathbf{G}(\mathsf{B}_r) \otimes \lambda}^{-1} \otimes 1_\mu) \circ \eta_{\mathbf{G}(\mathsf{B}_r \otimes \lambda) \otimes \mu}^{-1} \overset{(4.8)}{=} \eta_{\mathbf{G}(\mathsf{B}_r) \otimes \lambda \otimes \mu}^{-1} = \omega_{\mathsf{B}_r,\lambda \otimes \mu}, \end{align*}$$

as desired.

5.1 The quantum enveloping superalgebra

Fix $m,n \in \mathbb {N}$ and let

$$\begin{align*}I_V = I_V(m|n) = \{m,m-1,\dotsc,1-n\}. \end{align*}$$

Define a parity function

$$\begin{align*}p \colon I_V \to \{0,1\} \subseteq \mathbb{Z},\qquad p(i) = \begin{cases} 1 & \text{if } i \le 0, \\ 0 & \text{if } i> 0. \end{cases} \end{align*}$$

The general linear Lie superalgebra $\mathfrak {g} = \mathfrak {gl}(m|n,\mathbb {C})$ has a basis given by the unit matrices $E_{ij}$ , $i,j \in I_V$ , where the parity of $E_{ij}$ is

$$\begin{align*}\bar{E}_{ij} = p(i) + p(j)\quad \mod 2. \end{align*}$$

Here, and in what follows, parities are always considered modulo $2$ .

Let $\mathfrak {h}$ be the Cartan subalgebra of $\mathfrak {g}$ consisting of diagonal matrices. Then the dual space $\mathfrak {h}^*$ has basis $\epsilon _i$ , $i \in I_V$ , given by $\epsilon _i(E_{jj}) = \delta _{ij}$ . We define a symmetric bilinear form on the weight lattice $P = \bigoplus _{i \in I_V} \mathbb {Z} \epsilon _i$ by

$$\begin{align*}(\epsilon_i, \epsilon_j) = (-1)^{p(i)} \delta_{ij}. \end{align*}$$

We set the parity of $\epsilon _i$ to be $\overline {\epsilon _i} = p(i)$ . We then extend parity to a homomorphism of additive groups $P \to \mathbb {Z}_2$ , $\lambda \mapsto \bar {\lambda }$ .

Let

$$\begin{align*}I = \{ i \in \mathbb{Z} : 1-n \le i \le m-1 \} \end{align*}$$

and choose the set of simple roots $\Pi = \{ \alpha _i : i \in I \}$ , where

$$\begin{align*}\alpha_i = \epsilon_i - \epsilon_{i+1}, \qquad i \in I. \end{align*}$$

It follows that $\overline {\alpha _0} = 1$ and $\overline {\alpha _i} = 0$ for $i \in I$ , $i \ne 0$ . The Dynkin diagram associated to this choice of simple roots is:

(5.1)

In the above diagram, the crossed node corresponds to an odd isotropic simple root and the other nodes correspond to even simple roots. We have the coweight lattice $P^\vee = \bigoplus _{i \in I_V} \mathbb {Z} \epsilon _i^\vee $ , with the pairing

$$\begin{align*}\langle\ ,\ \rangle \colon P^\vee \times P \to \mathbb{Z},\qquad \langle \epsilon_i^\vee, \epsilon_j \rangle = \delta_{i,j}. \end{align*}$$

The set of simple coroots is $\Pi ^\vee = \{h_i : i \in I\}$ , where

$$\begin{align*}h_i = \epsilon_i^\vee - (-1)^{\delta_{i,0}} \epsilon_{i+1}^\vee,\qquad i \in I. \end{align*}$$

We set

$$\begin{align*}a_{ij} = \langle h_i, \alpha_j \rangle, \qquad i,j \in I. \end{align*}$$

We let $X = \mathbb {Z} \Pi $ and $Y = \mathbb {Z} \Pi ^\vee $ denote the root lattice and coroot lattice, respectively. We define

$$\begin{align*}d_i = \begin{cases} 1 & \text{if } i> 0, \\ -1 & \text{if } i \le 0, \end{cases} \qquad i \in I. \end{align*}$$

(The $d_i$ are uniquely determined by the condition $(\alpha _i, \alpha _j) = d_i a_{ij}$ for all $i,j \in I$ .) Then set $q_i = q^{d_i}$ for all $i \in I$ . We define the quantum integers

(5.2) $$ \begin{align} [a]=\frac{q^{a}-q^{-a}}{q-q^{-1}},\qquad a \in \mathbb{Z}. \end{align} $$

Following [Reference YamaneYam94, Th. 10.5.1], we define the quantum enveloping superalgebra $\mathrm {U} = U_q(\mathfrak {g})$ to be the unital associative superalgebra over $\mathbb {C}(q)$ with generators

$$\begin{align*}E_i, F_i, \quad i \in I, \qquad K_h,\quad h \in Y, \end{align*}$$

of parities

$$\begin{align*}\overline{E_i} = \overline{F_i} = \overline{\alpha_i},\quad i \in I, \qquad \overline{K_h} = 0,\quad h \in Y, \end{align*}$$

subject to the following relations for $h,h' \in Y$ , $i,j \in I$ :

(5.3) $$ \begin{align} K_0 = 1,\qquad K_h K_h = K_{h+h'}, \end{align} $$

(5.4) $$ \begin{align} K_h E_i = q^{\langle h, \alpha_i \rangle} E_i K_h,\qquad K_h F_i = q^{- \langle h, \alpha_i \rangle} F_i F_h, \end{align} $$

(5.5) $$ \begin{align} [E_i,F_j] = \delta_{i,j} \frac{K_i - K_i^{-1}}{q_i-q_i^{-1}},\qquad \text{where } K_i := K_{h_i}^{d_i}, \end{align} $$

(5.6) $$ \begin{align} [E_i,E_j] = 0,\qquad [F_i,F_j] = 0,\qquad \text{ for } a_{ij}=0 \end{align} $$

(5.7) $$ \begin{align} E_i^2 E_j - [2] E_i E_j E_i + E_j E_i^2 = 0 = F_i^2 F_j - [2] F_i F_j F_i + F_j F_i^2,\qquad \text{for } |a_{ij}|=1,\ i \ne 0, \end{align} $$

(5.8) $$ \begin{align} [[[E_{-1},E_0]_{q_0},E_1]_{q_1}],E_0]=0,\quad [[[F_{-1},F_0]_{q_0},F_1]_{q_1}],F_0]=0,\qquad \text{if } n \ge 1, \end{align} $$

where

$$\begin{align*}[X,Y]_a := XY-(-1)^{\bar{X} \bar{Y}} a YX, \quad a \in \Bbbk, \qquad \text{and} \qquad [X,Y] := [X,Y]_1. \end{align*}$$

Then $\mathrm {U}$ is a Hopf superalgebra with coproduct $\Delta $ , counit $\varepsilon $ , and antipode S given by

(5.9) $$ \begin{align} \Delta(E_i) = E_i \otimes 1 + K_i \otimes E_i,\quad \Delta(F_i) = F_i \otimes K_i^{-1} + 1 \otimes F_i,\quad \Delta(K_h) = K_h \otimes K_h, \end{align} $$

(5.10) $$ \begin{align} \varepsilon(E_i) = 0,\qquad \varepsilon(F_i) = 0,\qquad \varepsilon(K_h) = 1, \end{align} $$

(5.11) $$ \begin{align} S(E_i) = -K_i^{-1} E_i,\qquad S(F_i) = -F_i K_i,\qquad S(K_h) = K_{-h}. \end{align} $$

Let $\sigma $ be the Hopf superalgebra automorphism of $\mathrm {U}$ given by

(5.12) $$ \begin{align} \sigma(E_i) = (-1)^{\delta_{i=m-1 \ge 0}} E_i,\quad \sigma(F_i) = (-1)^{\delta_{i=m-1 \ge 0}} F_i,\quad \sigma(K_h) = K_h,\qquad i \in I,\ h \in Y. \end{align} $$

We define

(5.13) $$ \begin{align} \mathrm{U}_\sigma = \mathrm{U} \rtimes \langle \sigma \rangle \end{align} $$

to be the superalgebra obtained from $\mathrm {U}$ by adjoining an even generator $\sigma $ , subject to the relations

$$\begin{align*}\sigma^2 = 1,\quad \sigma x \sigma = \sigma(x),\qquad x \in \mathrm{U}. \end{align*}$$

We can extend the Hopf superalgebra structure of $\mathrm {U}$ to $\mathrm {U}_\sigma $ by defining

$$\begin{align*}\Delta(\sigma) = \sigma \otimes \sigma,\quad \varepsilon(\sigma) = 1,\quad S(\sigma) = \sigma. \end{align*}$$

The reason for introducing $\sigma $ will become apparent when we consider the iquantum enveloping superalgebra; see Remark 5.4.

For $i \ne 0$ , we have an automorphism of superalgebras $T_i \colon \mathrm {U} \to \mathrm {U}$ given by

(5.14) $$ \begin{align} \begin{gathered} T_i (E_i) = -F_i K_{i},\qquad T_i (F_i) = - K_{i}^{-1}E_i, \\ T_i(E_j) = E_j,\qquad T_i(F_j)=F_j, \qquad \text{for} \quad |j-i|>1, \\ T_i(E_j) = E_i E_j - q^{(\alpha_i,\alpha_j)} E_j E_i,\qquad T_i(F_j) = F_i F_j - q^{-(\alpha_i,\alpha_j)} F_j F_i, \qquad \text{for} \quad |j-i|=1, \\ T_i (K_h) = K_{s_i(h)},\quad h \in Y, \end{gathered} \end{align} $$

where $s_i$ is the reflection corresponding to the simple root $\alpha _i$ . The $T_i$ are super versions of the automorphisms $T_{i,1}"$ of [Reference LusztigLus10, §37.1.3] defining a braid group action; see [Reference YamaneYam99, Prop. 7.4.1] and [Reference ShenShe25, Th. 3.4].

5.2 The natural module and its dual

We now recall the quantum analogue of the natural module and its dual. The quantum analogue $V^+$ of the natural module has basis $\{v_j^+ : j \in I_V\}$ , with the action of $\mathrm {U}_\sigma $ given by

(5.15) $$ \begin{align} \begin{gathered} E_i v_j^+ = \delta_{i+1,j} v_{j-1}^+,\qquad F_i v_j^+ = \delta_{i,j} v_{j+1}^+,\qquad K_h v_j^+ = q^{\langle h, \epsilon_j \rangle} v_j^+, \\ K_i v_j^+ = q^{(-1)^{\delta_{j \le 0}}(\delta_{i,j} - \delta_{i+1,j})} v_j^+,\qquad \sigma v_j^+ = (-1)^{\delta_{j=m>0}} v_j^+. \end{gathered} \end{align} $$

We remind the reader that $K_i = K_{h_i}^{d_i}$ ; see (5.5). The dual module $V^-$ has basis $\{ v_j^- : j \in I_V \}$ , with the action of $\mathrm {U}_\sigma $ given by

(5.16) $$ \begin{align} \begin{gathered} E_i v_j^- = \delta_{i,j} v_{j+1}^-,\qquad F_i v_j^- = \delta_{i+1,j} (-1)^{\delta_{i,0}} v_{j-1}^-,\qquad K_h v_j^- = q^{-\langle h, \epsilon_j \rangle} v_j^-, \\ K_i v_j^- = q^{(-1)^{\delta_{j> 0}}(\delta_{i,j} - \delta_{i+1,j})} v_j^-,\qquad \sigma v_j^- = (-1)^{\delta_{j=m>0}} v_j^-. \end{gathered} \end{align} $$

We have a homomorphism of $\mathrm {U}_\sigma $ -modules

(5.17) $$ \begin{align} \operatorname{\mathrm{ev}}^+ \colon V^+ \otimes V^- \to \text{triv},\qquad \operatorname{\mathrm{ev}}^+(v_i^+ \otimes v_j^-) = \delta_{i,j} (-q)^{|i|}, \end{align} $$

where $\text {triv}$ denotes the trivial $\mathrm {U}_\sigma $ -module. Since $V^+$ and $V^-$ are simple, the homomorphism space $\operatorname {\mathrm {Hom}}_{\mathrm {U}}(V^+ \otimes V^-,\text {triv})$ is one-dimensional, spanned by $\operatorname {\mathrm {ev}}^+$ . We also have a homomorphism of $\mathrm {U}_\sigma $ -modules

(5.18) $$ \begin{align} \operatorname{\mathrm{ev}}^- \colon V^- \otimes V^+ \to \text{triv},\qquad \operatorname{\mathrm{ev}}^- (v_i^- \otimes v_j^+) = \delta_{i,j} (-1)^{i+p(i)} q^{m+n-|i-1|}, \end{align} $$

and $\operatorname {\mathrm {Hom}}_{\mathrm {U}}(V^- \otimes V^+,\text {triv})$ is one-dimensional, spanned by $\operatorname {\mathrm {ev}}^-$ .

For a basis $B^\pm $ of $V^\pm $ , we let $\{ v^\vee : v \in B^\pm \}$ denote the dual basis of $V^\mp $ determined by

$$\begin{align*}\operatorname{\mathrm{ev}}^\mp( v^\vee \otimes w ) = \delta_{v,w},\qquad v,w \in B^\pm. \end{align*}$$

It follows from (5.17) and (5.18) that the bases dual to $\{v_i^+ : i \in I_V\}$ and $\{v_i^- : i \in I_V\}$ are given by

(5.19) $$ \begin{align} (v_i^+)^\vee = (-1)^{i+p(i)} q^{|i-1|-m-n} v_i^-,\qquad (v_i^-)^\vee = (-q)^{-|i|} v_i^+. \end{align} $$

We have $\mathrm {U}_\sigma $ -module homomorphisms

(5.20) $$ \begin{align} \operatorname{\mathrm{coev}}_\pm \colon \text{triv} \to V^\mp \otimes V^\pm,\qquad 1 \mapsto \sum_{v \in B^\mp} v \otimes v^\vee. \end{align} $$

This definition is independent of the basis $B^\mp $ .

Let $\mathrm {U}_\sigma $ -tmod denote the category of tensor $\mathrm {U}_\sigma $ -modules. By definition, this is the full subcategory of the category of $\mathrm {U}_\sigma $ -modules whose objects are finite direct sums of summands of tensor products of $V^+$ and $V^-$ . The category $\mathrm {U}_\sigma $ -tmod is braided monoidal, where the braiding is given by the universal R-matrix. Define

$$\begin{align*}p(i,j) := \delta_{i,j} (1-2p(i)) = \begin{cases} 0, & i \ne j, \\ 1, & i=j> 0, \\ -1, & i=j \le 0, \end{cases} \qquad i,j \in I_V. \end{align*}$$

Then the action of the braiding on $V^+ \otimes V^+$ is

(5.21) $$ \begin{align} \begin{gathered} T_{++} \colon V^+ \otimes V^+ \to V^+ \otimes V^+, \\ T_{++}(v_i^+ \otimes v_j^+) = (-1)^{p(i)p(j)} q^{p(i,j)} v_j^+ \otimes v_i^+ + \delta_{i<j} (q-q^{-1}) v_i^+ \otimes v_j^+. \end{gathered} \end{align} $$

See, for example, [Reference MitsuhashiMit06, (1)]. One can verify by direct computation that

(5.22) $$ \begin{align} T_{++}^{-1}(v_i^+ \otimes v_j^+) = (-1)^{p(i)p(j)} q^{-p(i,j)} v_j^+ \otimes v_i^+ - \delta_{i>j} (q-q^{-1}) v_i^+ \otimes v_j^+. \end{align} $$

5.3 The iquantum enveloping superalgebra

Following [Reference Shen and WangSW25, §7.1], we consider the following super Satake diagram of type AI-II:

(5.23)

where $I_{\bullet } = \{1-2a : 1 \leq a \leq n\}$ and $I_\circ = I \backslash I_{\bullet }$ . The diagram automorphism $\tau $ that is part of the data of the Satake diagram is the identity in our case. The diagram (5.23) corresponds to an involution on $\mathfrak {gl}(m|2n)$ ; this is the involution denoted $\theta (I,\tau )$ in [Reference Shen and WangSW25, (2.5)]. Note that the underlying Dynkin diagram of (5.23) is (5.1), with n replaced by $2n$ . In the extreme case where $n=0$ , we obtain a Satake diagram of type AI; when $m=0$ , we obtain a Satake diagram of type AII; see [Reference Bao and WangBW18, Table 4].

The following definition, given in [Reference Shen and WangSW25, Def. 4.1], was inspired by [Reference LetzterLet99, §4] and [Reference KolbKol14, Def. 5.1], which treated the nonsuper case.

Definition 5.1. Fix $\varsigma _i \in \mathbb {C}(q)^\times $ for $i \in I_\circ $ . The corresponding iquantum enveloping superalgebra $\mathrm {U}^\imath $ of type AI-II is the $\mathbb {C}(q)$ -subalgebra of $\mathrm {U}$ generated by the elements

(5.24) $$ \begin{align} \begin{gathered} B_i = F_i + \varsigma_i E_{i}K_i^{-1},\qquad 1 \le i \le m-1,\\ B_0 = F_0 + \varsigma_0 T_{-1}(E_0)K_0^{-1}, \\ B_{2k} = F_{2k} + \varsigma_{2k} T_{2k+1} \big( T_{2k-1}(E_{2k}) \big) K_{2k}^{-1},\qquad 1-n \le k \le -1,\\ E_{2k+1}, F_{2k+1}, K_{2k+1}^{\pm 1},\qquad -n \le k \le -1. \end{gathered} \end{align} $$

We define $\mathrm {U}^\imath _\sigma $ to be the subalgebra of $\mathrm {U}_\sigma $ generated by $\mathrm {U}^\imath $ and $\sigma $ .

The restriction of the automorphism $\sigma $ of (5.12) to $\mathrm {U}^\imath $ is given by

(5.25) $$ \begin{align} \sigma(B_i) = (-1)^{\delta_{i=m-1 \ge 0}} B_i,\qquad i \in I_\circ, \end{align} $$

(5.26) $$ \begin{align} \sigma(E_i) = E_i,\qquad \sigma(F_i) = F_i,\qquad \sigma(K_i^{\pm 1}) = K_i^{\pm 1},\qquad i \in I_{\bullet}. \end{align} $$

The braid group actions appearing in (5.24) can be computed explicitly, using (5.14):

(5.27) $$ \begin{align} T_{-1}(E_0) = E_{-1} E_0 - q E_0 E_{-1}, \end{align} $$

(5.28) $$ \begin{align} T_{2k+1}(T_{2k-1}(E_k)) &= E_{2k-1}E_{2k+1}E_{2k} - q E_{2k-1}E_{2k}E_{2k+1} \nonumber\\ & - qE_{2k+1}E_{2k}E_{2k-1} + q^2E_{2k}E_{2k+1}E_{2k-1}. \end{align} $$

By [Reference Shen and WangSW25, Prop. 4.2], $\mathrm {U}^\imath $ is a right coideal subalgebra of $\mathrm {U}$ since

$$\begin{align*}\Delta(\mathrm{U}^\imath) \subseteq \mathrm{U}^\imath \otimes \mathrm{U}. \end{align*}$$

Thus $\mathrm {U}^\imath _\sigma $ is also a right coideal subalgebra of $\mathrm {U}_\sigma $ . Let $\mathrm {U}^\imath _\sigma $ -tmod denote the full subcategory of $\mathrm {U}^\imath $ -modules whose objects are restrictions of objects in $\mathrm {U}_\sigma \text {-tmod}$ . Then $\mathrm {U}^\imath _\sigma \text {-tmod}$ is naturally a right module category over $\mathrm {U}_\sigma \text {-tmod}$ . Given $M \in \mathrm {U}^\imath _\sigma \text {-tmod}$ and $N \in \mathrm {U}_\sigma \text {-tmod}$ , the bifunctor

$$\begin{align*}\otimes \colon \mathrm{U}^\imath_\sigma\text{-tmod} \times \mathrm{U}_\sigma\text{-tmod} \to \mathrm{U}^\imath_\sigma\text{-tmod} \end{align*}$$

sends $(M,N)$ to $M \otimes N := M \otimes _\Bbbk N$ , which is naturally a $\mathrm {U}^\imath _\sigma $ -module via $\Delta $ .

We note that the superalgebra $\mathrm {U}^\imath $ is a quantum analogue of the enveloping superalgebra of the orthosymplectic Lie superalgebra $\mathfrak {osp}(m|2n,\mathbb {C})$ ; see [Reference Shen and WangSW25, Ex. 2.16 and Rem. 7.8] and the proof of Theorem 8.1.

Remark 5.2. The superalgebra $\mathrm {U}^\imath $ is sometimes called an iquantum supergroup. Let us explain how Definition 5.1 is obtained from [Reference Shen and WangSW25, Def. 4.1]. First note that, as defined in [Reference Shen and WangSW25, §4.1], $\mathrm {U}^\imath $ also depends on a set of parameters $\{\kappa _i \in \mathbb {C}(q) : i \in I_\circ \}$ . However, the condition [Reference Shen and WangSW25, (4.10)] forces all $\kappa _i=0$ in our case. The diagram automorphism $\tau $ appearing in [Reference Shen and WangSW25, Def. 4.1] is the identity for us. The $w_{\bullet }$ there is the longest element of the Weyl group associated to the subdiagram of (5.23) containing the black nodes. Thus, for us, $T_{w_{\bullet }} = T_{-1} T_{-3} \dotsm T_{1-2n}$ and the $T_{1-2j}$ , $1 \le j \le n$ , pairwise commute. For $i \ne j$ , we have $T_i(E_j) = E_j$ whenever $a_{ij}=0$ . Thus

$$\begin{align*}T_{w_{\bullet}}(E_0) = T_{-1}(E_0),\quad T_{w_{\bullet}}(E_{2k}) = T_{2k+1} (T_{2k-1} (E_{2k})),\qquad -1 \le k \le 1-n. \end{align*}$$

Remark 5.3. Up to isomorphisms of coideal subalgebras, $\mathrm {U}^\imath $ is independent of the parameters $\varsigma _i$ . More precisely, for two choices $\varsigma = (\varsigma _i)_{i \in I_\circ }$ and $\varsigma ' = (\varsigma ^{\prime }_i)_{i \in I_\circ }$ , there is a Hopf algebra automorphism of $\mathrm {U}$ sending $\mathrm {U}^\imath $ for the choice $\varsigma $ to $\mathrm {U}^\imath $ for the choice $\varsigma '$ . See [Reference WatanabeWat21, Lem. 2.51 and Rem. 2.5.2] for details. While the treatment there is for the nonsuper case, the same automorphism applies in our setting. Because of this independence, one loses no generality in choosing specific parameters. The choice

(5.29) $$ \begin{align} \varsigma_i = \begin{cases} q^{-1} & \text{if } 0 < i < m-1, \\ -q^{-1} & \text{if } i \in \{0,-2,-4,\dotsc,2-2n\}, \end{cases} \end{align} $$

simplifies some of the formulas in the current paper. However, we work with general parameters since it does not involve substantially more work and allows the reader to make whatever choice is more convenient for their purposes.

5.4 Modules over the iquantum enveloping superalgebra

We have a restriction functor

$$\begin{align*}\operatorname{\mathrm{Res}} \colon \mathrm{U}_\sigma\text{-tmod} \to \mathrm{U}^\imath_\sigma\text{-tmod}. \end{align*}$$

When there is no chance for confusion, we will sometimes continue to denote $\operatorname {\mathrm {Res}}(V^\pm )$ by $V^\pm $ . Direct computation using (5.15), (5.16), (5.27), and (5.28) shows that the actions of $B_i$ , $i\in I_\circ $ , on $V^+$ and $V^-$ are given by

(5.30) $$ \begin{align} B_i v^+_j = \begin{cases} v_{j+1}^+ & \text{if } j=i, \\ - q \varsigma_i v_{j-3}^+ & \text{if } i<0,\ j=i+2, \\ - q \varsigma_0 v_{-1}^+ & \text{if } i=0,\ j=1, \\ q \varsigma_i v_{j-1}^+ & \text{if } i>0,\ j=i+1, \\ 0 & \text{otherwise}, \end{cases} \quad B_i v^-_j = \begin{cases} (-1)^{\delta_{i,0}} v_{j-1}^- & \text{if } j=i+1, \\ - q \varsigma_i v_{j+3}^- & \text{if } i<0,\ j=i-1, \\ - q \varsigma_0 v_1^- & \text{if } i=0,\ j=-1, \\ q \varsigma_i v_{j+1}^- & \text{if } i>0,\ j=i, \\ 0 & \text{otherwise}. \end{cases} \end{align} $$

Define the involution

(5.31) $$ \begin{align} \phi \colon I_V \to I_V,\quad \phi(i) = i - \delta_{i \le 0} (-1)^i = \begin{cases} i, & i>0, \\ i-1, & i \in \{0,-2,-4,\dotsc,2-2n\}, \\ i+1, & i \in \{-1,-3,-5,\dotsc,1-2n\}. \end{cases} \end{align} $$

For $i \in I_V$ , define

(5.32) $$ \begin{align} \tilde{\varsigma}_i := \begin{cases} \prod_{k=1}^{i-1} (q \varsigma_k)^{-1}, & i> 0, \\ \prod_{k = \lfloor \frac{i+1}{2} \rfloor}^0 (-q \varsigma_{2k}), & i \le 0. \end{cases} \end{align} $$

Note that $\tilde {\varsigma }_{\phi (i)} = \tilde {\varsigma }_i$ for all $i \in I_V.$

Lemma 5.6. The linear map $\varphi \colon V^- \to V^+$ determined by

(5.33) $$ \begin{align} \varphi(v_i^-) = \tilde{\varsigma}_i v_{\phi(i)}^+ \end{align} $$

is a $\mathrm {U}^\imath _\sigma $ -module isomorphism. Its inverse is determined by $\varphi ^{-1}(v_i^+) = \tilde {\varsigma }_i^{-1} v_{\phi (i)}^-$ .

Proof. By Lemma 5.6, it suffices to show that $V^+$ is simple. Suppose M is a nonzero submodule of $V^+$ . Since $V^+$ is generated by $v_m^+$ , to show that $M=V^+$ , it suffices to show that $v_m^+ \in M$ . Let v be a nonzero element of M. If $v=v_m^+$ , we are done. Otherwise, multiplying by a nonzero scalar if necessary, we may assume

$$\begin{align*}v = v_i^+ + \sum_{j>i} c_j v_j^+ \end{align*}$$

for some $i \in I_V$ , $i<m$ , and $c_j \in \Bbbk $ . If $i<m-1$ , then, by (5.30), we have

$$\begin{align*}B_{m-1} B_{m-2} \dotsm B_{i+1} B_i v = v_m^+, \end{align*}$$

where we interpret $B_{2k-1}$ as $F_{2k-1}$ for $k \le 0$ . On the other hand, if $i=m-1$ , then $v = v_{m-1}^+ + c_m v_m^+$ . First suppose $c_m \ne 0$ . If $m>0$ , we have

$$\begin{align*}(1-\sigma)v = 2 v_m^+. \end{align*}$$

If $m=0$ , we have

$$\begin{align*}B_{-1} v = v_0^+. \end{align*}$$

Finally, if $c_m = 0$ , then $B_{m-1} v = B_{m-1} v_{m-1}^+ = v_m^+$ . In all cases, we have shown that $v_m^+ \in M$ .

6.1 The oriented incarnation functor

The following proposition is known to experts. However, since we could not locate a proof in the literature, we have included one.

Proposition 6.1. There is a unique $\Bbbk $ -linear monoidal functor given on objects by ${\mathord {\uparrow }} \mapsto V^+$ , ${\mathord {\downarrow }} \mapsto V^-$ , and on morphisms by

Proof. We must show that respects the relations (2.1) to (2.4). The first three equalities in (2.1) follow immediately from the fact that $T_{++}$ is the action of the braiding on $V^+ \otimes V^+$ . Furthermore, it follows from (2.5) that and are the components of the braiding on $V^+ \otimes V^-$ and $V^- \otimes V^+$ , respectively. Indeed, if X and Y are objects in a rigid braided monoidal category, and $X^*$ is the dual of X, then naturality of the braiding implies that

Tensoring on the left with $X^*$ , then composing on the bottom with

and using the adjunction relation, gives

This shows that is the braiding on $V^+ \otimes V^-$ . The argument for is analogous. Then the last two equalities in (2.1) follow from the properties of a braided monoidal category.

The fact that respects (2.2) follows easily from (5.21) and (5.22). For the first relation in (2.3), first note that, since $V^+$ is simple, we have $\dim _\Bbbk \operatorname {\mathrm {End}}_{\mathrm {U}}(V^+) = 1$ . Thus, there exists $c \in \Bbbk $ such that

(6.1)

Using (5.18) to (5.21), we compute that the action of the left-hand side of (6.1) on $v_{1-n}^+$ is given by

Thus, $c=q^{m-n}$ , as desired. The proof that respects the second equality in (2.3) is similar.

To show that respects the last relation in (2.3), we compute that

as desired.

The verification that respects (2.4) is a standard direct verification.

The following result will be used in the proof of Theorem 6.4.

Lemma 6.2. We have

Proof. Using (2.6) and (5.19), we compute

The second equation is proved similarly.

As explained in the first paragraph of the proof of Proposition 6.1, the $V^+ \otimes V^-$ and $V^- \otimes V^-$ components of the braiding on $\mathrm {U}\text {-tmod}$ are

6.2 The disoriented incarnation functor

The composition of functors

(6.2)

endows $\mathrm {U}^\imath _\sigma \text {-tmod}$ with the structure of a right -module category.

The following lemma will allow us to simplify an argument in the proof of Theorem 6.4.

Lemma 6.3. As a $\mathrm {U}^\imath $ -module (hence, also as a $\mathrm {U}^\imath _\sigma $ -module), $\operatorname {\mathrm {Res}}(V^- \otimes V^-)$ is generated by

(6.3) $$ \begin{align} \{v_i^-\otimes v_j^- : \phi(i)\neq j\} \cup \{v_i^-\otimes v_i^-: i>0\}. \end{align} $$

Proof. Let W be the $\mathrm {U}^\imath $ -submodule generated by the given vectors. By the definition (5.31) of $\phi $ , it suffices to show that

(6.4) $$ \begin{align} v_{-2k}^- \otimes v_{-2k-1}^- \in W \quad \text{and} \quad v_{-2k-1}^- \otimes v_{-2k}^- \in W \end{align} $$

for $0 \le k \le n-1$ . We prove this by induction on k.

By (5.24) and (5.27), we have

$$\begin{align*}B_0 = F_0 + \varsigma_0 (E_{-1}E_0-qE_0E_{-1}) K_0^{-1}. \end{align*}$$

Thus

$$\begin{align*}B_0(v_{-1}^-\otimes v_1^-) \overset{(5.9)}{\underset{(5.16)}{=}} - v_{-1}^-\otimes v_0^- - \varsigma_0 v_1^-\otimes v_1^-. \end{align*}$$

Since $v_{-1}^-\otimes v_1^-,v_1^-\otimes v_1^-\in W$ , we conclude that $v_{-1}^-\otimes v_0^-\in W$ . On the other hand, we have

$$\begin{align*}E_{-1}(v_{-1}^-\otimes v_{-1}^-) \overset{(5.9)}{=} (E_{-1}\otimes 1+K_{-1}\otimes E_{-1})(v_{-1}^-\otimes v_{-1}^-)=v_0^-\otimes v_{-1}^-+qv_{-1}^-\otimes v_0^-. \end{align*}$$

Since $v_{-1}^-\otimes v_{-1}^-\in W$ , we see that $v_0^-\otimes v_{-1}^-\in W$ . Thus, (6.4) holds for $k=0$ .

Next suppose that $1 \le k \le n-1$ and that (6.4) holds for $k-1$ . Let $\mathrm {U} = \bigoplus _{\alpha \in X} \mathrm {U}_\alpha $ be the usual grading on $\mathrm {U}$ by the root lattice and, for $M \in \mathrm {U}\text {-tmod}$ and a weight $\mu $ , let $M_\mu $ denote the $\mu $ -weight space of M. Note that

$$\begin{align*}B_{-2k} \in F_{-2k} + \mathrm{U}_{\epsilon_{-2k-1}-\epsilon_{-2k+2}}. \end{align*}$$

Since

$$\begin{align*}F_{-2k}(v_{-2k+1}^-\otimes v_{-2k-1}^-) \overset{(5.9)}{=} (F_{-2k}\otimes K_{-2k}^{-1} + 1 \otimes F_{-2k})(v_{-2k+1}^- \otimes v_{-2k-1}^-) \overset{(5.16)}{=} v_{-2k+1}^-\otimes v_{-2k}^-, \end{align*}$$

we have

$$\begin{align*}B_{-2k} (v_{-2k+1}^-\otimes v_{-2k-1}^-) \in v_{-2k+1}^-\otimes v_{-2k}^- + (V^- \otimes V^-)_{-\epsilon_{-2k+1}-\epsilon_{-2k+2}}. \end{align*}$$

Because $(V^- \otimes V^-)_{-\epsilon _{-2k+1}-\epsilon _{-2k+2}}$ is spanned by $v_{-2k+1}^- \otimes v_{-2k+2}^-$ and $v_{-2k+2}^- \otimes v_{-2k+1}^-$ , both of which lie in W by the inductive hypothesis, we conclude that $v_{-2k+1}^-\otimes v_{-2k-1}^-\in W$ .

Finally, we calculate that

$$ \begin{align*} E_{-2k+1} (v_{-2k+1}^-\otimes v_{-2k+1}^-) &\overset{(5.9)}{=} (E_{-2k+1}\otimes 1 + K_{-2k+1} \otimes E_{-2k+1})(v_{-2k+1}^-\otimes v_{-2k+1}^-) \\& \overset{(5.16)}{=} v_{-2k}^-\otimes v_{-2k+1}^- + q v_{-2k+1}^- \otimes v_{-2k}^-. \end{align*} $$

Since $v_{-2k+1}^- \otimes v_{-2k+1}^- \in W$ and $v_{-2k+1}^- \otimes v_{-2k}^- \in W$ , we conclude that $v_{-2k}^- \otimes v_{-2k+1}^- \in W$ as well. Thus, (6.4) holds, completing the proof of the induction step.

Theorem 6.4. There is a unique strict morphism of -modules such that

(6.5)

Proof. The property of being a strict morphism of -modules, together with the definition (6.2), means that the diagram

commutes, where the horizontal arrows are the right actions. It follows that is uniquely determined by (6.5), since $B_0$ , , and generate as an -module. In particular, . It remains to show that respects the relations (2.17) and (2.18). The first two relations in (2.17) are immediate.

Next we verify the first relation in (2.18). The image under of the left-hand side is the map

and is the map

verifying the first relation in (2.18).

Now consider the second relation in (2.18). The image under of the left-hand side is the map

and is the map

verifying the second relation in (2.18).

It remains to verify the last relation in (2.17). By Lemma 6.3, it suffices to show that the images under of the two sides of the relation agree on the set (6.3). Note that $p(\phi (i)) = p(i)$ for all $i \in I_V$ . Using Lemma 6.2, we compute, for $i>0$ ,

and

which agree. If $\phi (i) \ne j$ , then

and

which also agree since the condition $\phi (i) \ne j$ implies that $i>j \iff \phi (i)>\phi (j)$ .

Remark 6.5. If either $m = 0$ or $n = 0$ , then the preservation of the last relation in (2.17) under follows from the reflection equation [Reference Balagović and KolbBK19, (9.16)] between the universal R-matrix of $\mathrm {U}$ and the universal K-matrix of $\mathrm {U}^\imath $ . Indeed, let $\tau _0$ be the algebra automorphism of $\mathrm {U}$ corresponding to the nontrivial involution of its Dynkin diagram. By [Reference Balagović and KolbBK19, Cor. 7.7], the universal K-matrix $\mathcal {K}$ defines an isomorphism of $\mathrm {U}^\imath $ -modules

$$\begin{align*}\mathcal{K}_M \colon M \to M^{\tau_0} \end{align*}$$

for any finite-dimensional $\mathrm {U}$ -module M, where $M^{\tau _0}$ has the same underlying vector space as M but with the action given by $(x, v) \mapsto \tau _0(x) v$ for $x \in \mathrm {U}$ and $v \in M^{\tau _0}$ . (Recall that the diagram automorphism $\tau $ , which is part of the data of the super Satake diagram (5.23), is the identity in our case.) It follows that the universal K-matrix $\mathcal {K}$ defines a $\mathrm {U}^\imath $ -isomorphism

$$\begin{align*}\mathcal{K}_{V^-} \colon V^- \to (V^-)^{\tau_0}. \end{align*}$$

However, it is straightforward to check that $(V^-)^{\tau _0} \cong V^+$ as $\mathrm {U}$ -modules. Since $V^- \cong V^+$ as $\mathrm {U}^\imath $ -modules and both are irreducible, Schur’s Lemma implies that one can identify $\mathcal {K}_{V^-}$ with the map $\varphi $ , up to a scalar. Then the last relation in (2.17) follows from the reflection equation established in [Reference Balagović and KolbBK19, (9.16)]. The proof of Theorem 6.4 could be made significantly shorter if the machinery of the K-matrix existed in the super setting; unfortunately, this is not yet the case.

6.3 The iquantum incarnation functor

Define

$$\begin{align*}V_r = \operatorname{\mathrm{Res}} \left( (V^+)^{\otimes r} \right), \qquad r \in \mathbb{N}. \end{align*}$$

Proposition 6.6. The composite morphism of -modules

(6.6)

is given on objects by $\mathsf {B}_r \mapsto V_r$ , $r \in \mathbb {N}$ , and on morphisms by

Note that is not a strict morphism of -modules, since $\mathbf {G}$ is not; see Remark 4.4. The map

recovers the operator $\Xi $ defined in [Reference Shen and WangSW25, §7.3].

7.1 Basis theorem

For $\lambda ,\mu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ , a $(\lambda ,\mu )$ -matching is a partition of the set

$$\begin{align*}E(\lambda,\mu) := \{-1,-2,\dotsc,-\ell(\lambda),1,2,\dotsc,\ell(\mu)\} \end{align*}$$

into subsets of size two. In a string diagram representing a morphism in , each nonclosed string has two endpoints. We view these endpoints as elements of $E(\lambda ,\mu )$ by numbering the ${\mathord {\uparrow }}$ , ${\mathord {\downarrow }}$ in $\lambda $ by $-1,-2,\dotsc ,-\ell (\lambda )$ from left to right and the ${\mathord {\uparrow }}$ , ${\mathord {\downarrow }}$ in $\mu $ by $1,2,\dotsc ,\ell (\mu )$ from left to right. A reduced $(\lambda ,\mu )$ -diagram for a given $(\lambda ,\mu )$ -matching is a string diagram representing a morphism in such that:

• • the endpoints of each string correspond under the given matching (i.e., they form one of the two-element subsets of the partition);

• • there are no closed strings (i.e., strings with no endpoints);

• • no string has more than one critical point (i.e., more than one point at which the tangent is horizontal);

• • there are no self-intersections of strings and no two strings cross each other more than once;

• • all toggles on strings connecting the top and bottom of the diagram are near their bottom endpoint;

• • all toggles on strings with both endpoints at the top of the diagram or both endpoints at the bottom of the diagram are near the left endpoint of the string.

For example, for $\lambda = {\mathord {\downarrow }} {\mathord {\uparrow }} {\mathord {\downarrow }} {\mathord {\downarrow }} {\mathord {\downarrow }} {\mathord {\uparrow }} {\mathord {\uparrow }}$ and $\mu = {\mathord {\uparrow }} {\mathord {\uparrow }} {\mathord {\uparrow }} {\mathord {\uparrow }} {\mathord {\downarrow }}$ ,

is a reduced $(\lambda ,\mu )$ -diagram for the $(\lambda ,\mu )$ -matching

$$\begin{align*}\big\{ \{-1,-5\}, \{-2,1\}, \{-3,4\}, \{-4,-7\}, \{-6,5\}, \{2,3\} \big\}. \end{align*}$$

Fix a set consisting of a choice of reduced $(\lambda ,\mu )$ -diagram for each of the $(\lambda ,\mu )$ -matchings.

Proof. Set . It suffices to consider the ground ring

$$\begin{align*}\Bbbk = \mathbb{Z}[q^{\pm 1}, t^{\pm 1}, (t-t^{-1})/(q-q^{-1})], \end{align*}$$

since the more general case then follows by base extension. The defining relations and the additional relations deduced in Sections 2.1 and 2.2 give Reidemeister-type relations modulo terms with fewer crossings, plus a skein relation. The relation (2.25), together with the skein relation (2.2), implies that we can slide toggles through crossings, modulo diagrams with fewer crossings. Furthermore, we can slide toggles over cups and caps, modulo diagrams with fewer crossings, by moving cups and caps to the left of the diagram, then using (2.25) and (2.26). These relations allow us to transform diagrams for morphisms in in way similar to the way oriented tangles are simplified in skein categories, modulo diagrams with fewer crossings. Therefore, there is a straightening algorithm to rewrite any diagram representing a morphism $\lambda \to \mu $ as a linear combination of the ones in .

It remains to prove linear independence. For $\mu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ , let $\mu '$ denote the word obtained from $\mu $ by rotating

. For example, $({\mathord {\uparrow }} {\mathord {\uparrow }} {\mathord {\downarrow }} {\mathord {\uparrow }} {\mathord {\downarrow }})' = ({\mathord {\uparrow }} {\mathord {\downarrow }} {\mathord {\uparrow }} {\mathord {\downarrow }} {\mathord {\downarrow }})$ . For $\lambda , \mu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ , we have a $\Bbbk $ -linear isomorphism

(7.1)

with inverse

Via the straightening algorithm mentioned above (e.g., using (2.4) to remove instances of multiple critical points and (2.2) to flip crossings if necessary), there is a bijection from to such that (7.1) acts by this bijection modulo diagrams with fewer crossings. Thus, it suffices to prove the linear independence of . Since when $\ell (\lambda ) \notin 2\mathbb {N}$ , we assume that $\ell (\lambda ) \in 2\mathbb {N}$ .

We will use the disoriented incarnation functor in the case that $n=0$ , which we assume throughout this proof. We also make the choice (5.29) for the $\varsigma _i$ . This implies that $\tilde {\varsigma }_i = 1$ for all $i \in I_V$ ; see (5.32).

For $\mu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ and $1 \le a \le \ell (\mu )$ , let

(7.2) $$ \begin{align} \pi_a(\mu) = \begin{cases} + &\text{if the } a\, \text{ th term in } \mu \text{ is } {\mathord{\uparrow}}, \\ - &\text{if the } a\, \text{ th term in } \mu \text{ is } {\mathord{\downarrow}}. \end{cases} \end{align} $$

Then, for $\mathbf {i} = (i_1,\dotsc ,i_{\ell (\mu )}) \in I_V^{\ell (\mu )}$ , let

We define

For a morphism $f \colon \mu \to \nu $ in , define

Let J be the ideal of $\mathbb {Z}[q^{\pm 1}]$ generated by $q-1$ . It follows from (5.21) and (5.22) that, for $\mu ,\nu \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ ,

and

where $\operatorname {\mathrm {flip}} \colon u \otimes w \to w \otimes u$ is the tensor flip. Similarly, the other crossings also induce the flip map. Thus, using also (5.17), (5.18), and (5.33), we see that, for and $\mathbf {i} = (i_1,\dotsc ,i_{\ell (\lambda )}) \in I_V^{\ell (\lambda )}$ ,

Now suppose that $m \ge \ell (\lambda )$ and that

(7.3)

Then, for each , evaluating (7.3) at $v_{\mathbf {i},\lambda }$ for some $\mathbf {i}$ whose entries are equal if and only if they are matched under the matching corresponding to f shows that $\gamma _f = 0$ . Thus, the , , are linearly independent if $m \ge \ell (\lambda )$ .

Now suppose that $\lambda \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ and that

Multiplying by an appropriate power of $(q-q^{-1})$ , we may assume that $c_f(q,t) \in \mathbb {Z}[q^{\pm 1}, t^{\pm 1}]$ for all . Applying , we have

Since the , , are linearly independent, we have $c_f(q,q^m)=0$ for all and $m \ge \ell (\lambda )$ . As there are infinitely many choices of m, it follows that $c_f(q,t)=0$ for all f. Thus, the set is linearly independent, as desired.

For $r,s \in \mathbb {N}$ , define

Let $A \subseteq \mathbb {C}(q) = \Bbbk $ be the $\mathbb {C}$ -subalgebra of rational functions regular at $q=1$ . This is a local ring with maximal ideal $\mathfrak {m} = A(q-1)$ . In what follows, we identify $\mathbb {C}$ with $A/\mathfrak {m}$ . For $d \in \mathbb {C}$ , let denote the Brauer category, as described in [Reference Lehrer and ZhangLZ15, Th. 2.6].

Corollary 7.3. There is an isomorphism of $\mathbb {C}$ -linear categories from to the Brauer category given by

Proof. It is straightforward to verify that the given functor is well defined (that is, the relations in Definition 2.7 are satisfied). It follows from [Reference Lehrer and ZhangLZ15, Th. 2.6] that, for each $r,s \in \mathbb {N}$ the image of under the above functor is a basis of . Here we use the fact that

and similarly for the other diagrams in appearing in (4.4) and (4.5). It follows that the functor in the statement of the lemma is an isomorphism.

7.2 Endomorphism algebras

For $r \in \mathbb {N}$ , the iquantum Brauer algebra $\mathrm {B}_r(q,t)$ is the associative $\Bbbk $ -algebra with generators $\sigma _1,\sigma _2,\dotsc ,\sigma _{r-1}$ and e, subject to the relations

$$ \begin{align*} \begin{gathered}\sigma_i \sigma_{i+1} \sigma_i = \sigma_{i+1} \sigma_i \sigma_{i+1},\qquad 1 \le i \le r-2, \\ \sigma_i \sigma_j = \sigma_j \sigma_i,\qquad 1 \le i,j \le r-1,\ |i-j|>1, \\ \sigma_i^2 = (q-q^{-1}) \sigma_i + 1,\qquad 1 \le i \le r-1, \\ e^2 = \frac{t-t^{-1}}{q-q^{-1}} e, \\ e \sigma_1 = \sigma_1 e = q e,\quad e \sigma_2 e = t e,\quad e \sigma_i = \sigma_i e,\qquad i > 2, \\ \sigma_2 \sigma_3 \sigma_1^{-1} \sigma_2^{-1} e_{(2)} = e_{(2)} = e_{(2)} \sigma_2 \sigma_3 \sigma_1^{-1} \sigma_2^{-1}, \quad \text{where } e_{(2)} = e \sigma_2 \sigma_3 \sigma_1^{-1} \sigma_2^{-1} e. \end{gathered}\end{align*} $$

Remark 7.4. The algebra $\mathrm {B}_r(q,t)$ is isomorphic to the algebra $Br_r(t^2,q^2)$ of [Reference WenzlWen12, §3.1] via the map

$$\begin{align*}\mathrm{B}_r(q,t) \to Br_r(t^2,q^2),\qquad e \mapsto qt^{-1} e,\quad \sigma_i \mapsto q^{-1} g_i,\quad 1 \le i \le r-1, \end{align*}$$

as can be checked by direct verification of the defining relations. Similar algebras appeared previously in [Reference MolevMol03, Def. 2.1]. The algebras $\mathrm {B}_r(q,t)$ have been called q-Brauer algebras in the literature, presumably because some authors view them as deformations of Brauer algebras and the notation used for the deformation parameter is often q. We prefer the term iquantum Brauer algebras to avoid possible confusion with Birman–Murakami–Wenzl (BMW) algebras, which are also deformations of Brauer algebras, and also to avoid terminology involving notation.

Proposition 7.5. For all $r \in \mathbb {N}$ and $\lambda \in \langle {\mathord {\uparrow }},{\mathord {\downarrow }} \rangle $ with $\ell (\lambda )=r$ , we have isomorphisms of algebras

Proof. By Theorem 4.5, it suffices to prove the result for . It is straightforward to verify that the map given by

satisfies the defining relations of $\mathrm {B}_r(q,t)$ . It then follows from the basis theorems [Reference WenzlWen12, Th. 3.8] and Corollary 7.2 that this map is in an isomorphism.