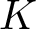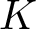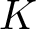1. Introduction
The combinatorial analysis of homotopy types dates back to the 1940s with Whitehead’s simple homotopy theory [Reference Whitehead35–Reference Whitehead38]. In an effort to describe homotopy equivalences through rigid transformations of combinatorial structures, Whitehead introduced collapses and expansions for finite simplicial complexes. These moves were inspired by Tietze transformations for group presentations. While Tietze’s theory provides a complete set of transformations between equivalent presentations, Whitehead’s simple homotopy theory is more restrictive and fails to capture all homotopy deformations. Nevertheless, it remains a powerful combinatorial framework, influencing classical problems [Reference Akbulut and Kirby1, Reference Milnor25]; such as Zeeman’s conjecture [Reference Zeeman39]; the Andrews–Curtis conjecture [Reference Andrews and Curtis2, Reference Hog-Angeloni and Metzler20]; and the Poincaré conjecture [Reference Poincaré30, Reference Zeeman40]; as well as modern computational approaches to analysing complexes and data [Reference Bauer and Edelsbrunner4, Reference Benedetti, Lai, Lofano and Lutz5, Reference Robins, Wood and Sheppard31].
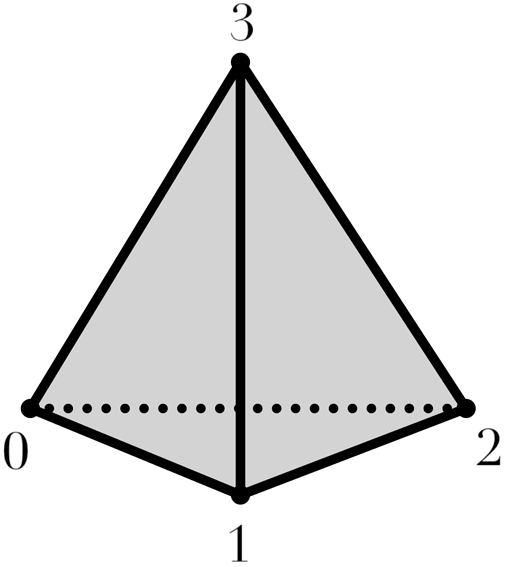
Whitehead’s elementary deformations are called collapses (and their reverse moves, expansions), which rely on the concept of a free face. If 
$\tau$ is the unique simplex of a simplicial complex 
$K$ properly containing 
$\sigma$, then both 
$\sigma$ and 
$\tau$ can be removed from 
$K$ while preserving its homotopy type and simplicial structure (see Figure 1, left). However, many simplicial complexes lack free faces (e.g., triangulations of closed manifolds). A more general concept is that of an internal free face, leading to an internal collapse [Reference Fernández16, Reference Kaczyński, Mrozek and Ślusarek21, Reference Kozlov23]. Here, 
$\sigma$ becomes a free face of 
$\tau$ in a subcomplex 
$L \subseteq K$. To preserve the homotopy type of 
$K$ after removing 
$\sigma$ and 
$\tau$, the simplices in 
$K \smallsetminus L$ must be re-attached, often losing the simplicial structure (see Figure 1, right). In general, there is no explicit or computable method to determine such attachments in arbitrary dimensions.
Figure 1. Collapse (left) vs internal collapse (right).
Discrete Morse theory [Reference Forman18, Reference Forman19, Reference Kozlov22], developed by Forman in the 1990s as a combinatorial analogue of smooth Morse theory for manifolds, is a tool for studying the homotopy type of simplicial complexes via real-valued functions defined on them. Concretely, given a simplicial complex 
$K$ and a discrete Morse function 
$f \colon K \to \mathbb{R}$, there exists a reduced CW-complex built from the critical simplices of 
$f$, denoted by 
${\mathrm{core}}_f(K)$, which is homotopy equivalent to 
$K$. Moreover, a recent result establishes a connection between discrete Morse theory and simple homotopy theory: if 
$K$ has dimension 
$N$, then there exists a sequence of collapses and expansions from 
$K$ to 
${\mathrm{core}}_f(K)$ through intermediate complexes of dimension at most 
$N+1$ (also called an 
$(N+1)$-deformation and denoted by 
$K \diagup\!\!\!\searrow^{^{N+1}} {\mathrm{core}}_f(K)$) [Reference Fernández16]. This result relies on the fact that discrete Morse functions are equivalent to well-ordered sequences of internal collapses, which encode the deformation from 
$K$ to 
${\mathrm{core}}_f(K)$ [Reference Fernández16, Reference Kozlov23]. The construction of the reduced complex 
${\mathrm{core}}_f(K)$, however, often sacrifices the original simplicial and combinatorial structure of 
$K$. The resulting attaching maps tend to be more intricate and are not explicitly determined, transferring the topological complexity of the space from many simplices with simple attaching maps to fewer cells (corresponding to the critical simplices) whose attaching maps are more complex. This work focuses on a particular case of discrete Morse theory in which it is possible to provide an explicit and computable method for describing these attaching maps, even in higher dimensions.
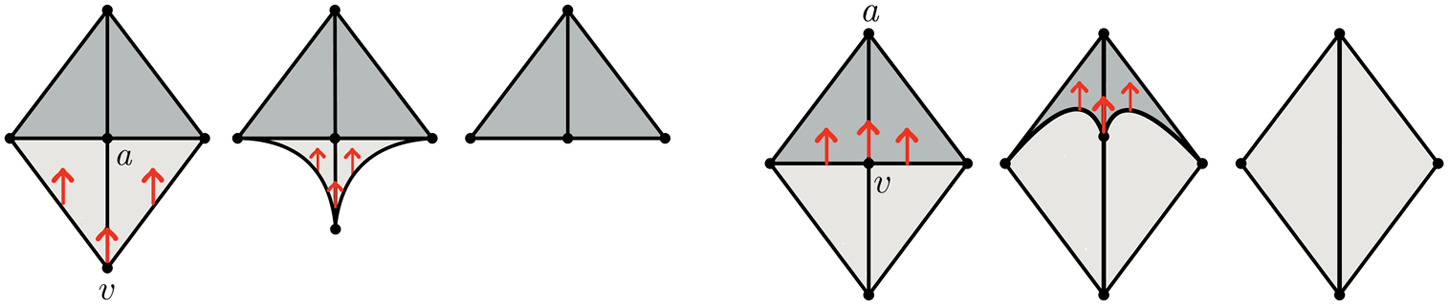
In 2012, a strong version of homotopy theory was developed by Barmak and Minian [Reference Barmak and Minian3]. This approach builds upon simple homotopy theory by introducing strong collapses of simplicial complexes. Inspired by vertex reductions on posets [Reference Stong33], strong collapses involve eliminating vertices 
$v$ (called dominated vertices) whose link is a simplicial cone. In general, removing (the open star of) vertices with a contractible link preserves the homotopy type, as a consequence of the Gluing Theorem [Reference Brown13]. Coned links, however, offer a systematic way to simple collapse 
$K$ to the subcomplex 
$K \smallsetminus v$ (see Figure 2, left).
Figure 2. Strong collapse (left) vs internal strong collapse (right).
Strong collapses, as collections of simultaneous collapses, are highly efficient. Unlike Whitehead’s collapses, strong collapses always yield the same minimal irreducible subcomplex — the strong core of 
$K$. However, the strong core of 
$K$ often coincides with 
$K$ itself, as many simplicial complexes lack dominated vertices. To overcome this limitation, one can consider performing strong collapses internally, where domination is restricted to a subcomplex of 
$K$ (see Figure 2, right). In such cases, a strategy must again be developed to recompute the attaching maps of the remaining cells, potentially compromising the simplicial structure of the reduced complex.
In this work, we establish a method for studying internal strong collapses and prove that the reduced CW-complex obtained from any sequence of such collapses is always regular (i.e., its attaching maps are homeomorphisms onto their images). As a consequence, the CW-structure of the reduced complex is fully combinatorially determined by the incidences of its cells. More broadly, we develop the theoretical foundations of strong Morse theory, a version of discrete Morse theory in which discrete Morse functions correspond to sequences of internal strong collapses. We propose an efficient algorithm for computing the reduced complex 
${\mathrm{core}}_f(K)$ for such discrete Morse functions 
$f$. To demonstrate its applicability, we use this method to identify more efficient regular models of the simplicial complexes in the Library of Triangulations [Reference Benedetti, Lai, Lofano and Lutz5–Reference Benedetti and Lutz7] by Benedetti and Lutz.
1.1. Motivation and related work
Classical discrete Morse theory does not provide an explicit description of the reduced homotopy equivalent CW-complex. A discrete Morse function on a simplicial complex 
$K$ induces a collection of critical simplices that correspond to the cells in the reduced CW-complex, along with information about their incidences, which is sufficient to determine the homology of the simplicial complex 
$K$. However, recovering the homotopy type of 
$K$ from the reduced CW-complex requires a more refined understanding of the attaching maps. Hence, except in special cases—such as when the homotopy type is fully determined by the list of critical cells (e.g., wedges of spheres)—the algorithmic reconstruction of homotopy types from discrete Morse data remains an open problem.
Some progress has been made toward addressing this challenge. In [Reference Fernández16], the author develops a combinatorial framework to describe the attaching maps of the reduced CW-complex for 2-dimensional simplicial complexes equipped with a discrete Morse function with a single critical 0-simplex. The approach makes strong use of the correspondence between 2-complexes and group presentations. However, it does not extend to higher dimensions, as the homotopy types of 
$N$-dimensional complexes with 
$N \gt 2$ generally cannot be fully captured combinatorially via group presentations. Rather than attempting to recover arbitrary attaching maps, the present work focuses on cases in which discrete Morse functions yield reduced complexes with particularly simple attaching maps—namely, homeomorphisms.
Our central goal is to develop a combinatorial and computable framework for a strong discrete Morse theory that allows for the explicit reconstruction of the reduced CW-complex. By restricting Morse functions to those induced by internal strong collapses, we prove that the resulting reduced complex is always a regular CW-complex, and hence its homotopy type can be entirely determined by the poset of incidence cells. Moreover, as strong Morse theory is a restricted version of classical discrete Morse theory, the reduced complex 
$(N+1)$-deforms to the original simplicial complex 
$K$, where 
$N$ is the dimension of 
$K$. Consequently, this theory also provides a computational method to perform 
$(N+1)$-dimensional deformations.
In [Reference Fernández-Ternero, Macías-Virgós, Scoville and Vilches17], the authors also establish connections between discrete Morse theory and strong collapses, focusing on general discrete Morse functions. Their work introduces a classification of internal collapses into critical and regular pairs, providing criteria to determine whether a sub-sequence of internal collapses is induced by a strong collapse. In contrast, our approach only focuses on the specific class of Morse functions derived from only internal strong collapses.
Our work builds on the main principles of Bestvina–Brady Morse theory [Reference Bestvina8, Reference Bestvina and Brady9]. In that framework, Morse functions are piecewise-linear (PL) functions defined on affine complexes, the critical points are the vertices, and changes in the topology of sublevel sets are studied through the descending links of vertices. Restricting to simplicial complexes and functions defined on their vertices, our theory refines this perspective by classifying vertices according to the structure of their descending links: either as descending dominated vertices (their descending links are simplicial cones, and induce internal strong collapses) or as strong critical vertices. While Bestvina–Brady Morse theory studies local changes in the homotopy type of sublevel sets, our approach also aims at the combinatorial and global reconstruction of a reduced complex induced by these local changes. In particular, instead of treating every vertex as critical, our theory identifies a potentially smaller subset of strong critical vertices that form the cells of the final reduced complex. The remaining descending dominated vertices are systematically collapsed, leading to a complete reconstruction of the homotopy type of the original complex.
A complementary perspective is presented in [Reference Nanda27, Reference Nanda, Tamaki and Tanaka28], where the authors encode the homotopy type of a simplicial complex endowed with a discrete Morse function into a combinatorially defined flow category. The classifying space of the flow category recovers the homotopy type of the original complex. However, these categories are often large and computationally challenging, limiting their application in algorithmic homotopy reconstruction. Indeed, while the computation of the nerve of a category can be exponential, the reconstruction of a regular CW-complex from its face poset is combinatorially direct.
1.2. Main results and outline
Let 
$K$ be a finite simplicial complex, and let 
$g \colon V(K) \to \mathbb{R}$ be a real-valued function on its set of vertices. The function 
$g$ induces a filtration of 
$K$ by subcomplexes, where each subcomplex consists of all simplices whose vertices lie below a given threshold in 
$g$. For each vertex 
$v \in V(K)$, we consider the first subcomplex in the filtration that contains 
$v$, and define its descending open star as the collection of simplices in that subcomplex that contain 
$v$. A vertex is called strong critical if, at the filtration step where it first appears, it is not dominated by any vertex from an earlier subcomplex.
This filtration of 
$K$ leads to a strong homotopy analogue of the classical discrete Morse lemmas (Lemma 2.4). Intervals in the filtration without strong critical vertices correspond to strong collapses, while those with strong critical vertices introduce changes in the homotopy type, determined by the simplices in its descending open stars (Lemma 3.6). This reduction process produces a sequence of internal strong collapses, resulting in a reduced complex, called the strong internal core and denoted by 
${\mathrm{core}}_g(K)$. Notably, we prove that this reduced CW-complex is regular, that is, its attaching maps are homeomorphisms with its image.
Our main result in strong Morse theory is as follows.
Theorem (Strong Morse Theory)
Let 
$K$ be a finite simplicial complex, and let 
$g \colon V(K) \to \mathbb{R}$ be a real-valued function on the vertex set of 
$K$. Then 
$K$ is homotopy equivalent to a regular CW-complex 
${\mathrm{core}}_g(K)$, whose cells are in one-to-one correspondence with the simplices in the descending open stars of the strong critical vertices of 
$g$. Moreover, if 
$\dim(K) = N$, then 
$K \diagup\!\!\!\searrow^{^{N+1}} {\mathrm{core}}_g(K)$.
We also show that this result is a particular case of classical discrete Morse theory (Theorem 3.9). More precisely, for every function 
$g \colon V(K) \to \mathbb{R}$, there exists a discrete Morse function 
$f \colon K \to \mathbb{R}$ such that the critical simplices of 
$f$ are exactly the simplices in the descending open stars of the strong critical vertices of 
$g$. Moreover, the CW-complexes 
${\mathrm{core}}_f(K)$ and 
${\mathrm{core}}_g(K)$ coincide. (By a slight abuse of notation, we denote both by 
${\mathrm{core}}$ depending on the context: 
${\mathrm{core}}_f(K)$ denotes the internal core obtained from a discrete Morse function 
$f$ on simplices, and 
${\mathrm{core}}_g(K)$ denotes the strong internal core obtained from a function 
$g$ on vertices.)
The combinatorial structure of the strong internal core admits a computational interpretation of internal strong collapses, which in turn leads to an efficient algorithm for their computation (Appendix A, Algorithms A1 and A2). An implementation is publicly available at https://github.com/ximenafernandez/Strong-Morse-Theory. To illustrate the effectiveness of this method, we apply it to examples from the Library of Triangulations [Reference Benedetti and Lutz7], a repository of challenging simplicial complexes frequently used in the study of homotopy types. The results of the reductions are presented in Tables 1 and 2.
Table 1 Comparison of reduction methods for simplicial complexes, averaged over 10 iterations. Bold values indicate cases where strong internal collapses yield the most significant size reduction. 
$Italicized$ values indicate cases where strong internal collapses also lead to a significant improvement in execution time compared to other methods
Table 2 Comparison of algorithmic reduction methods for simplicial complexes, averaged over 100 iterations. Bold values highlight cases where significant reduction is achieved via strong internal collapses (compared to other methods). 
$Italicized$ values indicate cases where significant reduction is only achieved through Whitehead collapses
Beyond its role in understanding homotopy types, the algorithmic reduction of simplicial complexes also has applications in topological data analysis, where the complexity of persistent homology computations increases rapidly with input size. For instance, computing degree-
$d$ persistent homology of the Vietoris–Rips filtration of a point cloud of size 
$N$ has worst-case complexity 
$O(N^{3(d+2)})$ [Reference Otter, Porter, Tillmann, Grindrod and Harrington29]. The method introduced in [Reference Boissonnat, Pritam and Pareek12] uses strong collapses to simplify Vietoris–Rips filtrations prior to computing persistent homology. Since our results extend algorithmic simplification of complexes via internal strong collapses, they have potential applications in further optimising such filtration-based computations.
The remainder of this manuscript is organized as follows. Section 2 presents discrete Morse theory as a generalization of Whitehead’s collapses. In Section 3, we introduce a strong version of discrete Morse theory, based on strong collapses, which enables the recovery of a regular structure in the reduced CW-complex (the strong internal core). Section 4 provides a combinatorial construction of the strong internal core in terms of posets and acyclic matchings. Finally, Section 5 discusses algorithms for the simplification of simplicial complexes and presents experiments on the Library of Triangulations [Reference Benedetti and Lutz7]. The Appendix details algorithms for constructing the critical poset and a random strong internal core.
Notation. We use 
$\simeq$ for homotopy equivalences, 
$\cong$ for homeomorphisms, and 
$|\cdot|$ for geometric realizations. The symbol 
$\sim$ is reserved for relations. The relation 
$\prec$ denotes the face relation between simplices of consecutive dimension.
2. Discrete Morse theory as generalized collapses
In this section, we revisit discrete Morse theory, framing it as a combinatorial generalization of collapsibility of simplicial complexes, in the context of Whitehead’s simple homotopy theory. The classical foundations of simple homotopy theory can be found in Whitehead’s seminal works [Reference Whitehead35, Reference Whitehead36, Reference Whitehead38], Milnor’s influential article [Reference Milnor25], and Cohen’s textbook [Reference Cohen15]. Throughout this manuscript, we will restrict our attention to finite simplicial complexes.
Definition 2.1. Let 
$K$ and 
$L$ be simplicial complexes. There is an elementary collapse from 
$K$ to 
$L$ if there exist simplices 
$\sigma, \tau \in K$ such that 
$L = K \smallsetminus \{\sigma, \tau\}$ and 
$\tau$ is the unique simplex containing 
$\sigma$ properly in 
$K$. In this case, 
$\sigma$ is called a free face of 
$\tau$.
A collapse, denoted 
$K {\searrow } L$, is a sequence 
$K = K_n { \searrow^e } K_{n-1} { \searrow^e } \dots { \searrow^e } K_0 = L$ of elementary collapses from 
$K$ to 
$L$. The inverse operation is called an expansion, denoted 
$L {\nearrow } K$. If 
$K {\searrow } L$ we say that 
$L$ is a weak core of 
$K$, and if 
$L$ has no free faces, we say it is minimal.
There is an 
$N$-deformation, denoted 
$K \diagup\!\!\!\searrow^{^{N}} L$, between 
$K$ and 
$L$ if there is a sequence 
$K = K_n, K_{n-1}, \dots, K_0 = L$ such that 
$K_i {\searrow } K_{i-1}$ or 
$K_i {\nearrow } K_{i-1}$, and 
$\dim(K_i) \leq N$ for all 
$i$. If there exists an 
$N$-deformation for some 
$N \in \mathbb{N}$ between 
$K$ and 
$L$, it is said that they have the same simple homotopy type.
Computing a minimal weak core of a simplicial complex provides a computational method for reducing its number of simplices while preserving its homotopy type. However, this approach is quite restrictive. For instance, many simplicial complexes lack free faces (e.g., triangulations of closed manifolds or famous examples such as the Dunce Hat [Reference Zeeman39] and Bing’s House [Reference Bing10]). Furthermore, a simplicial complex may have different (non-isomorphic) weak cores. For instance, if 
$D$ is any triangulation of the Dunce Hat, then 
$D \times I$ collapses to both 
$D$ and the singleton 
$*$. Thus, the order of collapses matters. A more general approach is provided by 
$N$-deformations (e.g., the above shows that 
$D \diagup\!\!\!\searrow^3 *$, even though its minimal weak core is 
$D$ itself). Nonetheless, the existence of an 
$N$-deformation between two simplicial complexes not computable, as this would imply being able to algorithmically determine the contractibility of spaces.
Discrete Morse theory [Reference Forman18, Reference Forman19], inspired by its smooth counterpart [Reference Milnor, Spivak and Wells26], provides a more general combinatorial framework for simplifying the structure of a simplicial complex while preserving its homotopy type. Here, deformations are encoded in terms of discrete Morse functions.
Definition 2.2. Let 
$K$ be a simplicial complex. A function 
$f \colon K \to \mathbb{R}$ defined on the simplices of 
$K$ is called a discrete Morse function if, for every simplex 
$\sigma \in K$, the set
\begin{equation*}
M(\sigma) = \{\tau \prec \sigma \colon f(\tau) \geq f(\sigma) \}
\cup \{\tau \succ \sigma \colon f(\tau) \leq f(\sigma) \},
\end{equation*} contains at most one element. A simplex 
$\sigma \in K$ is said to be critical if 
$M(\sigma) = \varnothing$.
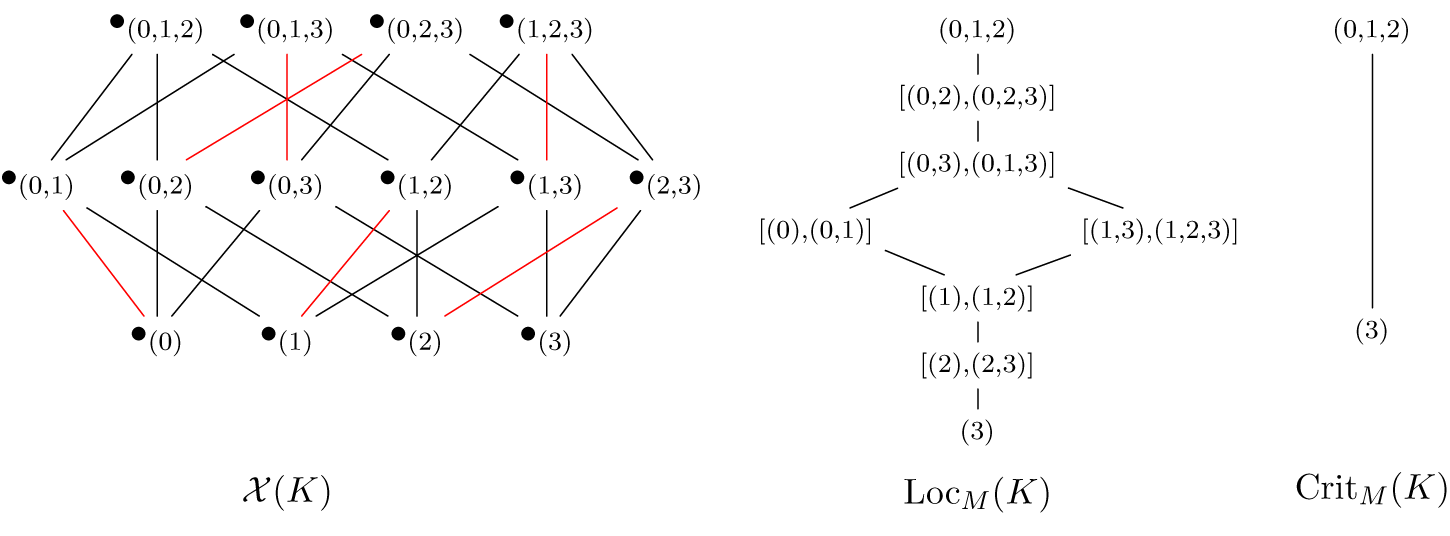
To every simplicial complex 
$K$, we associate its face poset 
${\mathcal X}(K)$, which is the poset of simplices of 
$K$ ordered by the face relation. Each Morse function determines a pairing of simplices 
$M = \big\{\{\sigma, \tau\} \colon M(\sigma) = \{\tau\}\big\}$. It can be shown that 
$M$ is a matching on the set of simplices of 
$K$. Moreover, the quotient of 
${\mathcal X}(K)$ obtained by identifying matched simplices inherits a poset structure (see Section 4 for more details). This matching is referred to as an acyclic matching Chari [Reference Chari14] proved that acyclic matchings are in correspondence with discrete Morse functions.
The main theorem in discrete Morse theory establishes the connection between critical simplices of discrete Morse functions and the homotopy type of the simplicial complex.
Theorem 2.3 (Forman [Reference Fernández16, Reference Forman18, Reference Forman19])
Let 
$K$ be a finite simplicial complex of dimension 
$N$, and let 
$f\colon K \to {\mathbb R}$ be a discrete Morse function. Then, there is an 
$(N+1)$-deformation from 
$K$ to a CW-complex with exactly one cell of dimension 
$d$ for every critical 
$d$-simplex of 
$f$.
We denote by 
${\mathrm{core}}_f(K)$ the CW-complex obtained from the critical simplices of 
$f$ in Theorem 2.3, and refer to it as the internal core of 
$K$ associated to 
$f$. It is important to note that Theorem 2.3 does not provide an explicit description of how the critical cells are attached along their boundaries in 
${\mathrm{core}}_f(K)$. In [Reference Fernández16, Prop. 1.3, Thm. 1.6], the author offers a recursive construction of the attaching maps for the critical cells, based on the finiteness of 
$K$; however, the construction is only made explicit for 2-dimensional cells.
The deformation from 
$K$ to 
${\mathrm{core}}_f(K)$ is described locally by the Morse Lemma 2.4. Any discrete Morse function 
$f \colon K \to \mathbb{R}$ induces a filtration of 
$K$ by sublevel subcomplexes: for each 
$\alpha \in \mathbb{R}$, 
$K_\alpha$ is the smallest subcomplex of 
$K$ containing all simplices 
$\sigma$ with 
$f(\sigma) \leq \alpha$. The following result describes the evolution of the homotopy type complex along the filtration: intervals that do not contain critical simplices correspond to collapses, while those containing a single critical simplex account for homotopy changes.
Lemma 2.4. (Thm. 3.3 and 3.4, [Reference Forman18])
Let 
$f \colon K \to \mathbb{R}$ be a discrete Morse function.
A. If
$f^{-1}\big((\alpha, \beta]\big)$ contains no critical simplices, then
$K_\beta {\searrow } K_\alpha$.B. If
$f^{-1}\big((\alpha, \beta]\big)$ contains exactly one critical
$k$-simplex, then
$K_\beta \simeq K_\alpha \cup e^k$, where
$e^k$ is a
$k$-dimensional cell.
From a combinatorial perspective, discrete Morse functions can be viewed as a totally ordered list of internal collapses.
Proposition 2.5. (Internal collapse [Reference Fernández16])
Let 
$K$ be a finite simplicial complex of dimension 
$N$. If a subcomplex 
$K_0 \subseteq K$ collapses to a subcomplex 
$L_0$, then 
$K \diagup\!\!\!\searrow^{^{N+1}} L$, where 
$L$ is a CW-complex obtained from 
$L_0$ by attaching one 
$k$-cell for each 
$k$-simplex in 
$K \smallsetminus K_0$.
Proposition 2.5 also admits a formulation in terms of CW-complexes; see [Reference Fernández16, Proposition 1.3]. We refer to the deformation from 
$K$ to 
$L$ as an internal collapse. The collapse takes place within a subcomplex 
$K_0 \subseteq K$, while the resulting deformation affects the entire complex through the reattachment of cells corresponding to the simplices in 
$K \smallsetminus K_0$.
Internal collapses arise naturally in discrete Morse theory: for any discrete Morse function 
$f \colon K \to \mathbb{R}$, the transitions between sublevel complexes as described in the Morse Lemma (Lemma 2.4) correspond to internal collapses. Specifically, if the interval 
$(\alpha, \beta]$ contains no critical simplices, then 
$K_\beta \simeq K_\alpha$, and there is an internal collapse from 
$K$ to a CW-complex obtained from 
$K_\alpha$ by attaching a 
$k$-cell for each 
$k$-simplex in 
$K \smallsetminus K_\beta$. In general, the entire deformation from 
$K$ to 
${\mathrm{core}}_f(K)$ can be interpreted as a well-ordered sequence of internal collapses.
We summarize the viewpoint of discrete Morse theory as a generalization of classical collapses in the following statement.
Proposition 2.6. Let 
$K$ be a finite simplicial complex.
(1) If
$K \searrow L$, then there exists a discrete Morse function
$f \colon K \to \mathbb{R}$ such that
${\mathrm{core}}_f(K) = L$.(2) If
$f \colon K \to \mathbb{R}$ is a discrete Morse function, then there exists a sequence of internal collapses from
$K$ to
${\mathrm{core}}_f(K)$.
3. Strong discrete Morse theory
Building on the strong homotopy theory for simplicial complexes introduced by Barmak and Minian [Reference Barmak and Minian3], we present a version of discrete Morse theory centred on the concept of internal strong collapses. We recall first the notion of strong collapses.
Given a simplicial complex 
$K$ and a vertex 
$v \in V(K)$, the open star of 
$v$, denoted 
${\mathrm{st}}(v, K)$, is the collection of simplices in 
$K$ that contain 
$v$. The subcomplex of simplices disjoint from 
$v$ is denoted 
$K \smallsetminus v$. The link of 
$v$ in 
$K$, denoted 
${\mathrm{lk}}(v, K)$, is the subcomplex of 
$K \smallsetminus v$ consisting of simplices 
$\sigma$ such that 
$\sigma \cup \{v\}$ is a simplex of 
$K$. A simplicial cone over 
$K$ with apex 
$a$ (a vertex not in 
$K$) is the complex 
$a*K$ consisting of all simplices of 
$K$, the vertex 
$\{a\}$, and all simplices of the form 
$\sigma \cup \{a\}$ with 
$\sigma \in K$. The closed star of 
$v$, denoted 
$\overline{{\mathrm{st}}}(v, K)$, is the subcomplex 
$v \ast {\mathrm{lk}}(v,K)$.
Definition 3.1. (Def. 2.1, [Reference Barmak and Minian3])
Let 
$K$ be a simplicial complex. A vertex 
$v$ of 
$K$ is dominated by a vertex 
$a$ if 
${\mathrm{lk}}(v,K)$ is a simplicial cone 
$a*K_0$, where 
$K_0$ is a subcomplex of 
$K$. In that case, there is an elementary strong collapse from 
$K$ to 
$K \smallsetminus v$, denoted 
$K \searrow K \smallsetminus v$. A strong collapse 
$K {\searrow \searrow} L$ from a simplicial complex 
$K$ to a subcomplex 
$L$ is a sequence of elementary strong collapses starting at 
$K$ and ending at 
$L$. In that case, we say that 
$L$ is a strong core of 
$K$. If 
$L$ has no dominated vertices, we say that 
$L$ is a minimal strong core of 
$K$. (Note that he strong core is simply called a core in [Reference Barmak and Minian3]. We will use the term minimal strong core in this manuscript to avoid confusion with other core constructions. In [Reference Barmak and Minian3], it is proved that the mimimal strong core of a complex is unique modulo homeomorphisms.)
If 
$v \in K$ is dominated by 
$a$, then there is an explicit strong deformation retraction 
$|r_a|\colon |K| \to |K \smallsetminus v|$ induced by the simplicial map
\begin{equation}
r_a(\sigma) =
\begin{cases}
\sigma & \text{if } v \notin \sigma, \\
\{a\} \cup \sigma \smallsetminus \{v\} & \text{if } v \in \sigma.
\end{cases}
\end{equation} More generally, if 
$K {\searrow\!\!\!\searrow} L$ via a sequence of elementary strong collapses
\begin{equation*}
K = K_0 {\searrow\searrow^e } K_1 {\searrow\searrow^e } \dots {\searrow\searrow^e } K_n = L,
\end{equation*} with 
$K_{i+1} = K_i \smallsetminus v_i$ and 
$v_i$ dominated by 
$a_i \in K_i$, then there is a strong deformation retraction 
$|r|\colon |K| \to |L|$ induced by the composition
\begin{equation}
r := r_{a_n} \circ r_{a_{n-1}} \circ \dots \circ r_{a_1}.
\end{equation} Moreover, if 
$K {\searrow \searrow} L$, then 
$K {\searrow } L$ [Reference Barmak and Minian3, Rmk. 2.4]. That is, Whitehead’s notion of collapse is weaker than the notion of strong collapse.
Theorem (Thm. 2.11. [Reference Barmak and Minian3])
Any sequence of strong collapses from a simplicial complex 
$K$ to a subcomplex without dominated vertices yields a unique (up to isomorphism) subcomplex of 
$K$. That is, the minimal strong core of a simplicial complex is unique up to isomorphism.
Recall that a CW-complex 
$K$ is regular if the attaching map 
$\varphi \colon S^{n-1} \to K^{(n-1)}$ of each open 
$n$-cell 
$e^n$ is a homeomorphism onto its image 
$\partial e^n$ in the 
$(n-1)$-skeleton. A regular CW-complex is said to be combinatorial if, for each cell 
$e^n$, the attaching map — regarded as a cellular map from 
$S^{n-1}$ endowed with a CW-structure — is a combinatorial map, meaning that it maps each open 
$k$-cell of 
$S^{n-1}$ homeomorphically onto an open 
$k$-cell of 
$K$ (see [Reference Hog-Angeloni and Metzler20, Ch. II]). The geometric realization 
$|K|$ of any simplicial complex 
$K$ is canonically a regular combinatorial CW-complex. Given a vertex 
$v$ in a regular CW-complex 
$K$, we define the open star 
${\mathrm{st}}(v,K)$ as the union of all open cells in 
$K$ that contain 
$v$ as a face. We denote by 
$\overline{e}$ the closure of a cell 
$e \in K$, i.e., the smallest subcomplex of 
$K$ containing 
$e$, which consists of 
$e$ together with all its faces. Similarly, we denote by 
$K \smallsetminus v$ the subcomplex of 
$K$ consisting of all cells 
$e$ such that 
$v \notin \overline{e}$.
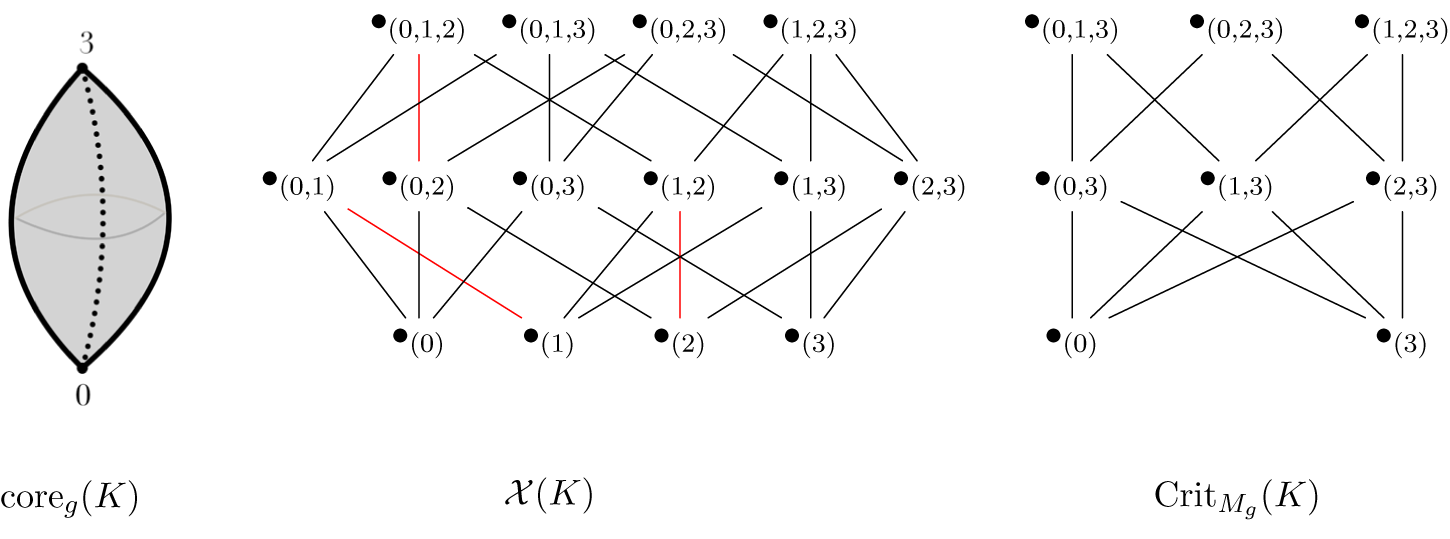
The following result formalizes the notion of an internal strong collapse, illustrated in Figure 2.
Theorem 3.3 Let 
$K$ be a regular combinatorial CW-complex, and let 
$w$ be a vertex of 
$K$ such that the subcomplex 
$K \smallsetminus w$ is a simplicial complex. Suppose there exists a subcomplex 
$L \subseteq K \smallsetminus w$ such that 
$K \smallsetminus w {\searrow \searrow} L$ via a sequence of strong collapses.
Then there exists a regular combinatorial CW-complex
\begin{equation*}
Z = L \cup \bigcup_{\ell} \tilde{e}_\ell,
\end{equation*} that is homotopy equivalent to 
$K$, where:
•
$L$ is embedded as a subcomplex of
$Z$,• for each cell
$e_\ell \in K$ such that
$w \in \overline{e_\ell}$, there is a corresponding
$\ell$-cell
$\tilde{e}_\ell$ in
$Z$ not contained in
$L$, and• the attaching map of each
$\tilde{e}_\ell$ is induced from that of
$e_\ell$ and the strong deformation retraction
$|r| \colon |K \smallsetminus w| \to |L|$ determined by the strong collapse.
Moreover, if 
$\dim(K) = N$, then 
$K \diagup\!\!\!\searrow^{^{N+1}} Z$.
Proof. Consider the pushout diagram
where 
$i$ is the inclusion map and 
$|r| \colon |K \smallsetminus w| \to |L|$ is the strong deformation retraction induced by the strong collapse. Since 
$|r|$ is a homotopy equivalence and 
$i$ is a closed cofibration, the Gluing Theorem (see, e.g., [Reference Brown13, 7.5.7, Corollary 2]) implies that 
$\bar{r}$ is also a homotopy equivalence.
We now define a regular combinatorial CW-structure on 
$Z$. Assume first that the collapse 
$K \smallsetminus w {\searrow \searrow} L$ is elementary, i.e., 
$L = (K \smallsetminus w) \smallsetminus v$ for some vertex 
$v$ dominated by 
$a \in K \smallsetminus w$.
The 
$0$-skeleton of 
$Z$ is defined as 
$Z^{(0)} = L^{(0)} \cup \{w\}$. We define a map 
$q \colon K^{(0)} \to Z^{(0)}$ by
\begin{equation*}
q(x) =
\begin{cases}
x & \text{if } x \in L^{(0)} \cup \{w\},\\
a & \text{if } x = v,
\end{cases}
\end{equation*} which agrees with the retraction 
$r$ on 
$K^{(0)} \smallsetminus \{w\}$.
Inductively, suppose that a regular combinatorial CW-structure has been defined on 
$Z^{(\ell-1)}$, and that the map 
$q \colon K^{(\ell -1)} \to Z^{(\ell-1)}$ is combinatorial and coincides with the simplicial retraction 
$r$ on 
$(K \smallsetminus w)^{(\ell-1)}$. Let 
$e$ be an 
$\ell$-cell in 
$K$ with attaching map 
$\varphi\colon S^{\ell-1} \to K^{(\ell-1)}$.
If 
$w \notin \overline{e}$, then 
$e$ belongs entirely to the subcomplex 
$K \smallsetminus w$, and its image in 
$Z$ is defined via 
$q = r$. Since 
$r \colon K \smallsetminus w \to L$ is simplicial, and the attaching maps in 
$K\smallsetminus w$ are simplicial, it follows that 
$q(e)$ inherits a regular combinatorial CW-structure. In particular, if 
$e \in L$, then 
$q$ acts as the identity on 
$e$.
If 
$w \in \overline{e}$, we distinguish three cases:
(1) If
$v \notin \overline{e}$, then
$q$ acts as the identity on
$e$, and the attaching map of
$e$ remains unchanged in
$Z$, inheriting the regular combinatorial CW-structure from
$K$.(2) If
$v \in \overline{e}$ but
$a \notin \overline{e}$, then
$r$ sends
$v$ to
$a$ in
$\partial e \cap (K\smallsetminus w)$, resulting in a relabelling, inducing a bijective identification on the boundary. The attaching map
$\tilde{\varphi} \colon S^{\ell - 1} \to Z^{(\ell - 1)}$ of
$\tilde e\in Z$ is given by
$\tilde{\varphi} := r \circ \varphi$, and the image cell
$q(e)$ is obtained from
$e$ via this relabelling.(3) If both
$v$ and
$a$ belong to
$\overline{e}$, then the retraction
$r$ modifies the attaching map non-trivially. Since
$K$ is regular and combinatorial, the boundary
$\partial e$ is a PL
$(\ell -1)$-sphere. Let
\begin{equation*}
A := |\overline{{\mathrm{st}}}(v, K \smallsetminus w)| \cap \partial e,\quad B := |{\mathrm{lk}}(v, K \smallsetminus w)| \cap \partial e.
\end{equation*}Then
$A$ is a PL
$(\ell -1)$-ball and
$B$ a PL
$(\ell-2)$-ball, and the strong collapse induces a retraction
$r|_A \colon A \to B$. By [Reference Rourke and Sanderson32, Ch. 3], there exist regular neighbourhoods
$U \supseteq A$ and
$V \supseteq B$ in
$\partial e$ and a map
$f \colon \partial e \to \partial e$ such that
$ f|_A = r|_A $, and
$ f|_{\partial e \setminus U} \colon \partial e \setminus U \to \partial e \setminus V $ is a PL homeomorphism. This induces a homeomorphism
\begin{equation*}
\bar{f} \colon \partial e / \!\sim\ \longrightarrow \partial e, \quad x \sim r(x)\ \text{for } x \in A.
\end{equation*}If
$ \varphi \colon S^{\ell -1} \to \partial e $ is the original attaching map of
$e$, then the modified attaching map is given by
\begin{equation*}
\tilde \varphi := \bar f^{-1} \circ \varphi \colon S^{\ell-1} \longrightarrow \partial e / \sim \subseteq Z^{(\ell-1)}.
\end{equation*}Therefore, the cell
$ \tilde{e}$ is attached regularly, and inherits a combinatorial CW-structure. Define
$q(e)= \tilde e$.
The general case follows by induction on the number of elementary strong collapses in the sequence
\begin{equation*}
K \smallsetminus w = K_0 {\searrow \searrow} K_1 {\searrow \searrow} \cdots {\searrow \searrow} K_n = L.
\end{equation*} At each step, the same argument applies to the retraction 
$ K_i \to K_{i+1} $, ensuring that the regularity and combinatorial structure are preserved. Since 
$w$ is not removed in the process, the identification maps never collapse an entire boundary sphere to a point.
Thus, 
$Z$ is a regular combinatorial CW-complex homotopy equivalent to 
$K$. The fact that this is an 
$(N+1)$-deformation follows from [Reference Fernández16, Prop. 1.3].
The previous result generalizes to the case where 
$K_0 {\searrow \searrow} L_0$ and 
$K_0$ is obtained from a simplicial complex 
$K$ by successively removing vertices (together with their open stars). In this case, 
$K_0$ is a full subcomplex of 
$K$, meaning that every simplex of 
$K$ whose vertices all belong to 
$V(K_0)$ is itself a simplex in 
$K_0$.
Theorem 3.4 (Strong internal collapse)
Let 
$K$ be a simplicial complex of dimension 
$N$, and let 
$K_0 \subseteq K$ be a full subcomplex. Suppose 
$K_0$ strong collapses to a subcomplex 
$L_0$. Then 
$K$ is 
$(N+1)$-homotopy equivalent to a combinatorial regular CW-complex 
$L$ obtained from 
$L_0$ by attaching one 
$k$-cell for each 
$k$-simplex in 
$K \smallsetminus K_0$.
Proof. Follows by induction on the vertices in 
$V(K)\smallsetminus V(K_0)$, applying Theorem 3.3 at each step.
Under the assumptions of Theorem 3.4, we say that there is a strong internal collapse from 
$K$ to 
$L$.
Let 
$K$ be a finite simplicial complex, and let 
$g \colon V(K) \to \mathbb{R}$ be a real-valued function on its vertex set. The function 
$g$ induces a filtration of 
$K$ by sublevel subcomplexes 
$\{K_\alpha\}_ {\alpha\in {\mathbb R}}$, where each 
$K_\alpha$ is the subcomplex spanned by the vertices in the sublevel set 
$g^{-1}\big((-\infty, \alpha]\big)$.
Definition 3.5. Let 
$g \colon V(K) \to \mathbb{R}$ be a real-valued function, and let 
$v \in V(K)$ be a vertex. The descending open star of 
$v$, denoted 
${\mathrm{st}}^\downarrow(v, K)$, is the open star of 
$v$ in the subcomplex 
$K_{g(v)}$. Similarly, the descending link of 
$v$, denoted 
${\mathrm{lk}}^\downarrow(v, K)$, is the link of 
$v$ in 
$K_{g(v)}$. We say that 
$v$ is descending dominated if it is dominated in 
$K_{g(v)}$ by a vertex 
$a$ with 
$g(a) \lt g(v)$. Otherwise, 
$v$ is called a strong critical vertex.
We have an analogous version of the classical discrete Morse Lemma 2.4 in this setting.
Lemma 3.6. Let 
$K$ be a simplicial complex and 
$g \colon V(K) \to \mathbb{R}$ a real-valued function.
A. If
$g^{-1}\big((\alpha, \beta]\big)$ contains no strong critical vertices, then
$K_\beta {\searrow \searrow} K_\alpha$.B. If
$g^{-1}\big((\alpha, \beta]\big)$ contains a single strong critical vertex
$w$, then
$K_\beta$ is homotopy equivalent to a CW-complex of the form
\begin{equation*}
K_\alpha \cup \bigcup_i e_i,
\end{equation*}where the cells
$e_i$ are in one-to-one correspondence with the simplices in
${\mathrm{st}}^{\downarrow}(w, K)$. This correspondence preserves dimensions, and the attaching maps of the cells are determined as in Theorem 3.3, resulting in a regular CW-complex structure.
Proof. The function 
$g$ induces a total order 
$\{v_1, v_2, \dots, v_n\}$ on 
$V(K)$ such that 
$g(v_i) \leq g(v_j)$ whenever 
$i \lt j$. For each 
$i$, let 
$K_i$ be the subcomplex of 
$K$ generated by all simplices whose vertices lie in 
$\{v_1, v_2, \dots, v_i\}$.
For part A., assume that 
$g^{-1}\big((\alpha, \beta]\big)$ contains no strong critical vertices. Then for each 
$v_i \in g^{-1}\big((\alpha, \beta]\big)$, the descending link 
${\mathrm{lk}}^{\downarrow}(v_i, K) = {\mathrm{lk}}(v_i, K_{g(v_i)})$ is a simplicial cone with apex 
$a_i$, where 
$g(a_i) \lt g(v_i)$. Since 
$K_i \subseteq K_{g(v_i)}$, we have
\begin{equation*}
{\mathrm{lk}}(v_i, K_i) = {\mathrm{lk}}(v_i, K_{g(v_i)}) \smallsetminus \{\sigma \in {\mathrm{lk}}(v_i, K_{g(v_i)}) \colon \sigma \ni v_j \text{with } j \gt i \text{and } g(v_j) = g(v_i)\}.
\end{equation*} This subcomplex remains a cone with apex 
$a_i$. Therefore, 
$v_i$ is dominated in 
$K_i$ by 
$a_i$, and 
$K_i {\searrow\searrow^e } K_i \smallsetminus v_i = K_{i-1}$. Applying this inductively, we obtain a sequence of strong collapses from 
$K_\beta$ to 
$K_\alpha$.
Part B. follows from part A. and Theorem 3.4.
Building on Theorem 3.4 and Lemma 3.6, we establish the following result, which formalize the relationship between internal strong collapses, regular CW-complexes, and discrete Morse theory.
Theorem 3.7 (Strong discrete Morse theory)
Let 
$K$ be a finite simplicial complex, and let 
$g \colon V(K) \to \mathbb{R}$ be a real-valued function. Then, 
$K$ is homotopy equivalent to a regular CW-complex 
${\mathrm{core}}_g(K)$, whose cells are in one-to-one correspondence with the simplices in the descending open star of the strong critical vertices of 
$g$.
Proof. Subdivide the image of 
$g$ into subintervals, each satisfying the conditions of Lemma 3.6 A. or B., and iteratively apply the corresponding deformations to 
$K$. The cells in the resulting CW-complex correspond to the simplices in 
$\{{\mathrm{st}}^\downarrow(w, K) \colon w \text{is a critical vertex in } K\}$.
We denote by 
${\mathrm{core}}_g(K)$ the regular CW-complex obtained from the critical simplices of 
$g \colon V(K) \to \mathbb{R}$ in Theorem 3.7, and refer to it as the strong internal core of 
$K$ associated to 
$g$. Notice that the strong internal core depends on a choice of dominating vertices for the strong internal collapses, but we omit this information unless necessary.
Proposition 3.8. (Connection to strong collapses)
If 
$K {\searrow \searrow} L$, then there exists a function 
$g \colon V(K) \to \mathbb{R}$ such that 
${\mathrm{core}}_g(K) = L$.
Proof. Let 
$v_1, v_2, \dots, v_n \in V(K)$ be the sequence of dominated vertices corresponding to a strong collapse from 
$K$ to 
$L$, i.e., define 
$K_n = K$ and 
$K_{i-1} = K_i \smallsetminus v_i$, with each 
$K_i {\searrow\searrow^e } K_{i-1}$ and 
$K_0 = L$. Define a function 
$g \colon V(K) \to \mathbb{R}$ by
\begin{equation*}
g(v) =
\begin{cases}
i & \text{if } v = v_i, \\
0 & \text{if } v \in V(L).
\end{cases}
\end{equation*} We claim that the strong internal core, 
${\mathrm{core}}_g(K)$, coincides with 
$L$. By construction, each 
$v_i$ is dominated in 
$K_i$ by some vertex 
$a_i \in K_i$. Since 
$v_i$ is removed at stage 
$i$, and 
$a_i \in K_j$ for some 
$j \lt i$, it follows that 
$g(a_i) \lt g(v_i)$. Therefore, 
$v_i$ is descending dominated. On the other hand, any vertex 
$v \in V(L)$ satisfies 
$g(v) = 0$, and hence 
$g^{-1}((-\infty, g(v))) = \varnothing$. Thus, 
$v$ cannot be descending dominated and is a strong critical vertex.
Hence, the only strong critical vertices of 
$g$ are those in 
$L$, and the strong internal core, 
${\mathrm{core}}_g(K)$, coincides with 
$L$.
Theorem 3.9 (Connection to discrete Morse theory)
Let 
$K$ be a finite simplicial complex and let 
$g\colon V(K) \to {\mathbb R}$ be a real-valued map. Then, there exists a discrete Morse function 
$f\colon K\to {\mathbb R}$ on 
$K$ such that its critical simplices are the simplices in 
$\{{\mathrm{st}}^\downarrow(w, K) : w \text{is a strong critical vertex of } g\}$. Moreover, 
${\mathrm{core}}_{g}(K)\cong {\mathrm{core}}_{f}(K)$, that is the strong internal core associated to 
$g$ is precisely the internal core associated to 
$f$.
Proof. Let 
$C = \{{\mathrm{st}}^\downarrow(w, K) : w \text{is a strong critical vertex of } g\}\subseteq K$. Given the correspondence between discrete Morse functions and acyclic matchings [Reference Chari14], we will construct an acyclic matching 
$M$ with critical simplices 
$C$ as follows. For each simplex 
$\sigma \in K$ containing descending dominated vertices, let
\begin{equation*}
v_\sigma = \arg \max\{g(v) \colon v \in \sigma \text{is a descending dominated vertex}\},
\end{equation*} and let 
$a_\sigma$ denote the vertex dominating 
$v_\sigma$. The pairing 
$M$ is then defined as follows: if 
$a_\sigma \in \sigma$, we include the pair 
$(\sigma \setminus \{a_\sigma\}, \sigma)$ in 
$M$; otherwise, we include the pair 
$(\sigma, \sigma \cup \{a_\sigma\})$ in 
$M$.
To verify that 
$M$ is a matching, assume for contradiction that a simplex in 
$K$ is matched to more than one simplex. Without loss of generality, suppose 
$(\sigma, \{a\}\cup \sigma) \in M$ with 
$v_\sigma$ the associated descending dominated vertex. If there exists another pair 
$(\{a\}\cup\sigma, \{a',a\}\cup\sigma) \in M$, then 
$a'$ dominates a vertex 
$v' \in \sigma$. Since 
$v'$ must also satisfy 
$v' = \arg\max\{g(v) \colon v \in \sigma$ is descending dominated
$\}$ this contradicts the uniqueness of 
$v_\sigma$. Alternatively, if there exists a pair 
$(\sigma', \{a\}\cup\sigma) \in M$, then 
$a\sigma = \{a'\}\cup\sigma'$ implies 
$\sigma = \{a'\}\cup\tau$ and 
$\sigma' = \{a\}\cup\tau$ for some simplex 
$\tau$. This forces 
$\tau$ to contain two distinct dominated vertices, 
$v_\sigma$ and 
$v'$, each maximizing 
$g(v)$, which is again a contradiction. Therefore, 
$M$ is a valid matching.
To establish that 
$M$ is acyclic, consider any pair 
$(\sigma, \{a\}\cup\sigma) \in M$. For any 
$\tau \succ \sigma$, we claim that 
$(\tau \smallsetminus \{a'\}, \tau) \notin M$ for any 
$a' \neq a$. Since 
$\tau \succ \sigma$, the simplex 
$\tau$ contains 
$v_\sigma$. If 
$v_\sigma$ also satisfies 
$v_\sigma = \arg \max\{g(v) \colon v \in \tau \text{is a descending dominated vertex}\}$, then 
$(\tau, \{a\}\cup\tau) \in M$, as 
$a$ dominates 
$v_\sigma$. Alternatively, if there exists another dominated vertex 
$w \in \tau$ such that 
$w \gt v_\sigma$, then 
$(\tau, \{a_w\}\cup \tau) \in M$, where 
$a_w$ dominates 
$w$. In either case, 
$(\tau \smallsetminus \{a'\}, \tau) \notin M$ for any 
$a' \neq a$, ensuring that 
$M$ is acyclic. This completes the proof.
Remark 3.10 (Connection to Bestvina–Brady Morse theory)
Let 
$K$ be a finite simplicial complex. A Bestvina–Brady Morse function 
$h \colon |K| \to \mathbb{R}$ is given by an injective function 
$g \colon V(K) \to \mathbb{R}$ that extends linearly over simplices. In this setting, the critical points of 
$h$ are precisely all the vertices of 
$K$, and the changes in homotopy type of sublevel sets occur at critical levels by attaching cones over the descending links of the corresponding vertices. In our framework, we also consider a vertex function 
$g$, but further classify each vertex as either strong critical or descending dominated, depending on whether its descending link forms a simplicial cone. This distinction not only describes the local homotopy behaviour (descending dominated vertices have coned descending links and, hence, do not change the homotopy type of sublevel complexes), but crucially allows a global, purely combinatorial reconstruction of the reduced complex 
${\mathrm{core}}_g(K)$. This leads to an efficient reduction, as changes to the homotopy type are introduced only by the subset of strong critical vertices, while the remaining dominated vertices are systematically collapsed.
Forman’s discrete Morse theory fits within the Bestvina–Brady framework, as observed by Zaremsky [Reference Matthew24], and can also be interpreted through the lens of strong discrete Morse theory. Specifically, any injective discrete Morse function 
$f \colon K \to \mathbb{R}$ induces a Bestvina–Brady Morse function 
$g \colon V(K') \to \mathbb{R}$ such that critical simplices of 
$f$ correspond to vertices in 
$K'$ whose descending links are barycentric subdivisions of the boundaries of those simplices — and hence homeomorphic to spheres. Each matched pair 
$(\sigma, \tau)$, with 
$\sigma \prec \tau$ and 
$f(\sigma) \gt f(\tau)$, satisfies that 
$\sigma$ is descending dominated by 
$\tau$, and 
${\mathrm{lk}}^\downarrow(\tau, K')$ is a topological cone on the unique vertex 
$v \in \tau \setminus \sigma$ (though not necessarily a simplicial one). This suggests a natural extension of our theory to cases where strong critical vertices have descending links that are topological cones.
4. The construction of the internal core
Given a CW-complex 
$K$, its face poset 
${\mathcal X}(K)$ encodes the incidence relations among its cells: 
$e \leq e'$ in 
${\mathcal X}(K)$ if 
$\overline{e} \subseteq \overline{e'}$. While this poset does not determine the homotopy type of 
$K$ in general, in the case of regular CW-complexes it serves as a complete combinatorial model: the order complex of 
${\mathcal X}(K)$, denoted 
${\mathcal K}({\mathcal X}(K))$, is homotopy equivalent to 
$K$ (see [Reference Björner11]).
Let 
$X$ be a finite poset. An matching on 
$X$ is a collection 
$M$ of disjoint pairs 
$\{x, y\} \subseteq X$ such that the quotient set 
$X/_\sim$, where 
$x \sim y$ if 
$\{x, y\} \in M$, admits a partial order induced by the original order on 
$X$ (the relation 
$[x]\leq [y]\in X/_\sim$ if 
$x\leq y$ in 
$X$ is antisymmetric).
Discrete Morse functions on a simplicial complex 
$K$ are in bijection with acyclic matchings on 
${\mathcal X}(K)$, where the unmatched elements correspond to the critical simplices [Reference Chari14]. Given an acyclic matching 
$M$ on 
${\mathcal X}(K)$, one can construct auxiliary posets that reflect the structure of the Morse reduced CW-complex. Inspired by Nanda’s work on discrete Morse theory and localization of categories [Reference Nanda27], we introduce the following definitions.
Definition 4.1. Let 
$K$ be a simplicial complex, and let 
$M$ be an acyclic matching on 
${\mathcal X}(K)$. The localization poset 
${\mathrm{Loc}}_M(K)$ is the poset obtained by identifying matched simplices in 
${\mathcal X}(K)$. The critical poset 
${\mathrm{Crit}}_M(K)$ is the subposet of 
${\mathrm{Loc}}_M(K)$ consisting of equivalence classes of unmatched (i.e., critical) simplices.
In general, neither 
${\mathrm{Crit}}_M(K)$ nor 
${\mathrm{Loc}}_M(K)$ determine the homotopy type of 
$K$, even when 
$K$ is regular or simplicial (see Example 4.3). However, when 
$M$ arises from internal strong collapses, Theorem 3.9 implies that 
${\mathrm{Crit}}_M(K)$ is a finite model of 
$K$.
Corollary 4.2. Let 
$K$ be a simplicial complex and let 
$g \colon V(K) \to \mathbb{R}$ be a real-valued function. Then, there exists an acyclic matching 
$M_g$ on 
${\mathcal X}(K)$ such that the critical poset 
${\mathrm{Crit}}_{M_g}(K)$ is the face poset of 
${\mathrm{core}}_g(K)$. In particular, 
${\mathrm{Crit}}_{M_g}(K)$ is a finite model of 
$K$.
For details on the algorithmic construction of the critical poset, see Appendix A, Algorithm A1.
Example 4.3. Let 
$K$ be the boundary of the 3-simplex with vertices labelled from 1 to 4 (see Figure 3). Consider the acyclic matching 
$M = \big\{\{(0), (0,1)\}, \{(1), (1,2)\}, \{(2), (2,3)\}, \{(0, 2), (0,2,3)\},\\ \{(0, 3), (0,2,3)\}\big\}$, depicted in Figure 4. The posets 
${\mathrm{Loc}}_M(K)$ and 
${\mathrm{Crit}}_M(K)$ are contractible, and do not reflect the homotopy type of 
$K\simeq S^2$.
On the other hand, consider the function 
$g\colon V(K)\to {\mathbb R}$ on the vertices depicted in Figure 3. For the associated acyclic matching 
$M_g$, the critical poset 
${\mathrm{Crit}}_{M_g}(K)$ recovers the homotopy type of 
$K$, and it is the face poset of the strong internal core (see Figure 5).
Remark 4.4. Consider the order-preserving maps
\begin{equation*}
{\mathcal Q} \colon {\mathcal X}(K) \to {\mathrm{Loc}}_M(K) \quad \text{and} \quad {\mathcal J} \colon {\mathrm{Crit}}_M(K) \to {\mathrm{Loc}}_M(K),
\end{equation*} where 
$ {\mathcal Q} $ denotes the quotient map and 
$ {\mathcal J} $ the inclusion map. In future work, we will establish general conditions on the acyclic matching 
$M$ under which these maps induce homotopy equivalences at the level of simplicial complexes. In particular, we will show that when 
$M$ is induced by internal strong collapses, both 
${\mathcal Q}$ and 
${\mathcal J}$ induce homotopy equivalences.
Figure 3. The boundary of a 3-simplex, 
$K$, endowed with a function 
$ g \colon V(K) \to \mathbb{R} $ on vertices. By abuse of notation, and due to the injectivity of 
$ g $, we identify each vertex with its image under 
$ g $.
Figure 4. Left: The face poset 
${\mathcal X}(K)$, for 
$K$ the boundary of a 3-smplex, with an acyclic matching 
$M$ depicted in red. Centre: The localization poset 
${\mathrm{Loc}}_M(K)$. Right: The critical poset 
${\mathrm{Crit}}_M(K)$ (c.f. Fig 3).
Figure 5. Left: The strong internal core associated to the map 
$g\colon V(K)\to {\mathbb R}$ on vertices (Fig. 3). Centre: The face poset 
${\mathcal X}(K)$, with the acyclic matching 
$M_g$ induced by internal strong collapses, in red. Right: The critical poset 
${\mathrm{Crit}}_{M_g}(K)$. Here, 
${\mathrm{core}}_g(K)$ has two 0-cells, three 1-cells and three 2-cells.
5. Algorithmic simplification of simplicial complexes
Let 
$K$ be a simplicial complex of dimension 
$N$. We summarize below the different core notions associated to 
$K$:
• Strong core: A subcomplex
$L \subseteq K$ such that
$K {\searrow \searrow} L$. The minimal strong core (i.e. with no dominated vertices) is unique up to isomorphism.• Weak core: A subcomplex
$L \subseteq K$ such that
$K {\searrow } L$. A minimal weak core (i.e. with no free faces) is not necessarily unique.• Internal core: Given a discrete Morse function
$f \colon K \to \mathbb{R}$, the internal core
${\mathrm{core}}_f(K)$ is the CW-complex obtained by performing the sequence of internal collapses determined by
$f$. It satisfies
$K \diagup\!\!\!\!\searrow^{^{N+1}} {\mathrm{core}}_f(K)$. The internal core is not necessarily regular.• Strong internal core: Given a function
$g \colon V(K) \to \mathbb{R}$ defined on the vertices of
$K$, the strong internal core,
${\mathrm{core}}_g(K)$, is obtained by the sequence of internal strong collapses guided by
$g$. It satisfies
$K \diagup\!\!\!\searrow^{^{N+1}} {\mathrm{core}}_g(K)$, and the resulting space is a regular CW-complex.
The diagram below shows implication relations among the core constructions.
For any method of reduction of simplicial complexes, computing the associated core requires the choice of an ordered sequence of collapses. While the minimal strong core is unique (up to isomorphism) regardless of the sequence of strong collapses, a minimal weak core does depend on the chosen sequence. Similarly, the internal core of a simplicial complex depends on the discrete Morse function. Note that (strong) discrete Morse theory can be seen as a systematic procedure for performing a sequence of (strong) reductions. These reductions may consist of (strong) internal collapses, or, when no free face (resp. dominated vertex) is available, the removal of a maximal simplex (resp. vertex). To address the dependence on the choice of the reduction sequence, one approach is to explore all possible sequences. However, this can be computationally prohibitive due to the exponential growth in the number of options. Alternatively, random reductions — where reductions are chosen randomly among the available options at each step — provide an efficient strategy to deal with this dependence.
To compute the minimal strong internal core, we iteratively apply a greedy algorithm that performs randomly chosen internal strong collapses whenever a dominated vertex is available. If no dominated vertex exists, we randomly select a vertex to be removed (see Appendix A, Algorithm A2 for further details). As part of this procedure, we construct the acyclic matching associated to the internal strong collapses as stated in Theorem 3.9. Notice that this algorithm can also be applied to study 
$(N+1)$-deformations, as the strong internal core 
$(N+1)$-deforms to the original complex. A similar procedure can be applied for the randomized computation of a minimal weak core of a simplicial complex.
In general, there is no combinatorial description of the internal core determined by a general discrete Morse function. Benedetti and Lutz [Reference Benedetti and Lutz6] performed a computational analysis of the topology of simplicial complexes using randomized discrete Morse theory, studying the number of critical cells arising from random discrete Morse functions.
We analyse the examples from the Library of Triangulations [Reference Benedetti and Lutz7] and compare the results of minimals weak core, strong core, and strong internal core, cases where the reduced complex can be completely reconstructed. We perform 10 iterations of the computation of random simple and strong internal cores for the simplicial complexes listed in Table 1, and 100 iterations for those in Table 2. Additionally, we implement a combined reduction strategy, where we first compute a random minimal weak core of the original complex and subsequently compute a random strong internal core of the resulting complex. Tables 1 and 2 present the mean sizes of the different cores and the corresponding computation times. The experiments were conducted on a MacBook Pro with an Apple M3 Pro chip, 12-core CPU, 18-core GPU, and 18 GB of unified memory. The implementation was developed in SageMath [34], and the code is available at https://github.com/ximenafernandez/Strong-Morse-Theory.
We observe that in cases where there are neither dominated vertices nor free faces, internal strong collapses allow significant reductions in the size of the complex, with reductions of 30% to 40% in instances as BH_3, BH_4, Bernadette_Sphere, and non_PL and 50% to 60% in the large examples trefoil_bsd and Hom_C5_K4. Notably, in many of these cases, the vector of critical simplices in a (classical) discrete Morse function does not fully determine the homotopy type. For example, the 18-vertex non-PL triangulation of the 5-dimensional sphere 
$S^5$ (non_PL) admits 
$(1, 0, 0, 2, 2, 1)$ as its smallest discrete Morse vector (see [Reference Benedetti and Lutz6]). Although this cellular decomposition is highly efficient in its cell count, this information alone is insufficient to reconstruct the reduced CW-complex and verify its homotopy type. By contrast, our strong Morse approach yields a regular CW-complex whose structure is fully determined, while still reducing the number of simplices in this example from 2608 to an average of 1690.56, a size reduction of 35% (see Table 2).
In several large cases with available simple collapses, the strong Morse theory approach yields a more efficient model, significantly reducing the original complex size by around 80% and computation times by over 90% compared to simple collapses in examples such as knot and bing. For the knot complex, for instance, applying simple collapses reduces the 6203 simplices to an average of 1946, while the strong internal core method reduces it even further to an average of 1184 simplices. Crucially, the latter reduction is achieved faster, taking an average of only 56 seconds, compared to the 2088 seconds (about 35 minutes) required for simple collapses (see Table 1).
On the other hand, a few cases exhibit simplicial complexes with small weak cores but large strong internal cores (on average). Examples include B_3_9_18, trefoil_arc, rudin, and triple_trefoil_arc. In these scenarios, the combined strategy emerges as the optimal choice: preprocessing the simplicial complex by computing its minimal weak core before determining the strong internal core.
Acknowledgements
The author thanks Robert Green for his enthusiasm for posets and for pointing out the earlier work of Nicholas Scoville on strong Morse theory during his visit to Oxford. This work was inspired by fruitful conversations with him at the Mathematical Institute. The author is also grateful to Vidit Nanda for engaging with early versions of this project and for suggesting the connection with the localization of categories, to Gabriel Minian for useful comments on the connection with Bestvina–Brady Morse theory, and to Eugenio Borghini for valuable discussions. This work was partially supported by Leverhulme Trust Research Project Grant RPG-2023-144 and the UK Centre for Topological Data Analysis EPSRC grant EP/R018472/1.
Appendix A. Algorithms
This appendix contains the pseudocode of the main algorithms used in the construction and computation of the critical poset associated with a strong internal core. An implementation in SageMath [34] can be found at https://github.com/ximenafernandez/Strong-Morse-Theory.
Algorithm 1 The critical poset
Remark A.1. Let 
$K$ be a finite simplicial complex with 
$V$ vertices, 
$F$ simplices, and dimension 
$N$. Algorithm 2 compute the strong internal core by repeatedly identifying descending dominated vertices and performing internal strong collapses. A domination test for a vertex 
$v$ inspects its (descending) open star and thus costs 
$O(S_v)$ time, where 
$S_v$ is the number of simplices containing 
$v$. Since each 
$k$-simplex has 
$k{+}1\le N{+}1$ vertices,
\begin{equation*}
\sum_{v\in V(K)} S_v = O(N\,F).
\end{equation*} Since every simplex belongs to at most 
$N+1$ vertex stars, the cumulative number of simplex inspections during the reduction is bounded by 
$O(N\,F)$. The overall runtime depends on the implementation. A naive approach that recomputes all domination tests after each collapse would have a worst-case complexity of 
$O(V\,N\,F)$. However, in practice, only the neighbourhood of the removed vertex needs updating. An efficient implementation using adjacency lists and a priority queue of candidate vertices to be tested yields an overall running time of
\begin{equation*}
O(N\,F + V\log V).
\end{equation*} For a fixed, small dimension 
$N$, this complexity is essentially linear in the number of simplices.
In contrast, classical discrete Morse algorithms construct an acyclic matching on the face poset 
${\mathcal X}(K)$. A basic implementation must inspect all cover relations between comparable simplices when iteratively attempting to form pairs, and test global acyclicity on the current directed graph after each addition. This may require 
$O(N^2\,F^2)$ time in the worst case. With optimized cycle–detection and data structures, the cost could be reduced to
\begin{equation*}O(N\,F\log F).\end{equation*}The strong-internal-collapse approach avoids global searches as reductions depend only on local vertex–link tests, leading to lower asymptotic complexity.
Algorithm 2 A random strong internal core
Open access
