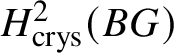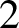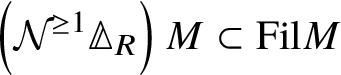1 Introduction
Let p be a prime which will be fixed throughout. Our beginning point is the classification of finite commutative group schemes of p-power rank over a perfect field k of characteristic p in terms of contravariant Dieudonné theory. This is achieved by defining an algebraic invariant associated to any given finite group scheme G (assumed to be commutative and of p-power rank, unless otherwise mentioned), which is called the Dieudonné module of G and will be denoted by 
$M(G)$. We will recall the classical construction of 
$M(G)$ in Section 3. The basic object of interest is the Dieudonné ring 
$\mathscr {D}_k$, which is an associative algebra over the ring of Witt vectors 
$W(k)$. The Dieudonné functor M which takes G to 
$M(G)$ transforms the study of finite group schemes over k to the study of semilinear algebraic objects. More precisely, we have the following:
Theorem 1.1 Dieudonné
The Dieudonné functor M induces an antiequivalence between the category of finite commutative group schemes over k of p-power rank and left 
$\mathscr {D}_k$-modules with finite 
$W(k)$ length.
Our primary goal in this paper is to provide a geometric construction of 
$M(G)$. In particular, we attempt to understand whether 
$M(G)$ can be constructed in terms of some cohomology theory associated to some ‘space’. Since 
$M(G)$ is a module over 
$W(k)$, it could be natural to take the naïve candidate, which is the ith crystalline cohomology of G for some i, denoted as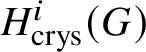 
$H^i_{\text {crys}}(G)$. However, one can see that this cannot not work for any i simply by taking discrete group schemes as input for 
$M(.)$. Moreover, any reasonable cohomology theory will suffer from exactly the same problems. The issue is that a cohomology theory will view any discrete group scheme just as a discrete space, and will be unable to detect its group structure. This suggests that we look for other spaces naturally associated to G instead of just G itself. In topology, one can get around this issue by considering the classifying space 
$BG$, as explained in Example 1.3. In category theory, the analogue of this would be to simply view a group G as a groupoid with one object and morphism set isomorphic to G. In algebraic geometry, for a group scheme G, a model of these constructions would be to consider the classifying stack 
$BG$. Our main goal is to prove the following:
Theorem 1.2. For a finite commutative group scheme G over k which is of p-power rank, the Dieudonné module 
$M(G)$ is naturally isomorphic (up to a Frobenius twist) to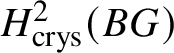 
$ H^2 _{\text {crys}}(BG)$, where 
$BG$ denotes the classifying stack of G (compare Section 3.1).
Example 1.3. We explain the topological analogue of Theorems 1.1 and 1.2. In the case where G is a finite abelian group, one can consider the classifying space 
$BG$ of G, which has the property that 
$\pi _1(BG) \simeq G$ and 
$\pi _i(BG) = 0$ for 
$i>1$. In this case, 
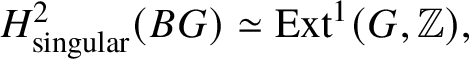$H^2_{\text {singular}}(BG) \simeq \text {Ext}^1 (G, \mathbb {Z}),$ which is noncanonically isomorphic to the group G. By using the short exact sequence 
$0 \to \mathbb {Z}\to \mathbb {Q} \to \mathbb {Q}/ \mathbb {Z}\to 0$, we obtain that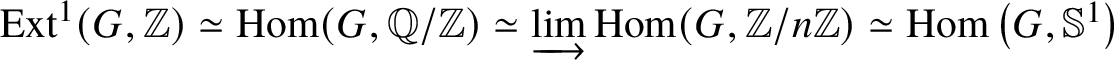 
$ \text {Ext}^1(G,\mathbb {Z}) \simeq \text {Hom}(G,\mathbb {Q}/ \mathbb {Z} ) \simeq \varinjlim \text {Hom}(G, \mathbb {Z}/n \mathbb {Z})\simeq \text {Hom}\left (G, \mathbb {S}^1\right )$. By Pontryagin duality, one obtains that sending 
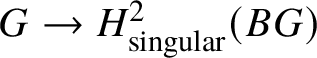$G \to H^2_{\text {singular}}(BG)$ gives an antiequivalence from the category of finite abelian groups to itself.
We also define the classifying stack 
$BG$ of a p-divisible group G and prove the following:
Theorem 1.4. Let G be a p-divisible group over k. Then 
$H^*_{\text {crys}}(BG) \simeq \text {Sym}^{*} (M(G)[-2]),$ where 
$M(G)$ denotes the Dieudonné module of G. Here 
$M(G)$ is considered to be in degree 
$2$. In particular, 
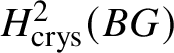$H^2_{\text {crys}}(BG)$ recovers the Dieudonné module 
$M(G)$ and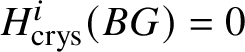 
$H^i _{\text {crys}} (BG)=0$ for odd i (compare Section 3.4).
In [Reference Scholze and WeinsteinSW14], Scholze and Weinstein defined a mixed-characteristic analogue of (covariant) Dieudonné modules for p-divisible groups over a perfectoid ring. More recently, in [Reference Anschütz and Le BrasALB19], Anschütz and Le Bras defined a mixed-characteristic analogue of contravariant Dieudonné modules over more general base rings. In Section 4.2 we briefly recall their work and the definition of the filtered prismatic Dieudonné module 
associated to a p-divisible group G as defined by them. Their main theorem is the following classification result:
Theorem 1.5 [Reference Anschütz and Le BrasALB19]
Let R be a quasiregular semiperfectoid ring. The filtered prismatic Dieudonné module functor
defines an antiequivalence between the category of p-divisible groups over R and the category of filtered prismatic Dieudonné modules over R.
Using the classifying stack 
$BG$ of a p-divisible group G, we prove the following:
Theorem 1.6. Let G be a p-divisible group over a quasiregular semiperfectoid ring R. Then the prismatic cohomology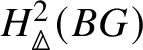 
is naturally isomorphic to the prismatic Dieudonné module 
. This isomorphism identifies the natural Frobenius on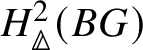 
with the endomorphism 
on 
. Further, the Nygaard filtration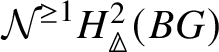 
on the prismatic cohomology of the stack 
$BG$ is isomorphic to 
(compare Section 4.2).
On the other hand, there has been some recent work involving computation of p-adic cohomology theories associated to the classifying stack of group schemes over p-adic base rings. For example, we refer to the work of Totaro [Reference TotaroTot18] and the work of Antieau, Bhatt and Mathew [Reference Antieau, Bhatt and MathewABM19]. Our results can also be viewed as some computations in this direction.
Outline of the paper
The statement of Theorem 1.2 presents the need for a theory of crystalline cohomology for stacks. This theory has already been developed by Olsson in [Reference OlssonOl07] using the lisse-étale crystalline site of an algebraic stack. In Section 2, we provide another definition of crystalline cohomology of algebraic stacks through syntomic descent, relying on the work of Fontaine and Messing [Reference Fontaine and MessingFM87]. In Proposition 2.16 we prove that the definition via syntomic descent and the definition via the lisse-étale crystalline site are equivalent.
In Section 3.1, we provide a brief review of crystalline Dieudonné theory and prove Theorem 1.2. Our proof uses a description of 
$M(G)$ obtained in the work of Berthelot, Breen and Messing [Reference Berthelot, Breen and MessingBBM82], which expresses 
$M(G)$ as a certain 
$\mathrm {Ext}$ group in the crystalline topos which is recalled in Theorem 3.8. The main ingredient of our proof of Theorem 1.2 is to obtain a suitable spectral sequence computing 
$H^*_{\text {crys}}(BG)$, which is done in Proposition 3.13. In order to obtain the spectral sequence in Proposition 3.13, we use Čech descent along the syntomic map 
$* \to BG$. In Section 3.2, we deduce the analogue of Theorem 1.2 for p-divisible groups. In Section 3.3, we provide a complete calculation of the crystalline cohomology of the classifying stack 
$B A$ of an abelian variety A. This is done in Proposition 3.28, where we prove that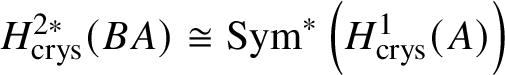 
$H^{2*}_{\text {crys}}(BA) \cong \text {Sym}^*\left (H^1_{\text {crys}}(A)\right )$ and 
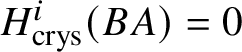$H^i_{\text {crys}}(BA) = 0$ for odd i. An analogue of this result in 
$\ell $-adic cohomology was proved by Behrend [Reference BehrendBeh03, Theorem 6.1.6]. Our proof of Proposition 3.28 uses different techniques. We rely on some explicit simplicial constructions and some computations from the theory of nonabelian derived functors. Using these calculations, in Section 3.4 we completely calculate the crystalline cohomology of 
$BG$ for a p-disivible group G.
In Section 4, we enter the mixed-characteristic situation. We begin by recalling the work of Anschütz and Le Bras and define the contravariant prismatic Dieudonné module 
for a p-divisible group G over a quasiregular semiperfectoid base ring R as an 
$\mathrm {Ext}^1$ group in the prismatic topos. This definition is compatible with the definition in [Reference Scholze and WeinsteinSW14] as proven in [Reference Anschütz and Le BrasALB19, Proposition 4.3.7]. We will then define quasisyntomic stacks and define the classifying stack 
$BG$ of G as a quasisyntomic stack in Definition 4.27. In Definition 4.13, we extend the notion of prismatic cohomology developed by Bhatt and Scholze [Reference Bhatt and ScholzeBS19] to quasisyntomic stacks via quasisyntomic descent. Then analogous to Proposition 3.16, in Proposition 4.33 we prove that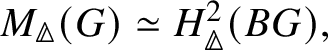 
where the latter denotes the prismatic cohomology of 
$BG$. Similar to the crystalline case, in Proposition 4.40 we obtain a complete calculation of the prismatic cohomology of the classifying stack 
$B \widehat {A}$, where 
$\widehat {A}$ is the p-adic completion of an abelian scheme A.
2 Crystalline cohomology
2.1 Crystalline cohomology for stacks
We gather some notation for this section. We fix a prime p. Let k be a perfect field of characteristic 
$p> 0$ and let 
$W(k)$ be the ring of Witt vectors of k. Let 
$\mathrm {SYNSch}_k$ denote the big Grothendieck site of schemes over k with the syntomic topology. Let 
$D (\mathrm {SYNSch}_k, W(k))$ denote the unbounded derived category of sheaves of 
$W(k)$-modules and let 
$D(W(k))$ denote the unbounded derived category of 
$W(k)$-modules (both can be equipped with natural 
$\infty $-categorical enhancements). For a given scheme 
$X \in \mathrm {SYNSch}_k$, there is a functor 
$R \Gamma (X, \cdot ):D (\mathrm {SYNSch}_k, W(k))\to D(W(k))$. Let 
$R \Gamma _{\text {crys}}(X) \in D(W(k))$ denote the crystalline cohomology of X.
Proposition 2.1. There is an object 
$R \mathcal {O}^{\text {crys}} \in D (\mathrm {SYNSch}_k, W(k))$ such that 
$R \Gamma (X, R \mathcal {O}^{\text {crys}}) \simeq R\Gamma _{\text {crys}}(X)$.
Proof. This is a formal corollary of a result of Fontaine and Messing. Using [Reference Fontaine and MessingFM87, Proposition 1.3], we get that for any n, there is a sheaf 
$\mathcal {O}^{\text {crys}}/W_n$ on 
$\mathrm {SYNSch}_k$ such that the n-truncated crystalline cohomology 
$\left (R \Gamma _{\text {crys}}/W_n\right )(X) \simeq R \Gamma (X, \mathcal {O}^{\text {crys}}/W_n)$. Now we define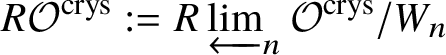 
$R\mathcal {O}^{\text {crys}}:= R \varprojlim _{n} \mathcal {O}^{\text {crys}}/W_n$. Then it follows that 
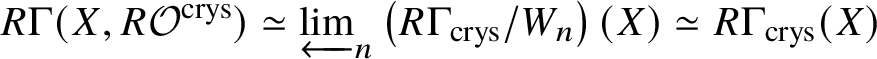$R \Gamma (X, R \mathcal {O}^{\text {crys}}) \simeq \varprojlim _{n} \left (R \Gamma _{\text {crys}}/W_n\right )(X) \simeq R \Gamma _{\text {crys}} (X)$.
Definition 2.2. Let 
$\mathscr X$ be an algebraic stack over k. Let 
$C_{\mathscr X}$ denote the category of schemes X over 
$\mathscr X$. We define the crystalline cohomology of the algebraic stack 
$\mathscr X$ as
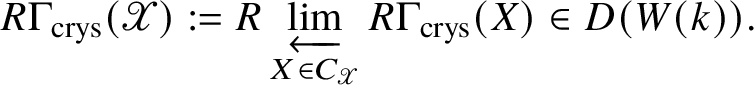$$ \begin{align*}R \Gamma_{\text{crys}} (\mathscr X):= R\varprojlim _{X \in C_{\mathscr X}} R \Gamma_{\text{crys}} (X) \in D(W(k)). \end{align*} $$Remark 2.3. Alternatively, given an algebraic stack 
$\mathscr {X}$ one can consider the slice site 
$\mathscr {X}_{\text {syn}}:=\mathrm {SYNSch}_{k_{/\mathscr {X}}}$. Then the object 
$R \mathcal {O}^{\text {crys}}$ induces an object in the derived category of sheaves of 
$W(k)$-modules on 
$\mathscr {X}_{\text {syn}}$, which by abuse of notation we again write as 
$R \mathcal {O}^{\text {crys}}$. Then 
$R \Gamma _{\text {crys}}(\mathscr {X}) \simeq R \Gamma \left (\mathscr {X}_{\text {syn}}, R\mathcal {O}^{\text {crys}}\right )$.
Remark 2.4. By Definition 2.2 and Zariski descent, we observe that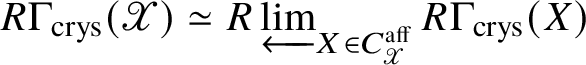 
$R \Gamma _{\text {crys}}(\mathscr {X}) \simeq R\varprojlim _{X \in C_{\mathscr X}^{\text {aff}}} R \Gamma _{\text {crys}} (X)$, where 
$C_{\mathscr {X}}^{\text {aff}}$ denotes the category of affine schemes over 
$\mathscr {X}$.
Remark 2.5. Let 
$X \to \mathscr {X}$ be a syntomic cover of the algebraic stack 
$\mathscr X$ by a scheme X. Let 
$X_\bullet $ be the simplicial algebraic space given by the Čech nerve of 
$X \to \mathscr {X}$ (so that 
$X_n$ is the n-fold fibre product of X over 
$\mathscr X$, which is, in general, only an algebraic space). Then we have that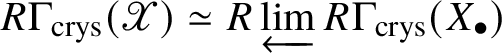 
$R \Gamma _{\text {crys}}(\mathscr {X}) \simeq R\varprojlim R \Gamma _{\text {crys}}(X_\bullet )$.
2.2 The crystalline site
In this section, we provide a brief reminder of definitions of the (big) crystalline site and the associated topos. We prefer to work with the big site because it is functorial and still computes the same cohomology groups. Our exposition roughly follows [Reference Berthelot, Breen and MessingBBM82].
We fix a prime p as before. Let k be a fixed field of characteristic p and let 
$W(k)$ be the ring of Witt vectors. Let 
$(W(k), p, \gamma )$ be the usual divided power structure on 
$W(k)$.
Definition 2.6. We denote by 
$\text {Crys}(k/ W(k))$ a category whose objects are given by the data of a k-scheme U; a 
$W(k)$-scheme T on which p is locally nilpotent; a closed 
$W(k)$-immerison 
$i : U \to T$; and a divided power structure 
$\delta $ on the ideal sheaf corresponding to the closed immersion 
$i,$ which we require to be compatible with the divided power structure 
$\gamma $. We will denote an object of 
$\text {Crys}(k/ W(k))$ by 
$(U,T, \delta )$, or simply by 
$(U,T)$ when no confusion is likely to arise. A morphism in this category is given by a pair of morphisms 
$u: U' \to U$ and 
$v: T' \to T$, where u is a k-morphism and v is a 
$W(k)$-morphism compatible with divided powers such that 
$v \circ i' = i \circ u$.
Definition 2.7. A family 
$(U_i, T_i) \to (U,T)$ of maps in 
$\text {Crys}(k/ W(k))$ is a 
$\tau $-covering if 
$U_i= U \times _T T_i$ for all i and 
$\left \{T_i \to T \right \}$ is a 
$\tau $-covering. Here 
$\tau $ could be Zariski, étale, smooth, syntomic or fppf. This equips the category 
$\text {Crys}(k/ W(k))$ with a Grothendieck topology, and we denote the site we obtain this way by 
$\text {Crys}(k/ W(k))_{\tau }$. We let 
$(k/ W(k))_{\text {Crys}, \tau }$ denote the associated topos. We define a presheaf 
$\mathcal {O}^{\text {crys}}(U,T) := \Gamma (T, \mathcal O_T)$. This is a sheaf of rings on the site 
$\text {Crys}(k/ W(k))_{\tau }$.
Definition 2.8. Let X be a scheme over k. By 
$\underline {X}$ we denote a sheaf on 
$\text {Crys}(k/ W(k))_{\tau }$ defined by 
$\underline {X}(U,T) := X(U) = \text {Hom}_{k}(U,X)$ (compare [Reference Berthelot, Breen and MessingBBM82, Section 1.1.4.5]). This is a sheaf for any 
$\tau ,$ where 
$\tau $ is from the list mentioned in Definition 2.7.
Remark 2.9. We will write 
$\tau \le \tau '$ when comparing different topologies to mean that 
$\tau '$ is finer than 
$\tau $.
Proposition 2.10. Let G be an abelian sheaf on 
$\text {Crys}(k/ W(k))_{\tau '}$. Then
$$ \begin{align*} \mathrm{RHom}_{\text{Crys}(k/ W(k))_{\tau}}(G, \mathcal O^{\text{crys}}) \simeq \mathrm{RHom}_{\text{Crys}(k/ W(k))_{\tau'}}(G, \mathcal O^{\text{crys}}) \end{align*} $$for 
$\tau \le \tau '$.
Proof. This is [Reference Berthelot, Breen and MessingBBM82, Proposition 1.3.6]. The proof relies on [Reference Berthelot, Breen and MessingBBM82, Proposition 1.1.19].
Proposition 2.11. Let X be a scheme over k. Then
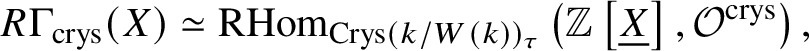$$ \begin{align*} R\Gamma_{\text{crys}}(X) \simeq \mathrm{RHom}_{\text{Crys}(k/ W(k))_{\tau}}\left(\mathbb Z \left[\underline{X}\right], \mathcal O^{\text{crys}}\right), \end{align*} $$where one can choose any topology 
$\tau $ from the list mentioned in Definition 2.7. Here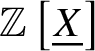 
$\mathbb Z\left [\underline {X}\right ] $ denotes the ‘free abelian group’ on 
$\underline {X}$ in the topos 
$(k/ W(k))_{\text{Crys}, \tau }$.
Proof. When 
$\tau $ is a Zariski topology, this follows from [Reference Berthelot, Breen and MessingBBM82, Proposition 1.3.4] and the definition of crystalline cohomology. The rest follows from Proposition 2.10.
Remark 2.12. Therefore, we see that it does not matter which topology 
$\tau $ we choose while computing crystalline cohomology. We will often choose 
$\tau =$ Zariski, and in this case we will omit 
$\tau $ from the notation and write the relevant site as 
$\text {Crys}(k/ W(k))$ and the topos as 
$(k/ W(k))_{\text {Crys}}$.
Remark 2.13. One can also define ‘truncated crystalline sites’ by replacing 
$W(k)$ by 
$W_n(k)$ in Definitions 2.6 and 2.7 for each 
$n \ge 1$. We denote the corresponding site (equipped with the Zariski topology for simplicity) by 
$\text {Crys}(k/W_n(k))$ and the associated topos by 
$(k/W_n(k))_{\text {Crys}}$. This has a sheaf of rings 
$\mathcal {O}^{\text {crys}}$ defined in a way similar to Definition 2.7. Analogous to Proposition 2.11, one has that for a scheme X over k,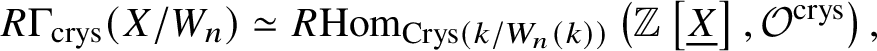 
$R \Gamma _{\text {crys}}(X/W_n) \simeq R\mathrm {Hom}_{\text {Crys}\left (k/W_n(k)\right )}\left (\mathbb {Z}\left [\underline {X}\right ], \mathcal O^{\text {crys}}\right ),$ where 
$\underline {X}$ is the sheaf on 
$\text {Crys}(k/W_n(k))$ defined in a way similar to Definition 2.8.
Now we provide a different definition of the crystalline cohomology of an algebraic stack, following [Reference OlssonOl07, Section 2.7.1]. Then we will prove that this definition is equivalent to Definition 2.2.
Definition 2.14. Let 
$\mathscr {X}$ be an algebraic stack over k. We define the lisse-étale crystalline site of 
$\mathscr X$ first as the category 
$\text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}{\rm t}}$ whose objects are the data of a k-scheme U with a smooth map 
$U \to \mathscr {X}$ over k; a 
$W(k)$-scheme T on which p is locally nilpotent; a closed 
$W(k)$-immersion 
$i: U \to T$; and a divided power structure 
$\delta $ on the ideal sheaf corresponding to the closed immersion i, which we require to be compatible with 
$(W(k), p, \gamma )$. We will denote an object of 
$\text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}{\rm t}}$ by 
$(U,T, \delta )$, or simply by 
$(U,T)$ when no confusion is likely to arise. The morphisms of this category is defined in the obvious way. A family 
$(U_i, T_i) \to (U,T)$ of maps in 
$\text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}{\rm t}}$ is a covering if 
$U_i = U \times _T T_i$ for all i and 
$\left \{T_i \to T \right \}$ is an étale covering. This equips 
$\text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}{\rm t}}$ with a Grothendieck topology, and the resulting site is called the lisse étale crystalline site. Let 
$\mathcal {O}^{\text {crys}}(U,T):= \Gamma (T, \mathcal O _T)$ be a sheaf of rings on 
$\text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}{\rm t}}$.
Definition 2.15. We define 
$R \Gamma _{\text{lis-}\acute{\rm e}\text{t-crys}} (\mathscr {X}):= R \Gamma (\text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}{\rm t}}, \mathcal {O}^{\text {crys}})$.
Proposition 2.16. 
$R\Gamma _{\text{lis-}\acute{\rm e}\text{t-crys}} (\mathscr {X}) \simeq R \Gamma _{\text {crys}} (\mathscr X)$ – that is, Definition 2.15 – is consistent with Definition 2.2.
Proof. We break down the proof into a few steps.
Step 1. First we fix some notations for the proof. We let 
$\text {Crys}(\mathscr {X})_{\acute{\rm e}{\rm t}}$ denote the big variant of the site in Definition 2.14, where we remove the hypothesis that for a pair 
$(U,T)$ the map 
$U \to \mathscr {X}$ must be smooth, and the covers are still given by étale covers. Sending 
$(U,T) \to \Gamma (T, \mathcal {O}_T)$ defines a sheaf of rings on both of these sites, which we will denote by 
$\mathcal {O}^{\text {crys}}$ in both cases when no confusion is likely to occur. Let 
$\text {Crys}(\mathscr {X})_{\text {{syn}}}$ denote the variant of 
$\text {Crys}(\mathscr {X})_{\acute{\rm e}{\rm t}}$ with the same underlying category, but now the covers are given by syntomic covers. Lastly, we denote the big syntomic site of 
$\mathscr {X}$ by 
$\mathscr X_{\text {syn}}$, which is the full subcategory of schemes over 
$\mathscr X$, and the topology is given by syntomic coverings.
Step 2. In this step, we show that crystalline cohomology can be computed in the big site 
$\text {Crys}(\mathscr {X})_{\acute{\rm e}{\rm t}}$. We have an inclusion functor
$$ \begin{align*} \text{Crys}(\mathscr{X})_{\text{lis-}\acute{\rm e}{\rm t}} \to \text{Crys}(\mathscr{X})_{\acute{\rm e}\text{t}}, \end{align*} $$which is continuous and cocontinuous and therefore gives a map of topoi
$$ \begin{align*} i:\text{ShvCrys}(\mathscr{X})_{\text{lis-}\acute{\rm e}{\rm t}} \to \text{ShvCrys}(\mathscr{X})_{\acute{\rm e}\text{t}}. \end{align*} $$We want to prove that there is a natural isomorphism 
$R \Gamma _{\text {lis-}\acute{\rm e}{\rm t}}\left (\mathscr {X},i^{-1} \mathcal {O}^{\text {crys}}\right ) \simeq R \Gamma _{\acute{\rm e}\text{t}}(\mathscr {X}, \mathcal {O}^{\text {crys}})$. Thus, it is enough to prove that 
$i^{-1}$ has a left adjoint 
$i_!$ which is exact. Following the method of proof in [SP, Tag 07IJ], it is enough to show that 
$i_! * = *$, where 
$*$ denotes the final object.
Let 
$Y \to \mathscr {X}$ be a smooth cover of 
$\mathscr {X}$ by a scheme Y. First we prove that for any given object 
$(U,T) \in \text {Crys}(\mathscr {X})_{\acute{\rm e}{\rm t}}$, there exists a cover 
$\left \{ (U_i, T_i ) \to (U,T) \right \}$ in 
$\text {Crys}(\mathscr {X})_{\acute{\rm e}\text{t}}$ such that for all i there are maps 
$U_i \to Y$ over 
$\mathscr {X}$. In order to show this, first we change base to get a smooth map 
$U\times _{\mathscr {X}} Y \to U$ which admits a projection map 
$U\times _{\mathscr {X}} Y \to Y$. Now we pick an étale cover 
$U' \to U \times _{\mathscr {X}} Y$, where 
$U'$ is a scheme, and thus we get a smooth map 
$U' \to U$. This can be refined further to obtain maps 
$U_i \to U'$ such that the composition 
$\left \{ U_i \to U' \to U \right \}$ is an étale cover. Now 
$i: U \to T$ is a divided-power thickening of U with p being locally nilpotent on T. Therefore 
$i: U \to T$ is a universal homeomorphism. By the invariance of étale sites [SP, Tag 04DY] for universal homeomorphisms, we get étale maps 
$T_i \to T$ such that 
$T_i \times _T U \simeq U_i$. This gives a thickening 
$U_i \to T_i$. Since the map 
$T_i \to T $ is étale, by [SP, Tag 07H1], the ideal of the thickening 
$U_i \to T_i$ has divided powers. Further, since 
$\left \{U_i \to U\right \}$ was an étale cover, 
$\left \{ T_i \to T \right \} $ is also an étale cover by construction. Thus we have constructed a refinement 
$\left \{(U_i , T_i) \to (U,T) \right \}$ in the site 
$\text {Crys}(\mathscr {X})_{\acute{\rm e}\text{t}}$. For all i, we have also constructed maps 
$U_i \to Y$ over 
$\mathscr X$.
Now by using the proof in [SP, Tag 07IJ], we fix a set of divided-power thickenings 
$(U_s,T_s)_{s \in S} $ by picking 
$(U_s)_{s \in S}= (\text {Spec} C_s)_{s\in S}$ to be an affine Zariski open cover of the scheme Y and, for each 
$s \in S$, building 
$T_s$ by using the algebra 
$C_s$ as in [SP, Tag 07HP]. Since the map 
$Y \to \mathscr {X}$ was smooth, it follows that 
$(U_s, T_s) \in \text {Crys}(\mathscr {X})_{\text{lis-}\acute{\rm e}\text{t}}$. Using the discussion from the previous paragraph and the construction of 
$(U_s, T_s)_{s\in S},$ we get an epimorphism 
$\coprod _{s \in S} h_{\left (U_s, T_s\right )} \to *$ in 
$\text {ShvCrys}(\mathscr {X})_{\acute{\rm e}{\rm t}},$ which implies 
$i_! * = *$, proving our main claim in step 2.
Step 3. In this step, we show that crystalline cohomology can also be computed in the finer site 
$\text {Crys}(\mathscr {X})_{\text {syn}}$. We have a map of topoi
$$ \begin{align*} v: \text{ShvCrys}(\mathscr{X})_{\text{syn}} \to \text{ShvCrys}(\mathscr{X})_{\acute{\rm e}{\rm t}}. \end{align*} $$Let 
$v_*$ denote the corresponding right adjoint. The left adjoint 
$v^{-1}$ is given by sheafification. Thus we obtain a natural isomorphism 
$R \Gamma _{\text {syn}}(\mathscr {X}, \mathcal {O}^{\text {crys}}) \simeq R \Gamma _{\acute{\rm e}{\rm t}}(\mathscr {X}, R v_* \mathcal {O}^{\text {crys}})$. We claim that 
$R v_* \mathcal {O}^{\text {crys}} \simeq v_* \mathcal {O}^{\text {crys}} = \mathcal {O}^{\text {crys}}$. This statement can be checked locally and thus follows from the scheme case, where it is already known. We refer to [Reference Berthelot, Breen and MessingBBM82, Proposition 1.1.19] for a proof in the case of schemes.
Step 4. In this step, we show that crystalline cohomology can be computed in 
$\mathscr {X}_{\text {syn}}$ as well and conclude the proof. We have a functor
$$ \begin{align*} h:\text{Crys}(\mathscr X)_{\text{syn}} \to \mathscr X_{\text{syn}} \end{align*} $$which sends 
$(V,T) \to V$. By the proof of [Reference Fontaine and MessingFM87, Proposition 1.3], this functor is cocontinuous. By [SP, Tag 00XI], there is a morphism of topoi
$$ \begin{align*} u: \text{ShvCrys}(\mathscr X)_{\text{syn}} \to \text{Shv} \mathscr X_{\text{syn}}, \end{align*} $$where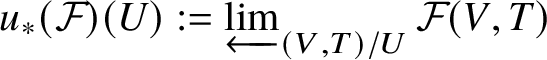 
$u_* (\mathcal F) (U):= \varprojlim _{\left (V,T\right )/U }\mathcal {F}(V,T)$. We write the left adjoint by 
$u^{-1}$, which is exact by [SP, Tag 00XL]. By adjunction, it follows that 
$u_*$ commutes with the global section functor: Indeed, we obtain 
$\text {Hom}(*, u_* \mathcal F) \simeq \text {Hom}(*, \mathcal F)$. Therefore it follows that 
$R \Gamma _{\text {syn}}(\mathscr X, \mathcal {O}^{\text {crys}}) \simeq R \Gamma Ru_* \mathcal {O}^{\text {crys}}$. Now the right-hand side is equivalent to Definition 2.2. Therefore we are done.
3 Application to crystalline Dieudonné theory
In this section, we apply the notion of the crystalline cohomology of stacks to describe the Dieudonné module of a finite group scheme of p-power order or a p-divisible group as the crystalline cohomology of the classifying stack. Before we do that, we briefly remind the reader of the main theorem of contravariant Dieudonné theory and the related definitions.
Definition 3.1. Let k be a perfect field and 
$W(k)$ the ring of Witt vectors of k. Let 
$\sigma $ denote the Witt vector Frobenius which is induced from the Frobenius in k. The Dieudonné ring 
$\mathscr {D}_k$ is defined to be the free noncommutative polynomial ring in two generators 
$F,V$ over 
$W(k)$ subjected to the relations 
$FV= VF = p$, 
$Fc = \sigma (c)F$ for 
$c \in W(k)$ and 
$cV = V \sigma (c) $ for 
$c \in W(k)$. The ring 
$\mathscr {D}_k$ is noncommutative when 
$k \neq \mathbb {F}_p$ and is 
$\mathbb {Z}_p[x, y]/(xy - p)$ when 
$k = \mathbb {F}_p$.
Definition 3.2. We let 
$W_n$ denote the group scheme that corepresents the functor that sends a k-algebra A to the ring of length n Witt vectors 
$W_n(A)$. These group schemes are naturally induced with a Frobenius endomorphism F on them, and we define 
$W_n^{m}$ to be the group scheme which is the kernel of 
$F^m$ on 
$W_n$. We also have a map 
$V: W_n \to W_{n+1}$ induced by the Witt vector Verschiebung which turns 
$\left \{W_n\right \}_{n\ge 1}$ into a directed system of group schemes. We define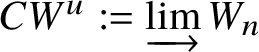 
$CW^u:= \varinjlim W_n$. One defines the formal p-group 
$CW$ of Witt covectors as a completion of 
$CW^u$ in a suitable sense. We refer to [Reference FontaineFo77] for details.
Example 3.3. By definition, 
$W_1$ is the additive group scheme 
$\mathbb {G}_a$. Also, 
$W_1^{1}$ is the finite additive group scheme with the underlying scheme given by 
$\text {Spec} k[x]/x^p$, which is usually denoted as 
$\alpha _p$. Similarly, 
$W_1^n$ is the finite additive group scheme with the underlying scheme given by 
$\text {Spec} k[x]/x^{p^n},$ which is denoted as 
$\alpha _{p^n}$. The Cartier dual of 
$\alpha _{p^n}$ is given by the group scheme 
$W_n^1$. More generally, the Cartier dual of 
$W_n^m$ is isomorphic to 
$W_m^n$ [Reference DemazureDem72, Chapter III, Section 4].
Definition 3.4. For a finite group scheme G over k, we define the Dieudonné module of G to be
$$ \begin{align*} M(G):= \text{Hom}(G,CW), \end{align*} $$where the 
$\text {Hom}$ is being taken in the category of formal groups.
Now we are ready the state the classical theorem of contravariant Dieudonné theory, which can be found in [Reference FontaineFo77, Chapitre III, Section 1, Theorem 1]:
Theorem 3.5. The functor 
$G \to M(G)$ induces an antiequivalence between the category of finite group schemes over k and left 
$\mathscr {D}_k$-modules with finite 
$W(k)$ length.
Example 3.6. Let us give some examples of Dieudonné modules associated to certain finite flat group schemes. For the group schemes 
$W_n^m$ from Example 3.3, we have 
$M\left (W_n^m\right ) \simeq \mathscr {D}_k / \mathscr {D}_k \cdot (F^m, V^n)$ [Reference OortOor66, Section 15.4]. In particular, 
$M \left (\alpha _{p^n}\right ) \simeq \mathscr {D}_k / \mathscr {D}_k \cdot (F^n, V)$. For the multiplicative group scheme underlying 
$p^n$th roots of unity denoted as 
$\mu _{p^n},$ we have 
$M\left (\mu _{p^n}\right ) \simeq \mathscr {D}_k / \mathscr {D}_k \cdot (F^n, (V-1))$. For the constant group scheme 
$\mathbb {Z}/p^n\mathbb {Z},$ we have 
$M(\mathbb {Z}/p^n\mathbb {Z}) \simeq \mathscr {D}_k / \mathscr {D}_k \cdot ((F-1), V^n)$.
Example 3.7. Let 
$E[p]$ denote the p-torsion group scheme of a supersingular elliptic curve E over k. Then 
$M (E[p]) \simeq \mathscr {D}_k / \mathscr {D}_k \cdot \left (F^2, F-V, V^2\right )$. We refer to [Reference OortOor66, Section 15.5] for more details.
In [Reference Berthelot, Breen and MessingBBM82], Berthelot, Breen and Messing obtained an alternative description of 
$M(G)$. Given a finite group scheme G, using Definition 2.8 we obtain an abelian group object 
$\underline {G}$ of the topos 
$(k/W(k))_{\text {Crys}}$. It proves the following theorem, which expresses 
$M(G)$ as a certain 
$\text {Ext}$ group in the crystalline topos.
Theorem 3.8 [Reference Berthelot, Breen and MessingBBM82, Theorem 4.2.14]
For a finite group scheme G for p-power rank, we have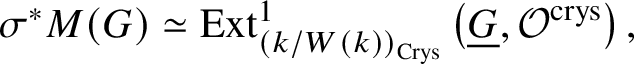 
$\sigma ^* M(G) \simeq \text {Ext}^1_{\left (k/W(k)\right )_{\text {Crys}}}\left (\underline {G},\mathcal {O}^{\text {crys}}\right ),$ where 
$\sigma ^* M(G)$ denotes the extension of scalars along the Witt vector Frobenius 
$\sigma $ – that is, 
$\sigma ^* M(G) := M(G)\otimes _{W(k), \sigma } W(k)$.
3.1 Dieudonné module of finite group schemes
In this subsection, we work with finite group schemes G of p-power rank over a perfect field k. Let 
$BG := [ \text {Spec} k / G ]$ be the classifying stack of G [SP, Tag 044O]. Any such group scheme is a local complete intersection and therefore it follows that the map 
$\text {Spec}k \to BG $ is a syntomic cover. Its Čech nerve is given by the following simplicial scheme:
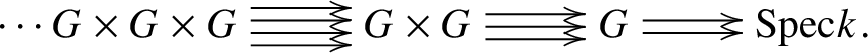
As in Definition 2.8, we can attach a sheaf 
$\underline {G}$ on 
$\text {Crys}(k/W(k))$ which can be viewed as an object of the topos 
$(k/W(k))_{\text {Crys}}$. Corresponding to this Čech nerve, we obtain by functoriality a simplicial object of the topos:
where 
$*$ is the final object. With this simplicial object, we can attach the free simplicial abelian group object
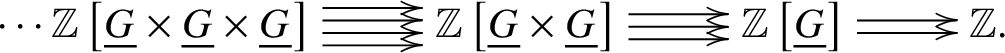
The alternating face map complex associated to this simplical object is as an object in the category of complexes of abelian objects of the topos 
$(k/W(k))_{\text {Crys}}$, which can also be viewed as an object in the derived category of abelian objects of 
$(k/W(k))_{\text {Crys}}$, denoted as 
$D(k/W(k))$. This object living in 
$D(k/W(k))$ is also isomorphic to the homotopy colimit of
viewed as a functor from 
$\Delta ^{op}$ to 
$D(k/W(k))$. We denote this object by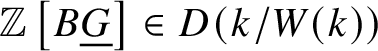 
$\mathbb Z \left [B \underline {G}\right ] \in D(k/W(k))$. If we work with the truncated crystalline site 
$\text {Crys}(k/W_n(k))$, all of these constructions remain valid, and one can associate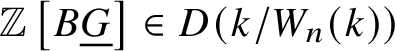 
$\mathbb Z \left [B \underline {G}\right ] \in D(k/W_n(k))$ as well.
Lemma 3.9.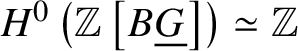 
$H^0 \left (\mathbb Z \left [B \underline {G}\right ]\right ) \simeq \mathbb Z$ and 
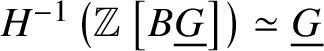$H^{-1} \left (\mathbb Z \left [B \underline {G}\right ]\right ) \simeq \underline {G}$.
Proof. First we work with the presheaf simplicial abelian group object
which is obtained by applying the free abelian presheaf functor to 
$B \underline {G}$ [SP, Tag 03CP]. Let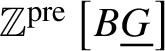 
$\mathbb {Z}^{\text {pre}}\left [B\underline {G}\right ]$ be the associated complex: 
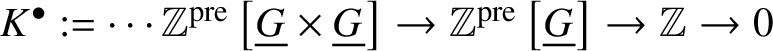$K^{\bullet }:=\dotsb \mathbb {Z}^{\text {pre}}\left [\underline {G}\times \underline {G}\right ] \to \mathbb {Z}^{\text {pre}}\left [\underline {G}\right ] \to \mathbb {Z} \to 0$. We see that 
$H^0$ of this complex is 
$\mathbb {Z}$, since the last differential is zero. One also notes that 
$K^\bullet $ computes the (presheaf) group cohomology of the (presheaf) abelian group 
$\underline {G}$ with constant coefficients in 
$\mathbb Z$, and hence 
$H^{-1}(K^\bullet ) \simeq \underline {G}$. Now since sheafification is exact, we obtain the required statements.
Lemma 3.10. Let G be a group scheme of order 
$p^m$. Then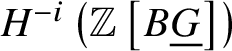 
$H^{-i}\left (\mathbb Z \left [B \underline {G}\right ]\right )$ is killed by 
$p^m$ for 
$i>0$.
Proof. We start by recalling some definitions for this proof. Let A be an ordinary n-torsion abelian group. Let us define 
$\mathbb {Z} [BA]$ to be the alternating face complex associated to the simplicial abelian group
Then, as noted previously, 
$H^{-i}(\mathbb Z [B A]) \simeq H_i ( A)$, where the latter denotes group cohomology with coefficients in 
$\mathbb Z$. This is also the homology of the Eilenberg–MacLane space 
$K(A,1)$. We will show that 
$H_i(A)$ is n-torsion (*). First, from the complex 
$\mathbb {Z}[BA]$, one notes that 
$H_i(A)$ commutes with filtered colimits as a functor defined on abelian groups. Since A is an n-torsion abelian group, it can be expressed as a filtered colimit of finite n-torsion abelian groups. Therefore, it is enough to check the statement for an n-torsion finite abelian group A. Further, one notes that 
$K(A_1,1) \times K(A_2,1) \simeq K(A_1 \times A_2, 1)$; therefore, by using the Künneth formula, we are reduced to checking this for n-torsion cyclic groups, where it follows from the well-known computation of group homology of finite cyclic groups using the Tate complex. The statement in the lemma now follows from applying (*) to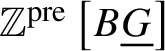 
$\mathbb {Z}^{\text {pre}}\left [B \underline {G}\right ]$ and noting that since G has order 
$p^m$, one has 
$p^m \cdot G=0$.
Remark 3.11. These lemmas clearly remain valid even if we were working with the truncated crystalline sites 
$\text {Crys}(k/W_n(k))$ mentioned in Remark 2.13.
Proposition 3.12.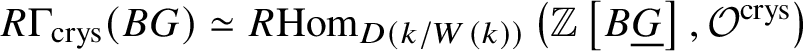 
$R \Gamma _{\text {crys}}(BG) \simeq R\text {Hom}_{D\left (k/W(k)\right )}\left (\mathbb {Z}\left [B \underline {G}\right ], \mathcal O^{\text {crys}}\right )$.
Proof. Since 
$\text {Spec} k \to B G$ is a syntomic map, we can apply Remark 2.5, which gives that
By Proposition 2.11, this is
We can take the 
$R \varprojlim $ inside as a homotopy colimit, which gives us that this is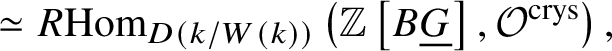 
$\simeq R \text {Hom}_{D\left (k/W(k)\right )}\left (\mathbb Z \left [B\underline {G}\right ], \mathcal O^{\text {crys}}\right ),$ as desired.
Proposition 3.13. There is a spectral sequence with 
$E_2$-page
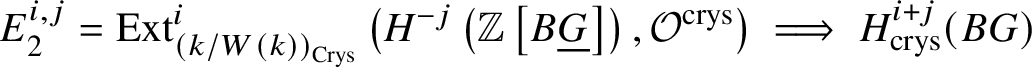$$ \begin{align*} E_2^{i,j}= \text{Ext}_{\left(k/W(k)\right)_{\text{Crys}}}^i \left(H^{-j}\left(\mathbb{Z}\left[B \underline{G}\right]\right), \mathcal{O}^{\text{crys}}\right)\implies H^{i+j}_{\text{crys}}(BG) \end{align*} $$and another spectral sequence with 
$E_1$-page
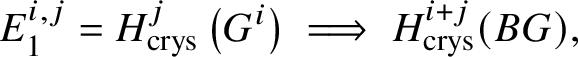$$ \begin{align*} E_1^{i,j}=H^j_{\text{crys}}\left(G^i\right) \implies H^{i+j}_{\text{crys}}(BG), \end{align*} $$where 
$G^i$ denotes the i-fold fibre product of G with itself. By convention, 
$G^0 = *$.
Proposition 3.14.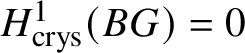 
$H^1_{\text {crys}}(BG) = 0$.
Proof. We can use the 
$E_2$ spectral sequence from Proposition 3.13 to compute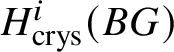 
$H^i_{\text {crys}} (BG)$. We note that 
$\text {Ext}^i (\mathbb Z, \mathcal O^{\text {crys}})=0$ for 
$i>0$, as it computes the cohomology of 
$\text {Spec} k$ for a perfect field k, by Proposition 2.11. Also, by [Reference Berthelot, Breen and MessingBBM82, Proposition 4.2.6], we have 
$\text {Hom}\left (\underline {G}, \mathcal O^{\text {crys}}\right )= 0$. These calculations, along with the spectral sequence and Lemma 3.9, imply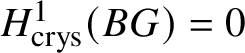 
$H^1_{\text {crys}}(BG) = 0$.
Proposition 3.15. If G is a finite group scheme of p-power order, then for any 
$i>0$, 
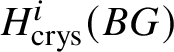$H^i_{\text {crys}}(BG)$ is killed by a power of p as an abelian group.
Proof. This follows from the spectral sequence in Proposition 3.13. Indeed, already in the 
$E_2$-page of the spectral sequence, all but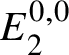 
$E_2^{0,0}$ is p-power torsion by Lemma 3.10. Hence, all but 
$E^{0,0}_{\infty }$ is p-power torsion as well. Therefore, for any 
$i>0$, 
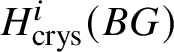$H^i_{\text {crys}}(BG)$ has a finite filtration whose successive quotients are p-power torsion, and hence is p-power torsion itself.
Proposition 3.16. If G is a finite group scheme of p-power order, then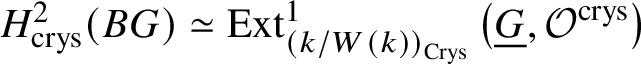 
$H^2_{\text {crys}}(BG) \simeq \text {Ext}^1_{\left (k/W(k)\right )_{\text {Crys}}}\left (\underline {G}, \mathcal {O}^{\text {crys}}\right )$.
Proof. First we note that there is a natural map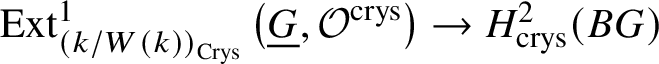 
$\text {Ext}^1_{\left (k/W(k)\right )_{\text {Crys}}}\left (\underline {G}, \mathcal {O}^{\text {crys}}\right ) \to H^2_{\text {crys}}(BG)$, which is injective. Indeed, from the 
$E_2$-spectral sequence (which is natural in G), we note that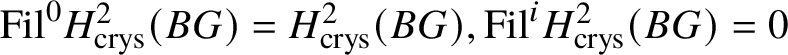 
$\mathrm {Fil}^0{H^2_{\text {crys}}(BG)} = H^2_{\text {crys}}(BG), \mathrm {Fil}^i{H^2_{\text {crys}}(BG)}= 0$ for 
$i \ge 2$, and therefore 
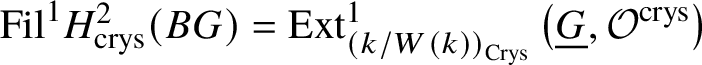$\mathrm {Fil}^1{H^2_{\text {crys}}(BG)} = \text {Ext}^1_{\left (k/W(k)\right )_{\text {Crys}}}\left (\underline {G}, \mathcal {O}^{\text {crys}}\right )$, which gives the required injective map. We proceed to proving that this natural map is an isomorphism.
Set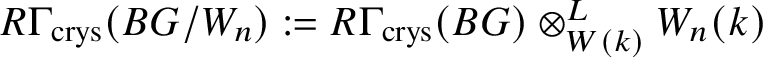 
$R\Gamma _{\text {crys}}(BG/W_n):= R\Gamma _{\text {crys}}(BG) \otimes ^{L}_{W(k)} W_n(k)$ and 
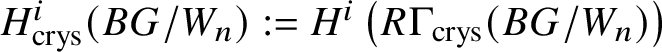$H^i_{\text {crys}}(BG/W_n):= H^i \left (R\Gamma _{\text {crys}}(BG/W_n)\right )$. Then we have the exact sequence
$$ \begin{align*} 0 \to H^1_{\text{crys}}(BG)/p^n \to H^1_{\text{crys}}(BG/W_n) \to H^2_{\text{crys}}(BG)[p^n]\to 0. \end{align*} $$Now we choose n large enough that 
$p^n G = 0$ and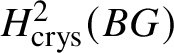 
$H^2_{\text {crys}}(BG)$ is 
$p^n$-torsion. This is possible by Proposition 3.15. Then the exact sequence, along with Proposition 3.14, gives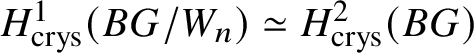 
$H^1_{\text {crys}}(BG/W_n) \simeq H^2 _{\text {crys}}(BG)$ for such an n. By [Reference Berthelot, Breen and MessingBBM82, Proposition 4.2.17], we have 
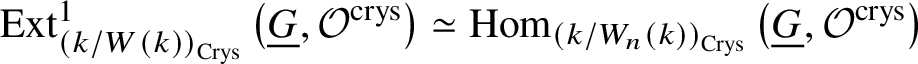$\text {Ext}^1_{\left (k/W(k)\right )_{\text {Crys}}}\left (\underline {G}, \mathcal {O}^{\text {crys}}\right ) \simeq \text {Hom}_{\left (k/W_n(k)\right )_{\text {Crys}}} \left (\underline {G}, \mathcal O^{\text {crys}}\right )$. Therefore, it is enough to show that 
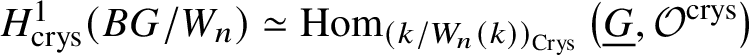$H^1_{\text {crys}}(BG/W_n) \simeq \text {Hom}_{\left (k/W_n(k)\right )_{\text {Crys}}} \left (\underline {G}, \mathcal O^{\text {crys}}\right )$.
Since
we obtain
In order to justify the last step, we note that 
$W_n(k)$ is quasi-isomorphic to the complex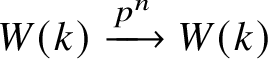 
$W(k) \xrightarrow {p^n} W(k)$; thus the functor 
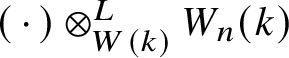$(\,\cdot \,) \otimes ^L_{W(k)} W_n(k)$ commutes with the 
$R \varprojlim $ as required.
Therefore, by Remark 3.11 and the proof of Proposition 3.12, one obtains
$$ \begin{align*} R \Gamma _{\text{crys}}(BG/W_n) \simeq R\text{Hom}_{D\left(k/W_n(k)\right)}\left(\mathbb{Z}\left[B \underline{G}\right], \mathcal O^{\text{crys}}\right), \end{align*} $$and, analogously to Proposition 3.13, a spectral sequence with 
$E_2$-page
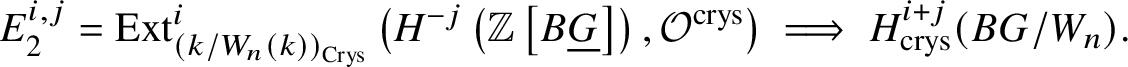$$ \begin{align*} E_2^{i,j}= \text{Ext}_{\left(k/W_n(k)\right)_{\text{Crys}}}^i \left(H^{-j}\left(\mathbb{Z}\left[B \underline{G}\right]\right), \mathcal{O}^{\text{crys}}\right)\implies H^{i+j}_{\text{crys}}(BG/W_n). \end{align*} $$Now applying Lemma 3.9 yields the desired isomorphism. To check this, we see that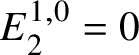 
$E^{1,0}_2 = 0$ and 
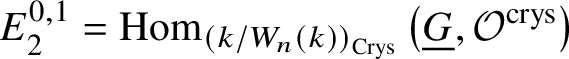$E^{0,1}_2 = \text {Hom}_{\left (k/W_n(k)\right )_{\text {Crys}}}\left (\underline {G}, \mathcal {O}^{\text {crys}}\right )$. Also, we have 
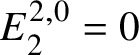$E_2^{2,0}= 0$. Since 
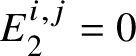$E^{i,j}_2 = 0$ for 
$i<0$ or 
$j<0$, we obtain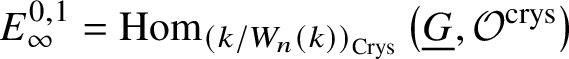 
$E^{0,1}_{\infty }= \text {Hom}_{\left (k/W_n(k)\right )_{\text {Crys}}}\left (\underline {G}, \mathcal {O}^{\text {crys}}\right )$. Therefore, we indeed obtain the required isomorphism 
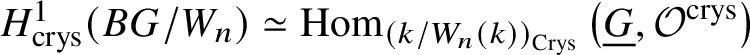$H^1_{\text {crys}}(BG/W_n) \simeq \text {Hom}_{\left (k/W_n(k)\right )_{\text {Crys}}} \left (\underline {G}, \mathcal O^{\text {crys}}\right )$. The relevant part of the 
$E_2$ page of the spectral sequence is depicted in the following diagram:
Remark 3.17. One can develop the theory of crystalline cohomology for higher stacks and study the cohomology of the n-stack 
$K(G,n)$ [Reference ToënTo06]. For a group scheme G, the n-stack 
$K(G,n)$ is supposed to be an analogue of the Eilenberg–MacLane space 
$K(G,n)$ for any discrete abelian group G which has the property that 
$\pi _i(K(G,n))= G$ for 
$i=n$ and 
$\pi _i(K(G,n))= 0$ for 
$i\ne \left \{n,0\right \} $. In the topological case, there exists a chain complex of abelian groups 
$\mathbb {Z}[B^n G]$ such that 
$H_i(\mathbb {Z}[B^n G])$ computes the singular homology of the CW complex 
$K(G,n)$. Here we do not define crystalline cohomology for higher stacks in general, but for a finite group scheme G, we can work with an ad hoc definition generalising Proposition 3.12. Similar to the definition of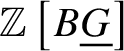 
$\mathbb {Z}\left [B \underline {G}\right ]$ as an object of the crystalline topos, one can also define 
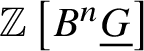$\mathbb {Z}\left [B^n \underline {G}\right ]$. Then we define 
$R\Gamma _{\text {crys}}(K(G,n)): = R\text {Hom}_{\left (k/W(k)\right )}(\mathbb {Z}[B^n G], \mathcal {O}^{\text {crys}})$. Then from the analogue of the spectral sequence in Proposition 3.13, we obtain that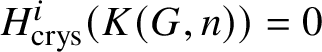 
$H^i_{\text {crys}}(K(G,n))=0$ for 
$0<i<n+1$ and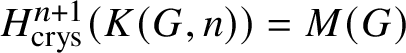 
$H^{n+1}_{\text {crys}}(K(G,n))= M(G)$. In order to prove this for 
$n \ge 2$, the computation with the spectral sequence relies on the fact that for an abelian group A, 
$H_i(K(A,n), \mathbb {Z})= 0$ for 
$0<i<n$, 
$H_n(K(A,n), \mathbb {Z})= A$ and 
$H_{n+1}(K(A,n), \mathbb {Z})=0$. The first two of these computations follow from the Hurewicz theorem, and the last one follows from applying the Serre fibration spectral sequence for the homotopy fibration sequence 
$K(A,n) \to * \to K(A, n+1)$.
3.2 Dieudonné theory of p-divisible groups
First, we recall the definition of a p-divisible group:
Definition 3.18. Let p be a prime and 
$h>0$ an integer. A p-divisible group (or Barsotti–Tate group) of height h over a scheme S is a directed system 
$G = \left \{ G_n\right \}$ of finite flat group schemes over S such that each 
$G_n$ is 
$p^n$-torsion of order 
$p^{nh}$ and the transition map 
$i_n : G_n \to G_{n+1}$ is an isomorphism of 
$G_n$ onto 
$G_{n+1}[p^n]$ for all 
$n \ge 1$. A morphism 
$f : G \to H $ between p-divisible groups is a compatible system of S-group maps 
$f_n : G_n \to H_n$ for all 
$n \ge 1$. If 
$S' \to S$ is a map of schemes, then 
$G \times _S S' := {G_n \times _S S'}$ is the p-divisible group of height h over 
$S'$ obtained by base change.
Example 3.19. If 
$A \to S$ is an abelian scheme with fibres of constant dimension 
$g> 0$ and p is a prime, then 
$G_n := A[p^n]$ is a finite flat 
$p^n$-torsion group scheme of order 
$p^{2gn}$ for all 
$n\ge 1$ and 
$\left \{G_n\right \}$ is a directed system via isomorphisms 
$G_n \cong G_{n+1}[p^n]$ for all 
$n\ge 1$. For an abelian variety A, we denote this p-divisible group by 
$A[p^\infty ]$. It has height 
$2g$, where 
$g = \dim A$.
We also recall the following theorem on the Dieudonné theory of p-divisible groups, which can be found in [Reference FontaineFo77, Chapitre III, Section 6, Proposition 6.1]:
Theorem 3.20. The functor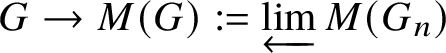 
$G \to M(G) := \varprojlim M(G_n)$ is an antiequivalence of categories between the category of p-divisible groups over k and the category of finite free 
$W(k)$-modules D equipped with a Frobenius semilinear endomorphism 
$F:D \to D$ such that 
$pD \subseteq F (D)$. The height of G is the 
$W(k)$-rank of 
$M(G)$.
Now in order to formulate the analogue of Theorem 1.2 for p-divisible groups, we begin by making a definition:
Definition 3.21. Let G be a p-divisible group over k. We define the classifying stack of G to be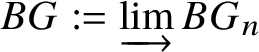 
$B G := \varinjlim B G_n $, where the colimit is being taken in the category of stacks.
Proposition 3.22. For a p-divisible group 
$G= \left \{G_n \right \}$, we have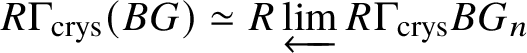 
$R\Gamma _{\text {crys}}(BG)\simeq R \varprojlim R \Gamma _{\text {crys}} B G_n$.
Proof. We write 
$\mathcal {F}_{n}:= BG_n$ and 
$\mathcal {F}:= BG$ for this proof. Using Remark 2.4, we see that the crystalline cohomology of a stack 
$\mathcal {Y}$ depends only on 
$\mathcal {Y}$ viewed as a presheaf of groupoids on the category of affine k-schemes 
$\text {Aff}_k$. If 
$\mathcal {Y}:= \text {colim} \mathcal {Y}_\alpha $ as presheaves of groupoids, then by the alternative definition in Remark 2.4 it follows that 
$R \Gamma _{\text {crys}}(\mathcal {Y}) \simeq R\text {lim}_{\alpha } R \Gamma _{\text {crys}}(\mathcal {Y}_{\alpha }) $. Therefore, in order to show that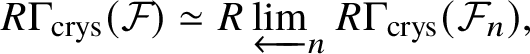 
$R \Gamma _{\text {crys}}(\mathcal {F}) \simeq R\varprojlim _{n} R \Gamma _{\text {crys}}(\mathcal {F}_{n}),$ it is enough to prove that 
$\mathcal {F}$ is the colimit of 
$\mathcal {F}_n$ in the category of presheaves of groupoids on 
$\text {Aff}_k$. This follows because affine schemes in the fpqc site of all schemes satisfy the property that any fpqc covering of an affine scheme has a finite subcovering by affine schemes. Indeed, by the property we mentioned, checking descent over an affine scheme is essentially a finite limit condition. Thus our claim follows, since filtered colimits commute with finite limits.
Proposition 3.23. We have a natural isomorphism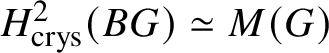 
$H^2_{\text {crys}}(BG) \simeq M(G)$.
Proof. We are interested in computing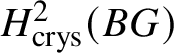 
$H^2_{\text {crys}}(BG)$, which is 
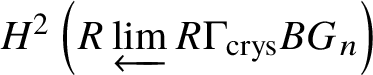$H^2 \left (R \varprojlim R \Gamma _{\text {crys}} B G_n\right )$ by Proposition 3.22. We compute the cohomology of this 
$\mathbb N$-indexed derived limit by using [SP, Tag 07KY], which gives us the short exact sequence
$$ \begin{align*} 0 \to R^1 \varprojlim H^1_{\text{crys}} (B G_n) \to H^2_{\text{crys}}(BG) \to \varprojlim H^2_{\text{crys}}(BG_n) \to 0. \end{align*} $$Therefore, our claim follows from Propositions 3.14 and 3.16 and Theorem 3.20.
3.3 Cohomology of the classifying stack of an abelian variety
Now we consider an abelian variety A over the field k. Let 
$BA$ denote the classifying stack of A. In this section, in Proposition 3.28, we prove that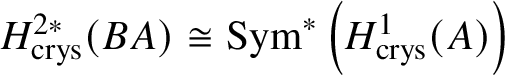 
$H^{2*}_{\text {crys}}(BA) \cong \text {Sym}^* \left (H^1_{\text {crys}}(A)\right )$, and 
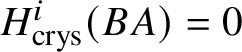$H^i_{\text {crys}}(BA) = 0$ for odd i. In other words, 
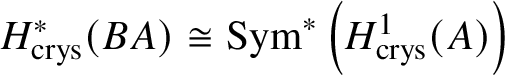$H^*_{\text {crys}} (BA) \cong \text {Sym}^* \left (H^1_{\text {crys}}(A)\right )$, where 
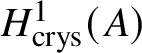$H^1_{\text {crys}}(A)$ is considered to be in degree 
$2$.
Remark 3.24. An analogue of this proposition was proved by Borel in topology [Reference BorelBo53] and by Behrend in 
$\ell $-adic cohomology using fibration spectral sequences [Reference BehrendBeh03, Theorem 6.1.6]. Here we take a different approach, based on descent theory. One knows that there is a functorial isomorphism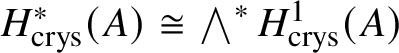 
$H^*_{\text {crys}}(A) \cong \bigwedge ^*H^1_{\text {crys}}(A)$. We show that Proposition 3.28 is a formal consequence of this isomorphism and the Künneth formula.
In this section, we will crucially use the theory of derived functors of nonadditive functors, which appears in [Reference Dold and PuppeDP61, Reference IllusieIl71]. Note that, analogously to Proposition 3.13, there is an 
$E_1$ spectral sequence with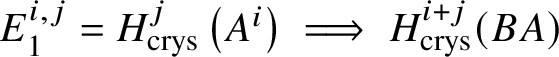 
$E_1^{i,j}= H^j_{\text {crys}}\left (A^i\right ) \implies H^{i+j}_{\text {crys}}(BA)$, where 
$A^i$ denotes the i-fold fibre product of A with itself. We note that by definition, for 
$j \ge 1$,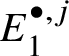 
$E_1^{\bullet ,j }$ is the alternating face complex associated to the cosimplicial object given by
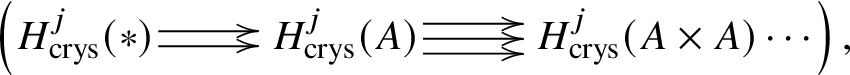
which is naturally isomorphic to the cosimplicial object
Lemma 3.25. The complex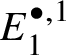 
$E_1^{\bullet , 1}$ is homotopy-equivalent to 
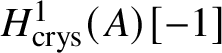$H^1_{\text {crys}}(A) [-1]$.
Proof. As already noted,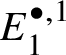 
$E_1^{\bullet , 1}$ is the alternating face complex associated to
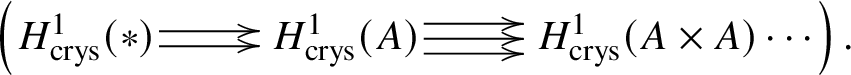
By the Künneth formula, one has a natural isomorphism 
$H^{1}_{\text {crys}} \left (A^i\right ) \cong \bigoplus _{s=1}^{i} H^1_{\text {crys}}(A)$, and 
$H^1(*) = 0$. Writing 
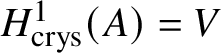$H^1_{\text {crys}}(A)=V$, we note that 
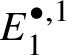$E_1^{\bullet ,1}$ is naturally isomoprphic to the following explicit complex (where V sits in cohomological degree 
$1$):
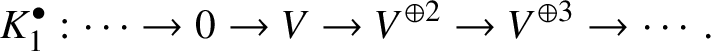$$ \begin{align*} K_1^{\bullet}: \dotsb \to 0 \to V \to V^{\oplus 2}\to V^{\oplus 3} \to \dotsb. \end{align*} $$Here the first differential 
$d_1: V \to V^{\oplus 2}$ is zero. In general, for 
$n \ge 2$, the differential 
$d_n: V^{\oplus n} \to V^{\oplus n+1}$ is given by
$$ \begin{align*} d_n(v_1, v_2, \dotsc, v_n)= (-v_1, 0, v_2 - v_3, 0, v_4 - v_5, 0, \dotsc, v_n)\quad \text{for even } n \end{align*} $$and
$$ \begin{align*} d_n(v_1, v_2, \dotsc, v_n) = (0, v_2, v_2, v_4, v_4, \dotsc, 0)\quad \text{for odd } n. \end{align*} $$One can check this by induction. Now we consider the complex 
$K_2^\bullet : \dotsb \to 0 \to V \to 0 \to 0 \dotsb $, where V sits in cohomological degree 
$1$. There are obvious maps 
$K_1^\bullet \to K_2^\bullet $ and 
$K_2^\bullet \to K_1^\bullet $ (induced by 
$\text {id}_V$ on cohomological degree 
$1$), and we prove that they induce the desired homotopy equivalence. There is nothing to prove for the composite map 
$K_2^\bullet \to K_2^\bullet $. For the other composite map, 
$K_1^\bullet \to K_1^\bullet $, our task is to prove that it is homotopic to 
$\text {id}_{K_1^{\bullet }}$. We construct the required homotopy 
$h_i$. We set 
$h_i = 0$ for 
$i \le 2$. For 
$i \ge 3,$ now we define 
$h_i: V^{\oplus i} \to V^{\oplus {i-1}}$. We let 
$h_3(v_1,v_2,v_3) = (-v_1, v_3)$ and 
$h_4(v_1, \ldots , v_4) = (0,v_2, 0)$. In general, we set
$$ \begin{align*} h_i(v_1, \dotsc, v_i)= (0, v_2,0, \dotsc, 0,v_{i-2}, 0)\quad \text{for even } i \ge 6 \end{align*} $$and
$$ \begin{align*} h_i(v_1, \dotsc, v_i)= (-v_1, 0 , -v_3,0, \dotsc,0,-v_{i-2}, v_i ) \quad \text{for odd } i \ge 5. \end{align*} $$One easily checks that this gives the required homotopy.
Remark 3.26. For the cohomology of the complex 
$K_1^\bullet ,$ one can also use a less explicit argument. If we write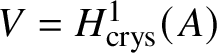 
$V= H^1_{\text {crys}}(A)$ as before, the addition 
$A \times A \to A$ induces a map 
$V \to V \oplus V$ which is dual to addition on 
$V^\vee $. Therefore, one sees that the complex 
$K_1^\bullet $ is the dual complex to 
$B V^\vee $ (whose cohomology is concentrated in cohomological degree 
$-1$ and is equal to 
$V^\vee $). Applying duals back, one sees that cohomology of 
$K_1^\bullet $ is concentrated in cohomological degree 
$1$ and is equal to V. In fact, one can also prove that 
$K_1^\bullet $ is homotopy-equivalent to 
$V[-1]$ in this manner by noting that 
$BV^\vee $ is homotopy-equivalent to 
$V^\vee [1]$. We thank the referee for pointing this out.
Lemma 3.27. The complex 
$E_1^{\bullet , n}$ is homotopy-equivalent to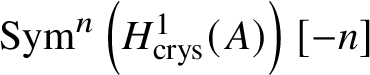 
$\text {Sym}^{n}\left (H^1_{\text {crys}}(A)\right )[-n]$.
Proof. Writing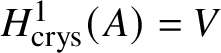 
$H^1_{\text {crys}}(A)= V$ again, we note that by Lemma 3.25, 
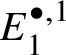$E_1^{\bullet , 1}$ is homotopy-equivalent to 
$V[-1]$. Therefore, the (derived) nth exterior power 
$\wedge ^n (V [-1]) $ is homotopy-equivalent to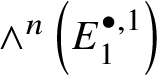 
$\wedge ^n \left (E_1^{\bullet , 1}\right )$ by [Reference IllusieIl71, Definition 4.1.3.2, Lemma 4.1.3.5]. It also follows from [Reference IllusieIl71, Definition 4.1.3.2, Section 1.3.4] that 
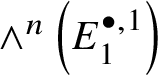$\wedge ^n \left (E_1^{\bullet , 1}\right )$ is homotopy-equivalent to the alternating face complex associated to
which is isomorphic to 
$E_1^{\bullet ,n}$. Now one also notes that 
$\wedge ^n (V[-1]) $ is homotopy-equivalent to 
$\text {Sym}^n (V)[-n]$, by the formula of décalage [Reference IllusieIl71, Proposition 4.3.2.1(i)]. This proves the lemma.
Proposition 3.28. We have a natural isomorphism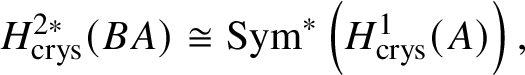 
$H^{2*}_{\text {crys}}(BA) \cong \text {Sym}^* \left (H^1_{\text {crys}}(A)\right ), $ and 
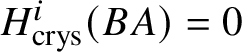$H^i_{\text {crys}}(BA) = 0$ for odd i.
Proof. This follows from the existence of the 
$E_1$ spectral sequence analogous to Proposition 3.13 (which degenerates at the 
$E_2$ page by Lemma 3.27) and the calculations from Lemmas 3.25 and 3.27. The spectral sequence also guarantees the naturality of the isomorphisms.
Corollary 3.29. For an abelian variety A over k,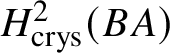 
$H^2_{\text {crys}}(BA)$ is naturally isomorphic to the Dieudonné module associated to the p-divisible group 
$A[p^\infty ]$.
Proof. This follows from Proposition 3.28 and the fact that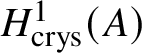 
$H^1_{\text {crys}}(A)$ is isomorphic to the Dieudonné module associated to the p-divisible group 
$A[p^\infty ]$.
3.4 Cohomology of the classifying stack of a p-divisible group
Let G be a p-disivisible group over a perfect field k. Using the calculation in Section 3.3, we are able to fully compute the cohomology ring 
$H^* _{\text {crys}}(BG)$. In this section, we prove that 
$H^*_{\text {crys}}(BG) \simeq \text {Sym}^{*} (M(G))$, where 
$M(G)$ is the Dieudonné module of G and is considered to be in degree 
$2$. Our strategy is to relate the p-divisible group to a suitable abelian variety and deduce the result from Proposition 3.28. First, we will record two lemmas:
Lemma 3.30. Let G be a uniquely p-divisible abelian group. Then 
$H_i (G, k)=0$ for 
$i>0$, where 
$H_i(G,k)$ denotes the group homology with coefficients in the field k equipped with trivial G action.
Proof. Since G is an abelian group, there is an exact sequence 
$ 0 \to \mathbb {Z}^{\oplus I} \to \mathbb {Z}^{\oplus J} \to G \to 0$. By taking colimits over multiplication by p, we obtain an exact sequence 
$0 \to \mathbb {Z}[1/p]^{\oplus I} \to \mathbb {Z}[1/p]^{\oplus J} \to G \to 0$. Using the Hochschild–Serre spectral sequence, we are reduced to checking the claim for 
$G = \mathbb Z[1/p]^{\oplus I}$. By taking filtered colimits, we can assume that I is finite. Then by the Künneth formula it is enough to check the claim for 
$\mathbb {Z}[1/p]$. Taking filtered colimits over multiplication by p, it follows from the fact that 
$H_1 (\mathbb {Z}, k)= k$ and 
$H_i (\mathbb {Z}, k)= 0$ for 
$i>0$.
Lemma 3.31. Let G be an abelian group such that multiplication by p is surjective on G. Then it follows that 
$W_n(k)[B G[p^\infty ]] \to W_n(k)[BG]$ is an isomorphism in the derived category 
$D(W_n(k))$ of 
$W_n(k)$-modules. Here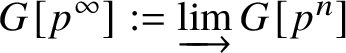 
$G[p^\infty ] := \varinjlim G[p^n]$.
Proof. Going modulo p, it would be enough to show that 
$k [B G[p^\infty ]] \to k[BG]$ is a quasi-isomorphism. For that, it would be enough to prove that the map induced on group homology 
$H_i (G[p^\infty ], k) \to H_i (G, k)$ is an isomorphism. Here in both cases, group cohomology is taken with constant coefficients in k. We have the exact sequence
$$ \begin{align*} 0 \to G[p^\infty] \to G \to \varinjlim_{p} G \to 0. \end{align*} $$We will write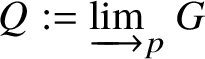 
$Q:=\varinjlim _{p} G$. By the Hochschild–Serre spectral sequence, we have a spectral sequence
$$ \begin{align*} E_2 = H_p \left(Q, H_q(G[p^\infty],k)\right) \implies H_{p+q}(G,k). \end{align*} $$Since G is abelian and G acts trivially on k, it follows that Q acts trivially on 
$H_q(G[p^\infty ], k)$. Since k is a field, 
$H_q(G[p^\infty ], k)$ is a direct sum of copies of k, and therefore we are done, by Lemma 3.30.
Proposition 3.32. Let A be an abelian variety over k. Let 
$A[p^\infty ]$ be the associated p-divisible group. Then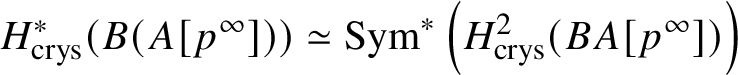 
$H^*_{\text {crys}}(B(A[p^\infty ])) \simeq \text {Sym}^{*}\left (H^2 _{\text {crys}}(BA[p^\infty ])\right )$, where 
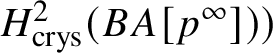$H^2_{\text {crys}} (BA[p^\infty ]))$ is considered to be in degree 
$2$.
Proof. We let 
$\mathcal {X}$ denote the topos 
$\text {Shv}(\mathrm {SYNSch}_k)$. Given the abelian variety A, we can associate an object in 
$\mathcal {X}$ (by considering functors of points), which will also be denoted by A. Similarly, by taking direct limits, we can associate an object in 
$\mathcal {X}$ corresponding to 
$A[p^\infty ]$, which will again be denoted by 
$A[p^\infty ]$. Since they both are group objects, we can consider the associated classifying objects as simplicial objects in 
$\mathcal {X}$, denoted respectively by 
$B A$ and 
$B A[p^\infty ]$. One can also consider the free 
$W_n(k)$-module on these objects and take the associated alternating face complex, which will be denoted by 
$W_n(k) [B A]$ and 
$W_n(k) [B A[p^\infty ]]$, respectively, and can both be viewed as objects in 
$D(W_n(k))_{\mathcal {X}}$; the derived category of 
$W_n(k)$-modules in 
$\mathcal {X}$. We set 
$R \Gamma _{\text {crys}}(B A[p^\infty ]/W_n):= R\text {Hom}_{D\left (W_n(k)\right )_{\mathcal {X}}}(W_n(k)[B A[p^\infty ]], \mathcal {O}^{\text {crys}}/W_n)$ and 
$R \Gamma _{\text {crys}}(BA/W_n) := R\text {Hom}_{D\left (W_n(k)\right )_{\mathcal {X}}}(W_n(k)[B A], \mathcal {O}^{\text {crys}}/W_n)$.
Lemma 3.33. There is a natural isomorphism 
$W_n(k)[B A[p^\infty ]] \simeq W_n(k) [B A]$ in 
$D(W_n(k))_{\mathcal {X}}$. Thus
$$ \begin{align*} R \Gamma _{\text{crys}} (B A[p^\infty]/W_n) \simeq R \Gamma_{\text{crys}} (BA/W_n). \end{align*} $$Proof. Since the multiplication-by-p map on the abelian variety A is a syntomic cover, it follows that as an abelian group object of 
$\mathcal {X},$ multiplication by p is surjective on A. Using the map 
$A[p^\infty ] \to A$, we obtain a natural map 
$W_n(k)[BA[p^\infty ]] \to W_n(k)[BA]$, and in order to prove that this map is a quasi-isomorphism, we need to check that 
$H^i (W_n(k)[BA[p^\infty ]]) \to H^i (W_n(k)[BA])$ is an isomorphism. Note that since the topos 
$\mathcal {X}$ can be generated by affine schemes, it is (locally) coherent, and by Deligne’s theorem [Reference Artin, Grothendieck and VerdierAGV72, Exposé VI, p. 336] it has enough points. Therefore, in order to check that the map 
$H^i (W_n(k)[BA[p^\infty ]]) \to H^i (W_n(k)[BA])$ is an isomorphism, it is enough to check it by taking stalks at a (geometric) point 
$x: \text {Sets} \to \mathcal {X}$. But since taking stalks is an exact functor, it commutes with taking cohomology. Therefore, we can take stalks levelwise on the complexes associated to 
$W_n(k)[B A[p^\infty ]]$ and 
$W_n(k)[BA]$ and then check that the map is a quasi-isomorphism. Again, noting that taking stalks commutes with the free 
$W_n(k)$-module object construction, we are reduced to proving that there is a natural quasi-isomorphism 
$W_n(k)[BA_x[p^\infty ]] \to W_n(k)[B A_x]$ of complexes of 
$W_n(k)$-modules. This follows from Lemma 3.31.
By taking inverse limits over n, we obtain 
$R \Gamma _{\text {crys}}(B A[p^\infty ]) \simeq R \Gamma _{\text {crys}}(BA)$. Now Proposition 3.32 follows from the fact that 
$H^*_{\text {crys}}(BA)$ is a symmetric algebra in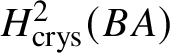 
$H^2_{\text {crys}}(BA)$ by Proposition 3.28.
Proposition 3.34. Let G be any p-divisible group over k. Then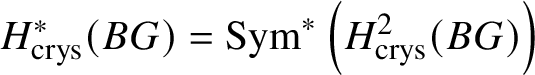 
$H^*_{\text {crys}} (BG)= \text {Sym}^{*} \left (H^2_{\text {crys}}(BG)\right )$, where 
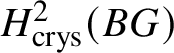$H^2_{\text {crys}}(BG)$ is considered to be in degree 
$2$.
Proof. At first we assume that the field k is algebraically closed. By the results proven in [Reference OortOor00], it follows that there exists a p-divisible group 
$G'$ such that there is an isomorphism 
$G \times G' \simeq A[p^\infty ]$ for some abelian variety A. Indeed, by taking 
$G'$ to be the dual of G, we get a p-divisible group 
$G \times G'$ which has a symmetric Newton polygon; therefore, by [Reference OortOor00, Section 5] there exists some abelian variety 
$A'$ such that 
$A'[p^\infty ]$ and 
$G \times G'$ have the same Newton polygon. By the Dieudonné–Manin classification, 
$A'$ is isogenous to 
$G \times G'$. Quotienting 
$A'$ by a finite flat group scheme if necessary, one obtains an abelian variety A as desired.
Using the zero section of 
$G'$ we have a map 
$G \to G \times G'$ which when composed with projection to G gives the identity map. Thus 
$BG$ is a retract of 
$BA[p^\infty ]$. Since 
$H^*_{\text {crys}}(BA[p^\infty ])$ is generated as a (commutative) symmetric algebra in degree 
$2$ classes, it follows that 
$H^*_{\text {crys}}BG$ is generated by degree 
$2$ classes – that is, there is a surjection 
$\text {Sym}^{*} \left (H^2 _{\text {crys}}(BG)\right ) \to H^*_{\text {crys}}(BG)$. Doing the same for 
$G'$, we arrive at the following commutative diagram:
The upper horizontal map is an isomorphism, since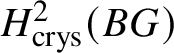 
$H^2_{\text {crys}}(BG)$ is isomorphic to the Dieudonné module (Proposition 3.23), and therefore 
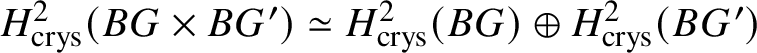$H^2_{\text {crys}}(BG \times BG') \simeq H^2_{\text {crys}}(BG) \oplus H^2_{\text {crys}}(BG')$. By Proposition 3.32, the right vertical map is an isomorphism, since 
$BG \times BG' \simeq B A[p^\infty ]$. This shows that the surjection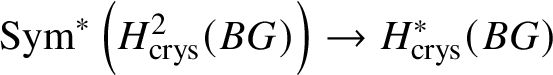 
$\text {Sym}^{*} \left (H^2 _{\text {crys}}(BG)\right ) \to H^*_{\text {crys}}(BG)$ must be an isomorphism, yielding the assertion of the proposition when k is algebraically closed.
We will now remove the assumption that k is algebraically closed. Let k be any perfect field and 
$\overline {k}$ denote the algebraic closure of k. Let 
$G_{\overline {k}}$ denote the base change of G to 
$\text {Spec} \overline {k}$. Our goal is to show that the natural map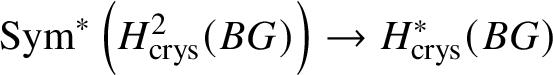 
$\text {Sym}^{*} \left (H^2 _{\text {crys}}(BG)\right ) \to H^*_{\text {crys}}(BG)$ is an isomorphism. By Proposition 3.23 and taking inverse limits over n, it would be enough to show that 
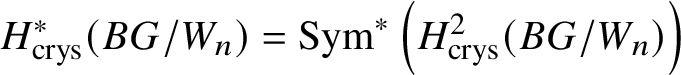$H^*_{\text {crys}}(BG/W_n) = \text {Sym}^* \left (H^2_{\text {crys}}(BG/W_n)\right )$. Since we already know that 
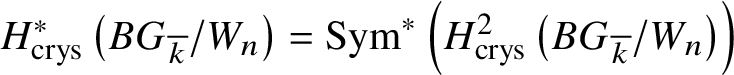$H^*_{\text {crys}}\left (BG_{\overline {k}}/W_n\right ) = \text {Sym}^* \left (H^2_{\text {crys}}\left (BG_{\overline {k}}/W_n\right )\right )$, it would be enough to prove that 
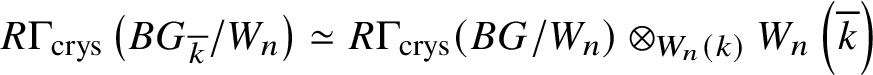$R\Gamma _{\text {crys}}\left (BG_{\overline {k}}/W_n\right ) \simeq R\Gamma _{\text {crys}}(BG/W_n) \otimes _{W_n(k)} W_n\left (\overline {k}\right )$. This reduces to the case when 
$n=1$, so it is enough to show that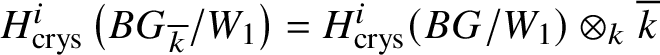 
$H_{\text {crys}}^i \left (BG_{\overline {k}}/W_1\right ) = H_{\text {crys}}^i(BG/W_1) \otimes _k \overline {k}$. We note the following lemma:
Lemma 3.35. Let M be a finite group scheme over a perfect field k. Then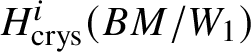 
$H_{\text {crys}}^i (BM/W_1)$ is a finite-dimensional vector space.
Proof. By using descent along the syntomic map 
$\text {Spec} k \to BM$ and [Reference Antieau, Bhatt and MathewABM19, Remark 2.4], it follows that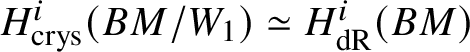 
$H^i_{\text {crys}}(BM/W_1) \simeq H^i _{\text {dR}} (BM)$. Here 
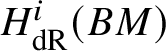$H^i _{\text {dR}} (BM)$ denotes the de Rham cohomology of the smooth stack 
$BM$ as in [Reference Antieau, Bhatt and MathewABM19, Construction 2.4]. In order to show the finiteness of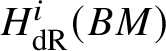 
$H^i_{\text {dR}}(BM)$, since 
$BM$ is smooth, using the Hodge–de Rham spectral sequence from [Reference Antieau, Bhatt and MathewABM19, Definition 3.1(b)] it is enough to show the finiteness of the Hodge cohomology groups of 
$BM$. But this finiteness follows because the cotangent complex of 
$BM$ and its exterior powers are perfect complexes on 
$BM$, and M is a finite group scheme (compare [Reference TotaroTot18, Theorem 3.1]).
Let us write G as the directed system 
$\left \{ G_n\right \}$ of finite group schemes 
$G_n$ over k. For a fixed 
$n,$ we have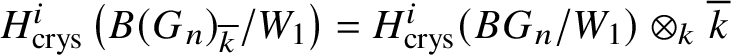 
$H_{\text {crys}}^i \left (B(G_n)_{\overline {k}}/W_1\right )= H_{\text {crys}}^i (BG_n/W_1)\otimes _k \overline {k}$. By the previous lemma, we have
$$ \begin{align*} H_{\text{crys}}^i \left(BG_{\overline{k}}/W_1\right) = \varprojlim_n H_{\text{crys}}^i \left(B(G_n)_{\overline{k}}/W_1\right)=\varprojlim_n \left( H_{\text{crys}}^i (BG_n/W_1) \otimes_k \overline{k} \right). \end{align*} $$ We note that the prosystem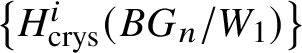 
$\left \{H_{\text {crys}}^i (B G_n/W_1)\right \}$ is essentially constant [SP, Tag 05PT]. Indeed, this can be seen by changing base to 
$\overline {k}$ and noting that the prosystem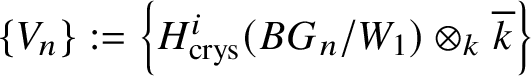 
$\left \{V_n\right \} := \left \{H_{\text {crys}}^i (B G_n/W_1)\otimes _k \overline {k} \right \}$ consists of finite-dimensional 
$\overline {k}$-vector spaces, and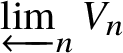 
$\varprojlim _n V_n$ is finite-dimensional as well. The first assertion follows from Lemma 3.35, and the second one follows from the statement of Proposition 3.34 for the algebraically closed field 
$\overline {k}$. Therefore,
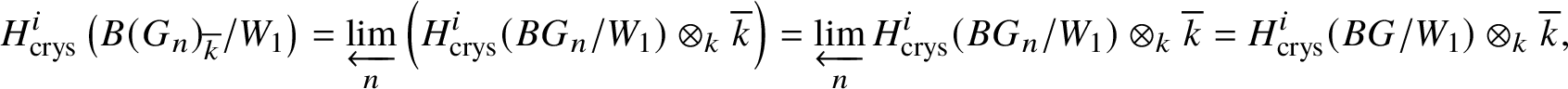$$ \begin{align*} H_{\text{crys}}^i \left(B(G_n)_{\overline{k}}/W_1\right)=\varprojlim_n \left( H_{\text{crys}}^i (BG_n/W_1) \otimes_k \overline{k} \right) = \varprojlim_n H_{\text{crys}}^i (BG_n/W_1) \otimes_k \overline{k}= H_{\text{crys}}^i (BG/W_1)\otimes_k \overline{k}, \end{align*} $$which finishes the proof.
4 Prismatic cohomology
4.1 Prismatic cohomology for stacks
In this section, we start by recalling the notion of prismatic cohomology and then extend it to stacks. The main references for this section are [Reference Bhatt and ScholzeBS19]. We will freely use the definitions and notations from those papers. Our somewhat terse exposition here is also loosely based on [Reference Anschütz and Le BrasALB19]. We will sometimes use the notion of derived p-completion in the proofs; for its basic properties, we refer to [SP, Tag 091N]. More details on notions such as p-complete flatness can be found in [Reference Bhatt, Morrow and ScholzeBMS19, Section 4].
Definition 4.1 [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.1]
Let 
$A \to B$ be a map of commutative rings. We will call this map p-completely (faithfully) flat if 
$B \otimes ^L_A A/p \in D(A/p)$ is concentrated in degree 
$0$, and is a (faithfully) flat 
$A/p$-algebra.
Definition 4.2 [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.1]
Let A be a commutative ring and M be an object in the derived category 
$D(A)$. Set 
$a,b \in \mathbb {Z} \sqcup \left \{ \pm \infty \right \}$. We will say that M has p-complete Tor-amplitude in 
$[a,b]$ if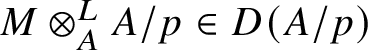 
$M \otimes ^L_{A} A/p \in D(A/p)$ has Tor-amplitude in 
$[a,b]$. The latter condition means that if we set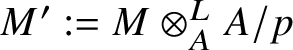 
$M':= M \otimes ^L_{A} A/p$, then 
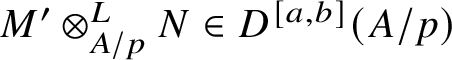$M' \otimes ^L_{A/p} N \in D^{\left [a,b\right ]}(A/p)$ for any 
$A/p$-module N.
Definition 4.3 [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.10]
A ring S is called quasisyntomic if it is p-complete with bounded 
$p^\infty $-torsion and the cotangent complex 
$\mathbb {L}_{S/\mathbb {Z}_p}$ has p-complete Tor-amplitude in 
$[-1,0]$. The category of all quasisyntomic rings is denoted by 
$\text {QSyn}$. A map 
$S \to S'$ of p-complete rings with bounded 
$p^\infty $-torsion is a quasisyntomic morphism if 
$S'$ is p-completely flat over S and the cotangent complex 
${\mathbb {L}_{S'/S}}$ has p-complete Tor-amplitutde in 
$[-1,0]$. A quasisyntomic morphism is called a quasisyntomic cover if the map 
$S \to S'$ is p-completely faithfully flat.
Remark 4.4. Note that since a quasisyntomic ring S is assumed to have bounded 
$p^\infty $-torsion, the notion of derived p-completeness is equivalent to classical p-completeness in this case (compare [SP, Tag 0923]).
Definition 4.5 [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.18]
A ring S is called an integral perfectoid if it is p-complete, such that 
$\pi ^p = p u$ for some 
$\pi \in S, u \in S ^\times $, the Frobenius is surjective on 
$S/p$ and the kernel of the map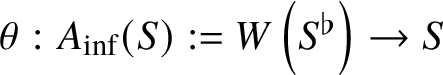 
$\theta : A_{\text {inf}}(S) := W\left (S^\flat \right ) \to S$ is principal.
Definition 4.6 [Reference Bhatt, Morrow and ScholzeBMS19, Definition 4.20]
A ring S is called a quasiregular semiperfectoid (QRSP) if 
$S \in \text {QSyn}$ and there exists a perfectoid ring R mapping surjectively onto S.
Definition 4.7. If R is any p-complete ring, we will let 
$(R)_{\text {qsyn}}$ denote the (opposite) category of all p-complete rings over R which are quasisyntomic. This category can be equipped with a Grothendieck topology generated by quasisyntomic covers, which turns this into a site.
Remark 4.8. By the results in [Reference Bhatt, Morrow and ScholzeBMS19, Section 4.4], QRSP rings form a basis for the site 
$(R)_{\text {qsyn}}$. Therefore, specifying a sheaf on 
$(R)_{\text {qsyn}}$ amounts to assigning values to the QRSP rings satisfying the descent condition.
In [Reference Bhatt and ScholzeBS19] the authors defined prismatic cohomology first for p-complete smooth algebras and then extended it to all p-complete algebras [Reference Bhatt and ScholzeBS19, Construction 7.6], calling it the derived prismatic cohomology. An important fact [Reference Bhatt and ScholzeBS19, Proposition 7.10] about this construction is that for every QRSP ring S, the derived prismatic cohomology, denoted as
, lives only in degree 
$0$ – that is, is discrete. Also, the functor
forms a quasisyntomic sheaf [Reference Bhatt and ScholzeBS19, Construction 7.6(3)]. Using these facts, the authors in [Reference Anschütz and Le BrasALB19] construct a sheaf of rings 
$\mathcal {O}^{\text {pris}}$ on 
$(R)_{\text {qsyn}}$ such that for any QRSP ring S over R, one has
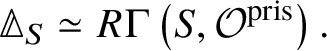
Further, we note that for any prism 
$(A,I)$, there is a decreasing filtration 
$\mathcal {N}^{\ge \bullet } A$, called the Nygaard filtration, which is defined as
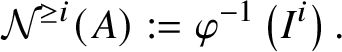$$ \begin{align*} \mathcal{N}^{\ge i}(A):= \varphi^{-1} \left(I^i\right). \end{align*} $$This equips the sheaf of rings 
$\mathcal {O}^{\text {pris}}$ with a decreasing filtration 
$\mathcal {N}^{\ge \bullet } \mathcal {O}^{\text {pris}}$ of sheaves.
Remark 4.9. We explain the construction of the Nygaard filtration in detail. Using [Reference Anschütz and Le BrasALB19, Corollary 3.3.10], we have a morphism of topoi
where
denotes the absolute prismatic site as in [Reference Anschütz and Le BrasALB19, Definition 3.1.4]. On
one defines a sheaf of rings
by sending a prism 
$(A,I) \to A$. Using the notion of Nygaard filtration on a prism, one can equip this sheaf of rings
with the Nygaard filtration
, which sends a prism 
$(A,I) \to \mathcal {N}^{\ge \bullet } A \subseteq A$. In order to prove that the presheaf 
$(A,I) \to \mathcal {N}^{\ge \bullet } A$ is indeed a sheaf, we note that 
$\mathcal {N}^{\ge i}(A)$ is the kernel of a map of a presheaf of rings 
$((A,I) \to A ) \to \left ((A,I) \to A/I^i\right )$ obtained by composing 
$\varphi : A \to A$ with the projection map 
$A \to A/I^i$. Therefore it will be enough to show that the presheaf 
$(A,I) \to A/I^i$ is a sheaf. This follows from the proof of [Reference Bhatt and ScholzeBS19, Corollary 3.12] by noting that for a map 
$(A,I) \to (B,J)$ of prisms, one has 
$I^i B = J^i$ by [Reference Bhatt and ScholzeBS19, Lemma 3.5]. One defines
By this definition and [Reference Bhatt and ScholzeBS19, Proposition 7.2], it follows that
for a QRSP ring 
$S \in (R)_{\text {qsyn}}$. In fact, by Remark 4.8 this description can be used to define the sheaves 
$\mathcal {N}^{\ge \bullet }\mathcal {O}^{\text {pris}}$ after one proves that it forms a sheaf on the basis objects. However, although a priori it is not obvious, actually more is true: The functor that sends a QRSP algebra
forms a sheaf with vanishing higher cohomology – that is,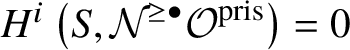 
$H^i \left (S, \mathcal {N}^{\ge \bullet } \mathcal {O}^{\text {pris}}\right ) = 0$ for 
$i \ge 1$ and a QRSP algebra S. This fact follows from [Reference Bhatt and ScholzeBS19, Theorem 12.2] and [Reference Bhatt, Morrow and ScholzeBMS19, Theorem 3.1].
Definition 4.10. We call 
$\mathcal {Y}$ a quasisyntomic stack over R if it is a stack with respect to the site 
$(R)_{\text {qsyn}}$.
Remark 4.11. If 
$A \in (R)_{\text {qsyn}}$, then by p-completely faithfully flat descent it follows that 
$h_{A}$ is a sheaf with respect to 
$(R)_{\text {qsyn}}$. If 
$\mathcal {Y}$ is a quasisyntomic stack, an arrow 
$h_A \to \mathcal {Y}$ will be denoted as 
$\text {Spf}A \to \mathcal {Y}$.
Remark 4.12. Let X be a p-adic formal scheme over R. Then setting 
$\underline {X}(A):= \text {Hom}_{\text {formal sch}}(\text {Spf} A, X)$ defines a quasisyntomic sheaf on 
$(R)_{\text {qsyn}}$, which we will denote by 
$\underline {X}$.
Definition 4.13. Let 
$\mathcal {Y}$ be a quasisyntomic stack. We define the prismatic cohomology of 
$\mathcal {Y}$ to be
where 
$A \in (R)_{\text {qsyn}}$ and the derived limit is taken in the derived category of abelian groups.
Remark 4.14. Let 
$\mathcal {Y}$ be a quasisyntomic stack. We give an alternative description of 
. One can define the quasisyntomic site of 
$\mathcal {Y}$, denoted as 
$(\mathcal {Y})_{\text {qsyn}}$, to be the category whose objects are 
$\text {Spf} A \to \mathcal {Y}$ for 
$A \in (R)_{\text {qsyn}}$ equipped with the quasisyntomic covers – that is, we let 
$(\mathcal {Y})_{\text {qsyn}}:= (R)_{{\text {qsyn}}_{/ \mathcal {Y}}}$. Then by the discussion preceding Definition 4.10, we obtain a sheaf of rings 
$\mathcal {O}^{\text {pris}}$ on 
$(\mathcal {Y})_{\text {qsyn}}$. Then it follows that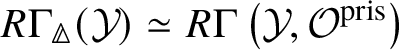 
.
Definition 4.15. Let 
$\mathcal {Y}$ be a quasisyntomic stack. The Nygaard filtration on the prismatic cohomology
is defined to be
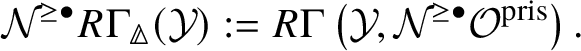
Definition 4.16. Now we consider an algebraic stack 
$\mathcal {X}$ over R. We will define the p-adic completion of 
$\mathcal {X}$ as a quasisyntomic stack, which will be denoted as 
$\widehat {\mathcal {X}}$. We define
$$ \begin{align*} \widehat{\mathcal{X}}(A):= \varprojlim \mathcal{X}(A/p^n), \end{align*} $$where 
$A \in (R)_{\text {qsyn}}$. This defines a sheaf of groupoids in the site 
$(R)_{\text {qsyn}}$. Indeed, 
$\widehat {\mathcal {X}}$ by definition is an inverse limit of the sheaves on 
$(R)_{\text {qsyn}}$ which sends 
$A \to \mathcal {X}(A/p^n)$ and therefore has to be a sheaf.
Definition 4.17. We define the prismatic cohomology of a stack 
$\mathcal {X}$ to be
Proposition 4.18. If X is a p-adic formal scheme over R, then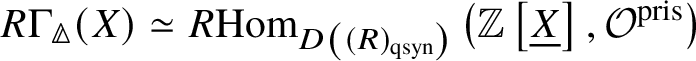 
, where 
$\underline {X}$ is the quasisyntomic sheaf associated to X on 
$(R)_{\text {qsyn}}$.
Remark 4.19. Instead of considering quasisyntomic stacks, one could also work with ‘p-adic formal stacks’, which can be defined to be stacks with respect to the Grothendieck site on the category of p-complete and bounded 
$p^\infty $-torsion rings equipped with p-completely faithfully flat covers. Any p-adic formal stack can also be regarded as a quasisyntomic stack. The reason we work with the notion of quasisyntomic stacks is that the notion of prismatic cohomology in Definition 4.13 would ultimately regard a p-adic formal stack as a quasisyntomic stack. Hence one might as well define prismatic cohomology for quasisyntomic stacks.
4.2 Application to prismatic Dieudonné theory
From now we will assume that the ring R is a QRSP ring. Let 
be the prism associated to R by taking prismatic cohomology. We briefly recall some definitions from [Reference Anschütz and Le BrasALB19] and review their theorem on classification of p-divisible groups in terms of filtered prismatic Dieudonné modules.
Definition 4.20 [Reference Anschütz and Le BrasALB19, Definition 4.1.10]
A filtered prismatic Dieudonné module over R is a collection 
$(M, \mathrm {Fil}M, \varphi _M)$ consisting of a finite locally free 
-module M, a 
-submodule 
$\mathrm {Fil}M$ and 
$\varphi $ a linear map 
$\varphi _M:M \to M$ satisfying the following:
(1)
$\varphi _M(\mathrm {Fil}M) \subset IM$ and $\varphi _M(\mathrm {Fil}M)$ generates $I M$ as a -module.(2)
and $M/ \mathrm {Fil}M$ is a finite locally free R-module.
Now let G be a p-divisible group. One makes the following definition:
Definition 4.21. The quasisyntomic sheaf 
$\underline {G} \in (R)_{\text {qsyn}}$ associated to a p-divisible group G is defined to be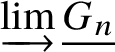 
$\varinjlim \underline {G_n}$, where 
$\underline {G_n} \in (R)_{\text {qsyn}}$ is the quasisyntomic sheaf associated to 
$\text {Spf}G_n$.
The authors in [Reference Anschütz and Le BrasALB19] make the following definition, which can be seen as a generalisation of Theorem 3.8:
Definition 4.22 [Reference Anschütz and Le BrasALB19, Definition 4.2.8]
Let G be a p-divisible group over R. We define
and
as the endomorphism induced by 
$\varphi $ on 
$\mathcal {O}^{\text {pris}}$. Then
is called the filtered prismatic Dieudonné module of G.
In this case, the main theorem of [Reference Anschütz and Le BrasALB19] says the following:
Theorem 4.23. The filtered prismatic Dieudonné module functor
defines an antiequivalence between the category of p-divisible groups over R and the category of filtered prismatic Dieudonné modules over R.
Example 4.24. For the étale p-divisible group 
$\mathbb {Q}_p/{\mathbb {Z}_p}$ over R, we have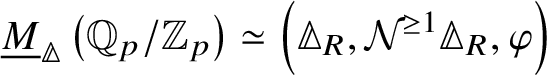 
. We refer to [Reference Anschütz and Le BrasALB19, Section 4.7, Remark 4.9.6] for more discussions.
Example 4.25. Let 
$\widehat {A}$ denote the p-adic completion of an abelian scheme A over R. Let us denote the p-divisible group associated to 
$\widehat {A}$ by 
$A[p^\infty ]$ for simplicity. In this case, the prismatic Dieudonné module 
is locally free of rank 
$2\cdot \text {dim} A$ and is isomorphic to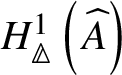 
, which identifies the natural Frobenius on both of these modules as well [Reference Anschütz and Le BrasALB19, Theorem 4.5.6]. Further, by using the proof of [Reference Anschütz and Le BrasALB19, Proposition 4.5.9], one obtains that 
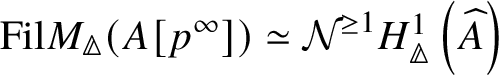, where 
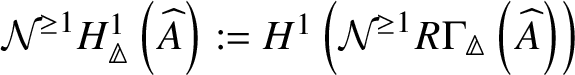(compare Proposition 4.39).
Now we proceed toward proving Theorem 1.6. Let 
$G= \text {Spec} B$ be a finite flat group scheme over R. Since G is syntomic, it follows that 
$\text {Spf} (B)$ is quasisyntomic. If 
${BG}$ denotes the associated quasisyntomic stack, then 
$* \to {BG}$ is a 
$\underline {G}$-torsor and is a quasisyntomic cover. The Čech nerve of the map 
$* \to {BG}$ is given by the simplicial quasi-syntomic sheaf
The associated simplicial abelian group object is
With this simplicial object we can associate an object of 
$D\left ((R)_{\text {qsyn}}\right )$, which we will denote simply by 
$\mathbb {Z}[{BG}]$.
Proposition 4.26. Let G be a finite flat group scheme over R. Then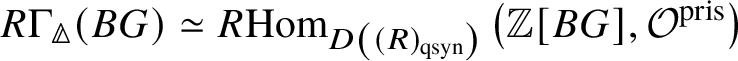 
.
Proof. By Čech descent along the quasisyntomic cover 
$* \to \underline {BG}$, we obtain
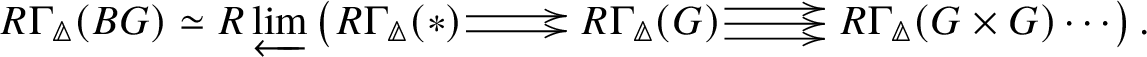
By Proposition 4.18, this is
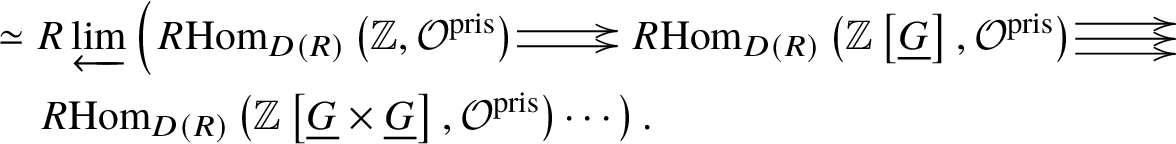
We can take the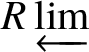 
$R \varprojlim $ inside as a homotopy colimit, which gives us that this is 
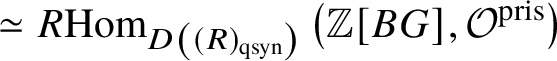${\simeq R\text {Hom}_{D\left ((R)_{\text {qsyn}}\right )}\left (\mathbb {Z}[{BG}], \mathcal {O}^{\text {pris}}\right )}$, as desired.
Definition 4.27. The classifying stack of a p-divisible group 
$G= \left \{G_n \right \}$ is defined to be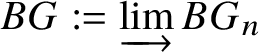 
$BG := \varinjlim {B G_n}$, where the filtered colimit is taken in the category of quasisyntomic stacks with respect to the site 
$(R)_{\text {qsyn}}$.
Proposition 4.28. For a p-divisible group 
$G= \left \{ G_n \right \}$, we have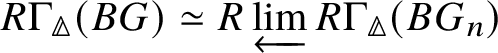 
.
Proof. This follows because 
$BG$ is defined to be the filtered colimit of the quasisyntomic stacks 
$BG_n$.
Since filtered colimits commute with finite limits, the Čech nerve of 
$* \to BG$ is given by the simplicial quasisyntomic sheaf
The associated simplicial abelian group object is
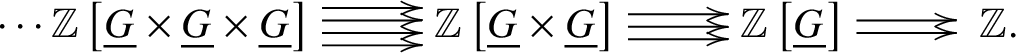
With this simplicial object, we can associate an object of 
$D\left ((R)_{\text {qsyn}}\right )$, which will be denoted by 
$\mathbb {Z}[BG]$. Since filtered colimits are exact in the category of abelian sheaves on 
$(R)_{\text {qsyn}}$, we have that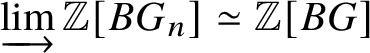 
$\varinjlim \mathbb {Z}[BG_n] \simeq \mathbb {Z}[BG]$.
Proposition 4.29. Let G be a p-divisible group over R. Then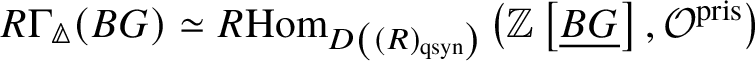 
.
Proof. By Propositions 4.26 and 4.28, we have
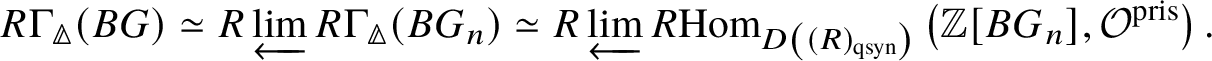
Now
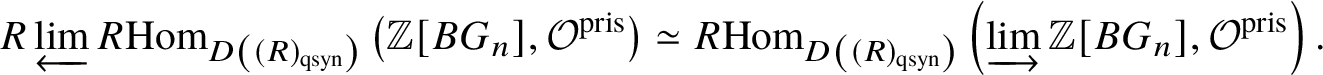$$ \begin{align*} R\varprojlim R\text{Hom}_{D\left((R)_{\text{qsyn}}\right)}\left(\mathbb{Z}[{BG_n}], \mathcal{O}^{\text{pris}}\right) \simeq R\text{Hom}_{D\left((R)_{\text{qsyn}}\right)}\left( \varinjlim\mathbb{Z}[{BG_n}], \mathcal{O}^{\text{pris}}\right). \end{align*} $$Since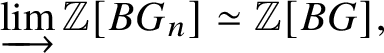 
$\varinjlim \mathbb {Z}[BG_n] \simeq \mathbb {Z}[BG],$ we obtain the required statement.
Remark 4.30. Alternatively, one could descend along the effective epimorphism 
$* \to BG$.
Proposition 4.31. There is a spectral sequence with 
$E_2$-page
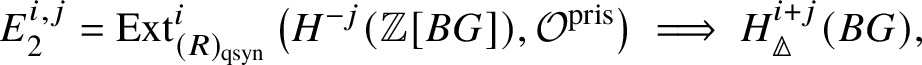
and another spectral sequence with 
$E_1$-page
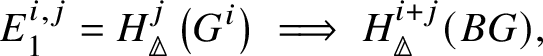
where 
$G^i$ denotes the i-fold fibre product of 
$\text {Spf} G$ with itself. By convention, 
$G^0 = *$.
Proof. This follows in a way similar to Proposition 3.13.
Lemma 4.32. 
$H^0 (\mathbb {Z}[BG]) \simeq \mathbb {Z}$, 
$H^{-1}(\mathbb {Z}[BG]) \simeq \underline {G}$ and 
$H^{-2}(\mathbb {Z}[BG]) \simeq \underline {G} \wedge \underline {G}$.
Proof. This follows exactly in the same ways as in the proof of Lemma 3.9, after further noting that for an abelian group G, the second group homology with integral coefficients 
$H_2 (G, \mathbb {Z}) \simeq G \wedge G$. This isomorphism can be found in [Reference MillerCM52, Theorem 3].
Proposition 4.33. There is a natural isomorphism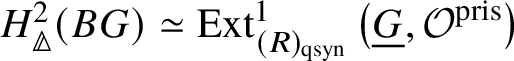 
.
Proof. By the 
$E_2$ spectral sequence from Proposition 4.31 and Lemma 4.32, this will follow once we prove that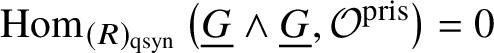 
$\text {Hom}_{(R)_{\text {qsyn}}}\left (\underline {G} \wedge \underline {G}, \mathcal {O}^{\text {pris}}\right )= 0$ and 
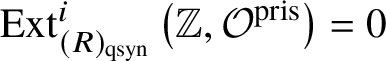$\text {Ext}^i_{(R)_{\text {qsyn}}}\left (\mathbb {Z}, \mathcal {O}^{\text {pris}}\right )=0$ for 
$i \ge 1$. We begin by proving the first vanishing. We have a surjection 
$\underline {G}\otimes \underline {G} \to \underline {G} \wedge \underline {G}\to 0$, which gives us an injection
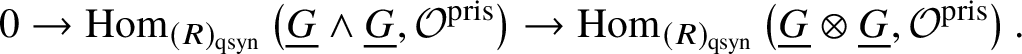$$ \begin{align*} 0 \to \text{Hom}_{(R)_{\text{qsyn}}}\left(\underline{G} \wedge \underline{G}, \mathcal{O}^{\text{pris}}\right) \to \text{Hom}_{(R)_{\text{qsyn}}}\left(\underline{G} \otimes \underline{G}, \mathcal{O}^{\text{pris}}\right). \end{align*} $$Thus it is enough to show that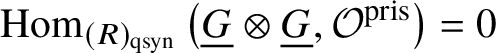 
$\text {Hom}_{(R)_{\text {qsyn}}}\left (\underline {G} \otimes \underline {G}, \mathcal {O}^{\text {pris}}\right ) = 0$. Indeed,
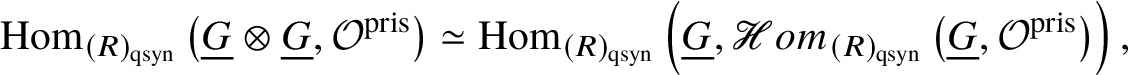$$ \begin{align*} \text{Hom}_{(R)_{\text{qsyn}}}\left(\underline{G} \otimes \underline{G}, \mathcal{O}^{\text{pris}}\right) \simeq \text{Hom}_{(R)_{\text{qsyn}}}\left(\underline{G}, \mathscr{H}{om}_{(R)_{\text{qsyn}}}\left( \underline{G}, \mathcal{O}^{\text{pris}}\right)\right), \end{align*} $$and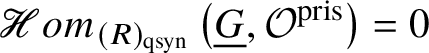 
$\mathscr {H}{om}_{(R)_{\text {qsyn}}}\left ( \underline {G}, \mathcal {O}^{\text {pris}}\right )= 0$, since G is p-divisible and 
$\mathcal {O}^{\text {pris}}$ is derived p-complete. Therefore, we obtain the required statement. Now the second vanishing follows from the fact that for a QRSP ring S, its prismatic cohomology 
is discrete – that is, lives only in degree 
$0$. This finishes the proof.
Proposition 4.34. In the foregoing situation,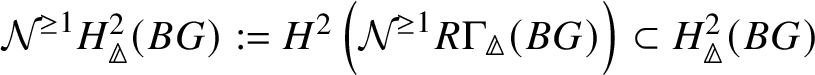 
and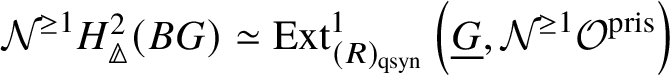 
.
Proof. By Definition 4.15, we have
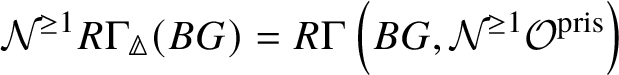
. Hence, analogous to Proposition 4.26, by descent along the effective epimorphism 
$* \to BG$ we obtain
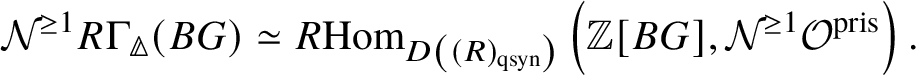
By the spectral sequence, analogous to Proposition 4.31 we obtain that in order to prove
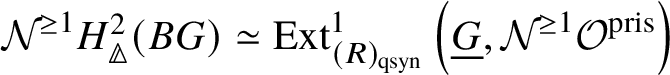
, by Lemma 4.32 it is enough to prove that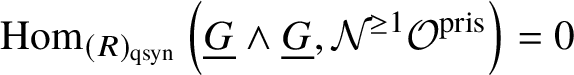 
$\text {Hom}_{(R)_{\text {qsyn}}} \left (\underline {G} \wedge \underline {G}, \mathcal {N}^{\ge 1}\mathcal {O}^{\text {pris}}\right )=0$ and 
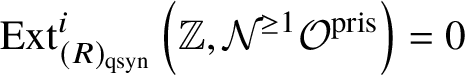$\text {Ext}^i_{(R)_{\text {qsyn}}} \left (\mathbb {Z}, \mathcal {N}^{\ge 1}\mathcal {O}^{\text {pris}}\right )=0$ for 
$i \ge 2$. By the proof of Proposition 4.33, in order to prove the first vanishing it is enough to prove that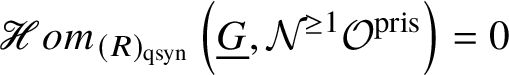 
$\mathscr {H}om_{(R)_{\text {qsyn}}}\left (\underline {G}, \mathcal {N}^{\ge 1}\mathcal {O}^{\text {pris}}\right )=0$. By the injection 
$0 \to \mathcal {N}^{\ge 1}\mathcal {O}^{\text {pris}} \to \mathcal {O}^{\text {pris}} $ of sheaves, the required vanishing follows from the fact that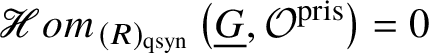 
$\mathscr {H}{om}_{(R)_{\text {qsyn}}}\left ( \underline {G}, \mathcal {O}^{\text {pris}}\right )= 0$, which was noted in the proof of Proposition 4.33. Now for proving 
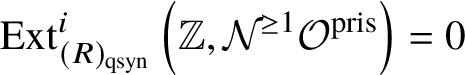$\text {Ext}^i_{(R)_{\text {qsyn}}} \left (\mathbb {Z}, \mathcal {N}^{\ge 1}\mathcal {O}^{\text {pris}}\right )=0$ for 
$i \ge 2$, using the exact sequence
$$ \begin{align*} 0 \to \mathcal{N}^{\ge 1}\mathcal{O}^{\text{pris}} \to \mathcal{O}^{\text{pris}} \to \mathcal{O} \to 0 \end{align*} $$from [Reference Anschütz and Le BrasALB19, Proposition 4.1.2], where 
$\mathcal {O}$ denotes the structure sheaf on 
$(R)_{\text {qsyn}},$ it is enough to show that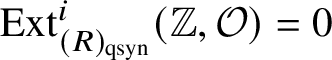 
$\text {Ext}^i_{(R)_{\text {qsyn}}}(\mathbb {Z}, \mathcal {O})=0$ for 
$i \ge 1$, which follows from p-completely faithfully flat descent for bounded 
$p^\infty $-torsion rings [Reference Bhatt, Morrow and ScholzeBMS19, Remark 4.9]. The inclusion
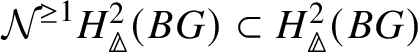
now follows from the exact sequence and the fact that 
$\text {Hom}\left (\underline {G}, \mathcal {O}\right )= 0$, since G is p-divisible and 
$\mathcal {O}$ is derived p-complete.
Remark 4.35. We note that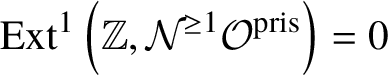 
$\text {Ext}^1\left (\mathbb {Z}, \mathcal {N}^{\ge 1} \mathcal {O}^{\text {pris}}\right )=0$ as well. This follows from the foregoing exact sequence and [Reference Anschütz and Le BrasALB19, Theorem 3.4.6].
Remark 4.36. Similar to Proposition 3.14, it follows that for a p-divisible group G over R, we have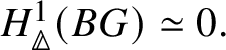 
Remark 4.37. One can define prismatic cohomology for higher quasisyntomic stacks as well. In particular, one can talk about prismatic cohomology of the n-stacks 
$K(G,n)$ for a p-divisible group G. Similar to Remark 3.17, one can prove that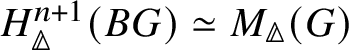 
and 
for 
$1 \le i \le n$.
Now we look at the case where 
$\widehat {A}$ is the p-adic completion of an abelian scheme A over R. In this situation one can consider the p-divisible group associated to 
$\widehat {A}$, which will be written as 
$ {A}[p^\infty ]. $ We let 
$B\widehat {A}$ denote the classifying stack of 
$\widehat {A}$, which we define to be the p-adic completion of the stack 
$BA$. The quasisyntomic sheaf represented by 
$\widehat {A}$ will simply be written as 
$\underline {A}$. Then we have the following:
Proposition 4.38. We have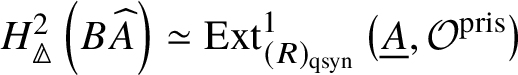 
and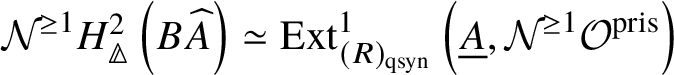 
.
Proof. This follows exactly in the same way as the proof of Proposition 4.33, after noting that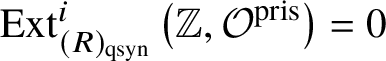 
$\text {Ext}^i_{(R)_{\text {qsyn}}}\left (\mathbb {Z}, \mathcal {O}^{\text {pris}}\right )=0$ for 
$i \ge 1$, as before, and 
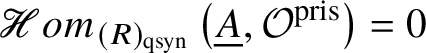$\mathscr {H}om_{(R)_{\text {qsyn}}}\left (\underline {A}, \mathcal {O}^{\text {pris}}\right )= 0$ by [Reference Anschütz and Le BrasALB19, Theorem 4.5.6]. The second part follows.
Proposition 4.39.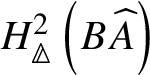 
is naturally isomorphic to the prismatic Dieudonné module associated to the p-divisible group 
${A}[p^\infty ]$. Further,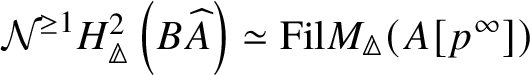 
.
Proof. Using Proposition 4.38, it is enough to prove that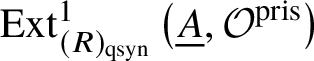 
$\text {Ext}^1_{(R)_{\text {qsyn}}}\left (\underline {A}, \mathcal {O}^{\text {pris}}\right )$ is isomorphic to 
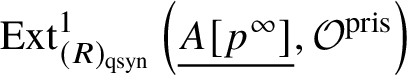$\text {Ext}^1_{(R)_{\text {qsyn}}}\left (\underline {{A}[p^\infty ]}, \mathcal {O}^{\text {pris}}\right )$. Note that we have
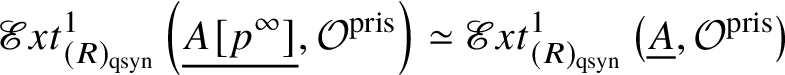$$ \begin{align*} \mathscr{E}xt^1_{(R)_{\text{qsyn}}}\left(\underline{{A}[p^\infty]}, \mathcal{O}^{\text{pris}}\right) \simeq \mathscr{E}xt^1_{(R)_{\text{qsyn}}}\left(\underline{A}, \mathcal{O}^{\text{pris}}\right) \end{align*} $$and
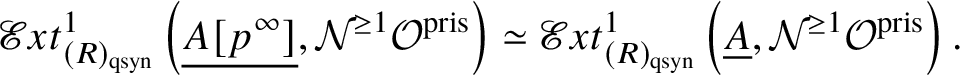$$ \begin{align*} \mathscr{E}xt^1_{(R)_{\text{qsyn}}}\left(\underline{{A}[p^\infty]}, \mathcal{N}^{\ge 1} \mathcal{O}^{\text{pris}}\right) \simeq \mathscr{E}xt^1_{(R)_{\text{qsyn}}}\left(\underline{A}, \mathcal{N}^{\ge 1} \mathcal{O}^{\text{pris}}\right). \end{align*} $$Indeed, to see these isomorphisms, we note that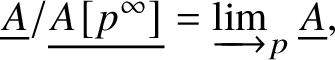 
$\underline {A}/ \underline {A[p^\infty ]} = \varinjlim _{p} \underline {A},$ and for any sheaf 
$\mathscr {F},$ we have
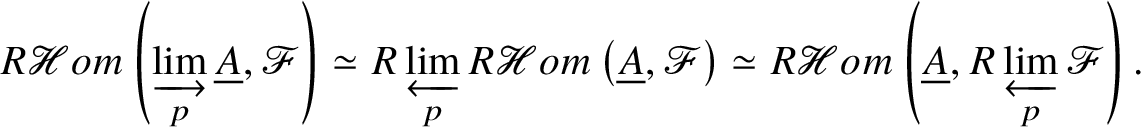$$ \begin{align*} R \mathscr{H}om \left(\varinjlim_{p} \underline{A}, \mathscr{F}\right) \simeq R\varprojlim_{p}R\mathscr{H}om \left(\underline{A}, \mathscr{F}\right) \simeq R\mathscr{H}om \left(\underline{A}, R\varprojlim_{p}\mathscr{F}\right). \end{align*} $$Now if 
$\mathscr {F}$ is further assumed to be a sheaf of derived p-complete abelian groups with vanishing higher cohomology on a collection of basis objects, then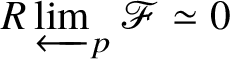 
$R\varprojlim _{p} \mathscr {F} \simeq 0$. To see this, it is enough to prove that for any such basis object 
$V,$ one has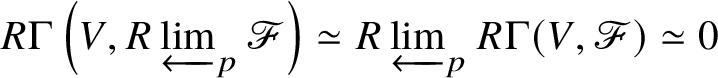 
$R\Gamma \left (V, R\varprojlim _{p} \mathscr {F}\right ) \simeq R\varprojlim _{p} R\Gamma (V, \mathscr {F}) \simeq 0$. But this follows from our assumptions, since 
$R\Gamma (V, \mathscr {F}) \simeq \mathscr {F}(V)$ and 
$\mathscr {F}(V)$ is derived p-complete [SP, Tag 091N]. Finally, by taking 
$\mathscr {F}$ to be 
$\mathcal {O}^{\text {pris}}$ or 
$\mathcal {N}^{\ge 1} \mathcal {O}^{\text {pris}}$ and using Remark 4.9, we obtain the required vanishings to yield the desired isomorphisms of 
$\mathscr {E}xt$-groups.
The proposition now follows by applying the global section functor and noting that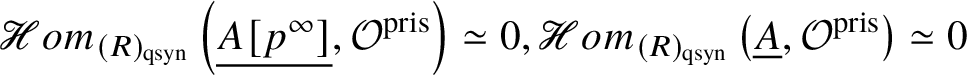 
$\mathscr {H}om_{(R)_{\text {qsyn}}}\left (\underline {{A}[p^\infty ]}, \mathcal {O}^{\text {pris}}\right ) \simeq 0, \mathscr {H}om_{(R)_{\text {qsyn}}}\left (\underline {A}, \mathcal {O}^{\text {pris}}\right ) \simeq 0$ and 
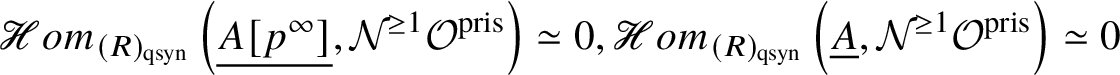$\mathscr {H}om_{(R)_{\text {qsyn}}}\left (\underline {{A}[p^\infty ]}, \mathcal {N}^{\ge 1} \mathcal {O}^{\text {pris}}\right ) \simeq 0, \mathscr {H}om_{(R)_{\text {qsyn}}}\left (\underline {A}, \mathcal {N}^{\ge 1}\mathcal {O}^{\text {pris}}\right ) \simeq 0$. These vanishings have been noted before in the proofs of Propositions 4.33, 4.34 and 4.38. This ends the proof.
As in Section 3.3, if 
$\widehat {A}$ is the p-adic completion of an abelian scheme A over R, we can explicitly compute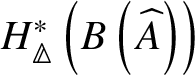 
.
Proposition 4.40. We have a natural isomorphism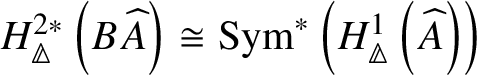 
, and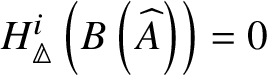 
for odd i.
Proof. This follows exactly in the same way as in the proof in the crystalline case in Section 3.3 from the 
$E_1$ spectral sequence in Proposition 4.31, the Künneth formula in prismatic cohomology [Reference Anschütz and Le BrasALB19, Corollary 3.5.2] and the calculations of the prismatic cohomology of abelian varieties in [Reference Anschütz and Le BrasALB19, Corollary 4.5.8].
Acknowledgments
I am grateful to Bhargav Bhatt for suggesting that Dieudonné modules could be recoverable via crystalline cohomology of classifying stacks, as well as for numerous helpful conversations regarding various aspects of this paper. I am also thankful to Igor Kriz, Arthur-César Le Bras, Shizhang Li and Martin Olsson for helpful conversations. Special thanks to the anonymous referee for offering many suggestions on an earlier version of this paper. During the preparation of this paper, I was partially supported by the Rackham International Students Fellowship.
Conflict of Interest
None.
Financial support
This research was partially supported by Bhargav Bhatt’s NSF grant DMS #1801689.
Open access
