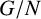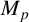1. Introduction
All groups in this note are finite and we refer to [Reference Isaacs5, Reference Navarro9] for notation. Let G be a group and
$\textrm {Irr}(G)$
be the set of irreducible (complex) characters of G. Recall that a character
$\chi $
of G is monomial when
$\chi $
is induced from a linear character of some subgroup of G. If every character
$\chi \in \textrm {Irr}(G)$
is monomial, then G is said to be an M-group. A well-known theorem of Taketa states that an M-group is solvable (see [Reference Isaacs5, Corollary 5.13]).
Let
$\chi \in \textrm {Irr}(G)$
and write
$$ \begin{align*}\textrm{cod}(\chi)=\frac{|G: \ker\chi|}{\chi(1)}\end{align*} $$
and
$\textrm {cod}(G)=\{\textrm {cod}(\chi )\mid \chi \in \textrm {Irr}(G)\}$
.
Qian et al. define
$\textrm {cod}(\chi )$
to be the codegree of the irreducible character
$\chi $
of G in [Reference Qian, Wang and Wei11], although the name codegree of a character was first used by Chillag et al. in [Reference Chillag, Mann and Manz3] with a slightly different definition. The properties of codegrees have gained some interest in recent years. For example, the codegrees of p-groups have been studied in [Reference Du and Lewis4, Reference Moretó8]; and the codegree analogue of Huppert’s
$\rho $
-
$\sigma $
conjecture has been studied in [Reference Yang and Qian14].
Alizadeh et al. in [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatara1] consider finite groups with few codegrees. In particular, they show that if
$|\textrm {cod} (G)| = 2$
, then G is elementary abelian, and they prove that if
$|\textrm {cod} (G)| = 3$
, then G is solvable. When a finite group G is such that
$|\textrm {cod} (G)| \leq 3$
, we show that G must be an M-group.
Theorem 1.1. If G is a group with
$|\mathrm {cod} (G)| \leq 3$
, then G is an M-group.
We observe that the bound on the hypothesis
$|\mathrm {cod}(G)| \leq 3$
in Theorem 2.1 cannot be sharpened. For example, when
$G = A_5$
, we have
$\textrm {cod} (G) = \{ 1, 12, 15, 20 \}$
, so G does not need to be solvable. Even if we assume G is solvable, it need not be the case that G is an M-group when
$|\textrm {cod} (G)| = 4$
. For example, take
$G = \textrm {SL}_{2}(3)$
. In this case, we have
$\textrm {cod}(G)=\{1, 3, 4, 12\}$
; however,
$\textrm {SL}(2, 3)$
is not an M-group.
Let p be a prime and denote by
$\textrm {IBr}(G)$
the set of irreducible p-Brauer characters of G. A p-Brauer character of G is monomial if it is induced from a linear p-Brauer character of some (not necessarily proper) subgroup of G. This definition was introduced by Okuyama in [Reference Okuyama10] using module theory.
A group G is called an
$M_{p}$
-group if every Brauer character
$\varphi \in \textrm {IBr}(G)$
is monomial. Okuyama proves in [Reference Okuyama10] that
$M_{p}$
-groups must be solvable. It is known using the Fong–Swan theorem that an M-group is necessarily an
$M_{p}$
-group for every prime p. However, an
$M_{p}$
-group need not be an M-group; for example,
$\textrm {SL}(2, 3)$
is an
$M_{2}$
-group, not an M-group. In fact, even when G is an
$M_p$
-group for every prime p, it is not necessarily the case that G is an M-group. (An example is given in [Reference Moretó7] of a
$\{ p, q \}$
-group that is both an
$M_p$
-group and an
$M_q$
-group, but is not an M-group.)
We next consider the relationship between
$M_{p}$
-groups and Brauer character degrees.
Theorem 1.2. Let G be a group and N be a normal subgroup of G. If every nonlinear irreducible p-Brauer character of G has prime degree, then either N is an
$M_{p}$
-group or
$G/N$
is an
$M_{p}$
-group.
Although Tong-Viet [Reference Tong-Viet12, Theorem C] has given the classification of groups all of whose nonlinear irreducible Brauer characters have prime degrees, the above result is not found in the literature.
2. Proofs
We first give a proof of Theorem 1.1 which we restate here.
Theorem 2.1. If G is a group with
$|\mathrm {cod} (G)| \leq 3$
, then G is an M-group and an
$M_{p}$
-group for every prime p.
Proof. When
$|\textrm {cod} (G)| = 1$
, we know
$G = 1$
and there is nothing to prove.
When
$|\textrm {cod}(G)| = 2$
, by [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatara1, Lemma 3.1], G is abelian. It follows that G is an M-group.
Now, assume that G is a group with
$|\textrm {cod} (G)| = 3$
. By [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatara1, Theorem 3.4], one of the following is true.
-
(i) G is a p-group of nilpotence class
$2$
with
$\textrm {cod}(G)=\{1, p, p^{s}\}$
, where
$s\geq 2$
. -
(ii) G is a Frobenius group with a Frobenius complement of prime order p, where
$|G|$
is divisible by exactly two primes p and q, and
$\textrm {cod}(G)=\{1, p, q^{s}\}$
for some integer
$s\geq 1$
.
From [Reference Alizadeh, Behravesh, Ghaffarzadeh, Ghasemi and Hekmatara1, Theorem 3.5], in case (ii), the Frobenius kernel
$G'$
is abelian, and in particular, all Sylow subgroups of G in case (ii) are abelian, so G is an M-group. In case (i), G is a p-group and so G is an M-group. Thus, in all cases, G is an M-group.
Finally, it follows by the Fong–Swan theorem (see [Reference Okuyama10, Remark 3.5(1)]) that G is an
$M_{p}$
-group for every prime p.
Note that our proof relies heavily on the classification of groups with two and three codegrees. Thus, our techniques are not really extendible to groups with more codegrees.
Now, we give the proof of Theorem 1.2.
Proof of Theorem 1.2.
We claim that either
$G'N\subseteq PN$
or
$N'\subseteq P$
, where
$G'$
is the derived subgroup of G and P is a Sylow p-subgroup of G. Suppose that
$G'N \nsubseteq PN$
; we want to prove that
$N'\subseteq P$
.
If there exists some Brauer character
$\theta \in \textrm {IBr}(N)$
with
$\theta (1)> 1$
, then there will exist a Brauer character
$\varphi \in \textrm {IBr}(G)$
such that
$\theta $
is an irreducible constituent of
$\varphi _{N}$
. Thus, by Clifford’s theorem [Reference Navarro9, Corollary 8.7],
$$ \begin{align*}\varphi_{N} = e \sum_{i=1}^{t} \theta_{i},\end{align*} $$
where
$\theta _{1} = \theta $
and the
$\theta _{i}$
are all conjugate to
$\theta $
in G for positive integers e and t. Since
$\varphi (1) = et \theta (1)> 1$
, we may assume without loss of generality that
$\varphi (1) = q$
, where q is a prime, and it follows that
$\theta (1) = q$
and
$e = t = 1$
, so that
$\varphi _{N}=\theta $
.
Thus, for distinct characters
$\beta \in \textrm {IBr} (G/N)$
, we see that the
$\varphi \beta $
are irreducible and distinct by [Reference Navarro9, Corollary 8.20]. Since
$(G/N)' = G'N/N \nsubseteq PN/N$
, we conclude by [Reference Wang, Chen and Zeng13, Lemma 2.1] that there exists some nonlinear irreducible Brauer character in
$\textrm {IBr}(G/N)$
. Then, we can choose characters
$\beta \in \textrm {IBr} (G/N)$
with
$\beta (1)> 1$
. Thus,
$$ \begin{align*}(\beta\varphi)(1)=\beta(1)\varphi(1)=\beta(1)\cdot q>q,\end{align*} $$
which is a contradiction to the hypothesis that every nonlinear irreducible Brauer character of G has prime degree. Therefore, we conclude that N has no nonlinear irreducible Brauer characters.
Again by [Reference Wang, Chen and Zeng13, Lemma 2.1], we deduce that the derived subgroup
$N'$
of N is contained in a Sylow p-subgroup S of N. Then, S is a characteristic subgroup of N. Since N is a normal subgroup of G, it follows that
$N'$
is contained in P, as desired.
If
$G'N\subseteq PN$
, where
$P \in \textrm {Syl}_{p} (G)$
, then
$$ \begin{align*} \frac{G}{PN} \cong \frac {G/N}{{PN}/N}\end{align*} $$
is abelian, and so it follows by the Fong–Swan theorem that
$\displaystyle G/{PN}$
is an
$M_{p}$
-group. Therefore,
$G/N$
is an
$M_{p}$
-group since
$PN/N$
is a normal Sylow p-subgroup of
$G/N$
. If
$N'\subseteq P$
, then
$N'=N'\cap N\subseteq P\cap N\in \textrm {Syl}_{p}(N)$
. Write
$P\cap N=S$
. Then,
$N/S$
is abelian and so N is an
$M_{p}$
-group.
In light of Theorem 1.2, the referee has asked if Tong-Viet’s classification can be used to determine when these groups are M-groups. In [Reference Tong-Viet12, Theorem C], Tong-Viet proves that if G is a group where
$O_p (G) = 1$
and the degrees of all the nonlinear irreducible p-Brauer characters of G are primes, then one of the following holds:
-
(1) G is solvable and the degrees of all the nonlinear irreducible characters of G are primes;
-
(2) G is solvable,
$G' \cong \textrm {SL}_2 (3)$
and
$|G: Z(G)G'| = 2$
with
$p = 3$
; or -
(3) G is nonsolvable with
$G' \cong \textrm {PSL}_2 (p)$
, where
$p \in \{ 5, 7 \}$
and
$|G:G'Z(G)| \le 2$
.
Obviously, there are no M-groups that satisfy condition (3). We know that
$\textrm {SL}_2 (3)$
is not an M-group and it is not difficult to show that the extensions of
$\textrm {SL}_2 (3)$
of degree
$2$
are also not M-groups, so there are no M-groups satisfying condition (2).
Groups satisfying condition (1), that is, groups where all the irreducible characters have prime degrees, are studied by Isaacs and Passman in [Reference Isaacs and Passman6] (the information in this paper is also in [Reference Isaacs5, Ch. 12]). Such groups are necessarily solvable and either have two or three character degrees. The groups with two character degrees are studied in [Reference Isaacs and Passman6, Section 3]. In Theorem 3.1 of that paper, it is shown that such a group is either nilpotent or has an abelian subgroup of prime index. Groups with three character degrees are studied in [Reference Isaacs and Passman6, Section 6]. It is shown that these groups either have Fitting height
$2$
or
$3$
. It is not difficult to see that the groups of Fitting height
$3$
will be M-groups. For the groups of Fitting height
$2$
, suppose p and q are the two primes that occur as degrees. In this case, the Fitting subgroup will have a nonabelian Sylow p-subgroup, and G is an M-group if and only if q divides
$p-1$
.
Under the hypothesis of Theorem 1.2, we do not necessarily find that G is an
$M_{p}$
-group. For example, when
$G = \textrm {SL} (2, 3)$
and
$p = 3$
, we see that
$\textrm {bcd}(G)=\{1, 2, 3\}$
, where
$\textrm {bcd} (G) = \{ \varphi (1) \mid \varphi \in \textrm {IBr}(G) \}$
, and
$\textrm {bcd}$
stands for p-Brauer character degree, but
$\textrm {SL} (2, 3)$
is not an
$M_{3}$
-group since it has an irreducible
$3$
-Brauer character of degree
$2$
.
In addition, we do not even necessarily find that G is solvable. For example, when G is the alternating group
$A_{5}$
and
$p=5$
, we see that
$\textrm {bcd} (G) = \{1, 3, 5\}$
. When
${|\textrm{bcd}(G)| = 2}$
, however, we have the following result.
Suppose N is a normal subgroup of G and consider a character
$\chi \in \textrm {Irr} (G)$
. Then,
$\chi $
is called a relative M-character with respect to N if there exists a subgroup H with
$N\subseteq H\subseteq G$
and a character
$\theta \in \textrm {Irr}(H)$
such that
$\theta ^{G} = \chi $
and
$\theta _{N} \in \textrm {Irr} (N)$
. When every character
$\chi \in \textrm {Irr}(G)$
is a relative M-character with respect to N, we say that G is a relative M-group with respect to N.
Observe that G is a relative M-group with respect to
$1$
if and only if it is an M-group. Also, if G is a relative M-group with respect to N, then
$G/N$
is an M-group. However, the converse is not true. For example, if
$G=\textrm {SL}(2, 3)$
and
$N=\textbf {Z}(G)$
, then
$G/N\cong A_{4}$
, which is an M-group, but G is not a relative M-group with respect to N since G has an irreducible character of degree
$2$
whose restriction to N is reducible.
Chen [Reference Chen2] proved that G is a relative M-group with respect to every normal subgroup of G if G is either metabelian (that is,
$G'$
is abelian) or an M-group G with
$\textrm {cd}(G)=\{1, u, v\}$
, where
$\textrm {cd}(G)=\{\chi (1)\mid \chi \in \textrm {Irr}(G)\}$
and
$u, v$
are different primes.
Proposition 2.2. Let G be a group and p be a prime. If
$\kern1pt\mathrm{bcd}(G) = \{ 1, m \}$
, where
$m>1$
and p does not divide m, then G is an
$M_{p}$
-group. In particular, G is solvable.
Proof. Since p does not divide the degree of any irreducible Brauer character of G, it follows by the Itô–Michler theorem that G has a normal Sylow p-subgroup P and
$$ \begin{align*}\textrm{cd} (G/P) = \textrm{bcd} (G/P) = \textrm{bcd} (G) = \{1, m\}.\end{align*} $$
Therefore,
$G/P$
is metabelian by [Reference Isaacs5, Corollary 12.6] and
$G/P$
is an M-group by [Reference Chen2, Theorem 1]. It follows that
$G/P$
is an
$M_{p}$
-group. Since P is a normal Sylow p-subgroup of G, we conclude that G is an
$M_{p}$
-group.
If p divides m, then we do not necessarily find that G is an
$M_{p}$
-group. For example, if G is the symmetric group
$S_{5}$
on five letters and
$p=2$
, then
$\textrm {bcd}(S_{5})=\{1, 4\}$
; however,
$S_{5}$
is not an
$M_{2}$
-group.
