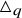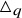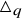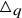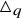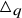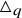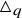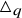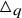1. Introduction
Throughout this article, we adopt the following conventions: A vacuous product is defined as the multiplicative identity. A vacuous sum is defined as the additive identity. Let
![]() $\mathbb N$
denote the set of all nonnegative integers. Assume that
$\mathbb N$
denote the set of all nonnegative integers. Assume that
![]() $\mathbb F$
is an algebraically closed field. Let
$\mathbb F$
is an algebraically closed field. Let
![]() $\mathbb F^\times $
denote the multiplicative group of all nonzero scalars in
$\mathbb F^\times $
denote the multiplicative group of all nonzero scalars in
![]() $\mathbb F$
. Fix a scalar
$\mathbb F$
. Fix a scalar
![]() $q\in \mathbb F^\times $
with
$q\in \mathbb F^\times $
with
![]() $q^4\not =1$
. Let x denote an indeterminate over
$q^4\not =1$
. Let x denote an indeterminate over
![]() $\mathbb F$
. For any
$\mathbb F$
. For any
![]() $a\in \mathbb F$
let
$a\in \mathbb F$
let
![]() $\sqrt {a}\in \mathbb F$
denote a fixed root of
$\sqrt {a}\in \mathbb F$
denote a fixed root of
![]() $x^2-a$
. For any finite-dimensional vector space V over
$x^2-a$
. For any finite-dimensional vector space V over
![]() $\mathbb F$
, let
$\mathbb F$
, let
![]() $\dim V$
denote the dimension of V. Given a left (resp. right) action of a group G on a set S, the notation
$\dim V$
denote the dimension of V. Given a left (resp. right) action of a group G on a set S, the notation
![]() $G\backslash S$
(resp.
$G\backslash S$
(resp.
![]() $S/G$
) stands for the set of all G-orbits in S.
$S/G$
) stands for the set of all G-orbits in S.
The Askey–Wilson algebras [Reference Lévy-Leblond and Lévy-Nahas35], [Reference Terwilliger41], [Reference Zhedanov49] are a family of unital associative algebras defined by generators and relations. These algebras describe the bispectral property of orthogonal polynomials in the Askey scheme [Reference Koekoek, Lesky and Swarttouw31]. Since the advent of Askey–Wilson algebras, they have been found to have applications in various fields, such as P- and Q-polynomial association schemes [Reference Bannai, Bannai, Ito and Tanaka2], [Reference Go13], [Reference Huang24–Reference Huang and Wen29], [Reference Miklavič36], [Reference Terwilliger and Žitnik47], spin models [Reference Curtin5], [Reference Curtin6], [Reference Nomura and Terwilliger39], [Reference Nomura and Terwilliger40], Leonard pairs [Reference Huang15], [Reference Leonard34], [Reference Terwilliger, Marcellán and Assche42], [Reference Terwilliger and Vidunas46], [Reference Vidūnas48], Lie algebras [Reference Alnajjar1], [Reference Bockting-Conrad and Huang3], [Reference Curtin4], [Reference Genest, Vinet and Zhedanov7], [Reference Genest, Vinet and Zhedanov10], [Reference Nomura and Terwilliger37], [Reference Terwilliger43], double affine Hecke algebras [Reference Genest, Vinet and Zhedanov12], [Reference Huang20], [Reference Huang22], [Reference Huang23], [Reference Ito and Terwilliger30], [Reference Koornwinder32], [Reference Koornwinder33], [Reference Nomura and Terwilliger38], [Reference Terwilliger45], coupling problems [Reference Granovskiĭ and Zhedanov14], [Reference Huang18], [Reference Huang19], [Reference Lévy-Leblond and Lévy-Nahas35], and superintegrable systems [Reference Genest, Vinet and Zhedanov8], [Reference Genest, Vinet and Zhedanov9], [Reference Genest, Vinet and Zhedanov11]. The universal Askey–Wilson algebra is a central extension of the Askey–Wilson algebras associated with the most general orthogonal polynomials in the Askey scheme, namely the Askey–Wilson polynomials and the q-Racah polynomials. The definition is presented as follows:
Definition 1.1 [Reference Terwilliger44, Definition 1.2]
The universal Askey–Wilson algebra
![]() $\triangle _q$
is a unital associative algebra over
$\triangle _q$
is a unital associative algebra over
![]() $\mathbb F$
defined by generators and relations. The generators are
$\mathbb F$
defined by generators and relations. The generators are
![]() $A,B,C$
and the relations assert that each of
$A,B,C$
and the relations assert that each of
 $$ \begin{align} A+ \frac{qBC-q^{-1}CB}{q^2-q^{-2}}, \qquad B+\frac{qCA-q^{-1}AC}{q^2-q^{-2}}, \qquad C+ \frac{qAB-q^{-1}BA}{q^2-q^{-2}} \end{align} $$
$$ \begin{align} A+ \frac{qBC-q^{-1}CB}{q^2-q^{-2}}, \qquad B+\frac{qCA-q^{-1}AC}{q^2-q^{-2}}, \qquad C+ \frac{qAB-q^{-1}BA}{q^2-q^{-2}} \end{align} $$
is central in
![]() $\triangle _q$
.
$\triangle _q$
.
Let
![]() $\alpha ,\beta ,\gamma $
denote the central elements of
$\alpha ,\beta ,\gamma $
denote the central elements of
![]() $\triangle _q$
obtained by multiplying the elements in (1.1) by
$\triangle _q$
obtained by multiplying the elements in (1.1) by
![]() $q+q^{-1}$
, respectively. Equivalently,
$q+q^{-1}$
, respectively. Equivalently,
 $$ \begin{align} \frac{\alpha}{q+q^{-1}} &= A+\frac{qBC-q^{-1}CB}{q^2-q^{-2}}, \end{align} $$
$$ \begin{align} \frac{\alpha}{q+q^{-1}} &= A+\frac{qBC-q^{-1}CB}{q^2-q^{-2}}, \end{align} $$
 $$ \begin{align} \frac{\beta}{q+q^{-1}}&=B+\frac{qCA-q^{-1}AC}{q^2-q^{-2}}, \end{align} $$
$$ \begin{align} \frac{\beta}{q+q^{-1}}&=B+\frac{qCA-q^{-1}AC}{q^2-q^{-2}}, \end{align} $$
 $$ \begin{align} \frac{\gamma}{q+q^{-1}}&=C+\frac{qAB-q^{-1}BA}{q^2-q^{-2}}. \end{align} $$
$$ \begin{align} \frac{\gamma}{q+q^{-1}}&=C+\frac{qAB-q^{-1}BA}{q^2-q^{-2}}. \end{align} $$
Proposition 1.2. The algebra
![]() $\triangle _q$
has a presentation given by generators
$\triangle _q$
has a presentation given by generators
![]() $A,B,\alpha ,\beta ,\gamma $
and the relations assert that
$A,B,\alpha ,\beta ,\gamma $
and the relations assert that
![]() $\alpha ,\beta ,\gamma $
are central in
$\alpha ,\beta ,\gamma $
are central in
![]() $\triangle _q$
and
$\triangle _q$
and
 $$ \begin{align} \alpha =& \frac{B^2A-(q^2+q^{-2})BAB+AB^2+(q^2-q^{-2})^2A+(q-q^{-1})^2B\gamma} {(q-q^{-1})(q^2-q^{-2})}, \end{align} $$
$$ \begin{align} \alpha =& \frac{B^2A-(q^2+q^{-2})BAB+AB^2+(q^2-q^{-2})^2A+(q-q^{-1})^2B\gamma} {(q-q^{-1})(q^2-q^{-2})}, \end{align} $$
 $$ \begin{align} \beta = & \frac{A^2B-(q^2+q^{-2})ABA+BA^2+(q^2-q^{-2})^2B+(q-q^{-1})^2A\gamma}{(q-q^{-1})(q^2-q^{-2})}. \end{align} $$
$$ \begin{align} \beta = & \frac{A^2B-(q^2+q^{-2})ABA+BA^2+(q^2-q^{-2})^2B+(q-q^{-1})^2A\gamma}{(q-q^{-1})(q^2-q^{-2})}. \end{align} $$
Proof. The relations (1.5) and (1.6) are obtained by applying (1.4) to eliminate C from (1.2) and (1.3).
Let V denote a
![]() $\triangle _q$
-module. For any
$\triangle _q$
-module. For any
![]() $\mu \in \mathbb F^\times $
define
$\mu \in \mathbb F^\times $
define
Note that
![]() $V(\mu )=V(\mu ^{-1})$
for any
$V(\mu )=V(\mu ^{-1})$
for any
![]() $\mu \in \mathbb F^\times $
. A scalar
$\mu \in \mathbb F^\times $
. A scalar
![]() $\mu \in \mathbb F^\times $
is called a weight of V whenever
$\mu \in \mathbb F^\times $
is called a weight of V whenever
![]() $V(\mu )\not =\{0\}$
. In this case,
$V(\mu )\not =\{0\}$
. In this case,
![]() $V(\mu )$
is called the weight space of V with weight
$V(\mu )$
is called the weight space of V with weight
![]() $\mu $
and every nonzero
$\mu $
and every nonzero
![]() $v\in V(\mu )$
is called a weight vector of V with weight
$v\in V(\mu )$
is called a weight vector of V with weight
![]() $\mu $
.
$\mu $
.
Lemma 1.3. For any
![]() $\triangle _q$
-module V and any weight
$\triangle _q$
-module V and any weight
![]() $\mu $
of V, the following relations hold:
$\mu $
of V, the following relations hold:
-
(i)
 $(B-\mu q^2-\mu ^{-1} q^{-2})(B-\mu q^{-2}-\mu ^{-1} q^2)A V(\mu )\subseteq V(\mu )$
.
$(B-\mu q^2-\mu ^{-1} q^{-2})(B-\mu q^{-2}-\mu ^{-1} q^2)A V(\mu )\subseteq V(\mu )$
. -
(ii)
 $(B-\mu q^2-\mu ^{-1} q^{-2}) (B-\mu -\mu ^{-1}) AV(\mu )\subseteq V(\mu q^{-2})$
.
$(B-\mu q^2-\mu ^{-1} q^{-2}) (B-\mu -\mu ^{-1}) AV(\mu )\subseteq V(\mu q^{-2})$
. -
(iii)
 $(B-\mu q^{-2}-\mu ^{-1} q^{2}) (B-\mu -\mu ^{-1}) AV(\mu )\subseteq V(\mu q^{2})$
.
$(B-\mu q^{-2}-\mu ^{-1} q^{2}) (B-\mu -\mu ^{-1}) AV(\mu )\subseteq V(\mu q^{2})$
.
Proof. (i): Let
![]() $v\in V(\mu )$
be given. Applying both sides of (1.5) to v, we find that
$v\in V(\mu )$
be given. Applying both sides of (1.5) to v, we find that
is equal to
![]() $(q-q^{-1})^2$
times
$(q-q^{-1})^2$
times
Since
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are central in
$\gamma $
are central in
![]() $\triangle _q$
, the vectors
$\triangle _q$
, the vectors
![]() $\alpha v$
and
$\alpha v$
and
![]() $\gamma v$
are in
$\gamma v$
are in
![]() $V(\mu )$
. Therefore, (1.8) lies in
$V(\mu )$
. Therefore, (1.8) lies in
![]() $V(\mu )$
. The relation (i) follows.
$V(\mu )$
. The relation (i) follows.
(ii), (iii): The relation (i) implies that
The relations (ii) and (iii) are immediate from the above equation.
Definition 1.4. A weight
![]() $\mu $
of a
$\mu $
of a
![]() $\triangle _q$
-module V is said to be marginal if there exists a weight vector v of V with weight
$\triangle _q$
-module V is said to be marginal if there exists a weight vector v of V with weight
![]() $\mu $
such that
$\mu $
such that
When q is not a root of unity, it has been shown that all finite-dimensional irreducible
![]() $\triangle _q$
-modules have marginal weights and can be constructed from the following infinite-dimensional
$\triangle _q$
-modules have marginal weights and can be constructed from the following infinite-dimensional
![]() $\triangle _q$
-modules up to isomorphism:
$\triangle _q$
-modules up to isomorphism:
Theorem 1.5 [Reference Huang16, §3]
For any
![]() $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
, there exists an infinite-dimensional
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
, there exists an infinite-dimensional
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $M_\lambda (a,b,c)$
satisfying the following conditions:
$M_\lambda (a,b,c)$
satisfying the following conditions:
-
(i) There exists a basis
 $\{m_i\}_{i\in \mathbb N}$
for the
$\{m_i\}_{i\in \mathbb N}$
for the
 $\triangle _q$
-module
$\triangle _q$
-module
 $M_\lambda (a,b,c)$
such that where
$M_\lambda (a,b,c)$
such that where $$ \begin{align*} (A-\theta_i) m_i&=m_{i+1} \qquad \text{for all } i\in \mathbb N,\\ (B-\theta_i^*) m_i&= \varphi_i m_{i-1}\qquad \text{for all }i\in \mathbb N, \end{align*} $$
$$ \begin{align*} (A-\theta_i) m_i&=m_{i+1} \qquad \text{for all } i\in \mathbb N,\\ (B-\theta_i^*) m_i&= \varphi_i m_{i-1}\qquad \text{for all }i\in \mathbb N, \end{align*} $$
 $m_{-1}$
is interpreted as any vector of
$m_{-1}$
is interpreted as any vector of
 $M_\lambda (a,b,c)$
and (1.9)
$M_\lambda (a,b,c)$
and (1.9) $$ \begin{align} \theta_i &= a\lambda^{-1} q^{2i}+ a^{-1} \lambda q^{-2i} \qquad \text{for all }i\in \mathbb N, \end{align} $$
(1.10)
$$ \begin{align} \theta_i &= a\lambda^{-1} q^{2i}+ a^{-1} \lambda q^{-2i} \qquad \text{for all }i\in \mathbb N, \end{align} $$
(1.10) $$ \begin{align} \theta_i^*&= b\lambda^{-1} q^{2i}+ b^{-1} \lambda q^{-2i}\qquad \text{for all }i\in \mathbb N, \end{align} $$
(1.11)
$$ \begin{align} \theta_i^*&= b\lambda^{-1} q^{2i}+ b^{-1} \lambda q^{-2i}\qquad \text{for all }i\in \mathbb N, \end{align} $$
(1.11) $$ \begin{align} \varphi_i &=a^{-1}b^{-1} \lambda q(q^i- q^{-i})(\lambda^{-1}q^{i-1}-\lambda q^{1-i})\\&\qquad \times \, (q^{-i}- abc\lambda^{-1}q^{i-1})(q^{-i} - abc^{-1}\lambda^{-1}q^{i-1})\qquad \text{for all } i\in \mathbb N.\nonumber \end{align} $$
$$ \begin{align} \varphi_i &=a^{-1}b^{-1} \lambda q(q^i- q^{-i})(\lambda^{-1}q^{i-1}-\lambda q^{1-i})\\&\qquad \times \, (q^{-i}- abc\lambda^{-1}q^{i-1})(q^{-i} - abc^{-1}\lambda^{-1}q^{i-1})\qquad \text{for all } i\in \mathbb N.\nonumber \end{align} $$
-
(ii) The elements
 $\alpha ,\beta ,\gamma $
act on
$\alpha ,\beta ,\gamma $
act on
 $M_\lambda (a,b,c)$
as scalar multiplication by (1.12)
$M_\lambda (a,b,c)$
as scalar multiplication by (1.12) $$ \begin{align} (b+b^{-1})(c+c^{-1}) +(a+a^{-1})(\lambda q+\lambda^{-1} q^{-1}), \end{align} $$
(1.13)
$$ \begin{align} (b+b^{-1})(c+c^{-1}) +(a+a^{-1})(\lambda q+\lambda^{-1} q^{-1}), \end{align} $$
(1.13) $$ \begin{align} (c+c^{-1})(a+a^{-1})+(b+b^{-1})(\lambda q+\lambda^{-1} q^{-1}), \end{align} $$
(1.14)respectively.
$$ \begin{align} (c+c^{-1})(a+a^{-1})+(b+b^{-1})(\lambda q+\lambda^{-1} q^{-1}), \end{align} $$
(1.14)respectively. $$ \begin{align} (a+a^{-1})(b+b^{-1})+(c+c^{-1})(\lambda q+\lambda^{-1} q^{-1}), \end{align} $$
$$ \begin{align} (a+a^{-1})(b+b^{-1})+(c+c^{-1})(\lambda q+\lambda^{-1} q^{-1}), \end{align} $$
By Theorem 1.5(i), the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $M_\lambda (a,b,c)$
has the marginal weight
$M_\lambda (a,b,c)$
has the marginal weight
![]() $b\lambda ^{-1}$
. In 2009, the present author conceived the initial idea for creating
$b\lambda ^{-1}$
. In 2009, the present author conceived the initial idea for creating
![]() $M_\lambda (a,b,c)$
during his work [Reference Huang15] on Leonard triples of q-Racah type. These Leonard triples provide a family of finite-dimensional irreducible
$M_\lambda (a,b,c)$
during his work [Reference Huang15] on Leonard triples of q-Racah type. These Leonard triples provide a family of finite-dimensional irreducible
![]() $\triangle _q$
-modules. In the 2015 paper [Reference Huang16], the
$\triangle _q$
-modules. In the 2015 paper [Reference Huang16], the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $M_\lambda (a,b,c)$
was formally introduced to classify the finite-dimensional irreducible
$M_\lambda (a,b,c)$
was formally introduced to classify the finite-dimensional irreducible
![]() $\triangle _q$
-modules when q is not a root of unity. The
$\triangle _q$
-modules when q is not a root of unity. The
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $M_\lambda (a,b,c)$
is called the Verma
$M_\lambda (a,b,c)$
is called the Verma
![]() $\triangle _q$
-module, in analogy with the role Verma modules play in the theory of semisimple Lie algebras.
$\triangle _q$
-module, in analogy with the role Verma modules play in the theory of semisimple Lie algebras.
In this article, we focus on those finite-dimensional irreducible
![]() $\triangle _q$
-modules with marginal weights under the condition that q is a root of unity. Henceforth, we assume that q is a root of unity with order
$\triangle _q$
-modules with marginal weights under the condition that q is a root of unity. Henceforth, we assume that q is a root of unity with order
![]() $d\not =1,2,4$
and set
$d\not =1,2,4$
and set

Note that ![]() is the order of the root of unity
is the order of the root of unity
![]() $q^2$
. Dividing the argument into the cases with and without marginal weights, it was shown that the dimension of every finite-dimensional irreducible
$q^2$
. Dividing the argument into the cases with and without marginal weights, it was shown that the dimension of every finite-dimensional irreducible
![]() $\triangle _q$
-module is less than or equal to
$\triangle _q$
-module is less than or equal to ![]() [Reference Huang21]. In particular, every nonzero
[Reference Huang21]. In particular, every nonzero
![]() $\triangle _q$
-module of dimension less than
$\triangle _q$
-module of dimension less than ![]() has a marginal weight. Please see Lemma 2.3. We will see that all finite-dimensional irreducible
has a marginal weight. Please see Lemma 2.3. We will see that all finite-dimensional irreducible
![]() $\triangle _q$
-modules with marginal weights can still be constructed from the Verma
$\triangle _q$
-modules with marginal weights can still be constructed from the Verma
![]() $\triangle _q$
-modules up to isomorphism.
$\triangle _q$
-modules up to isomorphism.
There are two natural families of finite-dimensional quotients of Verma
![]() $\triangle _q$
-modules. One of the two families was first released in [Reference Huang16, §4] and the description is as follows: Pick a triple
$\triangle _q$
-modules. One of the two families was first released in [Reference Huang16, §4] and the description is as follows: Pick a triple
![]() $(a,b,c)\in {\mathbb F^\times }^3$
and any
$(a,b,c)\in {\mathbb F^\times }^3$
and any
![]() $n\in \mathbb N$
. Set the parameter
$n\in \mathbb N$
. Set the parameter
![]() $\lambda =q^n$
. Let
$\lambda =q^n$
. Let
![]() $N_\lambda (a,b,c)$
denote the subspace of
$N_\lambda (a,b,c)$
denote the subspace of
![]() $M_\lambda (a,b,c)$
spanned by
$M_\lambda (a,b,c)$
spanned by
![]() $\{m_i\}_{i=n+1}^\infty $
. By construction,
$\{m_i\}_{i=n+1}^\infty $
. By construction,
![]() $N_\lambda (a,b,c)$
is invariant under A. By (1.11), the scalar
$N_\lambda (a,b,c)$
is invariant under A. By (1.11), the scalar
![]() $\varphi _{n+1}=0$
. Combined with Theorem 1.5(i), this implies that
$\varphi _{n+1}=0$
. Combined with Theorem 1.5(i), this implies that
![]() $N_\lambda (a,b,c)$
is invariant under B. By Theorem 1.5(ii), the elements
$N_\lambda (a,b,c)$
is invariant under B. By Theorem 1.5(ii), the elements
![]() $\alpha ,\beta ,\gamma $
act on
$\alpha ,\beta ,\gamma $
act on
![]() $N_\lambda (a,b,c)$
as scalar multiplication. Thus
$N_\lambda (a,b,c)$
as scalar multiplication. Thus
![]() $N_\lambda (a,b,c)$
is a
$N_\lambda (a,b,c)$
is a
![]() $\triangle _q$
-submodule of
$\triangle _q$
-submodule of
![]() $M_\lambda (a,b,c)$
by Proposition 1.2. Moreover,
$M_\lambda (a,b,c)$
by Proposition 1.2. Moreover,
![]() $N_\lambda (a,b,c)$
is the
$N_\lambda (a,b,c)$
is the
![]() $\triangle _q$
-submodule of
$\triangle _q$
-submodule of
![]() $M_\lambda (a,b,c)$
generated by
$M_\lambda (a,b,c)$
generated by
![]() $m_{n+1}$
. Therefore,
$m_{n+1}$
. Therefore,
is an
![]() $(n+1)$
-dimensional
$(n+1)$
-dimensional
![]() $\triangle _q$
-module that has the basis
$\triangle _q$
-module that has the basis
In this article, we will prove that all irreducible
![]() $\triangle _q$
-modules with dimensions less than
$\triangle _q$
-modules with dimensions less than ![]() are contained in the first family of finite-dimensional quotients of Verma
are contained in the first family of finite-dimensional quotients of Verma
![]() $\triangle _q$
-modules up to isomorphism:
$\triangle _q$
-modules up to isomorphism:
Theorem 1.6. Suppose that V is an irreducible
![]() $\triangle _q$
-module of dimension less than
$\triangle _q$
-module of dimension less than ![]() . Then there exist a triple
. Then there exist a triple
![]() $(a,b,c)\in {\mathbb F^\times }^3$
and an integer n with
$(a,b,c)\in {\mathbb F^\times }^3$
and an integer n with ![]() such that V is isomorphic to the
such that V is isomorphic to the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $V_n(a,b,c)$
.
$V_n(a,b,c)$
.
Let
![]() $\{\pm 1\}$
denote the multiplicative group consisting of the integers
$\{\pm 1\}$
denote the multiplicative group consisting of the integers
![]() $1$
and
$1$
and
![]() $-1$
. There exists a unique left
$-1$
. There exists a unique left
![]() $\{\pm 1\}^3$
-action on
$\{\pm 1\}^3$
-action on
![]() ${\mathbb F^{\times }}^3$
given by
${\mathbb F^{\times }}^3$
given by
 $$ \begin{align*} (-1,1,1)\cdot (a,b,c)&=(a^{-1},b,c), \\ (1,-1,1)\cdot (a,b,c)&=(a,b^{-1},c), \\ (1,1,-1)\cdot (a,b,c)&=(a,b,c^{-1}) \end{align*} $$
$$ \begin{align*} (-1,1,1)\cdot (a,b,c)&=(a^{-1},b,c), \\ (1,-1,1)\cdot (a,b,c)&=(a,b^{-1},c), \\ (1,1,-1)\cdot (a,b,c)&=(a,b,c^{-1}) \end{align*} $$
for all
![]() $(a,b,c)\in {\mathbb F^{\times }}^3$
. An irreducibility criterion for
$(a,b,c)\in {\mathbb F^{\times }}^3$
. An irreducibility criterion for
![]() $V_n(a,b,c)$
can be expressed in terms of the
$V_n(a,b,c)$
can be expressed in terms of the
![]() $\{\pm 1\}^3$
-action on
$\{\pm 1\}^3$
-action on
![]() ${\mathbb F^{\times }}^3$
:
${\mathbb F^{\times }}^3$
:
Theorem 1.7. For any triple
![]() $(a,b,c)\in {\mathbb F^\times }^3$
and any integer n with
$(a,b,c)\in {\mathbb F^\times }^3$
and any integer n with ![]() , the following conditions are equivalent:
, the following conditions are equivalent:
-
(i) The
 $\triangle _q$
-module
$\triangle _q$
-module
 $V_n(a,b,c)$
is irreducible.
$V_n(a,b,c)$
is irreducible. -
(ii)
 $\bar {a}\bar {b}\bar {c}\not \in \{q^{n-2i+1}\,|\,i=1,2,\ldots ,n\}$
for all
$\bar {a}\bar {b}\bar {c}\not \in \{q^{n-2i+1}\,|\,i=1,2,\ldots ,n\}$
for all
 $(\bar {a},\bar {b},\bar {c})\in \{\pm 1\}^3\cdot (a,b,c)$
.
$(\bar {a},\bar {b},\bar {c})\in \{\pm 1\}^3\cdot (a,b,c)$
.
Proof. The proof is similar to that of [Reference Huang16, Theorem 4.4].
Fix an integer n with ![]() . Define
. Define
![]() $\mathbf I_n$
as the set of all isomorphism classes of
$\mathbf I_n$
as the set of all isomorphism classes of
![]() $(n+1)$
-dimensional irreducible
$(n+1)$
-dimensional irreducible
![]() $\triangle _q$
-modules. Define
$\triangle _q$
-modules. Define
![]() $\mathbf P_n$
to be the set of all triples
$\mathbf P_n$
to be the set of all triples
![]() $(a,b,c)\in {\mathbb F^\times }^3$
satisfying Theorem 1.7(i), (ii). Clearly,
$(a,b,c)\in {\mathbb F^\times }^3$
satisfying Theorem 1.7(i), (ii). Clearly,
![]() $\mathbf P_n$
is closed under the
$\mathbf P_n$
is closed under the
![]() $\{\pm 1\}^3$
-action on
$\{\pm 1\}^3$
-action on
![]() ${\mathbb F^{\times }}^3$
. By analogy with the case where q is not a root of unity, Theorems 1.6 and 1.7 result in a classification of all irreducible
${\mathbb F^{\times }}^3$
. By analogy with the case where q is not a root of unity, Theorems 1.6 and 1.7 result in a classification of all irreducible
![]() $\triangle _q$
-modules of dimensions less than
$\triangle _q$
-modules of dimensions less than ![]() :
:
Theorem 1.8. For any integer n with ![]() , there is a bijection
, there is a bijection
![]() $\{\pm 1\}^3 \backslash \mathbf P_n\to \mathbf I_n$
given by
$\{\pm 1\}^3 \backslash \mathbf P_n\to \mathbf I_n$
given by
for all
![]() $(a,b,c)\in \mathbf P_n$
.
$(a,b,c)\in \mathbf P_n$
.
Proof. The proof is similar to that of [Reference Huang16, Theorem 4.7].
We now turn to the second family of finite-dimensional quotients of Verma
![]() $\triangle _q$
-modules. Pick any quadruple
$\triangle _q$
-modules. Pick any quadruple
![]() $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
. Since
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
. Since ![]() , the parameters (1.9)–(1.11) satisfy the cyclic properties:
, the parameters (1.9)–(1.11) satisfy the cyclic properties:

Let
![]() $\delta \in \mathbb F$
denote an additional parameter. Define
$\delta \in \mathbb F$
denote an additional parameter. Define
![]() $O_{\lambda }^\delta (a,b,c)$
to be the subspace of
$O_{\lambda }^\delta (a,b,c)$
to be the subspace of
![]() $M_\lambda (a,b,c)$
spanned by
$M_\lambda (a,b,c)$
spanned by ![]() . Applying Theorem 1.5(i) along with the cyclic properties, it is routine to verify that
. Applying Theorem 1.5(i) along with the cyclic properties, it is routine to verify that
![]() $O_\lambda ^\delta (a,b,c)$
is invariant under A and B. By Theorem 1.5(ii), the elements
$O_\lambda ^\delta (a,b,c)$
is invariant under A and B. By Theorem 1.5(ii), the elements
![]() $\alpha ,\beta ,\gamma $
act on
$\alpha ,\beta ,\gamma $
act on
![]() $O_\lambda ^\delta (a,b,c)$
as scalar multiplication. Thus
$O_\lambda ^\delta (a,b,c)$
as scalar multiplication. Thus
![]() $O_\lambda ^\delta (a,b,c)$
is a
$O_\lambda ^\delta (a,b,c)$
is a
![]() $\triangle _q$
-submodule of
$\triangle _q$
-submodule of
![]() $M_\lambda (a,b,c)$
by Proposition 1.2. Moreover,
$M_\lambda (a,b,c)$
by Proposition 1.2. Moreover,
![]() $O_\lambda ^\delta (a,b,c)$
is the
$O_\lambda ^\delta (a,b,c)$
is the
![]() $\triangle _q$
-submodule of
$\triangle _q$
-submodule of
![]() $M_\lambda (a,b,c)$
generated by
$M_\lambda (a,b,c)$
generated by ![]() . Therefore,
. Therefore,
is a ![]() -dimensional
-dimensional
![]() $\triangle _q$
-module that has the basis
$\triangle _q$
-module that has the basis
In this article, we will prove that all ![]() -dimensional irreducible
-dimensional irreducible
![]() $\triangle _q$
-modules with marginal weights are contained in this second family up to isomorphism:
$\triangle _q$
-modules with marginal weights are contained in this second family up to isomorphism:
Theorem 1.9. Suppose that V is a ![]() -dimensional irreducible
-dimensional irreducible
![]() $\triangle _q$
-module with marginal weights. Then there exists a quintuple
$\triangle _q$
-module with marginal weights. Then there exists a quintuple
![]() $(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
such that V is isomorphic to the
$(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
such that V is isomorphic to the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_{\lambda }^\delta (a,b,c)$
.
$W_{\lambda }^\delta (a,b,c)$
.
There is a unique left
![]() $\{\pm 1\}$
-action on
$\{\pm 1\}$
-action on
![]() ${\mathbb F^{\times }}^4$
given by
${\mathbb F^{\times }}^4$
given by
for all
![]() $(a,b,c,\lambda )\in {\mathbb F^{\times }}^4$
. Recall that the symmetric group
$(a,b,c,\lambda )\in {\mathbb F^{\times }}^4$
. Recall that the symmetric group
![]() $\mathfrak S_4$
of degree four has a presentation with the transpositions
$\mathfrak S_4$
of degree four has a presentation with the transpositions
![]() $(1\, 2), (2\, 3), (3\, 4)$
subject to the relations
$(1\, 2), (2\, 3), (3\, 4)$
subject to the relations
 $$ \begin{align*} (1\, 2)^2=(2\, 3&)^2=(3\, 4)^2=1,\\(1\, 2)(3\, 4)&=(3\, 4)(1\, 2),\\(1\, 2)(2\, 3)(1\, 2)&=(2\, 3)(1\, 2)(2\, 3),\\(2\, 3)(3\, 4)(2\, 3)&=(3\, 4)(2\, 3)(3\, 4). \end{align*} $$
$$ \begin{align*} (1\, 2)^2=(2\, 3&)^2=(3\, 4)^2=1,\\(1\, 2)(3\, 4)&=(3\, 4)(1\, 2),\\(1\, 2)(2\, 3)(1\, 2)&=(2\, 3)(1\, 2)(2\, 3),\\(2\, 3)(3\, 4)(2\, 3)&=(3\, 4)(2\, 3)(3\, 4). \end{align*} $$
Applying the presentation, it is straightforward to verify that there exists a unique right
![]() $\mathfrak S_4$
-action on
$\mathfrak S_4$
-action on
![]() $\{\pm 1\}\backslash {\mathbb F^{\times }}^4$
given by
$\{\pm 1\}\backslash {\mathbb F^{\times }}^4$
given by
 $$ \begin{align*} (\{\pm 1\}\cdot (a,b,c,\lambda))\cdot {(1\, 2)} &= \{\pm 1\}\cdot (a,b,c^{-1},\lambda), \\ (\{\pm 1\}\cdot (a,b,c,\lambda))\cdot {(2\, 3)} &= \{\pm 1\}\cdot \textstyle (\frac{a}{\sqrt{a b c\lambda q}}, \frac{b}{\sqrt{a b c\lambda q}}, \frac{c}{\sqrt{a b c\lambda q}}, \frac{\lambda}{\sqrt{a b c\lambda q}}), \\ (\{\pm 1\}\cdot (a,b,c,\lambda))\cdot {(3\, 4)} &= \{\pm 1\}\cdot (a^{-1},b,c,\lambda) \end{align*} $$
$$ \begin{align*} (\{\pm 1\}\cdot (a,b,c,\lambda))\cdot {(1\, 2)} &= \{\pm 1\}\cdot (a,b,c^{-1},\lambda), \\ (\{\pm 1\}\cdot (a,b,c,\lambda))\cdot {(2\, 3)} &= \{\pm 1\}\cdot \textstyle (\frac{a}{\sqrt{a b c\lambda q}}, \frac{b}{\sqrt{a b c\lambda q}}, \frac{c}{\sqrt{a b c\lambda q}}, \frac{\lambda}{\sqrt{a b c\lambda q}}), \\ (\{\pm 1\}\cdot (a,b,c,\lambda))\cdot {(3\, 4)} &= \{\pm 1\}\cdot (a^{-1},b,c,\lambda) \end{align*} $$
for all
![]() $(a,b,c,\lambda )\in {\mathbb F^{\times }}^4$
.
$(a,b,c,\lambda )\in {\mathbb F^{\times }}^4$
.
Definition 1.10.
-
(i) For any
 $(a,b,c,\lambda ),(\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^{\times }}^4$
, we define whenever
$(a,b,c,\lambda ),(\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^{\times }}^4$
, we define whenever
 $(\{\pm 1\}\cdot (a,b,c,\lambda ))\cdot \mathfrak S_4=(\{\pm 1\}\cdot (\bar {a},\bar {b},\bar {c},\bar {\lambda }))\cdot \mathfrak S_4$
in
$(\{\pm 1\}\cdot (a,b,c,\lambda ))\cdot \mathfrak S_4=(\{\pm 1\}\cdot (\bar {a},\bar {b},\bar {c},\bar {\lambda }))\cdot \mathfrak S_4$
in
 $(\{\pm 1\}\backslash {\mathbb F^{\times }}^4)/ \mathfrak S_4$
. The binary relation
$(\{\pm 1\}\backslash {\mathbb F^{\times }}^4)/ \mathfrak S_4$
. The binary relation  is an equivalence relation on
is an equivalence relation on
 ${\mathbb F^{\times }}^4$
.
${\mathbb F^{\times }}^4$
.
-
(ii) For any
 $(a,b,c,\lambda ,\delta ),(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^{\times }}^4\times \mathbb F$
, we define whenever
$(a,b,c,\lambda ,\delta ),(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^{\times }}^4\times \mathbb F$
, we define whenever
 and (1.15)
and (1.15)
The binary relation is an equivalence relation on
 ${\mathbb F^{\times }}^4\times \mathbb F$
.
${\mathbb F^{\times }}^4\times \mathbb F$
.
An irreducibility criterion for the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
can be expressed in terms of the equivalence relation
$W_\lambda ^\delta (a,b,c)$
can be expressed in terms of the equivalence relation ![]() :
:
Theorem 1.11. For any
![]() $(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
, the following conditions are equivalent:
$(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
, the following conditions are equivalent:
-
(i) The
 $\triangle _q$
-module
$\triangle _q$
-module
 $W_\lambda ^\delta (a,b,c)$
is irreducible.
$W_\lambda ^\delta (a,b,c)$
is irreducible. -
(ii)
 $\bar {\delta }\not =0$
or
$\bar {\delta }\not =0$
or  for all
for all  .
.
Define ![]() to be the set of all quintuples
to be the set of all quintuples
![]() $(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
satisfying Theorem 1.11(i), (ii). Let
$(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
satisfying Theorem 1.11(i), (ii). Let ![]() . It can be shown that if
. It can be shown that if ![]() , then the
, then the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is isomorphic to
$W_\lambda ^\delta (a,b,c)$
is isomorphic to
![]() $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
. Please see Theorem 7.4. However, the converse is not true. Extending the equivalence relation
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
. Please see Theorem 7.4. However, the converse is not true. Extending the equivalence relation ![]() by adding the following two additional rules, we will derive a classification of all
by adding the following two additional rules, we will derive a classification of all ![]() -dimensional irreducible
-dimensional irreducible
![]() $\triangle _q$
-modules with marginal weights up to isomorphism.
$\triangle _q$
-modules with marginal weights up to isomorphism.
Definition 1.12. For any
![]() $ (a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) \in {\mathbb F^{\times }}^4\times \mathbb F$
, we declare
$ (a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) \in {\mathbb F^{\times }}^4\times \mathbb F$
, we declare
![]() $ (a,b,c,\lambda ,\delta ) \sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) $
whenever any of the following conditions holds:
$ (a,b,c,\lambda ,\delta ) \sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) $
whenever any of the following conditions holds:
-
(i)
 .
. -
(ii)
 $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a^{-1},b,c,\lambda ^{-1}q^{-2},\delta )$
and
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a^{-1},b,c,\lambda ^{-1}q^{-2},\delta )$
and  .
. -
(iii)
 $ (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) = (a^{-1},b^{-1},c,\lambda ^{-1}q^{-2},\delta )$
and the following conditions hold:
$ (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) = (a^{-1},b^{-1},c,\lambda ^{-1}q^{-2},\delta )$
and the following conditions hold:-
(a)
 .
. -
(b)
 .
.
-
Definition 1.13. Define
![]() $\simeq $
to be the equivalence relation on
$\simeq $
to be the equivalence relation on
![]() ${\mathbb F^\times }^4\times \mathbb F$
generated by
${\mathbb F^\times }^4\times \mathbb F$
generated by
![]() $\sim $
.
$\sim $
.
It can be shown that ![]() is closed under
is closed under
![]() $\simeq $
. Please see Lemma 10.3. Let
$\simeq $
. Please see Lemma 10.3. Let ![]() denote the set of all equivalence classes of
denote the set of all equivalence classes of ![]() under
under
![]() $\simeq $
. Define
$\simeq $
. Define ![]() as the set of the isomorphism classes of all
as the set of the isomorphism classes of all ![]() -dimensional irreducible
-dimensional irreducible
![]() $\triangle _q$
-modules with marginal weights.
$\triangle _q$
-modules with marginal weights.
Theorem 1.14. There is a bijection from ![]() to
to ![]() given by
given by
for all ![]() .
.
The outline of this article is as follows: In Section 2, we recall some properties of marginal weights and their closely related vectors called marginal weight vectors. In Section 3, we reinterpret the universal property of
![]() $M_\lambda (a,b,c)$
and relate the property to a functional relation called the feasible relation. In Section 4, we give a proof of Theorem 1.6. In Section 5, we establish a polynomial characterization for the feasible relation; consequently, the feasible relation can be expressed in terms of the equivalence relation
$M_\lambda (a,b,c)$
and relate the property to a functional relation called the feasible relation. In Section 4, we give a proof of Theorem 1.6. In Section 5, we establish a polynomial characterization for the feasible relation; consequently, the feasible relation can be expressed in terms of the equivalence relation ![]() . In Section 6, we give a proof of Theorem 1.9. In Section 7, we characterize the equivalence relations
. In Section 6, we give a proof of Theorem 1.9. In Section 7, we characterize the equivalence relations ![]() and
and ![]() in terms of the
in terms of the
![]() $\triangle _q$
-modules
$\triangle _q$
-modules
![]() $M_\lambda (a,b,c)$
and
$M_\lambda (a,b,c)$
and
![]() $W_\lambda ^\delta (a,b,c)$
. In Section 8, we give a proof of Theorem 1.11. In Section 9, we relate the binary relation
$W_\lambda ^\delta (a,b,c)$
. In Section 8, we give a proof of Theorem 1.11. In Section 9, we relate the binary relation
![]() $\sim $
to the marginal weight vectors of
$\sim $
to the marginal weight vectors of
![]() $W_\lambda ^\delta (a,b,c)$
. In Section 10, we give a proof of Theorem 1.14. In addition, the
$W_\lambda ^\delta (a,b,c)$
. In Section 10, we give a proof of Theorem 1.14. In addition, the
![]() $\mathfrak S_4$
-action on
$\mathfrak S_4$
-action on
![]() $\{\pm 1\}\backslash {\mathbb F^{\times }}^4$
is fully displayed in Appendix A.
$\{\pm 1\}\backslash {\mathbb F^{\times }}^4$
is fully displayed in Appendix A.
2. The marginal weights and the marginal weight vectors
Recall the marginal weights of
![]() $\triangle _q$
-modules from Definition 1.4.
$\triangle _q$
-modules from Definition 1.4.
Theorem 2.1 [Reference Huang21, Theorem 6.10]
The dimension of any finite-dimensional irreducible
![]() $\triangle _q$
-module without marginal weights is equal to
$\triangle _q$
-module without marginal weights is equal to ![]() .
.
Lemma 2.2. Let V denote a
![]() $\triangle _q$
-module and W denote a
$\triangle _q$
-module and W denote a
![]() $\triangle _q$
-submodule of V. For any
$\triangle _q$
-submodule of V. For any
![]() $\mu \in \mathbb F^\times $
, the following statements are true:
$\mu \in \mathbb F^\times $
, the following statements are true:
-
(i)
 $W(\mu )=W\cap V(\mu )$
.
$W(\mu )=W\cap V(\mu )$
. -
(ii) If
 $\mu $
is a weight of W, then
$\mu $
is a weight of W, then
 $\mu $
is a weight of V.
$\mu $
is a weight of V. -
(iii) If
 $\mu $
is a marginal weight of W, then
$\mu $
is a marginal weight of W, then
 $\mu $
is a marginal weight of V.
$\mu $
is a marginal weight of V.
Proof.
Lemma 2.3. Every nonzero
![]() $\triangle _q$
-module of dimension less than
$\triangle _q$
-module of dimension less than ![]() has marginal weights.
has marginal weights.
Proof. Let V denote a nonzero
![]() $\triangle _q$
-module of dimension less than
$\triangle _q$
-module of dimension less than ![]() . Then V contains an irreducible
. Then V contains an irreducible
![]() $\triangle _q$
-submodule W. Since
$\triangle _q$
-submodule W. Since ![]() , the
, the
![]() $\triangle _q$
-module W has a marginal weight by Theorem 2.1. The lemma is now immediate from Lemma 2.2(iii).
$\triangle _q$
-module W has a marginal weight by Theorem 2.1. The lemma is now immediate from Lemma 2.2(iii).
Definition 2.4. Let
![]() $\mu $
denote a weight of a
$\mu $
denote a weight of a
![]() $\triangle _q$
-module V. A weight vector v of V with weight
$\triangle _q$
-module V. A weight vector v of V with weight
![]() $\mu $
is said to be marginal whenever v is an eigenvector of
$\mu $
is said to be marginal whenever v is an eigenvector of
By Definitions 1.4 and 2.4, if a
![]() $\triangle _q$
-module V contains a marginal weight vector with weight
$\triangle _q$
-module V contains a marginal weight vector with weight
![]() $\mu $
, then
$\mu $
, then
![]() $\mu $
is a marginal weight of V.
$\mu $
is a marginal weight of V.
Lemma 2.5 [Reference Huang21, Lemma 6.1]
Assume that V is a finite-dimensional irreducible
![]() $\triangle _q$
-module. For any weight
$\triangle _q$
-module. For any weight
![]() $\mu $
of V, the following conditions are equivalent:
$\mu $
of V, the following conditions are equivalent:
-
(i)
 $\mu $
is a marginal weight of V.
$\mu $
is a marginal weight of V. -
(ii) There exists a marginal weight vector of V with weight
 $\mu $
.
$\mu $
.
Lemma 2.6. Assume that a finite-dimensional irreducible
![]() $\triangle _q$
-module V contains a marginal weight vector v with weight
$\triangle _q$
-module V contains a marginal weight vector v with weight
![]() $\mu $
. For all
$\mu $
. For all
![]() $i\in \mathbb N$
, the following statements hold:
$i\in \mathbb N$
, the following statements hold:
-
(i)
 $ (B-\mu q^{2i}-\mu ^{-1} q^{-2i})A^i v $
is a linear combination of
$ (B-\mu q^{2i}-\mu ^{-1} q^{-2i})A^i v $
is a linear combination of
 $v, Av,\ldots , A^{i-1} v$
.
$v, Av,\ldots , A^{i-1} v$
. -
(ii)
 $ \prod \limits _{h=0}^i (B-\mu q^{2h}-\mu ^{-1} q^{-2h}) $
vanishes at
$ \prod \limits _{h=0}^i (B-\mu q^{2h}-\mu ^{-1} q^{-2h}) $
vanishes at
 $v, Av,\ldots , A^i v$
.
$v, Av,\ldots , A^i v$
.
Proof.
-
(i): Immediate from [Reference Huang21, Lemma 6.2].
-
(ii): By Lemma 2.6(i), a routine induction on i yields (ii).
Lemma 2.7. If a finite-dimensional irreducible
![]() $\triangle _q$
-module V contains a marginal weight vector v, then the vectors
$\triangle _q$
-module V contains a marginal weight vector v, then the vectors
![]() $\{A^i v\}_{i=0}^{\dim V-1}$
are a basis for V.
$\{A^i v\}_{i=0}^{\dim V-1}$
are a basis for V.
Proof. Let W denote the subspace of V spanned by
![]() $\{A^i v\}_{i\in \mathbb N}$
. Then W is A-invariant and the vectors
$\{A^i v\}_{i\in \mathbb N}$
. Then W is A-invariant and the vectors
![]() $\{A^i v\}_{i=0}^{\dim W-1}$
are a basis for W. By Lemma 2.6(i), W is B-invariant. By Schur’s lemma, the central elements
$\{A^i v\}_{i=0}^{\dim W-1}$
are a basis for W. By Lemma 2.6(i), W is B-invariant. By Schur’s lemma, the central elements
![]() $\alpha ,\beta ,\gamma $
act on V, as well as W, as scalar multiplication. Hence W is a
$\alpha ,\beta ,\gamma $
act on V, as well as W, as scalar multiplication. Hence W is a
![]() $\triangle _q$
-submodule of V by Proposition 1.2. Since
$\triangle _q$
-submodule of V by Proposition 1.2. Since
![]() $v\in W$
and
$v\in W$
and
![]() $v\not =0$
, it follows that
$v\not =0$
, it follows that
![]() $W=V$
. The lemma follows.
$W=V$
. The lemma follows.
3. The universal property of
 $M_\lambda (a,b,c)$
and the feasible relation
$M_\lambda (a,b,c)$
and the feasible relation
For the sake of brevity, the following notational agreements will be used throughout the rest of this article. Whenever the quadruple
![]() $(a,b,c,\lambda )$
is used to represent an element of
$(a,b,c,\lambda )$
is used to represent an element of
![]() ${\mathbb F^\times }^4$
, the notation
${\mathbb F^\times }^4$
, the notation
![]() $\{m_i\}_{i\in \mathbb N}$
denotes the basis for
$\{m_i\}_{i\in \mathbb N}$
denotes the basis for
![]() $M_\lambda (a,b,c)$
mentioned in Theorem 1.5(i) and
$M_\lambda (a,b,c)$
mentioned in Theorem 1.5(i) and
![]() $\{\theta _i\}_{i\in \mathbb N}$
,
$\{\theta _i\}_{i\in \mathbb N}$
,
![]() $\{\theta _i^*\}_{i\in \mathbb N}$
,
$\{\theta _i^*\}_{i\in \mathbb N}$
,
![]() $\{\varphi _i\}_{i\in \mathbb N}$
stand for the accompanying parameters (1.9)–(1.11).
$\{\varphi _i\}_{i\in \mathbb N}$
stand for the accompanying parameters (1.9)–(1.11).
We begin this section with a simplified description of [Reference Huang16, Proposition 3.2], which is called the universal property of the Verma
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $M_\lambda (a,b,c)$
.
$M_\lambda (a,b,c)$
.
Proposition 3.1. Let
![]() $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
be given. For any
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
be given. For any
![]() $\triangle _q$
-module V and
$\triangle _q$
-module V and
![]() $v\in V$
, the following conditions are equivalent:
$v\in V$
, the following conditions are equivalent:
-
(i) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ M_\lambda (a,b,c)\to V $
that sends
$ M_\lambda (a,b,c)\to V $
that sends
 $m_0$
to v.
$m_0$
to v. -
(ii) The following equations hold on V:
(3.1) $$ \begin{align} B v&=\theta_0^* v, \end{align} $$
(3.2)
$$ \begin{align} B v&=\theta_0^* v, \end{align} $$
(3.2) $$ \begin{align} (B-\theta_1^*)A v&=(\theta_0(\theta_0^*-\theta_1^*)+\varphi_1) v, \end{align} $$
(3.3)
$$ \begin{align} (B-\theta_1^*)A v&=(\theta_0(\theta_0^*-\theta_1^*)+\varphi_1) v, \end{align} $$
(3.3) $$ \begin{align} \beta v&=\omega^* v, \end{align} $$
(3.4)where
$$ \begin{align} \beta v&=\omega^* v, \end{align} $$
(3.4)where $$ \begin{align} \gamma v&=\omega^\varepsilon v, \end{align} $$
$$ \begin{align} \gamma v&=\omega^\varepsilon v, \end{align} $$
 $\omega ^*$
and
$\omega ^*$
and
 $\omega ^\varepsilon $
are the scalars (1.13) and (1.14), respectively.
$\omega ^\varepsilon $
are the scalars (1.13) and (1.14), respectively.
Proof. By Theorem 1.5, condition (i) implies (3.1), (3.3), (3.4) and the following equations:
where
![]() $\omega $
is the scalar (1.12). By [Reference Huang16, Proposition 3.2], equations (3.1) and (3.3)–(3.6) imply condition (i). Observe that (3.2) is identical to (3.5) when (3.1) holds. Applying both sides of (1.5) to v and evaluating the resulting equation using (3.1), (3.2), and (3.4), we obtain equation (3.6). Therefore (3.1)–(3.4) hold if and only if (3.1) and (3.3)–(3.6) hold. The proposition follows.
$\omega $
is the scalar (1.12). By [Reference Huang16, Proposition 3.2], equations (3.1) and (3.3)–(3.6) imply condition (i). Observe that (3.2) is identical to (3.5) when (3.1) holds. Applying both sides of (1.5) to v and evaluating the resulting equation using (3.1), (3.2), and (3.4), we obtain equation (3.6). Therefore (3.1)–(3.4) hold if and only if (3.1) and (3.3)–(3.6) hold. The proposition follows.
Since the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $M_\lambda (a,b,c)$
is generated by
$M_\lambda (a,b,c)$
is generated by
![]() $m_0$
, if Proposition 3.1(i) holds then the mentioned map is unique. The coefficient of v on the right-hand side of (3.2) is equal to
$m_0$
, if Proposition 3.1(i) holds then the mentioned map is unique. The coefficient of v on the right-hand side of (3.2) is equal to
![]() $q-q^{-1}$
times
$q-q^{-1}$
times
Inspired by Proposition 3.1, we study the following functional relation:
Definition 3.2. For any
![]() $(a,b,c,\lambda )\in \mathbb F^{\times 4}$
and any
$(a,b,c,\lambda )\in \mathbb F^{\times 4}$
and any
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^3$
, we say that
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^3$
, we say that
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
whenever the following equations hold:
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
whenever the following equations hold:
-
(i)
 $\mu =b\lambda ^{-1}$
.
$\mu =b\lambda ^{-1}$
. -
(ii)
 $\varphi = (c+c^{-1})(\lambda -\lambda ^{-1})-(a+a^{-1})(b q-b^{-1} q^{-1})$
.
$\varphi = (c+c^{-1})(\lambda -\lambda ^{-1})-(a+a^{-1})(b q-b^{-1} q^{-1})$
. -
(iii)
 $\omega ^{*}= (c+c^{-1})(a+a^{-1})+(b+b^{-1})(\lambda q+\lambda ^{-1} q^{-1})$
.
$\omega ^{*}= (c+c^{-1})(a+a^{-1})+(b+b^{-1})(\lambda q+\lambda ^{-1} q^{-1})$
. -
(iv)
 $\omega ^{\varepsilon }=(a+a^{-1})(b+b^{-1})+(c+c^{-1})(\lambda q+\lambda ^{-1} q^{-1})$
.
$\omega ^{\varepsilon }=(a+a^{-1})(b+b^{-1})+(c+c^{-1})(\lambda q+\lambda ^{-1} q^{-1})$
.
Theorem 3.3. Let
![]() $(a,b,c,\lambda )\in \mathbb F^{\times 4}$
and
$(a,b,c,\lambda )\in \mathbb F^{\times 4}$
and
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^3$
be given. Suppose that a
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^3$
be given. Suppose that a
![]() $\triangle _q$
-module V contains a nonzero vector v satisfying the following equations:
$\triangle _q$
-module V contains a nonzero vector v satisfying the following equations:
Then
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
if and only if the following conditions hold:
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
if and only if the following conditions hold:
-
(i)
 $\mu =b\lambda ^{-1}$
.
$\mu =b\lambda ^{-1}$
. -
(ii) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ M_\lambda (a,b,c)\to V $
that sends
$ M_\lambda (a,b,c)\to V $
that sends
 $m_0$
to v.
$m_0$
to v.
Proof. Statement (i) is exactly Definition 3.2(i).
(
![]() $\Rightarrow $
): Statement (ii) is immediate from Proposition 3.1 and Definition 3.2.
$\Rightarrow $
): Statement (ii) is immediate from Proposition 3.1 and Definition 3.2.
(
![]() $\Leftarrow $
): Since (ii) holds, it follows from Proposition 3.1 that equations 3.1–3.4 hold. By (i), the scalar
$\Leftarrow $
): Since (ii) holds, it follows from Proposition 3.1 that equations 3.1–3.4 hold. By (i), the scalar
![]() $\theta _1^*$
is equal to
$\theta _1^*$
is equal to
![]() $\mu q^2+\mu ^{-1}q^{-2}$
. Since
$\mu q^2+\mu ^{-1}q^{-2}$
. Since
![]() $v\not =0$
, comparing (3.2) with (3.8) yields Definition 3.2(ii). For similar reasons, Definition 3.2(iii) and (iv) follow. Therefore
$v\not =0$
, comparing (3.2) with (3.8) yields Definition 3.2(ii). For similar reasons, Definition 3.2(iii) and (iv) follow. Therefore
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
.
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
.
We end this section with the following lemmas related to Theorem 3.3:
Lemma 3.4. Suppose that V is a finite-dimensional irreducible
![]() $\triangle _q$
-module with a marginal weight
$\triangle _q$
-module with a marginal weight
![]() $\mu $
. Then there exist a nonzero vector
$\mu $
. Then there exist a nonzero vector
![]() $v\in V$
and three scalars
$v\in V$
and three scalars
![]() $\varphi ,\omega ^*,\omega ^\varepsilon \in \mathbb F$
satisfying equations (3.7)–(3.10).
$\varphi ,\omega ^*,\omega ^\varepsilon \in \mathbb F$
satisfying equations (3.7)–(3.10).
Proof. By Lemma 2.5, there exists a marginal weight vector v of V with weight
![]() $\mu $
. Hence (3.7) follows. By Definition 2.4 and since
$\mu $
. Hence (3.7) follows. By Definition 2.4 and since
![]() $q^2\not =1$
, there is a scalar
$q^2\not =1$
, there is a scalar
![]() $\varphi \in \mathbb F$
such that (3.8) holds. By Schur’s lemma, there are
$\varphi \in \mathbb F$
such that (3.8) holds. By Schur’s lemma, there are
![]() $\omega ^*,\omega ^\varepsilon \in \mathbb F$
such that (3.9) and (3.10) hold.
$\omega ^*,\omega ^\varepsilon \in \mathbb F$
such that (3.9) and (3.10) hold.
Lemma 3.5. Let
![]() $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
be given. For any
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
be given. For any
![]() $\triangle _q$
-submodule O of
$\triangle _q$
-submodule O of
![]() $M_\lambda (a,b,c)$
with
$M_\lambda (a,b,c)$
with
![]() $m_0\not \in O$
, the following statements are true:
$m_0\not \in O$
, the following statements are true:
-
(i)
 $m_0+O$
is a marginal weight vector of
$m_0+O$
is a marginal weight vector of
 $M_\lambda (a,b,c)/O$
with weight
$M_\lambda (a,b,c)/O$
with weight
 $b\lambda ^{-1}$
.
$b\lambda ^{-1}$
. -
(ii)
 $m_0+O$
is a marginal weight vector of
$m_0+O$
is a marginal weight vector of
 $M_\lambda (a,b,c)/O$
with weight
$M_\lambda (a,b,c)/O$
with weight
 $b^{-1}\lambda $
if and only if
$b^{-1}\lambda $
if and only if
 $b\lambda ^{-1}=b^{-1}\lambda $
or
$b\lambda ^{-1}=b^{-1}\lambda $
or
 $m_1+O$
is a scalar multiple of
$m_1+O$
is a scalar multiple of
 $m_0+O$
.
$m_0+O$
.
Proof.
-
(i): By Theorem 1.5(i), it is routine to verify statement (i).
-
(ii): By Theorem 1.5(i), a straightforward calculation shows that
 $$ \begin{align*} (B-b^{-1}\lambda q^2-b\lambda^{-1}q^{-2}) Am_0= \varphi m_0 + (q^2-q^{-2})(b\lambda^{-1}-b^{-1}\lambda) m_1 \end{align*} $$
$$ \begin{align*} (B-b^{-1}\lambda q^2-b\lambda^{-1}q^{-2}) Am_0= \varphi m_0 + (q^2-q^{-2})(b\lambda^{-1}-b^{-1}\lambda) m_1 \end{align*} $$
for some scalar
![]() $\varphi \in \mathbb F$
. Statement (ii) follows from the above equation.
$\varphi \in \mathbb F$
. Statement (ii) follows from the above equation.
4. Proof for Theorem 1.6
Lemma 4.1. There exists a unique algebra automorphism
![]() $\vee $
of
$\vee $
of
![]() $\triangle _q$
that sends
$\triangle _q$
that sends
Proof. It is routine to verify the lemma by using Proposition 1.2.
For any
![]() $\triangle _q$
-module V, the notation
$\triangle _q$
-module V, the notation
stands for the
![]() $\triangle _q$
-module obtained by twisting the
$\triangle _q$
-module obtained by twisting the
![]() $\triangle _q$
-module V via
$\triangle _q$
-module V via
![]() $\vee $
.
$\vee $
.
Lemma 4.2. Let n denote an integer with ![]() . Suppose that
. Suppose that
![]() $\{h_i\}_{i=0}^{n+1}$
is a sequence in
$\{h_i\}_{i=0}^{n+1}$
is a sequence in
![]() $\mathbb F$
satisfying the following conditions:
$\mathbb F$
satisfying the following conditions:
-
(i)
 $h_{i+2} -h_{i-1} = (q^2+1+q^{-2})(h_{i+1}-h_i) $
for all
$h_{i+2} -h_{i-1} = (q^2+1+q^{-2})(h_{i+1}-h_i) $
for all
 $i=1,2,\ldots ,n-1$
.
$i=1,2,\ldots ,n-1$
. -
(ii) There are three integers
 $j,k,\ell $
with
$j,k,\ell $
with
 $0\leq j<k<\ell \leq n+1$
such that
$0\leq j<k<\ell \leq n+1$
such that
 $h_j=h_k=h_\ell =0$
.
$h_j=h_k=h_\ell =0$
.
Then
![]() $ h_i=0$
for all
$ h_i=0$
for all
![]() $i=0,1,\ldots ,n+1$
.
$i=0,1,\ldots ,n+1$
.
Proof. If
![]() $n=1$
, then the lemma is immediate from (ii). Now suppose that
$n=1$
, then the lemma is immediate from (ii). Now suppose that
![]() $n\geq 2$
. Since
$n\geq 2$
. Since
![]() $q^4\not =1$
, the roots
$q^4\not =1$
, the roots
![]() $1$
,
$1$
,
![]() $q^2$
,
$q^2$
,
![]() $q^{-2}$
of the characteristic equation for the linear homogeneous recurrence (i) are mutually distinct. Thus there are
$q^{-2}$
of the characteristic equation for the linear homogeneous recurrence (i) are mutually distinct. Thus there are
![]() $c_0,c_1,c_2\in \mathbb F$
such that
$c_0,c_1,c_2\in \mathbb F$
such that
By (ii), the following linear equations hold:
 $$ \begin{align*} \left\{ \begin{array}{ll} c_0 + q^{2j}c_1 + q^{-2j} c_2 =0, \\ c_0 + q^{2k}c_1 + q^{-2k} c_2 =0, \\ c_0 + q^{2\ell}c_1 + q^{-2\ell} c_2 =0. \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} c_0 + q^{2j}c_1 + q^{-2j} c_2 =0, \\ c_0 + q^{2k}c_1 + q^{-2k} c_2 =0, \\ c_0 + q^{2\ell}c_1 + q^{-2\ell} c_2 =0. \end{array} \right. \end{align*} $$
The determinant of the coefficient matrix for the above linear equations is equal to
Since each of
![]() $k-j$
,
$k-j$
,
![]() $\ell -k$
,
$\ell -k$
,
![]() $\ell -j$
is a positive integer less than
$\ell -j$
is a positive integer less than ![]() , none of
, none of
![]() $q^{2(k-j)}$
,
$q^{2(k-j)}$
,
![]() $q^{2(\ell -k)}$
,
$q^{2(\ell -k)}$
,
![]() $q^{2(\ell -j)}$
is equal to one. Therefore the determinant is nonzero. Since the coefficient matrix is invertible, each of
$q^{2(\ell -j)}$
is equal to one. Therefore the determinant is nonzero. Since the coefficient matrix is invertible, each of
![]() $c_0, c_1, c_2$
is zero. The lemma follows.
$c_0, c_1, c_2$
is zero. The lemma follows.
Proof of Theorem 1.6
By Lemma 2.3, there exists a marginal weight
![]() $\mu $
of the
$\mu $
of the
![]() $\triangle _q$
-module V. By Lemma 3.4, there are a nonzero vector v of V and three scalars
$\triangle _q$
-module V. By Lemma 3.4, there are a nonzero vector v of V and three scalars
![]() $\varphi ,\omega ^*,\omega ^\varepsilon \in \mathbb F$
satisfying equations (3.7)–(3.10).
$\varphi ,\omega ^*,\omega ^\varepsilon \in \mathbb F$
satisfying equations (3.7)–(3.10).
By Lemma 2.3, there exists a marginal weight
![]() $\kappa $
of the
$\kappa $
of the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $V^\vee $
. Let n denote the dimension of V minus one. Set
$V^\vee $
. Let n denote the dimension of V minus one. Set
and let c be the scalar in
![]() $\mathbb F^\times $
satisfying
$\mathbb F^\times $
satisfying
 $$ \begin{align} c+c^{-1}=&\left\{ \begin{array}{ll} \displaystyle \frac{\omega^\varepsilon-(a+a^{-1})(b+b^{-1})}{\lambda q+\lambda^{-1}q^{-1}} \qquad &\text{if } n=0, \\ \displaystyle \frac{\varphi+(a+a^{-1})(bq-b^{-1}q^{-1})}{\lambda-\lambda^{-1}} \qquad &\text{if }n\geq 1. \end{array} \right. \end{align} $$
$$ \begin{align} c+c^{-1}=&\left\{ \begin{array}{ll} \displaystyle \frac{\omega^\varepsilon-(a+a^{-1})(b+b^{-1})}{\lambda q+\lambda^{-1}q^{-1}} \qquad &\text{if } n=0, \\ \displaystyle \frac{\varphi+(a+a^{-1})(bq-b^{-1}q^{-1})}{\lambda-\lambda^{-1}} \qquad &\text{if }n\geq 1. \end{array} \right. \end{align} $$
Since ![]() , it follows that
, it follows that
![]() $\lambda ^2=1$
if and only if
$\lambda ^2=1$
if and only if
![]() $n=0$
. Since
$n=0$
. Since
![]() $q^4\not =1$
, it follows that
$q^4\not =1$
, it follows that
![]() $\lambda ^2 \not =-q^{-2}$
when
$\lambda ^2 \not =-q^{-2}$
when
![]() $n=0$
. Hence the denominators in the right-hand side of (4.2) are nonzero. Since
$n=0$
. Hence the denominators in the right-hand side of (4.2) are nonzero. Since
![]() $\mathbb F$
is algebraically closed, the existence of c follows.
$\mathbb F$
is algebraically closed, the existence of c follows.
We are now going to show that
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. Apparently, Definition 3.2(i) is immediate from (4.1). Due to (4.2), we divide the argument into two cases:
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. Apparently, Definition 3.2(i) is immediate from (4.1). Due to (4.2), we divide the argument into two cases:
![]() $n=0$
and
$n=0$
and
![]() $n\geq 1$
.
$n\geq 1$
.
![]() $(n=0)$
: In this case, v is a basis for V and
$(n=0)$
: In this case, v is a basis for V and
![]() $(a,b,\lambda )=(\kappa ,\mu ,1)$
. Definition 3.2(iv) is immediate from (4.2). Since a is a weight of
$(a,b,\lambda )=(\kappa ,\mu ,1)$
. Definition 3.2(iv) is immediate from (4.2). Since a is a weight of
![]() $V^\vee $
, it follows from Lemma 4.1 that
$V^\vee $
, it follows from Lemma 4.1 that
on V. Evaluating the left-hand side of (3.8) by using (3.7) and (4.3) yields
Definition 3.2(ii) follows. Applying both sides of (1.6) to v, we evaluate the resulting equation by using (3.7) and (4.3). It follows that
![]() $\omega ^*$
is equal to
$\omega ^*$
is equal to
 $$ \begin{align*}(a+a^{-1}) \cdot \frac{\omega^\varepsilon-(a+a^{-1})(b+b^{-1})}{q+q^{-1}} + (q+q^{-1})(b+b^{-1}). \end{align*} $$
$$ \begin{align*}(a+a^{-1}) \cdot \frac{\omega^\varepsilon-(a+a^{-1})(b+b^{-1})}{q+q^{-1}} + (q+q^{-1})(b+b^{-1}). \end{align*} $$
Definition 3.2(iii) follows by substituting Definition 3.2(iv) into the above scalar. Therefore
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
when
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
when
![]() $n=0$
.
$n=0$
.
![]() $(n\geq 1)$
: Definition 3.2(ii) is immediate from (4.2). Set
$(n\geq 1)$
: Definition 3.2(ii) is immediate from (4.2). Set
By Lemma 2.7, the vectors
![]() $\{v_i\}_{i=0}^n$
are a basis for V. By Lemma 2.5, there exists a marginal weight vector w of the
$\{v_i\}_{i=0}^n$
are a basis for V. By Lemma 2.5, there exists a marginal weight vector w of the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $V^\vee $
with weight
$V^\vee $
with weight
![]() $\kappa $
. It follows from Lemma 2.6(ii) that
$\kappa $
. It follows from Lemma 2.6(ii) that
![]() $\prod _{i=0}^n (A-\theta _i)$
vanishes at
$\prod _{i=0}^n (A-\theta _i)$
vanishes at
![]() $\{B^i w\}_{i=0}^n$
on the
$\{B^i w\}_{i=0}^n$
on the
![]() $\triangle _q$
-module V. By Lemma 2.7, the vectors
$\triangle _q$
-module V. By Lemma 2.7, the vectors
![]() $\{B^i w\}_{i=0}^n$
are also a basis for V. Hence
$\{B^i w\}_{i=0}^n$
are also a basis for V. Hence
![]() $ \prod _{i=0}^n (A-\theta _i) $
vanishes on V. Combined with (4.4), this implies that
$ \prod _{i=0}^n (A-\theta _i) $
vanishes on V. Combined with (4.4), this implies that
Let
![]() $\varphi ^{(i)}_j\in \mathbb F$
for all integers
$\varphi ^{(i)}_j\in \mathbb F$
for all integers
![]() $i,j$
with
$i,j$
with
![]() $0\leq i,j\leq n$
such that
$0\leq i,j\leq n$
such that
 $$ \begin{align} (B-\theta_i^*)v_i= & \sum_{j=0}^n \varphi^{(i)}_j v_j. \end{align} $$
$$ \begin{align} (B-\theta_i^*)v_i= & \sum_{j=0}^n \varphi^{(i)}_j v_j. \end{align} $$
By Lemma 2.6(i), the coefficients
Applying (3.7) and (3.8) yields that
Evaluating the right-hand side of the above equation by using Definition 3.2(ii) yields that
For any integer i with
![]() $1\leq i\leq n$
, we apply both sides of (1.6) to
$1\leq i\leq n$
, we apply both sides of (1.6) to
![]() $v_{i-1}$
and evaluate the coefficient of
$v_{i-1}$
and evaluate the coefficient of
![]() $v_i$
in the resulting equation using (3.7) and (4.4)–(4.7). It follows that
$v_i$
in the resulting equation using (3.7) and (4.4)–(4.7). It follows that
Here,
![]() $\varphi ^{(0)}_{-1}=\varphi ^{(n+1)}_n=0$
and
$\varphi ^{(0)}_{-1}=\varphi ^{(n+1)}_n=0$
and
Applying (4.9) yields that
On the other hand, a direct calculation shows that
![]() $\{\varphi _i\}_{i=0}^{n+1}$
also satisfy the same recurrence. Hence the scalars
$\{\varphi _i\}_{i=0}^{n+1}$
also satisfy the same recurrence. Hence the scalars
satisfy Lemma 4.2(i). By (4.8) and since
![]() $\varphi _0=\varphi _{n+1}=\varphi ^{(0)}_{-1}=\varphi ^{(n+1)}_n=0$
, it follows that
$\varphi _0=\varphi _{n+1}=\varphi ^{(0)}_{-1}=\varphi ^{(n+1)}_n=0$
, it follows that
![]() $h_0=h_1=h_{n+1}=0$
. Applying Lemma 4.2 yields
$h_0=h_1=h_{n+1}=0$
. Applying Lemma 4.2 yields
It is now routine to verify Definition 3.2(iv) by substituting the above equations into (4.9).
For any integer i with
![]() $0\leq i\leq n$
, we apply both sides of (1.6) to
$0\leq i\leq n$
, we apply both sides of (1.6) to
![]() $v_i$
and evaluate the coefficient of
$v_i$
and evaluate the coefficient of
![]() $v_i$
in the resulting equation. It follows that
$v_i$
in the resulting equation. It follows that
Here,
![]() $\varphi ^{(0)}_{-2}=\varphi ^{(1)}_{-1}=\varphi ^{(n+1)}_{n-1}=\varphi ^{(n+2)}_n=0$
and
$\varphi ^{(0)}_{-2}=\varphi ^{(1)}_{-1}=\varphi ^{(n+1)}_{n-1}=\varphi ^{(n+2)}_n=0$
and
 $$ \begin{align*} \begin{split} c_i &= (\theta_i-\theta_{i+1})\varphi_i +(\theta_i-\theta_{i-1})\varphi_{i+1} -(q-q^{-1})^2\theta_i^2\theta_i^* \\ & \qquad +\,(q^2-q^{-2})^2\theta_i^* +(q-q^{-1})^2\theta_i\omega^\varepsilon \end{split} \qquad (0\leq i\leq n), \end{align*} $$
$$ \begin{align*} \begin{split} c_i &= (\theta_i-\theta_{i+1})\varphi_i +(\theta_i-\theta_{i-1})\varphi_{i+1} -(q-q^{-1})^2\theta_i^2\theta_i^* \\ & \qquad +\,(q^2-q^{-2})^2\theta_i^* +(q-q^{-1})^2\theta_i\omega^\varepsilon \end{split} \qquad (0\leq i\leq n), \end{align*} $$
where
![]() $\theta _{-1}=a q^{-n-2}+a^{-1} q^{n+2}$
. A direct calculation shows that
$\theta _{-1}=a q^{-n-2}+a^{-1} q^{n+2}$
. A direct calculation shows that
![]() $c_i$
is equal to
$c_i$
is equal to
![]() $(q-q^{-1})(q^2-q^{-2})$
times the right-hand side of Definition 3.2(iii) for each
$(q-q^{-1})(q^2-q^{-2})$
times the right-hand side of Definition 3.2(iii) for each
![]() $i=0,1,\ldots ,n$
. Combined with (4.10), this implies that the values of
$i=0,1,\ldots ,n$
. Combined with (4.10), this implies that the values of
![]() $ \varphi ^{(i+2)}_i -(q^2+q^{-2})\varphi ^{(i+1)}_{i-1} +\varphi ^{(i)}_{i-2} $
are identical for all
$ \varphi ^{(i+2)}_i -(q^2+q^{-2})\varphi ^{(i+1)}_{i-1} +\varphi ^{(i)}_{i-2} $
are identical for all
![]() $i=0,1,\ldots ,n$
. It follows that
$i=0,1,\ldots ,n$
. It follows that
Applying Lemma 4.2 yields
Definition 3.2(iii) follows by substituting the above equations into (4.10). Therefore,
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
when
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
when
![]() $n\geq 1$
.
$n\geq 1$
.
Since
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, it follows from Theorem 3.3 that there exists a
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, it follows from Theorem 3.3 that there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
that sends
![]() $m_0$
to v. By (4.3) and (4.5), the vector
$m_0$
to v. By (4.3) and (4.5), the vector
![]() $m_{n+1}$
lies in the kernel of (4.11). Recall from Section 1 that the
$m_{n+1}$
lies in the kernel of (4.11). Recall from Section 1 that the
![]() $\triangle _q$
-submodule
$\triangle _q$
-submodule
![]() $N_\lambda (a,b,c)$
of
$N_\lambda (a,b,c)$
of
![]() $M_\lambda (a,b,c)$
is generated by
$M_\lambda (a,b,c)$
is generated by
![]() $m_{n+1}$
. Hence (4.11) induces the
$m_{n+1}$
. Hence (4.11) induces the
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
that sends
![]() $m_0+N_\lambda (a,b,c)$
to v. Since
$m_0+N_\lambda (a,b,c)$
to v. Since
![]() $V_n(a,b,c)$
and V have the same dimension
$V_n(a,b,c)$
and V have the same dimension
![]() $n+1$
and by the irreducibility of the
$n+1$
and by the irreducibility of the
![]() $\triangle _q$
-module V, the map (4.12) is a
$\triangle _q$
-module V, the map (4.12) is a
![]() $\triangle _q$
-module isomorphism. The result follows.
$\triangle _q$
-module isomorphism. The result follows.
5. A polynomial characterization for the feasible relation
Theorem 5.1. Assume that
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^3$
. For any scalars
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^3$
. For any scalars
![]() $\kappa ,\lambda ,c\in \mathbb F^\times $
, the quadruple
$\kappa ,\lambda ,c\in \mathbb F^\times $
, the quadruple
![]() $ (\kappa \lambda ,\mu \lambda ,c,\lambda ) $
is feasible for
$ (\kappa \lambda ,\mu \lambda ,c,\lambda ) $
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
if and only if the following conditions hold:
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
if and only if the following conditions hold:
-
(i)
 $\kappa $
is a root of the polynomial
$\kappa $
is a root of the polynomial  $$ \begin{align*}\frac{x^4}{\mu q} -\frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}}x^3 +(\omega^*-\mu q^{-1}-\mu^{-1} q)x^2 -\frac{\omega^\varepsilon-q\varphi}{q+q^{-1}}x +\mu q. \end{align*} $$
$$ \begin{align*}\frac{x^4}{\mu q} -\frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}}x^3 +(\omega^*-\mu q^{-1}-\mu^{-1} q)x^2 -\frac{\omega^\varepsilon-q\varphi}{q+q^{-1}}x +\mu q. \end{align*} $$
-
(ii)
 $\lambda $
is a root of the polynomial
$\lambda $
is a root of the polynomial  $$ \begin{align*}\kappa\mu q x^6 + \left( \kappa^{-1}\mu q -\frac{\omega^\varepsilon-q\varphi}{q+q^{-1}} \right)x^4 + \left( \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} - \kappa\mu^{-1} q^{-1} \right)x^2 -\frac{1}{\kappa\mu q}. \end{align*} $$
$$ \begin{align*}\kappa\mu q x^6 + \left( \kappa^{-1}\mu q -\frac{\omega^\varepsilon-q\varphi}{q+q^{-1}} \right)x^4 + \left( \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} - \kappa\mu^{-1} q^{-1} \right)x^2 -\frac{1}{\kappa\mu q}. \end{align*} $$
-
(iii) c is a root of
 $x^2-rx+1$
, where
$x^2-rx+1$
, where  $$ \begin{align*} r= \left\{ \begin{array}{ll} \displaystyle \frac{\omega^\varepsilon-(\kappa \lambda+\kappa^{-1}\lambda^{-1})(\mu\lambda+\mu^{-1}\lambda^{-1})}{\lambda q+\lambda^{-1} q^{-1}} \qquad &\text{if }\lambda^2=1, \\ \displaystyle \frac{\varphi+(\kappa\lambda +\kappa^{-1}\lambda^{-1})(\mu\lambda q-\mu^{-1}\lambda^{-1}q^{-1})}{\lambda-\lambda^{-1}} \qquad &\text{if }\lambda^2\not=1. \end{array} \right. \end{align*} $$
$$ \begin{align*} r= \left\{ \begin{array}{ll} \displaystyle \frac{\omega^\varepsilon-(\kappa \lambda+\kappa^{-1}\lambda^{-1})(\mu\lambda+\mu^{-1}\lambda^{-1})}{\lambda q+\lambda^{-1} q^{-1}} \qquad &\text{if }\lambda^2=1, \\ \displaystyle \frac{\varphi+(\kappa\lambda +\kappa^{-1}\lambda^{-1})(\mu\lambda q-\mu^{-1}\lambda^{-1}q^{-1})}{\lambda-\lambda^{-1}} \qquad &\text{if }\lambda^2\not=1. \end{array} \right. \end{align*} $$
Proof. Let
Clearly, Definition 3.2(i) holds. Then
![]() $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
if and only if Definition 3.2(ii)–(iv) hold.
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
if and only if Definition 3.2(ii)–(iv) hold.
(
![]() $\Rightarrow $
): Suppose that Definition 3.2(ii)–(iv) hold and we show (i)–(iii). Condition (iii) is immediate from Definition 3.2(ii) if
$\Rightarrow $
): Suppose that Definition 3.2(ii)–(iv) hold and we show (i)–(iii). Condition (iii) is immediate from Definition 3.2(ii) if
![]() $\lambda ^2\not =1$
; condition (iii) is immediate from Definition 3.2(iv) if
$\lambda ^2\not =1$
; condition (iii) is immediate from Definition 3.2(iv) if
![]() $\lambda ^2=1$
.
$\lambda ^2=1$
.
Using Definition 3.2(ii) and (iv), it is routine to verify that
 $$ \begin{align} \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}}&=\lambda(c+c^{-1})+b^{-1}q^{-1}(a+a^{-1}). \end{align} $$
$$ \begin{align} \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}}&=\lambda(c+c^{-1})+b^{-1}q^{-1}(a+a^{-1}). \end{align} $$
We multiply (5.2) and (5.3) by
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda ^{-1}$
, respectively. The difference between the resulting equations gives
$\lambda ^{-1}$
, respectively. The difference between the resulting equations gives
 $$ \begin{align*}\lambda\frac{\omega^\varepsilon-q\varphi}{q+q^{-1}}-\lambda^{-1}\frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} =(a+a^{-1})(b\lambda q-b^{-1} \lambda^{-1} q^{-1}). \end{align*} $$
$$ \begin{align*}\lambda\frac{\omega^\varepsilon-q\varphi}{q+q^{-1}}-\lambda^{-1}\frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} =(a+a^{-1})(b\lambda q-b^{-1} \lambda^{-1} q^{-1}). \end{align*} $$
Condition (ii) follows by substituting (5.1) into the above equation.
We multiply (5.2) and (5.3) by
![]() $a^{-1}\lambda $
and
$a^{-1}\lambda $
and
![]() $a\lambda ^{-1}$
, respectively. The sum of the resulting equations gives
$a\lambda ^{-1}$
, respectively. The sum of the resulting equations gives
 $$ \begin{align} a^{-1}\lambda \frac{\omega^\varepsilon-q\varphi}{q+q^{-1}}+a\lambda^{-1} \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} =& (a+a^{-1})(a^{-1}b\lambda q+ab^{-1}\lambda^{-1}q^{-1}+c+c^{-1}). \end{align} $$
$$ \begin{align} a^{-1}\lambda \frac{\omega^\varepsilon-q\varphi}{q+q^{-1}}+a\lambda^{-1} \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} =& (a+a^{-1})(a^{-1}b\lambda q+ab^{-1}\lambda^{-1}q^{-1}+c+c^{-1}). \end{align} $$
Subtracting Definition 3.2(iii) from (5.4) yields
 $$ \begin{align*}a^{-1}\lambda \frac{\omega^\varepsilon-q\varphi}{q+q^{-1}} +a\lambda^{-1} \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} -\omega^* = (ab^{-1}-a^{-1}b)(a\lambda^{-1}q^{-1}-a^{-1}\lambda q). \end{align*} $$
$$ \begin{align*}a^{-1}\lambda \frac{\omega^\varepsilon-q\varphi}{q+q^{-1}} +a\lambda^{-1} \frac{\omega^\varepsilon+q^{-1}\varphi}{q+q^{-1}} -\omega^* = (ab^{-1}-a^{-1}b)(a\lambda^{-1}q^{-1}-a^{-1}\lambda q). \end{align*} $$
Condition (i) follows by substituting (5.1) into the above equation. The “only if” part follows.
(
![]() $\Leftarrow $
): Suppose that (i)–(iii) hold. We show Definition 3.2(ii)–(iv). Definition 3.2(ii) is immediate from (iii) if
$\Leftarrow $
): Suppose that (i)–(iii) hold. We show Definition 3.2(ii)–(iv). Definition 3.2(ii) is immediate from (iii) if
![]() $\lambda ^2\not =1$
; Definition 3.2(ii) is obtained from condition (ii) if
$\lambda ^2\not =1$
; Definition 3.2(ii) is obtained from condition (ii) if
![]() $\lambda ^2=1$
.
$\lambda ^2=1$
.
Definition 3.2(iv) is immediate from (iii) if
![]() $\lambda ^2=1$
. Suppose that
$\lambda ^2=1$
. Suppose that
![]() $\lambda ^2\not =1$
. Applying (ii) yields
$\lambda ^2\not =1$
. Applying (ii) yields
 $$ \begin{align*}\frac{\lambda-\lambda^{-1}}{q+q^{-1}}\omega^\varepsilon=(\kappa\lambda+\kappa^{-1}\lambda^{-1})(\mu\lambda^2 q-\mu^{-1}\lambda^{-2} q^{-1}) +\frac{\lambda q+\lambda^{-1} q^{-1}}{q+q^{-1}}\varphi. \end{align*} $$
$$ \begin{align*}\frac{\lambda-\lambda^{-1}}{q+q^{-1}}\omega^\varepsilon=(\kappa\lambda+\kappa^{-1}\lambda^{-1})(\mu\lambda^2 q-\mu^{-1}\lambda^{-2} q^{-1}) +\frac{\lambda q+\lambda^{-1} q^{-1}}{q+q^{-1}}\varphi. \end{align*} $$
To get Definition 3.2(iv), we evaluate the right-hand side of the above equation by using Definition 3.2(ii) and replacing
![]() $\kappa $
and
$\kappa $
and
![]() $\mu $
with
$\mu $
with
![]() $a\lambda ^{-1}$
and
$a\lambda ^{-1}$
and
![]() $b\lambda ^{-1}$
.
$b\lambda ^{-1}$
.
Applying (i) yields
 $$ \begin{align*}\omega^*=(\kappa^{-1}q-\kappa q^{-1}) \left( \kappa\mu^{-1}-\kappa^{-1}\mu-\frac{\varphi}{q+q^{-1}} \right) +\frac{\kappa+\kappa^{-1}}{q+q^{-1}}\omega^\varepsilon. \end{align*} $$
$$ \begin{align*}\omega^*=(\kappa^{-1}q-\kappa q^{-1}) \left( \kappa\mu^{-1}-\kappa^{-1}\mu-\frac{\varphi}{q+q^{-1}} \right) +\frac{\kappa+\kappa^{-1}}{q+q^{-1}}\omega^\varepsilon. \end{align*} $$
To get Definition 3.2(iii), we evaluate the right-hand side of the above equation by using Definition 3.2(ii) and (iv) and replacing
![]() $\kappa $
and
$\kappa $
and
![]() $\mu $
with
$\mu $
with
![]() $a\lambda ^{-1}$
and
$a\lambda ^{-1}$
and
![]() $b\lambda ^{-1}$
. The “if” part follows.
$b\lambda ^{-1}$
. The “if” part follows.
By Theorem 5.1, there are at most
![]() $48$
elements of
$48$
elements of
![]() ${\mathbb F^\times }^4$
that are feasible for a given element of
${\mathbb F^\times }^4$
that are feasible for a given element of
![]() $\mathbb F^\times \times \mathbb F^{3}$
. By Definition 1.10(i), each equivalence class under
$\mathbb F^\times \times \mathbb F^{3}$
. By Definition 1.10(i), each equivalence class under ![]() consists of at most
consists of at most
![]() $48$
elements.
$48$
elements.
Theorem 5.2. For any
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^{3}$
, the following statements are true:
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )\in \mathbb F^\times \times \mathbb F^{3}$
, the following statements are true:
-
(i) There exists a quadruple
 $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
that is feasible for
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
that is feasible for
 $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
.
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. -
(ii) If
 $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
 $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, then the equivalence class of
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, then the equivalence class of
 $(a,b,c,\lambda )$
under
$(a,b,c,\lambda )$
under  consists of all quadruples in
consists of all quadruples in
 ${\mathbb F^\times }^4$
that are feasible for
${\mathbb F^\times }^4$
that are feasible for
 $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
.
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
.
Proof.
-
(i): Since
 $\mathbb F$
is algebraically closed, statement (i) is immediate from Theorem 5.1.
$\mathbb F$
is algebraically closed, statement (i) is immediate from Theorem 5.1. -
(ii): Since
 $(a,b,c,\lambda )$
is feasible for
$(a,b,c,\lambda )$
is feasible for
 $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, we may substitute Definition 3.2(i)–(iv) into the polynomials given in Theorem 5.1(i)–(iii). By Theorem 5.1, one may factor those polynomials into linear factors to obtain all quadruples that are feasible for
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, we may substitute Definition 3.2(i)–(iv) into the polynomials given in Theorem 5.1(i)–(iii). By Theorem 5.1, one may factor those polynomials into linear factors to obtain all quadruples that are feasible for
 $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. By Table A1, these quadruples are all elements of the equivalence class of
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. By Table A1, these quadruples are all elements of the equivalence class of
 $(a,b,c,\lambda )$
under
$(a,b,c,\lambda )$
under  .
.
6. Proof for Theorem 1.9
While using the quintuple
![]() $(a,b,c,\lambda ,\delta )$
to represent an element of
$(a,b,c,\lambda ,\delta )$
to represent an element of
![]() ${\mathbb F^\times }^4\times \mathbb F$
, we simply write
${\mathbb F^\times }^4\times \mathbb F$
, we simply write
Recall from Section 1 that ![]() is a basis for
is a basis for
![]() $W_\lambda ^\delta (a,b,c)$
.
$W_\lambda ^\delta (a,b,c)$
.
Lemma 6.1. For any
![]() $(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
, the following statements hold on
$(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
, the following statements hold on
![]() $W_\lambda ^\delta (a,b,c)$
:
$W_\lambda ^\delta (a,b,c)$
:
-
(i) The actions of A and B on
 $W_\lambda ^\delta (a,b,c)$
are as follows:
$W_\lambda ^\delta (a,b,c)$
are as follows: 
-
(ii) The elements
 $\alpha ,\beta ,\gamma $
act on
$\alpha ,\beta ,\gamma $
act on
 $W_\lambda ^\delta (a,b,c)$
as scalar multiplication by (1.12)–(1.14), respectively.
$W_\lambda ^\delta (a,b,c)$
as scalar multiplication by (1.12)–(1.14), respectively. -
(iii) The element
 acts on
acts on
 $W_\lambda ^\delta (a,b,c)$
as scalar multiplication by
$W_\lambda ^\delta (a,b,c)$
as scalar multiplication by
 $\delta $
.
$\delta $
.
Proof.
Proposition 6.2. Let
![]() $(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
be given. For any
$(a,b,c,\lambda ,\delta )\in {\mathbb F^\times }^4\times \mathbb F$
be given. For any
![]() $\triangle _q$
-module V and
$\triangle _q$
-module V and
![]() $v\in V$
, there exists a
$v\in V$
, there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $W_\lambda ^\delta (a,b,c)\to V$
that sends
$W_\lambda ^\delta (a,b,c)\to V$
that sends
![]() $w_0$
to v if and only if the following conditions hold:
$w_0$
to v if and only if the following conditions hold:
-
(i) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $M_\lambda (a,b,c)\to V$
that sends
$M_\lambda (a,b,c)\to V$
that sends
 $m_0$
to v.
$m_0$
to v. -
(ii)
 .
.
Proof. (
![]() $\Rightarrow $
): Composing the
$\Rightarrow $
): Composing the
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $W_\lambda ^\delta (a,b,c)\to V$
with the canonical map
$W_\lambda ^\delta (a,b,c)\to V$
with the canonical map
![]() $M_\lambda (a,b,c)\to W_\lambda ^\delta (a,b,c)$
yields condition (i). Condition (ii) is immediate from Lemma 6.1(iii).
$M_\lambda (a,b,c)\to W_\lambda ^\delta (a,b,c)$
yields condition (i). Condition (ii) is immediate from Lemma 6.1(iii).
(
![]() $\Leftarrow $
): By (ii), the vector
$\Leftarrow $
): By (ii), the vector

lies in the kernel of the
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $M_\lambda (a,b,c)\to V$
described in (i). By Theorem 1.5(i), the above subtrahend is equal to
$M_\lambda (a,b,c)\to V$
described in (i). By Theorem 1.5(i), the above subtrahend is equal to ![]() . Since the
. Since the
![]() $\triangle _q$
-submodule
$\triangle _q$
-submodule
![]() $O_\lambda ^{\delta }(a,b,c)$
of
$O_\lambda ^{\delta }(a,b,c)$
of
![]() $M_\lambda (a,b,c)$
is generated by
$M_\lambda (a,b,c)$
is generated by ![]() , this induces the desired
, this induces the desired
![]() $\triangle _q$
-module homomorphism. The proposition follows.
$\triangle _q$
-module homomorphism. The proposition follows.
For each
![]() $n\in \mathbb N$
, there exists a unique polynomial
$n\in \mathbb N$
, there exists a unique polynomial
![]() $T_n(x)\in \mathbb F[x]$
such that
$T_n(x)\in \mathbb F[x]$
such that
Specifically, the polynomials
![]() $\{T_n(x)\}_{n\in \mathbb N}$
satisfy the recurrence
$\{T_n(x)\}_{n\in \mathbb N}$
satisfy the recurrence
with
![]() $T_0(x)=2$
and
$T_0(x)=2$
and
![]() $T_1(x)=x$
. In particular,
$T_1(x)=x$
. In particular,
![]() $T_n(x)$
is a monic polynomial of degree n for each integer
$T_n(x)$
is a monic polynomial of degree n for each integer
![]() $n\geq 1$
.
$n\geq 1$
.
Lemma 6.3.
![]() for any
for any
![]() $\mu \in \mathbb F^{\times }$
.
$\mu \in \mathbb F^{\times }$
.
Proof. Let y be another indeterminate over
![]() $\mathbb F$
commuting with x. In the proof, we view
$\mathbb F$
commuting with x. In the proof, we view ![]() as a polynomial in x with coefficients in the Laurent polynomial ring
as a polynomial in x with coefficients in the Laurent polynomial ring
![]() $\mathbb F[y^{\pm 1}]$
. Since
$\mathbb F[y^{\pm 1}]$
. Since ![]() , it follows from (6.1) that
, it follows from (6.1) that
Since ![]() are mutually distinct elements of
are mutually distinct elements of
![]() $\mathbb F[y^{\pm 1}]$
and
$\mathbb F[y^{\pm 1}]$
and ![]() is a monic polynomial of degree
is a monic polynomial of degree ![]() , it follows that
, it follows that

The lemma follows.
Theorem 6.4 [Reference Huang17, Theorem 3.2]
The elements ![]() ,
, ![]() ,
, ![]() are central in
are central in
![]() $\triangle _q$
.
$\triangle _q$
.
Lemma 6.5. For any scalar
![]() $\mu \in \mathbb F^{\times }$
, the elements
$\mu \in \mathbb F^{\times }$
, the elements

are central in
![]() $\triangle _q$
.
$\triangle _q$
.
Proof of Theorem 1.9
Let
![]() $\mu $
denote a marginal weight of the
$\mu $
denote a marginal weight of the
![]() $\triangle _q$
-module V. By Lemma 3.4, there are a nonzero vector v of V and three scalars
$\triangle _q$
-module V. By Lemma 3.4, there are a nonzero vector v of V and three scalars
![]() $\varphi ,\omega ^*,\omega ^\varepsilon \in \mathbb F$
satisfying equations (3.7)–(3.10).
$\varphi ,\omega ^*,\omega ^\varepsilon \in \mathbb F$
satisfying equations (3.7)–(3.10).
By Theorem 5.2(i), there exists a quadruple
![]() $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
that is feasible for
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
that is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. By Theorem 3.3, there exists a unique
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
. By Theorem 3.3, there exists a unique
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
that sends
![]() $m_0$
to v. By Lemma 6.5, the element
$m_0$
to v. By Lemma 6.5, the element ![]() is central in
is central in
![]() $\triangle _q$
. By Schur’s lemma, this central element acts on V as scalar multiplication by some
$\triangle _q$
. By Schur’s lemma, this central element acts on V as scalar multiplication by some
![]() $\delta \in \mathbb F$
. Consequently, by Proposition 6.2, there exists a unique
$\delta \in \mathbb F$
. Consequently, by Proposition 6.2, there exists a unique
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
that sends
![]() $w_0$
to v. Since
$w_0$
to v. Since
![]() $W_\lambda ^\delta (a,b,c)$
and V have the same dimension
$W_\lambda ^\delta (a,b,c)$
and V have the same dimension ![]() and by the irreducibility of the
and by the irreducibility of the
![]() $\triangle _q$
-module V, the map (6.2) is a
$\triangle _q$
-module V, the map (6.2) is a
![]() $\triangle _q$
-module isomorphism. The result follows.
$\triangle _q$
-module isomorphism. The result follows.
7. The representation-theoretical characterizations of  and
and 
Starting from this section, we add a few more notational agreements. Whenever the quadruple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
is used to represent an element of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
is used to represent an element of
![]() ${\mathbb F^\times }^4$
, the notation
${\mathbb F^\times }^4$
, the notation
![]() $\{\bar {m}_i\}_{i\in \mathbb N}$
denotes the basis for
$\{\bar {m}_i\}_{i\in \mathbb N}$
denotes the basis for
![]() $M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c})$
mentioned in Theorem 1.5(i) and
$M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c})$
mentioned in Theorem 1.5(i) and
![]() $\{\bar {\theta }_i\}_{i\in \mathbb N}$
,
$\{\bar {\theta }_i\}_{i\in \mathbb N}$
,
![]() $\{\bar {\theta }_i^*\}_{i\in \mathbb N}$
,
$\{\bar {\theta }_i^*\}_{i\in \mathbb N}$
,
![]() $\{\bar {\varphi }_i\}_{i\in \mathbb N}$
stand for the accompanying parameters (1.9)–(1.11). Similarly, whenever the quintuple
$\{\bar {\varphi }_i\}_{i\in \mathbb N}$
stand for the accompanying parameters (1.9)–(1.11). Similarly, whenever the quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
is used to represent an element of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
is used to represent an element of
![]() ${\mathbb F^\times }^4\times \mathbb F$
, we write
${\mathbb F^\times }^4\times \mathbb F$
, we write
Recall the equivalence relation ![]() on
on
![]() ${\mathbb F^\times }^4$
from Definition 1.10(i).
${\mathbb F^\times }^4$
from Definition 1.10(i).
Theorem 7.1. For any
![]() $(a,b,c,\lambda ),(\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^\times }^4$
, the following conditions are equivalent:
$(a,b,c,\lambda ),(\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^\times }^4$
, the following conditions are equivalent:
-
(i)
 .
. -
(ii) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ M_\lambda (a,b,c)\to M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) $
that maps
$ M_\lambda (a,b,c)\to M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) $
that maps
 $m_0$
to
$m_0$
to
 $\bar {m}_0$
.
$\bar {m}_0$
. -
(iii) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) \to M_\lambda (a,b,c) $
that maps
$ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) \to M_\lambda (a,b,c) $
that maps
 $\bar {m}_0$
to
$\bar {m}_0$
to
 $m_0$
.
$m_0$
. -
(iv) There exists a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $ M_\lambda (a,b,c)\to M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) $
that maps
$ M_\lambda (a,b,c)\to M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) $
that maps
 $m_0$
to
$m_0$
to
 $\bar {m}_0$
.
$\bar {m}_0$
. -
(v) There exists a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) \to M_\lambda (a,b,c) $
that maps
$ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) \to M_\lambda (a,b,c) $
that maps
 $\bar {m}_0$
to
$\bar {m}_0$
to
 $m_0$
.
$m_0$
.
Proof. (ii) and (iii)
![]() $\Leftrightarrow $
(iv) and (v): Trivial.
$\Leftrightarrow $
(iv) and (v): Trivial.
(i)
![]() $\Rightarrow $
(ii) and (iii): By Theorem 5.2(ii), condition (i) implies that
$\Rightarrow $
(ii) and (iii): By Theorem 5.2(ii), condition (i) implies that
![]() $(a,b,c,\lambda )$
and
$(a,b,c,\lambda )$
and
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
are feasible for the same element of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
are feasible for the same element of
![]() $\mathbb F^\times \times \mathbb F^3$
. Conditions (ii) and (iii) then follow from Theorem 3.3.
$\mathbb F^\times \times \mathbb F^3$
. Conditions (ii) and (iii) then follow from Theorem 3.3.
(ii)
![]() $\Rightarrow $
(i): By Lemma 3.5(i), the vector
$\Rightarrow $
(i): By Lemma 3.5(i), the vector
![]() $m_0$
is a marginal weight vector of
$m_0$
is a marginal weight vector of
![]() $M_\lambda (a,b,c)$
with weight
$M_\lambda (a,b,c)$
with weight
![]() $b\lambda ^{-1}$
. By Lemma 3.5(ii) and since
$b\lambda ^{-1}$
. By Lemma 3.5(ii) and since
![]() $\bar {m}_0$
and
$\bar {m}_0$
and
![]() $\bar {m}_1$
are linearly independent, condition (ii) implies that
$\bar {m}_1$
are linearly independent, condition (ii) implies that
![]() $\bar {b}\bar {\lambda }^{-1}=b\lambda ^{-1}$
. Applying Theorem 3.3 yields that
$\bar {b}\bar {\lambda }^{-1}=b\lambda ^{-1}$
. Applying Theorem 3.3 yields that
![]() $(a,b,c,\lambda )$
and
$(a,b,c,\lambda )$
and
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
are feasible for the same element of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
are feasible for the same element of
![]() $\mathbb F^\times \times \mathbb F^3$
. Condition (i) then follows from Theorem 5.2(ii).
$\mathbb F^\times \times \mathbb F^3$
. Condition (i) then follows from Theorem 5.2(ii).
(iii)
![]() $\Rightarrow $
(i): Similar to the proof of (ii)
$\Rightarrow $
(i): Similar to the proof of (ii)
![]() $\Rightarrow $
(i).
$\Rightarrow $
(i).
Lemma 7.2. For any
![]() $(a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
, if there exists a
$(a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
, if there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ W_\lambda ^\delta (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that sends
$ W_\lambda ^\delta (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that sends
![]() $w_0$
to
$w_0$
to
![]() $\bar {w}_0$
then
$\bar {w}_0$
then ![]() .
.
Proof. Composing the given
![]() $\triangle _q$
-module homomorphism with the canonical map
$\triangle _q$
-module homomorphism with the canonical map
![]() $M_\lambda (a,b,c)\to W_\lambda ^\delta (a,b,c)$
yields the
$M_\lambda (a,b,c)\to W_\lambda ^\delta (a,b,c)$
yields the
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ M_\lambda (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that sends
$ M_\lambda (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that sends
![]() $m_0$
to
$m_0$
to
![]() $\bar {w}_0$
. By Lemma 3.5(i), the vector
$\bar {w}_0$
. By Lemma 3.5(i), the vector
![]() $m_0$
is a marginal weight vector of
$m_0$
is a marginal weight vector of
![]() $M_\lambda (a,b,c)$
with weight
$M_\lambda (a,b,c)$
with weight
![]() $b\lambda ^{-1}$
. Since
$b\lambda ^{-1}$
. Since
![]() $\bar {w}_0$
and
$\bar {w}_0$
and
![]() $\bar {w}_1$
are linearly independent and by Lemma 3.5(ii), the scalar
$\bar {w}_1$
are linearly independent and by Lemma 3.5(ii), the scalar
![]() $\bar {b}\bar {\lambda }^{-1}=b\lambda ^{-1}$
. Applying Theorem 3.3 yields that
$\bar {b}\bar {\lambda }^{-1}=b\lambda ^{-1}$
. Applying Theorem 3.3 yields that
![]() $(a,b,c,\lambda )$
and
$(a,b,c,\lambda )$
and
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
are feasible for the same element of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
are feasible for the same element of
![]() $\mathbb F^\times \times \mathbb F^3$
. The lemma then follows from Theorem 5.2(ii).
$\mathbb F^\times \times \mathbb F^3$
. The lemma then follows from Theorem 5.2(ii).
Proposition 7.3. For any
![]() $(a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
and any nonzero
$(a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
and any nonzero
![]() $\bar {w}\in W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
, there exists a
$\bar {w}\in W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
, there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ W_\lambda ^\delta (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that sends
$ W_\lambda ^\delta (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that sends
![]() $w_0$
to
$w_0$
to
![]() $\bar {w}$
if and only if the following conditions hold:
$\bar {w}$
if and only if the following conditions hold:
-
(i) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ M_\lambda (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
$ M_\lambda (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
 $m_0$
to
$m_0$
to
 $\bar {w}$
.
$\bar {w}$
. -
(ii) Equation (1.15) holds.
Proof. By Proposition 6.2, it suffices to show that equation (1.15) holds if and only if the following equation holds:

To see this, we utilize the following two equations: It follows from Lemma 6.1(iii) that

It follows from Lemma 6.3 that

(7.1)
![]() $\Rightarrow $
(1.15): We replace x by A and then apply both sides of (7.3) to
$\Rightarrow $
(1.15): We replace x by A and then apply both sides of (7.3) to
![]() $\bar {w}$
. Simplifying the resulting equation using (7.1) and (7.2), we obtain
$\bar {w}$
. Simplifying the resulting equation using (7.1) and (7.2), we obtain
Since
![]() $\bar {w}\not =0$
, equation (1.15) follows.
$\bar {w}\not =0$
, equation (1.15) follows.
(1.15)
![]() $\Rightarrow $
(7.1): Simplifying (7.3) by using (1.15) yields that
$\Rightarrow $
(7.1): Simplifying (7.3) by using (1.15) yields that

We replace x by A and then apply both sides of the above equation to
![]() $\bar {w}$
. Since the right-hand side of the resulting equation is equal to the zero vector by (7.2), equation (7.1) follows.
$\bar {w}$
. Since the right-hand side of the resulting equation is equal to the zero vector by (7.2), equation (7.1) follows.
Recall the equivalence relation ![]() on
on
![]() ${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.10(ii).
${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.10(ii).
Theorem 7.4. For any
![]() $(a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
, the following conditions are equivalent:
$(a,b,c,\lambda ,\delta ), (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
, the following conditions are equivalent:
-
(i)
 .
. -
(ii) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ W_\lambda ^{\delta }(a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
$ W_\lambda ^{\delta }(a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
 $w_0$
to
$w_0$
to
 $\bar {w}_0$
.
$\bar {w}_0$
. -
(iii) There exists a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) \to W_\lambda ^{\delta }(a,b,c) $
that maps
$ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) \to W_\lambda ^{\delta }(a,b,c) $
that maps
 $\bar {w}_0$
to
$\bar {w}_0$
to
 $w_0$
.
$w_0$
. -
(iv) There exists a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $ W_\lambda ^{\delta }(a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
$ W_\lambda ^{\delta }(a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
 $w_0$
to
$w_0$
to
 $\bar {w}_0$
.
$\bar {w}_0$
. -
(v) There exists a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) \to W_\lambda ^{\delta }(a,b,c) $
that maps
$ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) \to W_\lambda ^{\delta }(a,b,c) $
that maps
 $\bar {w}_0$
to
$\bar {w}_0$
to
 $w_0$
.
$w_0$
.
Proof. (ii) and (iii)
![]() $\Leftrightarrow $
(iv) and (v): Trivial.
$\Leftrightarrow $
(iv) and (v): Trivial.
(ii) and (iii)
![]() $\Rightarrow $
(i): Immediate from Lemma 7.2 and Proposition 7.3.
$\Rightarrow $
(i): Immediate from Lemma 7.2 and Proposition 7.3.
(i)
![]() $\Rightarrow $
(ii): Since
$\Rightarrow $
(ii): Since ![]() by Definition 1.10(ii), the map mentioned in Theorem 7.1(ii) exists. Composing this map with the canonical map
by Definition 1.10(ii), the map mentioned in Theorem 7.1(ii) exists. Composing this map with the canonical map
![]() $ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
yields the
$ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c}) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
yields the
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ M_\lambda (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
$ M_\lambda (a,b,c) \to W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) $
that maps
![]() $m_0$
to
$m_0$
to
![]() $\bar {w}_0$
. Since (1.15) holds by Definition 1.10(ii), condition (ii) is now immediate from Proposition 7.3.
$\bar {w}_0$
. Since (1.15) holds by Definition 1.10(ii), condition (ii) is now immediate from Proposition 7.3.
(i)
![]() $\Rightarrow $
(iii): Similar to the proof of (i)
$\Rightarrow $
(iii): Similar to the proof of (i)
![]() $\Rightarrow $
(ii).
$\Rightarrow $
(ii).
8. Proof for Theorem 1.11
Throughout the remainder of this article, for convenience, we assume that
![]() $(a,b,c,\lambda ,\delta )$
denotes a fixed element of
$(a,b,c,\lambda ,\delta )$
denotes a fixed element of
![]() ${\mathbb F^\times }^4\times \mathbb F$
.
${\mathbb F^\times }^4\times \mathbb F$
.
Lemma 8.1. If the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is irreducible then
$W_\lambda ^\delta (a,b,c)$
is irreducible then
![]() $\delta \not =0$
or
$\delta \not =0$
or ![]() .
.
Proof. Suppose, to the contrary, that
![]() $\delta =0$
and
$\delta =0$
and
![]() $\lambda ^2=q^{2(i-1)}$
for some integer i with
$\lambda ^2=q^{2(i-1)}$
for some integer i with ![]() . Let W be the subspace of
. Let W be the subspace of
![]() $W_\lambda ^\delta (a,b,c)$
spanned by
$W_\lambda ^\delta (a,b,c)$
spanned by ![]() . By Lemma 6.1(ii), the elements
. By Lemma 6.1(ii), the elements
![]() $\alpha ,\beta ,\gamma $
act on W as scalar multiplication. Since
$\alpha ,\beta ,\gamma $
act on W as scalar multiplication. Since
![]() $\delta =0$
and
$\delta =0$
and
![]() $\varphi _i=0$
by (1.11), it follows from Lemma 6.1(i) that W is invariant under A and B. Hence W is a proper
$\varphi _i=0$
by (1.11), it follows from Lemma 6.1(i) that W is invariant under A and B. Hence W is a proper
![]() $\triangle _q$
-submodule of
$\triangle _q$
-submodule of
![]() $W_\lambda ^\delta (a,b,c)$
by Proposition 1.2, a contradiction.
$W_\lambda ^\delta (a,b,c)$
by Proposition 1.2, a contradiction.
After Theorem 7.4 and Lemma 8.1, Theorem 1.11(ii) is an evident necessary condition for the irreducibility of the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
.
$W_\lambda ^\delta (a,b,c)$
.
Proof of the implication (i)
 $\Rightarrow $
(ii) of Theorem 1.11
$\Rightarrow $
(ii) of Theorem 1.11
By Theorem 7.4, the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^{\delta }(a,b,c)$
is isomorphic to
$W_\lambda ^{\delta }(a,b,c)$
is isomorphic to
![]() $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
for any
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
for any ![]() . Combining this with Lemma 8.1, the implication (i)
. Combining this with Lemma 8.1, the implication (i)
![]() $\Rightarrow $
(ii) follows.
$\Rightarrow $
(ii) follows.
Theorem 1.11(ii) can be expanded as follows by using Table A1:
Lemma 8.2. Theorem 1.11(ii) holds if and only if each of the following conditions holds:
-
(i)
 $\delta \not =0$
or (8.1)
$\delta \not =0$
or (8.1)
-
(ii)
 or (8.2)
or (8.2)
-
(iii)
 or (8.3)
or (8.3)
-
(iv)
 or (8.4)
or (8.4)
It is not immediately obvious that Theorem 1.11(ii) is a sufficient condition for the irreducibility of the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
. To establish this, we proceed to study the
$W_\lambda ^\delta (a,b,c)$
. To establish this, we proceed to study the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)^\vee $
, where
$W_\lambda ^\delta (a,b,c)^\vee $
, where
![]() $\vee $
is the algebra automorphism of
$\vee $
is the algebra automorphism of
![]() $\triangle _q$
given in Lemma 4.1. Define
$\triangle _q$
given in Lemma 4.1. Define
![]() $\nu $
to be a scalar in
$\nu $
to be a scalar in
![]() $\mathbb F^\times $
satisfying
$\mathbb F^\times $
satisfying
The existence of
![]() $\nu $
is guaranteed since
$\nu $
is guaranteed since
![]() $\mathbb F$
is algebraically closed. Set
$\mathbb F$
is algebraically closed. Set
Lemma 8.3. The characteristic polynomial of A on
![]() $W_\lambda ^\delta (a,b,c)$
is equal to
$W_\lambda ^\delta (a,b,c)$
is equal to

Proof. By Lemma 6.1(iii), the characteristic polynomial of A on
![]() $W_\lambda ^\delta (a,b,c)$
is equal to the right-hand side of (8.6). According to Lemma 6.3, we have
$W_\lambda ^\delta (a,b,c)$
is equal to the right-hand side of (8.6). According to Lemma 6.3, we have

Combining this with (8.5), the lemma follows.
By Lemma 8.3, the weights of
![]() $W_\lambda ^\delta (a,b,c)^\vee $
are
$W_\lambda ^\delta (a,b,c)^\vee $
are ![]() and
and ![]() . Define
. Define

Lemma 8.4. For any integer i with ![]() , the coefficient of
, the coefficient of ![]() in
in
![]() $e_i$
with respect to the basis
$e_i$
with respect to the basis ![]() for
for
![]() $W_\lambda ^\delta (a,b,c)$
is equal to one.
$W_\lambda ^\delta (a,b,c)$
is equal to one.
Proof. Immediate from (8.7).
By Lemma 8.4, the vector
![]() $e_i$
is nonzero for each integer i with
$e_i$
is nonzero for each integer i with ![]() .
.
Lemma 8.5. For any integer i with ![]() , the following statements are true:
, the following statements are true:
-
(i) The weight space of
 $W_\lambda ^\delta (a,b,c)^\vee $
with weight
$W_\lambda ^\delta (a,b,c)^\vee $
with weight
 $\nu ^{-1} q^{2i}$
is spanned by
$\nu ^{-1} q^{2i}$
is spanned by
 $e_i$
.
$e_i$
. -
(ii) The weight space of
 $W_\lambda ^\delta (a,b,c)^\vee $
with weight
$W_\lambda ^\delta (a,b,c)^\vee $
with weight
 $\nu q^{-2i}$
is spanned by
$\nu q^{-2i}$
is spanned by
 $e_i$
.
$e_i$
.
Proof. Applying Lemma 6.1(i), a direct calculation shows that
![]() $(A-\vartheta _i)e_i$
is equal to
$(A-\vartheta _i)e_i$
is equal to

A change of indices shows that the above vector is equal to the scalar multiple of
![]() $w_0$
by
$w_0$
by

which is equal to zero by (8.6). Therefore,
![]() $e_i$
is a weight vector of
$e_i$
is a weight vector of
![]() $W_\lambda ^\delta (a,b,c)^\vee $
with weight
$W_\lambda ^\delta (a,b,c)^\vee $
with weight
![]() $\nu ^{-1} q^{2i}$
or
$\nu ^{-1} q^{2i}$
or
![]() $\nu q^{-2i}$
. By Lemma 6.1(i), the rank of
$\nu q^{-2i}$
. By Lemma 6.1(i), the rank of
![]() $A-\vartheta _i$
on
$A-\vartheta _i$
on
![]() $W_\lambda ^\delta (a,b,c)$
is at least
$W_\lambda ^\delta (a,b,c)$
is at least ![]() . The lemma now follows from the rank-nullity theorem.
. The lemma now follows from the rank-nullity theorem.
Lemma 8.6. For any integer i with ![]() , the following conditions are equivalent:
, the following conditions are equivalent:
-
(i)
 $\nu ^{-1} q^{2i}$
is a marginal weight of
$\nu ^{-1} q^{2i}$
is a marginal weight of
 $W_\lambda ^\delta (a,b,c)^\vee $
.
$W_\lambda ^\delta (a,b,c)^\vee $
. -
(ii)
 $(A-\vartheta _{i+1})(A-\vartheta _i)Be_i=0$
on
$(A-\vartheta _{i+1})(A-\vartheta _i)Be_i=0$
on
 $W_\lambda ^\delta (a,b,c)$
.
$W_\lambda ^\delta (a,b,c)$
. -
(iii)
 $e_i$
is a marginal weight vector of
$e_i$
is a marginal weight vector of
 $W_\lambda ^\delta (a,b,c)^\vee $
with weight
$W_\lambda ^\delta (a,b,c)^\vee $
with weight
 $\nu ^{-1} q^{2i}$
.
$\nu ^{-1} q^{2i}$
. -
(iv)
 $\nu q^{-2i}\in \{ a \lambda ^{-1} q^{-2}, a^{-1} \lambda ^{-1} q^{-2}, b c q^{-1}, b c^{-1} q^{-1} \}$
.
$\nu q^{-2i}\in \{ a \lambda ^{-1} q^{-2}, a^{-1} \lambda ^{-1} q^{-2}, b c q^{-1}, b c^{-1} q^{-1} \}$
.
Proof. (i)
![]() $\Leftrightarrow $
(ii): Immediate from Definition 1.4 and Lemma 8.5(i).
$\Leftrightarrow $
(ii): Immediate from Definition 1.4 and Lemma 8.5(i).
(ii)
![]() $\Leftrightarrow $
(iii): Immediate from Definition 2.4 and Lemma 8.5(i).
$\Leftrightarrow $
(iii): Immediate from Definition 2.4 and Lemma 8.5(i).
(ii)
![]() $\Leftrightarrow $
(iv): Applying Lemma 1.3(ii) to
$\Leftrightarrow $
(iv): Applying Lemma 1.3(ii) to
![]() $W_\lambda ^\delta (a,b,c)^\vee $
yields that
$W_\lambda ^\delta (a,b,c)^\vee $
yields that
By Lemma 8.5(i), the left-hand side of (8.8) is a scalar multiple of
![]() $e_{i-1}$
, where
$e_{i-1}$
, where
![]() $e_{i-1}$
is interpreted as
$e_{i-1}$
is interpreted as ![]() if
if
![]() $i=0$
. In view of Lemma 8.4, condition (ii) holds if and only if the coefficient of
$i=0$
. In view of Lemma 8.4, condition (ii) holds if and only if the coefficient of ![]() in the left-hand side of (8.8) is equal to zero. Applying Lemma 6.1(i), a direct calculation shows that this coefficient is equal to
in the left-hand side of (8.8) is equal to zero. Applying Lemma 6.1(i), a direct calculation shows that this coefficient is equal to
![]() $b^{-1}\lambda ^{-1} q^{-1}(q-q^{-1})(q^2-q^{-2})$
times
$b^{-1}\lambda ^{-1} q^{-1}(q-q^{-1})(q^2-q^{-2})$
times
The equivalence of (ii) and (iv) follows.
Lemma 8.7. For any integer i with ![]() , the following conditions are equivalent:
, the following conditions are equivalent:
-
(i)
 $\nu q^{-2i}$
is a marginal weight of
$\nu q^{-2i}$
is a marginal weight of
 $W_\lambda ^\delta (a,b,c)^\vee $
.
$W_\lambda ^\delta (a,b,c)^\vee $
. -
(ii)
 $(A-\vartheta _{i-1})(A-\vartheta _i)Be_i=0$
on
$(A-\vartheta _{i-1})(A-\vartheta _i)Be_i=0$
on
 $W_\lambda ^\delta (a,b,c)$
.
$W_\lambda ^\delta (a,b,c)$
. -
(iii)
 $e_i$
is a marginal weight vector of
$e_i$
is a marginal weight vector of
 $W_\lambda ^\delta (a,b,c)^\vee $
with weight
$W_\lambda ^\delta (a,b,c)^\vee $
with weight
 $\nu q^{-2i}$
.
$\nu q^{-2i}$
. -
(iv)
 $\nu q^{-2i}\in \{ a \lambda q^{2}, a^{-1} \lambda q^{2}, b^{-1} c q, b^{-1} c^{-1} q \}$
.
$\nu q^{-2i}\in \{ a \lambda q^{2}, a^{-1} \lambda q^{2}, b^{-1} c q, b^{-1} c^{-1} q \}$
.
Proof. Similar to the proof of Lemma 8.6.
Lemma 8.8. For any integer i with ![]() , the following conditions are equivalent:
, the following conditions are equivalent:
-
(i)
 $\nu ^{-1} q^{2i}$
or
$\nu ^{-1} q^{2i}$
or
 $\nu q^{-2i}$
is a marginal weight of
$\nu q^{-2i}$
is a marginal weight of
 $W_\lambda ^\delta (a,b,c)^\vee $
.
$W_\lambda ^\delta (a,b,c)^\vee $
. -
(ii)
 $e_i$
is a marginal weight vector of the
$e_i$
is a marginal weight vector of the
 $\triangle _q$
-module
$\triangle _q$
-module
 $W_\lambda ^\delta (a,b,c)^\vee $
.
$W_\lambda ^\delta (a,b,c)^\vee $
. -
(iii)
 $\nu q^{-2i}\in \{ a \lambda ^{-1} q^{-2}, a^{-1} \lambda q^{2}, a \lambda q^{2}, a^{-1}\lambda ^{-1} q^{-2}, b c q^{-1}, b^{-1} c^{-1} q, b c^{-1} q^{-1}, b^{-1} c q\}$
.
$\nu q^{-2i}\in \{ a \lambda ^{-1} q^{-2}, a^{-1} \lambda q^{2}, a \lambda q^{2}, a^{-1}\lambda ^{-1} q^{-2}, b c q^{-1}, b^{-1} c^{-1} q, b c^{-1} q^{-1}, b^{-1} c q\}$
.
There exist unique scalars
![]() $L_{jk}^{(i)}\in \mathbb F$
for all integers
$L_{jk}^{(i)}\in \mathbb F$
for all integers
![]() $i,j,k$
with
$i,j,k$
with ![]() satisfying
satisfying

Let i denote an integer with ![]() . In view of Lemma 6.1(i), it follows that
. In view of Lemma 6.1(i), it follows that
![]() $L_{jk}^{(i)}=0$
for all integers
$L_{jk}^{(i)}=0$
for all integers
![]() $j,k$
with
$j,k$
with ![]() . In particular,
. In particular,

Theorem 8.9. The
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is reducible if and only if there exists an integer i with
$W_\lambda ^\delta (a,b,c)$
is reducible if and only if there exists an integer i with ![]() satisfying the following conditions:
satisfying the following conditions:
-
(i)
 $e_i$
is a marginal weight vector of the
$e_i$
is a marginal weight vector of the
 $\triangle _q$
-module
$\triangle _q$
-module
 $W_\lambda ^\delta (a,b,c)^\vee $
.
$W_\lambda ^\delta (a,b,c)^\vee $
. -
(ii)
 .
.
Proof. (
![]() $\Rightarrow $
): Since the
$\Rightarrow $
): Since the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is reducible, there exists a proper irreducible
$W_\lambda ^\delta (a,b,c)$
is reducible, there exists a proper irreducible
![]() $\triangle _q$
-submodule W of
$\triangle _q$
-submodule W of
![]() $W_\lambda ^\delta (a,b,c)$
. By Lemma 2.3, there exists a marginal weight
$W_\lambda ^\delta (a,b,c)$
. By Lemma 2.3, there exists a marginal weight
![]() $\mu $
of
$\mu $
of
![]() $W^\vee $
. It follows from Lemma 2.2(iii) that
$W^\vee $
. It follows from Lemma 2.2(iii) that
![]() $\mu $
is also a marginal weight of
$\mu $
is also a marginal weight of
![]() $W_\lambda ^\delta (a,b,c)^\vee $
. By Lemma 8.3, there exists an integer i with
$W_\lambda ^\delta (a,b,c)^\vee $
. By Lemma 8.3, there exists an integer i with ![]() such that
such that
![]() $\mu =\nu q^{-2i}$
or
$\mu =\nu q^{-2i}$
or
![]() $\mu =\nu ^{-1}q^{2i}$
. Combining this with Lemma 8.8, condition (i) follows.
$\mu =\nu ^{-1}q^{2i}$
. Combining this with Lemma 8.8, condition (i) follows.
Since
![]() $\mu $
is a weight of
$\mu $
is a weight of
![]() $W^\vee $
, it follows from Lemma 8.5 that
$W^\vee $
, it follows from Lemma 8.5 that
![]() $e_i\in W$
. Combined with (8.10), the vector
$e_i\in W$
. Combined with (8.10), the vector ![]() . Since the
. Since the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is generated by
$W_\lambda ^\delta (a,b,c)$
is generated by
![]() $w_0$
, the vector
$w_0$
, the vector
![]() $w_0\not \in W$
. Condition (ii) follows.
$w_0\not \in W$
. Condition (ii) follows.
(
![]() $\Leftarrow $
): Suppose, to the contrary, that the
$\Leftarrow $
): Suppose, to the contrary, that the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is irreducible. Applying Lemma 2.7 to
$W_\lambda ^\delta (a,b,c)$
is irreducible. Applying Lemma 2.7 to
![]() $W_\lambda ^\delta (a,b,c)^\vee $
, the vectors
$W_\lambda ^\delta (a,b,c)^\vee $
, the vectors ![]() form a basis for
form a basis for
![]() $W_\lambda ^\delta (a,b,c)$
. However, by condition (ii), the right-hand side of (8.10) is zero. This implies that
$W_\lambda ^\delta (a,b,c)$
. However, by condition (ii), the right-hand side of (8.10) is zero. This implies that ![]() are linearly dependent, a contradiction.
are linearly dependent, a contradiction.
Proposition 8.10. For any integer i with ![]() , the following statements are true:
, the following statements are true:
-
(i) Suppose that
 $\nu q^{-2i}\in \{a \lambda ^{-1} q^{-2}, a^{-1} \lambda q^{2}\}$
. Then
$\nu q^{-2i}\in \{a \lambda ^{-1} q^{-2}, a^{-1} \lambda q^{2}\}$
. Then 
-
(ii) Suppose that
 $\nu q^{-2i}\in \{ a\lambda q^{2}, a^{-1} \lambda ^{-1} q^{-2}\}$
. Then
$\nu q^{-2i}\in \{ a\lambda q^{2}, a^{-1} \lambda ^{-1} q^{-2}\}$
. Then
 $L_{jk}^{(i)}$
is equal to
$L_{jk}^{(i)}$
is equal to 
-
(iii) Suppose that
 $\nu q^{-2i}\in \{b c q^{-1},b^{-1} c^{-1} q\}$
. Then
$\nu q^{-2i}\in \{b c q^{-1},b^{-1} c^{-1} q\}$
. Then
 $L_{jk}^{(i)}$
is equal to
$L_{jk}^{(i)}$
is equal to 
-
(iv) Suppose that
 $\nu q^{-2i}\in \{b c^{-1} q^{-1},b^{-1} c q\}$
. Then
$\nu q^{-2i}\in \{b c^{-1} q^{-1},b^{-1} c q\}$
. Then
 $L_{jk}^{(i)}$
is equal to
$L_{jk}^{(i)}$
is equal to 
Proof. Fix an integer i with ![]() . Recall the coefficients
. Recall the coefficients ![]() from (8.9). Applying Lemma 6.1(i) yields that
from (8.9). Applying Lemma 6.1(i) yields that
By (8.7), we have

The coefficients ![]() are uniquely determined by the recurrence (8.12) and the initial conditions (8.11) and (8.13). To see (i)–(iv), it is routine but tedious to verify that the given formulas satisfy (8.11)–(8.13).
are uniquely determined by the recurrence (8.12) and the initial conditions (8.11) and (8.13). To see (i)–(iv), it is routine but tedious to verify that the given formulas satisfy (8.11)–(8.13).
Proof of the implication (ii)
 $\Rightarrow $
(i) of Theorem 1.11
$\Rightarrow $
(i) of Theorem 1.11
Suppose, to the contrary, that Theorem 1.11(i) fails. By Theorem 8.9, there is an integer i with ![]() such that Theorem 8.9(i) and (ii) hold. By Lemma 8.8, there are four possible cases: (a)
such that Theorem 8.9(i) and (ii) hold. By Lemma 8.8, there are four possible cases: (a)
![]() $\nu q^{-2i}\in \{a\lambda ^{-1}q^{-2},a^{-1}\lambda q^2\}$
; (b)
$\nu q^{-2i}\in \{a\lambda ^{-1}q^{-2},a^{-1}\lambda q^2\}$
; (b)
![]() $\nu q^{-2i}\in \{a\lambda q^2,a^{-1}\lambda ^{-1} q^{-2}\}$
; (c)
$\nu q^{-2i}\in \{a\lambda q^2,a^{-1}\lambda ^{-1} q^{-2}\}$
; (c)
![]() $\nu q^{-2i}\in \{bcq^{-1},b^{-1}c^{-1}q\}$
; and (d)
$\nu q^{-2i}\in \{bcq^{-1},b^{-1}c^{-1}q\}$
; and (d)
![]() $\nu q^{-2i}\in \{bc^{-1}q^{-1},b^{-1}cq\}$
.
$\nu q^{-2i}\in \{bc^{-1}q^{-1},b^{-1}cq\}$
.
(a): Since ![]() is the order of
is the order of
![]() $q^2$
, the scalar
$q^2$
, the scalar ![]() . It follows from (8.5) that
. It follows from (8.5) that
![]() $\delta =0$
. By Lemma 8.2(i), condition (8.1) holds. Hence
$\delta =0$
. By Lemma 8.2(i), condition (8.1) holds. Hence
![]() $\varphi _h\not =0$
for all
$\varphi _h\not =0$
for all ![]() by (1.11). Then
by (1.11). Then ![]() by Proposition 8.10(i), which contradicts Theorem 8.9(ii).
by Proposition 8.10(i), which contradicts Theorem 8.9(ii).
(b): Since ![]() is the order of
is the order of
![]() $q^2$
, it follows that
$q^2$
, it follows that ![]() . Using (8.5) yields
. Using (8.5) yields ![]() . By Lemma 8.2(ii), condition (8.2) holds. Then
. By Lemma 8.2(ii), condition (8.2) holds. Then ![]() by Proposition 8.10(ii), which contradicts Theorem 8.9(ii).
by Proposition 8.10(ii), which contradicts Theorem 8.9(ii).
(c): Since ![]() is the order of
is the order of
![]() $q^2$
, it follows that
$q^2$
, it follows that ![]() . Using (8.5) yields
. Using (8.5) yields ![]() . By Lemma 8.2(iii), condition (8.3) holds. Then
. By Lemma 8.2(iii), condition (8.3) holds. Then ![]() by Proposition 8.10(iii), which contradicts Theorem 8.9(ii).
by Proposition 8.10(iii), which contradicts Theorem 8.9(ii).
(d): Since ![]() is the order of
is the order of
![]() $q^2$
, it follows that
$q^2$
, it follows that ![]() . Using (8.5) yields
. Using (8.5) yields ![]() . By Lemma 8.2(iv), condition (8.4) holds. Then
. By Lemma 8.2(iv), condition (8.4) holds. Then ![]() by Proposition 8.10(iv), which contradicts Theorem 8.9(ii).
by Proposition 8.10(iv), which contradicts Theorem 8.9(ii).
9. The binary relation
 $\sim $
and the marginal weight vectors of
$\sim $
and the marginal weight vectors of
 $W_\lambda ^\delta (a,b,c)$
$W_\lambda ^\delta (a,b,c)$
Lemma 9.1. The characteristic polynomial of B on
![]() $W_\lambda ^\delta (a,b,c)$
is equal to
$W_\lambda ^\delta (a,b,c)$
is equal to

Proof. Immediate from Lemma 6.1(i).
Define

Note that
![]() $w_{ii}=w_i$
for all
$w_{ii}=w_i$
for all ![]() . Applying Lemma 6.1(i), a straightforward calculation yields the following three lemmas:
. Applying Lemma 6.1(i), a straightforward calculation yields the following three lemmas:
Lemma 9.2. If there exists an integer i with ![]() such that
such that
![]() $\varphi _i=0$
, then
$\varphi _i=0$
, then
for any integer j with ![]() . In particular,
. In particular,
![]() $(B-\theta _i^*)w_{0i}=0$
for each integer i with
$(B-\theta _i^*)w_{0i}=0$
for each integer i with ![]() .
.
Lemma 9.3. For each integer i with ![]() , the vector
, the vector
![]() $(B-\theta _{i+1}^*)(B-\theta _i^*)A w_{0i}$
is equal to the scalar multiple of
$(B-\theta _{i+1}^*)(B-\theta _i^*)A w_{0i}$
is equal to the scalar multiple of
![]() $w_{0,i-1}$
by
$w_{0,i-1}$
by
 $$ \begin{align*} &a b^{-1}\lambda q (q-q^{-1}) (q^2-q^{-2}) (q^i-q^{-i}) \varphi_i \\ &\quad \times\, (b q^i-b^{-1} q^{-i}) (q^{-i}-a^{-1}bc^{-1} \lambda^{-1} q^{i-1}) (q^{-i}-a^{-1}bc \lambda^{-1} q^{i-1}). \end{align*} $$
$$ \begin{align*} &a b^{-1}\lambda q (q-q^{-1}) (q^2-q^{-2}) (q^i-q^{-i}) \varphi_i \\ &\quad \times\, (b q^i-b^{-1} q^{-i}) (q^{-i}-a^{-1}bc^{-1} \lambda^{-1} q^{i-1}) (q^{-i}-a^{-1}bc \lambda^{-1} q^{i-1}). \end{align*} $$
Lemma 9.4. The following statements hold on
![]() $W_\lambda ^\delta (a,b,c)$
:
$W_\lambda ^\delta (a,b,c)$
:
-
(i)
 .
. -
(ii) For each integer i with
 , the vector
, the vector
 $(B-\theta _{i-1}^*)(B-\theta _i^*)A w_{0i}$
is equal to
$(B-\theta _{i-1}^*)(B-\theta _i^*)A w_{0i}$
is equal to  $$ \begin{align*} \frac{(q-q^{-1})(q^2-q^{-2})}{(q^i-q^{-i})(q^{i+1}-q^{-i-1})}(\theta_i^*-\theta_0^*) w_{0,i+1}. \end{align*} $$
$$ \begin{align*} \frac{(q-q^{-1})(q^2-q^{-2})}{(q^i-q^{-i})(q^{i+1}-q^{-i-1})}(\theta_i^*-\theta_0^*) w_{0,i+1}. \end{align*} $$
-
(iii)
 is equal to the scalar multiple of
is equal to the scalar multiple of
 $w_0$
by
$w_0$
by 
Lemma 9.5. Let
![]() $i,j$
denote two integers with
$i,j$
denote two integers with ![]() . Suppose that
. Suppose that
![]() $\varphi _i=0$
. Then the subspace W of
$\varphi _i=0$
. Then the subspace W of
![]() $W_\lambda ^\delta (a,b,c)$
spanned by
$W_\lambda ^\delta (a,b,c)$
spanned by
![]() $\{w_h\}_{h=i}^j$
is B-invariant. Moreover, if one of the following conditions holds, then
$\{w_h\}_{h=i}^j$
is B-invariant. Moreover, if one of the following conditions holds, then
![]() $w_{ij}$
is a basis for the
$w_{ij}$
is a basis for the
![]() $\theta _j^*$
-eigenspace of B on W:
$\theta _j^*$
-eigenspace of B on W:
-
(i)
 $\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
.
$\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. -
(ii)
 $\theta _j^*\not \in \{\theta _h^*\,|\,h=i,i+1,\ldots ,j-1\}$
.
$\theta _j^*\not \in \{\theta _h^*\,|\,h=i,i+1,\ldots ,j-1\}$
.
Proof. Since
![]() $\varphi _i=0$
, the first assertion follows from Lemma 6.1(i) and the characteristic polynomial of B on W is
$\varphi _i=0$
, the first assertion follows from Lemma 6.1(i) and the characteristic polynomial of B on W is
 $$ \begin{align} \prod_{h=i}^j(x-\theta_h^*). \end{align} $$
$$ \begin{align} \prod_{h=i}^j(x-\theta_h^*). \end{align} $$
Recall from (9.1) that
![]() $w_{ij}$
is a linear combination of
$w_{ij}$
is a linear combination of
![]() $\{w_h\}_{h=i}^j$
. Hence
$\{w_h\}_{h=i}^j$
. Hence
![]() $w_{ij}\in W$
. It follows from Lemma 9.2 that
$w_{ij}\in W$
. It follows from Lemma 9.2 that
![]() $(B-\theta _j^*)w_{ij}=0$
. To see the second assertion, under assumption (i) or (ii), we need to show that (a) the
$(B-\theta _j^*)w_{ij}=0$
. To see the second assertion, under assumption (i) or (ii), we need to show that (a) the
![]() $\theta _j^*$
-eigenspace of B on W is one-dimensional and (b) the vector
$\theta _j^*$
-eigenspace of B on W is one-dimensional and (b) the vector
![]() $w_{ij}$
is nonzero.
$w_{ij}$
is nonzero.
Suppose that (i) holds. Then the rank of
![]() $B-\theta _j^*$
on W is equal to
$B-\theta _j^*$
on W is equal to
![]() $j-i$
. By the rank-nullity theorem, condition (a) follows. Since the coefficient of
$j-i$
. By the rank-nullity theorem, condition (a) follows. Since the coefficient of
![]() $w_i$
in
$w_i$
in
![]() $w_{ij}$
is
$w_{ij}$
is
![]() $\varphi _{i+1}\varphi _{i+2}\dots \varphi _j \not =0$
, condition (b) follows. Suppose that (ii) holds. Then
$\varphi _{i+1}\varphi _{i+2}\dots \varphi _j \not =0$
, condition (b) follows. Suppose that (ii) holds. Then
![]() $\theta _j^*$
is a simple root of (9.2). Hence condition (a) follows. Since the coefficient of
$\theta _j^*$
is a simple root of (9.2). Hence condition (a) follows. Since the coefficient of
![]() $w_j$
in
$w_j$
in
![]() $w_{ij}$
is
$w_{ij}$
is
![]() $ (\theta _j^*-\theta _i^*)(\theta _j^*-\theta _{i+1}^*)\dots (\theta _j^*-\theta _{j-1}^*) \not =0 $
, condition (b) follows. The lemma follows.
$ (\theta _j^*-\theta _i^*)(\theta _j^*-\theta _{i+1}^*)\dots (\theta _j^*-\theta _{j-1}^*) \not =0 $
, condition (b) follows. The lemma follows.
Recall the binary relation
![]() $\sim $
on
$\sim $
on
![]() ${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.12.
${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.12.
Lemma 9.6. Suppose that there exists an integer i with ![]() such that
such that
![]() $\lambda ^2=q^{2(i-1)}$
. Then
$\lambda ^2=q^{2(i-1)}$
. Then
![]() $ (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a^{-1},b,c,\lambda ^{-1}q^{-2},\delta )$
satisfies the following statements:
$ (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a^{-1},b,c,\lambda ^{-1}q^{-2},\delta )$
satisfies the following statements:
-
(i)
 $\bar {\theta }_h^*=\theta _{i+h}^*$
for all
$\bar {\theta }_h^*=\theta _{i+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(ii)
 $w_i$
is a marginal weight vector of
$w_i$
is a marginal weight vector of
 $W_\lambda ^\delta (a,b,c)$
with weight
$W_\lambda ^\delta (a,b,c)$
with weight
 $\bar {b}\bar {\lambda }^{-1}$
.
$\bar {b}\bar {\lambda }^{-1}$
. -
(iii) There is a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
 $\bar {w}_0$
to
$\bar {w}_0$
to
 $w_i$
.
$w_i$
.
Proof. Since
![]() $\lambda ^2=q^{2(i-1)}$
and
$\lambda ^2=q^{2(i-1)}$
and
![]() $(\bar {b},\bar {\lambda })=(b,\lambda ^{-1}q^{-2})$
, it follows that
$(\bar {b},\bar {\lambda })=(b,\lambda ^{-1}q^{-2})$
, it follows that
Condition (i) follows from this and (1.10). Let
![]() $\mu $
denote the scalar (9.3). Then
$\mu $
denote the scalar (9.3). Then
![]() $(\mu +\mu ^{-1},\mu q^2+\mu ^{-1} q^{-2})=(\theta _i^*,\theta _{i+1}^*)$
. Since
$(\mu +\mu ^{-1},\mu q^2+\mu ^{-1} q^{-2})=(\theta _i^*,\theta _{i+1}^*)$
. Since
![]() $\lambda ^2=q^{2(i-1)}$
, it follows from (1.11) that
$\lambda ^2=q^{2(i-1)}$
, it follows from (1.11) that
![]() $\varphi _i=0$
. By Lemma 9.2, the vector
$\varphi _i=0$
. By Lemma 9.2, the vector
![]() $w_i$
is a weight vector of
$w_i$
is a weight vector of
![]() $W_\lambda ^{\delta }(a,b,c)$
with weight
$W_\lambda ^{\delta }(a,b,c)$
with weight
![]() $\mu $
. Let
$\mu $
. Let
 $$ \begin{align*}\varphi=\frac{\varphi_{i+1}+\theta_i(\theta_i^*-\theta_{i+1}^*)}{q-q^{-1}}. \end{align*} $$
$$ \begin{align*}\varphi=\frac{\varphi_{i+1}+\theta_i(\theta_i^*-\theta_{i+1}^*)}{q-q^{-1}}. \end{align*} $$
Using Lemma 6.1(i), a routine calculation yields that
![]() $ (B-\theta _{i+1}^*)Aw_i=(q-q^{-1})\varphi \, w_i. $
Condition (ii) follows.
$ (B-\theta _{i+1}^*)Aw_i=(q-q^{-1})\varphi \, w_i. $
Condition (ii) follows.
Under the hypothesis
![]() $\lambda ^2=q^{2(i-1)}$
, the quadruple
$\lambda ^2=q^{2(i-1)}$
, the quadruple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
is feasible for
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, where
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, where
![]() $\omega ^*$
and
$\omega ^*$
and
![]() $\omega ^{\varepsilon }$
are the scalars (1.13) and (1.14), respectively. By Theorem 3.3, there exists a
$\omega ^{\varepsilon }$
are the scalars (1.13) and (1.14), respectively. By Theorem 3.3, there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^{\delta }(a,b,c) $
that sends
$ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^{\delta }(a,b,c) $
that sends
![]() $\bar {m}_0$
to
$\bar {m}_0$
to
![]() $w_i$
. Since
$w_i$
. Since ![]() , equation (1.15) holds. Condition (iii) now follows from Proposition 7.3.
, equation (1.15) holds. Condition (iii) now follows from Proposition 7.3.
Lemma 9.7. Suppose that conditions (a) and (b) of Definition 1.12(iii) hold. Then
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a^{-1},b^{-1},c,\lambda ^{-1}q^{-2},\delta )$
satisfies the following statements:
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a^{-1},b^{-1},c,\lambda ^{-1}q^{-2},\delta )$
satisfies the following statements:
-
(i)
 for all
for all  .
. -
(ii)
 is a marginal weight vector of
is a marginal weight vector of
 $W_\lambda ^\delta (a,b,c)$
with weight
$W_\lambda ^\delta (a,b,c)$
with weight
 $\bar {b}\bar {\lambda }^{-1}$
.
$\bar {b}\bar {\lambda }^{-1}$
. -
(iii) There is a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
 $\bar {w}_0$
to
$\bar {w}_0$
to  .
.
Proof. Since
![]() $(\bar {b},\bar {\lambda })=(b^{-1},\lambda ^{-1}q^{-2})$
, it follows that
$(\bar {b},\bar {\lambda })=(b^{-1},\lambda ^{-1}q^{-2})$
, it follows that
Condition (i) follows. Let
![]() $\mu $
denote the scalar (9.4). Then
$\mu $
denote the scalar (9.4). Then ![]() . Observe that condition (a) of Definition 1.12(iii) is equivalent to
. Observe that condition (a) of Definition 1.12(iii) is equivalent to
By Lemma 9.5, the vector ![]() is a basis for the weight space
is a basis for the weight space
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
. Under condition (b) of Definition 1.12(iii), Lemma 9.4(iii) implies that
$W_\lambda ^\delta (a,b,c)(\mu )$
. Under condition (b) of Definition 1.12(iii), Lemma 9.4(iii) implies that
Since
![]() $q^2\not =1$
and
$q^2\not =1$
and ![]() is a basis for
is a basis for
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
, there exists a scalar
$W_\lambda ^\delta (a,b,c)(\mu )$
, there exists a scalar
![]() $\varphi \in \mathbb F$
such that
$\varphi \in \mathbb F$
such that ![]() Condition (ii) follows.
Condition (ii) follows.
Applying Lemma 6.1(i), a direct calculation shows that

By Definition 3.2, it is straightforward to verify that
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
is feasible for
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
is feasible for
![]() $(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, where
$(\mu ,\varphi ,\omega ^*,\omega ^\varepsilon )$
, where
![]() $\omega ^*$
and
$\omega ^*$
and
![]() $\omega ^{\varepsilon }$
are the scalars (1.13) and (1.14), respectively. By Theorem 3.3, there exists a
$\omega ^{\varepsilon }$
are the scalars (1.13) and (1.14), respectively. By Theorem 3.3, there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^{\delta }(a,b,c) $
that sends
$ M_{\bar {\lambda }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^{\delta }(a,b,c) $
that sends
![]() $\bar {m}_0$
to
$\bar {m}_0$
to ![]() . Since
. Since ![]() , equation (1.15) holds. Condition (iii) now follows from Proposition 7.3.
, equation (1.15) holds. Condition (iii) now follows from Proposition 7.3.
Proposition 9.8. For any
![]() $(a,b,c,\lambda ,\delta ),(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
satisfying
$(a,b,c,\lambda ,\delta ),(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
satisfying
![]() $(a,b,c,\lambda ,\delta )\sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
, there exists a
$(a,b,c,\lambda ,\delta )\sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
, there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
![]() $\bar {w}_0$
to a marginal weight vector of
$\bar {w}_0$
to a marginal weight vector of
![]() $W_\lambda ^\delta (a,b,c)$
.
$W_\lambda ^\delta (a,b,c)$
.
10. Proof for Theorem 1.14
Recall the equivalence relation ![]() on
on
![]() ${\mathbb F^\times }^4$
from Definition 1.10(i).
${\mathbb F^\times }^4$
from Definition 1.10(i).
Lemma 10.1. Suppose that
![]() $(a,b,c,\lambda ), (\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^\times }^4$
satisfy
$(a,b,c,\lambda ), (\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^\times }^4$
satisfy ![]() . Then
. Then
![]() $\theta _i^*=\bar {\theta }_i^*$
for all
$\theta _i^*=\bar {\theta }_i^*$
for all
![]() $i\in \mathbb N$
.
$i\in \mathbb N$
.
Proof. According to Table A1, the scalar
![]() $b\lambda ^{-1}=\bar {b}\bar {\lambda }^{-1}$
. Together with (1.10), this implies the lemma.
$b\lambda ^{-1}=\bar {b}\bar {\lambda }^{-1}$
. Together with (1.10), this implies the lemma.
Recall the equivalence relation ![]() on
on
![]() ${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.10(ii).
${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.10(ii).
Lemma 10.2. Suppose that there exists an integer i with ![]() such that
such that
![]() $\varphi _i=0$
. Then there exists a quintuple
$\varphi _i=0$
. Then there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that ![]() and the following conditions hold:
and the following conditions hold:
-
(i)
 $\bar {\lambda }^2=q^{2(i-1)}$
.
$\bar {\lambda }^2=q^{2(i-1)}$
. -
(ii)
 $\bar {\theta }_h=\theta _h$
for all
$\bar {\theta }_h=\theta _h$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(iii)
 $\bar {\theta }_h^*=\theta _h^*$
for all
$\bar {\theta }_h^*=\theta _h^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(iv)
 $\bar {\varphi }_h=\varphi _h$
for all
$\bar {\varphi }_h=\varphi _h$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(v) There is a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps 
Proof. Since
![]() $\varphi _i=0$
, it follows from (1.11) that
$\varphi _i=0$
, it follows from (1.11) that
We set
![]() $\bar {\delta }=\delta $
and select
$\bar {\delta }=\delta $
and select
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
from the
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })$
from the
![]() $2$
nd,
$2$
nd,
![]() $4$
th, and
$4$
th, and
![]() $7$
th rows of Table A1 as follows:
$7$
th rows of Table A1 as follows:
 $$ \begin{align*} (\bar{a},\bar{b},\bar{c},\bar{\lambda}) =\left\{ \begin{array}{ll} (a,b,c,\lambda) \qquad &\text{if }q^{2(i-1)}=\lambda^2, \\ (\frac{a}{\sqrt{abc\lambda q}}, \frac{b}{\sqrt{abc\lambda q}}, \frac{c}{\sqrt{abc\lambda q}}, \frac{\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=a^{-1}b^{-1}c^{-1}\lambda q^{-1}, \\ (\frac{ac}{\sqrt{abc\lambda q}}, \frac{bc}{\sqrt{abc\lambda q}}, \frac{1}{\sqrt{abc\lambda q}}, \frac{c\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=a^{-1}b^{-1}c\lambda q^{-1}. \end{array} \right. \end{align*} $$
$$ \begin{align*} (\bar{a},\bar{b},\bar{c},\bar{\lambda}) =\left\{ \begin{array}{ll} (a,b,c,\lambda) \qquad &\text{if }q^{2(i-1)}=\lambda^2, \\ (\frac{a}{\sqrt{abc\lambda q}}, \frac{b}{\sqrt{abc\lambda q}}, \frac{c}{\sqrt{abc\lambda q}}, \frac{\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=a^{-1}b^{-1}c^{-1}\lambda q^{-1}, \\ (\frac{ac}{\sqrt{abc\lambda q}}, \frac{bc}{\sqrt{abc\lambda q}}, \frac{1}{\sqrt{abc\lambda q}}, \frac{c\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=a^{-1}b^{-1}c\lambda q^{-1}. \end{array} \right. \end{align*} $$
By construction, condition (i) holds. Since
![]() $\bar {a}\bar {\lambda }^{-1}=a\lambda ^{-1}$
, condition (ii) holds by (1.9). Since
$\bar {a}\bar {\lambda }^{-1}=a\lambda ^{-1}$
, condition (ii) holds by (1.9). Since ![]() by Definition 1.10(i), condition (iii) is immediate from Lemma 10.1. It is straightforward to verify condition (iv) using (1.11).
by Definition 1.10(i), condition (iii) is immediate from Lemma 10.1. It is straightforward to verify condition (iv) using (1.11).
Since
![]() $(\bar {a}\bar {\lambda }^{-1},\bar {\delta })=(a\lambda ^{-1},\delta )$
, equation (1.15) holds. Hence
$(\bar {a}\bar {\lambda }^{-1},\bar {\delta })=(a\lambda ^{-1},\delta )$
, equation (1.15) holds. Hence ![]() by Definition 1.10(ii). By Theorem 7.4, there exists a
by Definition 1.10(ii). By Theorem 7.4, there exists a
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
that maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $w_0$
. Applying (ii) and Lemma 6.1(i) yields that
$w_0$
. Applying (ii) and Lemma 6.1(i) yields that
![]() $f(\bar {w}_h)=w_h$
for all
$f(\bar {w}_h)=w_h$
for all ![]() . Condition (v) follows.
. Condition (v) follows.
Recall the set ![]() defined after Theorem 1.11. Recall the equivalence relation
defined after Theorem 1.11. Recall the equivalence relation
![]() $\simeq $
on
$\simeq $
on
![]() ${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.13.
${\mathbb F^\times }^4\times \mathbb F$
from Definition 1.13.
Lemma 10.3. For any ![]() and any
and any
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
satisfying
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
satisfying
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
, the
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
, the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is isomorphic to
$W_\lambda ^\delta (a,b,c)$
is isomorphic to
![]() $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
. Moreover,
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
. Moreover, ![]() is closed under
is closed under
![]() $\simeq $
.
$\simeq $
.
Lemma 10.4. Suppose that there is an integer i with ![]() such that
such that
![]() $\varphi _i=0$
. Then there exists a quintuple
$\varphi _i=0$
. Then there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^{\times }}^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^{\times }}^4\times \mathbb F$
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
-
(i)
 $\bar {\theta }_h^*=\theta _{i+h}^*$
for all
$\bar {\theta }_h^*=\theta _{i+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(ii) There is a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $ f:W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$ f:W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
 $\bar {w}_0$
to
$\bar {w}_0$
to
 $w_i$
.
$w_i$
.
Proof. If
![]() $i=0$
, then the lemma follows by selecting
$i=0$
, then the lemma follows by selecting
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a,b,c,\lambda ,\delta )$
. Suppose that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a,b,c,\lambda ,\delta )$
. Suppose that
![]() $i\geq 1$
. By Lemma 10.2, we may assume that
$i\geq 1$
. By Lemma 10.2, we may assume that
![]() $\lambda ^2=q^{2(i-1)}$
instead of
$\lambda ^2=q^{2(i-1)}$
instead of
![]() $\varphi _i=0$
. The lemma is now immediate from Lemma 9.6.
$\varphi _i=0$
. The lemma is now immediate from Lemma 9.6.
Whenever
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
is used to denote an element of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
is used to denote an element of
![]() ${\mathbb F^\times }^4\times \mathbb F$
, the notation
${\mathbb F^\times }^4\times \mathbb F$
, the notation
![]() $\bar {w}_{ij}$
stands for the vector of
$\bar {w}_{ij}$
stands for the vector of
![]() $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
corresponding to the vector
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
corresponding to the vector
![]() $w_{ij}$
of
$w_{ij}$
of
![]() $W_\lambda ^\delta (a,b,c)$
for any integers
$W_\lambda ^\delta (a,b,c)$
for any integers
![]() $i,j$
with
$i,j$
with ![]() . Similarly, whenever the quintuple
. Similarly, whenever the quintuple
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
is used to denote an element of
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
is used to denote an element of
![]() ${\mathbb F^\times }^4\times \mathbb F$
, the notations
${\mathbb F^\times }^4\times \mathbb F$
, the notations
![]() $\{\hat {\theta }_i\}_{i\in \mathbb N}$
,
$\{\hat {\theta }_i\}_{i\in \mathbb N}$
,
![]() $\{\hat {\theta }_i^*\}_{i\in \mathbb N}$
,
$\{\hat {\theta }_i^*\}_{i\in \mathbb N}$
,
![]() $\{\hat {\varphi }_i\}_{i\in \mathbb N}$
,
$\{\hat {\varphi }_i\}_{i\in \mathbb N}$
, ![]() ,
, ![]() will follow a similar convention.
will follow a similar convention.
Lemma 10.5. Suppose that ![]() and there exist two integers
and there exist two integers
![]() $i,j$
with
$i,j$
with ![]() such that
such that
![]() $\varphi _i=0$
and
$\varphi _i=0$
and
![]() $\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. Then there exist an integer k with
$\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. Then there exist an integer k with
![]() $i\leq k\leq j$
and a quintuple
$i\leq k\leq j$
and a quintuple ![]() such that
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
-
(i)
 $\bar {\varphi }_1\bar {\varphi }_2\dots \bar {\varphi }_{j-k}\not =0$
.
$\bar {\varphi }_1\bar {\varphi }_2\dots \bar {\varphi }_{j-k}\not =0$
. -
(ii)
 $\bar {\theta }_h^*=\theta _{k+h}^*$
for all
$\bar {\theta }_h^*=\theta _{k+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(iii) There is a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c)$
that maps
 $\bar {w}_{0,j-k}$
to
$\bar {w}_{0,j-k}$
to
 $w_{ij}$
.
$w_{ij}$
.
Proof. The proof proceeds by induction on
![]() $j-i$
. By Lemma 10.4, there exists a quintuple
$j-i$
. By Lemma 10.4, there exists a quintuple
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
and the following conditions hold:
$(a,b,c,\lambda ,\delta )\simeq (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
and the following conditions hold:
-
(1)
 $\hat {\theta }_h^*=\theta _{i+h}^*$
for all
$\hat {\theta }_h^*=\theta _{i+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(2) There is a
 $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
 $f_1:W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})\to W_\lambda ^\delta (a,b,c)$
that maps
$f_1:W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})\to W_\lambda ^\delta (a,b,c)$
that maps
 $\hat {w}_0$
to
$\hat {w}_0$
to
 $w_i$
.
$w_i$
.
Since ![]() and by Lemma 10.3, the quintuple
and by Lemma 10.3, the quintuple ![]() . Since the
. Since the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W_\lambda ^\delta (a,b,c)$
is irreducible by Theorem 1.11, it follows that
$W_\lambda ^\delta (a,b,c)$
is irreducible by Theorem 1.11, it follows that
![]() $f_1$
is a
$f_1$
is a
![]() $\triangle _q$
-module isomorphism. If
$\triangle _q$
-module isomorphism. If
![]() $i=j$
, then the lemma follows by selecting
$i=j$
, then the lemma follows by selecting
![]() $k=i$
and
$k=i$
and
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
.
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
.
Suppose that
![]() $j> i$
. Since
$j> i$
. Since
![]() $\hat {\varphi }_0=0$
, there is an integer
$\hat {\varphi }_0=0$
, there is an integer
![]() $i'$
with
$i'$
with
![]() $0\leq i'\leq j-i$
such that
$0\leq i'\leq j-i$
such that
![]() $\hat {\varphi }_{i'}=0$
and
$\hat {\varphi }_{i'}=0$
and
![]() $\hat {\varphi }_{i'+1}\hat {\varphi }_{i'+2}\dots \hat {\varphi }_{j-i}\not =0$
. Suppose that
$\hat {\varphi }_{i'+1}\hat {\varphi }_{i'+2}\dots \hat {\varphi }_{j-i}\not =0$
. Suppose that
![]() $i'\geq 1$
. By the induction hypothesis, there are an integer
$i'\geq 1$
. By the induction hypothesis, there are an integer
![]() $k'$
with
$k'$
with
![]() $i'\leq k'\leq j-i$
and a quintuple
$i'\leq k'\leq j-i$
and a quintuple ![]() such that
such that
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
-
(1’)
 $\bar {\varphi }_1\bar {\varphi }_2\dots \bar {\varphi }_{j-i-k'}\not =0$
.
$\bar {\varphi }_1\bar {\varphi }_2\dots \bar {\varphi }_{j-i-k'}\not =0$
. -
(2’)
 $\bar {\theta }_h^*=\hat {\theta }_{k'+h}^*$
for all
$\bar {\theta }_h^*=\hat {\theta }_{k'+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(3’) There is a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $f_2:W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})$
that maps
$f_2:W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})$
that maps
 $\bar {w}_{0,j-i-k'}$
to
$\bar {w}_{0,j-i-k'}$
to
 $\hat {w}_{i',j-i}$
.
$\hat {w}_{i',j-i}$
.
If
![]() $i'=0$
, then the above statement remains true by selecting
$i'=0$
, then the above statement remains true by selecting
![]() $k'=0$
and
$k'=0$
and
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
. By the transitivity of
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
. By the transitivity of
![]() $\simeq $
, the quintuple
$\simeq $
, the quintuple
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
. Set
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
. Set
Then condition (i) is exactly condition (1’). Condition (ii) is immediate from (1) and (2’).
It follows from Lemma 9.2 that
![]() $(B-\bar {\theta }_{j-k}^*)\bar {w}_{0,j-k}=0$
. Since
$(B-\bar {\theta }_{j-k}^*)\bar {w}_{0,j-k}=0$
. Since
![]() $\bar {\theta }_{j-k}^*=\theta _j^*$
by (1) and (2’), applying
$\bar {\theta }_{j-k}^*=\theta _j^*$
by (1) and (2’), applying
![]() $f_1\circ f_2$
to the above equation yields
$f_1\circ f_2$
to the above equation yields
Applying Lemma 9.5 to (1’) yields that
![]() $\bar {w}_{0,j-k}$
is nonzero. Since
$\bar {w}_{0,j-k}$
is nonzero. Since
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are two
$f_2$
are two
![]() $\triangle _q$
-module isomorphisms, the vector
$\triangle _q$
-module isomorphisms, the vector
![]() $(f_1\circ f_2)(\bar {w}_{0,j-k})$
is nonzero. By (3’), the vector
$(f_1\circ f_2)(\bar {w}_{0,j-k})$
is nonzero. By (3’), the vector
![]() $(f_1\circ f_2)(\bar {w}_{0,j-k})=f_1(\hat {w}_{i',j-i})$
. Applying Lemma 6.1(i) to (2) yields that
$(f_1\circ f_2)(\bar {w}_{0,j-k})=f_1(\hat {w}_{i',j-i})$
. Applying Lemma 6.1(i) to (2) yields that
![]() $f_1(\hat {w}_{i',j-i})$
is a linear combination of
$f_1(\hat {w}_{i',j-i})$
is a linear combination of
![]() $\{w_h\}_{h=i}^{j}$
. Since
$\{w_h\}_{h=i}^{j}$
. Since
![]() $\varphi _i=0$
and
$\varphi _i=0$
and
![]() $\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
, it follows from Lemma 9.5 that there exists
$\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
, it follows from Lemma 9.5 that there exists
![]() $\varepsilon \in \mathbb F^\times $
such that
$\varepsilon \in \mathbb F^\times $
such that
The
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
![]() $\varepsilon ^{-1}\cdot (f_1\circ f_2)$
satisfies condition (iii). The lemma follows.
$\varepsilon ^{-1}\cdot (f_1\circ f_2)$
satisfies condition (iii). The lemma follows.
Lemma 10.6. Suppose that there is an integer i with ![]() such that
such that
![]() $\varphi _1\varphi _2\dots \varphi _i\not =0$
. Then the following conditions are equivalent:
$\varphi _1\varphi _2\dots \varphi _i\not =0$
. Then the following conditions are equivalent:
-
(i)
 $(B-\theta _{i+1}^*)(B-\theta _i^*) A w_{0i}=0$
.
$(B-\theta _{i+1}^*)(B-\theta _i^*) A w_{0i}=0$
. -
(ii)
 $q^{2(i-1)}\in \{b^{-2}q^{-2}, ab^{-1}c\lambda q^{-1}, ab^{-1}c^{-1}\lambda q^{-1}\}$
.
$q^{2(i-1)}\in \{b^{-2}q^{-2}, ab^{-1}c\lambda q^{-1}, ab^{-1}c^{-1}\lambda q^{-1}\}$
.
Proof. (ii)
![]() $\Rightarrow $
(i): Immediate from Lemma 9.3.
$\Rightarrow $
(i): Immediate from Lemma 9.3.
(i)
![]() $\Rightarrow $
(ii): Since
$\Rightarrow $
(ii): Since
![]() $\varphi _1\varphi _2\dots \varphi _{i-1}\not =0$
, it follows from Lemma 9.5 that
$\varphi _1\varphi _2\dots \varphi _{i-1}\not =0$
, it follows from Lemma 9.5 that
![]() $w_{0,i-1}$
is nonzero. Together with the assumption
$w_{0,i-1}$
is nonzero. Together with the assumption
![]() $\varphi _i\not =0$
, the implication (i)
$\varphi _i\not =0$
, the implication (i)
![]() $\Rightarrow $
(ii) follows from (1.11) and Lemma 9.3.
$\Rightarrow $
(ii) follows from (1.11) and Lemma 9.3.
Lemma 10.7. Assume that there exists an integer i with ![]() such that
such that
![]() $\varphi _1\varphi _2\dots \varphi _i\not =0$
. If
$\varphi _1\varphi _2\dots \varphi _i\not =0$
. If
then there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c) $
that maps
$ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c) $
that maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $w_{0i}$
.
$w_{0i}$
.
Proof. If
![]() $i=0$
, then the lemma follows by selecting
$i=0$
, then the lemma follows by selecting
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a,b,c,\lambda ,\delta )$
. Suppose that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })=(a,b,c,\lambda ,\delta )$
. Suppose that
![]() $i\geq 1$
. It follows from Lemma 10.6 that
$i\geq 1$
. It follows from Lemma 10.6 that
![]() $q^{2(i-1)}\in \{b^{-2}q^{-2}, ab^{-1}c\lambda q^{-1}, ab^{-1}c^{-1}\lambda q^{-1}\}$
. We select
$q^{2(i-1)}\in \{b^{-2}q^{-2}, ab^{-1}c\lambda q^{-1}, ab^{-1}c^{-1}\lambda q^{-1}\}$
. We select
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda })$
from the
$(\hat {a},\hat {b},\hat {c},\hat {\lambda })$
from the
![]() $10$
th,
$10$
th,
![]() $13$
th, and
$13$
th, and
![]() $18$
th rows of Table A1 as follows:
$18$
th rows of Table A1 as follows:
 $$ \begin{align*} (\hat{a},\hat{b},\hat{c},\hat{\lambda}) =\left\{ \begin{array}{ll} (c, \lambda^{-1}q^{-1}, a, b^{-1}q^{-1}) \qquad &\text{if }q^{2(i-1)}=b^{-2}q^{-2}, \\ (\frac{c}{\sqrt{abc\lambda q}}, \frac{abc}{\sqrt{abc\lambda q}}, \frac{a}{\sqrt{abc\lambda q}}, \frac{ac\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=ab^{-1}c\lambda q^{-1}, \\ (\frac{1}{\sqrt{abc\lambda q}}, \frac{ab}{\sqrt{abc\lambda q}}, \frac{ac}{\sqrt{abc\lambda q}}, \frac{a\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=ab^{-1}c^{-1}\lambda q^{-1}. \end{array} \right. \end{align*} $$
$$ \begin{align*} (\hat{a},\hat{b},\hat{c},\hat{\lambda}) =\left\{ \begin{array}{ll} (c, \lambda^{-1}q^{-1}, a, b^{-1}q^{-1}) \qquad &\text{if }q^{2(i-1)}=b^{-2}q^{-2}, \\ (\frac{c}{\sqrt{abc\lambda q}}, \frac{abc}{\sqrt{abc\lambda q}}, \frac{a}{\sqrt{abc\lambda q}}, \frac{ac\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=ab^{-1}c\lambda q^{-1}, \\ (\frac{1}{\sqrt{abc\lambda q}}, \frac{ab}{\sqrt{abc\lambda q}}, \frac{ac}{\sqrt{abc\lambda q}}, \frac{a\lambda}{\sqrt{abc\lambda q}}) \qquad &\text{if }q^{2(i-1)}=ab^{-1}c^{-1}\lambda q^{-1}. \end{array} \right. \end{align*} $$
By construction,
![]() $\hat {\lambda }^2=q^{2(i-1)}$
. Note that
$\hat {\lambda }^2=q^{2(i-1)}$
. Note that ![]() by Definition 1.10(i). Set
by Definition 1.10(i). Set
Then ![]() by Definition 1.10(ii). By Theorem 7.4, there exists a
by Definition 1.10(ii). By Theorem 7.4, there exists a
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
that maps
![]() $\hat {w}_0$
to
$\hat {w}_0$
to
![]() $w_0$
. Applying Lemma 9.6, there exists a quintuple
$w_0$
. Applying Lemma 9.6, there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there is a
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there is a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
that maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $\hat {w}_i$
. Since
$\hat {w}_i$
. Since
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\sim (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and
![]() $(a,b,c,\lambda ,\delta )\sim (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
by Definition 1.12(i), it follows from Definition 1.13 that
$(a,b,c,\lambda ,\delta )\sim (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
by Definition 1.12(i), it follows from Definition 1.13 that
![]() $ (a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
.
$ (a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
.
Since
![]() $\hat {\lambda }^2=q^{2(i-1)}$
, it follows from (1.11) that
$\hat {\lambda }^2=q^{2(i-1)}$
, it follows from (1.11) that
![]() $\hat {\varphi }_i=0$
. Hence
$\hat {\varphi }_i=0$
. Hence
![]() $ (B-\hat {\theta }_i^*)\hat {w}_i=0$
by Lemma 9.2. Since
$ (B-\hat {\theta }_i^*)\hat {w}_i=0$
by Lemma 9.2. Since
![]() $\theta _i^*=\hat {\theta }_i^*$
by Lemma 10.1, applying
$\theta _i^*=\hat {\theta }_i^*$
by Lemma 10.1, applying
![]() $f_1$
to the above equation yields
$f_1$
to the above equation yields
Since
![]() $f_1$
is a
$f_1$
is a
![]() $\triangle _q$
-module isomorphism, the vector
$\triangle _q$
-module isomorphism, the vector
![]() $f_1(\hat {w}_i)$
is nonzero. Since
$f_1(\hat {w}_i)$
is nonzero. Since
![]() $f_1(\hat {w}_0)=w_0$
and by Lemma 6.1(i), the vector
$f_1(\hat {w}_0)=w_0$
and by Lemma 6.1(i), the vector
![]() $f_1(\hat {w}_i)$
is a linear combination of
$f_1(\hat {w}_i)$
is a linear combination of
![]() $\{w_h\}_{h=0}^i$
. Since
$\{w_h\}_{h=0}^i$
. Since
![]() $\varphi _1\varphi _2\dots \varphi _i\not =0$
, it follows from Lemma 9.5 that there exists
$\varphi _1\varphi _2\dots \varphi _i\not =0$
, it follows from Lemma 9.5 that there exists
![]() $\varepsilon \in \mathbb F^\times $
such that
$\varepsilon \in \mathbb F^\times $
such that
The
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $\varepsilon ^{-1}\cdot (f_1\circ f_2)$
maps
$\varepsilon ^{-1}\cdot (f_1\circ f_2)$
maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $w_{0i}$
. The lemma follows.
$w_{0i}$
. The lemma follows.
Proposition 10.8. Assume that ![]() and there exist two integers
and there exist two integers
![]() $i,j$
with
$i,j$
with ![]() such that
such that
![]() $\varphi _i=0$
and
$\varphi _i=0$
and
![]() $\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. If
$\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. If
then there exists a quintuple ![]() such that
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
![]() $ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c) $
that maps
$ W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W_\lambda ^\delta (a,b,c) $
that maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $w_{ij}$
.
$w_{ij}$
.
Proof. By Lemma 10.5, there exist an integer k with
![]() $i\leq k\leq j$
and a quintuple
$i\leq k\leq j$
and a quintuple ![]() such that
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
and the following conditions hold:
$(a,b,c,\lambda ,\delta )\simeq (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
and the following conditions hold:
-
(i)
 $\hat {\varphi }_1\hat {\varphi }_2\dots \hat {\varphi }_{j-k}\not =0$
.
$\hat {\varphi }_1\hat {\varphi }_2\dots \hat {\varphi }_{j-k}\not =0$
. -
(ii)
 $\hat {\theta }_h^*=\theta _{k+h}^*$
for all
$\hat {\theta }_h^*=\theta _{k+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(iii) There is a
 $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
 $f_1:W^{\hat {\delta }}_{\hat {\lambda }}(\hat {a},\hat {b},\hat {c})\to W^\delta _\lambda (a,b,c)$
that maps
$f_1:W^{\hat {\delta }}_{\hat {\lambda }}(\hat {a},\hat {b},\hat {c})\to W^\delta _\lambda (a,b,c)$
that maps
 $\hat {w}_{0,j-k}$
to
$\hat {w}_{0,j-k}$
to
 $w_{ij}$
.
$w_{ij}$
.
By (ii) and (iii), applying
![]() $f_1^{-1}$
to equation (10.1) yields
$f_1^{-1}$
to equation (10.1) yields
Due to (i) and the above equation, it follows from Lemma 10.7 that there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $f_2:W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W^{\hat {\delta }}_{\hat {\lambda }}(\hat {a},\hat {b},\hat {c})$
that maps
$f_2:W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})\to W^{\hat {\delta }}_{\hat {\lambda }}(\hat {a},\hat {b},\hat {c})$
that maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $\hat {w}_{0,j-k}$
.
$\hat {w}_{0,j-k}$
.
Since ![]() and by Lemma 10.3, the quintuple
and by Lemma 10.3, the quintuple ![]() . By Lemma 9.5, the vector
. By Lemma 9.5, the vector
![]() $\hat {w}_{0,j-k}$
is nonzero. Since the
$\hat {w}_{0,j-k}$
is nonzero. Since the
![]() $\triangle _q$
-module
$\triangle _q$
-module
![]() $W^{\hat {\delta }}_{\hat {\lambda }}(\hat {a},\hat {b},\hat {c})$
is irreducible by Theorem 1.11, it follows that
$W^{\hat {\delta }}_{\hat {\lambda }}(\hat {a},\hat {b},\hat {c})$
is irreducible by Theorem 1.11, it follows that
![]() $f_2$
is a
$f_2$
is a
![]() $\triangle _q$
-module isomorphism. The composition
$\triangle _q$
-module isomorphism. The composition
![]() $f_1\circ f_2$
maps
$f_1\circ f_2$
maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $w_{ij}$
. The proposition follows.
$w_{ij}$
. The proposition follows.
Proposition 10.9. Suppose that there exist two integers
![]() $i,j$
with
$i,j$
with ![]() such that
such that
![]() $\varphi _{i+1}=0$
and
$\varphi _{i+1}=0$
and
![]() $\theta _i^*=\theta _j^*$
. Then there exists a quintuple
$\theta _i^*=\theta _j^*$
. Then there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
-
(i)
 $\bar {\theta }_h^*=\theta _{j+h}^*$
for all
$\bar {\theta }_h^*=\theta _{j+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(ii) If
 $j=i+1$
, then the following equation holds:
$j=i+1$
, then the following equation holds:  $$ \begin{align*}\frac{\varphi_i+\theta_i(\theta_i^*-\theta_{i+2}^*)}{q-q^{-1}}=(\bar{c}+\bar{c}^{-1})(\bar{\lambda}-\bar{\lambda}^{-1})-(\bar{a}+\bar{a}^{-1})(\bar{b}q-\bar{b}^{-1}q^{-1}). \end{align*} $$
$$ \begin{align*}\frac{\varphi_i+\theta_i(\theta_i^*-\theta_{i+2}^*)}{q-q^{-1}}=(\bar{c}+\bar{c}^{-1})(\bar{\lambda}-\bar{\lambda}^{-1})-(\bar{a}+\bar{a}^{-1})(\bar{b}q-\bar{b}^{-1}q^{-1}). \end{align*} $$
Proof. By Lemma 10.2, we may assume that
instead of
![]() $\varphi _{i+1}=0$
. Since
$\varphi _{i+1}=0$
. Since
![]() $\theta _i^*=\theta _j^*$
, it follows that
$\theta _i^*=\theta _j^*$
, it follows that
![]() $\lambda ^2=b^2q^{2(i+j)}$
. Substituting (10.2) into the above equation yields
$\lambda ^2=b^2q^{2(i+j)}$
. Substituting (10.2) into the above equation yields
Set
![]() $ (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) = (a,b^{-1},c,\lambda ,\delta ). $
Then
$ (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta }) = (a,b^{-1},c,\lambda ,\delta ). $
Then
![]() $\bar {b}\bar {\lambda }^{-1}=b\lambda ^{-1}q^{2j}$
by (10.3). Condition (i) holds. Using (10.2) and (10.3), it is straightforward to verify condition (ii). It remains to show that
$\bar {b}\bar {\lambda }^{-1}=b\lambda ^{-1}q^{2j}$
by (10.3). Condition (i) holds. Using (10.2) and (10.3), it is straightforward to verify condition (ii). It remains to show that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
. Let
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
. Let
By the
![]() $23$
rd row of Table A1 and Definition 1.10(ii),
$23$
rd row of Table A1 and Definition 1.10(ii),
Since (10.3) holds, it follows from Definition 1.12(ii) that
By the
![]() $18$
th row of Table A1 and Definition 1.10(ii),
$18$
th row of Table A1 and Definition 1.10(ii),
By the transitivity of
![]() $\simeq $
, the relation
$\simeq $
, the relation
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
holds.
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
holds.
Recall the statement of Theorem 1.14.
Proof of Theorem 1.14
By Lemma 10.3, the function from ![]() into
into ![]() exists. By Theorem 1.9, this function is onto. To see the injectivity, we assume that
exists. By Theorem 1.9, this function is onto. To see the injectivity, we assume that
![]() $(a,b,c,\lambda ,\delta )$
and
$(a,b,c,\lambda ,\delta )$
and
![]() $(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
are in
$(\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
are in ![]() and there exists a
and there exists a
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
![]() $ f:W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})\to W_\lambda ^\delta (a,b,c). $
We need to show that
$ f:W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})\to W_\lambda ^\delta (a,b,c). $
We need to show that
We claim that there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and there exists a
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
that maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $f(\hat {w}_0)$
. Suppose that the claim is true. Then the
$f(\hat {w}_0)$
. Suppose that the claim is true. Then the
![]() $\triangle _q$
-module homomorphism
$\triangle _q$
-module homomorphism
![]() $ f^{-1}\circ g: W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) \to W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c}) $
maps
$ f^{-1}\circ g: W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c}) \to W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c}) $
maps
![]() $\bar {w}_0$
to
$\bar {w}_0$
to
![]() $\hat {w}_0$
. Applying Theorem 7.4 yields
$\hat {w}_0$
. Applying Theorem 7.4 yields ![]() . In particular,
. In particular,
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\sim (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
by Definition 1.12(i). Together with the relation
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\sim (\hat {a},\hat {b},\hat {c},\hat {\lambda },\hat {\delta })$
by Definition 1.12(i). Together with the relation
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
, the relation (10.4) follows from the transitivity of
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
, the relation (10.4) follows from the transitivity of
![]() $\simeq $
. Thus, it suffices to prove the claim.
$\simeq $
. Thus, it suffices to prove the claim.
By Lemma 3.5(i), the vector
![]() $\hat {w}_0$
is a marginal weight vector of
$\hat {w}_0$
is a marginal weight vector of
![]() $W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})$
with weight
$W_{\hat {\lambda }}^{\hat {\delta }}(\hat {a},\hat {b},\hat {c})$
with weight
Hence
![]() $f(\hat {w}_0)$
is a marginal weight vector of
$f(\hat {w}_0)$
is a marginal weight vector of
![]() $W_\lambda ^\delta (a,b,c)$
with weight
$W_\lambda ^\delta (a,b,c)$
with weight
![]() $\mu $
. Since any scalar appears in
$\mu $
. Since any scalar appears in ![]() at most twice, it follows that
at most twice, it follows that
![]() $\dim W_\lambda ^\delta (a,b,c)(\mu )\leq 2$
. Let
$\dim W_\lambda ^\delta (a,b,c)(\mu )\leq 2$
. Let
Since
![]() $f(\hat {w}_0)\in K$
, it follows that
$f(\hat {w}_0)\in K$
, it follows that
![]() $\dim K\geq 1$
. By Lemma 9.1, there is an integer j with
$\dim K\geq 1$
. By Lemma 9.1, there is an integer j with ![]() such that
such that
![]() $\theta _j^*=\mu +\mu ^{-1}$
. Hence
$\theta _j^*=\mu +\mu ^{-1}$
. Hence
![]() $\mu \in \{b\lambda ^{-1}q^{2j},b^{-1}\lambda q^{-2j}\}$
and
$\mu \in \{b\lambda ^{-1}q^{2j},b^{-1}\lambda q^{-2j}\}$
and

To prove the claim, we divide the argument into four cases: (a)
![]() $\dim W_\lambda ^\delta (a,b,c)(\mu )=\dim K=1$
and
$\dim W_\lambda ^\delta (a,b,c)(\mu )=\dim K=1$
and
![]() $\mu =b\lambda ^{-1} q^{2j}$
; (b)
$\mu =b\lambda ^{-1} q^{2j}$
; (b)
![]() $\dim W_\lambda ^\delta (a,b,c)(\mu )=\dim K=1$
and
$\dim W_\lambda ^\delta (a,b,c)(\mu )=\dim K=1$
and
![]() $\mu =b^{-1}\lambda q^{-2j}$
; (c)
$\mu =b^{-1}\lambda q^{-2j}$
; (c)
![]() $\dim W_\lambda ^\delta (a,b,c)(\mu )=2$
and
$\dim W_\lambda ^\delta (a,b,c)(\mu )=2$
and
![]() $\dim K=1$
; and (d)
$\dim K=1$
; and (d)
![]() $\dim W_\lambda ^\delta (a,b,c)(\mu )=\dim K=2$
.
$\dim W_\lambda ^\delta (a,b,c)(\mu )=\dim K=2$
.
(a): Since
![]() $\varphi _0=0$
, there exists an integer i with
$\varphi _0=0$
, there exists an integer i with
![]() $0\leq i\leq j$
such that
$0\leq i\leq j$
such that
![]() $\varphi _i=0$
and
$\varphi _i=0$
and
![]() $\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. Since
$\varphi _{i+1}\varphi _{i+2}\dots \varphi _j\not =0$
. Since
![]() $\dim W_\lambda ^\delta (a,b,c)(\mu )=1$
and by Lemma 9.5, the vector
$\dim W_\lambda ^\delta (a,b,c)(\mu )=1$
and by Lemma 9.5, the vector
![]() $w_{ij}$
is a basis for
$w_{ij}$
is a basis for
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
as well as for K. Hence
$W_\lambda ^\delta (a,b,c)(\mu )$
as well as for K. Hence
![]() $f(\hat {w}_0)$
is a nonzero scalar multiple of
$f(\hat {w}_0)$
is a nonzero scalar multiple of
![]() $w_{ij}$
. The claim now follows from Proposition 10.8.
$w_{ij}$
. The claim now follows from Proposition 10.8.
(b): Since the former case has been done, we may assume that ![]() . In other words,
. In other words,
Then
![]() $\theta _j^*\not =\theta _h^*$
for all
$\theta _j^*\not =\theta _h^*$
for all
![]() $h=0,1,\ldots ,j-1$
. By Lemma 9.5 the vector
$h=0,1,\ldots ,j-1$
. By Lemma 9.5 the vector
![]() $w_{0j}$
is a basis for
$w_{0j}$
is a basis for
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
as well as for K.
$W_\lambda ^\delta (a,b,c)(\mu )$
as well as for K.
Suppose that ![]() . Then
. Then
![]() $\theta _{j+1}^*\not =\theta _h^*$
for all
$\theta _{j+1}^*\not =\theta _h^*$
for all
![]() $h=0,1,\ldots ,j$
by (10.5). By Lemma 9.5, the vector
$h=0,1,\ldots ,j$
by (10.5). By Lemma 9.5, the vector
![]() $w_{0,j+1}$
is nonzero. Since
$w_{0,j+1}$
is nonzero. Since
![]() $w_{0j}\in K$
, it follows from Lemma 9.4(i), (ii) that
$w_{0j}\in K$
, it follows from Lemma 9.4(i), (ii) that

which contradicts (10.5). Therefore, ![]() . It follows that condition (a) of Definition 1.12(iii) is satisfied by (10.5). Since
. It follows that condition (a) of Definition 1.12(iii) is satisfied by (10.5). Since ![]() and
and ![]() , condition (b) of Definition 1.12(iii) follows from Lemma 9.4(iii). Since
, condition (b) of Definition 1.12(iii) follows from Lemma 9.4(iii). Since
![]() $f(\hat {w}_0)$
is a nonzero scalar multiple of
$f(\hat {w}_0)$
is a nonzero scalar multiple of ![]() , the claim now follows from Lemma 9.7.
, the claim now follows from Lemma 9.7.
Before proceeding to cases (c) and (d), we provide some comments on
In this case, there exist two integers i and j with ![]() such that
such that
![]() $\theta _i^*=\theta _j^*=\mu +\mu ^{-1}$
. Then
$\theta _i^*=\theta _j^*=\mu +\mu ^{-1}$
. Then
![]() $\theta _h^*=\theta _{\ell }^*$
if and only if
$\theta _h^*=\theta _{\ell }^*$
if and only if
![]() $q^{2(h+\ell )}=q^{2(i+j)}$
for all distinct
$q^{2(h+\ell )}=q^{2(i+j)}$
for all distinct ![]() . It follows that:
. It follows that:
-
(1)
 $\theta _i^*\not =\theta _h^*$
for all
$\theta _i^*\not =\theta _h^*$
for all  ;
; -
(2)
 $\theta _{i+1}^*\not =\theta _h^*$
for all
$\theta _{i+1}^*\not =\theta _h^*$
for all
 $h=0,1,\ldots ,i-1$
;
$h=0,1,\ldots ,i-1$
; -
(3)
 provided that
provided that
 $i=0$
.
$i=0$
.
By the rank-nullity theorem, there exists an integer k with
![]() $i<k\leq j$
such that
$i<k\leq j$
such that
![]() $\varphi _k=0$
. Moreover, we may assume that
$\varphi _k=0$
. Moreover, we may assume that
![]() $\varphi _{k+1}\varphi _{k+2}\dots \varphi _j\not =0$
. In view of (1) and the condition
$\varphi _{k+1}\varphi _{k+2}\dots \varphi _j\not =0$
. In view of (1) and the condition
![]() $\varphi _{k+1}\varphi _{k+2}\dots \varphi _j\not = 0$
, Lemma 9.5 implies that the vectors
$\varphi _{k+1}\varphi _{k+2}\dots \varphi _j\not = 0$
, Lemma 9.5 implies that the vectors
![]() $w_{0i}$
and
$w_{0i}$
and
![]() $w_{kj}$
are nonzero. Since
$w_{kj}$
are nonzero. Since
![]() $i<k$
, these vectors are linearly independent and thus form a basis for
$i<k$
, these vectors are linearly independent and thus form a basis for
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
.
$W_\lambda ^\delta (a,b,c)(\mu )$
.
Observe that
![]() $ \mu =b\lambda ^{-1}q^{2i}=b^{-1}\lambda q^{-2j}$
or
$ \mu =b\lambda ^{-1}q^{2i}=b^{-1}\lambda q^{-2j}$
or
![]() $ \mu =b^{-1}\lambda q^{-2i}=b\lambda ^{-1}q^{2j}$
. We may assume the latter case by applying Lemma 10.4 to
$ \mu =b^{-1}\lambda q^{-2i}=b\lambda ^{-1}q^{2j}$
. We may assume the latter case by applying Lemma 10.4 to
![]() $\varphi _k=0$
if necessary. Then
$\varphi _k=0$
if necessary. Then

Furthermore, the following conditions are equivalent:

The proof for the equivalence of (i)–(v) is as follows: The implication (i)
![]() $\Rightarrow $
(ii) is obvious. In view of (1) and (3), Lemma 9.4(i) and (ii) imply the equivalence of (ii) and (iii). By (2) and (9.1), the equivalence of (iii)–(v) follows. Suppose that (ii)–(v) hold. Then
$\Rightarrow $
(ii) is obvious. In view of (1) and (3), Lemma 9.4(i) and (ii) imply the equivalence of (ii) and (iii). By (2) and (9.1), the equivalence of (iii)–(v) follows. Suppose that (ii)–(v) hold. Then
![]() $\varphi _{i+1}=0$
and
$\varphi _{i+1}=0$
and
![]() $w_{kj}=w_{i+1}$
, which implies that
$w_{kj}=w_{i+1}$
, which implies that
![]() $w_{i+1}\in K$
. The implication (ii)–(v)
$w_{i+1}\in K$
. The implication (ii)–(v)
![]() $\Rightarrow $
(i) then follows.
$\Rightarrow $
(i) then follows.
(c): Since (ii) fails, there exists a scalar
![]() $\varepsilon \in \mathbb F$
such that
$\varepsilon \in \mathbb F$
such that
![]() $\varepsilon w_{0i}+w_{kj}$
is a basis for K. Then
$\varepsilon w_{0i}+w_{kj}$
is a basis for K. Then
![]() $f(\hat {w}_0)$
is a nonzero scalar multiple of
$f(\hat {w}_0)$
is a nonzero scalar multiple of
![]() $\varepsilon w_{0i}+w_{kj}$
. If
$\varepsilon w_{0i}+w_{kj}$
. If
![]() $\varepsilon =0$
, the claim is immediate from Proposition 10.8.
$\varepsilon =0$
, the claim is immediate from Proposition 10.8.
Suppose that
![]() $\varepsilon \not =0$
. Since (ii) fails, it follows from Lemma 9.4(i) and (ii) that
$\varepsilon \not =0$
. Since (ii) fails, it follows from Lemma 9.4(i) and (ii) that
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})(B-\mu -\mu ^{-1})A w_{0i}$
is a nonzero scalar multiple of
$(B-\mu q^2-\mu ^{-1}q^{-2})(B-\mu -\mu ^{-1})A w_{0i}$
is a nonzero scalar multiple of
![]() $w_{0,i+1}$
. Since (iv) fails and by (2) and (9.1), the coefficient of
$w_{0,i+1}$
. Since (iv) fails and by (2) and (9.1), the coefficient of
![]() $w_{i+1}$
in
$w_{i+1}$
in
![]() $w_{0,i+1}$
is nonzero. Since
$w_{0,i+1}$
is nonzero. Since
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})(B-\mu -\mu ^{-1})A w_{kj}$
is a linear combination of
$(B-\mu q^2-\mu ^{-1}q^{-2})(B-\mu -\mu ^{-1})A w_{kj}$
is a linear combination of
![]() $\{w_h\}_{h=k}^{j-1}$
, this forces
$\{w_h\}_{h=k}^{j-1}$
, this forces
![]() $k=i+1$
. By Proposition 10.9, there exists a quintuple
$k=i+1$
. By Proposition 10.9, there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
with
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
with
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
satisfying
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
satisfying
![]() $\bar {\theta }_h^*=\theta _{j+h}^*$
for all
$\bar {\theta }_h^*=\theta _{j+h}^*$
for all
![]() $h\in \mathbb N$
. By Lemma 10.3, there exists a
$h\in \mathbb N$
. By Lemma 10.3, there exists a
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
Since
![]() $(\bar {\theta }_0^*,\bar {\theta }_1^*)=(\theta _j^*,\theta _{j+1}^*)$
, the vector
$(\bar {\theta }_0^*,\bar {\theta }_1^*)=(\theta _j^*,\theta _{j+1}^*)$
, the vector
![]() $\bar {w}_0$
is a marginal weight vector of
$\bar {w}_0$
is a marginal weight vector of
![]() $W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
with weight
$W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})$
with weight
![]() $\mu $
. Since
$\mu $
. Since
![]() $\dim K=1$
, the vector
$\dim K=1$
, the vector
![]() $g(\bar {w}_0)$
must be a nonzero scalar multiple of
$g(\bar {w}_0)$
must be a nonzero scalar multiple of
![]() $f(\hat {w}_0)$
. The claim follows.
$f(\hat {w}_0)$
. The claim follows.
(d): By (v), the scalar
![]() $\varphi _{i+1}=0$
and
$\varphi _{i+1}=0$
and
![]() $w_{kj}=w_{i+1}$
. Since
$w_{kj}=w_{i+1}$
. Since
![]() $K=W_\lambda ^\delta (a,b,c)(\mu )$
, the space
$K=W_\lambda ^\delta (a,b,c)(\mu )$
, the space
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
is
$W_\lambda ^\delta (a,b,c)(\mu )$
is
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})A$
-invariant. Using Lemma 6.1(i), a direct calculation shows that the matrix representing
$(B-\mu q^2-\mu ^{-1}q^{-2})A$
-invariant. Using Lemma 6.1(i), a direct calculation shows that the matrix representing
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})A$
with respect to the ordered basis
$(B-\mu q^2-\mu ^{-1}q^{-2})A$
with respect to the ordered basis
![]() $w_{i+1}, w_{0i}$
for
$w_{i+1}, w_{0i}$
for
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
is
$W_\lambda ^\delta (a,b,c)(\mu )$
is
 $$ \begin{align*}\begin{pmatrix} \varphi_{i+2}+\theta_{i+1}(\theta_i^*-\theta_{i+2}^*) &(\theta_i^*-\theta_{i+2}^*)\prod\limits_{h=0}^{i-1}(\theta_i^*-\theta_h^*) \\ 0 &\varphi_i+\theta_i(\theta_i^*-\theta_{i+2}^*) \end{pmatrix}. \end{align*} $$
$$ \begin{align*}\begin{pmatrix} \varphi_{i+2}+\theta_{i+1}(\theta_i^*-\theta_{i+2}^*) &(\theta_i^*-\theta_{i+2}^*)\prod\limits_{h=0}^{i-1}(\theta_i^*-\theta_h^*) \\ 0 &\varphi_i+\theta_i(\theta_i^*-\theta_{i+2}^*) \end{pmatrix}. \end{align*} $$
The eigenvalues of
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})A$
on
$(B-\mu q^2-\mu ^{-1}q^{-2})A$
on
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
are
$W_\lambda ^\delta (a,b,c)(\mu )$
are
Since the upper-right entry of the
![]() $2\times 2$
matrix is nonzero by (1), the geometric multiplicities of (10.6) and (10.7) are equal to one, even if (10.6) and (10.7) coincide. By Definition 2.4, the vector
$2\times 2$
matrix is nonzero by (1), the geometric multiplicities of (10.6) and (10.7) are equal to one, even if (10.6) and (10.7) coincide. By Definition 2.4, the vector
![]() $f(\hat {w}_0)$
is an eigenvector of
$f(\hat {w}_0)$
is an eigenvector of
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})A$
in
$(B-\mu q^2-\mu ^{-1}q^{-2})A$
in
![]() $W_\lambda ^\delta (a,b,c)(\mu )$
. If the eigenvalue corresponding to
$W_\lambda ^\delta (a,b,c)(\mu )$
. If the eigenvalue corresponding to
![]() $f(\hat {w}_0)$
is (10.6), then
$f(\hat {w}_0)$
is (10.6), then
![]() $f(\hat {w}_0)$
is a nonzero scalar multiple of
$f(\hat {w}_0)$
is a nonzero scalar multiple of
![]() $w_{i+1}$
and the claim follows from Lemma 10.4. Suppose that the eigenvalue corresponding to
$w_{i+1}$
and the claim follows from Lemma 10.4. Suppose that the eigenvalue corresponding to
![]() $f(\hat {w}_0)$
is (10.7). By Proposition 10.9, there exists a quintuple
$f(\hat {w}_0)$
is (10.7). By Proposition 10.9, there exists a quintuple
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
$(\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })\in {\mathbb F^\times }^4\times \mathbb F$
such that
![]() $(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
$(a,b,c,\lambda ,\delta )\simeq (\bar {a},\bar {b},\bar {c},\bar {\lambda },\bar {\delta })$
and the following conditions hold:
-
(1’)
 $\bar {\theta }_h^*=\theta _{j+h}^*$
for all
$\bar {\theta }_h^*=\theta _{j+h}^*$
for all
 $h\in \mathbb N$
.
$h\in \mathbb N$
. -
(2’) (10.7) is equal to
 $(q-q^{-1})$
times
$(q-q^{-1})$
times
 $ (\bar {c}+\bar {c}^{-1})(\bar {\lambda }-\bar {\lambda }^{-1}) - (\bar {a}+\bar {a}^{-1})(\bar {b}q-\bar {b}^{-1}q^{-1})$
.
$ (\bar {c}+\bar {c}^{-1})(\bar {\lambda }-\bar {\lambda }^{-1}) - (\bar {a}+\bar {a}^{-1})(\bar {b}q-\bar {b}^{-1}q^{-1})$
.
By condition (1’), the vector
![]() $\bar {w}_0\in W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})(\mu )$
. By condition (2’) and the remark following Proposition 3.1, the vector
$\bar {w}_0\in W_{\bar {\lambda }}^{\bar {\delta }}(\bar {a},\bar {b},\bar {c})(\mu )$
. By condition (2’) and the remark following Proposition 3.1, the vector
![]() $\bar {w}_0$
is an eigenvector of
$\bar {w}_0$
is an eigenvector of
![]() $(B-\mu q^2-\mu ^{-1}q^{-2})A$
corresponding to the eigenvalue (10.7). By Lemma 10.3, there exists a
$(B-\mu q^2-\mu ^{-1}q^{-2})A$
corresponding to the eigenvalue (10.7). By Lemma 10.3, there exists a
![]() $\triangle _q$
-module isomorphism
$\triangle _q$
-module isomorphism
According to the above arguments, the vector
![]() $g(\bar {w}_0)$
must be a nonzero scalar multiple of
$g(\bar {w}_0)$
must be a nonzero scalar multiple of
![]() $f(\hat {w}_0)$
. The claim follows.
$f(\hat {w}_0)$
. The claim follows.
We have shown that the claim holds in all cases. Thus, Theorem 1.14 is established.
The article ends with a question.
Question 10.10. Consider the Askey–Wilson algebras or their central extensions associated with hypergeometric orthogonal polynomials, such as the Krawtchouk algebras, the universal Hahn algebra, and the universal Racah algebra. Suppose that the underlying field is algebraically closed and of positive characteristic. Under this assumption, define the marginal weights of their modules and classify their finite-dimensional irreducible modules with marginal weights up to isomorphism.
Funding statement
This research was supported by the National Science and Technology Council of Taiwan under grant NSTC 114-2115-M-008-011.
Competing interests
The author has no relevant financial or non-financial interests to disclose.
A. The right
 $\mathfrak S_4$
-action on
$\mathfrak S_4$
-action on
 $\{\pm 1\}\backslash {\mathbb F^\times }^4$
$\{\pm 1\}\backslash {\mathbb F^\times }^4$
Recall the left
![]() $\{\pm 1\}$
-action on
$\{\pm 1\}$
-action on
![]() ${\mathbb F^\times }^4$
and the right
${\mathbb F^\times }^4$
and the right
![]() $\mathfrak S_4$
-action on
$\mathfrak S_4$
-action on
![]() $\{\pm 1\}\backslash {\mathbb F^\times }^4$
given immediately preceding Definition 1.10. Let
$\{\pm 1\}\backslash {\mathbb F^\times }^4$
given immediately preceding Definition 1.10. Let
![]() $(a,b,c,\lambda )\in {\mathbb F^\times }^4$
be given. In the table below, we list each element
$(a,b,c,\lambda )\in {\mathbb F^\times }^4$
be given. In the table below, we list each element
![]() $\sigma \in \mathfrak S_4$
along with a corresponding element
$\sigma \in \mathfrak S_4$
along with a corresponding element
![]() $(\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^\times }^4$
satisfying
$(\bar {a},\bar {b},\bar {c},\bar {\lambda })\in {\mathbb F^\times }^4$
satisfying
Table A1 The
![]() $\mathfrak S_4$
-orbit of
$\mathfrak S_4$
-orbit of
![]() $\{\pm 1\}\cdot (a,b,c,\lambda )$
$\{\pm 1\}\cdot (a,b,c,\lambda )$