2.1 Notation

Random variables are denoted by uppercase letters, X, and their realizations by the corresponding lowercase letters, x. Analogously, uppercase letters, P, denote probability distributions and the corresponding lowercase letters, p, denote probability density functions (PDFs). Occasionally, subscripts are used to indicate a distribution or density of a certain random variable, say, $P_X$ and $p_X$ . We use $Q_X$ and $q_X$ to indicate that the corresponding distribution or density is closely related but not identical to $P_X$ or $p_X$ , respectively. For example, $q_X$ might be an approximation or unnormalized version of $p_X$ . The expected value of a random variable is written as $E[X]$ . Again, a subscript is used to explicitly indicate the random variable, say, $E_X[c + X]$ . Equality in distribution is denoted by $\stackrel {d}{=}$ . Unless stated otherwise, collections of variables, such as vectors and matrices, are indicated by bold font. We write $\mathcal {A}^n$ to denote the n-fold Cartesian product of a set $\mathcal {A}$ with itself. The n-dimensional probability simplex is denoted by $\Delta ^n$ . The set of Boolean vectors of length N whose elements sum to K is denoted by $\mathcal {S}_K^N$ . The set of all positive semi-definite matrices of size M is denoted by $\mathbb {S}_+^M$ . We further define the elliptope of correlation matrices as , and the projection of a matrix $\boldsymbol {\Sigma } \in \mathbb {S}_+^M$ on $\mathcal {E}_M$ as . Here, $\boldsymbol {I}_M$ denotes the identity matrix of size M and $\operatorname {\mathrm {diag}}(\boldsymbol {X})$ denotes the diagonal matrix with the same main diagonal elements as $\boldsymbol {X}$ . Additional symbols and notations will be defined when they occur in the text.

We assume that a test is administered periodically at time instances $t = 1, 2,\ldots , T$ . Each administration is assumed to have $N \geq 1$ test takers.Footnote ¹ An unknown share of test takers is assumed to belong to the critical group whose members we seek to flag. In order to formalize the flagging problem, we introduce the following random variables:

• • $R \in [0, 1]$ denotes the rate of critical group members, that is, the probability that a randomly selected test taker is a member of the critical group. R is assumed to be a latent variable.

• • $C_{t,n} \in \{0, 1\}$ indicates whether the nth test taker in the tth administration is a member of the critical group ( $C_{t,n} = 1$ ) or not ( $C_{t,n} = 0$ ). $C_{t,n}$ is assumed to be a latent variable.

• • $\boldsymbol {X}_{t,n} \in \mathbb {R}^M$ , $M \geq 1$ , denotes the vector of features associated with the nth test taker in the tth administration. $X_{t,n}$ is assumed to be observable and provided by a given mechanism.

• • $S_{t,n} \in \{0, 1\}$ indicates whether the nth test taker in the tth administration was selected for review ( $S_{t,n} = 1$ ) or not ( $S_{t,n} = 0$ ). $S_{t,n}$ is set according to the chosen selection policy.

• • $D_{t,n} \in \{0, 1\}$ denotes whether the nth test taker of the tth administration was detected as being a member of the critical group ( $D_{t,n} = 1$ ) or not ( $D_{t,n} = 0$ ). $D_{t,n}$ is the outcome of an expert review and can be observed.

For the sake of a more compact notation, variables corresponding to the same administration are also written as column vectors:

Analogously, horizontal stacks of vectors of the first t administrations are written as

2.2 Information flow

Before going into more details of the model underlying the random variables defined in the previous section, it is useful to highlight how the available information evolves over time. Before the administration at time instant $t+1$ , the available data consist of the features of all previous test takers, $\boldsymbol {X}_{1:t}$ , the subset of test takers selected for review, $\boldsymbol {S}_{1:t}$ , and the outcomes of these reviews, $\boldsymbol {D}_{1:t}$ . We denote the $\sigma $ -algebra of events generated by these random variables by

(1)

After the administration at time instant $t+1$ is completed and all responses are processed, the extracted features, $\boldsymbol {X}_{t+1}$ , become available. We denote this refined $\sigma $ -algebra by

(2)

Note that the decision about which test takers to select for review should take $\boldsymbol {X}_{t+1}$ into account, hence, it can use all information available in $\mathcal {F}^{\prime }_t$ , not just $\mathcal {F}_t$ . Finally, the selected responses, $\boldsymbol {S}_{t+1}$ , and the outcomes of the corresponding reviews, $\boldsymbol {D}_{t+1}$ , are observed. This refines the $\sigma $ -algebra to $\mathcal {F}_{t+1}$ and completes the cycle. Note that $\mathcal {F}_t \subset \mathcal {F}^{\prime }_t \subset \mathcal {F}_{t+1}$ for all $t = 1, \ldots , T-1$ .

2.3 Assumptions

Throughout the article, we make the following assumptions:

1. 1. All group membership indicators, $C_{t,n}$ , are independent and identically distributed Bernoulli random variables with success probability R so that $P(C_{t,n} = 1 \,|\, R = r) = r$ .

2. 2. All feature vectors, $\boldsymbol {X}_{t,n}$ , are independent and identically distributed conditioned on the group membership indicator $C_{t,n}$ . That is, there exist two random vectors, $\boldsymbol {X}_0$ and $\boldsymbol {X}_1$ , such that $\boldsymbol {X}_{t,n} | (C_{t,n} = 0) \stackrel {d}{=} \boldsymbol {X}_0$ and $\boldsymbol {X}_{t,n} | (C_{t,n} = 1) \stackrel {d}{=} \boldsymbol {X}_1$ for all t and n. The distributions of $\boldsymbol {X}_0$ and $\boldsymbol {X}_1$ are denoted by $P_0$ and $P_1$ , respectively.

3. 3. $P_0$ and $P_1$ are assumed to be members of two, not necessarily identical, parametric families of distributions. That is, there exist two (vector) parameters in suitably defined spaces, $\theta _0 \in \mathcal {T}_0$ and $\theta _1 \in \mathcal {T}_1$ , such that

   (3) $$ \begin{align} \begin{aligned} P_0 = P( \bullet \,|\, \theta_0),\\ P_1 = P( \bullet \,|\, \theta_1). \end{aligned} \end{align} $$

4. 4. The selection process is modeled as follows: After each administration, $K \leq N$ test takers are selected for review. The corresponding selection policy is a function $\xi _t \colon \mathcal {S}^N \to \Delta ^N$ that assigns a probability to every possible selection vector. Each $\xi _t$ is assumed to be $\mathcal {F}^{\prime }_{t-1}$ -measurable, that is, the selection policy can depend only on events whose occurrence can be established based on knowledge of $\boldsymbol {X}_{1:t}$ , $\boldsymbol {S}_{1:t-1}$ , and $\boldsymbol {D}_{1:t-1}$ . Note that this implies that $\boldsymbol {S}_t$ and $\boldsymbol {C}_t$ are conditionally independent since

   (4) $$ \begin{align} P(\boldsymbol{S}_t = \boldsymbol{s}, \boldsymbol{C}_t = \boldsymbol{c} \,|\, \mathcal{F}^{\prime}_{t-1}) &= P(\boldsymbol{S}_t = \boldsymbol{s} \,|\, \mathcal{F}^{\prime}_{t-1}) \, P(\boldsymbol{C}_t = \boldsymbol{c} \,|\, \boldsymbol{S}_t = \boldsymbol{s}, \mathcal{F}^{\prime}_{t-1}) \notag \\ &= \xi_t(\boldsymbol{s}) \, P(\boldsymbol{C}_t = \boldsymbol{c} \,|\, \mathcal{F}^{\prime}_{t-1}), \end{align} $$
   where the second equality holds since $\boldsymbol {S}_t$ can only provide information that is already contained in $\mathcal {F}^{\prime }_{t-1}$ .

5. 5. The review process is modeled as follows: All flagged test takers are reviewed and the review resolves any ambiguity about the test taker’s group membership. Test takers that did not get flagged are automatically assumed to be members of the reference group. Unflagged members of the critical group remain undetected. This means

   (5) $$ \begin{align} D_{t,n} = \begin{cases} 1, & S_{t,n} = 1, C_{t,n} = 1\\ 0, & \text{otherwise} \end{cases} \end{align} $$
   or, using Hadamard’s element-wise vector product notation,
   (6) $$ \begin{align} \boldsymbol{D}_t = \boldsymbol{S}_t \odot \boldsymbol{C}_t. \end{align} $$

Assumptions 1 and 2 are made to simplify the mathematical analysis and to keep the model general. Possible relaxations, such as allowing dependencies between test takers (and possibly re-takers), or considering sub-populations with different feature distributions or rates of critical group members, will significantly complicate the analysis and likely depend on what behavior or phenomenon underpins the definition of the critical group. A brief outlook on possible research avenues in this direction will be given in Section 7.

Assumption 3 enables us to formulate the flagging problem in a standard Bayesian setting. An extension to a non-parametric formulation is beyond the scope of the article.

Assumption 4 is common in sequential decision making and ensures that the policy does not use information that is not available at the time the selection decision needs to be made.

Assumption 5 is likely the most controversial, and it will not always hold in practice. However, at least in the context of test security, various standards and criteria have been established according to which an expert or a panel of experts can evaluate the evidence and arrive at a well-justified decision whether or not a certain response or behavior constitutes cheating. Alternatively, one can define the critical group as those test takers who an expert considers “sufficiently curious” to be reviewed in detail, irrespective of the outcome of the review. This criterion is less sharp, but can be more applicable in practice. In general, we assume that some, potentially expensive and time-consuming, process exists that assigns “true positive” and “false positive” labels to the selected cases. The proposed procedure is agnostic to the exact meaning of these labels and the process used to assign them.

2.4 Problem formulation

As mentioned before, we adopt a Bayesian perspective in this article. That is, we assume that unknown quantities are themselves random variables, and that the joint distribution of all random variables, latent and observable, is known. We denote this joint distribution by P, so that

(7) $$ \begin{align} \big( \boldsymbol{X}_{1:T}, \boldsymbol{S}_{1:T}, \boldsymbol{D}_{1:T}, \boldsymbol{C}_{1:T}, R, \Theta_0, \Theta_1, \big) \sim P, \end{align} $$

where $\boldsymbol {X}_{1:T}, \boldsymbol {C}_{1:T}, \boldsymbol {S}_{1:T}, \boldsymbol {D}_{1:T}$ , and R are defined in Section 2.1, and $\Theta _0$ and $\Theta _1$ denote the parameters of the conditional feature distributions in (3).

Our aim is to design a selection policy, $\boldsymbol {\xi }_{1:T}$ , that maximizes the expected number of detected members of the critical group, while limiting the number of expert reviews per test administration to at most $K \leq N$ . This leads to the following optimization problem:

(8) $$ \begin{align} \max_{\boldsymbol{\xi}_{1:T}} \; E\left[ \sum_{t=1}^T \sum_{n = 1}^N D_{t,n} \right] \quad \text{s.\ t.} \quad \sum_{n = 1}^N S_{t,n} \leq K, \end{align} $$

where the constraint needs to hold almost surely for all $t = 1, \ldots , T$ .

Clearly, (8) is by no means the only way of formalizing the flagging problem. For example, one could relax the constraint to hold in expectation, constrain the false or true positive rate instead of the absolute number of reviews, or, in a more traditional Bayesian formulation, define costs of reviews, detections, false alarms, and so on. Nevertheless, we believe that the problem formulation in (8) strikes a good balance between transparency, tractability, and applicability. In particular, the question of how to set K, that is, the number of reviews one is willing to afford, is well-defined and can be understood and discussed without deeper technical knowledge. By contrast, choosing Bayesian costs is typically less straightforward and can lead to confusion about what these cost should and should not reflect. Moreover, we believe that the optimal and approximate selection policies presented in this article provide a blueprint that can be adapted to variations of the problem in (8) in a relatively straightforward manner.

3.1 Posterior update

As more tests are administered and more reviews are conducted, more information is gathered that needs to be incorporated into the underlying Bayesian model. In this section, we detail the corresponding updates and provide expressions for the respective distributions. Of particular interest is the joint posterior distribution of $\Theta _0$ , $\Theta _1$ , and R since the latter are assumed to persist between test administrations. That is, $\Theta _0$ , $\Theta _1$ , and R can be learned from the data, while the uncertainty about the group indicators, $\boldsymbol {C}_t$ , will not be resolved completely in general.

Assume that the administration at time instant $t-1$ was completed, and let the corresponding conditional PDF of the persistent random variables be denoted by $p(r, \theta _0, \theta _1 \,|\, \mathcal {F}_{t-1})$ . Now, consider the joint distribution of $\boldsymbol {X}_t$ and $\boldsymbol {C}_t$ conditioned on the model parameters:

(12) $$ \begin{align} p(\boldsymbol{x} , \boldsymbol{c} \,|\, r, \theta_0, \theta_1) &= p(\boldsymbol{c}\,|\, r, \theta_0, \theta_1) \, p(\boldsymbol{x} \,|\, r, \theta_0, \theta_1, \boldsymbol{c}) \end{align} $$

(13) $$ \begin{align} &= p(\boldsymbol{c}\,|\, r) \, p(\boldsymbol{x} \,|\, \theta_0, \theta_1, \boldsymbol{c}) \end{align} $$

(14) $$ \begin{align} &= \prod_{n=1}^N \left[ r \, p(x_n \,|\, \theta_{1}) \right]^{c_n} \left[ (1 - r) \, p(x_n \,|\, \theta_{0}) \right]^{1 - c_n}\end{align} $$

(15) $$ \begin{align} &= r^{\lVert \boldsymbol{c} \rVert_1} (1-r)^{N - \lVert \boldsymbol{c} \rVert_1} \, \prod_{n=1}^N p(x_n \,|\, \theta_{1})^{c_n} p(x_n \,|\, \theta_{0})^{1 - c_n}. \end{align} $$

Since conditioning on the model parameters renders the distribution independent of the specific administration, we dropped the time index in the notation. By marginalizing out the unknown group membership, we obtain the feature distribution for a given set of model parameters:

(16) $$ \begin{align} p(\boldsymbol{x} \,|\, r, \theta_0, \theta_1) &= \sum_{\boldsymbol{c} \in \mathcal{S}^N} p(\boldsymbol{x} , \boldsymbol{c} \,|\, r, \theta_0, \theta_1) \end{align} $$

(17) $$ \begin{align} &= \sum_{\boldsymbol{c} \in \mathcal{S}^N} r^{\lVert \boldsymbol{c} \rVert_1} (1-r)^{N - \lVert \boldsymbol{c} \rVert_1} \, \prod_{n=1}^N p(x_n \,|\, \theta_{1})^{c_n} p(x_n \,|\, \theta_{0})^{1 - c_n}. \end{align} $$

Averaging over the unknown model parameters yields the posterior predictive distribution of the features at time instant t:

(18) $$ \begin{align} p(\boldsymbol{x}_t \,|\, \mathcal{F}_{t-1}) = E\big[ p(\boldsymbol{x}_t \,|\, R, \Theta_0, \Theta_1) \,|\, \mathcal{F}_{t-1}\big], \end{align} $$

where the expected value is taken with respect to the current model posterior, $p(r, \theta _0, \theta _1 \,|\, \mathcal {F}_{t-1})$ . Note that the posterior predictive in (18) is needed for the look-ahead step in (10).

Now, assume that the test administration at time instant t was completed and that $\boldsymbol {X}_t = \boldsymbol {x}_t$ was observed. In order to determine the optimal selection policy in (9), we require the posterior distribution of the group memberships, $\boldsymbol {C}_t$ , conditioned on all previous observations. According to Bayes’ rule, this distribution is given by

(19) $$ \begin{align} p(\boldsymbol{c}_t \,|\, \mathcal{F}_{t-1}') = \frac{p(\boldsymbol{x}_t, \boldsymbol{c}_t \,|\, \mathcal{F}_{t-1})}{p(\boldsymbol{x}_t \,|\, \mathcal{F}_{t-1})} = \frac{E\big[ p(\boldsymbol{c}_t, \boldsymbol{x}_t \,|\, R, \Theta_0, \Theta_1) \,|\, \mathcal{F}_{t-1}\big]}{E\big[ p(\boldsymbol{x}_t \,|\, R, \Theta_0, \Theta_1) \,|\, \mathcal{F}_{t-1}\big]}, \end{align} $$

where, again, all expected values are taken with respect to $p(r, \theta _0, \theta _1 \,|\, \mathcal {F}_{t-1})$ .

Given (19), the optimal selection vector can, in principle, be determined by finding the maximum in (9), and the corresponding test takers can be reviewed. In our model, this corresponds to observing $\boldsymbol {S}_t = \boldsymbol {s}_t$ and $\boldsymbol {D}_t = \boldsymbol {d}_t$ . This new information leads to the model update

(20) $$ \begin{align} p(r, \theta_0, \theta_1 \,|\, \mathcal{F}_t) = \frac{p(\boldsymbol{x}_t, \boldsymbol{s}_t, \boldsymbol{d}_t \,|\, r, \theta_0, \theta_1, \mathcal{F}_{t-1})}{p(\boldsymbol{x}_t, \boldsymbol{s}_t, \boldsymbol{d}_t \,|\, \mathcal{F}_{t-1})} p(r, \theta_0, \theta_1 \,|\, \mathcal{F}_{t-1}). \end{align} $$

The likelihood in the numerator of (20) is given by

(21) $$ \begin{align} p(\boldsymbol{x}_t, \boldsymbol{s}_t, \boldsymbol{d}_t \,|\, r, \theta_0, \theta_1, \mathcal{F}_{t-1}) &= \sum_{\boldsymbol{c}_t \in \mathcal{S}^N} p(\boldsymbol{x}_t, \boldsymbol{c}_t, \boldsymbol{s}_t, \boldsymbol{d}_t \,|\, r, \theta_0, \theta_1, \mathcal{F}_{t-1}) \end{align} $$

(22) $$ \begin{align} &= \sum_{\boldsymbol{c}_t \in \mathcal{S}^N}p(\boldsymbol{d}_t \,|\, \boldsymbol{s}_t, \boldsymbol{c}_t) \, \xi_t(\boldsymbol{s}_t) \, p(\boldsymbol{x}_t, \boldsymbol{c}_t \,|\, r, \theta_0, \theta_1) \end{align} $$

(23) $$ \begin{align} &= \xi_t(\boldsymbol{s}_t) \sum_{\boldsymbol{c}_t \in \mathcal{S}^N} [\boldsymbol{d}_t = \boldsymbol{s}_t \odot \boldsymbol{c}_t] \, p(\boldsymbol{x}_t, \boldsymbol{c}_t \,|\, r, \theta_0, \theta_1), \end{align} $$

where we used Iverson bracket notation as a shorthand for the indicator function, meaning that the summands on the right-hand side of (23) are zero unless $\boldsymbol {d}_t = \boldsymbol {s}_t \odot \boldsymbol {c}_t$ holds. Now, define

(24) $$ \begin{align} q(\boldsymbol{x}, \boldsymbol{s}, \boldsymbol{d} \,|\, r, \theta_0, \theta_1) = \sum_{\boldsymbol{c} \in \mathcal{C}(\boldsymbol{d}, \boldsymbol{s})} p(\boldsymbol{x}, \boldsymbol{c} \,|\, r, \theta_0, \theta_1), \end{align} $$

where . Note that $q(\boldsymbol {x}, \boldsymbol {s}, \boldsymbol {d} \,|\, r, \theta _1, \theta _1)$ in (24) and $p(\boldsymbol {x} \,|\, r, \theta _1, \theta _1)$ in (17) are closely related. While the latter is obtained by summing over all possible group memberships, the former is obtained by summing only over those that are compatible with the observed review outcomes. This implies that (24) needs to be normalized to be a valid PDF. The final posterior update is then given by

(25) $$ \begin{align} p(r, \theta_0, \theta_1 \,|\, \mathcal{F}_t) = \frac{q(\boldsymbol{x}_t, \boldsymbol{s}_t, \boldsymbol{d}_t \,|\, r, \theta_0, \theta_1)}{E\big[ q(\boldsymbol{x}_t, \boldsymbol{s}_t, \boldsymbol{d}_t \,|\, R, \Theta_0, \Theta_1) \,|\, \mathcal{F}_{t-1} \big]} \, p(r, \theta_0, \theta_1 \,|\, \mathcal{F}_{t-1}). \end{align} $$

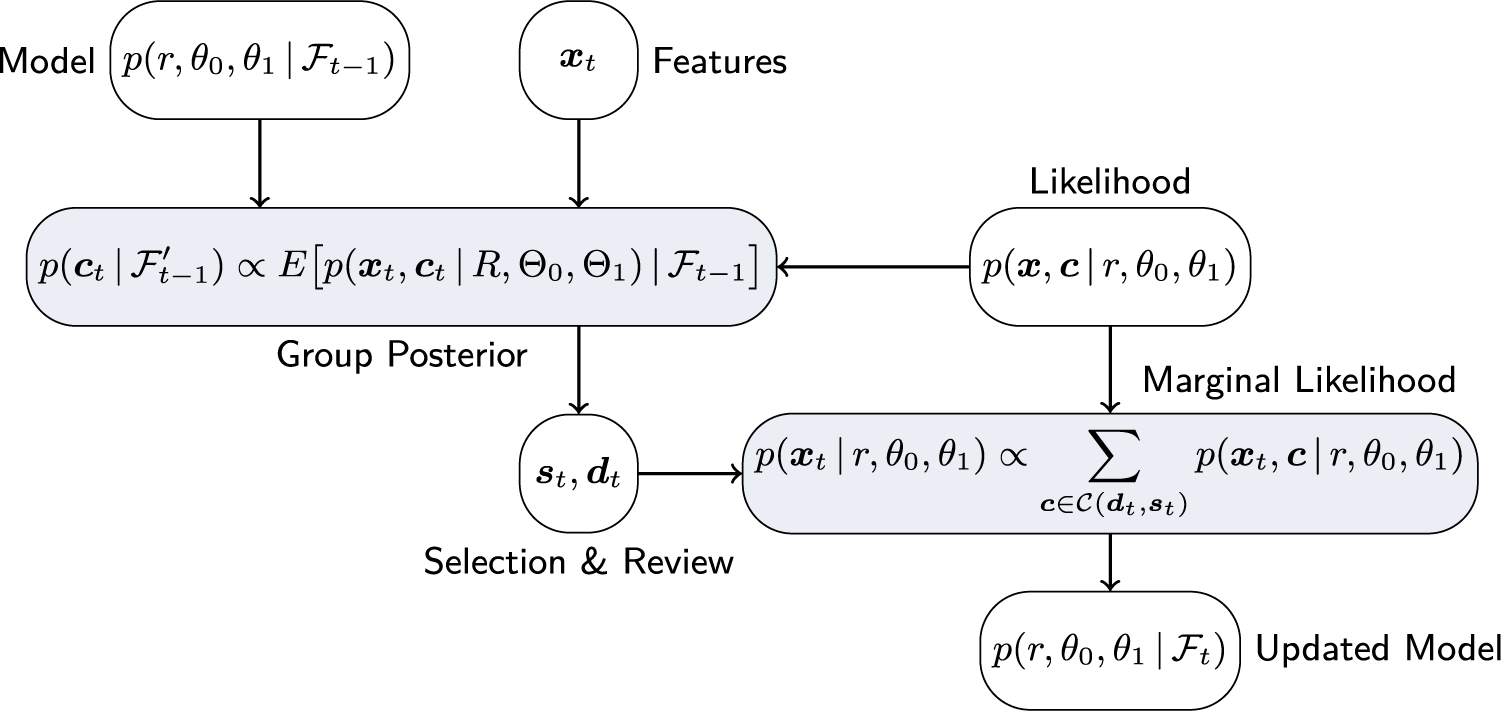
The factor $\xi _t(\boldsymbol {s}_t)$ in (23) is $\mathcal {F}_{t-1}$ -measurable and cancels out in the normalization. The update steps now repeat with $t \leftarrow t+1$ (see Figure 1 for a graphical illustration of the process).

Figure 1

Graphical illustration of information flow and posterior update of the Bayesian model.

3.2 Discussion

In this section, we briefly discuss the general structure and some properties of the optimal selection policy stated in Theorem 1. This discussion will also provide qualitative insights that can inform the design of approximate procedures.

By inspection, the optimal selection policy in (9) maximizes the expected value of a sum of two terms, $\boldsymbol {s}^\intercal \boldsymbol {C}_t$ and $\rho _t$ . The first term corresponds to the number of critical group members detected in the current administration; the second term corresponds to the expected number of critical group members detected in all future administrations. This trade-off between immediate and future rewards is typical for sequential decision-making procedures. However, there are a few aspects that are non-standard:

• • In general, the optimal policy at time t depends on all data observed so far and requires averaging over all future data. This results in extremely high complexity, even for small T and N, making strictly optimal policies virtually impossible to compute in practice.

• • In line with the information evolving in two steps, compare Section 2.2, the calculation of the expected reward in Theorem 1 is split into two parts. First, in (9), the review outcomes are predicted based on the observed features, $\boldsymbol {X}_t$ . Then, in (10), the features themselves are predicted based on the data from previous administrations. These two expectations correspond to two different sources of uncertainty: feature vectors need to be estimated to predict future rewards, but can in principle be observed. In contrast, the group memberships need to be estimated because they are unobservable to begin with.

• • The optimization over the selection vector, $\boldsymbol {s}$ , is “sandwiched” between the two expected values discussed in the previous bullet point. It happens inside the expectation over the feature vectors, which are available at the time the selection is made, but outside the expectation over the unknown group memberships.

• • There always exists a deterministic optimal selection policy. This follows directly from the fact that in (A.13) a function that is linear in the optimization variable, $\xi _t$ , is maximized over a probability simplex. Therefore, at least one vertex attains the maximum, and any vertex of a probability simplex corresponds to a single point mass on the respective outcome.

• • The update of the posterior distribution detailed in Section 3.1 depends on the selection, but not on the selection policy. This is the case since the selected test takers only enter via the marginalization in (24). The latter requires knowledge of the selection, $\boldsymbol {s}$ , but is independent of how this selection was made.

• • In principle, it is not necessary to track $\boldsymbol {S}_t$ and $\boldsymbol {D}_t$ separately. Both can be combined into a single vector that indicates if the respective test taker is known to be a member of the critical group, of the reference group, or if their group membership is unknown. We decided to go with the slightly lengthier notation since we believe it to be conceptually simpler.

This concludes the discussion of the optimal selection policy. Based on the insights gained, we now turn to the design of approximate selection policies that are practical to implement.

4.1 Approximate posterior update

The approximation method proposed in this section is essentially an expectation maximization (EM) algorithm (Dempster et al., Reference Dempster, Laird and Rubin2018). However, it also incorporates ideas from the mixture-based extended auto-regressive model, see (Šmídl & Quinn, Reference Šmídl and Quinn2006, Chapter 8), and basic copula theory (Jaworski et al., Reference Jaworski, Durante, Hardle and Rychlik2010). First, each element of the feature vector, $\boldsymbol {X}$ , is assumed to follow a distribution from the exponential family. That is,

(26) $$ \begin{align} p_{X_m}(x \,|\, \eta_m) = h_m(x) \exp\big(\eta_m^\intercal T_m(x) - A_m(\eta)\big), \end{align} $$

with natural parameters $\eta _m \in \mathcal {T}_m$ , base measure $h_m$ , sufficient statistic $T_m$ , log-partition $A_m$ and $m = 1, \ldots , M$ . Correlations between the elements of $\boldsymbol {X}$ are modeled via a Gaussian copula. To this end, we define the random vector $\boldsymbol {Z} \in \mathbb {R}^M$ as

(27) $$ \begin{align} Z_m = \Phi^{-1}\big( F_{\boldsymbol{\eta}_m}(X_m) \big), \end{align} $$

where $F_{\boldsymbol {\eta }_m}$ denotes the cumulative distribution function (CDF) of $P_{X_m}$ , and $\Phi $ denotes the CDF of the standard normal distribution. The random vector $\boldsymbol {Z}$ is then modeled as normally distributed with mean zero and covariance $\boldsymbol {\Sigma }$ , that is, $\boldsymbol {Z} \sim \mathcal {N}(\boldsymbol {0}, \boldsymbol {\Sigma })$ . It can be shown that (26) and (27) define a class of distributions with PDFs

(28) $$ \begin{align} p_{\boldsymbol{X}}(\boldsymbol{x} \,|\, \theta) = p_{\boldsymbol{X}}(\boldsymbol{x} \,|\, \boldsymbol{\eta}, \boldsymbol{\Sigma}) = p_{\boldsymbol{Z}}(\boldsymbol{z} \,|\, \boldsymbol{\Sigma}) \, \prod_{m=1}^M g(x_m \,|\, \eta_m). \end{align} $$

Here, $\boldsymbol {z}$ is calculated from $\boldsymbol {x}$ according to (27), $p_{\boldsymbol {Z}}( \bullet \,|\, \boldsymbol {\Sigma })$ denotes the PDF of a zero-mean multivariate normal distribution with covariance matrix $\boldsymbol {\Sigma }$ , and we defined

(29)

where $\operatorname {\mathrm {erfc}}$ denotes the complementary error function.

The model in (28) is assumed to hold under both hypotheses, that is, for test takers in the critical group and in the reference group. The corresponding parameters and functions are denoted by an additional subscript $i \in \{0,1\}$ , for example, $\eta _{i,m}$ . Note that the exponential families of distributions do not need to be of the same type under both hypotheses.

A priori, we assume the free parameters to be independent and distributed according to

(30) $$ \begin{align} R &\sim \operatorname{\mathrm{Beta}}\big(\nu_1^{(0)}, \nu_0^{(0)}\big), \end{align} $$

(31) $$ \begin{align} \boldsymbol{\Sigma}_i &\sim \mathcal{W}^{-1}\big(\nu_i^{(0)}, \boldsymbol{\Psi}_i^{(0)}\big),\end{align} $$

(32) $$ \begin{align} H_{i,m} &\sim \Pi_m\big(\nu_i^{(0)}, \chi_{i,m}^{(0)} \big),\end{align} $$

where Beta denotes the beta distribution, $\mathcal {W}^{-1}$ denotes the inverse Wishart distribution, and $\Pi _m$ denotes the conjugate prior of the exponential family distribution corresponding to the density in (26). This distribution exists and its density is of the form

(33) $$ \begin{align} \pi_{H}(\eta \,|\, \nu, \chi) \propto \exp\Big( \eta^\intercal \chi - \nu A(\eta) \Big). \end{align} $$

The parameters $\nu _0$ and $\nu _1$ , which represent the effective number of observed samples under each hypothesis, are shared across all priors. Allowing for different initial effective sample sizes, $\nu _0^{(0)}$ and $\nu _1^{(0)}$ , is straightforward. We do not introduce this modification here, as it would significantly complicate the notation. In practice, however, it can be the case that, for example, one has more prior knowledge about the cheating rate distribution than the feature distribution.

While not guaranteed to accurately reflect the true prior knowledge in general, we consider the conjugate priors in (30)–(32) a useful and robust choice in practice—mainly for two reasons: First, as will become clear later in this section, conjugate priors significantly reduce computational complexity and eliminate the need for Monte Carlo sampling or numerical optimization in the inference step. Second, they are arguably a good fit for the problem at hand. Since the flagging procedure is assumed to run periodically, a natural prior for the parameters at time t is simply the posterior from the previous time instant, $t-1$ . In this chain, later priors are more accurate, as they incorporate more information. This effect is captured by the conjugate priors, which, by construction, remain of the same type after each administration, but increase their effective sample size, reflecting the larger set of training data. In the absence of training data, the least informative prior is obtained by setting the effective sample size to its minimum feasible value.

Based on the model specified above, we propose the following approximate posterior update. At time instant t, the approximate posterior distributions of R, $\boldsymbol {\Sigma }_i$ , and $H_{m,i}$ are given by

(34) $$ \begin{align} Q_R^{(t)} &= \text{Beta}\Big(\nu_1^{(t)}, \nu_0^{(t)}\Big), \end{align} $$

(35) $$ \begin{align} Q_{\boldsymbol{\Sigma}_i}^{(t)} &= \mathcal{W}^{-1}\Big(\nu_i^{(t)}, \boldsymbol{\Psi}_t^{(t)}\Big), \end{align} $$

(36) $$ \begin{align} Q_{H_{i,m}}^{(t)} &= \Pi_m\big(\nu_i^{(t)}, \chi_{i,m}^{(t)} \Big). \end{align} $$

The distribution parameters on the right-hand side, $\chi _{i,m}^{(t)}$ , $\boldsymbol {\Psi }_t^{(t)}$ , and $\nu _i^{(t)}$ , are obtained from their previous values, $\chi _{i,m}^{(t-1)}$ , $\boldsymbol {\Psi }_t^{(t-1)}$ , and $\nu _i^{(t-1)}$ , by solving the following system of equations:

(37) $$ \begin{align} q_{C_{t,n}}(1) &= s_{t,n} d_{t,n} + (1 - s_{t,n}) \frac{\nu_{1}^{(t)} \, p_{\boldsymbol{X}}\Big(\boldsymbol{x}_{t,n} \,|\, \hat{\boldsymbol{\eta}}_1^{(t)}, \mathcal{P}_{\mathcal{E}}\big( \boldsymbol{\Psi}_1^{(t)}\big) \Big)}{\sum_{j=0}^1 \nu_{j}^{(t)} \, p_{\boldsymbol{X}}\Big(\boldsymbol{x}_{t,n} \,|\, \hat{\boldsymbol{\eta}}_j^{(t)}, \mathcal{P}_{\mathcal{E}}\big( \boldsymbol{\Psi}_j^{(t)}\big) \Big)}, \end{align} $$

(38) $$ \begin{align} \hat{\eta}_{i,m}^{(t)} &\in \operatorname*{\mbox{arg max}}_{\eta \in \mathcal{T}_m} \; \eta^\intercal \chi_{i,m}^{(t)} - \nu_i^{(t)} A_{i,m}(\eta), \end{align} $$

(39) $$ \begin{align} \boldsymbol{\Psi}_i^{(t)} &= \boldsymbol{\Psi}_i^{(t-1)} + \sum_{n=1}^n q_{C_{t,n}}(i) \, \boldsymbol{z}_{i,t,n}^{\phantom{\intercal}} \boldsymbol{z}_{i,t,n}^\intercal, \end{align} $$

(40) $$ \begin{align} \nu_i^{(t)} &= \nu_i^{(t-1)} + \sum_{n=1}^N q_{C_{t,n}}(i), \end{align} $$

(41) $$ \begin{align} \chi_i^{(t)} &= \chi_i^{(t-1)} + \sum_{n=1}^n q_{C_{t,n}}(i) \, T(x_{t,n}), \end{align} $$

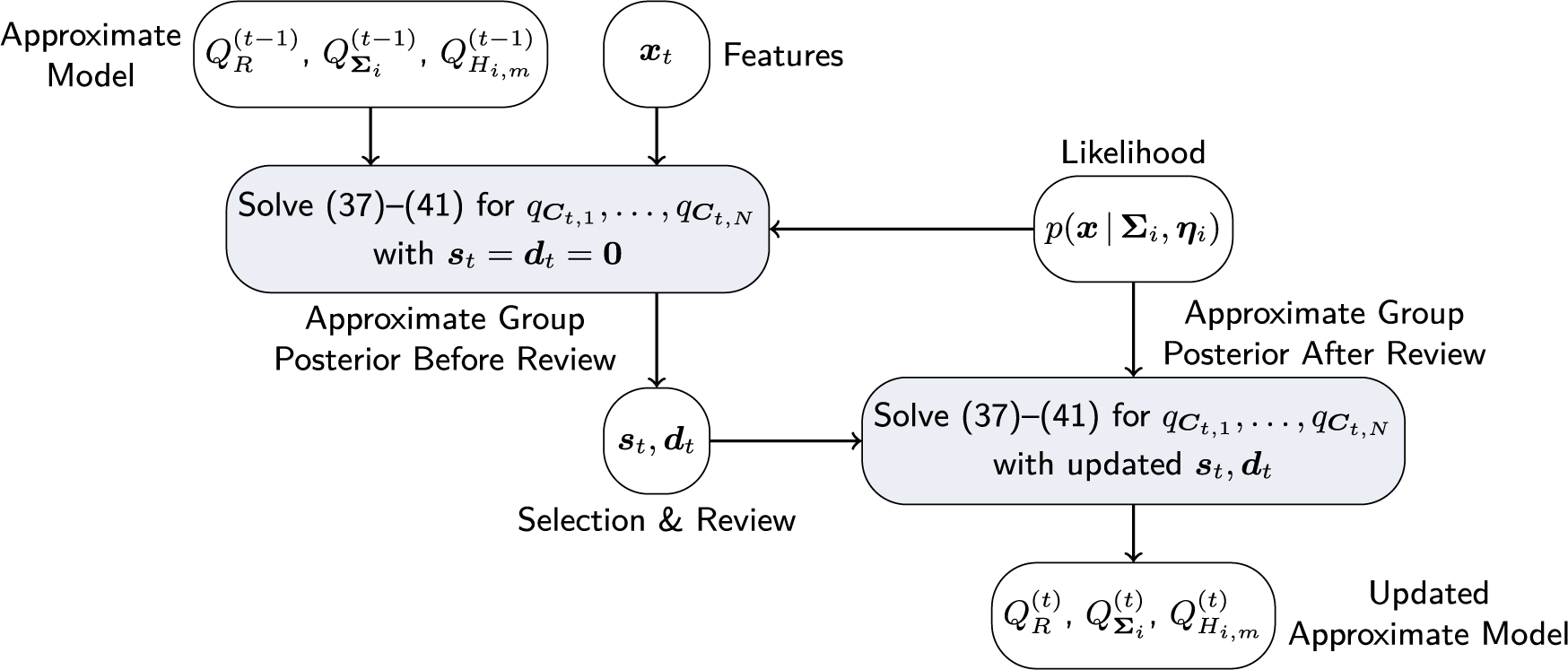
where $i \in \{0,1\}$ and $\boldsymbol {z}_{i,t,n} = \Phi ^{-1}\big ( F_{\hat {\boldsymbol {\eta }}_i^{(t)}}(\boldsymbol {x}_{t,n} ) \big )$ . The proposed approximate posterior update for a given selection policy is summarized in Algorithm 1, a graphical illustration in analogy to Figure 1 is shown in Figure 2.

Figure 2

Graphical illustration of the approximate posterior update in (37)–(41).

Note that the posterior update in Algorithm 1 is run twice—once before the test takers are selected and once after the reviews are completed. The purpose of the first update is to obtain the approximate posterior distributions of the group indicator variables, $q_{C_{t,n}}$ . The selection policies discussed in the next section are all based on these distributions. The purpose of the second update is to refine the estimates of $\nu _i^{(t)}$ , $\chi _i^{(t)}$ , and $\boldsymbol {\Psi }_i^{(t)}$ by incorporating the outcomes of the reviews. The difference between the first and second runs is reflected in (37), where the probability that the nth test taker of the tth administration is a member of the critical group is estimated from the observed features in case the test taker has not been reviewed ( $s_{t,n} = 0$ ), or is set to the true label, $d_{t,n}$ , if the review outcome is known ( $s_{t,n} = 1$ ).

The idea underlying the update equations in (37)–(41) is to start with the priors in (30)–(32) and approximate the posterior distributions via a mean-field variational approximation (Blei et al., Reference Blei, Kucukelbir and McAuliffe2017; Šmídl & Quinn, Reference Šmídl and Quinn2006). By construction, this approximation yields posterior distributions that are of the same type as the priors, and whose parameters are determined implicitly by a system of equations. However, this system is still hard to solve since it involves expectations taken with respect to the current posterior distribution. In order to simplify the evaluation of the latter, we use maximum a posteriori probability (MAP) estimates as an approximation of the expected values. More precisely, to evaluate the posterior group membership probabilities in (37), we calculate MAP estimates of the marginal parameters in (38). Once the marginal parameters are fixed, the observations, $\boldsymbol {x}_{t,n}$ , can be mapped to the “Gaussian domain,” $\boldsymbol {z}_{t,n}$ , via (27). The latter can then be used to update the covariance posterior in (39). The effective sample sizes and the parameters of the posterior distributions of the marginal parameters are updated according to (40) and (41). Of course, since all updates are coupled, they cannot simply be performed in sequence, but need to be solved jointly. We will further elaborate on this aspect later in this section.

Finally, note that in the model updates (39)–(41), the posterior group probabilities are used as weights, that is, the observation $x_{t,n}$ contributes to the model of the critical group with weight $q_{C_{n,t}}(1)$ and to the model of the reference group with weight $q_{C_{n,t}}(0) = 1 - q_{C_{n,t}}(1)$ . This observation will later be used in the derivation of heuristic selection policies.

Before concluding this section, we briefly discuss some implementation aspects of Algorithm 1:

• • There are various ways of solving the equation system in (37)–(41) in practice. A natural approach is to iterate over the updates until all parameters and probabilities have converged. Alternatively, one can use standard numerical solvers. In this case, it is useful to consider only $q_{C_{t,n}}(1)$ , ${n = 1, \ldots , N}$ , as free variables since all other variables are fixed once all $q_{C_{t,n}}(1)$ are given. Note that this means that the equation system is of size N in the first update step of Algorithm 1 and of size $N - K$ in the second.

• • Depending on the choice of the marginal distributions, the optimization problems in (38) may not have a closed-form solution. However, even if (38) needs to be solved numerically, the underlying distributions are univariate so the number of parameters is typically small. Moreover, for given $\chi _{i,m}$ and $\nu _{i,m}$ , the $2 M$ problems in (38) can be solved in parallel.

• • In (37), the covariance matrix of the feature distribution is projected on the elliptope of correlation matrices. This projection is not strictly necessary. However, in our experiments, it leads to an improved performance. This is likely the case because the true $\boldsymbol {\Sigma }$ has unit diagonal elements if the model in (26) holds exactly. However, in practice, replacing the projection in (37) with the maximum likelihood estimate, $\frac {\boldsymbol {\Psi }_i}{\nu _i + M + 1}$ might improve the performance in some cases.

• • In practice, $\theta _0$ , $\theta _1$ , and r do not necessarily remain constant for all $t = 1, \ldots , T$ . While initially the Bayesian model can and will adapt to variations, the more samples are observed, the higher its “inertia” becomes. In order to counteract this effect, past observations can be down-weighted in the posterior update. For example, an exponential decay can be introduced by making the substitutions $\nu _i^{(t-1)} \leftarrow \omega \nu _i^{(t-1)}$ , $\chi _i^{(t-1)} \leftarrow \omega \chi _i^{(t-1)}$ , and $\boldsymbol {\Psi }_i^{(t-1)} \leftarrow \omega \boldsymbol {\Psi }_i^{(t-1)}$ in (39)–(41), where ${0 < \omega < 1}$ is a weight that balances adaptivity and steady-state performance—compare (Šmídl & Quinn, Reference Šmídl and Quinn2006, Section 8.6).

4.2 Approximate selection policies

The algorithm proposed in the previous section offers a mechanism to track the posterior distributions of the model parameters for a given selection policy. However, it does not answer the question of how to choose a selection policy in the first place. This question will be addressed in this section.

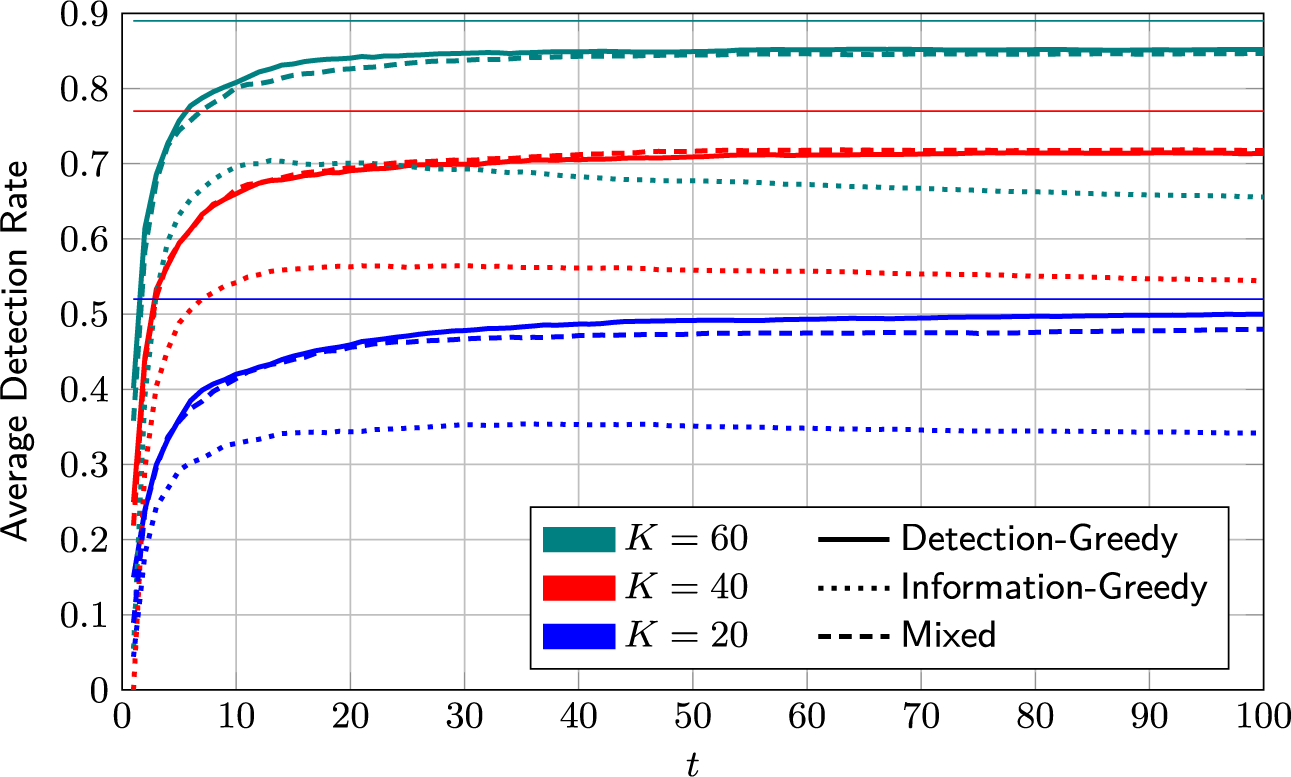
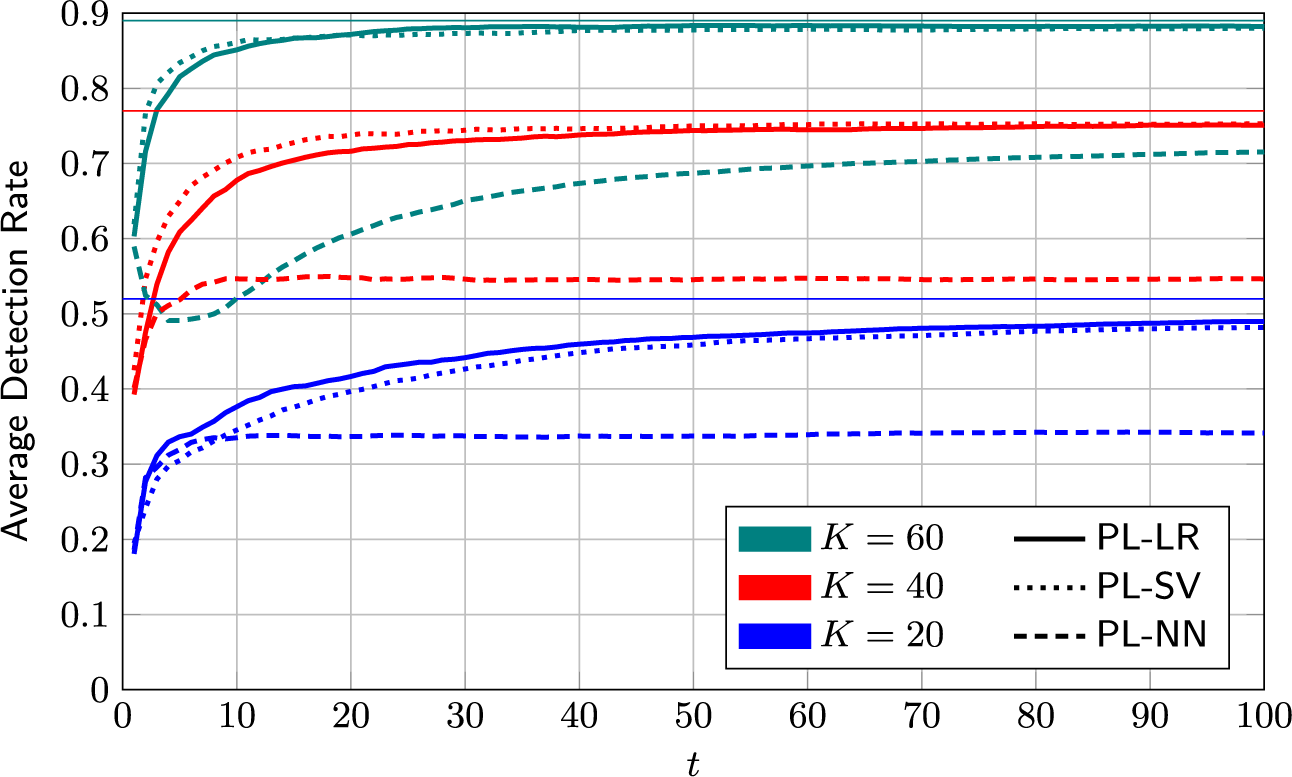
We propose three selection policies: A detection-greedy policy, an information-greedy policy, and a mixed policy that balances the information-greedy and detection-greedy approaches depending on the estimated accuracy of the current model.

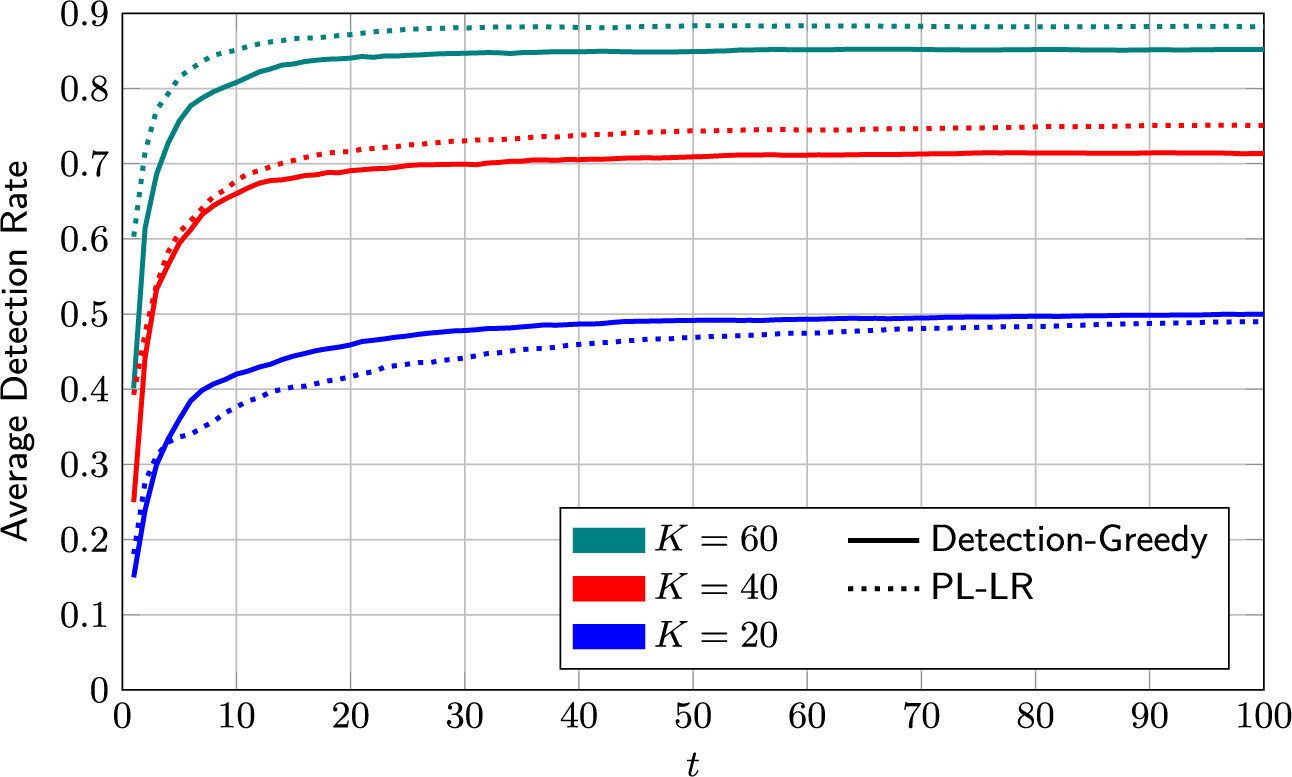
4.2.1 Detection-greedy selection policy

Consider the optimal selection policy defined by the optimization problem (9). Adopting a greedy approach and ignoring the expected future rewards, this problem simplifies to

(42) $$ \begin{align} \max_{\boldsymbol{s} \in \mathcal{S}_K^N} \; E_{\boldsymbol{C}_t}\big[ \boldsymbol{s}^\intercal \boldsymbol{C}_t \,|\, \mathcal{F}_{t-1}' \big] &= \max_{\boldsymbol{s} \in \mathcal{S}_K^N} \boldsymbol{s}^\intercal E_{\boldsymbol{C}_t} \big[ \boldsymbol{C}_t \,|\, \mathcal{F}_{t-1}' \big] \end{align} $$

(43) $$ \begin{align} &= \max_{\boldsymbol{s} \in \mathcal{S}_K^N} \; \sum_{n=1}^N s_{t,n} P(C_{t,n} = 1 \,|\, \mathcal{F}_{t-1}'). \end{align} $$

That is, the optimal greedy selection policy is to select the K test takers with the highest posterior probability of being members of the critical group.

Although the detection-greedy policy is much simpler than the optimal one, evaluating ${P(C_{t,N} = 1 \,|\, \mathcal {F}_{t-1}')}$ will still be too complex in most practical cases. Therefore, the heuristic policy suggested here is to select test takers based on the approximate probability $q_{C_{t,n}}(1)$ . This leads to the following selection policy:

Selection Policy 1 (Detection-Greedy).

At time instant t, the detection-greedy selection policy, $\xi _t^\dagger $ , is defined as

(44) $$ \begin{align} \xi_t^\dagger(\mathcal{S}_t^\dagger) = 1, \end{align} $$

where

(45)

with $q_{C_{t,n}}(1)$ defined in (38). In words, $\xi _t^\dagger $ flags the K test takers that are most likely to be members of the critical group according to the approximate posterior probability $q_{C_{t,n}}(1)$ .

The detection-greedy policy is a natural choice, and, as the numerical examples in Section 6 will demonstrate, works well in many cases. However, by design, it does not take into account the benefits of potential model improvements that could be achieved by reviewing particularly informative cases. The second policy aims to identify the latter.

4.2.2 Information-greedy selection policy

The idea underlying this selection policy is not to review the cases that are most likely to lead to detections, but to review the cases that provide the most information. In terms of the optimal selection policy in (9), this roughly corresponds to maximizing only the expected reward term, $\rho _t$ , and ignoring the immediate reward $\boldsymbol {s}^\intercal \boldsymbol {C}_t$ . In this sense, the information-greedy policy complements the detection-greedy policy. However, as was the case for the latter, directly maximizing $\rho _t$ is computationally infeasible. We propose the following heuristic:

Selection Policy 2 (Information-Greedy).

At time instant t, the information-greedy selection policy, $\xi _t^\ddagger $ , is defined as

(46) $$ \begin{align} \xi_t^\ddagger(\mathcal{S}_t^\ddagger) = 1, \end{align} $$

where

(47)

$H_b$ denotes the binary entropy function, and $q_{C_{t,n}}(1)$ is defined in (37). In words, $\xi _t^\ddagger $ flags the K test takers whose approximate posterior group-membership distribution admits the highest entropy.

The rationale for the information-greedy selection policy is that resolving cases with the highest ambiguity has the greatest effect on model updates. More specifically, in (39)–(41), observed samples contribute to the parameter updates of the posterior distributions with weights $q_{C_{t,n}}$ . Reviewing cases that are highly likely to belong to a certain group has little effect on these weights. For example, reviewing a case with $q_{C_{t,n}}(1) = 0.99$ will most likely result in a detection, changing the weight from $0.99$ to $1.0$ . This small change has a negligible impact on the model. In contrast, reviewing cases with high entropy, that is, $q_{C_{t,n}}(1) \approx 0.5$ , has a strong impact: Without review, the sample contributes equally to both models, reducing separability. With review, it contributes exclusively to the correct model, increasing separability.

On its own, the information-greedy policy is of limited use, as it does not explicitly aim to maximize the number of detections.Footnote ² However, it serves as a useful building block for an adaptive policy that balances model fit and detection rate (DR). Such a policy is proposed next.

4.2.3 Mixed selection policy

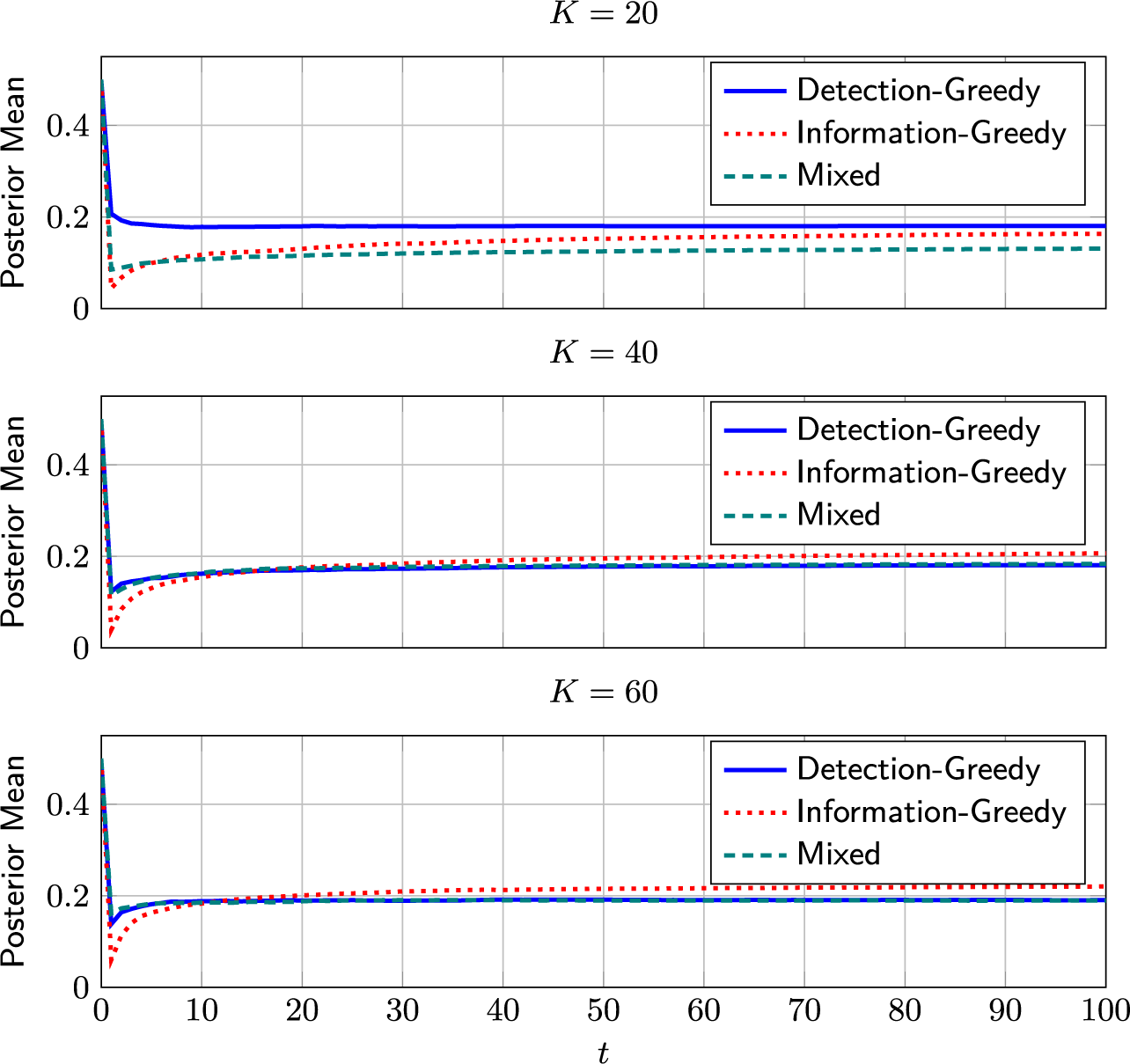
The detection-greedy selection policy is a good choice when the learned model is close enough to the true one to produce sufficiently reliable predictions. However, the information-greedy selection policy might be useful to reduce the time and samples needed to reach this point. The idea underlying the proposed mixed policy is to track the model fit and balance the two policies accordingly. However, quantifying model fit is not straightforward. As discussed before, the optimal measure in (9) is too complex to evaluate in practice. Possible proxy measures include, for example, the variance or entropy of the posterior distribution. However, translating the latter into a useful exploration/exploitation trade-off is a non-trivial problem itself.

The heuristic proposed here is to use the detector calibration as a measure of the model accuracy. The underlying idea is the following: If the learned model is a good fit, the resulting (approximate) posterior probabilities will be reasonably accurate. That is, assuming that the posterior probabilities of the K selected test takers being critical group members are $q_1, \ldots , q_K$ , the number of critical group members detected in the review process should be close to the sum of these probabilities. More precisely, it should hold that

(48) $$ \begin{align} E\!\left[ \sum_{n=1}^N D_{t,n} \right] = \sum_{k=1}^K q_k \quad \text{and} \quad \text{Var}\!\left[ \sum_{n=1}^N D_{t,n} \right] = \sum_{k=1}^K q_k(1-q_k). \end{align} $$

If the number of true positives is significantly lower than one would expect according to (48), the model likely needs improvement. This motivates the following selection policy:

Selection Policy 3 (Mixed).

Let be the number of detected critical group members in the administration at time instant $t-1$ , and let

(49) $$ \begin{align} \phi_t = \begin{cases} \displaystyle 1, & \mu_{t-1} - d_{t-1} \leq \sigma_{t-1}, \\ \displaystyle \frac{\sigma_{t-1}}{\mu_{t-1} - d_{t-1}}, & \text{otherwise}, \end{cases} \end{align} $$

where $\mu _t$ and $\sigma ^2_t$ denote mean and variance defined in (48). In the administration at time instant t, first select $\lceil \phi _t K \rceil $ test takers according to Selection Policy 1, then select the remaining $K - \lceil \phi _t K \rceil $ test takers according to Selection Policy 2, where $ \lceil\cdot \rceil $ denotes the ceiling operation.

In words, $\phi _t$ is the reciprocal of the number of standard deviations $d_{t-1}$ falls short of its mean. Note that, as long as $d_{t-1}$ remains within one standard deviation, the mixed policy reduces to the detection-greedy policy.

Instead of fixing the shares of test takers selected according to each policy, one can also use a randomized strategy, where test takers are selected sequentially and selection policies 1 and 2 are used with probabilities $\phi $ and $1 - \phi $ , respectively.

Finally, note that the distribution of $\sum _{n=1}^N D_{t,n}$ is known, namely, it is a Poisson binomial distribution with parameters $q_1, \ldots , q_K$ (Tang & Tang, Reference Tang and Tang2023). Therefore, the probability of observing a certain number of critical group members can be calculated exactly, and can be used to refine Selection Policy 3. However, given the heuristic nature of the proposed selection policies, such refinements are unlikely to be worth the extra computational cost.

6.1 Reference procedure

As discussed in Section 1, the sequential semi-supervised flagging problem addressed in this article is non-standard, and none of the methods found in the literature met all our requirements. Thus, there is no obvious reference procedure to compare the proposed one to.

In order to at least establish a performance baseline, we propose combining off-the-shelf classifiers with pseudo labeling (PL), a generic method for learning from partially labeled data. PL was proposed by Lee (Reference Lee2013) and is still widely used today (Kage et al., Reference Kage, Rothenberger, Andreadis and Diochnos2025; Zhai et al., Reference Zhai, Oliver, Kolesnikov and Beyer2019). Its idea is to use a model trained on labeled data to assign labels to unlabeled data. The predicted labels, called pseudo-labels, are then treated as if they were true and used to train the model alongside the original, labeled samples. To reduce noise, pseudo-labeling is usually applied selectively, for example, by only assigning pseudo-labels to samples that were classified with high confidence.

In principle, PL can be combined with any classifier. However, given the complications of the flagging problem, we consider classifiers with the following properties:

1. 1. The classifier outputs soft labels (probabilities or scores) that allow samples to be ordered from least to most likely to belong to the critical group.

2. 2. The classifier can be trained via stochastic gradient descent (SGD) (or a variant thereof), which naturally lends itself to learning from sequential data.

3. 3. The classifier can operate in a small-to-medium sample size regime, minimizing the need for pretraining before use in operation.

Note that some advanced methods that are routinely used in more standard settings do not meet the requirements stated above. For example, deep neural networks typically require large datasets to reach their full potential (Sun et al., Reference Sun, Shrivastava, Singh and Gupta2017); many ensemble methods, such as random forests and boosting, are inherently designed for static datasets and not well-suited for sequential learning without substantial modification (Dietterich, Reference Dietterich2000; Saffari et al., Reference Saffari, Leistner, Santner, Godec and Bischof2009); and methods such as k-nearest-neighbors or decision-tree classifiers require additional, often sample-hungry calibration procedures to convert hard labels to soft labels (Niculescu-Mizil & Caruana, Reference Niculescu-Mizil and Caruana2005; Zadrozny & Elkan, Reference Zadrozny and Elkan2002).

For the experiments in this section, we used three different classifiers: logistic regression, a linear support vector machine, and a fully-connected neural network with a single hidden layer and rectified linear unit (ReLU) activation function. These classifiers are well-established, highly popular among practitioners, and efficient implementations are readily available in various programming languages. The resulting procedures are referred to as PL-LR, PL-SV, and PL-NN, respectively. The underlying algorithm for combining PL with SGD-based classifiers is summarized in Algorithm 2.

All three reference procedures were implemented via the scikit-learn framework (Pedregosa et al., Reference Pedregosa, Varoquaux, Gramfort, Michel, Thirion, Grisel, Blondel, Prettenhofer, Weiss, Dubourg, Vanderplas, Passos, Cournapeau, Brucher, Perrot and Duchesnay2011). PL was implemented as follows: During the first 10 administrations, only reviewed samples were used for training. After this warm-up period, the threshold for PL positive samples (critical group members) was set to the lowest predicted probability or score among the confirmed positive samples in the current administration. For example, if three cases were identified as critical group members during the review, and the classifier had predicted these outcomes with probabilities $0.75$ , $0.8$ , and $0.9$ , then all samples whose predicted probability of belonging to the critical group exceeds $0.75$ were assigned a positive pseudo-label. Negative pseudo-labels (reference group members) were assigned analogously.

The reference procedures were combined with a detection-greedy flagging policy, that is, the K samples with the highest likelihood of belonging to the critical group were selected for review. We chose this policy because it can be implemented irrespective of whether a classifier outputs probabilities or scores and, as will be shown shortly, the proposed Bayesian procedure typically performed best with a detection-greedy policy.

In addition to the PL and selection rules, all three classifiers have hyper-parameters that need to be set. However, in the sequential settings of the flagging problem, hyper-parameter optimization is non-trivial and requires custom methods (Gama et al., Reference Gama, Žliobaitė, Bifet, Pechenizkiy and Bouchachia2014) or substantial modifications of methods for static datasets (Shumway & Stoffer, Reference Shumway and Stoffer2022). Since these complications are well beyond the scope of this article, we decided to set the hyper-parameters by directly optimizing the observed performance. This is clearly not possible in practice, but provides useful insights into the potential performance of different methods.

Finally, we focused on tuning two important hyper-parameters: the learning rate used in the SGD steps, which is critical for balancing fast learning with good steady-state performance, and the width of the hidden layer of the neural network. The remaining hyper-parameters were left at their default values in scikit-learn (version 1.6.1). The learning rate was optimized via a grid-search over the interval $[10^{-5}, 10^{1}]$ with 61 logarithmically-spaced grid-points. The width of the hidden network layer was optimized via a grid search over the interval $[M, 10M]$ in steps of $\lfloor \tfrac {M}{2} \rfloor $ , where $\lfloor \bullet \rfloor $ denotes the flooring operation. Results are reported for the parameter values that, averaged over 20 runs, showed the best performance. More details will be discussed in the course of this section.

While clearly not exhaustive, we believe that the three PL procedures detailed above provide a useful baseline for how well the flagging problem can be solved by combining off-the-shelf components.

6.2 Synthetic data

For the first example, we consider $T = 100$ test administrations with $N = 100$ test takers each, approximately 20% of which are members of the critical group ( $r = 0.2$ ). The selection is made based on $M = 10$ features that admit beta-distributed marginals with the following, randomly generated parameters:

(59) $$ \begin{align} \begin{bmatrix} \boldsymbol{\eta}_0^\intercal \\ \boldsymbol{\eta}_1^\intercal \end{bmatrix} = \begin{bmatrix} \boldsymbol{\alpha}_0^\intercal \\ \boldsymbol{\beta}_0^\intercal \\ \boldsymbol{\alpha}_1^\intercal \\ \boldsymbol{\beta}_1^\intercal \end{bmatrix} = \begin{bmatrix} 1.73 & 3.16 & 2.46 & 2.58 & 3.08 & 3.02 & 2.10 & 5.27 & 2.78 & 2.24 \\ 1.56 & 2.93 & 2.80 & 3.28 & 3.89 & 5.10 & 1.82 & 1.92 & 2.58 & 3.25 \\ 2.50 & 3.84 & 3.72 & 2.95 & 3.54 & 3.33 & 2.16 & 2.95 & 2.47 & 3.77 \\ 1.75 & 3.49 & 2.07 & 2.43 & 2.75 & 4.02 & 3.36 & 3.71 & 2.80 & 3.08 \\ \end{bmatrix}. \end{align} $$

For members of the reference group, the features were assumed to be uncorrelated, $\boldsymbol {\Sigma }_0 = \boldsymbol {I}$ . For members of the critical group, the correlations were modeled as $\big [ \boldsymbol {\Sigma }_1 \big ]_{ij} = 0.9^{\lvert i - j \rvert }$ .

Figure 3 shows the average DR of the selection procedure as a function of the number of administrations. Note that DR here refers to the accumulated fraction of detected members of the critical group, that is,

(60)

The results were averaged over 20 runs, and identical feature distributions were used for every run. By inspection of Figure 3, it can be seen that the detection-greedy policy performs best in this example, irrespective of the number of reviewed test takers. The DR of the mixed policy, which balances detection and model improvement, first grows significantly more slowly than that of the detection-greedy policy, but ultimately converges to approximately the same value. This means that the mixed policy first focuses on learning the model, at the expense of a lower DR. However, once the model is sufficiently accurate, it performs just as well or even better than the detection-greedy policy. In contrast, the information-greedy policy shows significantly lower DRs across all experiments. This is expected, as it is not designed to maximize the DR. In fact, it might be somewhat unexpected that the DR does not converge to 50%. In this example, this is the case because the entropy of the posterior group distribution tends to be higher for members of the critical group than for members of the reference group. As a consequence, the information-greedy policy flags more test takers from the former. In general, we observed that the information-greedy policy tends to flag more members of the smaller group, which is the critical group in this case.

Figure 3

Average accumulated detection rate of the proposed policies against the number of administrations for different review sizes K.

Note: Here, $N = 100$ , $r=0.2$ , and the parameters of the feature distributions are given in (59). The thin horizontal lines indicate the upper bound on the detection rate in (56).

From Figure 3, one may draw the conclusion that the mixed selection policy is redundant, given that it performs worse than the simpler detection-greedy policy. However, this result does not convey the whole picture. First, for both $K = 10$ and $K = 20$ , the mixed policy only performs worse than the detection-greedy policy in the early test administrations, with the largest gap between the two occurring at around $t \approx 10$ . As t increases, the gap between the two curves narrows, meaning that the mixed policy performs equally well or even better for virtually all later administrations. Consequently, the mixed policy can be preferable in cases where the first administrations are less critical and can be used primarily for data collection. For example, new items are commonly piloted before being used in high-stakes tests (von Davier, Reference von Davier2010).

A second advantage of the mixed policy is that it leads to a more accurate model. Figure 4 shows plots of the average mean squared error (MSE) of two parameters, R and $\boldsymbol {\Sigma }_1$ , over the number of administrations. The MSE was calculated with respect to the posterior distribution at the time and again averaged over 20 runs. For all three policies, the large initial model errors steadily decrease, meaning the procedure does indeed learn the model from the data. However, the information-greedy and the mixed policy learn the parameters faster. Consider, for example, the MSE of R in the top plot of Figure 4. While it takes the detection-greedy policy approximately 75 administrations to reach $-$ 40dB, the information-greedy and mixed policy only need half as many samples to reach the same error level. For the error in the covariance matrix estimate, shown in the lower plot of Figure 4, this difference is less pronounced, but still noticeable. For example, the information-greedy and mixed policy reach the 0dB level approximately 10 administrations or 1000 samples earlier than the detection-greedy policy.

Figure 4

Average MSE against the number of administrations.

Note: Here, $N = 100$ , $r=0.2$ , $K = 20$ , and the parameters of the feature distributions are given in (59).

Finally, some insight into the mixed selection policy can be gained by observing $\phi _t$ , defined in (49). Its value, averaged over 20 runs, is plotted against the number of administrations in Figure 5. It can be seen that initially a substantial share of samples is selected according to the information-greedy policy, which is in line with the quicker model fit/learning discussed above. However, after approximately 30 administrations, $\phi _t$ reaches a steady state in which it fluctuates around approximately $0.95$ , meaning that most reviewed samples are selected according to the detection-greedy policy. Interestingly, the observed $\phi _t$ curves are almost identical for $K =20$ and $K = 40$ . Only for $K = 10$ the behavior is slightly different, with $\phi _t$ being strictly one for most administrations. This is likely a consequence of the second-order moment approximation used to calculate $\phi _t$ , which becomes more accurate as K increases. Nevertheless, the observed quick convergence to a purely detection-greedy policy is beneficial in this case since for $K = 10$ the procedure operates in a regime where the number of reviews, not the model fit, constitutes the main bottleneck.

Figure 5

Average values of $\phi _t$ in (49) against the number of administrations.

Note: Here, $N = 100$ , $r=0.2$ , $K = 20$ , and the parameters of the feature distributions are given in (59).

The results discussed so far illustrate the trade-off between DR and model accuracy. On the one hand, the model needs to be “good enough” to reliably detect critical group members. On the other hand, investing too many samples into model improvements can lead to situations in which an unreasonable number of administrations is required to compensate for the lower initial DR. Based on our experiments, we conjecture that, as a rule of thumb, in cases where a high DR is the main or only goal, the detection-greedy policy should be used. In cases where early administrations can be used for training, or when an accurate model is of concern, for example, to track error rates, feature correlations, or shares of critical group members, the mixed policy can be preferable.

To put the results shown so far into perspective, average DRs of the three reference procedures detailed in Section 6.1 are shown in Figure 6. The corresponding hyper-parameters are given in Table 1. By inspection, PL-SV and PL-LR achieve virtually identical performances for all values of K. PL-NN performs notably worse. We conjecture that this is the case because neural networks have significantly more free parameters and in turn require more training data. In this example, even the smallest neural network, with a hidden layer of width 30, has well over 300 free parameters. For comparison, the proposed Bayesian method has approximately 60 free parameters, and PL-LR and PL-SV both have fewer than 20.

Figure 6

Average accumulated detection rates of reference procedures against the number of administrations for different review sizes K.

Note: Here, $N = 100$ , $r=0.2$ , and the parameters of the feature distributions are given in (59). The thin horizontal lines indicate the upper bound on the detection rate in (56).

Table 1

Hyper-parameters of reference procedures for different values of K

In Figure 7, we compare one of the best-performing baseline methods, PL-SV, to the detection-greedy variant of the proposed method. For large and small values of K, there are no significant performance differences. For $K = 10$ , both procedures appear limited mainly by the small number of reviews rather than their respective flagging or learning strategies. At the other end, for $K = 40$ , there are enough labeled data points for both to quickly achieve virtually perfect separation. Only for $K = 20$ does the proposed method significantly outperform PL-SV. We conjecture that in this case, in which the share of reviewed cases equals the rate of critical group members ( $\tfrac {K}{N} = r$ ), the proposed procedure’s more principled approach to data processing and model tracking pays off. Arguably, the case $\tfrac {K}{N} \approx r$ is also of practical relevance, as one would normally expect to review about as many cases as there are critical group members.

Figure 7

Comparison of average accumulated detection rates of the proposed detection-greedy policy and support-vector-based reference procedure.

Note: Here, $N = 100$ , $r=0.2$ , and the parameters of the feature distributions are given in (59).

6.3 Real-world data

For the second example, we used real-world data collected from a large language assessment between November 2022 and March 2023. The dataset contains 2,595 data points, each a three-dimensional vector representing different similarity metrics between a submitted response and a potential source text it may have been copied from. Of the 2,595 responses, 745 ( $\approx $ 30%) were labeled as plagiarized (true positives) by human experts, and 1,850 ( $\approx $ 70%) as authentic (false positives), meaning the similarities did not constitute plagiarism under the program’s guidelines.Footnote ³ The three similarity metrics used in this example all take values in the unit interval, with one corresponding to identical texts. For security reasons, we do not detail how the features were computed from the responses or which items were used for the study. For the purpose of illustrating the proposed flagging procedure, these specifics are of little importance. Interested readers may contact the authors directly.

An additional complication compared to the first example is introduced by the fact that, owing to pre-processing steps that will not be detailed here, the elements of the similarity vectors are left-truncated at $0.13$ , $0.7$ , and $0.3$ , respectively. In principle, the proposed algorithm can be adapted to use truncated exponential distributions. However, this extension is non-trivial and beyond the scope of this article. Instead, in this example, we disregarded the model mismatch and ran the flagging procedure with the same marginal distributions and parameters as in the first example. This approach is clearly suboptimal. However, we still consider the experiment meaningful since, in practice, model mismatches are inevitable and the flagging procedure should still perform acceptably well under such conditions.

We again used $N = 100$ , $r=0.2$ , and $T = 100$ . The number of features, $M = 3$ , was determined by the data. Samples from the critical and reference groups were generated via bootstrapping. That is, for each administration, we first sampled a vector $\boldsymbol {c}_t$ whose elements are independent Bernoulli random variables with success probability r. For each $c_{n,t}$ , the corresponding feature vector $\boldsymbol {x}_t$ was then drawn uniformly and with replacement from the respective data set. In order to investigate the effect of the model mismatch, we fitted two multivariate truncated beta distributions to the true and false positives in our data set. These distributions were defined in analogy to those in Section 3.1, that is, the marginals are truncated beta distributions and the correlations are modeled via a Gaussian copula. This model largely eliminates the model mismatch and, in line with the assumptions underlying Lemma 1, was used to simulate the case in which the distributions $P_0$ and $P_1$ are known.

In Figure 8, the average DRs of the three proposed policies are plotted against the number of administrations for different values of K. For comparison, we included bounds obtained by assuming $P_0$ and $P_1$ to be known, as explained above. In general, the DR curves behave similar to their counterparts in the first example, which corroborates the findings obtained from synthetic data. Interestingly, in the sample-rich regime ( $K = 60$ ), the performance of the information-greedy policy is on par with that of the detection-greedy and mixed policies. We conjecture that this is the case because samples from the smaller group tend to be more informative. For $K=60$ , the sample size is large enough for the policy to “saturate” the samples from the critical group.

Figure 8

Average detection rate of the proposed policies against the number of administrations for different review sizes K.

Note: Here, $N = 100$ , $M=3$ , and $r=0.2$ . The thin horizontal lines indicate upper bounds on the detection rate obtained by an “oracle” version of the proposed method that uses a fitted model from the beginning instead of learning it from the data.

Next, we compare the model fit of the different policies. In lack of a ground truth for the other parameters, we look at the posterior mean of R. As can be seen in Figure 9, for all policies, the estimated rate of critical group members starts high, then quickly drops, and finally converges to a value close to $0.2$ . This behavior can be explained as follows: Since R is assumed to have been drawn from a uniform prior, the initial mean is $0.5$ , which is significantly larger than the true value of $0.2$ . As samples start coming in, the model adjusts to the lower observed rate of critical group members. However, for the first administrations, the uncertainty in the model is large, and the detection accuracy is still low. Therefore, only a fraction of the critical group members is detected, and the model goes from overestimating r to underestimating it. This overshoot effect is least pronounced for the detection-greedy policy, which has the highest DR in early administrations (compare Figure 8). We conjecture that this effect also contributes to the higher overall accuracy of the detection-greedy policy when $K = 20$ .

Figure 9

Average posterior mean of R against the number of administrations for different selection policies and values of K, with $N = 100$ and $M=3$ .

The average DRs of the three reference procedures detailed in Section 6.1 are shown in Figure 10, and the corresponding hyper-parameters in Table 2. By inspection, PL-NN performs significantly worse than PL-SV and PL-LR. The latter admit virtually identical performance, with PL-LR performing slightly better for $K = 20$ . This finding corroborates that neural networks do not seem to be a good fit for the sequential flagging problem: large networks require too many samples to learn the underlying model, and small networks lack the required expressive power. This problem could possibly be addressed by adaptively growing the network as more data become available, but exploring this approach is well beyond the scope of this section.

Figure 10

Average detection rate of reference procedures against the number of administrations for different review sizes K.

Note: Here, $N = 100$ , $M=3$ , and $r=0.2$ . The thin horizontal lines indicate upper bounds on the detection rate obtained by an “oracle” version of the proposed method that uses a fitted model from the beginning instead of learning it from the data.

Table 2

Hyper-parameters of reference procedures for different values of K

In Figure 11, we compare the proposed detection-greedy policy to the best-performing reference method, PL-LR. Interestingly, the latter slightly outperforms the former for larger values of K. We conjecture that this performance gap is mainly caused by the model mismatch discussed above. On the one hand, this result shows that, unsurprisingly, the proposed procedure is not necessarily the best choice under all circumstances. On the other hand, it is reassuring to see that even under moderate model mismatch, the proposed method admits DRs within three percentage points of the best reference method, and accurately estimates the share of critical group members among the test population (compare Figure 9). Also, note that PL-LR uses a close-to-optimal learning rate, which is unlikely to be the case in practice.

Figure 11

Comparison of average accumulated detection rates of the proposed detection-greedy policy and logistic-regression-based reference procedure.

Note: Here, $N = 100$ , $M=3$ , and $r=0.2$ .

6.4 Summary

In summary, we conclude from the experiments in this section that the main strengths of the proposed procedure are as follows:

• Simplicity: The proposed procedure can be used without modifications for all sample sizes, time horizons, numbers of conducted reviews, feature dimensions, etc. In contrast, many alternative approaches, including the ones presented here, require the user to tune various hyper-parameters. For example, as can be seen from Tables 1 and 2, the optimal learning rates vary widely between different scenarios and can be far from common defaults, such as $0.01$ (TensorFlow Contributors, 2025) or $0.001$ (PyTorch Contributors, 2025).

• Robustness: While not always being the best choice, the proposed procedure performed well in all of our experiments, even under moderate model mismatch. In combination with its simplicity, we believe that this makes it an excellent choice in practice.

• Fully Bayesian model: At any point in time, the user has access to the approximate posterior distributions of the quantities of interest and can perform additional inference as desired. While not always necessary, this allows for a much more systematic analysis of both the flagging decisions and the test taker population. Moreover, in particular when using the mixed policy, the procedure self-calibrates so that predicted probabilities can validly be interpreted as such.

As potential weaknesses, we identified the following issues:

• Model mismatch: While our experiments showed that the procedure can handle moderate model mismatch, it will break down under severe model mismatch. This means that the user should not apply the procedure blindly, but have some familiarity with the data of interest. For example, a simple sanity check is to verify that the assumed exponential family distributions roughly fit the true marginal distributions of the features.

• Compute: In our experiments, the proposed procedure typically took more time to run than the alternatives. This is partly due to its higher complexity and partly because our implementation is not as optimized as those provided by mature machine learning libraries. However, the time required to process a single administration averaged around 2s for $M = 10$ and 0.5s for $M = 3$ , making it real-time capable for most practical purposes.

• Numerical stability: The proposed procedure requires solving the equation system in (37)–(41). In our experiments, a simple fixed-point iteration converged most of the time. When it did not (fewer than 10 occasions across all experiments), the output of the last iteration was used. The effect of these inaccuracies appears negligible, but, in principle, one should be aware of potential numerical issues.