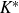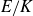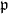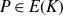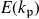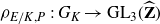1. Introduction
Under the Generalised Riemann Hypothesis (GRH), every non-zero rational number that is not
![]() $-1$
or a square is a primitive root modulo infinitely many primes p. This was proved in 1967 by Hooley [
Reference Hooley6
], forty years after Artin had stated it as a conjecture. For general number fields K, there are counterexamples to the direct analogue of this statement, i.e., number fields K with non-torsion elements
$-1$
or a square is a primitive root modulo infinitely many primes p. This was proved in 1967 by Hooley [
Reference Hooley6
], forty years after Artin had stated it as a conjecture. For general number fields K, there are counterexamples to the direct analogue of this statement, i.e., number fields K with non-torsion elements
![]() $x\in K^*$
that are not
$x\in K^*$
that are not
![]() $\ell$
th powers for any prime
$\ell$
th powers for any prime
![]() $\ell$
for which K contains a primitive
$\ell$
for which K contains a primitive
![]() $\ell$
th root of unity, but that are nevertheless a primitive root in only finitely many residue class fields
$\ell$
th root of unity, but that are nevertheless a primitive root in only finitely many residue class fields
![]() $k_{\mathfrak{p}}$
. The direct analogue of Artin’s conjecture does however hold for
$k_{\mathfrak{p}}$
. The direct analogue of Artin’s conjecture does however hold for
![]() $x\in K^*$
that are globally primitive, i.e., not in
$x\in K^*$
that are globally primitive, i.e., not in
![]() ${K^*}^\ell$
for any prime
${K^*}^\ell$
for any prime
![]() $\ell$
.
$\ell$
.
Theorem 1.1. Let K be a number field and
![]() $x\in K^*$
globally primitive, and assume GRH. Then x is a primitive root modulo
$x\in K^*$
globally primitive, and assume GRH. Then x is a primitive root modulo
![]() ${\mathfrak{p}}$
for a set primes
${\mathfrak{p}}$
for a set primes
![]() ${\mathfrak{p}}$
of K of positive density.
${\mathfrak{p}}$
of K of positive density.
Informally stated: globally primitive elements in
![]() $K^*$
are locally primitive in
$K^*$
are locally primitive in
![]() $k_{\mathfrak{p}}^*$
at infinitely many places
$k_{\mathfrak{p}}^*$
at infinitely many places
![]() ${\mathfrak{p}}$
, with an element being ‘locally primitive’ in
${\mathfrak{p}}$
, with an element being ‘locally primitive’ in
![]() $k_{\mathfrak{p}}^*$
meaning that it generates a subgroup that is not contained in a strictly larger cyclic subgroup of
$k_{\mathfrak{p}}^*$
meaning that it generates a subgroup that is not contained in a strictly larger cyclic subgroup of
![]() $k_{\mathfrak{p}}^*$
. Section 3 provides a proof of Theorem 1.1, and counterexamples to stronger statements.
$k_{\mathfrak{p}}^*$
. Section 3 provides a proof of Theorem 1.1, and counterexamples to stronger statements.
Now replace the multiplicative group
![]() $K^*$
by the point group E(K) of an elliptic curve
$K^*$
by the point group E(K) of an elliptic curve
![]() $E/K$
, and the unit group
$E/K$
, and the unit group
![]() $k_{\mathfrak{p}}^*$
of the residue class field at
$k_{\mathfrak{p}}^*$
of the residue class field at
![]() ${\mathfrak{p}}$
by the point group
${\mathfrak{p}}$
by the point group
![]() $E(k_{\mathfrak{p}})$
at the primes of good reduction
$E(k_{\mathfrak{p}})$
at the primes of good reduction
![]() ${\mathfrak{p}}$
of E. Then we can add two natural questions to Artin’s to obtain the following three problems: for a number field K, determine the infinitude (or natural density) of the set of primes
${\mathfrak{p}}$
of E. Then we can add two natural questions to Artin’s to obtain the following three problems: for a number field K, determine the infinitude (or natural density) of the set of primes
![]() ${\mathfrak{p}}$
in K for which:
${\mathfrak{p}}$
in K for which:
-
I. (Artin) a given element
 $x\in K^*$
is a primitive root modulo
$x\in K^*$
is a primitive root modulo
 ${\mathfrak{p}}$
, i.e.,
${\mathfrak{p}}$
, i.e.,
 $k_{\mathfrak{p}}^*=\langle\bar x\rangle$
;
$k_{\mathfrak{p}}^*=\langle\bar x\rangle$
; -
II. (Serre [ Reference Serre16 ]) a given elliptic curve
 $E/K$
has cyclic reduction modulo
$E/K$
has cyclic reduction modulo
 ${\mathfrak{p}}$
;
${\mathfrak{p}}$
; -
III. (Lang–Trotter [ Reference Lang and Trotter9 ]) a given point
 $P\in E(K)$
generates the group
$P\in E(K)$
generates the group
 $E(k_{\mathfrak{p}})$
at
$E(k_{\mathfrak{p}})$
at
 ${\mathfrak{p}}$
.
${\mathfrak{p}}$
.
We will refer to the cases I, II and III as the multiplicative primitive root, the cyclic reduction and the elliptic primitive root case, and denote the corresponding sets of primes by
![]() $S_{K, x}$
,
$S_{K, x}$
,
![]() $S_{E/K}$
and
$S_{E/K}$
and
![]() $S_{E/K, P}$
, respectively. By definition, the finitely many primes of bad reduction for which we have
$S_{E/K, P}$
, respectively. By definition, the finitely many primes of bad reduction for which we have
![]() $\mathrm{ord}_{\mathfrak{p}}(x)\ne 0$
(in case I) or
$\mathrm{ord}_{\mathfrak{p}}(x)\ne 0$
(in case I) or
![]() $\mathrm{ord}_{\mathfrak{p}}(\Delta_E)\ne0$
(in case II and III, with
$\mathrm{ord}_{\mathfrak{p}}(\Delta_E)\ne0$
(in case II and III, with
![]() $\Delta_E$
the discriminant of E) are excluded from these sets. Note that we have an obvious inclusion
$\Delta_E$
the discriminant of E) are excluded from these sets. Note that we have an obvious inclusion
![]() $S_{E/K, P}\subset S_{E/K}$
.
$S_{E/K, P}\subset S_{E/K}$
.
In each of the three cases, we have a group theoretical statements that can be checked prime-wise at the primes
![]() $\ell$
dividing the order of the groups
$\ell$
dividing the order of the groups
![]() $k_{\mathfrak{p}}^*$
and
$k_{\mathfrak{p}}^*$
and
![]() $E(k_{\mathfrak{p}})$
involved. The statement ‘at
$E(k_{\mathfrak{p}})$
involved. The statement ‘at
![]() $\ell$
’ has a translation in terms of the splitting behaviour of
$\ell$
’ has a translation in terms of the splitting behaviour of
![]() ${\mathfrak{p}}$
in a finite Galois extension
${\mathfrak{p}}$
in a finite Galois extension
![]() $K\subset K_\ell$
that we describe in Section 2. Combining the requirements for all
$K\subset K_\ell$
that we describe in Section 2. Combining the requirements for all
![]() $\ell$
leads to (conjectural) density statements based on the Chebotarev density theorem [
Reference Stevenhagen and Lenstra17
].
$\ell$
leads to (conjectural) density statements based on the Chebotarev density theorem [
Reference Stevenhagen and Lenstra17
].
Imposing infinitely many splitting conditions, one for each prime
![]() $\ell$
, leads to analytic problems with error terms that have been mastered under assumption of GRH in cases I [
Reference Cooke and Weinberger1
,
Reference Hooley6
,
Reference Lenstra10
] and II [
Reference Campagna and Stevenhagen2
,
Reference Gupta and Ram Murty4
,
Reference Serre16
], and that remain largely open [
Reference Chen and Yu3
,
Reference Gupta and Ram Murty5
,
Reference Lang and Trotter9
] in case III. In each case, there is a conjectural density
$\ell$
, leads to analytic problems with error terms that have been mastered under assumption of GRH in cases I [
Reference Cooke and Weinberger1
,
Reference Hooley6
,
Reference Lenstra10
] and II [
Reference Campagna and Stevenhagen2
,
Reference Gupta and Ram Murty4
,
Reference Serre16
], and that remain largely open [
Reference Chen and Yu3
,
Reference Gupta and Ram Murty5
,
Reference Lang and Trotter9
] in case III. In each case, there is a conjectural density
![]() $\delta_{K, x}$
,
$\delta_{K, x}$
,
![]() $\delta_{E/K}$
, or
$\delta_{E/K}$
, or
![]() $\delta_{E/K, P}$
that is an upper bound for the upper density of the set of primes
$\delta_{E/K, P}$
that is an upper bound for the upper density of the set of primes
![]() ${\mathfrak{p}}$
. Proving unconditionally that the set is infinite when the conjectural density is positive is an open problem in cases I and III. If the density is zero, we can however prove unconditionally that the corresponding set of primes is finite.
${\mathfrak{p}}$
. Proving unconditionally that the set is infinite when the conjectural density is positive is an open problem in cases I and III. If the density is zero, we can however prove unconditionally that the corresponding set of primes is finite.
This paper focuses on the vanishing of
![]() $\delta_{E/K, P}$
in the elliptic primitive root case, which is much more subtle than the vanishing in the cases I and II. We call a global point
$\delta_{E/K, P}$
in the elliptic primitive root case, which is much more subtle than the vanishing in the cases I and II. We call a global point
![]() $P\in E(K)$
locally imprimitive if it is a generator of the local point group
$P\in E(K)$
locally imprimitive if it is a generator of the local point group
![]() $E(k_{\mathfrak{p}})$
for only finitely many primes
$E(k_{\mathfrak{p}})$
for only finitely many primes
![]() ${\mathfrak{p}}$
of K. Our analysis will yield ‘elliptic counterexamples’
${\mathfrak{p}}$
of K. Our analysis will yield ‘elliptic counterexamples’
![]() $(E/K, P)$
to Theorem 1.1, i.e., elliptic curves
$(E/K, P)$
to Theorem 1.1, i.e., elliptic curves
![]() $E/K$
for which the cyclic reduction density
$E/K$
for which the cyclic reduction density
![]() $\delta_{E/K}$
is positive but for which a globally primitive point
$\delta_{E/K}$
is positive but for which a globally primitive point
![]() $P\in E(K)$
is locally imprimitive.
$P\in E(K)$
is locally imprimitive.
Just as in the multiplicative primitive root and the cyclic reduction cases I and II, obstructions to local primitivity of a point
![]() $P\in E(K)$
become visible in an associated Galois representation. In the elliptic primitive root case, the absolute Galois group
$P\in E(K)$
become visible in an associated Galois representation. In the elliptic primitive root case, the absolute Galois group
![]() $G_K=\mathrm{Gal}(\overline K/K)$
of the number field K acts on the subgroup of
$G_K=\mathrm{Gal}(\overline K/K)$
of the number field K acts on the subgroup of
![]() $E(\overline K)$
consisting of the points
$E(\overline K)$
consisting of the points
![]() $Q\in E(\overline K)$
satisfying
$Q\in E(\overline K)$
satisfying
![]() $kQ\in\langle P\rangle\subset E(K)$
for some
$kQ\in\langle P\rangle\subset E(K)$
for some
![]() $k\in{\mathbf{Z}}_{\ge1}$
. As explained in the next Section (equation (2·8)), this yields a representation
$k\in{\mathbf{Z}}_{\ge1}$
. As explained in the next Section (equation (2·8)), this yields a representation
![]() $\rho_{E/K, P}\,:\, G_K\to\mathrm{GL}_3({\widehat {{\mathbf{Z}}}}).$
Just as in the two other cases [
Reference Campagna and Stevenhagen2
], it suffices to consider the residual representation
$\rho_{E/K, P}\,:\, G_K\to\mathrm{GL}_3({\widehat {{\mathbf{Z}}}}).$
Just as in the two other cases [
Reference Campagna and Stevenhagen2
], it suffices to consider the residual representation
modulo a suitable squarefree integer N that is divisible by all ‘critical primes’.
Unlike the cases I and II, case III already allows non-trivial obstructions to local primitivity at prime level
![]() $N=\ell$
. In the multiplicative case I, the index
$N=\ell$
. In the multiplicative case I, the index
![]() $[k_{\mathfrak{p}}^*\,:\,\langle\overline x\rangle]$
can only be divisible by
$[k_{\mathfrak{p}}^*\,:\,\langle\overline x\rangle]$
can only be divisible by
![]() $\ell$
for almost all
$\ell$
for almost all
![]() ${\mathfrak{p}}$
for the ‘trivial reason’ that K contains an
${\mathfrak{p}}$
for the ‘trivial reason’ that K contains an
![]() $\ell$
th root of unity and x is an
$\ell$
th root of unity and x is an
![]() $\ell$
th power in
$\ell$
th power in
![]() $K^*$
. In the cyclic reduction case II, the group
$K^*$
. In the cyclic reduction case II, the group
![]() $E(k_{\mathfrak{p}})$
can only have a non-cyclic
$E(k_{\mathfrak{p}})$
can only have a non-cyclic
![]() $\ell$
-part for almost all
$\ell$
-part for almost all
![]() ${\mathfrak{p}}$
for the ‘trivial reason’ that the full
${\mathfrak{p}}$
for the ‘trivial reason’ that the full
![]() $\ell$
-torsion of
$\ell$
-torsion of
![]() $E/K$
is K-rational. In the elliptic primitive root case III however, there is a third reason why a point
$E/K$
is K-rational. In the elliptic primitive root case III however, there is a third reason why a point
![]() $P\in E(K)$
can be locally
$P\in E(K)$
can be locally
![]() $\ell$
-imprimitive, meaning that
$\ell$
-imprimitive, meaning that
![]() $\ell$
divides the index
$\ell$
divides the index
![]() $[E(k_{\mathfrak{p}})\,:\,\langle \bar P\rangle]$
for all but finitely many
$[E(k_{\mathfrak{p}})\,:\,\langle \bar P\rangle]$
for all but finitely many
![]() ${\mathfrak{p}}$
. It is a less obvious one, and it was numerically discovered in 2015 in the case
${\mathfrak{p}}$
. It is a less obvious one, and it was numerically discovered in 2015 in the case
![]() $\ell=2$
by Meleleo [
Reference Meleleo12
], who restricted himself to the basic case
$\ell=2$
by Meleleo [
Reference Meleleo12
], who restricted himself to the basic case
![]() $K={\mathbf{Q}}$
.
$K={\mathbf{Q}}$
.
Theorem 1.2. Let
![]() $P\in E(K)$
be a non-torsion point of an elliptic curve E defined over a number field K, and
$P\in E(K)$
be a non-torsion point of an elliptic curve E defined over a number field K, and
![]() $\ell$
a prime number. Then P is locally
$\ell$
a prime number. Then P is locally
![]() $\ell$
-imprimitive if and only if at least one of the following conditions hold:
$\ell$
-imprimitive if and only if at least one of the following conditions hold:
-
A. E(K) contains a torsion point of order
 $\ell$
and
$\ell$
and
 $P\in \ell\cdot E(K)$
;
$P\in \ell\cdot E(K)$
; -
B. E has complete rational
 $\ell$
-torsion over K;
$\ell$
-torsion over K; -
C. there exists an isogeny
 $\phi\,:\, E'\to E$
defined over K with kernel generated by a torsion point of
$\phi\,:\, E'\to E$
defined over K with kernel generated by a torsion point of
 $E^{\prime}$
(K) of order
$E^{\prime}$
(K) of order
 $\ell$
and
$\ell$
and
 $P\in\phi[E'(K)]$
.
$P\in\phi[E'(K)]$
.
Condition A in Theorem 1.2 is the analogue of the trivial condition from case I: if E(K) has non-trivial
![]() $\ell$
-torsion, then almost all
$\ell$
-torsion, then almost all
![]() $E(k_{\mathfrak{p}})$
are groups of order divisible by
$E(k_{\mathfrak{p}})$
are groups of order divisible by
![]() $\ell$
, and for these
$\ell$
, and for these
![]() ${\mathfrak{p}}$
a point
${\mathfrak{p}}$
a point
![]() $P\in \ell\cdot E(K)$
will have its reduction in the subgroup
$P\in \ell\cdot E(K)$
will have its reduction in the subgroup
![]() $\ell E(k_{\mathfrak{p}}) \subset E(k_{\mathfrak{p}})$
of index divisible by
$\ell E(k_{\mathfrak{p}}) \subset E(k_{\mathfrak{p}})$
of index divisible by
![]() $\ell$
. Condition B bears no relation to P, and is well known from case II: non-cyclicity of the
$\ell$
. Condition B bears no relation to P, and is well known from case II: non-cyclicity of the
![]() $\ell$
-part of the global torsion subgroup
$\ell$
-part of the global torsion subgroup
![]() $E(K)^\text{tor}$
implies non-cyclicity of the
$E(K)^\text{tor}$
implies non-cyclicity of the
![]() $\ell$
-part of
$\ell$
-part of
![]() $E(k_{\mathfrak{p}})$
at almost all
$E(k_{\mathfrak{p}})$
at almost all
![]() ${\mathfrak{p}}$
. At these
${\mathfrak{p}}$
. At these
![]() ${\mathfrak{p}}$
, no single point can generate it.
${\mathfrak{p}}$
, no single point can generate it.
In the multiplicative primitive root case, condition C is just the same as condition A, but in the elliptic primitive root case, it is a truly different condition as it includes cases in which we have both
![]() $P\notin \ell\cdot E(K)$
and
$P\notin \ell\cdot E(K)$
and
![]() $E[\ell](K)=0$
. If it holds, the dual isogeny
$E[\ell](K)=0$
. If it holds, the dual isogeny
![]() $\widehat\phi\,:\, E\to E'$
maps P into
$\widehat\phi\,:\, E\to E'$
maps P into
![]() $\ell E'(K)$
, and the pair (E,P) is
$\ell E'(K)$
, and the pair (E,P) is
![]() $\ell$
-isogenous to the curve-point pair
$\ell$
-isogenous to the curve-point pair
![]() $(E',\widehat\phi(P))$
satisfying condition A.
$(E',\widehat\phi(P))$
satisfying condition A.
We call a locally
![]() $\ell$
-imprimitive non-torsion point
$\ell$
-imprimitive non-torsion point
![]() $P\in E(K)$
non-trivial if condition C is satisfied, but not condition A or B. By Theorem 1.2, non-trivial locally 2-imprimitive points
$P\in E(K)$
non-trivial if condition C is satisfied, but not condition A or B. By Theorem 1.2, non-trivial locally 2-imprimitive points
![]() $P\in E(K)$
can only exist for
$P\in E(K)$
can only exist for
![]() $E/K$
having a single K-rational point of order 2, i.e., a 2-torsion subgroup of order
$E/K$
having a single K-rational point of order 2, i.e., a 2-torsion subgroup of order
![]() $\#E(K)[2]\ne 1, 4$
. Examples of such points are actually surprisingly abundant.
$\#E(K)[2]\ne 1, 4$
. Examples of such points are actually surprisingly abundant.
Theorem 1.3. Let
![]() $E/K$
be any elliptic curve with
$E/K$
be any elliptic curve with
![]() $\#E(K)[2]=2$
. Then there are infinitely many quadratic twists of E over K that have a non-trivial locally 2-imprimitive point.
$\#E(K)[2]=2$
. Then there are infinitely many quadratic twists of E over K that have a non-trivial locally 2-imprimitive point.
The proof of this Theorem, which we give in Section 5, uses the fact that it is easy to create non-torsion points on twists of E, and exploits the particularly explicit description of K-rational 2-isogenies.
For primes
![]() $\ell>2$
, it is harder to obtain families of elliptic curves with points of infinite order that are locally
$\ell>2$
, it is harder to obtain families of elliptic curves with points of infinite order that are locally
![]() $\ell$
-imprimitive in non-trivial ways. In Section 6 we provide an approach in the case
$\ell$
-imprimitive in non-trivial ways. In Section 6 we provide an approach in the case
![]() $\ell=3$
. It can be extended to higher values of
$\ell=3$
. It can be extended to higher values of
![]() $\ell$
(Section 7), but the examples rapidly become unwieldy.
$\ell$
(Section 7), but the examples rapidly become unwieldy.
Non-torsion points that are locally imprimitive but not locally
![]() $\ell$
-imprimitive for any single prime
$\ell$
-imprimitive for any single prime
![]() $\ell$
do exist, but they are not easily found. They involve restrictions arising from reductions of
$\ell$
do exist, but they are not easily found. They involve restrictions arising from reductions of
![]() $\rho_{E/K,P}$
of composite level caused by non-trivial entanglement between the fields
$\rho_{E/K,P}$
of composite level caused by non-trivial entanglement between the fields
![]() $K_\ell$
. In the context of the easier cyclic reduction case II, this is discussed in [
Reference Campagna and Stevenhagen2
], and we present a first type of examples for our Lang-Trotter case III in our final Section 8.
$K_\ell$
. In the context of the easier cyclic reduction case II, this is discussed in [
Reference Campagna and Stevenhagen2
], and we present a first type of examples for our Lang-Trotter case III in our final Section 8.
2. Characterisation by splitting conditions
In each of the three cases discussed in the introduction, we can characterise the corresponding sets of primes
![]() $S_{K, x}$
,
$S_{K, x}$
,
![]() $S_{E/K}$
, and
$S_{E/K}$
, and
![]() $S_{E/K, P}$
of K in terms of the splitting behaviour of their elements
$S_{E/K, P}$
of K in terms of the splitting behaviour of their elements
![]() ${\mathfrak{p}}$
in suitable extensions
${\mathfrak{p}}$
in suitable extensions
![]() $K\subset K_\ell$
, with
$K\subset K_\ell$
, with
![]() $\ell$
ranging over all prime numbers.
$\ell$
ranging over all prime numbers.
I. Multiplicative primitive root case. Let K be a number field and
![]() $x\in K^*$
non-torsion. Define
$x\in K^*$
non-torsion. Define
![]() $K_m={\mathbf{Q}}(\zeta_m,\root m \of x)$
for
$K_m={\mathbf{Q}}(\zeta_m,\root m \of x)$
for
![]() $m\in{\mathbf{Z}}_{\ge1}$
as the ‘m-division field of x’, i.e., the splitting field over K of the polynomial
$m\in{\mathbf{Z}}_{\ge1}$
as the ‘m-division field of x’, i.e., the splitting field over K of the polynomial
![]() $X^m-x\in K[X]$
. If
$X^m-x\in K[X]$
. If
![]() ${\mathfrak{p}}$
is a prime of K of characteristic p for which x is a
${\mathfrak{p}}$
is a prime of K of characteristic p for which x is a
![]() ${\mathfrak{p}}$
-adic unit, the index
${\mathfrak{p}}$
-adic unit, the index
![]() $[k_{\mathfrak{p}}^*\,:\,\langle \overline x\rangle]$
is divisible by a prime
$[k_{\mathfrak{p}}^*\,:\,\langle \overline x\rangle]$
is divisible by a prime
![]() $\ell\ne p$
if and only if
$\ell\ne p$
if and only if
![]() ${\mathfrak{p}}$
splits completely in
${\mathfrak{p}}$
splits completely in
![]() $K\subset K_\ell$
.
$K\subset K_\ell$
.
Note that
![]() $[k_{\mathfrak{p}}^*\,:\,\langle \overline x\rangle]$
is never divisible by
$[k_{\mathfrak{p}}^*\,:\,\langle \overline x\rangle]$
is never divisible by
![]() $p=\mathrm{char} ({\mathfrak{p}})$
, even though
$p=\mathrm{char} ({\mathfrak{p}})$
, even though
![]() ${\mathfrak{p}}$
may split completely in
${\mathfrak{p}}$
may split completely in
![]() $K_p$
. Example:
$K_p$
. Example:
![]() $x=17$
is a primitive root modulo the prime
$x=17$
is a primitive root modulo the prime
![]() ${\mathfrak{p}}_3$
of norm 3 in
${\mathfrak{p}}_3$
of norm 3 in
![]() $K={\mathbf{Q}}(\sqrt{-21})$
, but
$K={\mathbf{Q}}(\sqrt{-21})$
, but
![]() ${\mathfrak{p}}_3$
splits completely in the sextic extension
${\mathfrak{p}}_3$
splits completely in the sextic extension
This can however only happen for primes
![]() ${\mathfrak{p}}|2\Delta_K$
, with
${\mathfrak{p}}|2\Delta_K$
, with
![]() $\Delta_K$
the discriminant of K, since
$\Delta_K$
the discriminant of K, since
![]() $K\subset K_p$
is ramified at all
$K\subset K_p$
is ramified at all
![]() ${\mathfrak{p}}|p$
for p coprime to
${\mathfrak{p}}|p$
for p coprime to
![]() $2\Delta_K$
. In other words: for almost all
$2\Delta_K$
. In other words: for almost all
![]() ${\mathfrak{p}}$
, the ‘condition at
${\mathfrak{p}}$
, the ‘condition at
![]() $\ell$
’ in the following Lemma is automatically satisfied at
$\ell$
’ in the following Lemma is automatically satisfied at
![]() $\ell=\mathrm{char}\ {{\mathfrak{p}}}$
.
$\ell=\mathrm{char}\ {{\mathfrak{p}}}$
.
Lemma 2.1. For
![]() ${\mathfrak{p}}$
a prime of K outside the support of x, we have
${\mathfrak{p}}$
a prime of K outside the support of x, we have
![]() $k_{\mathfrak{p}}^*=\langle \overline x\rangle $
if and only if
$k_{\mathfrak{p}}^*=\langle \overline x\rangle $
if and only if
![]() ${\mathfrak{p}}$
does not split completely in
${\mathfrak{p}}$
does not split completely in
![]() $K\subset K_\ell$
for any prime
$K\subset K_\ell$
for any prime
![]() $\ell\ne\mathrm{char}\ {{\mathfrak{p}}}$
.
$\ell\ne\mathrm{char}\ {{\mathfrak{p}}}$
.
By Lemma 2.1, the set
![]() $S_{K, x}$
of primes in K for which x is a primitive root is up to finitely many primes equal to the set of primes that do not split completely in
$S_{K, x}$
of primes in K for which x is a primitive root is up to finitely many primes equal to the set of primes that do not split completely in
![]() $K\subset K_\ell$
for any prime
$K\subset K_\ell$
for any prime
![]() $\ell$
. For
$\ell$
. For
![]() $m\in{\mathbf{Z}}_{\ge1}$
, the set of primes
$m\in{\mathbf{Z}}_{\ge1}$
, the set of primes
![]() ${\mathfrak{p}}$
of K that split completely in
${\mathfrak{p}}$
of K that split completely in
![]() $K\subset K_m$
has natural density
$K\subset K_m$
has natural density
![]() $1/[K_m\,:\,K]$
. Under GRH, it follows from [
Reference Lenstra10
] that the set
$1/[K_m\,:\,K]$
. Under GRH, it follows from [
Reference Lenstra10
] that the set
![]() $S_{K, x}$
has a natural density that is given by the inclusion-exclusion sum
$S_{K, x}$
has a natural density that is given by the inclusion-exclusion sum
 \begin{equation}\delta_{K,x}=\sum_{m=1}^{\infty} \frac{\mu(m)}{[K_m\,:\,K]}\end{equation}
\begin{equation}\delta_{K,x}=\sum_{m=1}^{\infty} \frac{\mu(m)}{[K_m\,:\,K]}\end{equation}
that converges slowly, but that can be rewritten in ‘factored form’ as
 \begin{equation}\delta_{K,x}=\sum_{m|N} \frac{\mu(m)}{[K_m\,:\,K]}\cdot \prod_{\ell\nmid N \text{ prime}} \left(1-\frac{1}{\ell(\ell-1)}\right).\end{equation}
\begin{equation}\delta_{K,x}=\sum_{m|N} \frac{\mu(m)}{[K_m\,:\,K]}\cdot \prod_{\ell\nmid N \text{ prime}} \left(1-\frac{1}{\ell(\ell-1)}\right).\end{equation}
Here we can take for N any integer divisible by the primes in some finite set of critical primes. One may take for this set the set of primes that are either in the support of x or divide
![]() $2\Delta_K$
, together with those primes
$2\Delta_K$
, together with those primes
![]() $\ell$
for which x is in
$\ell$
for which x is in
![]() ${K^*}^\ell$
. The essential feature of N is that the family
${K^*}^\ell$
. The essential feature of N is that the family
![]() $\{K_\ell\}_{\ell\nmid N}$
of ‘
$\{K_\ell\}_{\ell\nmid N}$
of ‘
![]() $\ell$
-division fields of x outside N’ is a linearly disjoint family over K with each
$\ell$
-division fields of x outside N’ is a linearly disjoint family over K with each
![]() $K_\ell$
having the full Galois group
$K_\ell$
having the full Galois group
![]() $\mathrm{Gal}(K_\ell/K)\cong \mathrm{Aff}_1({\mathbf{F}}_\ell)={\mathbf{F}}_\ell\rtimes {\mathbf{F}}_\ell^*$
of order
$\mathrm{Gal}(K_\ell/K)\cong \mathrm{Aff}_1({\mathbf{F}}_\ell)={\mathbf{F}}_\ell\rtimes {\mathbf{F}}_\ell^*$
of order
![]() $\ell(\ell-1)$
, and that the compositum L of the fields in this family satisfies
$\ell(\ell-1)$
, and that the compositum L of the fields in this family satisfies
![]() $L\cap K_N=K$
.
$L\cap K_N=K$
.
II. Cyclic reduction case. For an elliptic curve
![]() $E/K$
, we consider the set
$E/K$
, we consider the set
![]() $S_{E/K}$
of primes of cyclic reduction of E, i.e., the primes
$S_{E/K}$
of primes of cyclic reduction of E, i.e., the primes
![]() ${\mathfrak{p}}$
of K for which E has good reduction and the reduced elliptic curve point group
${\mathfrak{p}}$
of K for which E has good reduction and the reduced elliptic curve point group
![]() $E(k_{\mathfrak{p}})$
is cyclic. The condition that E have good reduction modulo
$E(k_{\mathfrak{p}})$
is cyclic. The condition that E have good reduction modulo
![]() ${\mathfrak{p}}$
only excludes the finitely many primes dividing the discriminant
${\mathfrak{p}}$
only excludes the finitely many primes dividing the discriminant
![]() $\Delta_E$
of E.
$\Delta_E$
of E.
For
![]() $m\in{\mathbf{Z}}_{\ge1}$
, we define
$m\in{\mathbf{Z}}_{\ge1}$
, we define
![]() $K_m=K(E[m](\overline {\mathbf{Q}}))$
in this case to be the m-division field of E over K. The following elementary lemma [
Reference Campagna and Stevenhagen2
, corollary 2.2] is the analogue of Lemma 2.1 It expresses the fact that a finite abelian group is cyclic if and only if its
$K_m=K(E[m](\overline {\mathbf{Q}}))$
in this case to be the m-division field of E over K. The following elementary lemma [
Reference Campagna and Stevenhagen2
, corollary 2.2] is the analogue of Lemma 2.1 It expresses the fact that a finite abelian group is cyclic if and only if its
![]() $\ell$
-primary part is cyclic for all primes
$\ell$
-primary part is cyclic for all primes
![]() $\ell$
.
$\ell$
.
Lemma 2.2. A prime
![]() ${\mathfrak{p}}$
of good reduction of
${\mathfrak{p}}$
of good reduction of
![]() $E/K$
is a prime of cyclic reduction if and only if
$E/K$
is a prime of cyclic reduction if and only if
![]() ${\mathfrak{p}}$
does not split completely in
${\mathfrak{p}}$
does not split completely in
![]() $K\subset K_\ell$
for any prime
$K\subset K_\ell$
for any prime
![]() $\ell\ne\mathrm{char}\ {{\mathfrak{p}}}$
.
$\ell\ne\mathrm{char}\ {{\mathfrak{p}}}$
.
As in the multiplicative case I, cyclicity of the p-primary part of the groups
![]() $E(k_{\mathfrak{p}})$
is automatic for
$E(k_{\mathfrak{p}})$
is automatic for
![]() $p=\mathrm{char} ({\mathfrak{p}})$
. Also here, total splitting of
$p=\mathrm{char} ({\mathfrak{p}})$
. Also here, total splitting of
![]() ${\mathfrak{p}}$
in non-trivial extensions
${\mathfrak{p}}$
in non-trivial extensions
![]() $K\subset K_p$
for
$K\subset K_p$
for
![]() $p=\mathrm{char}\ {{\mathfrak{p}}}$
does occur: it suffices to base change any elliptic curve
$p=\mathrm{char}\ {{\mathfrak{p}}}$
does occur: it suffices to base change any elliptic curve
![]() $E/K$
with
$E/K$
with
![]() $K\subset K_p=K[X]/(f)$
non-trivial by an extension
$K\subset K_p=K[X]/(f)$
non-trivial by an extension
![]() $K\subset L= K[X]/(g)$
with f and g polynomials of the same degree that are
$K\subset L= K[X]/(g)$
with f and g polynomials of the same degree that are
![]() ${\mathfrak{p}}$
-adically close, but with g Eisenstein at a prime
${\mathfrak{p}}$
-adically close, but with g Eisenstein at a prime
![]() ${\mathfrak{q}}$
that is unramified in
${\mathfrak{q}}$
that is unramified in
![]() $K\subset K_p$
. For
$K\subset K_p$
. For
![]() $E/L$
, the non-trivial extension
$E/L$
, the non-trivial extension
![]() $L\subset L_p$
will be totally split at all primes dividing
$L\subset L_p$
will be totally split at all primes dividing
![]() ${\mathfrak{p}}$
. Again, this can happen only at primes
${\mathfrak{p}}$
. Again, this can happen only at primes
![]() ${\mathfrak{p}}|2\Delta_K$
, as otherwise
${\mathfrak{p}}|2\Delta_K$
, as otherwise
![]() $K\subset K_p$
will be ramified at all primes
$K\subset K_p$
will be ramified at all primes
![]() ${\mathfrak{p}}$
of characteristic p by the fact that
${\mathfrak{p}}$
of characteristic p by the fact that
![]() $K_p$
contains
$K_p$
contains
![]() $\zeta_p$
. Thus, for almost all
$\zeta_p$
. Thus, for almost all
![]() ${\mathfrak{p}}$
, the ‘condition at
${\mathfrak{p}}$
, the ‘condition at
![]() $\ell$
’ in Lemma 2.2 is again automatically satisfied at
$\ell$
’ in Lemma 2.2 is again automatically satisfied at
![]() $\ell=\mathrm{char}\ {{\mathfrak{p}}}$
. The finitely many primes dividing
$\ell=\mathrm{char}\ {{\mathfrak{p}}}$
. The finitely many primes dividing
![]() $2\Delta_K$
are clearly irrelevant when dealing with the density of the set
$2\Delta_K$
are clearly irrelevant when dealing with the density of the set
![]() $S_{E/K}$
, which, just like in the previous case, coincides up to finitely many primes with the set of primes
$S_{E/K}$
, which, just like in the previous case, coincides up to finitely many primes with the set of primes
![]() ${\mathfrak{p}}$
of K that do not split completely in
${\mathfrak{p}}$
of K that do not split completely in
![]() $K\subset K_\ell$
for any prime
$K\subset K_\ell$
for any prime
![]() $\ell$
.
$\ell$
.
Under GRH, the density of
![]() $S_{E/K}$
is again given [
Reference Campagna and Stevenhagen2
, Section 2] by an inclusion-exclusion sum that we already know from (2·1):
$S_{E/K}$
is again given [
Reference Campagna and Stevenhagen2
, Section 2] by an inclusion-exclusion sum that we already know from (2·1):
 \begin{equation}\delta_{E/K}=\sum_{m=1}^{\infty} \frac{\mu(m)}{[K_m\; :\; K]}.\end{equation}
\begin{equation}\delta_{E/K}=\sum_{m=1}^{\infty} \frac{\mu(m)}{[K_m\; :\; K]}.\end{equation}
If E is without CM over
![]() $\overline{\mathbf{Q}}$
, or has CM by an order
$\overline{\mathbf{Q}}$
, or has CM by an order
![]() $\mathcal{O}\subset K$
, there is in each case a factorisation of
$\mathcal{O}\subset K$
, there is in each case a factorisation of
![]() $\delta_{E/K}$
that is typographically identical to (2·1), provided that N is divisible by all primes from an appropriately defined finite set of critical primes [
Reference Campagna and Stevenhagen2
, theorems 1.1 and 1.2]. If E has CM by an order
$\delta_{E/K}$
that is typographically identical to (2·1), provided that N is divisible by all primes from an appropriately defined finite set of critical primes [
Reference Campagna and Stevenhagen2
, theorems 1.1 and 1.2]. If E has CM by an order
![]() $\mathcal{O}\not\subset K$
, there is a hybrid formula [
Reference Campagna and Stevenhagen2
, theorem 1.4] with different contributions from ordinary and supersingular primes.
$\mathcal{O}\not\subset K$
, there is a hybrid formula [
Reference Campagna and Stevenhagen2
, theorem 1.4] with different contributions from ordinary and supersingular primes.
A ‘factorisation formula’ for
![]() $\delta_{K, x}$
and
$\delta_{K, x}$
and
![]() $\delta_{E/K}$
as in (2·2) shows that the vanishing of these densities is always caused by an obstruction at some finite level N. For such N, no element in
$\delta_{E/K}$
as in (2·2) shows that the vanishing of these densities is always caused by an obstruction at some finite level N. For such N, no element in
![]() $\mathrm{Gal}(K_N/K)$
restricts for all
$\mathrm{Gal}(K_N/K)$
restricts for all
![]() $\ell|N$
to a non-trivial element of
$\ell|N$
to a non-trivial element of
![]() $\mathrm{Gal}(K_\ell/K)$
. As a consequence, there are no non-critical primes in
$\mathrm{Gal}(K_\ell/K)$
. As a consequence, there are no non-critical primes in
![]() $S_{K,x}$
or
$S_{K,x}$
or
![]() $S_{E/K}$
: the Frobenius elements of such primes in
$S_{E/K}$
: the Frobenius elements of such primes in
![]() $\mathrm{Gal}(K_N/K)$
cannot exist for group theoretical reasons.
$\mathrm{Gal}(K_N/K)$
cannot exist for group theoretical reasons.
An obstruction at prime level
![]() $N=\ell$
, which means an equality
$N=\ell$
, which means an equality
![]() $K=K_\ell$
, amounts in the cases I and II to a ‘trivial’ reason that we already mentioned in the context of conditions A and B in Theorem 1.2. For
$K=K_\ell$
, amounts in the cases I and II to a ‘trivial’ reason that we already mentioned in the context of conditions A and B in Theorem 1.2. For
![]() $K={\mathbf{Q}}$
, vanishing of
$K={\mathbf{Q}}$
, vanishing of
![]() $\delta_{{\mathbf{Q}}, x}$
and
$\delta_{{\mathbf{Q}}, x}$
and
![]() $\delta_{E/{\mathbf{Q}}}$
only occurs if we have
$\delta_{E/{\mathbf{Q}}}$
only occurs if we have
![]() $K=K_\ell$
for a prime
$K=K_\ell$
for a prime
![]() $\ell$
, which in this case has to be
$\ell$
, which in this case has to be
![]() $\ell=2$
.
$\ell=2$
.
Over general number fields, vanishing may be caused by obstructions that occur only at composite levels. Typical examples can be constructed by base changing a non-vanishing example (K, x) or
![]() $E/K$
to a suitable extension field
$E/K$
to a suitable extension field
![]() $K\subset L$
. Example 3.1 accomplishes vanishing of
$K\subset L$
. Example 3.1 accomplishes vanishing of
![]() $\delta_{K,x}$
by an obstruction at level
$\delta_{K,x}$
by an obstruction at level
![]() $30=2\cdot 3\cdot 5$
for the field
$30=2\cdot 3\cdot 5$
for the field
![]() $K={\mathbf{Q}}(\sqrt 5)$
that does not arise at lower level by cleverly choosing x. In [
Reference Campagna and Stevenhagen2
, example 5.4] we find a base change of an elliptic curve
$K={\mathbf{Q}}(\sqrt 5)$
that does not arise at lower level by cleverly choosing x. In [
Reference Campagna and Stevenhagen2
, example 5.4] we find a base change of an elliptic curve
![]() $E/{\mathbf{Q}}$
to a field K of degree 48 with a similar level 30 obstruction to cyclic reduction.
$E/{\mathbf{Q}}$
to a field K of degree 48 with a similar level 30 obstruction to cyclic reduction.
III. Elliptic primitive root case. In addition to the elliptic curve
![]() $E/K$
, we are now given a point
$E/K$
, we are now given a point
![]() $P\in E(K)$
of infinite order. We consider the set
$P\in E(K)$
of infinite order. We consider the set
![]() $S_{E/K, P}$
of primes
$S_{E/K, P}$
of primes
![]() ${\mathfrak{p}}$
of K for which E has cyclic reduction and the reduction of the point P modulo
${\mathfrak{p}}$
of K for which E has cyclic reduction and the reduction of the point P modulo
![]() ${\mathfrak{p}}$
generates the group
${\mathfrak{p}}$
generates the group
![]() $E(k_{\mathfrak{p}})$
. Note the obvious inclusion
$E(k_{\mathfrak{p}})$
. Note the obvious inclusion
![]() $S_{E/K, P}\subset S_{E/K}$
.
$S_{E/K, P}\subset S_{E/K}$
.
For
![]() $m\in{\mathbf{Z}}_{\ge1}$
, we let
$m\in{\mathbf{Z}}_{\ge1}$
, we let
![]() $K_m=K(m^{-1}P)$
be the m-division field of P, i.e., the extension of K generated by the points of the subgroup of
$K_m=K(m^{-1}P)$
be the m-division field of P, i.e., the extension of K generated by the points of the subgroup of
![]() $E(\overline K)$
defined as
$E(\overline K)$
defined as
Note that this extension
![]() $K_m$
contains the m-division field of the elliptic curve E that we encountered in the cyclic reduction case II. The m-division field
$K_m$
contains the m-division field of the elliptic curve E that we encountered in the cyclic reduction case II. The m-division field
![]() $K_m=K(m^{-1}P)$
of P is again unramified over K at primes
$K_m=K(m^{-1}P)$
of P is again unramified over K at primes
![]() ${\mathfrak{p}}$
of good reduction coprime to m. The proof of this fact is as for the m-division field of E: as the m-th roots
${\mathfrak{p}}$
of good reduction coprime to m. The proof of this fact is as for the m-division field of E: as the m-th roots
![]() $Q\in E(\overline K)$
of P that generate
$Q\in E(\overline K)$
of P that generate
![]() $K_m$
over K differ by m-torsion points, their reductions modulo a prime over
$K_m$
over K differ by m-torsion points, their reductions modulo a prime over
![]() ${\mathfrak{p}}$
remain different, so inertia acts trivially on the set of such Q.
${\mathfrak{p}}$
remain different, so inertia acts trivially on the set of such Q.
The quotient group
![]() $V_m=\langle m^{-1} P\rangle / \langle P\rangle$
is a free module of rank 3 over
$V_m=\langle m^{-1} P\rangle / \langle P\rangle$
is a free module of rank 3 over
![]() ${\mathbf{Z}}/m{\mathbf{Z}}$
. It comes with a natural
${\mathbf{Z}}/m{\mathbf{Z}}$
. It comes with a natural
![]() ${\mathbf{Z}}/m{\mathbf{Z}}$
-linear action of the absolute Galois group
${\mathbf{Z}}/m{\mathbf{Z}}$
-linear action of the absolute Galois group
![]() $G_K$
of K, and this mod-m Galois representation induces an embedding
$G_K$
of K, and this mod-m Galois representation induces an embedding
As
![]() $G_K$
stabilises the rank 2 subspace
$G_K$
stabilises the rank 2 subspace
![]() $U_m=E[m](\overline K)\subset V_m$
, this is a ‘reducible’ representation. Write
$U_m=E[m](\overline K)\subset V_m$
, this is a ‘reducible’ representation. Write
![]() $V_m=U_m\oplus ({\mathbf{Z}}/m{\mathbf{Z}})\cdot \bar Q$
with
$V_m=U_m\oplus ({\mathbf{Z}}/m{\mathbf{Z}})\cdot \bar Q$
with
![]() $\bar Q = (Q\bmod \langle P\rangle) \in V_m$
the image of a point
$\bar Q = (Q\bmod \langle P\rangle) \in V_m$
the image of a point
![]() $Q\in E(\overline K)$
satisfying
$Q\in E(\overline K)$
satisfying
![]() $m Q=P$
. We then have a split exact sequence
$m Q=P$
. We then have a split exact sequence
of free
![]() ${\mathbf{Z}}/m{\mathbf{Z}}$
-modules that is split as a sequence of
${\mathbf{Z}}/m{\mathbf{Z}}$
-modules that is split as a sequence of
![]() $({\mathbf{Z}}/m{\mathbf{Z}})[G_m]$
-modules if and only if we have
$({\mathbf{Z}}/m{\mathbf{Z}})[G_m]$
-modules if and only if we have
![]() $P\in m \cdot E(K)$
. After choosing a
$P\in m \cdot E(K)$
. After choosing a
![]() ${\mathbf{Z}}/m{\mathbf{Z}}$
-basis
${\mathbf{Z}}/m{\mathbf{Z}}$
-basis
![]() $\{T_1, T_2\}$
of
$\{T_1, T_2\}$
of
![]() $U_m$
and extending it by some
$U_m$
and extending it by some
![]() $\bar Q$
as above to a
$\bar Q$
as above to a
![]() ${\mathbf{Z}}/m{\mathbf{Z}}$
-basis for
${\mathbf{Z}}/m{\mathbf{Z}}$
-basis for
![]() $V_m$
, the matrix representation of
$V_m$
, the matrix representation of
![]() $\sigma\in G_m$
becomes
$\sigma\in G_m$
becomes
 \begin{equation}\sigma=\sigma_{A,b}=\begin{pmatrix}a_{11} & & & a_{12} && & b_1 \\a_{21} && & a_{22} && & b_2 \\0 && & 0 && & 1\end{pmatrix},\end{equation}
\begin{equation}\sigma=\sigma_{A,b}=\begin{pmatrix}a_{11} & & & a_{12} && & b_1 \\a_{21} && & a_{22} && & b_2 \\0 && & 0 && & 1\end{pmatrix},\end{equation}
in which the linear action of
![]() $\sigma$
on
$\sigma$
on
![]() $U_m$
with respect to some
$U_m$
with respect to some
![]() ${\mathbf{Z}}/m{\mathbf{Z}}$
-basis
${\mathbf{Z}}/m{\mathbf{Z}}$
-basis
![]() $\{T_1, T_2\}$
of
$\{T_1, T_2\}$
of
![]() $U_m$
is described by
$U_m$
is described by
![]() $A=\begin{pmatrix}a_{11} && & a_{12} \\a_{21} && & a_{22}\end{pmatrix}\in \mathrm{GL}(U_m)$
, and
$A=\begin{pmatrix}a_{11} && & a_{12} \\a_{21} && & a_{22}\end{pmatrix}\in \mathrm{GL}(U_m)$
, and
is the translation action of
![]() $\sigma$
on some chosen ‘m-th root’ Q of P with respect to that same basis. In other words,
$\sigma$
on some chosen ‘m-th root’ Q of P with respect to that same basis. In other words,
![]() $V_m$
gives a Galois representation of
$V_m$
gives a Galois representation of
![]() $G_K$
with image
$G_K$
with image
![]() $G_m\subset \mathrm{GL}(V_m)$
that is contained in the 2-dimensional affine group
$G_m\subset \mathrm{GL}(V_m)$
that is contained in the 2-dimensional affine group
In the important case where
![]() $m=\ell$
is prime, we are in the classical situation of a 3-dimensional Galois representation over the finite field
$m=\ell$
is prime, we are in the classical situation of a 3-dimensional Galois representation over the finite field
![]() ${\mathbf{F}}_\ell$
.
${\mathbf{F}}_\ell$
.
The analogue in the elliptic primitive root case of Lemmas 2.1 and 2.2 is a little bit more involved. We have to impose a condition on the Frobenius elements
![]() $\mathrm{Frob}_{{\mathfrak{p}}, \ell}\in G_\ell$
at all primes
$\mathrm{Frob}_{{\mathfrak{p}}, \ell}\in G_\ell$
at all primes
![]() $\ell\ne\mathrm{char}\ {{\mathfrak{p}}}$
different from being equal to the identity element
$\ell\ne\mathrm{char}\ {{\mathfrak{p}}}$
different from being equal to the identity element
![]() $\mathrm{id}_\ell\in G_\ell$
: in this case it only needs to be ‘sufficiently close’ to it.
$\mathrm{id}_\ell\in G_\ell$
: in this case it only needs to be ‘sufficiently close’ to it.
Lemma 2.3. For
![]() $P\in E(K)$
of infinite order and
$P\in E(K)$
of infinite order and
![]() ${\mathfrak{p}}$
a prime of good reduction of E of characteristic different from
${\mathfrak{p}}$
a prime of good reduction of E of characteristic different from
![]() $\ell$
we have
$\ell$
we have
Proof. As all
![]() $V_\ell$
are 3-dimensional over
$V_\ell$
are 3-dimensional over
![]() ${\mathbf{F}}_\ell$
, the condition
${\mathbf{F}}_\ell$
, the condition
![]() $\mathrm{rank} (\mathrm{Frob}_{{\mathfrak{p}},\ell} - \mathrm{id}_\ell)\le 1$
means that
$\mathrm{rank} (\mathrm{Frob}_{{\mathfrak{p}},\ell} - \mathrm{id}_\ell)\le 1$
means that
![]() $\mathrm{Frob}_{{\mathfrak{p}},\ell}$
is the identity on an
$\mathrm{Frob}_{{\mathfrak{p}},\ell}$
is the identity on an
![]() ${\mathbf{F}}_\ell$
-subspace of
${\mathbf{F}}_\ell$
-subspace of
![]() $V_\ell$
of dimension at least 2. If this subspace contains
$V_\ell$
of dimension at least 2. If this subspace contains
![]() $U_\ell$
, then
$U_\ell$
, then
![]() $E(k_{\mathfrak{p}})$
has complete
$E(k_{\mathfrak{p}})$
has complete
![]() $\ell$
-torsion of order
$\ell$
-torsion of order
![]() $\ell^2$
and every cyclic subgroup
$\ell^2$
and every cyclic subgroup
![]() $\langle {\bar P}\rangle$
has index divisible by
$\langle {\bar P}\rangle$
has index divisible by
![]() $\ell$
. If not, it intersects
$\ell$
. If not, it intersects
![]() $U_\ell$
in a 1-dimensional subspace, so we have a point of order
$U_\ell$
in a 1-dimensional subspace, so we have a point of order
![]() $\ell$
in
$\ell$
in
![]() $E(k_{\mathfrak{p}})$
and a point
$E(k_{\mathfrak{p}})$
and a point
![]() $\bar Q\in E(k_{\mathfrak{p}})$
satisfying
$\bar Q\in E(k_{\mathfrak{p}})$
satisfying
![]() $\ell\bar Q=\bar P$
. This also implies that
$\ell\bar Q=\bar P$
. This also implies that
![]() $[E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle]$
is divisible by
$[E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle]$
is divisible by
![]() $\ell$
.
$\ell$
.
Conversely, if
![]() $\ell$
divides
$\ell$
divides
![]() $[E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle]$
then either
$[E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle]$
then either
![]() $E(k_{\mathfrak{p}})$
has complete
$E(k_{\mathfrak{p}})$
has complete
![]() $\ell$
-torsion or
$\ell$
-torsion or
![]() $E(k_{\mathfrak{p}})$
has a cyclic non-trivial
$E(k_{\mathfrak{p}})$
has a cyclic non-trivial
![]() $\ell$
-part and
$\ell$
-part and
![]() $\bar P$
is contained in
$\bar P$
is contained in
![]() $\ell\cdot E(k_{\mathfrak{p}})$
. In both cases
$\ell\cdot E(k_{\mathfrak{p}})$
. In both cases
![]() $\mathrm{Frob}_{{\mathfrak{p}},\ell}$
is the identity on a subspace of
$\mathrm{Frob}_{{\mathfrak{p}},\ell}$
is the identity on a subspace of
![]() $V_\ell$
of dimension at least 2.
$V_\ell$
of dimension at least 2.
This time, it is not clear that in the case
![]() $\ell={\mathfrak{p}}$
, the condition
$\ell={\mathfrak{p}}$
, the condition
![]() $\ell \mid [E(k_{\mathfrak{p}}) : \langle \bar{P} \rangle]$
of the Lemma will automatically not be satisfied for almost all primes
$\ell \mid [E(k_{\mathfrak{p}}) : \langle \bar{P} \rangle]$
of the Lemma will automatically not be satisfied for almost all primes
![]() ${\mathfrak{p}}$
of
${\mathfrak{p}}$
of
![]() $K$
. In order to have this, we will restrict our attention to primes
$K$
. In order to have this, we will restrict our attention to primes
![]() ${\mathfrak{p}}$
of K of degree one, i.e., primes
${\mathfrak{p}}$
of K of degree one, i.e., primes
![]() ${\mathfrak{p}}$
of prime norm
${\mathfrak{p}}$
of prime norm
![]() $\mathrm{char}\ {{\mathfrak{p}}}$
.
$\mathrm{char}\ {{\mathfrak{p}}}$
.
Corollary 2.4. Let
![]() $P\in E(K)$
be of infinite order and
$P\in E(K)$
be of infinite order and
![]() ${\mathfrak{p}}$
a prime of good reduction of E of prime norm
${\mathfrak{p}}$
a prime of good reduction of E of prime norm
![]() $\mathrm{char}\ {{\mathfrak{p}}}>5$
for which
$\mathrm{char}\ {{\mathfrak{p}}}>5$
for which
![]() $\bar P\ne \bar O\in E(k_{\mathfrak{p}})$
. Then we have
$\bar P\ne \bar O\in E(k_{\mathfrak{p}})$
. Then we have
Proof. By Lemma 2.3, the condition on the right-hand side says that
![]() $p=\mathrm{char}\ {{\mathfrak{p}}}$
is the only possible prime divisor of the index
$p=\mathrm{char}\ {{\mathfrak{p}}}$
is the only possible prime divisor of the index
![]() $[E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle ]$
. For a prime
$[E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle ]$
. For a prime
![]() ${\mathfrak{p}}$
of degree one, i.e., of prime norm p, the index of a subgroup of
${\mathfrak{p}}$
of degree one, i.e., of prime norm p, the index of a subgroup of
![]() $E(k_{\mathfrak{p}})=E({\mathbf{F}}_p)$
can only be divisible by p if it is the trivial subgroup, as we have
$E(k_{\mathfrak{p}})=E({\mathbf{F}}_p)$
can only be divisible by p if it is the trivial subgroup, as we have
![]() $\#E({\mathbf{F}}_p)< p+1+2\sqrt p<2p$
for
$\#E({\mathbf{F}}_p)< p+1+2\sqrt p<2p$
for
![]() $p>5$
. So we have
$p>5$
. So we have
![]() $E(k_{\mathfrak{p}})=\langle {\bar P}\rangle$
unless
$E(k_{\mathfrak{p}})=\langle {\bar P}\rangle$
unless
![]() ${\mathfrak{p}}$
is one of the finitely many primes for which we have
${\mathfrak{p}}$
is one of the finitely many primes for which we have
![]() $\bar P = \bar O\in E(k_{\mathfrak{p}})$
.
$\bar P = \bar O\in E(k_{\mathfrak{p}})$
.
In density questions, we can disregard any finite set of primes, and more generally a set of primes of density zero. The set of primes in a number field of degree bigger than one is such a zero density set. For this reason, the density of the set
![]() $S_{E/K,P}$
only depends on the primes of degree one outside any finite set of ‘critical primes’ that it contains. Thus, Corollary 2.4 can play the same role as Lemmas 2.1 and 2.2.
$S_{E/K,P}$
only depends on the primes of degree one outside any finite set of ‘critical primes’ that it contains. Thus, Corollary 2.4 can play the same role as Lemmas 2.1 and 2.2.
In order to express the ‘heuristical density’
![]() $\delta_{E/K, P}$
of
$\delta_{E/K, P}$
of
![]() $S_{E/K,P}$
, we define the subset
$S_{E/K,P}$
, we define the subset
![]() $S_\ell\subset G_\ell=\mathrm{Gal}(K_\ell/K)$
of ‘bad’ elements at the prime
$S_\ell\subset G_\ell=\mathrm{Gal}(K_\ell/K)$
of ‘bad’ elements at the prime
![]() $\ell$
as
$\ell$
as
For arbitrary
![]() $m\in{\mathbf{Z}}_{\ge1}$
and
$m\in{\mathbf{Z}}_{\ge1}$
and
![]() $\ell|m$
prime we let
$\ell|m$
prime we let
![]() $\pi_{m,\ell}\,:\,G_m\to G_\ell$
be the natural restriction map, and define
$\pi_{m,\ell}\,:\,G_m\to G_\ell$
be the natural restriction map, and define
![]() $S_m\subset G_m$
as
$S_m\subset G_m$
as
With
![]() $s_m=\#S_m$
denoting the cardinality of
$s_m=\#S_m$
denoting the cardinality of
![]() $S_m$
, the elliptic primitive root density is now given by the inclusion-exclusion sum
$S_m$
, the elliptic primitive root density is now given by the inclusion-exclusion sum
 \begin{equation}\delta_{E/K,P}=\sum_{m=1}^{\infty} \frac{\mu(m)s_m}{[K_m\,:\,K]}.\end{equation}
\begin{equation}\delta_{E/K,P}=\sum_{m=1}^{\infty} \frac{\mu(m)s_m}{[K_m\,:\,K]}.\end{equation}
It is the elliptic analogue of the multiplicative primitive root density (2·1). It is an upper density for
![]() $S_{E/K,P}$
that has not been proven to be its true density in cases with
$S_{E/K,P}$
that has not been proven to be its true density in cases with
![]() $\delta_{E/K, P}>0$
, not even under GRH.
$\delta_{E/K, P}>0$
, not even under GRH.
We can compute
![]() $\delta_{E/K, P}$
using the methods of [
Reference Campagna and Stevenhagen2
]. This is not directly relevant for us, as our focus in this paper is on cases where
$\delta_{E/K, P}$
using the methods of [
Reference Campagna and Stevenhagen2
]. This is not directly relevant for us, as our focus in this paper is on cases where
![]() $\delta_{E/K, P}$
vanishes in ‘non-trivial’ ways, so we will merely sketch this here. In order to obtain a factorisation
$\delta_{E/K, P}$
vanishes in ‘non-trivial’ ways, so we will merely sketch this here. In order to obtain a factorisation
 \begin{equation}\delta_{E/K,P}=\sum_{m|N} \frac{\mu(m)s_m}{[K_m\,:\,K]}\cdot \prod_{\ell\nmid N \text{ prime}} \left(1-\frac{s_\ell}{[K_\ell\,:\,K]}\right),\end{equation}
\begin{equation}\delta_{E/K,P}=\sum_{m|N} \frac{\mu(m)s_m}{[K_m\,:\,K]}\cdot \prod_{\ell\nmid N \text{ prime}} \left(1-\frac{s_\ell}{[K_\ell\,:\,K]}\right),\end{equation}
as in (2·2), it suffices to have an ‘open-image theorem’ for the Galois representation
![]() $\rho_{E,P}$
arising from the action of
$\rho_{E,P}$
arising from the action of
![]() $G_K$
on the subgroup
$G_K$
on the subgroup
of
![]() $E(\bar K)$
generated by all the roots of P in
$E(\bar K)$
generated by all the roots of P in
![]() $E(\bar K)$
. The Galois action of
$E(\bar K)$
. The Galois action of
![]() $G_K$
on the quotient group
$G_K$
on the quotient group
![]() $V=R_P/\langle P\rangle$
, which is free of rank 3 over
$V=R_P/\langle P\rangle$
, which is free of rank 3 over
![]() ${\mathbf{Q}}/{\mathbf{Z}}$
, gives rise to a Galois representation
${\mathbf{Q}}/{\mathbf{Z}}$
, gives rise to a Galois representation
which has (2·4) as its mod-m representation. It factors via
![]() $\mathrm{Gal}(K(R_P)/K)$
, with
$\mathrm{Gal}(K(R_P)/K)$
, with
![]() $K(R_P)=\bigcup_m K_m\subset \bar K$
the compositum of all ‘m-division fields’ of P inside
$K(R_P)=\bigcup_m K_m\subset \bar K$
the compositum of all ‘m-division fields’ of P inside
![]() $\bar K$
. The group
$\bar K$
. The group
![]() $U=E(\overline K)^\text{tor}\cong ({\mathbf{Q}}/{\mathbf{Z}})^2$
is a direct summand of V, and if we choose a
$U=E(\overline K)^\text{tor}\cong ({\mathbf{Q}}/{\mathbf{Z}})^2$
is a direct summand of V, and if we choose a
![]() ${\mathbf{Q}}/{\mathbf{Z}}$
-basis for
${\mathbf{Q}}/{\mathbf{Z}}$
-basis for
![]() $V=U\oplus {\mathbf{Q}}/{\mathbf{Z}}$
as we did for
$V=U\oplus {\mathbf{Q}}/{\mathbf{Z}}$
as we did for
![]() $V_m=U_m\oplus {\mathbf{Z}}/m{\mathbf{Z}}\cdot\bar Q$
, the image of
$V_m=U_m\oplus {\mathbf{Z}}/m{\mathbf{Z}}\cdot\bar Q$
, the image of
![]() $\rho_{E,P}$
is in
$\rho_{E,P}$
is in
![]() $\mathrm{Aff}_2({\widehat {{\mathbf{Z}}}})={\widehat {{\mathbf{Z}}}}^2\rtimes \mathrm{GL}_2({\widehat {{\mathbf{Z}}}})$
. For E without CM over
$\mathrm{Aff}_2({\widehat {{\mathbf{Z}}}})={\widehat {{\mathbf{Z}}}}^2\rtimes \mathrm{GL}_2({\widehat {{\mathbf{Z}}}})$
. For E without CM over
![]() $\bar K$
, one deduces from Serre’s open image theorem that this image is of finite index in
$\bar K$
, one deduces from Serre’s open image theorem that this image is of finite index in
![]() $\mathrm{Aff}_2({\widehat {{\mathbf{Z}}}})$
, which yields (2·7) for any N divisible by some finite product
$\mathrm{Aff}_2({\widehat {{\mathbf{Z}}}})$
, which yields (2·7) for any N divisible by some finite product
![]() $N_{E/K,P}\in{\mathbf{Z}}_{>0}$
of critical primes. As in [
Reference Campagna and Stevenhagen2
], one deduces that all non-CM-densities
$N_{E/K,P}\in{\mathbf{Z}}_{>0}$
of critical primes. As in [
Reference Campagna and Stevenhagen2
], one deduces that all non-CM-densities
![]() $\delta_{E,P}$
are rational multiples of a universal constant. If E has CM over
$\delta_{E,P}$
are rational multiples of a universal constant. If E has CM over
![]() $\bar K$
by an order
$\bar K$
by an order
![]() $\mathcal{O}\subset K$
, one replaces
$\mathcal{O}\subset K$
, one replaces
![]() $\mathrm{Aff}_2({\widehat {{\mathbf{Z}}}})$
by
$\mathrm{Aff}_2({\widehat {{\mathbf{Z}}}})$
by
![]() $\mathrm{Aff}_1(\mathcal{O})$
, and in the case of CM by an order
$\mathrm{Aff}_1(\mathcal{O})$
, and in the case of CM by an order
![]() $\mathcal{O}\not\subset K$
, one separates the contribution of ordinary and supersingular primes of
$\mathcal{O}\not\subset K$
, one separates the contribution of ordinary and supersingular primes of
![]() $E/K$
as in [
Reference Campagna and Stevenhagen2
].
$E/K$
as in [
Reference Campagna and Stevenhagen2
].
3. Multiplicative primitivity
Before focusing on the Lang-Trotter case III, we first settle the multiplicative primitive root case: under GRH, globally primitive elements
![]() $x\in K^*$
are locally primitive for a set of primes of positive density
$x\in K^*$
are locally primitive for a set of primes of positive density
![]() $\delta_{K,x}$
.
$\delta_{K,x}$
.
Proof of Theorem
1.1. Let
![]() $x\in K^*$
be globally primitive. As we assume GRH, the primitive root density for
$x\in K^*$
be globally primitive. As we assume GRH, the primitive root density for
![]() $x\in K^*$
exists and is equal to
$x\in K^*$
exists and is equal to
![]() $\delta_{K,x}$
defined in (2·1), by the results of [
Reference Lenstra10
]. We need to show that
$\delta_{K,x}$
defined in (2·1), by the results of [
Reference Lenstra10
]. We need to show that
![]() $\delta_{K,x}$
does not vanish. In view of the factorisation formula (2·2), it suffices to show that for any squarefree integer
$\delta_{K,x}$
does not vanish. In view of the factorisation formula (2·2), it suffices to show that for any squarefree integer
![]() $N>1$
, the fraction
$N>1$
, the fraction
![]() $\sum_{m|N} \mu(m)[K_m\,:\,K]^{-1}$
of elements in
$\sum_{m|N} \mu(m)[K_m\,:\,K]^{-1}$
of elements in
![]() $\mathrm{Gal}(K_N/K)$
that have non-trivial restriction to
$\mathrm{Gal}(K_N/K)$
that have non-trivial restriction to
![]() $K_\ell$
for all primes
$K_\ell$
for all primes
![]() $\ell|N$
does not vanish.
$\ell|N$
does not vanish.
As x is not an
![]() $\ell$
th power in
$\ell$
th power in
![]() $K^*$
, the polynomial
$K^*$
, the polynomial
![]() $X^\ell-x$
is irreducible in K[X]. It therefore gives rise to an extension
$X^\ell-x$
is irreducible in K[X]. It therefore gives rise to an extension
![]() $K\subset K_\ell=\mathrm{Split}_K(X^\ell-x)=K(\zeta_\ell,\root \ell \of x)$
of degree
$K\subset K_\ell=\mathrm{Split}_K(X^\ell-x)=K(\zeta_\ell,\root \ell \of x)$
of degree
![]() $\ell\cdot c_\ell$
, with
$\ell\cdot c_\ell$
, with
![]() $c_\ell$
a divisor of
$c_\ell$
a divisor of
![]() $\ell-1$
. If
$\ell-1$
. If
![]() $\ell$
is the largest prime dividing the squarefree number N, we conclude that
$\ell$
is the largest prime dividing the squarefree number N, we conclude that
![]() $K_{N/\ell}\subset K_N$
is Galois of degree divisible by
$K_{N/\ell}\subset K_N$
is Galois of degree divisible by
![]() $\ell$
.
$\ell$
.
Showing that
![]() $\mathrm{Gal}(K_N/K)$
contains an element of the required type is now easily done by induction on the number of of primes dividing the squarefree integer
$\mathrm{Gal}(K_N/K)$
contains an element of the required type is now easily done by induction on the number of of primes dividing the squarefree integer
![]() $N>1$
. If N is prime, then
$N>1$
. If N is prime, then
![]() $\mathrm{Gal}(K_N/K)$
contains a non-trivial element of order N. If not, we let
$\mathrm{Gal}(K_N/K)$
contains a non-trivial element of order N. If not, we let
![]() $\ell$
be the largest prime dividing N and observe that an automorphism of the required type in
$\ell$
be the largest prime dividing N and observe that an automorphism of the required type in
![]() $\mathrm{Gal}(K_{N/\ell}/K)$
, which exists by the induction hypothesis, always possesses an extension to the compositum
$\mathrm{Gal}(K_{N/\ell}/K)$
, which exists by the induction hypothesis, always possesses an extension to the compositum
![]() $K_N$
of
$K_N$
of
![]() $K_{N/\ell}$
and
$K_{N/\ell}$
and
![]() $K_\ell$
that is non-trivial on
$K_\ell$
that is non-trivial on
![]() $K_\ell$
.
$K_\ell$
.
The assumption of global primitivity in Theorem 1.1 cannot be weakened to the assumption
![]() $K\ne K_\ell$
for all prime numbers
$K\ne K_\ell$
for all prime numbers
![]() $\ell$
. The resulting stronger statement is correct for
$\ell$
. The resulting stronger statement is correct for
![]() $K={\mathbf{Q}}$
, but counterexamples to it exist for general number fields K, as the cyclotomic extensions
$K={\mathbf{Q}}$
, but counterexamples to it exist for general number fields K, as the cyclotomic extensions
![]() $K\subset K(\zeta_\ell)$
for different
$K\subset K(\zeta_\ell)$
for different
![]() $\ell$
may all be non-trivial, but ‘entangled’ over K. The following counterexample takes K to be quadratic.
$\ell$
may all be non-trivial, but ‘entangled’ over K. The following counterexample takes K to be quadratic.
Example 3.1. The quadratic field
![]() $K={\mathbf{Q}}(\sqrt 5)$
has fundamental unit
$K={\mathbf{Q}}(\sqrt 5)$
has fundamental unit
![]() $\varepsilon=({1+\sqrt 5})/{2}$
. The element
$\varepsilon=({1+\sqrt 5})/{2}$
. The element
![]() $\pi=\varepsilon^2-4=({-5+\sqrt 5})/{2}\in K$
has norm 5 and is a square modulo 4. The field
$\pi=\varepsilon^2-4=({-5+\sqrt 5})/{2}\in K$
has norm 5 and is a square modulo 4. The field
![]() $K(\sqrt\pi)$
, which is cyclic of degree 4 over
$K(\sqrt\pi)$
, which is cyclic of degree 4 over
![]() ${\mathbf{Q}}$
and unramified outside 5, is therefore equal to
${\mathbf{Q}}$
and unramified outside 5, is therefore equal to
![]() $K(\zeta_5)$
. Take
$K(\zeta_5)$
. Take
![]() $y=-3\pi\in K$
and choose
$y=-3\pi\in K$
and choose
![]() $x=y^{15}$
. We then have
$x=y^{15}$
. We then have
so
![]() $K_2=K(\sqrt x)=K(\sqrt y)=K(\sqrt{-3\pi})$
and
$K_2=K(\sqrt x)=K(\sqrt y)=K(\sqrt{-3\pi})$
and
![]() $K_3$
and
$K_3$
and
![]() $K_5$
are three different quadratic extensions of K contained in the biquadratic extension
$K_5$
are three different quadratic extensions of K contained in the biquadratic extension
![]() $K\subset K_6=K_{10}=K_{15}=K_{30}$
. We have
$K\subset K_6=K_{10}=K_{15}=K_{30}$
. We have
![]() $\mu_K=\{\pm1\}$
and, even though x is not a square in
$\mu_K=\{\pm1\}$
and, even though x is not a square in
![]() $K^*$
, there is exactly one prime of K modulo which x is a primitive root: (2). For the primes
$K^*$
, there is exactly one prime of K modulo which x is a primitive root: (2). For the primes
![]() ${\mathfrak{p}}=(3)$
and
${\mathfrak{p}}=(3)$
and
![]() ${\mathfrak{p}}=(\sqrt 5)$
the element x is not in
${\mathfrak{p}}=(\sqrt 5)$
the element x is not in
![]() $k_{\mathfrak{p}}^*$
, and for all primes of characteristic
$k_{\mathfrak{p}}^*$
, and for all primes of characteristic
![]() $p>5$
the index
$p>5$
the index
![]() $[{\mathbf{F}}_p\,:\,\langle\bar x\rangle]$
is divisible by at least one of 2, 3 or 5. Indeed, no prime can be inert in all three quadratic subfields of an extension with group
$[{\mathbf{F}}_p\,:\,\langle\bar x\rangle]$
is divisible by at least one of 2, 3 or 5. Indeed, no prime can be inert in all three quadratic subfields of an extension with group
![]() ${\mathbf{Z}}/2{\mathbf{Z}}\times{\mathbf{Z}}/2{\mathbf{Z}}$
.
${\mathbf{Z}}/2{\mathbf{Z}}\times{\mathbf{Z}}/2{\mathbf{Z}}$
.
The simple observation that no prime
![]() ${\mathfrak{p}}$
of a number field K can be inert in all three quadratic subextensions of an extension
${\mathfrak{p}}$
of a number field K can be inert in all three quadratic subextensions of an extension
![]() $K\subset L$
with group
$K\subset L$
with group
![]() ${\mathbf{Z}}/2{\mathbf{Z}}\times{\mathbf{Z}}/2{\mathbf{Z}}$
underlies many ‘entanglement obstructions’, including the one in Section 8.
${\mathbf{Z}}/2{\mathbf{Z}}\times{\mathbf{Z}}/2{\mathbf{Z}}$
underlies many ‘entanglement obstructions’, including the one in Section 8.
4. Proof of Theorem 1.2
In the Lang-Trotter situation, Lemma 2.3 shows that a point
![]() $P\in E(K)$
will generate a subgroup of the local point group
$P\in E(K)$
will generate a subgroup of the local point group
![]() $E(k_{\mathfrak{p}})$
of index divisible by
$E(k_{\mathfrak{p}})$
of index divisible by
![]() $\ell$
when
$\ell$
when
![]() $\mathrm{Frob}_{{\mathfrak{p}}, \ell}\in G_\ell$
pointwise fixes a 2-dimensional subspace of the 3-dimensional
$\mathrm{Frob}_{{\mathfrak{p}}, \ell}\in G_\ell$
pointwise fixes a 2-dimensional subspace of the 3-dimensional
![]() ${\mathbf{F}}_\ell$
-vector space
${\mathbf{F}}_\ell$
-vector space
![]() $V_\ell$
. Vanishing of the density
$V_\ell$
. Vanishing of the density
![]() $\delta_{E/K,P}$
can therefore occur ‘because of
$\delta_{E/K,P}$
can therefore occur ‘because of
![]() $K_\ell$
’ in cases where
$K_\ell$
’ in cases where
![]() $G_\ell=\mathrm{Gal}(K_\ell/K)$
is non-trivial, but only contains elements that pointwise fix a 2-dimensional subspace of
$G_\ell=\mathrm{Gal}(K_\ell/K)$
is non-trivial, but only contains elements that pointwise fix a 2-dimensional subspace of
![]() $V_\ell$
.
$V_\ell$
.
Our proof of Theorem 1.2 is based on a general lemma that we phrase and prove in the generality that was suggested to us by Hendrik Lenstra. It describes the linear group actions on vector spaces of finite dimension over arbitrary fields that have ‘many fixpoints’ in the sense of the 3-dimensional example
![]() $V_\ell$
that we have at hand.
$V_\ell$
that we have at hand.
Let V be any vector space on which a group G acts linearly, and denote by
the maximal subspace and quotient space of V on which G acts trivially. For every
![]() $\sigma \in G$
, we have an exact sequence of vector spaces
$\sigma \in G$
, we have an exact sequence of vector spaces
showing that for V of finite dimension n, we have
Lemma 4.1. Let G be a group acting linearly on a vector space V of dimension
![]() $n\in{\mathbf{Z}}_{\ge0}$
. Then the following are equivalent:
$n\in{\mathbf{Z}}_{\ge0}$
. Then the following are equivalent:
-
(i)
 $\dim V^{\langle\sigma\rangle}\ge n-1$
for all
$\dim V^{\langle\sigma\rangle}\ge n-1$
for all
 $\sigma \in G$
;
$\sigma \in G$
; -
(ii)
 $\dim V^G\ge n-1$
or
$\dim V^G\ge n-1$
or
 $\dim V_G\ge n-1$
.
$\dim V_G\ge n-1$
.
Proof. The implication
![]() $(\textrm{ii})\Rightarrow(\textrm{i})$
is immediate, as the inequality
$(\textrm{ii})\Rightarrow(\textrm{i})$
is immediate, as the inequality
![]() $\dim V_G\ge n-1$
implies that, for all
$\dim V_G\ge n-1$
implies that, for all
![]() $\sigma\in G$
, we have
$\sigma\in G$
, we have
![]() $\dim (\sigma-1)V \le 1$
and, by (4·1),
$\dim (\sigma-1)V \le 1$
and, by (4·1),
![]() $\dim V^{\langle\sigma\rangle}\ge n-1$
.
$\dim V^{\langle\sigma\rangle}\ge n-1$
.
For
![]() $(\textrm{i})\Rightarrow (\textrm{ii})$
, we can assume there exists
$(\textrm{i})\Rightarrow (\textrm{ii})$
, we can assume there exists
![]() $\sigma\in G$
acting non-trivially on V, and define subgroups
$\sigma\in G$
acting non-trivially on V, and define subgroups
![]() $A_\sigma, B_\sigma \subset G$
by
$A_\sigma, B_\sigma \subset G$
by
The equality
![]() $A_\sigma=G$
implies that
$A_\sigma=G$
implies that
![]() $V^G=V^{\langle\sigma\rangle}$
has dimension
$V^G=V^{\langle\sigma\rangle}$
has dimension
![]() $n-1$
, and the equality
$n-1$
, and the equality
![]() $B_\sigma=G$
implies that
$B_\sigma=G$
implies that
![]() $V_G=V/(\sigma-1)V$
has dimension
$V_G=V/(\sigma-1)V$
has dimension
![]() $n-1$
. In order to show that we have one of these equalities, and therefore (ii), we argue by contradiction. Assume
$n-1$
. In order to show that we have one of these equalities, and therefore (ii), we argue by contradiction. Assume
![]() $A_\sigma$
and
$A_\sigma$
and
![]() $B_\sigma$
are strict subgroups of G, and pick
$B_\sigma$
are strict subgroups of G, and pick
![]() $\tau\in G$
outside
$\tau\in G$
outside
![]() $A_\sigma\cup B_\sigma$
. Then there exist
$A_\sigma\cup B_\sigma$
. Then there exist
![]() $s\in V^{\langle\sigma\rangle}\setminus V^{\langle\tau\rangle}$
and
$s\in V^{\langle\sigma\rangle}\setminus V^{\langle\tau\rangle}$
and
![]() $t\in V^{\langle\tau\rangle}\setminus V^{\langle\sigma\rangle}$
, and
$t\in V^{\langle\tau\rangle}\setminus V^{\langle\sigma\rangle}$
, and
![]() $(\sigma-1)V$
and
$(\sigma-1)V$
and
![]() $(\tau-1)V$
are different 1-dimensional subspaces of V spanned by
$(\tau-1)V$
are different 1-dimensional subspaces of V spanned by
![]() $(\sigma-1) t$
and
$(\sigma-1) t$
and
![]() $(\tau-1)s$
, respectively.
$(\tau-1)s$
, respectively.
The subspace
![]() $(\tau\sigma-1)V$
is 1-dimensional and spanned by
$(\tau\sigma-1)V$
is 1-dimensional and spanned by
![]() $(\tau\sigma-1)s=(\tau-1)s$
, so it equals
$(\tau\sigma-1)s=(\tau-1)s$
, so it equals
![]() $(\tau-1)V$
. It contains
$(\tau-1)V$
. It contains
![]() $(\tau\sigma-1)t=\tau(\sigma-1)t$
, but since
$(\tau\sigma-1)t=\tau(\sigma-1)t$
, but since
![]() $\tau$
acts on
$\tau$
acts on
![]() $(\sigma-1)t\notin (\tau-1)V$
by translation along a vector in
$(\sigma-1)t\notin (\tau-1)V$
by translation along a vector in
![]() $(\tau-1)V$
, we have
$(\tau-1)V$
, we have
![]() $\tau(\sigma-1)t\notin (\tau-1)V$
. Contradiction.
$\tau(\sigma-1)t\notin (\tau-1)V$
. Contradiction.
For those who like to think of Lemma 4.1 in terms of matrices, Condition (i) means that every element of G has a matrix representation with respect to a suitable basis that, according to (4·1), can be given in one of the equivalent forms

The first form shows
![]() $n-1$
linearly independent vectors in
$n-1$
linearly independent vectors in
![]() $V^{\langle\sigma\rangle}$
, the second starts from a vector spanning
$V^{\langle\sigma\rangle}$
, the second starts from a vector spanning
![]() $(\sigma-1)V$
. The lemma then states that under this condition, a single basis for V can be chosen such that either all elements of G have a matrix representation of the first form, or they all have one of the second form.
$(\sigma-1)V$
. The lemma then states that under this condition, a single basis for V can be chosen such that either all elements of G have a matrix representation of the first form, or they all have one of the second form.
Example 4.2. For an elliptic curve
![]() $E/K$
, we can apply Lemma 4.1 to the action of the Galois group G of the
$E/K$
, we can apply Lemma 4.1 to the action of the Galois group G of the
![]() $\ell$
-division field of E over K on the 2-dimensional
$\ell$
-division field of E over K on the 2-dimensional
![]() ${\mathbf{F}}_\ell$
-vector space
${\mathbf{F}}_\ell$
-vector space
![]() $V=E[\ell](\overline K)$
of
$V=E[\ell](\overline K)$
of
![]() $\ell$
-torsion points of E. In this case the point group
$\ell$
-torsion points of E. In this case the point group
![]() $E(k_{\mathfrak{p}})$
at a prime
$E(k_{\mathfrak{p}})$
at a prime
![]() ${\mathfrak{p}}\nmid \ell$
of good reduction is of order divisible by
${\mathfrak{p}}\nmid \ell$
of good reduction is of order divisible by
![]() $\ell$
if and only if
$\ell$
if and only if
![]() $\mathrm{Frob}_{\mathfrak{p}}\in G$
pointwise fixes a 1-dimensional subspace of V. We find that
$\mathrm{Frob}_{\mathfrak{p}}\in G$
pointwise fixes a 1-dimensional subspace of V. We find that
![]() $E(k_{\mathfrak{p}})$
has order divisible by
$E(k_{\mathfrak{p}})$
has order divisible by
![]() $\ell$
for almost all primes
$\ell$
for almost all primes
![]() ${\mathfrak{p}}$
of K if and only if the Galois representation
${\mathfrak{p}}$
of K if and only if the Galois representation
![]() $\rho_{E/K,\ell}$
of
$\rho_{E/K,\ell}$
of
![]() $G_K$
on the group of
$G_K$
on the group of
![]() $\ell$
-torsion points of E can be given in matrix form as
$\ell$
-torsion points of E can be given in matrix form as
In words: either E(K) contains an
![]() $\ell$
-torsion point, or it is
$\ell$
-torsion point, or it is
![]() $\ell$
-isogenous over K to an elliptic curve with a K-rational
$\ell$
-isogenous over K to an elliptic curve with a K-rational
![]() $\ell$
-torsion point. Moreover, for
$\ell$
-torsion point. Moreover, for
![]() $E/K$
of the first kind, with a point
$E/K$
of the first kind, with a point
![]() $T\in E(K)$
of order
$T\in E(K)$
of order
![]() $\ell$
, the quotient curve
$\ell$
, the quotient curve
![]() $E'=E/\langle T\rangle$
is of the second kind, with the dual isogeny
$E'=E/\langle T\rangle$
is of the second kind, with the dual isogeny
![]() $E'\to E$
being the
$E'\to E$
being the
![]() $\ell$
-isogeny in question. This is a well-known fact that occurs as the very first exercise in [
Reference Serre15
, p. I-2.]
$\ell$
-isogeny in question. This is a well-known fact that occurs as the very first exercise in [
Reference Serre15
, p. I-2.]
Proof of Theorem
1.2. Let
![]() $E/K$
be an elliptic curve, and
$E/K$
be an elliptic curve, and
![]() $P\in E(K)$
a non-torsion point that is locally
$P\in E(K)$
a non-torsion point that is locally
![]() $\ell$
-imprimitive. We define
$\ell$
-imprimitive. We define
![]() $K_\ell=K(\ell^{-1}P)$
as in Section 2, and view
$K_\ell=K(\ell^{-1}P)$
as in Section 2, and view
![]() $G_\ell=\mathrm{Gal}(K_\ell/K)\subset \mathrm{GL}(V_\ell)$
as a group of
$G_\ell=\mathrm{Gal}(K_\ell/K)\subset \mathrm{GL}(V_\ell)$
as a group of
![]() ${\mathbf{F}}_\ell$
-linear automorphisms of the 3-dimensional vector space
${\mathbf{F}}_\ell$
-linear automorphisms of the 3-dimensional vector space
![]() $V_\ell= \langle \ell^{-1}P\rangle/\langle P \rangle$
. As every element of
$V_\ell= \langle \ell^{-1}P\rangle/\langle P \rangle$
. As every element of
![]() $G_\ell$
occurs as the Frobenius of infinitely many primes of good reduction, it follows from Lemma 2.3 that all elements of
$G_\ell$
occurs as the Frobenius of infinitely many primes of good reduction, it follows from Lemma 2.3 that all elements of
![]() $G_\ell$
leave a 2-dimensional subspace of
$G_\ell$
leave a 2-dimensional subspace of
![]() $V_\ell$
pointwise invariant. We can now apply our Lemma 4.1 for
$V_\ell$
pointwise invariant. We can now apply our Lemma 4.1 for
![]() $n=3$
with
$n=3$
with
![]() $G=G_\ell$
and
$G=G_\ell$
and
![]() $V=V_\ell$
to conclude that at least one of the following occurs: either
$V=V_\ell$
to conclude that at least one of the following occurs: either
![]() $G_\ell$
acts trivially on a 2-dimensional subspace of
$G_\ell$
acts trivially on a 2-dimensional subspace of
![]() $V_\ell$
, or
$V_\ell$
, or
![]() $G_\ell$
acts trivially on a 2-dimensional quotient space of
$G_\ell$
acts trivially on a 2-dimensional quotient space of
![]() $V_\ell$
.
$V_\ell$
.
In the first case, if
![]() $U_\ell=E[\ell](\overline K)\subset V_\ell$
is a subspace with trivial
$U_\ell=E[\ell](\overline K)\subset V_\ell$
is a subspace with trivial
![]() $G_\ell$
-action, then E(K) has complete
$G_\ell$
-action, then E(K) has complete
![]() $\ell$
-torsion and condition B is satisfied. If
$\ell$
-torsion and condition B is satisfied. If
![]() $G_\ell$
acts trivially on a different 2-dimensional subspace
$G_\ell$
acts trivially on a different 2-dimensional subspace
![]() $S_\ell\subset V_\ell$
, than
$S_\ell\subset V_\ell$
, than
![]() $S_\ell$
is spanned by a non-zero vector in
$S_\ell$
is spanned by a non-zero vector in
![]() $U_\ell\cap S_\ell$
and the non-zero image of a point of infinite order
$U_\ell\cap S_\ell$
and the non-zero image of a point of infinite order
![]() $Q\in \langle \ell^{-1}P\rangle$
in the
$Q\in \langle \ell^{-1}P\rangle$
in the
![]() ${\mathbf{F}}_\ell$
-vector space
${\mathbf{F}}_\ell$
-vector space
![]() $V_\ell$
. In other words: E(K) contains a torsion point of order
$V_\ell$
. In other words: E(K) contains a torsion point of order
![]() $\ell$
and a point Q with
$\ell$
and a point Q with
![]() $\ell Q=mP$
for some
$\ell Q=mP$
for some
![]() $m\in{\mathbf{Z}}$
that is not divisible by
$m\in{\mathbf{Z}}$
that is not divisible by
![]() $\ell$
. Writing
$\ell$
. Writing
![]() $am+b\ell=1$
in
$am+b\ell=1$
in
![]() ${\mathbf{Z}}$
, the point
${\mathbf{Z}}$
, the point
![]() $Q'=aQ+bP\in E(K)$
satisfies
$Q'=aQ+bP\in E(K)$
satisfies
![]() $\ell Q'= a\ell Q+b\ell P=amP+b\ell P=P$
, so condition A is satisfied.
$\ell Q'= a\ell Q+b\ell P=amP+b\ell P=P$
, so condition A is satisfied.
In the second case, where
![]() $G_\ell$
acts trivially on a 2-dimensional quotient space
$G_\ell$
acts trivially on a 2-dimensional quotient space
![]() $V_\ell/T_\ell$
, it acts on
$V_\ell/T_\ell$
, it acts on
![]() $V_\ell$
by translation along the 1-dimensional subspace
$V_\ell$
by translation along the 1-dimensional subspace
![]() $T_\ell$
. We will assume that
$T_\ell$
. We will assume that
![]() $G_\ell$
does not act trivially on the subspace
$G_\ell$
does not act trivially on the subspace
![]() $U_\ell$
, as this would bring us back in the first case, with condition B holding. As
$U_\ell$
, as this would bring us back in the first case, with condition B holding. As
![]() $U_\ell=E[\ell](\overline K)\subset V_\ell$
is
$U_\ell=E[\ell](\overline K)\subset V_\ell$
is
![]() $G_\ell$
-stable, we have strict inclusions
$G_\ell$
-stable, we have strict inclusions
![]() $0\subsetneq T_\ell\subsetneq U_\ell$
of
$0\subsetneq T_\ell\subsetneq U_\ell$
of
![]() ${\mathbf{F}}_\ell[G_\ell]$
-modules, so
${\mathbf{F}}_\ell[G_\ell]$
-modules, so
![]() $T_\ell$
is a K-rational subgroup of
$T_\ell$
is a K-rational subgroup of
![]() $E(\overline K)$
of order
$E(\overline K)$
of order
![]() $\ell$
. The corresponding isogeny
$\ell$
. The corresponding isogeny
![]() $E\to E'=E/T_\ell$
is defined over K, and identifies the
$E\to E'=E/T_\ell$
is defined over K, and identifies the
![]() ${\mathbf{F}}_\ell[G_\ell]$
-module
${\mathbf{F}}_\ell[G_\ell]$
-module
![]() $U_\ell/ T_\ell$
, which has trivial
$U_\ell/ T_\ell$
, which has trivial
![]() $G_\ell$
-action, with the subgroup of
$G_\ell$
-action, with the subgroup of
![]() $E^{\prime}$
(K) of order
$E^{\prime}$
(K) of order
![]() $\ell$
that is the kernel of the isogeny
$\ell$
that is the kernel of the isogeny
![]() $\phi\,:\, E'\to E$
dual to
$\phi\,:\, E'\to E$
dual to
![]() $\widehat\phi\,:\, E\to E'=E/T_\ell$
. If
$\widehat\phi\,:\, E\to E'=E/T_\ell$
. If
![]() $Q\in E(\overline K)$
satisfies
$Q\in E(\overline K)$
satisfies
![]() $\ell Q=P$
, then
$\ell Q=P$
, then
![]() $P'=\widehat\phi(Q)$
is in
$P'=\widehat\phi(Q)$
is in
![]() $E^{\prime}$
(K), as it is the image of any point in the Galois orbit
$E^{\prime}$
(K), as it is the image of any point in the Galois orbit
![]() $G_\ell\cdot Q\subset Q+T_\ell$
. Moreover, we have
$G_\ell\cdot Q\subset Q+T_\ell$
. Moreover, we have
![]() $\phi(P')=\phi\widehat\phi(Q)=\ell Q=P$
, so condition C of Theorem 1.2 is satisfied.
$\phi(P')=\phi\widehat\phi(Q)=\ell Q=P$
, so condition C of Theorem 1.2 is satisfied.
Conversely, each of the conditions A, B and C guarantees that
![]() $P\in E(K)$
is locally
$P\in E(K)$
is locally
![]() $\ell$
-imprimitive. For A and B this is immediate. If condition C holds, we have an
$\ell$
-imprimitive. For A and B this is immediate. If condition C holds, we have an
![]() $\ell$
-isogeny
$\ell$
-isogeny
![]() $\phi\,:\, E'\to E$
defined over K and a point
$\phi\,:\, E'\to E$
defined over K and a point
![]() $P'\in E'(K)$
with
$P'\in E'(K)$
with
![]() $\phi(P')=P$
. Pick
$\phi(P')=P$
. Pick
![]() $Q'\in E'(\overline K)$
with
$Q'\in E'(\overline K)$
with
![]() $\ell Q'=P'$
and put
$\ell Q'=P'$
and put
![]() $Q=\phi(Q')\in E(\overline K)$
. Writing
$Q=\phi(Q')\in E(\overline K)$
. Writing
![]() $\widehat\phi\,:\, E\to E'$
for the dual isogeny, we are in the situation of Example 4.2, and we have
$\widehat\phi\,:\, E\to E'$
for the dual isogeny, we are in the situation of Example 4.2, and we have
As Q is in the fibre
![]() $\widehat\phi^{-1}(P')$
, the
$\widehat\phi^{-1}(P')$
, the
![]() $G_\ell$
-action on
$G_\ell$
-action on
![]() $Q \bmod \langle P\rangle\in V_\ell$
, which is by translation over
$Q \bmod \langle P\rangle\in V_\ell$
, which is by translation over
![]() $\ell$
-torsion points, gives rise to a Galois orbit of length dividing
$\ell$
-torsion points, gives rise to a Galois orbit of length dividing
![]() $\ell$
. If the length is 1, then condition A is satisfied, and
$\ell$
. If the length is 1, then condition A is satisfied, and
![]() $P\in E(K)$
is locally
$P\in E(K)$
is locally
![]() $\ell$
-imprimitive. If the length is
$\ell$
-imprimitive. If the length is
![]() $\ell$
, then
$\ell$
, then
![]() $G_\ell$
acts on
$G_\ell$
acts on
![]() $V_\ell$
by translation along the K-rational subgroup
$V_\ell$
by translation along the K-rational subgroup
![]() $T_\ell=\ker\widehat\phi\subset U_\ell=E[\ell](\overline K)$
, and the matrix representation of
$T_\ell=\ker\widehat\phi\subset U_\ell=E[\ell](\overline K)$
, and the matrix representation of
![]() $G_\ell$
on
$G_\ell$
on
![]() $V_\ell$
with respect to the filtration
$V_\ell$
with respect to the filtration
![]() $T_\ell\subset U_\ell\subset V_\ell$
is
$T_\ell\subset U_\ell\subset V_\ell$
is
 \[\rho_{E/K,\ell} \sim\begin{pmatrix}* & && * & && * \\0 && & 1 & && 0 \\0 & && 0 & && 1\end{pmatrix}.\]
\[\rho_{E/K,\ell} \sim\begin{pmatrix}* & && * & && * \\0 && & 1 & && 0 \\0 & && 0 & && 1\end{pmatrix}.\]
By Lemma 2.3, we find that we have
![]() $\ell | [E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle ]$
for every prime
$\ell | [E(k_{\mathfrak{p}})\,:\,\langle {\bar P}\rangle ]$
for every prime
![]() ${\mathfrak{p}}$
of good reduction of E that is of characteristic different from
${\mathfrak{p}}$
of good reduction of E that is of characteristic different from
![]() $\ell$
, so
$\ell$
, so
![]() $P\in E(K)$
is locally
$P\in E(K)$
is locally
![]() $\ell$
-imprimitive.
$\ell$
-imprimitive.
5. Locally 2-imprimitive points
A non-trivial locally
![]() $\ell$
-imprimitive point on an elliptic curve
$\ell$
-imprimitive point on an elliptic curve
![]() $E/K$
is a non-torsion point
$E/K$
is a non-torsion point
![]() $P\in E(K)$
for which condition C of Theorem 1.2 holds, but not conditions A or B. If P is such a point, E admits a K-rational
$P\in E(K)$
for which condition C of Theorem 1.2 holds, but not conditions A or B. If P is such a point, E admits a K-rational
![]() $\ell$
-isogeny
$\ell$
-isogeny
![]() $E\to E'$
, and the Galois representation
$E\to E'$
, and the Galois representation
![]() $\bar\rho_{E, \ell}$
of
$\bar\rho_{E, \ell}$
of
![]() $G_K$
on
$G_K$
on
![]() $U_\ell=E[\ell](\bar K)$
is non-trivial, with image contained in a Borel subgroup of
$U_\ell=E[\ell](\bar K)$
is non-trivial, with image contained in a Borel subgroup of
![]() $\mathrm{GL}(U_\ell)$
.
$\mathrm{GL}(U_\ell)$
.
In the case
![]() $\ell=2$
, a Borel subgroup of
$\ell=2$
, a Borel subgroup of
![]() $\mathrm{GL}(U_2)\cong \mathrm{GL}_2({\mathbf{F}}_2)$
has order 2, and the existence of a non-trivial locally 2-imprimitive point
$\mathrm{GL}(U_2)\cong \mathrm{GL}_2({\mathbf{F}}_2)$
has order 2, and the existence of a non-trivial locally 2-imprimitive point
![]() $P\in E(K)$
implies that we have
$P\in E(K)$
implies that we have
![]() $\#E(K)[2]=2$
, and that
$\#E(K)[2]=2$
, and that
![]() $\bar\rho_{E, 2}$
is a non-trivial quadratic character.
$\bar\rho_{E, 2}$
is a non-trivial quadratic character.
If
![]() $T\in E(K)$
is a point of order 2, we can choose a Weierstrass model
$T\in E(K)$
is a point of order 2, we can choose a Weierstrass model
for
![]() $E/K$
in which we have
$E/K$
in which we have
![]() $T=(0,0)$
. The representation
$T=(0,0)$
. The representation
![]() $\bar \rho_{E, 2}$
corresponds to the 2-division field of E over K, which equals
$\bar \rho_{E, 2}$
corresponds to the 2-division field of E over K, which equals
![]() $K(\sqrt d)$
, and we have
$K(\sqrt d)$
, and we have
![]() $\#E(\overline K)[2]=2$
if and only
$\#E(\overline K)[2]=2$
if and only
![]() $d\in K^*$
is not a square.
$d\in K^*$
is not a square.
Addition by (0, 0) induces an involution
on the function field
![]() $K(E)=K(x,y)$
of E, and the invariant field
$K(E)=K(x,y)$
of E, and the invariant field
![]() $K(x+x_1, y+y_1)$
is the function field of the 2-isogenous curve
$K(x+x_1, y+y_1)$
is the function field of the 2-isogenous curve
![]() $E'=E/\langle(0,0)\rangle$
. Choosing
$E'=E/\langle(0,0)\rangle$
. Choosing
![]() $u=x+x_1+a$
and
$u=x+x_1+a$
and
![]() $v=y+y_1$
as generators for K(
$v=y+y_1$
as generators for K(
![]() $E^{\prime}$
), we obtain a Weierstrass model
$E^{\prime}$
), we obtain a Weierstrass model
for
![]() $E^{\prime}$
that is of the same form (5·1), and an explicit 2-isogeny
$E^{\prime}$
that is of the same form (5·1), and an explicit 2-isogeny
![]() $\varphi\,:\, E\to E'$
given by
$\varphi\,:\, E\to E'$
given by
An affine point
![]() $(u,v)\in E'(K)$
different from (0, 0) is in the image of E(K) under this isogeny if and only if
$(u,v)\in E'(K)$
different from (0, 0) is in the image of E(K) under this isogeny if and only if
![]() $u\in K^*$
is a square. The point (0, 0) is in the image if and only if d is a square in
$u\in K^*$
is a square. The point (0, 0) is in the image if and only if d is a square in
![]() $K^*$
, which amounts to saying that E(K) has full 2-torsion.
$K^*$
, which amounts to saying that E(K) has full 2-torsion.
As
![]() $E^{\prime}$
is again of the form (5·1), one sees that the isogeny
$E^{\prime}$
is again of the form (5·1), one sees that the isogeny
![]() $\widehat\varphi\,:\, E'\to E$
dual to
$\widehat\varphi\,:\, E'\to E$
dual to
![]() $\varphi$
is given by
$\varphi$
is given by
Proof of Theorem
1.3. Let
![]() $E/K$
be an elliptic curve with
$E/K$
be an elliptic curve with
![]() $\#E(K)[2]=2$
. We take (0, 0) as the point of order 2 in a Weierstrass model of E in order to obtain an equation
$\#E(K)[2]=2$
. We take (0, 0) as the point of order 2 in a Weierstrass model of E in order to obtain an equation
![]() $E\,:\, y^2=x(x^2+ax+b)$
as in (5·1), with
$E\,:\, y^2=x(x^2+ax+b)$
as in (5·1), with
![]() $d=a^2-4b\in K^*\setminus {K^*}^2$
. Any quadratic twist of E over K is of the form
$d=a^2-4b\in K^*\setminus {K^*}^2$
. Any quadratic twist of E over K is of the form
for some
![]() $D\in K^*$
that we may still rescale by squares in
$D\in K^*$
that we may still rescale by squares in
![]() $K^*$
, and we can define the 2-isogeny
$K^*$
, and we can define the 2-isogeny
![]() $\varphi\,:\, E_D \to E_D'=E_D/\langle (0,0)\rangle$
as above by replacing (a, b) in (5·1), (5·2) and (5·3) by
$\varphi\,:\, E_D \to E_D'=E_D/\langle (0,0)\rangle$
as above by replacing (a, b) in (5·1), (5·2) and (5·3) by
![]() $(aD, bD^2)$
. Any point
$(aD, bD^2)$
. Any point
![]() $P\in E_D(K)$
satisfying condition C from Theorem 1.2 is in the image
$P\in E_D(K)$
satisfying condition C from Theorem 1.2 is in the image
![]() $\widehat\varphi(E_D'(K))$
of the isogeny
$\widehat\varphi(E_D'(K))$
of the isogeny
![]() $\widehat\varphi\,:\, E_D'\to E_D$
dual to
$\widehat\varphi\,:\, E_D'\to E_D$
dual to
![]() $\varphi$
. This means that its x-coordinate is a square in
$\varphi$
. This means that its x-coordinate is a square in
![]() $K^*$
, which we can take to be 1 after rescaling the model of E over K. Thus, the twists that are relevant for us are those for which the point
$K^*$
, which we can take to be 1 after rescaling the model of E over K. Thus, the twists that are relevant for us are those for which the point
![]() $P=(1,\pm Y)\in E_D(\bar K)$
is K-rational.
$P=(1,\pm Y)\in E_D(\bar K)$
is K-rational.
We want (D, Y) to be a K-rational point on the conic
![]() $Y^2=1+aD+bD^2$
different from
$Y^2=1+aD+bD^2$
different from
![]() $(0,\pm 1)$
. Such points are obtained as the second point of intersection of this conic with the line
$(0,\pm 1)$
. Such points are obtained as the second point of intersection of this conic with the line
![]() $Y-1=\lambda D$
through (0, 1) with slope
$Y-1=\lambda D$
through (0, 1) with slope
![]() $\lambda \in K$
. We find that the twists
$\lambda \in K$
. We find that the twists
![]() $E_\lambda=E_{D_\lambda}$
of E by
$E_\lambda=E_{D_\lambda}$
of E by
come by construction with a K-rational point
We can find
![]() $K_2=K(\frac{1}{2} P_\lambda)$
by solving
$K_2=K(\frac{1}{2} P_\lambda)$
by solving
![]() $2Q=\widehat\varphi(\varphi Q) = P_\lambda$
in
$2Q=\widehat\varphi(\varphi Q) = P_\lambda$
in
![]() $E_\lambda(\overline K)$
. The equation
$E_\lambda(\overline K)$
. The equation
![]() $\widehat\varphi(u,v)=P_\lambda$
has 2 solutions in
$\widehat\varphi(u,v)=P_\lambda$
has 2 solutions in
![]() $E'_\lambda(K)$
, since we chose for the first coordinate of
$E'_\lambda(K)$
, since we chose for the first coordinate of
![]() $P_\lambda$
the square value 1. By (5·4), these are the K-rational points (u, v) different from (0, 0) that have
$P_\lambda$
the square value 1. By (5·4), these are the K-rational points (u, v) different from (0, 0) that have
![]() $v^2=4u^2$
and satisfy the equation
$v^2=4u^2$
and satisfy the equation
defining
![]() $E'_\lambda$
. With
$E'_\lambda$
. With
![]() $d=a^2-4b$
, the resulting equation
$d=a^2-4b$
, the resulting equation
for u yields two solutions
![]() $u_1, u_2 = aD_\lambda+2 \pm Y_\lambda \in K$
with product
$u_1, u_2 = aD_\lambda+2 \pm Y_\lambda \in K$
with product
![]() $u_1u_2=dD_\lambda^2$
. Writing
$u_1u_2=dD_\lambda^2$
. Writing
![]() $D_\lambda$
and
$D_\lambda$
and
![]() $P_\lambda$
as in (5·5) and (5·6), we find
$P_\lambda$
as in (5·5) and (5·6), we find
![]() $aD_\lambda+2 - Y_\lambda=d/(\lambda^2-b)$
, so the minimal extension
$aD_\lambda+2 - Y_\lambda=d/(\lambda^2-b)$
, so the minimal extension
![]() $K\subset K_2$
for which the corresponding points are in
$K\subset K_2$
for which the corresponding points are in
![]() $\varphi[E(K_2)]$
is
$\varphi[E(K_2)]$
is
If we avoid the values
![]() $\lambda\in K$
for which
$\lambda\in K$
for which
![]() $\lambda^2 - b$
is either a square or d times a square in K–this includes the 3 values excluded in (5·5) then
$\lambda^2 - b$
is either a square or d times a square in K–this includes the 3 values excluded in (5·5) then
![]() $K_2$
is a biquadratic extension of K which, unsurprisingly, has the 2-division field
$K_2$
is a biquadratic extension of K which, unsurprisingly, has the 2-division field
![]() $K(\sqrt d)$
of
$K(\sqrt d)$
of
![]() $E/K$
as one of its quadratic subextensions. For these
$E/K$
as one of its quadratic subextensions. For these
![]() $\lambda$
, our matrix representation from (2·4) and (2·5) of
$\lambda$
, our matrix representation from (2·4) and (2·5) of
![]() $G_2=\mathrm{Gal}(K_2/K)$
becomes
$G_2=\mathrm{Gal}(K_2/K)$
becomes
 \[\mathrm{Gal}(K_2/K)=\left\{ \begin{bmatrix}1 & && x &&& y \\0 &&& 1 &&& 0 \\0 &&& 0 &&& 1\end{bmatrix}\,:\, x,y\in{\mathbf{F}}_2 \right\},\]
\[\mathrm{Gal}(K_2/K)=\left\{ \begin{bmatrix}1 & && x &&& y \\0 &&& 1 &&& 0 \\0 &&& 0 &&& 1\end{bmatrix}\,:\, x,y\in{\mathbf{F}}_2 \right\},\]
which implies that
![]() $P_\lambda\in E_\lambda(K)$
is globally 2-primitive, but locally 2-imprimitive.
$P_\lambda\in E_\lambda(K)$
is globally 2-primitive, but locally 2-imprimitive.
There is still the possibility that
![]() $P_\lambda$
, though globally 2-primitive, is a torsion point of even order
$P_\lambda$
, though globally 2-primitive, is a torsion point of even order
![]() $m>2$
. Examples: the point
$m>2$
. Examples: the point
![]() $(1,-3)$
on
$(1,-3)$
on
![]() $y^2=x(x^2-7x+3)$
has order 4, and the point (1, 1) on
$y^2=x(x^2-7x+3)$
has order 4, and the point (1, 1) on
![]() $y^2=x(x^2+3x-3)$
has order 6. However, for fixed K there are only finitely many possibilities for m by Merel’s theorem. For every given even m, the point
$y^2=x(x^2+3x-3)$
has order 6. However, for fixed K there are only finitely many possibilities for m by Merel’s theorem. For every given even m, the point
![]() $P_\lambda$
is of order m if and only if the m-th division polynomial
$P_\lambda$
is of order m if and only if the m-th division polynomial
![]() $\psi_m(x)=y^{-1}f(x, E_\lambda)$
vanishes at
$\psi_m(x)=y^{-1}f(x, E_\lambda)$
vanishes at
![]() $x=1$
. This happens for only finitely many values of
$x=1$
. This happens for only finitely many values of
![]() $\lambda$
, as
$\lambda$
, as
![]() $f(1,E_\lambda)$
is a non-constant rational function of
$f(1,E_\lambda)$
is a non-constant rational function of
![]() $\lambda$
if we fix
$\lambda$
if we fix
![]() $a,b \in K$
.
$a,b \in K$
.
Our understanding of local 2-imprimitivity is more or less complete, as every non-trivial 2-locally imprimitive point on an elliptic curve arises as in the construction in the proof of Theorem 1.3. Indeed, the hypothesis
![]() $\#E[2](\overline K)=2$
implies that E has a model as in (5·1), and as the x-coordinate of a point P satisfying condition C of Theorem 1.2 is a square, the model can be scaled over K to have
$\#E[2](\overline K)=2$
implies that E has a model as in (5·1), and as the x-coordinate of a point P satisfying condition C of Theorem 1.2 is a square, the model can be scaled over K to have
![]() $P=(1,y)\in E(K)$
.
$P=(1,y)\in E(K)$
.
6. Locally 3-imprimitive points
By Theorem 1.2, every pair (E,P) of an elliptic curve
![]() $E/K$
with a non-trivial locally
$E/K$
with a non-trivial locally
![]() $\ell$
-imprimitive point
$\ell$
-imprimitive point
![]() $P\in E(K)$
arises as the
$P\in E(K)$
arises as the
![]() $\ell$
-isogenous image of a K-rational curve-point-pair (
$\ell$
-isogenous image of a K-rational curve-point-pair (
![]() $E^{\prime},P^{\prime}$
) for which the kernel
$E^{\prime},P^{\prime}$
) for which the kernel
![]() $E'\to E$
is generated by an
$E'\to E$
is generated by an
![]() $\ell$
-torsion point
$\ell$
-torsion point
![]() $T\in E'(K)$
. In this situation, the Galois representations of
$T\in E'(K)$
. In this situation, the Galois representations of
![]() $G_K$
on the
$G_K$
on the
![]() $\ell$
-torsion subgroups of
$\ell$
-torsion subgroups of
![]() $E^{\prime}$
and
$E^{\prime}$
and
![]() $E=E'/\langle T\rangle$
are, with respect to a suitable basis, of the form
$E=E'/\langle T\rangle$
are, with respect to a suitable basis, of the form
Here
![]() $\omega_\ell$
is the cyclotomic character corresponding to the extension
$\omega_\ell$
is the cyclotomic character corresponding to the extension
![]() $K\subset K(\zeta_\ell)$
. For
$K\subset K(\zeta_\ell)$
. For
![]() $\ell > 2$
, the K-rationality of
$\ell > 2$
, the K-rationality of
![]() $\ell$
-torsion points of E is not preserved under twisting of E, so there is no direct analogue of Theorem 1.3 for
$\ell$
-torsion points of E is not preserved under twisting of E, so there is no direct analogue of Theorem 1.3 for
![]() $\ell\ne2$
. In this section we focus on the case
$\ell\ne2$
. In this section we focus on the case
![]() $\ell=3$
.
$\ell=3$
.
Lemma 6.1. Let
![]() $E/K$
be an elliptic curve of discriminant
$E/K$
be an elliptic curve of discriminant
![]() $\Delta_{E}$
for which the Galois representation
$\Delta_{E}$
for which the Galois representation
![]() $\rho_{E/K, 3}$
on
$\rho_{E/K, 3}$
on
![]() $U_3=E[3](\overline K)$
is of one of the two forms in (6·1). Then the 3-division field of E over K equals the splitting field of the polynomial
$U_3=E[3](\overline K)$
is of one of the two forms in (6·1). Then the 3-division field of E over K equals the splitting field of the polynomial
![]() $X^3-\Delta_{E}$
.
$X^3-\Delta_{E}$
.
Proof. Let
![]() $H_3=\mathrm{Gal}(K(E[3])/K)\subset \mathrm{GL}(U_3)\cong \mathrm{GL}_2({\mathbf{F}}_3)$
be the image of
$H_3=\mathrm{Gal}(K(E[3])/K)\subset \mathrm{GL}(U_3)\cong \mathrm{GL}_2({\mathbf{F}}_3)$
be the image of
![]() $\rho_{E/K, 3}$
, and denote by
$\rho_{E/K, 3}$
, and denote by
![]() $\psi_3=\prod_{i=1}^4 (X- x_i)\in K[X]$
the 3-division polynomial of E over K. The quartic polynomial
$\psi_3=\prod_{i=1}^4 (X- x_i)\in K[X]$
the 3-division polynomial of E over K. The quartic polynomial
![]() $\psi_3$
comes with a Galois resolvent
$\psi_3$
comes with a Galois resolvent
![]() $\delta_3\in K[X]$
, a cubic having
$\delta_3\in K[X]$
, a cubic having
as its roots. Under the permutation action of
![]() $\mathrm{GL}(U_3)/\langle -1\rangle=S_4$
on the roots of
$\mathrm{GL}(U_3)/\langle -1\rangle=S_4$
on the roots of
![]() $\psi_3$
, the normal subgroup
$\psi_3$
, the normal subgroup
![]() $V_4\triangleleft S_4$
of order 4 fixes each of these 3 roots
$V_4\triangleleft S_4$
of order 4 fixes each of these 3 roots
![]() $\alpha_i$
. The two natural surjections of Galois groups
$\alpha_i$
. The two natural surjections of Galois groups
are isomorphisms as they arise as a restriction to suitable subgroups of the generic group theoretical maps
More precisely, the first surjection in (6·2) is injective as we have
![]() $-1\notin H_3$
for
$-1\notin H_3$
for
![]() $H_3$
as in (6·1), and the second is because we have
$H_3$
as in (6·1), and the second is because we have
![]() $\mathrm{Gal}(\psi_3)\cap V_4= 1 $
in
$\mathrm{Gal}(\psi_3)\cap V_4= 1 $
in
![]() $S_4$
: the x-coordinate of the 3-torsion point spanning the Galois invariant subspace corresponding to the first column of the matrices is fixed by
$S_4$
: the x-coordinate of the 3-torsion point spanning the Galois invariant subspace corresponding to the first column of the matrices is fixed by
![]() $\mathrm{Gal}(\psi_3)$
. Viewing
$\mathrm{Gal}(\psi_3)$
. Viewing
![]() $H_3$
as
$H_3$
as
![]() $\mathrm{Gal}(\delta_3)$
, we may finish the proof by quoting a classical formula [
Reference Serre14
, p. 305] that expresses the three cube roots of
$\mathrm{Gal}(\delta_3)$
, we may finish the proof by quoting a classical formula [
Reference Serre14
, p. 305] that expresses the three cube roots of
![]() $\Delta_E$
as
$\Delta_E$
as
![]() $b_4-3\alpha_i$
(
$b_4-3\alpha_i$
(
![]() $i=1,2,3$
), with
$i=1,2,3$
), with
![]() $b_i\in K$
a coefficient from the Weierstrass model of E. This yields
$b_i\in K$
a coefficient from the Weierstrass model of E. This yields
![]() $K(E[3])=\mathrm{Split}_K(\delta_3)=\mathrm{Split}_K(X^3-\Delta_{E})$
.
$K(E[3])=\mathrm{Split}_K(\delta_3)=\mathrm{Split}_K(X^3-\Delta_{E})$
.
From Lemma 6.1, we see that for the representations in (6·1), the subgroup
![]() $\binom{1\ *}{0\ 1}$
corresponds to the extension
$\binom{1\ *}{0\ 1}$
corresponds to the extension
![]() $K(\zeta_3)\subset K(\zeta_3,\root 3 \of \Delta)$
for the discriminant values
$K(\zeta_3)\subset K(\zeta_3,\root 3 \of \Delta)$
for the discriminant values
![]() $\Delta=\Delta_{E'}$
and
$\Delta=\Delta_{E'}$
and
![]() $\Delta_E$
.
$\Delta_E$
.
We can write the curve
![]() $E^{\prime}$
in Deuring normal form [
Reference Husemöller7
, p. 89] as
$E^{\prime}$
in Deuring normal form [
Reference Husemöller7
, p. 89] as
Here
![]() $T=(0,0)\in E'(K)$
is the point of order 3, and the quotient curve
$T=(0,0)\in E'(K)$
is the point of order 3, and the quotient curve
![]() $E=E'/\langle T\rangle$
has Weierstrass equation
$E=E'/\langle T\rangle$
has Weierstrass equation
with the explicit formula for the 3-isogeny
![]() $\varphi_3\,:\, E'\to E=E'/\langle T\rangle$
being given by
$\varphi_3\,:\, E'\to E=E'/\langle T\rangle$
being given by
As E has discriminant
![]() $\Delta_E=b(a^3-27b)^3$
, the 3-division field K(E[3]) over K equals
$\Delta_E=b(a^3-27b)^3$
, the 3-division field K(E[3]) over K equals
![]() $K(\zeta_3)$
if and only if
$K(\zeta_3)$
if and only if
![]() $b\in K^*$
is a cube and different from
$b\in K^*$
is a cube and different from
![]() $(a/3)^3$
.
$(a/3)^3$
.
If a is non-zero, we can rescale
![]() $(x, y)\mapsto (a^2x, a^3y)$
and simplify (6·3) to
$(x, y)\mapsto (a^2x, a^3y)$
and simplify (6·3) to
For K a number field, we have infinitely many pairwise different 3-isogenous images
![]() $(E_b, P_b)=\varphi_3[(E_b', P_b')]$
for which
$(E_b, P_b)=\varphi_3[(E_b', P_b')]$
for which
![]() $P_b\in E_b(K)$
is non-trivially locally 3-imprimitive.
$P_b\in E_b(K)$
is non-trivially locally 3-imprimitive.
Theorem 6.2. For K a number field, take
![]() $b=b(X)=(1-X-X^2)/X\in K(X)$
and define the associated elliptic curve over K(X) as
$b=b(X)=(1-X-X^2)/X\in K(X)$
and define the associated elliptic curve over K(X) as
Then for infinitely many
![]() $t\in K^*$
, the specialisation
$t\in K^*$
, the specialisation
![]() $E_{b(t)}$
of
$E_{b(t)}$
of
![]() $E_b$
is an elliptic curve over K for which
$E_b$
is an elliptic curve over K for which
 \begin{equation} \left(\frac{(t^2+t)(t^2-1)+1}{t^2}, \frac{(1-t^2)\left(t^4+2 t^3+t-1\right)}{t^3}\right)\in E_{b(t)}(K)\end{equation}
\begin{equation} \left(\frac{(t^2+t)(t^2-1)+1}{t^2}, \frac{(1-t^2)\left(t^4+2 t^3+t-1\right)}{t^3}\right)\in E_{b(t)}(K)\end{equation}
is a non-trivial locally 3-imprimitive point.
Proof. For the curve
![]() $E'_b$
in (6·6) with
$E'_b$
in (6·6) with
![]() $b\in K(X)$
as defined, the point
$b\in K(X)$
as defined, the point
![]() $P'_b=(1, X)$
lies on
$P'_b=(1, X)$
lies on
![]() $E'_b$
by the very choice of b: it satisfies
$E'_b$
by the very choice of b: it satisfies
![]() $X^2+X+bX=1$
. Under the 3-isogeny
$X^2+X+bX=1$
. Under the 3-isogeny
![]() $\varphi_3\,:\, E'_b\to E_b$
from (6·5) to the curve
$\varphi_3\,:\, E'_b\to E_b$
from (6·5) to the curve
![]() $E_b$
obtained by putting
$E_b$
obtained by putting
![]() $a=1$
in (6·4), it is mapped to
$a=1$
in (6·4), it is mapped to
Under the specialisation
![]() $X=t\in K^*$
, we obtain a point
$X=t\in K^*$
, we obtain a point
![]() $P_{b(t)}$
, on the curve
$P_{b(t)}$
, on the curve
![]() $E_{b(t)}$
defined over K that is given by (6·7). We are only interested in those specialisations for which
$E_{b(t)}$
defined over K that is given by (6·7). We are only interested in those specialisations for which
![]() $E_{b(t)}$
is an elliptic curve. As these are all
$E_{b(t)}$
is an elliptic curve. As these are all
![]() $t\in K^*$
for which
$t\in K^*$
for which
![]() $b(t)\notin \{0, 1/27\}$
, at most 4 ‘bad’ values of t are excluded. Also, by the same argument as we gave for
$b(t)\notin \{0, 1/27\}$
, at most 4 ‘bad’ values of t are excluded. Also, by the same argument as we gave for
![]() $P_\lambda$
in the case
$P_\lambda$
in the case
![]() $\ell=2$
, there are only finitely many
$\ell=2$
, there are only finitely many
![]() $t\in K^*$
for which
$t\in K^*$
for which
![]() $P_t$
is torsion point. These finitely many t we also exclude as ‘bad’ values.
$P_t$
is torsion point. These finitely many t we also exclude as ‘bad’ values.
We saw already that
![]() $E_b$
has 3-division field
$E_b$
has 3-division field
![]() $K(\zeta_3, \root 3 \of b)$
, and an explicit computation shows that the 3-division field of the point
$K(\zeta_3, \root 3 \of b)$
, and an explicit computation shows that the 3-division field of the point
![]() $P_b\in E_b(K(X))$
equals
$P_b\in E_b(K(X))$
equals
Over
![]() $K(\zeta_3, X)$
, the elements X and
$K(\zeta_3, X)$
, the elements X and
![]() $X^2+X-1$
have ‘independent’ cube roots – it suffices look at their ramification locus. It follows that the Galois group of the 3-division field of
$X^2+X-1$
have ‘independent’ cube roots – it suffices look at their ramification locus. It follows that the Galois group of the 3-division field of
![]() $P_b$
over K(X) may be described as
$P_b$
over K(X) may be described as
 \[\mathrm{Gal}\left(K(X)\left(\dfrac13 P_b\right)/K(X)\right)=\left\{ \begin{bmatrix}\omega_3 &&& x &&& y \\0 &&& 1 &&& 0 \\0 &&& 0 &&& 1\end{bmatrix}\,:\, x,y\in{\mathbf{F}}_3 \right\},\]
\[\mathrm{Gal}\left(K(X)\left(\dfrac13 P_b\right)/K(X)\right)=\left\{ \begin{bmatrix}\omega_3 &&& x &&& y \\0 &&& 1 &&& 0 \\0 &&& 0 &&& 1\end{bmatrix}\,:\, x,y\in{\mathbf{F}}_3 \right\},\]
with
![]() $\omega_3$
denoting the
$\omega_3$
denoting the
![]() ${\mathbf{F}}_3^*$
-valued character corresponding to the (possibly trivial) extension
${\mathbf{F}}_3^*$
-valued character corresponding to the (possibly trivial) extension
![]() $K(X)\subset K(X, \zeta_3)$
. By Hilbert irreducibility, it follows that for infinitely many
$K(X)\subset K(X, \zeta_3)$
. By Hilbert irreducibility, it follows that for infinitely many
![]() $t\in K^*$
outside the finite set of ‘bad’ values, the 3-division field of the point
$t\in K^*$
outside the finite set of ‘bad’ values, the 3-division field of the point
![]() $P_{b(t)}\in E_{b(t)}(K)$
has the ‘same’ Galois group over K, making it into a point that is globally 3-primitive, but locally 3-imprimitive. As
$P_{b(t)}\in E_{b(t)}(K)$
has the ‘same’ Galois group over K, making it into a point that is globally 3-primitive, but locally 3-imprimitive. As
![]() $E_{b(t)}$
does not have complete 3-torsion over K, we conclude that the point
$E_{b(t)}$
does not have complete 3-torsion over K, we conclude that the point
![]() $P_{b(t)}$
given in (6·7) is a non-trivial locally 3-imprimitive point.
$P_{b(t)}$
given in (6·7) is a non-trivial locally 3-imprimitive point.
Remark 6.3.
The construction in the proof of Theorem 6.2 excludes all specialisations for which
![]() $b=b(t)\in K^*$
is a cube and the elliptic curve in (6·6) has 3-division field
$b=b(t)\in K^*$
is a cube and the elliptic curve in (6·6) has 3-division field
![]() $K(\zeta_3)$
. In this special case, we can also equip
$K(\zeta_3)$
. In this special case, we can also equip
![]() $E=E_b$
with a non-trivial locally 3-imprimitive point for infinitely many
$E=E_b$
with a non-trivial locally 3-imprimitive point for infinitely many
![]() $b\in {K^*}^3$
. We first write
$b\in {K^*}^3$
. We first write
![]() $b=c^{-3}$
and transform the curve under
$b=c^{-3}$
and transform the curve under
![]() $(x,y)\mapsto (c^{-2}x, c^{-3}y)$
into
$(x,y)\mapsto (c^{-2}x, c^{-3}y)$
into
![]() $E'\,:\,y^2+cxy+y=x^3$
. As in the previous case, we have
$E'\,:\,y^2+cxy+y=x^3$
. As in the previous case, we have
![]() $P'=(1,t)\in E'(K)$
for
$P'=(1,t)\in E'(K)$
for
![]() $c=({-}t^2-t+1)/t$
, and the image of
$c=({-}t^2-t+1)/t$
, and the image of
![]() $P^{\prime}$
under the map
$P^{\prime}$
under the map
is the point
![]() $P=\varphi_3(P')=(({-}t^2 + t + 1)/t, (t^2 - 1)/t^2)\in E(K)$
, for which the 3-division field
$P=\varphi_3(P')=(({-}t^2 + t + 1)/t, (t^2 - 1)/t^2)\in E(K)$
, for which the 3-division field
![]() $K(\frac13P)$
is equal to
$K(\frac13P)$
is equal to
![]() $K(\zeta_3,\sqrt[3]t)$
. For almost all
$K(\zeta_3,\sqrt[3]t)$
. For almost all
![]() $t\notin {K^*}^3$
, this makes P into a globally 3-primitive point that is locally 3-imprimitive.
$t\notin {K^*}^3$
, this makes P into a globally 3-primitive point that is locally 3-imprimitive.
We conclude our discussion for
![]() $\ell=3$
with the remaining case in which the curve
$\ell=3$
with the remaining case in which the curve
![]() $E^{\prime}$
in (6·3) has
$E^{\prime}$
in (6·3) has
![]() $a=0$
. In this case
$a=0$
. In this case
![]() $E^{\prime}$
has j-invariant 0, and writing
$E^{\prime}$
has j-invariant 0, and writing
![]() $c=b/2$
we may rescale the equation by
$c=b/2$
we may rescale the equation by
![]() $y\mapsto y-c$
to the more familiar shape
$y\mapsto y-c$
to the more familiar shape
![]() $E'\,:\, y^2=x^3+c^2$
, with 3-torsion point
$E'\,:\, y^2=x^3+c^2$
, with 3-torsion point
![]() $T=(0,c)$
and CM by
$T=(0,c)$
and CM by
![]() ${\mathbf{Z}}[\zeta_3]$
. We equip
${\mathbf{Z}}[\zeta_3]$
. We equip
![]() $E^{\prime}$
with a K-rational point
$E^{\prime}$
with a K-rational point
![]() $(c, c\sqrt{c+1})$
by putting
$(c, c\sqrt{c+1})$
by putting
![]() $c=s^2-1$
with
$c=s^2-1$
with
![]() $s\in K$
. This leads to a 1-parameter family of 3-isogenies
$s\in K$
. This leads to a 1-parameter family of 3-isogenies
between CM-curves with j-invariant 0. In this case the 3-division field of
![]() $E_s$
over K is
$E_s$
over K is
![]() $K(\zeta_3, \root 3 \of {2(s^2-1)})$
, and the 3-division field of
$K(\zeta_3, \root 3 \of {2(s^2-1)})$
, and the 3-division field of
![]() $P_s$
over K equals
$P_s$
over K equals
Again, for
![]() $s\in K$
outside a thin set, the point
$s\in K$
outside a thin set, the point
![]() $P_s\in E_s(K)$
is globally 3-primitive but locally 3-imprimitive.
$P_s\in E_s(K)$
is globally 3-primitive but locally 3-imprimitive.
7. Further examples
Over
![]() $K={\mathbf{Q}}$
, non-trivial locally
$K={\mathbf{Q}}$
, non-trivial locally
![]() $\ell$
-imprimitive points can only occur for primes
$\ell$
-imprimitive points can only occur for primes
![]() $\ell\le 7$
. Examples for
$\ell\le 7$
. Examples for
![]() $\ell=5$
and also
$\ell=5$
and also
![]() $\ell=7$
can be found by the techniques that we employed for
$\ell=7$
can be found by the techniques that we employed for
![]() $\ell=3$
, but the formulas and resulting curves rapidly become less suitable for presentation on paper.
$\ell=3$
, but the formulas and resulting curves rapidly become less suitable for presentation on paper.
7.1. Curves with a locally 5-imprimitive point
In this case, we start from Tate’s normal form
that parametrises elliptic curves with (0, 0) as a 5-rational point (see Kulesz [
Reference Kulesz8
]). It has further points (0, c), (c, 0) and
![]() $(c,\, c^2)$
of order 5, and its discriminant equals
$(c,\, c^2)$
of order 5, and its discriminant equals
![]() $\Delta_{E'}=c^5 \left(c^2-11 c-1\right)$
. Using Vélu’s formula [
Reference Vélu20
] or invoking Pari-GP, we compute the Weierstrass equation for the 5-isogenous curve
$\Delta_{E'}=c^5 \left(c^2-11 c-1\right)$
. Using Vélu’s formula [
Reference Vélu20
] or invoking Pari-GP, we compute the Weierstrass equation for the 5-isogenous curve
![]() $E=E'/\langle(0,0)\rangle$
$E=E'/\langle(0,0)\rangle$
and also the explicit 5-isogeny
![]() $\varphi_5\,:\, E'\rightarrow E$
. The discriminants involved are
$\varphi_5\,:\, E'\rightarrow E$
. The discriminants involved are
![]() $\Delta_{E'}=c^5 (c^2-11c-1)$
and
$\Delta_{E'}=c^5 (c^2-11c-1)$
and
![]() $\Delta_{E}=c(c^2-11c-1)^5$
, much like we saw for
$\Delta_{E}=c(c^2-11c-1)^5$
, much like we saw for
![]() $\ell=3$
. The 5-torsion representations of
$\ell=3$
. The 5-torsion representations of
![]() $E^{\prime}$
and E are as in (6·1), and even though the proof of Lemma 6 for
$E^{\prime}$
and E are as in (6·1), and even though the proof of Lemma 6 for
![]() $\ell=3$
does not generalise to
$\ell=3$
does not generalise to
![]() $\ell=5$
, we found by a direct calculation that the 5-division field is
$\ell=5$
, we found by a direct calculation that the 5-division field is
![]() $K(E[5])=K(\zeta_5,\sqrt[5]{c})$
: generated over
$K(E[5])=K(\zeta_5,\sqrt[5]{c})$
: generated over
![]() $K(\zeta_5)$
by the 5-th root of the discriminant.
$K(\zeta_5)$
by the 5-th root of the discriminant.
We can equip
![]() $E^{\prime}$
with a K-rational point
$E^{\prime}$
with a K-rational point
![]() $P_t'=(t,t)$
by putting
$P_t'=(t,t)$
by putting
![]() $c=t(2-t)$
, and compute its image
$c=t(2-t)$
, and compute its image
![]() $P_t=\varphi_5(P')\in E_{t(2-t)}(K)$
as
$P_t=\varphi_5(P')\in E_{t(2-t)}(K)$
as
The corresponding 5-division field of
![]() $P_t$
is
$P_t$
is
If this is an extension of degree 5 of
![]() $K(\zeta_5, \root 5 \of c)=K(\zeta_5, \root 5 \of {t(t-2)})$
, then
$K(\zeta_5, \root 5 \of c)=K(\zeta_5, \root 5 \of {t(t-2)})$
, then
![]() $P_t$
is a globally 5-primitive but locally 5-imprimitive point in
$P_t$
is a globally 5-primitive but locally 5-imprimitive point in
![]() $E_{t(2-t)}(K)$
.
$E_{t(2-t)}(K)$
.
Example 7.1. Take
![]() $K={\mathbf{Q}}$
. For
$K={\mathbf{Q}}$
. For
![]() $t=1$
the point
$t=1$
the point
![]() $P_t$
above is the zero point as
$P_t$
above is the zero point as
![]() $P'_t$
is 5-torsion, for
$P'_t$
is 5-torsion, for
![]() $t=2$
we have
$t=2$
we have
![]() $c=0$
and E is singular, while for
$c=0$
and E is singular, while for
![]() $t=3$
and 4 we encounter the ‘accidents’
$t=3$
and 4 we encounter the ‘accidents’
![]() $t=-c$
and
$t=-c$
and
![]() $tc=2^5$
leading to points
$tc=2^5$
leading to points
![]() $P_t\in 5E_{t(2-t)}({\mathbf{Q}})$
. For
$P_t\in 5E_{t(2-t)}({\mathbf{Q}})$
. For
![]() $t=5$
we obtain the point
$t=5$
we obtain the point
![]() $P_5=(497/16, -73441/64)$
on
$P_5=(497/16, -73441/64)$
on
which is the curve 5835.c2 in the LMFDB-database [
19
]. Note that for
![]() $c=-15$
we have
$c=-15$
we have
The locally 5-imprimitive point
![]() $P_5$
is a generator of
$P_5$
is a generator of
![]() $E_{-15}({\mathbf{Q}})\cong{\mathbf{Z}}$
. In fact,
$E_{-15}({\mathbf{Q}})\cong{\mathbf{Z}}$
. In fact,
![]() $P_t$
will be globally 5-primitive but locally 5-imprimitive in
$P_t$
will be globally 5-primitive but locally 5-imprimitive in
![]() $E_{t(2-t)}({\mathbf{Q}})$
for all
$E_{t(2-t)}({\mathbf{Q}})$
for all
![]() $t\in{\mathbf{Z}}_{\ge5}$
that are not a fifth power or a fifth power plus 2, as for these t the subgroup of
$t\in{\mathbf{Z}}_{\ge5}$
that are not a fifth power or a fifth power plus 2, as for these t the subgroup of
![]() ${\mathbf{Q}}^*/{{\mathbf{Q}}^*}^5$
generated by t and
${\mathbf{Q}}^*/{{\mathbf{Q}}^*}^5$
generated by t and
![]() $t-2$
has order 25.
$t-2$
has order 25.
7.2. Curves with a locally 7-imprimitive point
Again we start from the Tate’s normal equation
but now we do not impose
![]() $b=c$
as for
$b=c$
as for
![]() $\ell=5$
, but instead
$\ell=5$
, but instead
The curve
![]() $E'=E_d'$
parametrises [
Reference Kulesz8
] elliptic curves with (0, 0) as point of order 7. A Weierstrass equation for the 7-isogenous curve
$E'=E_d'$
parametrises [
Reference Kulesz8
] elliptic curves with (0, 0) as point of order 7. A Weierstrass equation for the 7-isogenous curve
![]() $E=E'/\langle(0,0)\rangle$
is
$E=E'/\langle(0,0)\rangle$
is
 \begin{align*}E\,:\, & y^2+(1-c)xy-by=x^3-bx^2-5 (2 b^2+b (c^2-3 c-2)+c (c^2+4 c+1))x\\& -b^2 (12 c^2+c+24)-6 b^3+b ({-}c^4+9 c^3+46 c^2+24 c+2)\\& - c (c^4+16 c^3+36 c^2+16 c+1).\end{align*}
\begin{align*}E\,:\, & y^2+(1-c)xy-by=x^3-bx^2-5 (2 b^2+b (c^2-3 c-2)+c (c^2+4 c+1))x\\& -b^2 (12 c^2+c+24)-6 b^3+b ({-}c^4+9 c^3+46 c^2+24 c+2)\\& - c (c^4+16 c^3+36 c^2+16 c+1).\end{align*}
It has discriminant
![]() $\Delta_E=d(d-1)(d^3-8d^2+5d+1)^7$
, and this time we find its 7-division field to be
$\Delta_E=d(d-1)(d^3-8d^2+5d+1)^7$
, and this time we find its 7-division field to be
![]() $K(E[7])=K(\zeta_7,\sqrt[7]{d(d-1)^2}).$
$K(E[7])=K(\zeta_7,\sqrt[7]{d(d-1)^2}).$
We equip
![]() $E^{\prime}$
with a K-rational point
$E^{\prime}$
with a K-rational point
![]() $P_t'=(d^2t,d^3t)$
by putting
$P_t'=(d^2t,d^3t)$
by putting
![]() $d=d(t)=({t+1)/(t^2-t+1})$
. The image of
$d=d(t)=({t+1)/(t^2-t+1})$
. The image of
![]() $P_t'$
under the 7-isogeny
$P_t'$
under the 7-isogeny
![]() $E'\to E$
is
$E'\to E$
is
 $$P_t=\left(-\frac{C(t)}{(2 t-1)^2 (t-1)^2 \left(t^2-t+1\right)^4},\frac{D(t)}{(t-1)^3 (2 t-1)^3 \left(t^2-t+1\right)^6}\right)\in E(K)$$
$$P_t=\left(-\frac{C(t)}{(2 t-1)^2 (t-1)^2 \left(t^2-t+1\right)^4},\frac{D(t)}{(t-1)^3 (2 t-1)^3 \left(t^2-t+1\right)^6}\right)\in E(K)$$
for certain polynomials C(t) and D(t) in
![]() ${\mathbf{Z}}[t]$
of degree 12 and 18. In terms of t, the 7-division field is
${\mathbf{Z}}[t]$
of degree 12 and 18. In terms of t, the 7-division field is
![]() $K(E[7])=K(\zeta_7, \root 7 \of {t^2(t+1)(t-2)^2(t^2-t+1)^4})$
, and the 7-division field of
$K(E[7])=K(\zeta_7, \root 7 \of {t^2(t+1)(t-2)^2(t^2-t+1)^4})$
, and the 7-division field of
![]() $P_t$
is
$P_t$
is
 \[K\left( \dfrac17 P_t\right)=K(E[7])\left(\root 7\of {\frac{t(t+1)}{t-2}}\right)=K\left(\zeta_7, \root 7 \of {\frac{t(t^2-t+1)}{(t+1)}}, \root 7 \of {\frac{t(t+1)}{(t-2)}}\right).\]
\[K\left( \dfrac17 P_t\right)=K(E[7])\left(\root 7\of {\frac{t(t+1)}{t-2}}\right)=K\left(\zeta_7, \root 7 \of {\frac{t(t^2-t+1)}{(t+1)}}, \root 7 \of {\frac{t(t+1)}{(t-2)}}\right).\]
The point
![]() $P_t$
is a globally 7-primitive but locally 7-imprimitive point when the extension
$P_t$
is a globally 7-primitive but locally 7-imprimitive point when the extension
![]() $K(\zeta_7)\subset K(\frac17 P_t)$
has its generic degree
$K(\zeta_7)\subset K(\frac17 P_t)$
has its generic degree
![]() $7^2$
.
$7^2$
.
Example 7.2. Take
![]() $K={\mathbf{Q}}$
. For
$K={\mathbf{Q}}$
. For
![]() $t=1$
the point
$t=1$
the point
![]() $P_t$
above is the zero point as
$P_t$
above is the zero point as
![]() $P'_t$
is 7-torsion, and for
$P'_t$
is 7-torsion, and for
![]() $t=2$
the curve
$t=2$
the curve
![]() $E^{\prime}$
is singular. For
$E^{\prime}$
is singular. For
![]() $t=3$
and
$t=3$
and
![]() $d=4/7$
however we obtain the point
$d=4/7$
however we obtain the point
![]() $P_3=(286019/490^2, 15951227/490^3)$
on
$P_3=(286019/490^2, 15951227/490^3)$
on
which is the curve 20622.j1 with minimal model
in the LMFDB-database [
19
]. Our locally 7-imprimitive point
![]() $P_3$
is a generator of
$P_3$
is a generator of
![]() $E({\mathbf{Q}})\cong{\mathbf{Z}}$
. On
$E({\mathbf{Q}})\cong{\mathbf{Z}}$
. On
![]() $E_0$
the corresponding generator is
$E_0$
the corresponding generator is
![]() $(328219/10^2, 109777927/10^3)$
.
$(328219/10^2, 109777927/10^3)$
.
8. A composite level obstruction
So far we have focused on non-trivial obstructions to local primitivity at prime level
![]() $\ell$
, as this is a new phenomenon in the elliptic primitive root case III that does not arise in the multiplicative primitive root case I and the cyclic reduction case II.
$\ell$
, as this is a new phenomenon in the elliptic primitive root case III that does not arise in the multiplicative primitive root case I and the cyclic reduction case II.
In all three cases, there exist obstructions of different nature at composite levels that arise from the entanglement between finitely many of the corresponding division fields
![]() $K_\ell$
. These obstructions do not arise over
$K_\ell$
. These obstructions do not arise over
![]() $K={\mathbf{Q}}$
, and most examples in the cases I and II are created by base changing to a well-chosen finite extension of the fields of definition
$K={\mathbf{Q}}$
, and most examples in the cases I and II are created by base changing to a well-chosen finite extension of the fields of definition
![]() ${\mathbf{Q}}(x)$
and
${\mathbf{Q}}(x)$
and
![]() ${\mathbf{Q}}(j_E)$
. Again, case III is different here, as entanglement obstructions already occur over
${\mathbf{Q}}(j_E)$
. Again, case III is different here, as entanglement obstructions already occur over
![]() ${\mathbf{Q}}$
. In this Section we construct a level 6 obstruction.
${\mathbf{Q}}$
. In this Section we construct a level 6 obstruction.
Let
![]() $E/K$
be an elliptic curve with
$E/K$
be an elliptic curve with
![]() $\#E[2](K)=2$
, and
$\#E[2](K)=2$
, and
![]() $P\in E(K)$
a point of infinite order. Then the 2 division field
$P\in E(K)$
a point of infinite order. Then the 2 division field
![]() $K(E[2](\overline K))$
is a quadratic extension of K. Assume that the 2-division field
$K(E[2](\overline K))$
is a quadratic extension of K. Assume that the 2-division field
![]() $K(\frac12 P)$
of P is of maximal degree 4 over it. Then
$K(\frac12 P)$
of P is of maximal degree 4 over it. Then
![]() $G_2=\mathrm{Gal}(K(\frac12 P)/K)$
is a dihedral group of order 8 for which the matrix representation (2·5) on
$G_2=\mathrm{Gal}(K(\frac12 P)/K)$
is a dihedral group of order 8 for which the matrix representation (2·5) on
![]() $V_2=\langle\frac12 P\rangle/\langle P\rangle$
has the form
$V_2=\langle\frac12 P\rangle/\langle P\rangle$
has the form
 \begin{equation}G_2=\left\{ \begin{bmatrix}1 &&& a &&& c \\0 &&& 1 &&& b \\0 &&& 0 &&& 1\end{bmatrix}\,:\, a,b,c \in{\mathbf{F}}_2 \right\}\subset \mathrm{GL}_3({\mathbf{F}}_2).\end{equation}
\begin{equation}G_2=\left\{ \begin{bmatrix}1 &&& a &&& c \\0 &&& 1 &&& b \\0 &&& 0 &&& 1\end{bmatrix}\,:\, a,b,c \in{\mathbf{F}}_2 \right\}\subset \mathrm{GL}_3({\mathbf{F}}_2).\end{equation}
There is a unique subfield of
![]() $L\subset K(\frac12 P)$
with Galois group over K isomorphic to the Klein 4-group
$L\subset K(\frac12 P)$
with Galois group over K isomorphic to the Klein 4-group
![]() $V_4=C_2\times C_2$
, and we can view a and b in the matrix representation (8.1) of
$V_4=C_2\times C_2$
, and we can view a and b in the matrix representation (8.1) of
![]() $G_2$
as
$G_2$
as
![]() ${\mathbf{F}}_2$
-valued quadratic characters on
${\mathbf{F}}_2$
-valued quadratic characters on
![]() $G_2$
that generate the character group of the quotient
$G_2$
that generate the character group of the quotient
![]() $\mathrm{Gal}(L/K)\cong V_4$
of
$\mathrm{Gal}(L/K)\cong V_4$
of
![]() $G_2$
.
$G_2$
.
For a prime
![]() ${\mathfrak{p}}\nmid 2\Delta_E$
, the point P generates a subgroup of odd index in
${\mathfrak{p}}\nmid 2\Delta_E$
, the point P generates a subgroup of odd index in
![]() $E(k_{\mathfrak{p}})$
if and only if for its Frobenius
$E(k_{\mathfrak{p}})$
if and only if for its Frobenius
![]() $\mathrm{Frob}_{{\mathfrak{p}},2}\in G_2$
, viewed as a matrix as in (8.1), the endomorphism
$\mathrm{Frob}_{{\mathfrak{p}},2}\in G_2$
, viewed as a matrix as in (8.1), the endomorphism
![]() $(\mathrm{Frob}_{{\mathfrak{p}},2}-\mathrm{id}_2)\,:\, V_2\to V_2$
has
$(\mathrm{Frob}_{{\mathfrak{p}},2}-\mathrm{id}_2)\,:\, V_2\to V_2$
has
![]() ${\mathbf{F}}_2$
-rank at least 2 (Lemma 2.3). We obtain the criterion
${\mathbf{F}}_2$
-rank at least 2 (Lemma 2.3). We obtain the criterion
More precisely,
![]() $a(\mathrm{Frob}_{{\mathfrak{p}},2})=1$
implies that
$a(\mathrm{Frob}_{{\mathfrak{p}},2})=1$
implies that
![]() $E(k_{\mathfrak{p}})$
does not have full 2-torsion, and
$E(k_{\mathfrak{p}})$
does not have full 2-torsion, and
![]() $b(\mathrm{Frob}_{{\mathfrak{p}},2})=1$
implies that P is not only not in
$b(\mathrm{Frob}_{{\mathfrak{p}},2})=1$
implies that P is not only not in
![]() $2E(k_{\mathfrak{p}})$
, but also not a 2-isogenous image as in condition C of Theorem 1.2.
$2E(k_{\mathfrak{p}})$
, but also not a 2-isogenous image as in condition C of Theorem 1.2.
Suppose further that E has a K-rational 3-torsion subgroup T, and let
![]() $\varphi_3\,:\,E'\to E$
be the isogeny dual to the quotient map
$\varphi_3\,:\,E'\to E$
be the isogeny dual to the quotient map
![]() $\phi\,:\,E\to E'=E/T$
. Assume that the point P is in
$\phi\,:\,E\to E'=E/T$
. Assume that the point P is in
![]() $\varphi_3[E'(K)]$
but not in 3E(K). Then the 3-division field
$\varphi_3[E'(K)]$
but not in 3E(K). Then the 3-division field
![]() $K(\frac13 P)$
of P has Galois group
$K(\frac13 P)$
of P has Galois group
![]() $G_3=\mathrm{Gal}(K(\frac13 P)/K)$
for which the matrix representation on
$G_3=\mathrm{Gal}(K(\frac13 P)/K)$
for which the matrix representation on
![]() $V_3=\langle\frac13 P\rangle/\langle P\rangle$
will ‘generically’ be the group
$V_3=\langle\frac13 P\rangle/\langle P\rangle$
will ‘generically’ be the group
 \begin{equation}G_3=\left\{ \begin{bmatrix}d &&& e &&& f \\0 &&& g &&& 0 \\0 &&& 0 &&& 1\end{bmatrix}: \quad d,g \in {\mathbf{F}}_3^*, e,f \in{\mathbf{F}}_3 \right\}\subset \mathrm{GL}_3({\mathbf{F}}_3)\end{equation}
\begin{equation}G_3=\left\{ \begin{bmatrix}d &&& e &&& f \\0 &&& g &&& 0 \\0 &&& 0 &&& 1\end{bmatrix}: \quad d,g \in {\mathbf{F}}_3^*, e,f \in{\mathbf{F}}_3 \right\}\subset \mathrm{GL}_3({\mathbf{F}}_3)\end{equation}
of order 36. In this case d and g can be viewed as a quadratic characters
![]() $G_3\to {\mathbf{F}}_3^*$
, and another application of Lemma 2.3 shows that for primes
$G_3\to {\mathbf{F}}_3^*$
, and another application of Lemma 2.3 shows that for primes
![]() ${\mathfrak{p}}\nmid 3\Delta_E$
, we have
${\mathfrak{p}}\nmid 3\Delta_E$
, we have
Thus, for primes
![]() ${\mathfrak{p}}\nmid 6\Delta_E$
, a necessary condition for
${\mathfrak{p}}\nmid 6\Delta_E$
, a necessary condition for
![]() $\bar P \in E(k_{\mathfrak{p}})$
to be an elliptic primitive root is that the three quadratic characters a, b and g occurring in (8.2) and (8.4) do not vanish on the Frobenius automorphism of
$\bar P \in E(k_{\mathfrak{p}})$
to be an elliptic primitive root is that the three quadratic characters a, b and g occurring in (8.2) and (8.4) do not vanish on the Frobenius automorphism of
![]() ${\mathfrak{p}}$
in
${\mathfrak{p}}$
in
![]() $K_6=K(\frac16P)$
. In other words: the prime
$K_6=K(\frac16P)$
. In other words: the prime
![]() ${\mathfrak{p}}$
has to be inert in the quadratic extensions
${\mathfrak{p}}$
has to be inert in the quadratic extensions
![]() $K_a$
,
$K_a$
,
![]() $K_b$
and
$K_b$
and
![]() $K_g$
of K corresponding to these 3 characters.
$K_g$
of K corresponding to these 3 characters.
Primes
![]() ${\mathfrak{p}}$
satisfying the condition above exist if the quadratic extensions
${\mathfrak{p}}$
satisfying the condition above exist if the quadratic extensions
![]() $K_a$
,
$K_a$
,
![]() $K_b$
and
$K_b$
and
![]() $K_g$
are linearly disjoint over K, but not if they are the three quadratic subfields of a
$K_g$
are linearly disjoint over K, but not if they are the three quadratic subfields of a
![]() $V_4$
-extension
$V_4$
-extension
![]() $K\subset K_a K_b K_g$
. In the latter case, we have a splitting obstruction to local primitivity of P in
$K\subset K_a K_b K_g$
. In the latter case, we have a splitting obstruction to local primitivity of P in
![]() $K_6$
that does not exist in one of the smaller fields
$K_6$
that does not exist in one of the smaller fields
![]() $K(\frac12 P)$
or
$K(\frac12 P)$
or
![]() $K(\frac13 P)$
: it has level 6, but not 2 or 3, making it an obstruction caused by entanglement of division fields.
$K(\frac13 P)$
: it has level 6, but not 2 or 3, making it an obstruction caused by entanglement of division fields.
Example 8.1. An example is provided by the elliptic curve
![]() $E/{\mathbf{Q}}$
with label 12100.j1 in the LMFDB data base. The curve E has discriminant
$E/{\mathbf{Q}}$
with label 12100.j1 in the LMFDB data base. The curve E has discriminant
and if we take (0, 0) to be its unique
![]() ${\mathbf{Q}}$
-rational 2-torsion point it has Weierstrass model
${\mathbf{Q}}$
-rational 2-torsion point it has Weierstrass model
For this curve we have
![]() $E({\mathbf{Q}})=\langle T_2\rangle\times\langle P\rangle \cong {\mathbf{Z}}/2{\mathbf{Z}}\times {\mathbf{Z}}$
with
$E({\mathbf{Q}})=\langle T_2\rangle\times\langle P\rangle \cong {\mathbf{Z}}/2{\mathbf{Z}}\times {\mathbf{Z}}$
with
![]() $T_2=(0,0)$
of order 2 and
$T_2=(0,0)$
of order 2 and
![]() $P=({-13475}/{36}, {1249325}/{216})$
a generator of infinite order. We have
$P=({-13475}/{36}, {1249325}/{216})$
a generator of infinite order. We have
![]() $K_a={\mathbf{Q}}(E[2])={\mathbf{Q}}(\sqrt{\Delta_E})={\mathbf{Q}}(\sqrt 5)$
, and over this field the 2-division field
$K_a={\mathbf{Q}}(E[2])={\mathbf{Q}}(\sqrt{\Delta_E})={\mathbf{Q}}(\sqrt 5)$
, and over this field the 2-division field
![]() ${\mathbf{Q}}(\frac12P)$
of P is the
${\mathbf{Q}}(\frac12P)$
of P is the
![]() $V_4$
extension
$V_4$
extension
generated by the square roots of
![]() $\pi=3+2\sqrt5$
and its conjugate. From
$\pi=3+2\sqrt5$
and its conjugate. From
![]() $\pi\bar\pi=-11$
we see that
$\pi\bar\pi=-11$
we see that
![]() ${\mathbf{Q}}(\frac12P)$
is cyclic of degree 4 over
${\mathbf{Q}}(\frac12P)$
is cyclic of degree 4 over
![]() ${\mathbf{Q}}(\sqrt{-55})$
, and that we have
${\mathbf{Q}}(\sqrt{-55})$
, and that we have
![]() $K_b={\mathbf{Q}}(\sqrt{-11})$
.
$K_b={\mathbf{Q}}(\sqrt{-11})$
.
As E acquires a 3-torsion point
![]() $T_3=({55}/{3}, {275}\sqrt{165}/{9})$
over the quadratic field
$T_3=({55}/{3}, {275}\sqrt{165}/{9})$
over the quadratic field
![]() ${\mathbf{Q}}(\sqrt{165})={\mathbf{Q}}(\sqrt{-3\cdot-55})$
that generates a
${\mathbf{Q}}(\sqrt{165})={\mathbf{Q}}(\sqrt{-3\cdot-55})$
that generates a
![]() ${\mathbf{Q}}$
-rational torsion subgroup of order 3, the 3-division field of E has quadratic subfields
${\mathbf{Q}}$
-rational torsion subgroup of order 3, the 3-division field of E has quadratic subfields
![]() $K_d={\mathbf{Q}}(\sqrt{165})$
and
$K_d={\mathbf{Q}}(\sqrt{165})$
and
![]() $K_g={\mathbf{Q}}(\sqrt{-55})$
, making
$K_g={\mathbf{Q}}(\sqrt{-55})$
, making
![]() $K_g$
the third quadratic subfield in the
$K_g$
the third quadratic subfield in the
![]() $V_4$
-extension
$V_4$
-extension
![]() ${\mathbf{Q}}\subset K_aK_b$
. Over the full 3-division field of E, the 3-division field of P is the cubic extension
${\mathbf{Q}}\subset K_aK_b$
. Over the full 3-division field of E, the 3-division field of P is the cubic extension
generated by a cube root of an element
![]() $\alpha=(3+\sqrt{-55})/2\in K_g$
of norm 16, which shows that its Galois group over
$\alpha=(3+\sqrt{-55})/2\in K_g$
of norm 16, which shows that its Galois group over
![]() ${\mathbf{Q}}$
is the group
${\mathbf{Q}}$
is the group
![]() $G_3$
in (8.3). We conclude that P is a locally never-primitive point of
$G_3$
in (8.3). We conclude that P is a locally never-primitive point of
![]() $E({\mathbf{Q}})$
as the index of
$E({\mathbf{Q}})$
as the index of
![]() $\langle\bar P\rangle$
in
$\langle\bar P\rangle$
in
![]() $E({\mathbf{F}}_p)$
is always divisible by 2 or 3.
$E({\mathbf{F}}_p)$
is always divisible by 2 or 3.
Acknowledgements
All authors received support from the Max-Planck-Institut für Mathematik in Bonn while working on this paper. They thank the institute for its financial support and for its very inspiring atmosphere.