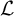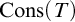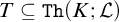1. Introduction
The author was motivated to consider this topic by the following question:
Problem 1.1. Does there exist an infinite, finitely axiomatisable field?
This (still open) problem was posed explicitly by I. Kaplan at the 2016 Oberwolfach workshop on Definability and Decidability Problems in Number Theory [Reference Koenigsmann, Pasten, Shlapentokh and Vidaux33, Q4], though existed as folklore before. This relates closely to another elementary question:
Problem 1.2. Does there exist a finitely axiomatisable theory of fields which is decidable and has an infinite model?
That is, this problem is to ascertain the existence of an infinite field F and a collection of first-order sentences T in the language of rings
$\mathcal {L}_r$
, such that
$T \subseteq {\mathtt{Th}}(F; \mathcal {L}_r)$
, T is finitely axiomatised, T models the field axioms, and there exists a decision procedure to determine membership of
$\mbox {Cons}(T)$
—the set of
$\mathcal {L}_r$
-sentences
$\phi $
such that
$T \models \phi $
.
Answering Problem 1.2
in the negative (as the empirical evidence suggests might indeed be the case) would answer Problem 1.1
in the negative too. This is the focus of modern investigations. One approach to this was established by Ziegler [Reference Ziegler49], and generalised further by Shlapentokh and Videla [Reference Shlapentokh and Videla43]. Ziegler’s idea was to take a finitely axiomatised subtheory of a sufficiently saturated field with a powerful model completeness property (he considered
$\operatorname {\mathbb {C}}$
,
$\widetilde {\mathbb {F}_p(t)}$
—where “
$\,\widetilde {F}\,$
” denotes the algebraic closure of a field F—
$\operatorname {\mathbb {R}}$
, and
$\operatorname {\mathbb {Q}}_p$
) and prove it to be a subtheory of a field interpreting arithmetic. By using a result of Tarski (see below), there is no nonempty finitely axiomatised subtheory (“finite subtheory”) of ACF
${}_0$
, ACF
${}_p$
, RCF, or p
CF that is decidable. With this in mind we forward the following definitionFootnote
1
:
Definition 1.3. A theory T in a language
$\mathcal {L}$
is finitely undecidable if every finitely axiomatised
$\mathcal {L}$
-subtheory of T is undecidable. (An
$\mathcal {L}$
-structure is finitely undecidable if its complete
$\mathcal {L}$
-theory is.)
What infinite fields are finitely undecidable (implicitly: in
$\mathcal {L}_r$
)? That is the motivating question for this paper and its sequel. If there exists a field satisfying Problem 1.1
or
1.2
, this field is not finitely undecidable; we will show, however, there is a considerably broad class of fields whose members have this undecidability property.
In particular, most (if not all) infinite fields whose model theory in the language of rings is well understood will be finitely undecidable, as we will argue. Following this philosophy, we are motivated by a long-standing model theory conjecture:
Conjecture (Shelah’s NIP Fields Conjecture)
Every infinite NIP field is either separably closed, real closed, or admits a nontrivial henselian valuation.
In [Reference Tyrrell47] we consider other classification-theoretic conjectures on field theories. Here, we adapt Ziegler’s argument to SCF
${}_{p, e}$
(Section 3) and the complete theories of certain henselian valued fields in the language
$\mathcal {L}_{val}$
; the language of rings with an additional unary predicate for the valuation ring (Sections 4 and 5). Our main result is:
Theorem (Corollary 4.10 + Theorem 5.3 + Theorem 5.8)
Let
$(K, v)$
be an
-
• equicharacteristic
$0$
, or -
• mixed characteristic, or
-
• equicharacteristic
$p>0$
separably defectless Kaplansky
henselian nontrivially valued field. Then
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
$\mathcal {O}_v$
is
$\mathcal {L}_r$
-definable, K is finitely undecidable as a field.
Thanks to some deeper results in classification theory, some immediate consequences of this are:
Corollary 5.9.
-
(1) If
$(K, v)$
is an NIP henselian nontrivially valued field,
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable. Furthermore if
$\mathcal {O}_v$
is
$\mathcal {L}_r$
-definable in K, then K is finitely undecidable as a field. -
(2) Every infinite dp-finite field is finitely undecidable.
-
(3) Assuming the NIP Fields Conjecture, every infinite NIP field is finitely undecidable.
We recall the notion of a dp-finite field L below (for a full, general discussion of dp-rank, see [Reference Kaplan, Onshuus and Usvyatsov31, Reference Simon45]). We work in a sufficiently saturated model of
${\mathtt{Th}}(L; \mathcal {L}_r)$
.
Definition 1.4. For
$n \in \operatorname {\mathbb {N}}_{>0}$
, let
$I_1, \dots , I_n$
be a list of sequences, and A a set of parameters. We say that the sequences
$I_1, \dots , I_n$
are mutually indiscernible over A if for each
$1 \leq t \leq n$
, the sequence
$I_t$
is indiscernible over
$A \cup I_{\neq t}$
.
If p is a partial type over A, we say p is of dp-rank
$\geq n$
if there exist
$a \models p$
and a list of sequences
$I_1, \dots , I_n$
mutually indiscernible over A such that
$I_k$
is not indiscernible over
$A \cup \{a\}$
for
$1 \leq k \leq n$
. (The dp-rank of a partial type is always
$\geq 0$
.)
This definition does not in fact depend on the parameter set A, as evidenced by Simon [Reference Simon45, Lemma 4.14].
Definition 1.5. A field L is of finite dp-rank if for some
$m \in \operatorname {\mathbb {N}}$
, “
$x = x$
” has dp-rank
$\geq \ m$
but does not have dp-rank
$\geq \ m+1$
.
See Example 5.10
for “interesting” examples of Theorem (Corollary 4.10
$+$
Theorem 5.3
$+$
Theorem 5.8
) and Corollary 5.9
in action.
All of our undecidability results rely on a theorem of Tarksi, which we now state: general references for this material are [Reference Ershov, Lavrov, Taimanov and Taitslin15, Reference Shoenfield44, Reference Tarski, Mostowski and Robinson46].
Theorem 1.6 (Tarski)
Let
$\mathcal {L}_1$
,
$\mathcal {L}_2$
be finite languages. The
$\mathcal {L}_2$
-theory
$T_2$
is hereditarily undecidable if there exist a finitely axiomatised essentially undecidable
$\mathcal {L}_1$
-theory
$T_1$
and models
$M_1 \models T_1$
,
$M_2 \models T_2$
such that
$M_1$
is interpretable in
$M_2$
.
Proof This is [Reference Ershov, Lavrov, Taimanov and Taitslin15, pp. 87–89], using different (but equivalent) terminology. Results such as this originate in [Reference Tarski, Mostowski and Robinson46, Sections I.3 and I.4]; cf.Theorems 6–8 ibid.
We will use this as follows:
Lemma 1.7 [Reference Shoenfield44, Proposition 11.2]
Let
$\mathcal {L}$
be a finite language and
$a_1, \dots , a_n$
constant symbols not in
$\mathcal {L}$
. Let M be an
$\mathcal {L}(a_1, \dots , a_n)$
-structure and
$M|_{\mathcal {L}}$
the reduct of M to
$\mathcal {L}$
. If
${\mathtt{Th}}(M; \mathcal {L}(a_1, \dots , a_n))$
is hereditarily undecidable, so too is
${\mathtt{Th}}(M|_{\mathcal {L}}; \mathcal {L})$
.
Corollary 1.8. Let K be a field of characteristic
$0$
, and L a field of characteristic
$p> 0$
such that there exists
$t \in L$
transcendental over
$\mathbb {F}_p$
. Let
$\mathcal {L}$
be a finite expansion of the language of rings. Suppose
$\operatorname {\mathbb {Z}}$
is
$\mathcal {L}$
-definable with parameters in K and
$\mathbb {F}_p[t]$
is
$\mathcal {L}$
-definable with parameters in L. Then
$ {{\mathtt{Th}}}(K;\mathcal {L})$
and
${\mathtt{Th}}(L; \mathcal {L})$
are hereditarily undecidable.
Proof This is an application of Theorem 1.6
with
$\mathcal {L}_2$
an expansion of
$\mathcal {L}$
by constant symbols,
$\mathcal {L}_1 = \mathcal {L}_r$
,
$T_1 = Q$
(Robinson arithmetic), and
$M_1 = \operatorname {\mathbb {N}}$
. Notice
$\operatorname {\mathbb {N}}$
is
$\emptyset $
-
$\mathcal {L}_r$
-definable in
$\operatorname {\mathbb {Z}}$
(e.g., by Lagrange’s Four Square Theorem) hence interpretable in
$\operatorname {\mathbb {Z}}$
. By [Reference Robinson41, Sections 4a and 4b],
$\operatorname {\mathbb {N}}$
is interpretable in the
$\mathcal {L}_r(t)$
-structure
$\mathbb {F}_p[t]$
. Thus, by assumption
$\operatorname {\mathbb {N}}$
is interpretable in K (with, say, parameters
$\overline {c} = \{c_1, \dots , c_k\}$
) and
$\operatorname {\mathbb {N}}$
is interpretable in L (with, say, parameters
$\overline {d} = \{d_1, \dots , d_l\}$
). By Theorem 1.6
,
${\mathtt{Th}}(K; \mathcal {L}(\overline {c}))$
and
${\mathtt{Th}}(L; \mathcal {L}(\overline {d}))$
are hereditarily undecidable. The hereditary undecidability of
${\mathtt{Th}}(K; \mathcal {L})$
and
${\mathtt{Th}}(L; \mathcal {L})$
follows from Lemma 1.7
exactly.
Remark 1.9. Notational remark. By “
$K \equiv _{\mathcal {L}} L$
” we denote that two
$\mathcal {L}$
-structures
$K, L$
are elementarily equivalent. If “
$K \equiv L$
” is written, the language is implicitly
$\mathcal {L}_r$
. In the case of valued fields, we will frequently write “
$(K, v) \equiv (L, w)$
” to denote an
$\mathcal {L}_{val}$
-elementary equivalence, where
$v, w$
are valuations on their respective fields.
2. First exploration by Ziegler
Ziegler’s main result of [Reference Ziegler49] is the construction of a field
$K_q$
satisfying the following theorem:
Theorem 2.1. Let L be the field
$\operatorname {\mathbb {C}}$
,
$\widetilde {\mathbb {F}_p(t)}$
,
$\operatorname {\mathbb {R}}$
, or
$\operatorname {\mathbb {Q}}_p$
, and
$q \neq p$
prime. There exists a field
$K_q \subseteq L$
such that:
-
(1)
$\operatorname {\mathbb {Z}}$
or
$\mathbb {F}_p[t]$
is definable (with parameters) in
$K_q$
. -
(2) If the intermediate field
$K_q \subseteq H \subseteq L$
is finite over
$K_q$
, either
$[H : K_q] = 1$
or
$q | [H : K_q]$
.
Proof This is [Reference Ziegler49, Theorem, p. 270] with a specified A. Cf. Theorems 3.3 and 4.4, and Section 5, of [Reference Shlapentokh and Videla43] (this paper, by Shlapentokh and Videla, generalises Ziegler’s construction).
Corollary 2.2 (Ziegler)
Let p be prime. ACF
${}_0$
, ACF
${}_p$
, RCF, and p
CF are finitely undecidable.
Proof [Reference Ziegler49, Corollary, p. 270]. Let T be a finite subtheory of L, which is one of the fields
$\operatorname {\mathbb {C}}$
,
$\widetilde {\mathbb {F}_p(t)}$
,
$\operatorname {\mathbb {R}}$
,
$\operatorname {\mathbb {Q}}_p$
. Let P be the set of primes distinct to p. For each
$q \in P$
, use Theorem 2.1
to obtain a field
$K_q$
satisfying (1) and (2). Let
$\mathcal {U}$
be a nonprincipal ultrafilter on P, and let
$\mathbb {K}$
be the ultraproduct
$\prod _{q \in P} K_q / \mathcal {U}$
.
We claim that
$\mathbb {K}$
is relatively algebraically closed in
$L^{\mathcal {U}}$
. Indeed, suppose
$f = (f_q) \in \mathbb {K}[X]$
has a root
$\alpha = (\alpha _q) \in L^{\mathcal {U}}$
. In which case,
$\{q\mbox { : } f_q(\alpha _q) = 0\} \in \mathcal {U}$
, hence
$\{q\mbox { : } [K_q(\alpha _q) : K_q] \leq \deg (f)\} \in \mathcal {U}$
. Consequently, as
$q | [H : K_q]$
for all proper finite extensions
$K_q \subset H \subseteq L$
,
$\{q\mbox { : } [K_q(\alpha _q) : K_q] =1 \} \in \mathcal {U}$
. Hence
$\alpha \in \mathbb {K}$
as desired.
By the model theory of algebraically/real closed/p-adically closed fields,Footnote
2
we deduce
$\mathbb {K} \equiv L^{\mathcal {U}}$
(
$\equiv L$
by Łoś’ Theorem; specifically [Reference Chang and Keisler6, Theorem 4.1.9]). Therefore
$\mathbb {K} \models T$
. As T is finitely axiomatised, by Łoś’ Theorem there must exist some
$q \in P$
such that
$K_q \models T$
. Thus by Theorem 2.1 and Corollary 1.8
,
${\mathtt{Th}}(K_q; \mathcal {L}_r)$
is hereditarily undecidable, making T undecidable as required.
One can see the key step in this corollary was using the following property inherent to the considered fields L:
$$ \begin{align} K\ \text{relatively algebraically closed in}\ L\ \implies\ K \ \equiv L. \end{align} $$
In Section 3 we will outline Ziegler’s construction of the field
$K_q$
, with a minor discrepancy for L a separably closed field. In Section 4 we outline Ziegler’s construction in the case
$L=\operatorname {\mathbb {Q}}_p$
but again with minor changes, so his method works for a general class of henselian valued fields. Later in the paper we will discuss extending this construction to more difficult cases that avoid property
$(\flat )$
.
3. Separably closed fields
To save referring the reader to another text, we will outline Ziegler’s construction in this subsection. To make this a more interesting exercise we shall prove the theory of any separably closed field is finitely undecidable, not considered by Ziegler in [Reference Ziegler49].
Let SCF denote the theory of separably closed fields, SCF
${}_{p}$
the theory of separably closed fields of characteristic p, and SCF
${}_{p, e}$
the theory of separably closed fields of characteristic p and degree of imperfection e. We shall assume for this section the reader is familiar with [Reference Delon and Bouscaren11]. As SCF
${}_{0}\ =$
ACF
${}_0$
and SCF
${}_{p, 0}\ =$
ACF
${}_p$
, we will not consider the cases
$p = 0$
or
$p> 0$
&
$e = 0$
(the case
$e = \infty $
will be considered separately in Corollary 3.8
).
Let
$q \neq p$
be a prime number,
$L = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)\right )^s$
where
$\{u_1, \dots , u_e\}$
are transcendental and algebraically independent over
$\widetilde {\mathbb {F}_p(t)}$
(and “
$\,F^s\,$
‘’ denotes the separable closure of a field F). Note
$L \models {\mathtt{SCF}}_{p,e}$
, as
$\widetilde {\mathbb {F}_p(t)}$
is perfect. First we have:
Proposition 3.1. For each prime
$q \neq p$
, there exists a field
$K_q \subseteq L$
such that:
-
(1)
$\mathbb {F}_p[t]$
is definable (with parameters) in
$K_q$
. -
(2) If the intermediate field
$K_q \subseteq H \subseteq L$
is finite and separable over
$K_q$
, then
$[H : K_q] = 1$
or is divisible by q.
To prove this, we require a construction. Let
$F = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_{e-1})\right )^s \subseteq L$
; we construct a field
$K_q \subseteq L$
such that
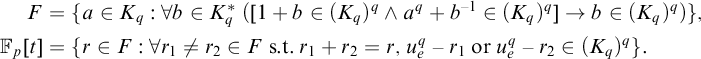$$ \begin{align*} F &= \{ a \in K_q \mbox{ : }\forall b \in K_q^* \mbox{ } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q] \rightarrow b \in (K_q)^q)\},\\ \mathbb{F}_p[t] &= \{r \in F \mbox{ : } \forall r_1 \neq r_2 \in F \mbox{ s.t. } r_1 + r_2 = r\mbox{, } u_e^q - r_1 \mbox{ or } u_e^q - r_2 \in (K_q)^q\}. \end{align*} $$
This will suffice to prove Proposition 3.1(1). We will take
$K_q$
to be the union of a sequence
$$\begin{align*}F(u_e) = E_0 \subseteq E_1 \subseteq E_2 \subseteq \cdots\end{align*}$$
within L of finite separable extensions
$E_i/F(u_e)$
. Obtaining Proposition 3.1(2) while ensuring F and
$\mathbb {F}_p[t]$
are definable in this way requires us to keep a tight rein on the q-th roots in
$K_q$
. To that end, we will also carefully construct a sequence:
$$\begin{align*}\emptyset = S_0 \subseteq S_1 \subseteq S_2 \subseteq \cdots\end{align*}$$
of finite subsets
$S_i \subseteq E_i$
, ultimately desiring
$K_q\setminus (K_q)^q = \bigcup _i S_i$
. To ensure we do not introduce an incompatibility between
$K_q \setminus (K_q)^q$
and F or
$\mathbb {F}_p[t]$
, we will ask the following rule [Reference Ziegler49, p. 273] to be obeyed at each point of the sequence
$(E_i, S_i)$
:
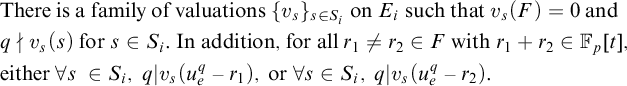$$ \begin{align} & \mbox{There is a family of valuations}\ \{v_s\}_{s \in S_i}\ \mbox{on}\ E_i\ \mbox{such that}\ v_s(F) = 0\ \mbox{and} \nonumber\\ & q \nmid v_s(s)\ \mbox{for}\ s \in S_i.\ \mbox{In addition, for all}\ r_1 \neq r_2 \in F\ \mbox{with}\ r_1 + r_2 \in \mathbb{F}_p[t], \hspace{7mm} \\ &\mbox{either}\ \forall s\ \in S_i,\ q | v_s(u_e^q - r_1),\ \text{or}\ \forall s \in S_i,\ q | v_s(u_e^q - r_2). \nonumber \end{align} $$
We will reference the following two standard lemmas, taken directly from [Reference Ziegler49, Section 3]:
Lemma 3.2 [Reference Ziegler49, Lemma 1]
Let
$(H_1, v_1)$
be a discretely valued field,
$H_2/H_1$
a finite extension, and q a prime such that
$q \nmid [H_2 : H_1]$
. Then there is an extension of
$v_1$
to
$H_2$
, which we denote
$v_2$
, such that
$q \nmid (v_2 H_2 : v_1 H_1)$
.
Lemma 3.3 [Reference Ziegler49, Lemma 2]
Let
$(H, v)$
be a valued field and q a prime distinct to
$\operatorname {\mathrm {char}}(Hv)$
. For
$a \in H \setminus (H)^q$
with
$q | v(a)$
, there is an extension of valued fields
$(H(\sqrt [q]{a}), w)/(H, v)$
such that
$wH(\sqrt [q]{a}) = vH$
.
We will also require the following fact:
Definition 3.4. Valuations
$v_1, v_2$
on a field K are dependent if
$\mathcal {O}_{v_1} \mathcal {O}_{v_2} \subsetneq K$
.
Lemma 3.5. If
$v_1, v_2$
are dependent discrete valuations on a field K, then
$v_1 = v_2$
(by which we mean
$\mathcal {O}_{v_1} = \mathcal {O}_{v_2})$
.
Proof The valuation ring of a discrete valuation is maximal [Reference Engler and Prestel13, Corollary 2.3.2], hence
$\mathcal {O}_{v_1} = \mathcal {O}_{v_1}\mathcal {O}_{v_2} = \mathcal {O}_{v_2}$
as desired.
The construction begins with an enumeration
$a_0, a_1, a_2, \dots $
of the elements of L separably algebraic over
$F(u_e)$
, each repeated countably infinitely many times. Suppose
$(E_i, S_i)$
is already constructed—Ziegler considers now four cases, based on the equivalence class of i mod
$4$
. These correspond to guaranteeing Proposition 3.1(1) (Case 1), Proposition 3.1(2) (Case 2), the definition of F by ensuring there is a “reason” b is excluded from
$(K_q)^q$
(Case 3 +
$\clubsuit $
), and the definition of
$\mathbb {F}_p[t]$
(Case 4 +
$\clubsuit $
); again, by ensuring there is a “reason”
$a_n$
is excluded.
Construction. (cf. [Reference Ziegler49, Section 3])
Case 1:
$i = 4n$
. If
$q | [E_i(a_n) : E_i]$
, then
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise set
$(E_{i+1}, S_{i+1})\ = (E_i(a_n), S_i)$
and using Lemma 3.2
extend each valuation
$v_s$
,
$s \in S_i$
, from
$E_i$
to
$E_{i+1}$
in a way preserving
$(\clubsuit )$
.
Case 2:
$i = 4n + 1$
. Unless
$a_n \in E_i \setminus S_i$
, set
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise, if for some
$v_s$
,
$s \in S_i$
, we have
$q \nmid v_s(a_n)$
then define
$(E_{i+1}, S_{i+1})= (E_i, S_i \cup \{a_n\})$
and set
$v_{a_n} \mathrel {\mathop :}= v_s$
. This ensures
$(\clubsuit )$
holds for
$i+1$
. If
$q| v_s(a_n)$
for all
$s \in S_i$
, then we take
$(E_{i+1}, S_{i+1}) = (E_i(\sqrt [q]{a_n}), S_i)$
Footnote
3
and extend every valuation according to Lemma 3.3
.
Case 3:
$i = 4n +2$
. Unless
$a_n \in E_i \setminus F$
, let
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. If
$a_n \in E_i \setminus F$
let v be a discrete valuation on
$E_i$
, trivial on F, which is negative on
$a_n$
. If the second condition in
$(\clubsuit )$
does not already hold for
$\{v, \{v_s\}_{s \in S_i}\}$
in
$E_i$
, then there exists
$r \in F$
such that
$q \nmid v(u_e^q - r)$
and
$q | v_s(u_e^q - r)$
for all
$s \in S_i$
. By the strong triangle inequality, there is at most one such r: indeed, for
$r \neq r' \in F$
,
$v(u_e^q - r') = v(u_e^q - r + r - r') = 0$
, as
$v(r - r') = 0$
and
$q \nmid v(u_e^q - r)$
. As
$L = (L)^q$
, we may set
$E = E_i(\sqrt [q]{u_e^q - r})$
and extend the valuations
$\{v, \{v_s\}_{s \in S_i}\}$
sensibly as above. We conclude the second condition of
$(\clubsuit )$
holds for
$(E, \{v, \{v_s\}_{s \in S_i}\})$
.
If v is independent to
$v_s$
for every
$s \in S_i$
: let
$\{v, v_{s_1}, \dots , v_{s_k}\}$
be the distinct valuations of
$\{v, \{v_s\}_{s \in S_i}\}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
$b \in E$
such that
$v(b)$
is the smallest positive element in the value group of v (hence
$q | v(1+b)$
,
$q|v(a_n^q + b^{-1})$
) and
$q|v_{s_j}(b)$
,
$q|v_{s_j}(1+b)$
,
$q|v_{s_j}(a_n^q + b^{-1})$
for
$1 \leq j \leq k$
. As
$b, 1+b, a_n^q + b^{-1} \in (L)^q = L$
, we may define
$$\begin{align*}(E_{i+1}, S_{i+1}) = \left(E\!\left(\sqrt[q]{1+b}, \sqrt[q]{a_n^q + b^{-1}}\right)\!,\, S_i \cup \{b\}\right).\end{align*}$$
Extending
$\{v_b = v, \{v_s\}_{s \in S_i}\}$
as above, we know
$(\clubsuit )$
holds as it did on E.
If v is dependent with
$v_{\widehat {s}}$
for some
$\widehat {s} \in S_i$
: by Lemma 3.5
$v = v_{\widehat {s}}$
. Let
$\{v_{s_1}, \dots , v_{s_l}\}$
be the distinct valuations of
$\{v, \{v_s\}_{s \in S_i}\}$
, assuming WLOG
$v = v_{s_1}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
$b \in E$
such that
$v_{s_1}(b)$
is the smallest positive element in the value group of
$v_{s_1}$
, and
$q|v_{s_j}(b)$
,
$q|v_{s_j}(1+b)$
,
$q|v_{s_j}(a_n^q + b^{-1})$
for
$2 \leq j \leq l$
. As
$b, 1+b, a_n^q + b^{-1} \in (L)^q = L$
, we may define
$$\begin{align*}(E_{i+1}, S_{i+1}) = \left(E\!\left(\sqrt[q]{1+b}, \sqrt[q]{a_n^q + b^{-1}}\right)\!,\, S_i \cup \{b\}\right).\end{align*}$$
Extending
$\{v_b = v_{s_1}, \{v_s\}_{s \in S_i}\}$
as above, again
$(\clubsuit )$
holds on
$(E_{i+1}, S_{i+1})$
. (This case allows
$b \in S_i$
without issue, by Lemma 3.5
.)
Case 4:
$i = 4n+3$
. Unless
$a_n \in F\setminus \mathbb {F}_p[t]$
we set
$(E_{i+1}, S_{i+1}) = (E_{i}, S_{i})$
. Otherwise, first observe
$B = \{r \in F \mbox { : } \exists s \in S_i \mbox { s.t. } q \nmid v_s(u_e^q - r)\}$
is finite. Next, for
$r \in F^*$
there exists a discrete valuation
$v_r$
on
$F(u_e)$
, trivial on F, for which
$v_r(u_e^q - r)$
is the smallest positive element of its valuation group (this follows as
$X^q - r \in F[X]$
has no multiple factors). For each such r, we choose an extension
$w_r$
of
$v_r$
to
$E_i$
, and by the construction of
$E_i/F$
, the set
$C =$
$\{r \in F^* \mbox { : } q|w_r(u_e^q - r)\}$
is finite. Choose
$r_1 \in F^*$
such that
$r_1 \neq a_n$
,
$2 r_1 \neq a_n$
, and
$r_1, a_n -r_1 \not \in C$
, and
$r_1, a_n - r_1 \not \in \mathbb {F}_p[t]$
. Let
$r_2 = a_n - r_1$
and finally define
$$\begin{align*}(E_{i+1}, S_{i+1}) = (E_i, S_i \cup \{ u_e^q - r_1, u_e^q - r_2\}).\end{align*}$$
One can prove
$\{w_{r_1}, w_{r_2}, \{v_s\}_{s \in S_i}\}$
satisfies
$(\clubsuit )$
based on this construction.⊣
Lemma 3.6. Set
$K_q = \bigcup _i E_i$
. The above construction ensures we have the following features of
$K_q$
, and the definitions of F and
$\mathbb {F}_p[t]$
we intended:
-
(1)
$F \subseteq (K_q)^q$
. -
(2)
$K_q \setminus (K_q)^q = \bigcup _i S_i$
. -
(3)
$F = \{a \in K_q : \forall b \in K_q^* \mbox { } [( 1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q) \rightarrow b \in (K_q)^q]\}$
. -
(4)
$\mathbb {F}_p[t]\! =\! \{r \in F\! :\! \forall r_1 \neq r_2 \in F\! \mbox { } (r_1 + r_2 = r)\! \rightarrow \! (u_e^q - r_1\! \in \! (K_q)^q \lor u_e^q - r_2\! \in \! (K_q)^q)\}$
.
Proof We follow [Reference Ziegler49, Section 4] as much as possible.
-
(1) As F is separably closed, and
$q \neq p$
,
$F = (F)^q$
. -
(2) Let
$a \in (K_q)^q$
. For all sufficiently large i,
$a \in (E_i)^q$
; hence
$q | v(a)$
for all v trivial on F. Therefore by
$(\clubsuit )$
we have
$a \not \in S_i$
; consequently
$a \not \in \bigcup _i S_i$
. Conversely if
$a \in K_q\setminus (K_q)^q$
, then for some n sufficiently large we have
$a = a_n$
and
$a \in E_{4n+1}$
. By Case 2 of the construction,
$a \in S_{4n+2}$
. This proves
$K_q \setminus (K_q)^q = \bigcup _i S_i$
. -
(3) Fix
$a \in F$
. Suppose for some nonzero
$b \in K_q$
that
$1 + b, a^q + b^{-1} \in (K_q)^q$
. Let i be so large that
$1+b, a^q + b^{-1} \in (E_i)^q$
. Let v be any valuation on
$E_i$
that is trivial on F. If
$v(b)> 0$
, then
$v(b) = -v(a^q + b^{-1})$
is divisible by q. If
$v(b) < 0$
, then
$v(b) = v(1+b)$
is divisible by q. Hence
$q| v(b)$
always. By
$(\clubsuit )$
,
$b \not \in S_i$
; by (2) therefore
$b \in (K_q)^q$
. Conversely, if
$a \in K_q \setminus F$
, we may choose n sufficiently large such that
$a = a_n \in E_{4n+2}$
. In Case 3 we make it such that in
$S_{4n+3}$
there is a (nonzero) b with
$1 + b, a^q + b^{-1} \in (E_{4n+3})^q$
. This concludes the proof. -
(4) Let
$r_1 + r_2 \in \mathbb {F}_p[t]$
, with
$r_1 \neq r_2 \in F$
. If it is the case that
$u_e^q - r_1, u_e^q - r_2 \not \in (K_q)^q$
, then for some sufficiently large i, they belong to
$S_i$
. However this contradicts
$(\clubsuit )$
. If we suppose
$r \in F \setminus \mathbb {F}_p[t]$
, for some sufficiently large n it is the case that
$a_n = r$
. Then by Case 4 there exists
$r_1 \neq r_2 \in F$
,
$r_1 + r_2 = r$
, such that
$u_e^q - r_1, u_e^q - r_2 \in S_{4n+4}$
. By (2) this ensures
$u_e^q - r_1, u_e^q - r_2 \not \in (K_q)^q$
; again a contradiction.
Proof of Proposition 3.1
First, as F and
$\mathbb {F}_p[t]$
are definable,
$\operatorname {\mathbb {N}}$
is interpretable (with parameters) as an
$\mathcal {L}_r$
-structure in
$K_q$
. Next, note that
$K_q/F(u_e)$
is a separable extension, as by construction it is a union of finite separable extensions, and
$K_q \subseteq F(u_e)^s$
. Let
$K_q \subset H \subseteq L$
be a finite separable extension. Then
$H = K_q(a)$
for some
$a \in L$
by the Primitive Element Theorem. As
$K_q(a)/F(u_e)$
is separable, for some n sufficiently large we have
$a = a_{n}$
and
$$\begin{align*}[E_{4n}(a_n) : E_{4n}] = [K_q(a) : K_q],\end{align*}$$
as we assume
$a \not \in K_q$
. By construction,
$q | [E_{4n}(a) : E_{4n}]$
.
Combining these fields in a nonprincipal ultraproduct, as will be done in the next corollary, allows us to conclude the desired undecidability result.
Corollary 3.7. Let p be a prime and
$e \in \operatorname {\mathbb {N}}_{>0}$
. Then
SCF
${}_{p, e}$
is finitely undecidable.
Proof Let
$L = \left (\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)\right )^s$
as before Proposition 3.1
. Let P be the set of primes distinct to p. For each
$q \in P$
, use Proposition 3.1
to obtain a field
$K_q$
satisfying (1) and (2) ibid. Let
$\mathcal {U}$
be a nonprincipal ultrafilter on P and let
$\mathbb {K}$
be the ultraproduct
$\prod _{q \in P} K_q / \mathcal {U}$
. We claim that
$\mathbb {K}$
is relatively separably closed in
$L^{\mathcal {U}}$
: indeed, suppose
$f = (f_q) \in \mathbb {K}[X]$
is separable and has a root
$\alpha = (\alpha _q) \in L^{\mathcal {U}}$
. In which case
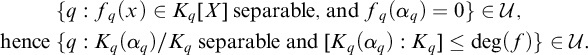$$ \begin{align*} &\{q \mbox{ : } f_q(x) \in K_q[X] \mbox{ separable, and } f_q(\alpha_q) = 0\} \in \mathcal{U},\\ \mbox{hence }&\{q \mbox{ : } K_q(\alpha_q)/K_q \mbox{ separable and } [K_q(\alpha_q) : K_q] \leq \deg(f)\} \in \mathcal{U}. \end{align*} $$
By Proposition 3.1(2),
$\{q \mbox { : } [K_q(\alpha _a) : K_q] = 1\} \in \mathcal {U}$
, and thus
$\alpha \in \mathbb {K}$
as desired.
Therefore
$\mathbb {K}$
is a separably closed field of characteristic p. Recall
$\{u_1, \dots , u_e\}$
is a p-basis for L. As they are p-independent in L, and by construction
$u_1, \dots , u_{e} \in K_q$
, they remain p-independent in
$K_q$
. Hence the degree of imperfection of
$K_q$
is at least e, for each q. Moreover, by construction
$K_q /\widetilde {\mathbb {F}_p(t)}(u_1, \dots , u_e)$
is an algebraic (separable) extension. As algebraic extensions do not increase the degree of imperfection, the degree of imperfection of
$K_q$
is at most e. Thus by Łoś’ Theorem, the degree of imperfection of
$\mathbb {K}$
is exactly e. We conclude that
$\mathbb {K} \models {\mathtt {SCF}}_{p, e}$
, and hence
$\mathbb {K} \models T$
for any finite subtheory
$T \subseteq {\mathtt {SCF}}_{p, e}$
.
Since T is finitely axiomatised, there exists some prime q such that
$K_q \models T$
. By Lemma 3.6 and Corollary 1.8
,
${\mathtt{Th}}(K_q; \mathcal {L}_r)$
is hereditarily undecidable, making T undecidable as required.
Corollary 3.8. Let p be prime. Then
SCF
${}_{p, \infty }$
is finitely undecidable.
Proof Let T be a finite subtheory of SCF
${}_{p, \infty }$
, which we assume is axiomatised by the axioms of a field of characteristic p, such that each separable polynomial over the field has a root in the field, and for each
$n \in \operatorname {\mathbb {N}}_{>0}$
the statement “the degree of imperfection is greater than n.” By the Compactness Theorem, there exists a finite subset
$\Delta $
of this axiomatisation such that
$\Delta \models T$
. For some finite
$\nu $
sufficiently large, SCF
${}_{p, \nu } \models \Delta $
; hence T is a finite subtheory of SCF
${}_{p, \nu }$
. The result follows from Corollary 3.7
.
Example 3.9. For all primes
$p> 0$
and
$e \in \operatorname {\mathbb {N}} \cup \,\{\infty \}$
, the theory
${\mathtt{SCF}}_{p,e}$
is known to be decidable (see [Reference Delon and Bouscaren11, pp. 146–153] for exposition). Therefore Corollaries 3.7 and 3.8
put a bound on further possible decidability results for these theories.
It is worth remarking that, modulo some conjectures, these results are in connection with aspects of classification theory. It is a theorem of Macintyre [Reference Macintyre35] that every infinite
$\omega $
-stable field is a model of ACF
${}_p$
for
$p = 0$
or prime. From the 1970s we have the following conjecture:
Conjecture (Stable Fields)
Every infinite stable field is separably closed.
This is known in some cases, such as for the aforementioned
$\omega $
-stable [Reference Macintyre35] or superstable infinite fields [Reference Cherlin and Shelah7], or for infinite stable fields of weight 1 [Reference Krupiński and Pillay34] or finite dp-rank [Reference Halevi and Palacín18], or most recently infinite large stable fields [Reference Johnson, Tran, Walsberg and Ye30].
Corollary 3.10. Assume the Stable Fields Conjecture. Then every infinite stable field is finitely undecidable.
Let us use this connection to classification theory to motivate which fields to consider next. Outside of stable theories, there are two orthogonal directions in which to travel: one direction attempts to extend the theories of forking, dividing and independence of types to more general contexts (e.g., [super]simple and [super]rosy), while the other direction aims to understand theories with a modest notion of order (e.g., o-minimal and NIP). The latter direction contains theories we are already familiar with: RCF in the language of ordered rings is o-minimal, and p CF in the language of valued fields is distal and dp-minimal (hence NIP). One might wonder what other field theories could be present under this banner—and there is a conjecture of Shelah that would answer this question:
Conjecture (Shelah/NIP Fields)
Every infinite NIP field is either separably closed, real closed, or admits a nontrivial henselian valuation.
Theorem 3.11. Assume the NIP Fields Conjecture. Then every infinite NIP field is either real closed, separably closed, or admits a nontrivial henselian valuation
$\emptyset $
-definable in the language of rings.
Proof (Here a valuation is definable if the valuation ring is a definable subset of the field.)
$\mathcal {L}_r$
-definability is [Reference Halevi, Hasson and Jahnke17, Proposition 6.2(2)], and the results cited in the proof (from [Reference Jahnke and Koenigsmann21]) in fact conclude
$\emptyset $
-definability.
Therefore a sensible goal would be to prove that every field with a nontrivial
$\emptyset $
-
$\mathcal {L}_r$
-definable henselian valuation is finitely undecidable. Or more so, that every henselian valued field is finitely undecidable in the language of valued fields
$\mathcal {L}_{val}$
.
4. Equicharacteristic 0 Henselian valued fields
The previous subsection did not address the aspects of Ziegler’s construction relevant to
$\operatorname {\mathbb {Q}}_p$
; these aspects will be seen in this subsection. In this subsection we will consider a pair of valued fields
$(R, v_R)$
,
$(Z, v_Z)$
, and an additional field F, under the following assumptions:
Assumption (
$\otimes $
)
-
(1)
$R \subseteq F \subseteq Z$
,
$v_R = v_Z|_R$
, and
$(Z, v_Z)$
is a henselian immediate extension of
$(R, v_R)$
. -
(2) R (thence
$v_R R$
and
$R v_R$
) is countable, and if
$\operatorname {\mathrm {char}}(R)> 0$
then R is transcendental over its prime subfield. -
(3) There are uncountably many elements of Z transcendental over R.
-
(4)
$F = Z \cap {R(\overline {x})}^s$
, where
$R(\overline {x})$
is a purely transcendental, finite transcendence degree extension of R. -
(5) Let
$q> \operatorname {\mathrm {char}}(Rv_R)$
be prime
$;$
then
$Z = (Z)^q \cdot F^*$
.
First we will give a concrete example of a pair of valued fields where these assumptions are satisfied. Let k be a field and
$\Gamma $
an ordered abelian group. Consider the multiplicative group of formal monomials
$\{t^{\gamma } \mbox { : } \gamma \in \Gamma \}$
, where
$t^0 = 1$
and
$t^{\gamma _1} \cdot t^{\gamma _2} = t^{\gamma _1 + \gamma _2}$
. Define
$k[\Gamma ]$
to be the set of formal series
$\sum _{\gamma } a_{\gamma } t^{\gamma }$
where
$a_{\gamma } \in k$
and only finitely many
$a_{\gamma }$
are nonzero. Addition and multiplication are defined by
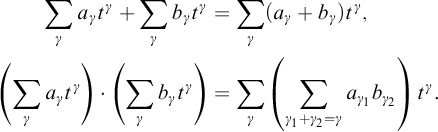$$ \begin{align*} \sum_{\gamma} a_{\gamma} t^{\gamma} + \sum_{\gamma} b_{\gamma} t^{\gamma} &= \sum_{\gamma} (a_{\gamma} + b_{\gamma}) t^{\gamma},\\ \left( \sum_{\gamma} a_{\gamma} t^{\gamma} \right) \cdot \left( \sum_{\gamma} b_{\gamma} t^{\gamma} \right) &= \sum_{\gamma} \left(\sum_{\gamma_1 + \gamma_2 = \gamma} a_{\gamma_1} b_{\gamma_2} \right) t^{\gamma}. \end{align*} $$
These operations are confirmed to be well-defined, and
$k[\Gamma ]$
an integral domain, by [Reference Marker37, Section 2.4]. This domain comes with a natural valuation
$v_{\Gamma }(\sum _{\gamma } a_{\gamma } t^{\gamma }) \mathrel {\mathop :}= \min \operatorname {\mathrm {supp}}(\sum _{\gamma } a_{\gamma } t^{\gamma })$
. Define
$k(\Gamma )$
to be the fraction field of this valued domain. Further define
$k((\Gamma ))$
as the set whose elements are formal series
$\sum _{\gamma } a_{\gamma } t^{\gamma }$
with well-ordered support. By [Reference Marker37, Section 2.4],
$(k((\Gamma )), v_{\Gamma })$
is a well-defined immediate henselian overfield of
$(k(\Gamma ), v_{\Gamma })$
.
Lemma 4.1. Let
$e \in \operatorname {\mathbb {N}}$
, k, and
$\Gamma $
be countable, and v be a henselian valuation on
$k((\Gamma ))$
which factors through
$v_{\Gamma }$
, i.e., there exists a valuation
$v'$
on k such thatFootnote
4
$v = v' \circ v_{\Gamma }$
. There exists
$t_1, \dots , t_e \in k((\Gamma ))$
transcendental over
$k(\Gamma )$
and algebraically independent such that the pair of valued fields
$(R, v_R) = (k(\Gamma ), v|_{k(\Gamma )})$
,
$(Z, v_Z) = (k((\Gamma )), v)$
, and
$F = k((\Gamma )) \cap \left (k(\Gamma )(t_1, \dots , t_e)\right )^s$
satisfy Assumption
$(\otimes )$
.
Proof Properties (1) and (4) follow by definition. Property (2) follows by construction, and as
$k(\Gamma )$
is countable (from its definition). Property (3) can be seen by a cardinality argument (cf. [Reference van den Dries, Macpherson and Toffalori12, p. 82]): fixing
$\gamma \in \Gamma ^{>0}$
, there is an injection
$(\operatorname {\mathbb {N}}; 0, +, <) \hookrightarrow (\Gamma; 0, +, <)$
given by
$n \mapsto n \cdot \gamma $
, and by definition
$|k((\Gamma ))| \geq |k|^{\aleph _0} \cdot 2^{\aleph _0} = 2^{\aleph _0}$
, while
$|\widetilde {k(\Gamma )}| = \aleph _0$
.
Property (5) requires more work: we adapt [Reference Ziegler49, Lemma 3]. Clearly
$(k((\Gamma )))^q \cdot F^* \subseteq k((\Gamma ))$
; we are required to show that for all
$a \in k((\Gamma ))^*$
, there exists
$b \in F^*$
such that
$a b^{-1} \in (k((\Gamma )))^q$
. Choose
$b \in F^*$
such that
$v_{\Gamma }(a - b)> v_{\Gamma }(a)$
; this can be done by setting
$b \in k(\Gamma )^* \subseteq F^*$
to be a sufficiently large finite truncation of a. Then
$v_{\Gamma }(a b^{-1} - 1)> v_{\Gamma }(a b^{-1})$
; hence
$ab^{-1} \equiv 1$
mod
$\mathfrak {m}_{v_{\Gamma }}$
. By Hensel’s Lemma (regardless of v,
$(k((\Gamma )), v_{\Gamma })$
is henselian),
$ab^{-1}$
is a q-th power in
$k((\Gamma ))$
, as desired.
Using Assumption
$(\otimes )$
, for
$q> p$
prime, we shall construct a field extension
$F \subseteq K_q \subseteq Z$
such that
$\operatorname {\mathbb {Z}}$
or
$\mathbb {F}_p[z]$
(where
$p = \operatorname {\mathrm {char}}(R)> 0$
and
$z \in Z$
is transcendental over
$\mathbb {F}_p$
) is
$\mathcal {L}_{val}$
-definable in
$K_q$
, and for some elements
$a \in Z$
algebraic over
$K_q$
,
$q|[K_q(a) : K_q]$
.
Remark 4.2. Notice that if Z is perfect, and for all
$a \in Z$
algebraic over
$K_q$
we have either
$K_q(a) = K_q$
or
$q | [K_q(a) : K_q]$
, then
$K_q$
is perfect:
$(K_q)^p = K_q$
. This will be a problem for Theorem 5.8
, where we will consider finite subtheories T of imperfect fields and prove
$K_q \models T$
. This problem will be resolved after Lemma 4.3
.
By Assumption
$(\otimes )$
there exists an element
$t \in Z$
transcendental over F. The field
$K_q$
will be the union of a specific sequence of finite extensions of
$F(t)$
in Z:
$$\begin{align*}R \subseteq F \subset F(t) = E_0 \subseteq E_1 \subseteq E_2 \subseteq \cdots \quad \subseteq Z.\end{align*}$$
As before, we will also construct a sequence
$\emptyset = S_0 \subseteq S_1 \subseteq S_2 \subseteq \cdots $
of finite subsets
$S_i \subseteq E_i \cap (Z)^q$
, ultimately desiring a close relationship between
$K_q \setminus (F^* \cdot (K_q)^q)$
,
$(K_q \cap (Z)^q) \setminus (K_q)^q$
, and
$\bigcup _i S_i$
. We will desire F &
$\operatorname {\mathbb {Z}}$
(if
$\operatorname {\mathrm {char}}(R) = 0$
;
$\mathbb {F}_p[z]$
otherwise) to have the following definitions, similar to as before:
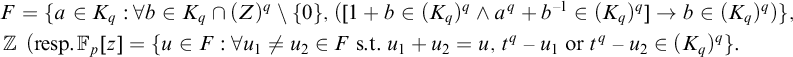$$ \begin{align*} &F = \{ a \in K_q \mbox{ : }\forall b \in K_q \cap (Z)^q\setminus\{0\} \mbox{, } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q] \rightarrow b \in (K_q)^q)\},\\&\operatorname{\mathbb{Z}} \mbox{ (resp.\!}\ \mathbb{F}_p[z] = \{u \in F \mbox{ : } \forall u_1 \neq u_2 \in F \mbox{ s.t. } u_1 + u_2 = u\mbox{, } t^q - u_1 \mbox{ or } t^q - u_2 \in (K_q)^q\}. \end{align*} $$
Denote by “
$v_Z|_{E_i}$
” the restriction of
$v_Z$
to
$E_i \subseteq Z$
. To again ensure we do not introduce an incompatibility between
$(K_q \cap (Z)^q) \setminus (K_q)^q$
and F or
$\operatorname {\mathbb {Z}}$
(resp.
$\mathbb {F}_p[z]$
), the following rule will be enforced during the construction:
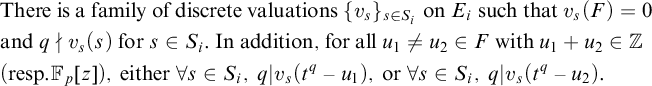$$ \begin{align} & \mbox{There is a family of discrete valuations}\ \{v_s\}_{s \in S_i}\ \text{on}\ E_i\ \text{such that}\ v_s(F) = 0 \nonumber\\& \mbox{and}\ q \nmid v_s(s)\ \text{for}\ s \in S_i.\ \text{In addition, for all}\ u_1 \neq u_2 \in F\ \text{with}\ u_1 + u_2 \in \operatorname{\mathbb{Z}} \\& \mbox{(resp.}\!\ \mathbb{F}_p[z]),\ \text{either}\ \forall s \in S_i,\ q | v_s(t^q - u_1),\ \text{or}\ \forall s \in S_i,\ q | v_s(t^q - u_2). \nonumber \end{align} $$
We have the following lemma:
Lemma 4.3. Let u be a nontrivial discrete valuation on
$E_i$
, considered as a (finite) function field extension of
$F(t)/F$
. Then u and
$v_Z|_{E_i}$
are independent (in the sense of Definition 3.4).
Proof Assume u and
$v_Z|_{E_i}$
are dependent: by [Reference Engler and Prestel13, Theorem 2.3.4] they induce the same topology on
$E_i$
. Thus there exists
$a \in E_i$
such that
$a \cdot \mathfrak {m}_{u} \subseteq \mathfrak {m}_{v_Z|_{E_i}}$
(
$= \mathfrak {m}_{v_Z} \cap E_i$
). However, as R is a subset of the constant subfield of
$E_i$
(and thus
$u(R) = 0$
, while
$v_R R = v_Z Z$
), there exists
$f \in a \cdot \mathfrak {m}_u$
with
$v_Z(f) = v_Z|_{E_i}(f) < 0$
; a contradiction.
To use the same construction of
$K_q$
throughout the paper, yet have
$K_q$
a model of a finite subtheory of either a perfect or imperfect field, we have the following definition:
Definition 4.4. The set of pliant elements over a field will denote either the separably algebraic or algebraic elements over the field, and be specified in Corollary 4.10/Theorem 5.3/Theorem 5.8.
Fix an enumeration
$a_0, a_1, \dots $
of the elements of Z pliant over
$F(t)$
, each repeated countably infinitely many times. Suppose
$(E_i, S_i)$
is already constructed—and consider the following modified construction.
Modified Construction.
Case 1:
$i = 4n$
. As on page 6.
Case 2:
$i = 4n + 1$
. If
$a_n \not \in E_i$
or
$a_n \not \in (Z)^q$
then set
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. Otherwise proceed as on page 6.
Case 3:
$i = 4n+2$
. Unless
$a_n \in E_i \setminus F$
, let
$(E_{i+1}, S_{i+1})= (E_i, S_i)$
. If
$a_n \in E_i \setminus F$
let w be a discrete valuation on
$E_i$
(considered as a function field extension of
$F(t)/F$
), trivial on F, which is negative on
$a_n$
. By Lemma 4.3
, w and
$v_Z|_{E_i}$
are independent. Let us define a finite separable extension
$E/E_i$
: if the second condition of (
) already holds for
$\{w, \{v_s\}_{s \in S_i}\}$
in
$E_i$
, set
$E = E_i$
. Otherwise there exists
$u \in F$
such that
$q \nmid w(t^q - u)$
and
$q | v_s(t^q - u)$
for all
$s \in S_i$
. By the strong triangle inequality, there is at most one such u.
Under Assumption
$(\otimes )(5)$
there exists
$d \in F^*$
such that
$d(t^q - u) \in (Z)^q$
. Thus we may set
$E = E_i(\sqrt [q]{d(t^q - u)})$
and extend the valuations
$\{v_s\}_{s \in S_i}$
sensibly as before (and let
$w'$
be any extension to E of w). We conclude the second condition of (
) now holds for
$(E, \{w', \{v_s\}_{s \in S_i}\})$
.
If
$w'$
is independent to
$v_s$
for every
$s \in S_i$
: let
$\{w', v_{s_1}, \dots , v_{s_k}\}$
be the distinct valuations of
$\{w', \{v_s\}_{s \in S_i}\}$
. By the Approximation Theorem [Reference Engler and Prestel13, Theorem 2.4.1], there exists
$b \in E$
such that
$w'(b)$
is the smallest positive element of its value group,
$q | v_{s_j}(b)$
and
$v_{s_j}(b) < 0, -v_{s_j}(a_n^q)$
for
$1 \leq j \leq k$
. Notice
$q | w'(1+b)$
,
$q|w'(a_n^q + b^{-1})$
, and
$q|v_s(a_n^q + b^{-1})$
,
$q|v_s(1+b)$
for all
$s \in S_i$
.
We also wish
$b, 1+b, a_n^q + b^{-1} \in (Z)^q$
. This can be achieved with further care by using the Approximation Theorem and Hensel’s Lemma: by Lemma 4.3
and [Reference Engler and Prestel13, Corollary 2.3.2],
$v_Z|_{E}$
,
$w'$
, and
$v_{s_j}$
for
$1 \leq j \leq k$
are pairwise independent. Let
$d \in (E)^q \subseteq (Z)^q$
have
$v_Z|_E(d)> 0$
. Using the Approximation Theorem, we choose
$b \in E$
so that in addition
$v_Z|_E(b - d)> v_Z|_E(d)$
. Then by Hensel’s Lemma,
$b \in E \cap (Z)^q$
, and since
$v_Z|_E((b+1) - 1) = v_Z|_E(b)$
and
$v_Z|_E((b + a_n^{-q}) - a_n^{-q}) = v_Z|_E(b)$
, we have
$1 + b, b + a_n^{-q} \in E \cap (Z)^q$
. (Hence
$a_n^q + b^{-1} \in E \cap (Z)^q$
.) We define
$$\begin{align*}(E_{i+1}, S_{i+1}) = (E(\sqrt[q]{1+b}, \sqrt[q]{a_n^q + b^{-1}}),\, S_i \cup \{b\}).\end{align*}$$
Extending
$\{v_b = w', \{v_s\}_{s \in S_i}\}$
as in Case 2, (
) holds as it did on E.
Now assume
$w'$
is dependent with
$v_{\widehat {s}}$
for some
$\widehat {s} \in S_i$
: in which case,
$w' = v_{\widehat {s}}$
by Lemma 3.5
. Let
$\{v_{s_1}, \dots , v_{s_l}\}$
be the distinct valuations of
$\{w', \{v_s\}_{s \in S_i}\}$
, assuming WLOG
$w' = v_{s_1}$
. By Lemma 4.3
and [Reference Engler and Prestel13, Corollary 2.3.2],
$v_Z|_{E}$
, and
$v_{s_j}$
for
$1 \leq j \leq l$
are pairwise independent. Let
$d \in (E)^q \subseteq (Z)^q$
have
$v_Z|_E(d)> 0$
. Using the Approximation Theorem, we choose
$b \in E$
so that
$v_Z|_E(b - d)> v_Z|_E(d)$
,
$v_{s_1}(b)$
is the smallest positive element of its value group,
$q | v_{s_j}(b)$
and
$v_{s_j}(b) < 0, -v_{s_j}(a_n^q)$
for
$2 \leq j \leq l$
. By Hensel’s Lemma,
$1 + b, a_n^q + b^{-1} \in E \cap (Z)^q$
, and we may define
$$\begin{align*}(E_{i+1}, S_{i+1}) = (E(\sqrt[q]{1+b}, \sqrt[q]{a_n^q + b^{-1}}),\, S_i \cup \{b\}).\end{align*}$$
Extending
$\{v_b = w', \{v_s\}_{s \in S_i}\}$
as in Case 2, (
) holds on
$(E_{i+1}, S_{i+1})$
. (Again this case allows for
$b \in S_i$
without issue, by Lemma 3.5
.)
Case 4:
$i = 4n +3$
. As on page 6. Recall this step extends
$\{v_s\}_{s \in S_i}$
to
$\{v_s\}_{s\in S_{i+1}} = \{w_{r_1}, w_{r_2}, \{v_s\}_{s \in S_i}\}$
. The valuations
$w_{r_1}, w_{r_2}$
are independent to
$v_Z|_{E_i}$
by Lemma 4.3
, and (
) is satisfied.⊣
Now we can show the following (cf. Lemma 3.6 ):
Lemma 4.5. Set
$K_q = \bigcup _i E_i$
. The above construction ensures we have the following features of
$K_q$
under Assumption
$(\otimes )$
:
-
(1)
$(K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
. -
(2)
$F^* \cdot \left ( \bigcup _i S_i \right ) = K_q \setminus (F^* \cdot (K_q)^q)$
. -
(3)
$F \!=\! \{ a \in {K_q}\!:\!\forall b \in K_q \cap (Z)^q\setminus \{0\} \mbox { } ([1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q]\! \rightarrow \! b \in (K_q)^q)\}$
. -
(4)
$\operatorname {\mathbb {Z}} \mbox{(resp.}\ \mathbb{F}_p[z]) = \{u \in F : \forall u_1 \neq u_2 \in F \mbox { s.t. } u_1 + u_2 = u\mbox {, } t^q - u_1 \mbox { or } t^q - u_2 \in F^* \cdot (K_q)^q\}$
.
Proof In [Reference Ziegler49, Section 4], but for exposition:
-
(1) Let
$a \in (K_q \cap (Z)^q)\setminus (K_q)^q$
. For some n sufficiently large,
$a_n = a$
and
$a_n \in E_{4n+1}$
. Case 2 of the above construction assures
$a_n \in S_{4n+2}$
, hence
$a \in \bigcup _i S_i$
as desired. Conversely, by construction
$\bigcup _i S_i \subseteq K_q \cap (Z)^q$
, and
$S_i \cap (K_q)^q = \emptyset $
for all i. -
(2) Let
$a \in F^* \cdot (K_q)^q$
. For all i sufficiently large,
$a \in F^* \cdot (E_i)^q$
and hence
$q|u(a)$
for all valuations u trivial on F. By design of (),
$a \not \in F^* \cdot S_i$
, hence
$F^* \cdot \left ( \bigcup _i S_i \right ) \subseteq K_q \setminus (F^* \cdot (K_q)^q)$
. Conversely, if
$a \in K_q \setminus (F^* \cdot (K_q)^q)$
, then by Assumption
$(\otimes )(5)$
there exists
$b \in F^*$
with
$ab \in (K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
by (1). -
(3) Let
$a \in F$
. Suppose for
$b \in {K_q} \cap (Z)^q \setminus \{0\}$
, we have
$1 + b, a^q + b^{-1} \in (K_q)^q$
. Let i be sufficiently large such that
$1 + b, a^q + b^{-1} \in (E_i)^q$
. Notice that, for any valuation u on
$E_i$
trivial on F,
$q|u(b)$
: indeed, if
$u(b) < 0$
then
$u(b) = u(1 + b)$
, and if
$u(b)> 0$
then
$u(b) = u(a^q + b^{-1})$
. By ()
$b \not \in S_i$
(for all subsequent i too), hence as
$b \in K_q \cap (Z)^q$
,
$b \in (K_q)^q$
by (1).Conversely, if
$a \in K_q \setminus F$
, then for some n sufficiently large we may assume
$a_n = a$
and
$a \in E_{4n+2}$
. By Case 3 of the construction, there exists
$b \in S_{4n+3}$
such that
$1+ b, a^q + b^{-1} \in (E_{4n+3})^q$
and
$b \in K_q \cap (Z)^q$
. Therefore by (1), as desired.
$$\begin{align*}\exists b \in K_q \cap (Z)^q\setminus\{0\} \mbox{, }(1 + b \in (K_q)^q \land a^q + b^{-1} \in (K_q)^q \land b \not\in (K_q)^q),\end{align*}$$
-
(4) Let
$u \in \operatorname {\mathbb {Z}}$
(resp.
$\mathbb {F}_p[z]$
),
$u_1 \neq u_2 \in F$
, and
$u_1 + u_2 = u$
. Assume for the purpose of contradiction both
$t^q - u_1, t^q - u_2 \not \in F^* \cdot (K_q)^q$
. By the argument in Case 4 there exist
$d_1, d_2$
such that
$d_1(t^q - u_1), d_2(t^q - u_2) \in (K_q \cap (Z)^q) \setminus (K_q)^q = \bigcup _i S_i$
, by (1). We conclude for some sufficiently large i that
$t^q - u_1, t^q - u_2 \in F^* \cdot S_i$
, contradicting ().Conversely, if
$u \in F \setminus \operatorname {\mathbb {Z}}$
(resp.
$F \setminus \mathbb {F}_{p}[z]$
), then for some n sufficiently large we may assume
$a_n = u$
and
$a_n \in E_{4n+3}$
. By Case 3 of the construction, deliberately there exists
$u_1 \neq u_2 \in F^*$
with
$u_1 + u_2 = u$
and
$t^q - u_1, t^q - u_2 \in S_{4n+4} \subseteq F^* \cdot S_{4n+4}$
. Therefore by (2),
$t^q - u_1, t^q - u_2 \not \in F^* \cdot (K_q)^q$
as required for this argument.
), 
) 
).
Let us return to the case
$(R, v_R) = (k(\Gamma ), v|_{k(\Gamma )})$
,
$(Z, v_Z) = (k((\Gamma )), v)$
,
$F = k((\Gamma )) \cap \left ({k(\Gamma )(t_1, \dots , t_e)}\right )^s$
. We have the following additional results:
Theorem 4.6 ((Ax–Kochen–Ershov) [Reference Ax and Kochen3, Reference Ershov14])
Let
$(K, v)$
,
$(L, w)$
be equicharacteristic
$0$
henselian valued fields. Then
$K \equiv _{\mathcal {L}_{val}} L$
if and only if
$Kv \equiv _{\mathcal {L}_r} Lw$
and
$vK \equiv _{\mathcal {L}_{oag}} wL$
.
Consequently,
$(K, v) \equiv (Kv((vK)), v_{vK})$
, the field of Hahn series in
$vK$
over
$Kv$
.
Lemma 4.7. Let
$q> \operatorname {\mathrm {char}}(k)$
be prime and v a henselian valuation on
$k((\Gamma ))$
which factors through
$v_{\Gamma }$
, where k and
$\Gamma $
are countable, and
$K_q$
as above. Then
$K_q \cap (k((\Gamma )))^q$
is
$\mathcal {L}_{val}$
-definable in
$(K_q, w)$
, where
$w = v|_{K_q}$
.
Proof Recall from Lemma 4.1
that Assumption
$(\otimes )$
is satisfied. It suffices to show
$c \in K_q \cap (k((\Gamma )))^q$
if and only if there exists
$d \in K_q$
such that
$w(c - d^q)> w(c)$
.
Assume there exists
$d \in K_q$
such that
$w(c - d^q)> w(c)$
; then (as elements of
$k((\Gamma ))$
) we have
$v(c - d^q)> v(c)$
, hence
$v(1 - \tfrac {d^q}{c})> 0$
, and thus
$1 \equiv {\tfrac {d^q}{c}}$
mod
$\mathfrak {m}_{v}$
. By Hensel’s Lemma, there exists
$e \in k((\Gamma ))$
such that
$e^q = \tfrac {d^q}{c}$
; we conclude
$c \in (k((\Gamma )))^q$
.
Conversely, let
$c \in K_q \cap (k((\Gamma )))^q$
and write
$c = \widehat {d}^q$
. Let
$d \in k(\Gamma )$
be a sufficiently large finite truncation of
$\widehat {d} \in k((\Gamma ))$
such that
$v_{\Gamma }(\widehat {d} - d)> v_{\Gamma }(\widehat {d})$
(and note
$v_{\Gamma }(\widehat {d}) = v_{\Gamma }(d)$
). Then
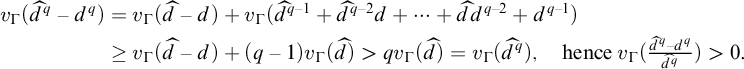$$ \begin{align*} v_{\Gamma}(\widehat{d}^q - d^q) &= v_{\Gamma}(\widehat{d} - d) + v_{\Gamma}(\widehat{d}^{q-1} + \widehat{d}^{q-2} d + \dots + \widehat{d} d^{q-2} + d^{q-1})\\ &\geq v_{\Gamma}(\widehat{d} - d) + (q-1) v_{\Gamma}(\widehat{d})> q v_{\Gamma}(\widehat{d}) = v_{\Gamma}(\widehat{d}^q), \quad \mbox{hence}\ v_{\Gamma}(\tfrac{\widehat{d}^q - d^q}{\widehat{d}^q}) > 0. \end{align*} $$
Consequently
$v(\tfrac {\widehat {d}^q - d^q}{\widehat {d}^q})> 0$
, i.e.,
$v(\widehat {d}^q - d^q)> v(\widehat {d}^q)$
; equivalently
$v(c - d^q)> v(c)$
and hence
$w(c - d^q)> w(c)$
as desired.
Theorem 4.8. Let
$q> \operatorname {\mathrm {char}}(k)$
be prime, v a henselian valuation on
$k((\Gamma ))$
which factors through
$v_{\Gamma }$
, where k and
$\Gamma $
are countable, and
$K_q$
as above. Then:
-
(1)
$(K_q, v_{\Gamma }|_{K_q})$
is an immediate extension of
$(k(\Gamma ), v_{\Gamma })$
. -
(2)
$(K_q, v|_{K_q})$
is an immediate extension of
$(k(\Gamma ), v)$
. -
(3)
$\operatorname {\mathbb {Z}}$
(resp.
$\mathbb {F}_p[z])$
is definable in
$K_q$
in the language
$\{0, 1, +, \times , \mathcal {O}_{v|_{K_q}}\}$
. -
(4) If
$a \in k((\Gamma ))\setminus K_q$
is pliant over
$K_q$
, then
$q | [K_q(a) : K_q]$
.
Proof (1) and (2) follow from the fact that
$k(\Gamma ) \subseteq K_q \subseteq k((\Gamma ))$
. For (3),
$\operatorname {\mathbb {Z}}$
(resp.
$\mathbb {F}_p[z]$
) is
$\mathcal {L}_{val}$
-definable in
$K_q$
as
$K_q \cap (k((\Gamma )))^q$
is
$\mathcal {L}_{val}$
-definable in
$K_q$
by Lemma 4.7
, and this is sufficient to define
$\operatorname {\mathbb {Z}}$
(resp.
$\mathbb {F}_p[z]$
) by Lemma 4.5
. Finally for (4), note for some n sufficiently large, we have
$a = a_{n}$
and
$[E_{4n}(a_n) : E_{4n}] = [K_q(a) : K_q]$
, as we assume
$a \not \in K_q$
. By construction (Case 1),
$q|[E_{4n}(a) : E_{4n}]$
as desired.
Remark 4.9 [Reference Engler and Prestel13, pp. 173–178]
Let S be an infinite set of indices and
$\mathcal {U}$
a nonprincipal ultrafilter on S. For
$s \in S$
, let
$(K_s, v_s)$
be a valued field. One may take an ultraproduct
$\prod _{s \in S} (K_s, v_s)/\mathcal {U}$
of valued fields, and obtain a (valued) field
$\mathbb {K} = \prod _{s \in S} K_s/\mathcal {U}$
with value group
$\prod _{s \in S} v_s K_s/\mathcal {U}$
and residue field
$\prod _{s \in S} K_s v_s/\mathcal {U}$
, under the valuation
$\prod v_s$
defined by:
$$ \begin{gather*} \textstyle\prod v_s ([(a_s)_{s \in S}]) = [(v_s(a_s))_{s \in S}], \quad \mbox{with residue}\\ res_{\textstyle\prod v_s} : \mathcal{O}_{\textstyle\prod v_s} \rightarrow \prod_{s \in S} K_s v_s/\mathcal{U};\quad [(x_s)] \mapsto [(res_{v_s}(x_s))]. \end{gather*} $$
(Here
$a_s \in K_s$
for
$s \in S$
, and
$[\cdot ]$
represents the equivalence class of tuples modulo
$\mathcal {U}$
.)
Corollary 4.10. Let
$(K, v)$
be an equicharacteristic
$0$
henselian nontrivially valued field.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
$\mathcal {O}_v$
is
$\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
Proof Writing
$k = Kv$
and
$\Gamma = vK$
, by Theorem 4.6
we have
$(K, v) \equiv (k((\Gamma )), v_{\Gamma })$
. By the Downwards Löwenheim–Skolem Theorem we may also assume
$k, \Gamma $
are countable. Set
$v'$
(on k) to be the trivial valuation, in which case
$v = v' \circ v_{\Gamma } = v_{\Gamma }$
. By Lemma 4.1
,
$(R, v_R)\! =\! (k(\Gamma ), v_{\Gamma }|_{k(\Gamma )}),(Z, v_Z)\! = \!(k((\Gamma )), v_{\Gamma }), F\! =\! k((\Gamma )) \cap \widetilde {k(\Gamma )}$
satisfy Assumption
$(\otimes )$
.
Let q be prime and consider
$(K_q, w = v_{\Gamma }|_{K_q}) \subseteq (k((\Gamma )), v_{\Gamma })$
arising from the Modified Construction, where now “pliant” means algebraic. In particular
$K_q$
is an equicharacteristic
$0$
valued field with residue field k and value group
$\Gamma $
. We will verify the henselianity axioms
$\varphi _1, \dots , \varphi _{q-1}$
are satisfied, where
$\varphi _n$
is
$$\begin{align*}\forall a_0, \dots, a_{n-2} \left( \bigwedge_i a_i \in \mathfrak{m}_v \rightarrow \exists x\, [x^n + x^{n-1} + a_{n-2} x^{n-2} + \dots + a_0 = 0]\right).\end{align*}$$
Take
$l \leq q-1$
and fix
$a_0, \dots , a_{l-2} \in \mathfrak {m}_{w}$
. Suppose
$X^l + X^{l-1} + a_{l-2} X^{l-2} + \dots + a_0 = 0$
has no solution in
$K_q$
, and
$\alpha \in k((\Gamma )) \setminus K_q$
satisfies this equation. Then
$K_q(\alpha )/K_q$
is a finite proper extension. By Theorem 4.8
,
$q| [K_q(\alpha ) : K_q]$
, however
$q> l$
and
$[K_q(\alpha ) : K_q] \leq l$
; a contradiction. We conclude that
$K_q \models \varphi _l$
for all
$l \leq q-1$
; in particular for
$n \geq 0$
fixed,
$K_q \models \varphi _n$
for all primes
$q> n$
.
Let
$\mathcal {U}$
be a nonprincipal ultrafilter on the set of primes, and let
$\mathbb {K}$
be the ultraproduct
$\prod _{q} K_q / \mathcal {U}$
. By Remark 4.9 and Łoś’ Theorem,
$\mathbb {K}$
is an equicharacteristic
$0$
henselian valued field with residue field (
$\mathcal {L}_r$
-elementarily equivalent to) k, and value group (
$\mathcal {L}_{oag}$
-elementarily equivalent to)
$\Gamma $
. Hence by Theorem 4.6
,
$\mathbb {K} \equiv _{\mathcal {L}_{val}} k((\Gamma ))$
. Thus
$\mathbb {K} \models T$
for any finite subtheory
$T \subseteq {\mathtt{Th}}(k((\Gamma )); \mathcal {L}_{val})$
, and hence for some prime q,
$K_q \models T$
. By Theorem 4.8 and Corollary 1.8
,
${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable, making T undecidable as required.
Finally, if
$\mathcal {O}_v \subseteq K$
is
$\mathcal {L}_r$
-definable by the formula
$\varpi (x, \overline {y})$
(where
$\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
$\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
$S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
$K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
5. Henselian valued fields: further discourse
We may extend the results of the previous section from equicharacteristic 0 henselian valued fields, to mixed characteristic henselian valued fields, using the standard decomposition Footnote 5 :
Let
$(K, v)$
be a valued field of mixed characteristic
$(0, p)$
with value group
$\Gamma $
. Define
$\Delta _0$
to be the minimal convex subgroup of
$\Gamma $
containing
$v(p)$
, and
$\Delta _p$
to be the maximal convex subgroup of
$\Gamma $
not containing
$v(p)$
. We will consider the valuation(s)
$v_0 : K \rightarrow \Gamma / \Delta _0$
(resp.
$v_p : K \rightarrow \Gamma / \Delta _p$
) corresponding to the coarsening(s) of v with respect to
$\Delta _0$
(resp.
$\Delta _p$
), and the induced valuation(s)
$\hat {v}_0 : K v_0 \rightarrow \Delta _0$
(resp.
$\hat {v}_p : K v_p \rightarrow \Delta _p$
) with residue field(s)
$Kv$
. Also consider
$\overline {v_p} : K v_0 \rightarrow \Delta _0 / \Delta _p$
with residue field
$K v_p$
; this arises as the coarsening of
$v_0$
with respect to
$\Delta _p$
(as
$\Delta _p < \Delta _0 \leq \Gamma $
). These fit together in the following way:
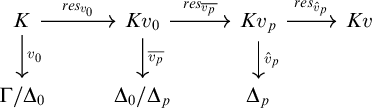
If
$\Delta _0 = vK$
then by the Compactness Theorem there is an elementary extension
$(K, v) \prec (K^{\flat }, v^{\flat })$
containing an element
$c^{\flat }$
such that
$n \cdot v^{\flat }(p) < v^{\flat }(c^{\flat }) < \infty $
for all
$n \geq 0$
. Hence the minimal convex subgroup of
$v^{\flat }K^{\flat }$
containing
$v^{\flat }(p)$
does not contain
$v^{\flat }(c^{\flat })$
, i.e.,
$\Delta _0 < v^{\flat }K^{\flat }$
. As
$(K, v) \equiv (K^{\flat }, v^{\flat })$
, for the purposes of proving finite undecidability we may assume WLOG
$\Delta _0 < vK$
. Consider:
Lemma 5.1 [Reference Anscombe and Jahnke2, Lemma 6.5]
Let T be a theory of bivalued fields
$(K, v', v)$
with
$v'$
an equicharacteristic
$0$
henselian coarsening of v, and suppose that T entails complete theories of valued fields
$(K, v')$
and
$(Kv', \overline {v})$
. Then T is complete.
Corollary 5.2. Let
$(K, v)$
be a mixed characteristic henselian nontrivially valued field, and
$v_0$
as above. There exists a nontrivial ordered abelian group
$\Omega $
such that
$(K, v_0, v) \equiv (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
.
Proof Define
$\Omega = vK/\Delta _0$
. By Theorem 4.6
,
$(K, v_0) \equiv (Kv_0((\Omega )), v_{\Omega })$
. Since
$v = \widehat {v}_0 \circ v_0$
in the standard decomposition of
$(K, v)$
,
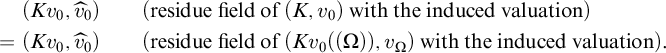$$ \begin{align*} &(Kv_0, \widehat{v}_0) \qquad \mbox{(residue field of}\ (K, v_0)\ \mbox{with the induced valuation)}\\ =\,\, &(Kv_0, \widehat{v}_0) \qquad \mbox{(residue field of}\ (Kv_0((\Omega)), v_{\Omega})\ \mbox{with the induced valuation).} \end{align*} $$
By Lemma 5.1
, we conclude
$(K, v_0, v) \equiv (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
as desired.
Theorem 5.3. Let
$(K, v)$
be a mixed characteristic henselian nontrivially valued field.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
$\mathcal {O}_v$
is
$\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
Proof As finite undecidability is a property of
${\mathtt{Th}}(K; \mathcal {L}_{val})$
, we may assume WLOG
$(K, v_0, v) = (Kv_0((\Omega )), v_{\Omega }, \widehat {v}_0 \circ v_{\Omega })$
where
$Kv_0$
and
$\Omega $
are countable, by the Downwards Löwenheim–Skolem Theorem and Corollary 5.2
. Let
$(Z, v_Z) = (Kv_0((\Omega )), \widehat {v}_0 \circ v_{\Omega })$
,
$(R, v_R) = (Kv_0(\Omega ),\, \widehat {v}_0 \circ v_{\Omega })$
and
$F = Z \cap \widetilde {R}$
. By Lemma 4.1
, Assumption
$(\otimes )$
is satisfied: for
$q> p$
prime, denote by
$K_q$
be the field given by the Modified Construction—where now “pliant” means algebraic—with valuation
$(\widehat {v}_0 \circ v_{\Omega })|_{K_q} = \widehat {v}_0 \circ v_{\Omega }|_{K_q}$
. We have the following diagram of fields:
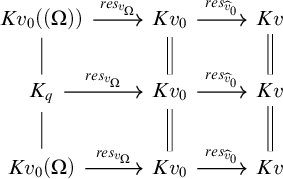
Consider
$K_q$
as a multisorted structure:
$$\begin{align*}\mathcal{K}_q = (K_q,\, Kv_0,\, Kv,\, \Omega,\, \Delta_0,\, vK;\,\, res_{v_{\Omega}|_{K_q}},\, res_{\widehat{v}_0},\, res_{(\widehat{v}_0 \circ v_{\Omega})|_{K_q}};\, v_{\Omega}|_{K_q},\, \widehat{v}_0,\, (\widehat{v}_0 \circ v_{\Omega})|_{K_q}),\end{align*}$$
which encompasses the diagram
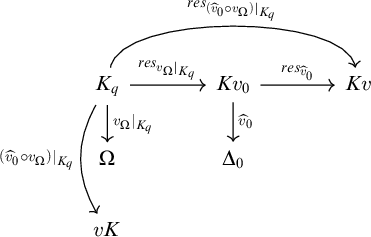
Let
$\mathcal {U}$
be a nonprincipal ultrafilter on the set of primes larger than p, and let
$\mathbb {K}$
be the ultraproduct
$\prod _{q>p} \mathcal {K}_q/\mathcal {U}$
. (We abuse notation to also denote the home sort of
$\mathbb {K}$
by
$\mathbb {K}$
.) We have the following properties of
$\mathbb {K}$
:
-
•
$\mathbb {K}$
has valuation
$\mathfrak {v}_0=\prod v_{\Omega }|_{K_q}$
with residue field
$\prod _{q>p} Kv_0/\mathcal {U} = Kv_0^{\mathcal {U}}$
and value group
$\prod _{q>p} \Omega /\mathcal {U} = \Omega ^{\mathcal {U}}$
. (This is Remark 4.9
.) Furthermore,
$(\mathbb {K}, \mathfrak {v}_0)$
is a henselian valued field. Indeed, we claim for
$q> p$
prime the henselianity axioms
$\varphi _1, \dots , \varphi _{q-1}$
are satisfied in
$K_q$
:Let
$l < q$
and fix
$a_0, \dots a_{l-2} \in \mathfrak {m}_{v_{\Omega }|_{K_q}}$
. Suppose
$X^l + X^{l-1} + a_{l-2}X^{l-2} + \dots + a_0 = 0$
has no solution in
$K_q$
—though there exists a solution
$\alpha \in K_q^h$
, and
$K_q^h \subseteq Kv_0((\Omega ))$
by the universal property of henselisations [Reference Engler and Prestel13, Theorem 5.2.2]. Then
$K_q(\alpha )/K_q$
is a finite proper extension. By Theorem 4.8
,
$q|[K_q(\alpha ) : K_q]$
; however
$q> l$
and
$[K_q(\alpha ) : K_q] \leq l$
; a contradiction.Therefore, by Łoś’ Theorem (i.e., [Reference Chang and Keisler6, Theorem 4.1.9])
$(\mathbb {K}, \mathfrak {v}_0)$
is an equicharacteristic 0 henselian valued field with
$\mathfrak {v}_0 \mathbb {K} \equiv _{\mathcal {L}_{oag}} \Omega $
and
$\mathbb {K}\mathfrak {v}_0 \equiv _{\mathcal {L}_r} Kv_0$
. By Theorem 4.6
we conclude
$(\mathbb {K}, \mathfrak {v}_0) \equiv (Kv_0((\Omega )), v_{\Omega })$
. -
•
$Kv_0^{\mathcal {U}}$
has valuation
$\widehat {v}_0^{\mathcal {U}} = \prod \widehat {v}_0$
with residue field
$vK^{\mathcal {U}}$
and value group
$\Delta _0^{\mathcal {U}}$
(Remark 4.9
). By [Reference Chang and Keisler6, Theorem 4.1.9],
$(Kv_0^{\mathcal {U}}, \widehat {v}_0^{\mathcal {U}}) \equiv (Kv_0, \widehat {v}_0)$
. -
• Hence
$\mathbb {K}$
can be equipped with a valuation
$\mathfrak {v}_1 := \widehat {v}_0^{\mathcal {U}} \circ \mathfrak {v}_0$
, and
$\mathfrak {v}_0$
is an equicharacteristic
$0$
henselian coarsening of
$\mathfrak {v}_1$
.
$\mathbb {K}$
also has a valuation
$\mathfrak {v}_2=\prod (\widehat {v}_0 \circ v_{\Omega })|_{K_q}$
, and we claim
$\mathcal {O}_{\mathfrak {v}_1} = \mathcal {O}_{\mathfrak {v}_2}$
, so
$(\mathbb {K}, \mathfrak {v}_1) \equiv (\mathbb {K}, \mathfrak {v}_2)$
. Indeed,
$$ \begin{align*} x = [(x_q)] \in \mathcal{O}_{\mathfrak{v}_1} &\iff [(x_q)] \in res_{\mathfrak{v}_0}^{-1}(\mathcal{O}_{\widehat{v}_0^{\mathcal{U}}})\\ &\iff res_{\mathfrak{v}_0}([(x_q)]) = [(res_{v_{\Omega}|_{K_q}}(x_q))] \in \mathcal{O}_{\widehat{v}_0^{\mathcal{U}}}\\ &\iff \{q \mbox{ : } res_{v_{\Omega}|_{K_q}}(x_q) \in \mathcal{O}_{\widehat{v}_0}\} \in \mathcal{U}\\ &\iff \{q \mbox{ : } x_q \in \mathcal{O}_{(\widehat{v}_0 \circ v_{\Omega})|_{K_q}}\} \in \mathcal{U} \iff [(x_q)] \in \mathcal{O}_{\mathfrak{v}_2}. \end{align*} $$
Considering
$(\mathbb {K}, \mathfrak {v}_0, \mathfrak {v}_1)$
as a bivalued field, by Lemma 5.1
$$\begin{align*}(\mathbb{K}, \mathfrak{v}_0, \mathfrak{v}_1) \equiv (Kv_0((\Omega)), v_{\Omega}, \widehat{v}_0 \circ v_{\Omega}) = (K, v_0, v).\end{align*}$$
Taking a reduct of the language,
$(\mathbb {K}, \mathfrak {v}_2) \equiv (\mathbb {K}, \mathfrak {v}_1) \equiv (K, v)$
. Therefore if T is a finite subtheory of
${\mathtt{Th}}(K; \mathcal {L}_{val})$
,
$(\mathbb {K}, \mathfrak {v}_2) \models T$
, and hence for some q sufficiently large,
$(K_q, \widehat {v}_0 \circ v_{\Omega }|_{K_q}) \models T$
. By Theorem 4.8 and Corollary 1.8
,
${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable, making T undecidable as required.
Finally, if
$\mathcal {O}_v \subseteq K$
is
$\mathcal {L}_r$
-definable by the formula
$\varpi (x, \overline {y})$
(where
$\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
$\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O}_{\mathfrak {v}_2} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
$S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
$K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
What remains is to handle the case of equicharacteristic
$p> 0$
henselian nontrivially valued fields. We will show this gap can be eliminated for certain fields of this type (e.g., those fields also satisfying NIP, by using a nice algebraic classification of such fields by Anscombe and Jahnke [Reference Anscombe and Jahnke2, Theorem 5.1]). We require the following definitions:
Definition 5.4. A valued field
$(K, v)$
is said to be (separably) defectless if whenever
$L/K$
is a finite (separable) extension,
$[L : K] = \sum _{w \supseteq v} e(w/v) f(w/v)$
, where w ranges over all prolongations of v to L,
$e(w/v) = (wL : vK)$
is the ramification degree and
$f(w/v) = [Lw : Kv]$
is the inertia degree of the valued field extension
$(L,w)/(K,v)$
.
Definition 5.5. A valued field
$(K, v)$
of residue characteristic
$p>0$
is Kaplansky
Footnote
6
if
$vK$
is p-divisible, and
$Kv$
is perfect and admits no proper separable algebraic extensions of degree divisible by p.
Theorem 5.6 (Anscombe–Jahnke)
Let
$(K, v)$
be a positive equicharacteristic NIP henselian nontrivially valued field. Then
$(K, v)$
is separably defectless Kaplansky.
Proof An immediate consequence of [Reference Anscombe and Jahnke2, Proposition 3.1].
A corollary to this, noted by Anscombe and Jahnke, is that by Delon [Reference Delon10, Théorème 3.1] the
$\mathcal {L}_{val}$
-theory of equicharacteristic
$p> 0$
henselian separably defectless valued fields
$(K,v)$
of imperfection degree e, with residue field
$\mathcal {L}_r$
-elementarily equivalent to
$Kv$
and value group
$\mathcal {L}_{oag}$
-elementarily equivalent to
$vK$
, is complete. (As we are concerned with finitely axiomatised subsets of
${\mathtt{Th}}(K; \mathcal {L}_{val})$
, we will assume WLOG
$e < \infty $
.)
For a valued field
$(B, v_B)$
to be separably defectless, it is sufficient for it to satisfy the first-order
$\mathcal {L}_{val}$
-statementsFootnote
7
for all
$M \geq 1$
:
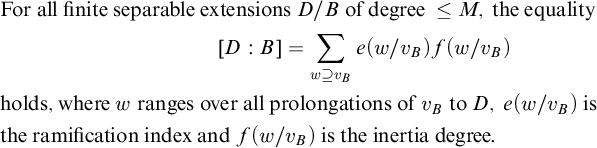$$\begin{align} & \mbox{For all finite separable extensions}\ D/B\ \text{of degree}\ \leq M,\ \text{the equality} \nonumber\\ &\hspace{37mm}[D : B] = \sum_{w \supseteq v_B} e(w/v_B) f(w/v_B)\hspace{7mm} \\ &\mbox{holds, where}\ w\ \text{ranges over all prolongations of}\ v_B\ \text{to}\ D,\ e(w/v_B)\ \text{is} \nonumber\\ &\mbox{the ramification index and}\ f(w/v_B)\ \text{is the inertia degree.} \nonumber \end{align}$$
Lemma 5.7. Fix
$M \in \operatorname {\mathbb {N}}_{>0}$
and
$q> M^M$
prime. Assume
$(R, v_R)$
,
$(Z, v_Z)$
, and F satisfy Assumption
$(\otimes )$
and let
$K_q$
be the field resulting from the Modified Construction. If Z is separably defectless Kaplansky, then 
.
Proof Let
$D/K_q$
be a separable extension of degree
$\leq M$
. By taking the normal closure may assume
$D/K_q$
is Galois and of degree
$d\leq M^M$
. If
$D/K_q$
is proper, by degree reasons
$Z \cap D = K_q$
. Indeed, if
$Z \supset D' \supset K_q$
is a separable extension of degree
$\leq M^M$
, by the Primitive Element Theorem there exists
$\alpha \in Z \cap K_q^s$
such that
$D' = K_q(\alpha )$
. By Theorem 4.8
, if
$\alpha \not \in K_q$
then
$q | [K_q(\alpha ) : K_q]$
; however
$q> M^M$
and
$[K_q(\alpha ) : K_q] \leq M^M$
. This is a contradiction; hence
$\alpha \in K_q$
. Thus Z and D are linearly disjoint over
$K_q$
. Consider the following tower of extensions:
By the tower property [Reference Fried and Jarden16, Lemma 2.5.3], D is linearly disjoint to
$K_q^h$
, a subfield of Z by the universal property of henselisations. Thus
$w = v_Z|_{K_q}$
extends uniquely to
$(D, w')$
, by, e.g., [Reference Blaszczok and Kuhlmann4, Lemma 2.1]. As
$(Z, v_Z)$
is henselian,
$v_Z$
extends uniquely to
$(ZD, v_Z')$
, and restricts to
$(D, w')$
. As
$Z/K_q$
is immediate, as the valuation extensions are unique, and as Z is linearly disjoint from D over
$K_q$
,
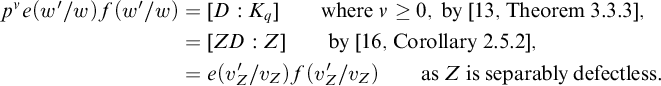$$ \begin{align*} p^{\nu} e(w'/w) f(w'/w) &= [D : K_q] \qquad\mbox{where}\ \nu \geq 0,\ \mbox{by [13, Theorem 3.3.3],}\\ &= [ZD : Z] \qquad \mbox{by [16, Corollary 2.5.2],}\\ &= e(v_Z'/v_Z) f(v_Z' / v_Z) \qquad\mbox{as}\ Z\ \mbox{is separably defectless}. \end{align*} $$
In addition, as Z is Kaplansky,
$p \nmid e(v_Z'/v_Z), f(v_Z' / v_Z)$
. Hence
$$\begin{align*}[D : K_q] = e(w'/w) f(w'/w) = \sum_{w' \supseteq w} e(w'/w) f(w'/w).\end{align*}$$
We conclude 
as desired.
We are ready to prove:
Theorem 5.8. Let
$(K, v)$
be an equicharacteristic
$p> 0$
separably defectless Kaplansky henselian nontrivially valued field.
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable.
Moreover, if
$\mathcal {O}_v$
is
$\mathcal {L}_r$
-definable, then K is finitely undecidable as a field.
Proof Fix
$e \in \operatorname {\mathbb {N}}$
, the imperfection degree of K. Let k,
$\Gamma $
be countable models of
${\mathtt{Th}}(Kv; \mathcal {L}_r)$
,
${\mathtt{Th}}(vK; \mathcal {L}_{oag})$
. By definition k is perfect and
$\Gamma $
is p-divisible, and thus
$k(\Gamma )$
and
$k((\Gamma ))$
are perfect. By Lemma 4.1
we may choose
$t_1, \dots , t_e \in k((\Gamma ))$
transcendental and algebraically independent over
$k(\Gamma )$
and consider the field
$k(\Gamma )(t_1, \dots , t_{e-1})$
—by [Reference Fried and Jarden16, Lemma 2.7.2] its imperfection degree is exactly
$e-1$
. Finally, set
$F = k((\Gamma )) \cap (k(\Gamma )(t_1, \dots , t_{e-1}))^s$
. With
$(R, v_R) = (k(\Gamma ), v_{\Gamma })$
,
$(Z, v_Z) = (k((\Gamma )), v_{\Gamma })$
, Assumption
$(\otimes )$
is satisfied by Lemma 4.1
. Note the imperfection degree of F is exactly
$e-1$
, and
$(Z, v_Z)$
is perfect separably defectless Kaplansky.
As there exists an element
$t \in k((\Gamma ))$
transcendental over F, by Theorem 4.8
there exists a field
$F(t) \subseteq K_q \subseteq k((\Gamma ))$
such that if
$w = v_{\Gamma }|_{K_q}$
, then
$K_q w = k$
,
$wK_q = \Gamma $
,
$\mathbb {F}_p[z]$
is
$\mathcal {L}_{val}$
-definable in
$K_q$
where
$z \in k(\Gamma )$
is transcendental over
$\mathbb {F}_p$
, and if
$a \in k((\Gamma ))\setminus K_q$
is pliant over
$K_q$
, then
$q | [K_q(a) : K_q]$
.
-
If e > 0: “pliant” will refer to separably algebraic elements. By the construction of
$K_q$
as a union of separable extensions of
$F(t)$
,
$K_q/k(\Gamma )(t_1, \dots , t_{e-1}, t)$
is separably algebraic and has degree of imperfection e by [Reference Fried and Jarden16, Lemma 2.7.3]. -
If e = 0: “pliant” will refer to algebraic elements. As noted in Remark 4.2 ,
$K_q$
is perfect.
In either case,
$K_q$
is an equicharacteristic p nontrivially valued field of imperfection degree e, with residue field k and value group
$\Gamma $
. We will verify the henselianity axioms
$\varphi _1, \dots , \varphi _{q-1}$
are satisfied. Let
$l < q$
and fix
$a_0, \dots a_{l-2} \in \mathfrak {m}_{w}$
. Suppose
$X^l + X^{l-1} + a_{l-2}X^{l-2} + \dots + a_0 = 0$
has no solution in
$K_q$
—however there exists a solution
$\alpha \in K_q^h$
, and
$K_q^h \subseteq k((\Gamma ))$
by the universal property of henselisations [Reference Engler and Prestel13, Theorem 5.2.2]. Then
$K_q(\alpha )/K_q$
is a finite proper extension; moreover,
$\alpha $
is pliant over
$K_q$
as
$K_q(\alpha ) \subseteq K_q^h \subseteq K_q^s \subseteq \widetilde {K_q}$
. By Theorem 4.8
,
$q|[K_q(\alpha ) : K_q]$
; however
$q> l$
and
$[K_q(\alpha ) : K_q] \leq l$
; a contradiction.
Let Q be the set of primes
$q> p$
and
$\mathcal {U}$
a nonprincipal ultrafilter on Q. Let
$\mathbb {K} = \prod _{q \in Q} K_q / \mathcal {U}$
; by Łoś’ Theorem,
$\mathbb {K}$
is an equicharacteristic p henselian nontrivially valued field, of imperfection degree e, and residue field
$\mathcal {L}_r$
-elementarily equivalent to
$Kv$
and value group
$\mathcal {L}_{oag}$
-elementarily equivalent to
$vK$
. Furthermore,
$\mathbb {K}$
is separably defectless. Indeed, given
$M \in \mathbb {N}_{>0}$
, 
for all primes
$q> M^M$
by Lemma 5.7
. Hence, by Łoś’ Theorem, 
for all
$M \geq 1$
. By [Reference Delon10, Théorème 3.1],
$\mathbb {K} \equiv _{\mathcal {L}_{val}}\! K$
.
Let T be a finite subtheory of
${\mathtt{Th}}(K; \mathcal {L}_{val})$
. As
$\mathbb {K} \models T$
, for some
$q \in Q$
we have
$K_q \models T$
. By Theorem 4.8 and Corollary 1.8
,
${\mathtt{Th}}(K_q; \mathcal {L}_{val})$
is hereditarily undecidable; hence T is undecidable as required.
Finally, if
$\mathcal {O}_v \subseteq K$
is
$\mathcal {L}_r$
-definable by the formula
$\varpi (x, \overline {y})$
(where
$\overline {y} = y_1, \dots , y_n$
denote parameter variables), then
$\mathbb {K} \models \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
too. For any finite subtheory
$S \subseteq {\mathtt{Th}}(K; \mathcal {L}_r)$
, by Łoś’ Theorem there exists a prime l such that
$K_l \models S \land \exists y_1, \dots , y_n \forall x\, (x \in \mathcal {O} \leftrightarrow \varpi (x, \overline {y}))$
. By Theorem 4.8 and Corollary 1.8
,
${\mathtt{Th}}(K_l; \mathcal {L}_r)$
is hereditarily undecidable, making S undecidable as desired.
Corollary 5.9.
-
(1) If
$(K, v)$
is an NIP henselian nontrivially valued field,
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable. Furthermore if
$\mathcal {O}_v$
is
$\mathcal {L}_r$
-definable in K, then K is finitely undecidable as a field. -
(2) Every infinite dp-finite field is finitely undecidable.
-
(3) Assuming the NIP Fields Conjecture, every infinite NIP field is finitely undecidable.
Proof
-
(1) If
$(K, v)$
is equicharacteristic 0 or mixed characteristic, this is a result of Corollary 4.10/Theorem 5.3
. If
$(K, v)$
is positive equicharacteristic then by Anscombe–Jahnke it is separably defectless Kaplansky (Theorem 5.6
); hence its
$\mathcal {L}_{val}$
-theory is finitely undecidable by Theorem 5.8
. -
(2) By the work of JohnsonFootnote 8 [Reference Johnson27, Corollary 4.16], every infinite dp-finite field K is either algebraically closed, real closed, or admits a non-trivial definable henselian valuation. If K is algebraically or real closed, it is finitely undecidable by [Reference Ziegler49, Corollary, p. 270]. Otherwise K has an
$\mathcal {L}_r$
-definable valuation v. As K is dp-finite,
${\mathtt{Th}}(K; \mathcal {L}_r)$
is NIP (following from [Reference Simon45, Observation 4.13]), and hence
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is NIP as the valuation is
$\mathcal {L}_r$
-definable. Thus K is finitely undecidable, from (1). -
(3) Recall Theorem 3.11 , where assuming the NIP Fields Conjecture one can conclude every infinite NIP field K is either separably closed (hence finitely undecidable by [Reference Ziegler49, Corollary, p. 270]/Corollaries 3.7 and 3.8 ), real closed (hence finitely undecidable by [Reference Ziegler49, Corollary, p. 270]), or admits a nontrivial
$\emptyset $
-
$\mathcal {L}_r$
-definable henselian valuation. In this case, K is finitely undecidable by (1).
Example 5.10. We present some finitely undecidable fields, and some open questions, as a consequence of this work.
-
(1) Let
$(K, v)$
be any algebraic valued field extension of
$(\operatorname {\mathbb {Q}}_p, v_p)$
with non-divisible value group. By [Reference Koenigsmann32, Lemma 3.6], the valuation is
$\emptyset $
-
$\mathcal {L}_r$
-definable. By Theorem 5.3
, K is a finitely undecidable field. -
(2) It is unknown if
$\mathbb {F}_p((t))$
is finitely undecidable. (Equally one can consider the finite undecidability of
${\mathtt{Th}}(\mathbb {F}_p((t)); \mathcal {L}_{val})$
, as the valuation ring
$\mathbb {F}_p[[t]]$
is
$\emptyset $
-
$\mathcal {L}_r$
-definable in
$\mathbb {F}_p((t))$
by, e.g., [Reference Koenigsmann32, Lemma 3.6].) More generally if
$F\!/\mathbb {F}_p$
is any algebraic extension, the finite undecidability of
$F((t))$
—or of
${\mathtt{Th}}(F((t)); \mathcal {L}_{val})$
—is an open question.
Recall the notion of t-henselianity: a field is t-henselian if it can be equipped with a topology compatible with the field operations, behaving very much like the topology arising from a nontrivial valuation, satisfying a “topological” Hensel’s Lemma. This notion was introduced by Prestel and Ziegler [Reference Prestel and Ziegler40], and the topology shown to be
$\mathcal {L}_r$
-definable in nonseparably closed fields in [Reference Prestel38, p. 203]. Using saturation we may equally state (as Anscombe and Jahnke [Reference Anscombe and Jahnke1, p. 872] do) that a field is t-henselian if it is
$\mathcal {L}_r$
-elementarily equivalent to a field L which admits a nontrivial henselian valuation, i.e., has a subset
$\mathcal {O} \subseteq L$
that satisfies the definition of a nontrivial henselian valuation ring. (Cf. the discussion in [Reference Prestel and Ziegler40, Section 7] and [Reference Koenigsmann32, Section 3.4].) In some cases we can use t-henselianity—a purely field-theoretic,
$\mathcal {L}_r$
-elementary property—to conclude finite undecidability of a field.
-
(3) Let K be a characteristic 0 t-henselian field with nonuniversal Footnote 9 absolute Galois group. FromFootnote 10 [Reference Jahnke20, Theorem 3.2.3], K is either real closed, separably (= algebraically) closed, or henselian with respect to a nontrivial
$\emptyset $
-
$\mathcal {L}_r$
-definable valuation. Thus K is finitely undecidable, by [Reference Ziegler49, Corollary, p. 270] or Corollary 4.10
or Theorem 5.3
. -
(4) Let K be a positive characteristic NIP t-henselian field. If K is separably closed, it is finitely undecidable by Corollary 3.7/3.8 . Otherwise let L be a field with nontrivial henselian valuation v such that
$L \equiv K$
; note L is not separably closed and NIP as a field. By [Reference Jahnke and Koenigsmann21, Corollary 3.18], L admits a nontrivial
$\emptyset $
-
$\mathcal {L}_r$
-definable henselian valuation. Hence K is finitely undecidable, by Corollary 5.9(1).
Two concrete examples of fields from (3) and (4) are
$\operatorname {\mathbb {C}}((t))$
and
$\widetilde {\mathbb {F}_p}((\tfrac {1}{p^{\infty }}\!\operatorname {\mathbb {Z}}))$
, respectively.
-
(5) Boissonneau [Reference Boissonneau5] has recently extended the Anscombe–Jahnke results towards n-dependent valued fields. The class of n-dependent theories was introduced by Shelah in [Reference Shelah42, Section 5(H)] (see [Reference Chernikov, Palacin and Takeuchi9] for further discussion), and is a proper generalisation of NIP (which corresponds to 1-dependent). n-dependence in groups and fields has been studied extensively by Hempel and Chernikov–Hempel [Reference Chernikov and Hempel8, Reference Hempel19].
If
$(K, v)$
is a positive characteristic n-dependent nontrivially valued field, it is henselian (by [Reference Chernikov and Hempel8, Theorem 3.1]) and separably defectless Kaplansky (by [Reference Boissonneau5, Lemma 3.10]). Thus
${\mathtt{Th}}(K; \mathcal {L}_{val})$
is finitely undecidable, by Theorem 5.8
. Furthermore, by [Reference Hempel19, Proposition 8.4], K is either separably closed (hence finitely undecidable, by Corollary 3.7/3.8
) or admits an
$\emptyset $
-
$\mathcal {L}_r$
-definable nontrivial henselian valuation (separably defectless Kaplansky, by [Reference Boissonneau5, Lemma 3.10]). We conclude from Theorem 5.8
if K is a positive characteristic n-dependent t-henselian field, it is finitely undecidable.
One may ask: is every nontrivially henselian valued field, which is finitely undecidable as an
$\mathcal {L}_{val}$
-structure, finitely undecidable as a field? This cannot be concluded easily from Corollary 4.10/Theorem 5.3/Theorem 5.8
, as there exist henselian valued fields which do not admit any nontrivial
$\mathcal {L}_r$
-definable henselian valuation, such as the Jahnke–Koenigsmann example [Reference Jahnke and Koenigsmann22, Example 6.2]. Anscombe and Jahnke discuss “henselianity in the language of rings” further in [Reference Anscombe and Jahnke1].
Acknowledgements
The author extends his thanks to Professor Ehud Hrushovski, Professor Jochen Koenigsmann, Professor Arno Fehm, Dr. Sylvy Anscombe, and Dr. Konstantinos Kartas for many helpful conversations. Further thanks is due to S. Anscombe for her excellent recommendations on presentation, organisation, and abstraction.
is a first-order 
Open access
