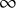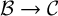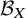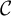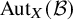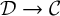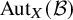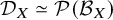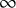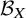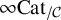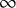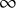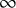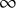1 Introduction
By Hasse’s famous local-global principle the natural commutative square

relating the integers, rationals, and p-adic numbers, is a cartesian square, known as the arithmetic fracture square. Hasse’s principle serves as a guiding principle in arithmetic and arithmetic geometry and was extended to a fundamental principle in unstable and stable homotopy theory fracturing an appropriate finite (stable) homotopy type into its rationalization and p-completion.
It is goal of this article to prove a local-global principle for parametrized
![]() $\infty $
-categories. It is a fundamental insight of [Reference Barwick, Dotto, Glasman, Nardin and Shah5], [Reference Barwick, Dotto, Glasman, Nardin and Shah6], [Reference Nardin and Shah30], [Reference Shah34], [Reference Shah33] that parametrized
$\infty $
-categories. It is a fundamental insight of [Reference Barwick, Dotto, Glasman, Nardin and Shah5], [Reference Barwick, Dotto, Glasman, Nardin and Shah6], [Reference Nardin and Shah30], [Reference Shah34], [Reference Shah33] that parametrized
![]() $\infty $
-category theory, that is, the systematic study of
$\infty $
-category theory, that is, the systematic study of
![]() $\infty $
-categories over a fixed base
$\infty $
-categories over a fixed base
![]() $\infty $
-category, is a powerful tool to perform constructions in equivariant and motivic homotopy theory [Reference Barwick and Glasman7], [Reference Quigley and Shah32], [Reference Cnossen, Haugseng, Lenz and Linskens10], [Reference Bachmann and Hoyois4]. Parametrized
$\infty $
-category, is a powerful tool to perform constructions in equivariant and motivic homotopy theory [Reference Barwick and Glasman7], [Reference Quigley and Shah32], [Reference Cnossen, Haugseng, Lenz and Linskens10], [Reference Bachmann and Hoyois4]. Parametrized
![]() $\infty $
-category theory relies on a deep understanding and efficient control of fibrations of
$\infty $
-category theory relies on a deep understanding and efficient control of fibrations of
![]() $\infty $
-categories. The latter play the role in higher category theory that Kan-fibrations play in homotopy theory but the complexity is drastically higher [Reference Ayala and Francis2]. The next diagram gives an impression of the plethora of fibrations of
$\infty $
-categories. The latter play the role in higher category theory that Kan-fibrations play in homotopy theory but the complexity is drastically higher [Reference Ayala and Francis2]. The next diagram gives an impression of the plethora of fibrations of
![]() $\infty $
-categories, where all sub-squares are cartesian:
$\infty $
-categories, where all sub-squares are cartesian:

All fibrations in the latter diagram have a common base
![]() $\infty $
-category. Choosing the base to be a space the latter diagram degenerates and only two types of fibrations remain: Kan-fibrations and bicartesian fibrations. Since any space splits as the disjoint union of path components, the first type of fibration classifies a family of spaces, the family of fibers over the path components, equipped with the action of the loop space. Similarly, the second type of fibration classifies a family of
$\infty $
-category. Choosing the base to be a space the latter diagram degenerates and only two types of fibrations remain: Kan-fibrations and bicartesian fibrations. Since any space splits as the disjoint union of path components, the first type of fibration classifies a family of spaces, the family of fibers over the path components, equipped with the action of the loop space. Similarly, the second type of fibration classifies a family of
![]() $\infty $
-categories equipped with the action of the loop space.
$\infty $
-categories equipped with the action of the loop space.
We prove a local-global principle for parametrized
![]() $\infty $
-categories following the next table of analogies:
$\infty $
-categories following the next table of analogies:
 $$ \begin{align*}\begin{array}{ l | c} \hline {\mathbb{Z}} & \{\infty\text{-categories over the base}\} \\ \hline {\mathbb Q} & \{\text{Locally cartesian fibrations whose fibers are presentable} \\ & \text{and whose fiber transports admit a right adjoint}\} \\ \hline \text{primes } p & \text{equivalence classes } p \text{ of objects of the base} \\ \hline {\mathbb{Z}}_p & \infty\mathrm{Cat}[\Omega_p], \text{ the } \infty\text{-category of small } \infty\text{-categories} \\ & \text{equipped with an action of the loop space at } p. \\ \hline {\mathbb Q}_p = {\mathbb Q} \otimes_{\mathbb{Z}} {\mathbb{Z}}_p & \mathrm{Pr}^L[\Omega_p], \text{ the } \infty\text{-category of presentable } \infty\text{-categories} \\ & \text{equipped with an action of the loop space at } p. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ l | c} \hline {\mathbb{Z}} & \{\infty\text{-categories over the base}\} \\ \hline {\mathbb Q} & \{\text{Locally cartesian fibrations whose fibers are presentable} \\ & \text{and whose fiber transports admit a right adjoint}\} \\ \hline \text{primes } p & \text{equivalence classes } p \text{ of objects of the base} \\ \hline {\mathbb{Z}}_p & \infty\mathrm{Cat}[\Omega_p], \text{ the } \infty\text{-category of small } \infty\text{-categories} \\ & \text{equipped with an action of the loop space at } p. \\ \hline {\mathbb Q}_p = {\mathbb Q} \otimes_{\mathbb{Z}} {\mathbb{Z}}_p & \mathrm{Pr}^L[\Omega_p], \text{ the } \infty\text{-category of presentable } \infty\text{-categories} \\ & \text{equipped with an action of the loop space at } p. \end{array}\end{align*} $$
We prove the following theorem, where for any small
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
we write
${\mathcal C}$
we write
![]() $\pi _0({\mathcal C})$
for the set of equivalence classes in
$\pi _0({\mathcal C})$
for the set of equivalence classes in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() $ \mathrm {LoCART}^L_{\mathcal C} $
for the
$ \mathrm {LoCART}^L_{\mathcal C} $
for the
![]() $\infty $
-category of locally cartesian fibrations whose fibers are presentable and whose fiber transports admit a right adjoint and arbitrary functors over
$\infty $
-category of locally cartesian fibrations whose fibers are presentable and whose fiber transports admit a right adjoint and arbitrary functors over
![]() ${\mathcal C}$
inducing left adjoints on every fiber:
${\mathcal C}$
inducing left adjoints on every fiber:
Theorem 1.1 (Theorem 4.1)
For every small
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
there is a pullback square of
${\mathcal C}$
there is a pullback square of
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories

Theorem 1.1 is useful since it reduces the theory of parametrized
![]() $\infty $
-categories to the theory of locally cartesian fibrations whose fibers are presentable and fiber transports admit a right adjoint. This correspondence restricts to several classes of fibrations of interest: Theorem 1.1 reduces the theory of exponentiable fibrations to the theory of cartesian fibrations whose fibers are presentable and fiber transports admit a right adjoint (Proposition 3.22). It reduces the theory of cocartesian fibrations to the theory of bicartesian fibrations whose fibers are presentable and fiber transports admit a right adjoint (Lemma 3.11). In particular, Theorem 1.1 relates several classes of relevant fibrations of
$\infty $
-categories to the theory of locally cartesian fibrations whose fibers are presentable and fiber transports admit a right adjoint. This correspondence restricts to several classes of fibrations of interest: Theorem 1.1 reduces the theory of exponentiable fibrations to the theory of cartesian fibrations whose fibers are presentable and fiber transports admit a right adjoint (Proposition 3.22). It reduces the theory of cocartesian fibrations to the theory of bicartesian fibrations whose fibers are presentable and fiber transports admit a right adjoint (Lemma 3.11). In particular, Theorem 1.1 relates several classes of relevant fibrations of
![]() $\infty $
-categories to each other and therefore helps to understand their relationships.
$\infty $
-categories to each other and therefore helps to understand their relationships.
Parametrized
![]() $\infty $
-category theory might be thought of as a generalization of
$\infty $
-category theory might be thought of as a generalization of
![]() $\infty $
-category theory and parametrized homotopy theory that studies
$\infty $
-category theory and parametrized homotopy theory that studies
![]() $\infty $
-categories over a fixed
$\infty $
-categories over a fixed
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}.$
For
${\mathcal C}.$
For
![]() ${\mathcal C}=[1]$
the walking arrow parametrized
${\mathcal C}=[1]$
the walking arrow parametrized
![]() $\infty $
-category theory specializes to the theory of correspondences of
$\infty $
-category theory specializes to the theory of correspondences of
![]() $\infty $
-categories, which are a crucial concept in the theory of dualities of
$\infty $
-categories, which are a crucial concept in the theory of dualities of
![]() $\infty $
-categories [Reference Heine, Lopez-Avila and Spitzweck21]. We apply Theorem 1.1 for
$\infty $
-categories [Reference Heine, Lopez-Avila and Spitzweck21]. We apply Theorem 1.1 for
![]() ${\mathcal C} =[1]$
to in [Reference Heine, Lopez-Avila and Spitzweck21, Theorem 5.21.] and [Reference Heine, Spitzweck and Verdugo22, Theorem 6.27.] to prove an equivalence between symmetric bilinear functors and dualities.
${\mathcal C} =[1]$
to in [Reference Heine, Lopez-Avila and Spitzweck21, Theorem 5.21.] and [Reference Heine, Spitzweck and Verdugo22, Theorem 6.27.] to prove an equivalence between symmetric bilinear functors and dualities.
We use Theorem 1.1 to construct a Grothendieck construction for parametrized
![]() $\infty $
-categories. The Grothendieck construction for cocartesian and cartesian fibrations of
$\infty $
-categories. The Grothendieck construction for cocartesian and cartesian fibrations of
![]() $\infty $
-categories [Reference Lurie27, Theorem 3.2.0.1.], [Reference Nuiten31], [Reference Moser, Rasekh and Rovelli29], [Reference Abellán, Gagna and Haugseng1] is a cornerstone in higher category theory and an essential and crucial tool to construct functors to the
$\infty $
-categories [Reference Lurie27, Theorem 3.2.0.1.], [Reference Nuiten31], [Reference Moser, Rasekh and Rovelli29], [Reference Abellán, Gagna and Haugseng1] is a cornerstone in higher category theory and an essential and crucial tool to construct functors to the
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \mathrm {Cat}$
of small
$\infty \mathrm {Cat}$
of small
![]() $\infty $
-categories that has ubiquitious applications. Due to its importance and relevance several extensions of the Grothendieck-construction have been studied: [Reference Lurie28, §3], [Reference Ayala, Mazel-Gee and Rozenblyum3, Theorem B.4.3.] offer a Grothendieck construction for locally cartesian fibrations. [Reference Ayala and Francis2, Theorem 0.8], [Reference Barwick and Shah8, 4.8. Proposition] construct a Grothendieck-construction for exponentiable fibrations.
$\infty $
-categories that has ubiquitious applications. Due to its importance and relevance several extensions of the Grothendieck-construction have been studied: [Reference Lurie28, §3], [Reference Ayala, Mazel-Gee and Rozenblyum3, Theorem B.4.3.] offer a Grothendieck construction for locally cartesian fibrations. [Reference Ayala and Francis2, Theorem 0.8], [Reference Barwick and Shah8, 4.8. Proposition] construct a Grothendieck-construction for exponentiable fibrations.
Since Theorem 1.1 reduces the theory of parametrized
![]() $\infty $
-categories to the theory of locally cartesian fibrations, we can apply Theorem 1.1 to extend the Grothendieck construction for locally cartesian fibrations to a Grothendieck construction for parametrized
$\infty $
-categories to the theory of locally cartesian fibrations, we can apply Theorem 1.1 to extend the Grothendieck construction for locally cartesian fibrations to a Grothendieck construction for parametrized
![]() $\infty $
-categories, which extends all Grothendieck constructions. While the Grothendieck-construction for cartesian fibrations classifies functors to the
$\infty $
-categories, which extends all Grothendieck constructions. While the Grothendieck-construction for cartesian fibrations classifies functors to the
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \mathrm {Cat}$
of small
$\infty \mathrm {Cat}$
of small
![]() $\infty $
-categories and functors, the Grothendieck-construction for exponentiable fibrations classifies functors to the
$\infty $
-categories and functors, the Grothendieck-construction for exponentiable fibrations classifies functors to the
![]() $\infty $
-precategory
$\infty $
-precategory
![]() ${\mathrm {Corr}}$
of small
${\mathrm {Corr}}$
of small
![]() $\infty $
-categories and correspondences. We extend all Grothendieck constructions via the concept of double
$\infty $
-categories and correspondences. We extend all Grothendieck constructions via the concept of double
![]() $\infty $
-category [Reference Gepner and Haugseng11, Definition 2.4.3.], which is a category object in
$\infty $
-category [Reference Gepner and Haugseng11, Definition 2.4.3.], which is a category object in
![]() $\infty \mathrm {Cat}$
, and a 2-categorical refinement of an
$\infty \mathrm {Cat}$
, and a 2-categorical refinement of an
![]() $\infty $
-precategory. We use Theorem 1.1 to construct a double
$\infty $
-precategory. We use Theorem 1.1 to construct a double
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {CORR}}$
(Theorem 7.6) that refines the
${\mathrm {CORR}}$
(Theorem 7.6) that refines the
![]() $\infty $
-precategory
$\infty $
-precategory
![]() ${\mathrm {Corr}}$
of correspondences, thereby answering a question of [Reference Ayala and Francis2, Question 0.14]. We apply Theorem 1.1 to prove the following Grothendieck-construction for parametrized
${\mathrm {Corr}}$
of correspondences, thereby answering a question of [Reference Ayala and Francis2, Question 0.14]. We apply Theorem 1.1 to prove the following Grothendieck-construction for parametrized
![]() $\infty $
-categories that classifies lax normal functors to the double
$\infty $
-categories that classifies lax normal functors to the double
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {CORR}},$
where
${\mathrm {CORR}},$
where
![]() ${\mathrm N}$
is the (derived version of the) nerve of an
${\mathrm N}$
is the (derived version of the) nerve of an
![]() $\infty $
-category:
$\infty $
-category:
Theorem 1.2 (Corollary 7.31)
Let
![]() ${\mathcal C}$
be a small
${\mathcal C}$
be a small
![]() $\infty $
-category. There is a canonical equivalence of
$\infty $
-category. There is a canonical equivalence of
![]() $\infty $
-categories
$\infty $
-categories
where the left hand side is the
![]() $\infty $
-category of lax normal functors.
$\infty $
-category of lax normal functors.
Blom [Reference Blom9] recently gave an alternative and very different proof of Theorem 1.2, which heavily relies on a universal property of the double
![]() $\infty $
-category of spans [Reference Haugseng13, Corollary 3.11.].
$\infty $
-category of spans [Reference Haugseng13, Corollary 3.11.].
Although Theorem 1.2 is interesting from a theoretical point of view, one might wonder why a Grothendieck construction for parametrized
![]() $\infty $
-categories is useful, and what kind of lax normal functors to
$\infty $
-categories is useful, and what kind of lax normal functors to
![]() ${\mathrm {CORR}}$
one might like to classify. We offer an instructive example (Example 7.19). Parametrized
${\mathrm {CORR}}$
one might like to classify. We offer an instructive example (Example 7.19). Parametrized
![]() $\infty $
-category theory studies for every small
$\infty $
-category theory studies for every small
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
the
${\mathcal C}$
the
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \mathrm {Cat}_{/{\mathcal C}}$
of small
$\infty \mathrm {Cat}_{/{\mathcal C}}$
of small
![]() $\infty $
-categories over
$\infty $
-categories over
![]() ${\mathcal C}.$
The
${\mathcal C}.$
The
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \mathrm {Cat}_{/{\mathcal C}}$
is not cartesian closed. However by the defining property of exponentiability for every exponentiable fibration
$\infty \mathrm {Cat}_{/{\mathcal C}}$
is not cartesian closed. However by the defining property of exponentiability for every exponentiable fibration
![]() ${\mathcal A} \to {\mathcal C}$
the functor
${\mathcal A} \to {\mathcal C}$
the functor
![]() ${\mathcal A} \times _{\mathcal C} (-) : \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
admits a right adjoint
${\mathcal A} \times _{\mathcal C} (-) : \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
admits a right adjoint
![]() $\mathrm {Fun}^{\mathcal C}({\mathcal A},-).$
For every functor
$\mathrm {Fun}^{\mathcal C}({\mathcal A},-).$
For every functor
![]() ${\mathcal B} \to {\mathcal C}$
the internal hom
${\mathcal B} \to {\mathcal C}$
the internal hom
![]() $\mathrm {Fun}^{{\mathcal C}}({\mathcal A},{\mathcal B}) \to {\mathcal C} $
is a parametrized
$\mathrm {Fun}^{{\mathcal C}}({\mathcal A},{\mathcal B}) \to {\mathcal C} $
is a parametrized
![]() $\infty $
-category that plays the role of the
$\infty $
-category that plays the role of the
![]() $\infty $
-category of functors in higher category theory, and therefore is a crucial and ubiquitious construction in parametrized
$\infty $
-category of functors in higher category theory, and therefore is a crucial and ubiquitious construction in parametrized
![]() $\infty $
-category theory, which is unfortunately generally hard to understand. The internal hom is generally not a cocartesian, cartesian, or even exponentiable fibration and therefore cannot be analyzed by means of the usual Grothendieck-construction. However, we can apply Theorem 1.2 to classify the internal hom
$\infty $
-category theory, which is unfortunately generally hard to understand. The internal hom is generally not a cocartesian, cartesian, or even exponentiable fibration and therefore cannot be analyzed by means of the usual Grothendieck-construction. However, we can apply Theorem 1.2 to classify the internal hom
![]() $\mathrm {Fun}^{{\mathcal C}}({\mathcal A},{\mathcal B})\to {\mathcal C} $
by a lax normal functor
$\mathrm {Fun}^{{\mathcal C}}({\mathcal A},{\mathcal B})\to {\mathcal C} $
by a lax normal functor
![]() ${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
, which can be used to analyze the internal hom. The classified lax normal functor
${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
, which can be used to analyze the internal hom. The classified lax normal functor
![]() ${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
sends any morphism
${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
sends any morphism
![]() $\theta : X \to Y$
in
$\theta : X \to Y$
in
![]() ${\mathcal C}$
to a pro-functor
${\mathcal C}$
to a pro-functor
corresponding to a functor
![]() $\gamma : \mathrm {Fun}({\mathcal A}_X,{\mathcal B}_X)^{\mathrm {op}} \times \mathrm {Fun}({\mathcal A}_Y,{\mathcal B}_Y) \to {\mathcal S}$
. The functors
$\gamma : \mathrm {Fun}({\mathcal A}_X,{\mathcal B}_X)^{\mathrm {op}} \times \mathrm {Fun}({\mathcal A}_Y,{\mathcal B}_Y) \to {\mathcal S}$
. The functors
![]() ${\mathcal A} \to {\mathcal C}, {\mathcal B} \to {\mathcal C}$
classify lax normal functors
${\mathcal A} \to {\mathcal C}, {\mathcal B} \to {\mathcal C}$
classify lax normal functors
![]() ${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
that send the morphism
${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
that send the morphism
![]() $\theta : X \to Y$
to pro-functors
$\theta : X \to Y$
to pro-functors
![]() $ {\mathrm A}_Y \to {\mathcal A}_X, {\mathcal B}_Y \to {\mathcal B}_X$
corresponding to functors
$ {\mathrm A}_Y \to {\mathcal A}_X, {\mathcal B}_Y \to {\mathcal B}_X$
corresponding to functors
![]() $\alpha : {\mathcal A}_X^{\mathrm {op}} \times {\mathcal A}_Y \to {\mathcal S}, \beta : {\mathcal B}_X^{\mathrm {op}} \times {\mathcal B}_Y \to {\mathcal S}.$
The functor
$\alpha : {\mathcal A}_X^{\mathrm {op}} \times {\mathcal A}_Y \to {\mathcal S}, \beta : {\mathcal B}_X^{\mathrm {op}} \times {\mathcal B}_Y \to {\mathcal S}.$
The functor
![]() $\gamma $
sends any pair
$\gamma $
sends any pair
![]() $(F,G) \in \mathrm {Fun}({\mathcal A}_X,{\mathcal B}_X)^{\mathrm {op}} \times \mathrm {Fun}({\mathcal A}_Y,{\mathcal B}_Y)$
to the limit of the functor
$(F,G) \in \mathrm {Fun}({\mathcal A}_X,{\mathcal B}_X)^{\mathrm {op}} \times \mathrm {Fun}({\mathcal A}_Y,{\mathcal B}_Y)$
to the limit of the functor
where
![]() $\rho : {\mathcal W} \to {\mathcal A}_X^{\mathrm {op}} \times {\mathcal A}_Y$
is the left fibration classified by
$\rho : {\mathcal W} \to {\mathcal A}_X^{\mathrm {op}} \times {\mathcal A}_Y$
is the left fibration classified by
![]() $\alpha $
. We use the latter description of the internal hom in
$\alpha $
. We use the latter description of the internal hom in
![]() $\infty \mathrm {Cat}_{/[1]}$
in [Reference Heine, Spitzweck and Verdugo23, Proposition 3.22.] to prove an equivalence between a real S-construction and hermitian
$\infty \mathrm {Cat}_{/[1]}$
in [Reference Heine, Spitzweck and Verdugo23, Proposition 3.22.] to prove an equivalence between a real S-construction and hermitian
![]() ${\mathcal Q}$
-construction.
${\mathcal Q}$
-construction.
2 Notation and terminology
We fix a hierarchy of Grothendieck universes whose objects we call small, large, very large, etc. We call a space small, large, etc. if its set of path components and its homotopy groups are small, large, etc. for any choice of base point. We call an
![]() $\infty$
-category small, large, etc if its maximal subspace and all its mapping spaces are small, large, etc.
$\infty$
-category small, large, etc if its maximal subspace and all its mapping spaces are small, large, etc.
We write
-
○
 $\mathrm {Set}$
for the category of small sets.
$\mathrm {Set}$
for the category of small sets. -
○
 $\Delta $
for (a skeleton of) the category of finite, nonempty, partially ordered sets and order preserving maps, whose objects we denote by
$\Delta $
for (a skeleton of) the category of finite, nonempty, partially ordered sets and order preserving maps, whose objects we denote by
 $[{n}] = \{0 < \cdots < {n}\}$
for
$[{n}] = \{0 < \cdots < {n}\}$
for
 ${n} \geq 0$
.
${n} \geq 0$
. -
○
 ${\mathcal S}$
for the
${\mathcal S}$
for the
 $\infty $
-category of small spaces.
$\infty $
-category of small spaces. -
○
 $ \infty \mathrm {Cat}$
for the
$ \infty \mathrm {Cat}$
for the
 $\infty $
-category of small
$\infty $
-category of small
 $\infty $
-categories.
$\infty $
-categories. -
○
 $\infty \mathrm {Cat}^{{c} {c}} $
for the
$\infty \mathrm {Cat}^{{c} {c}} $
for the
 $\infty $
-category of large
$\infty $
-category of large
 $\infty $
-categories with small colimits and small-colimits-preserving functors.
$\infty $
-categories with small colimits and small-colimits-preserving functors.
We often indicate
![]() $\infty $
-categories of large objects by
$\infty $
-categories of large objects by
![]() $\widehat {(-)}$
, for example, we write
$\widehat {(-)}$
, for example, we write
![]() $\widehat {{\mathcal S}}, \infty \widehat {\mathrm {Cat}}$
for the
$\widehat {{\mathcal S}}, \infty \widehat {\mathrm {Cat}}$
for the
![]() $\infty $
-categories of large spaces,
$\infty $
-categories of large spaces,
![]() $\infty $
-categories.
$\infty $
-categories.
For any
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
containing objects
${\mathcal C}$
containing objects
![]() ${\mathrm A}, {\mathrm B}$
we write
${\mathrm A}, {\mathrm B}$
we write
-
○
 ${\mathcal C}({\mathrm A},{\mathrm B})$
for the space of maps
${\mathcal C}({\mathrm A},{\mathrm B})$
for the space of maps
 ${\mathrm A} \to {\mathrm B}$
in
${\mathrm A} \to {\mathrm B}$
in
 ${\mathcal C}$
,
${\mathcal C}$
, -
○
 ${\mathcal C}_{/{\mathrm A}}$
for the
${\mathcal C}_{/{\mathrm A}}$
for the
 $\infty $
-category of objects over
$\infty $
-category of objects over
 ${\mathrm A}$
,
${\mathrm A}$
, -
○
 ${\mathrm {Ho}}({\mathcal C})$
for its homotopy category,
${\mathrm {Ho}}({\mathcal C})$
for its homotopy category, -
○
 ${\mathcal C}^{\mathrm {op}}$
for the opposite
${\mathcal C}^{\mathrm {op}}$
for the opposite
 $\infty $
-category,
$\infty $
-category, -
○
 ${\mathcal C}^{\triangleleft }, {\mathcal C}^{\triangleright }$
for the
${\mathcal C}^{\triangleleft }, {\mathcal C}^{\triangleright }$
for the
 $\infty $
-category arising from
$\infty $
-category arising from
 ${\mathcal C}$
by adding an initial, final object, respectively,
${\mathcal C}$
by adding an initial, final object, respectively, -
○
 $\iota ({\mathcal C}) $
for the maximal subspace in
$\iota ({\mathcal C}) $
for the maximal subspace in
 ${\mathcal C}$
,
${\mathcal C}$
, -
○
 $\infty \mathrm {Cat}^{\mathrm {cocart}}_{/{\mathcal C}} \subset \infty \mathrm {Cat}_{/{\mathcal C}}$
the subcategory of cocartesian fibrations over
$\infty \mathrm {Cat}^{\mathrm {cocart}}_{/{\mathcal C}} \subset \infty \mathrm {Cat}_{/{\mathcal C}}$
the subcategory of cocartesian fibrations over
 ${\mathcal C}$
and functors over
${\mathcal C}$
and functors over
 ${\mathcal C}$
preserving cocartesian morphisms,
${\mathcal C}$
preserving cocartesian morphisms, -
○
 $\infty \mathrm {Cat}^{\mathrm {cart}}_{/{\mathcal C}} \subset \infty \mathrm {Cat}_{/{\mathcal C}}$
the subcategory of cartesian fibrations over
$\infty \mathrm {Cat}^{\mathrm {cart}}_{/{\mathcal C}} \subset \infty \mathrm {Cat}_{/{\mathcal C}}$
the subcategory of cartesian fibrations over
 ${\mathcal C}$
and functors over
${\mathcal C}$
and functors over
 ${\mathcal C}$
preserving cartesian morphisms.
${\mathcal C}$
preserving cartesian morphisms.
Note that
![]() ${\mathrm {Ho}}(\infty \mathrm {Cat})$
is cartesian closed and for small
${\mathrm {Ho}}(\infty \mathrm {Cat})$
is cartesian closed and for small
![]() $\infty $
-categories
$\infty $
-categories
![]() ${\mathcal C},{\mathcal D}$
we write
${\mathcal C},{\mathcal D}$
we write
![]() $\mathrm {Fun}({\mathcal C},{\mathcal D})$
for the internal hom, the
$\mathrm {Fun}({\mathcal C},{\mathcal D})$
for the internal hom, the
![]() $\infty $
-category of functors
$\infty $
-category of functors
![]() ${\mathcal C} \to {\mathcal D}.$
${\mathcal C} \to {\mathcal D}.$
We often call a fully faithful functor an embedding. We call a functor an inclusion if if it induces an embedding on maximal subspaces and on all mapping spaces.
3 Parametrized
 $\infty $
-categories of presheaves
$\infty $
-categories of presheaves
Our key tool to prove a local global principle for parametrized
![]() $\infty $
-categories, that is,
$\infty $
-categories, that is,
![]() $\infty $
-categories over a given base
$\infty $
-categories over a given base
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C},$
is a parametrized version of presheaf
${\mathcal C},$
is a parametrized version of presheaf
![]() $\infty $
-category. In this section we define this parametrized version of presheaf
$\infty $
-category. In this section we define this parametrized version of presheaf
![]() $\infty $
-category (Definition 3.5, Corollary 3.37) and establish a universal property (Proposition 3.16). Moreover we use this parametrized version of presheaf
$\infty $
-category (Definition 3.5, Corollary 3.37) and establish a universal property (Proposition 3.16). Moreover we use this parametrized version of presheaf
![]() $\infty $
-category to relate several types of fibrations of
$\infty $
-category to relate several types of fibrations of
![]() $\infty $
-categories to each other (Proposition 3.22, Corollary 3.27).
$\infty $
-categories to each other (Proposition 3.22, Corollary 3.27).
We first recall the Grothendieck construction [Reference Lurie27, Theorem 3.2.0.1.].
For every
![]() ${\mathcal C} \in \infty \mathrm {Cat}$
the Grothendieck construction is an equivalence
${\mathcal C} \in \infty \mathrm {Cat}$
the Grothendieck construction is an equivalence
that sends a functor
![]() ${\mathcal C} \to \infty \mathrm {Cat}$
to a cocartesian fibration over
${\mathcal C} \to \infty \mathrm {Cat}$
to a cocartesian fibration over
![]() ${\mathcal C},$
which we call the classifying cocartesian fibration. There is also a Grothendieck construction for cartesian fibrations
${\mathcal C},$
which we call the classifying cocartesian fibration. There is also a Grothendieck construction for cartesian fibrations
sending a functor
![]() ${\mathcal C}^{\mathrm {op}} \to \infty \mathrm {Cat}$
to a cartesian fibration over
${\mathcal C}^{\mathrm {op}} \to \infty \mathrm {Cat}$
to a cartesian fibration over
![]() ${\mathcal C},$
which we call the classifying cartesian fibration.
${\mathcal C},$
which we call the classifying cartesian fibration.
Remark 3.1. The Grothendieck construction for cartesian fibrations 3.2 is by definition the composite
where the middle functor is the Grothendieck construction 3.1 for
![]() ${\mathcal C}^{\mathrm {op}}$
, and the first and last functors are induced by the opposite
${\mathcal C}^{\mathrm {op}}$
, and the first and last functors are induced by the opposite
![]() $\infty $
-category involution
$\infty $
-category involution
![]() $(-)^{\mathrm {op}}: \infty \mathrm {Cat} \to \infty \mathrm {Cat}$
.
$(-)^{\mathrm {op}}: \infty \mathrm {Cat} \to \infty \mathrm {Cat}$
.
Remark 3.2. For every functor
![]() $\psi : {\mathcal C} \to {\mathcal D}$
there is a commutative square
$\psi : {\mathcal C} \to {\mathcal D}$
there is a commutative square

where the horizontal functors form the Grothendieck construction and the left vertical functor is precomposition along
![]() $\psi $
and the right vertical functor forms the base change along
$\psi $
and the right vertical functor forms the base change along
![]() $\psi .$
$\psi .$
For
![]() ${\mathcal C}$
the final
${\mathcal C}$
the final
![]() $\infty $
-category the equivalence (3.1) identifies with the identity. Hence for every object
$\infty $
-category the equivalence (3.1) identifies with the identity. Hence for every object
![]() ${\mathrm X} \in {\mathcal D}$
the commutative square (3.3) identifies with the commutative triangle
${\mathrm X} \in {\mathcal D}$
the commutative square (3.3) identifies with the commutative triangle

where the left vertical functor evaluates at
![]() ${\mathrm X}$
and the right vertical functor takes the fiber over
${\mathrm X}$
and the right vertical functor takes the fiber over
![]() ${\mathrm X}.$
${\mathrm X}.$
Definition 3.1. A functor
![]() ${\mathcal A} \to {\mathcal B}$
is a right fibration if the induced commutative square
${\mathcal A} \to {\mathcal B}$
is a right fibration if the induced commutative square

is a pullback square, where the vertical functors evaluate at the target.
Remark 3.3. A functor
![]() ${\mathcal C}^{\mathrm {op}} \to \infty \mathrm {Cat}$
lands in the full subcategory of
${\mathcal C}^{\mathrm {op}} \to \infty \mathrm {Cat}$
lands in the full subcategory of
![]() $\infty $
-groupoids if and only if the classifying cartesian fibration over
$\infty $
-groupoids if and only if the classifying cartesian fibration over
![]() ${\mathcal C}$
is a right fibration [Reference Lurie27, Proposition 2.4.2.4.].
${\mathcal C}$
is a right fibration [Reference Lurie27, Proposition 2.4.2.4.].
Definition 3.2. A right fibration
![]() ${\mathcal A} \to {\mathcal B}$
is representable if
${\mathcal A} \to {\mathcal B}$
is representable if
![]() ${\mathcal A}$
has a final object.
${\mathcal A}$
has a final object.
Remark 3.4. A right fibration
![]() ${\mathcal A} \to {\mathcal B}$
is representable if and only if
${\mathcal A} \to {\mathcal B}$
is representable if and only if
![]() ${\mathcal A} \to {\mathcal B}$
classifies a representable presheaf.
${\mathcal A} \to {\mathcal B}$
classifies a representable presheaf.
Notation 3.3. Let
be the full subcategory of right fibrations and
the full subcategory of representable right fibrations.
Lemma 3.4. Evaluation at the target
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
is a cocartesian and cartesian fibration that restricts to a cocartesian fibration
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
is a cocartesian and cartesian fibration that restricts to a cocartesian fibration
![]() $\kappa : {\mathcal U} \to \infty \mathrm {Cat}$
with the same cocartesian morphisms.
$\kappa : {\mathcal U} \to \infty \mathrm {Cat}$
with the same cocartesian morphisms.
Proof. The functor
![]() $\gamma : \mathrm {Fun}([1],\infty \mathrm {Cat}) \to \infty \mathrm {Cat}$
evaluating at the target is a cartesian fibration because
$\gamma : \mathrm {Fun}([1],\infty \mathrm {Cat}) \to \infty \mathrm {Cat}$
evaluating at the target is a cartesian fibration because
![]() $\infty \mathrm {Cat}$
admits pullbacks. Since right fibrations are stable under pullback,
$\infty \mathrm {Cat}$
admits pullbacks. Since right fibrations are stable under pullback,
![]() $\gamma $
restricts to a cartesian fibration
$\gamma $
restricts to a cartesian fibration
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
with the same cartesian morphisms. For any functor
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
with the same cartesian morphisms. For any functor
![]() $\psi : {\mathcal C} \to {\mathcal D}$
the fiber transport
$\psi : {\mathcal C} \to {\mathcal D}$
the fiber transport
![]() ${\mathcal R}_{\mathcal D} \to {\mathcal R}_{\mathcal C}$
of
${\mathcal R}_{\mathcal D} \to {\mathcal R}_{\mathcal C}$
of
![]() ${\mathcal R} \to \infty \mathrm {Cat}$
admits a left adjoint
${\mathcal R} \to \infty \mathrm {Cat}$
admits a left adjoint
![]() $\psi _!$
that takes the left Kan extension along the functor
$\psi _!$
that takes the left Kan extension along the functor
![]() ${\mathcal C}^{\mathrm {op}} \to {\mathcal D}^{\mathrm {op}}.$
This guarantees that the cartesian fibration
${\mathcal C}^{\mathrm {op}} \to {\mathcal D}^{\mathrm {op}}.$
This guarantees that the cartesian fibration
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
is also a cocartesian fibration. Since
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
is also a cocartesian fibration. Since
![]() $\psi _!$
preserves representables, the cocartesian fibration
$\psi _!$
preserves representables, the cocartesian fibration
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
restricts to a cocartesian fibration
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
restricts to a cocartesian fibration
![]() $\kappa : {\mathcal U} \to \infty \mathrm {Cat}$
with the same cocartesian morphisms.
$\kappa : {\mathcal U} \to \infty \mathrm {Cat}$
with the same cocartesian morphisms.
Definition 3.5. For every cocartesian fibration
![]() ${\mathcal D} \to {\mathcal C}$
classifying a functor
${\mathcal D} \to {\mathcal C}$
classifying a functor
![]() $\psi : {\mathcal C} \to \infty \mathrm {Cat}$
let
$\psi : {\mathcal C} \to \infty \mathrm {Cat}$
let
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
be the pullback of
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
be the pullback of
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
along
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
along
![]() $\psi : {\mathcal C} \to \infty \mathrm {Cat}.$
$\psi : {\mathcal C} \to \infty \mathrm {Cat}.$
Notation 3.6. Let
![]() ${\mathcal P}: \infty \mathrm {Cat} \to \infty \widehat {\mathrm {Cat}}$
be the functor classifying the cocartesian fibration
${\mathcal P}: \infty \mathrm {Cat} \to \infty \widehat {\mathrm {Cat}}$
be the functor classifying the cocartesian fibration
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
.
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
.
Remark 3.5. For every cocartesian fibration
![]() ${\mathcal D} \to {\mathcal C}$
classifying a functor
${\mathcal D} \to {\mathcal C}$
classifying a functor
![]() $\psi : {\mathcal C} \to \infty \mathrm {Cat}$
by Lemma 3.4 the pullback
$\psi : {\mathcal C} \to \infty \mathrm {Cat}$
by Lemma 3.4 the pullback
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is a cocartesian and cartesian fibration. By definition the cocartesian fibration
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is a cocartesian and cartesian fibration. By definition the cocartesian fibration
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
classifies the functor
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
classifies the functor
![]() ${\mathcal C} \xrightarrow {\psi } \infty \mathrm {Cat} \xrightarrow {{\mathcal P}} \infty \widehat {\mathrm {Cat}}. $
${\mathcal C} \xrightarrow {\psi } \infty \mathrm {Cat} \xrightarrow {{\mathcal P}} \infty \widehat {\mathrm {Cat}}. $
Remark 3.6. Evaluation at the target
![]() ${\mathcal R} \to \infty \mathrm {Cat}$
is a cocartesian and cartesian fibration by Lemma 3.4. So for every cocartesian fibration
${\mathcal R} \to \infty \mathrm {Cat}$
is a cocartesian and cartesian fibration by Lemma 3.4. So for every cocartesian fibration
![]() ${\mathcal D} \to {\mathcal C}$
whose fibers are small, the functor
${\mathcal D} \to {\mathcal C}$
whose fibers are small, the functor
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is a cocartesian and cartesian fibration.
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is a cocartesian and cartesian fibration.
For the next lemma we use the following notation:
Notation 3.7. For every functor
![]() ${\mathcal A} \to {\mathcal B}$
and
${\mathcal A} \to {\mathcal B}$
and
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm K}$
let
${\mathrm K}$
let
![]() ${\mathcal A}^{\mathrm K} \to {\mathcal B}$
be the pullback
${\mathcal A}^{\mathrm K} \to {\mathcal B}$
be the pullback
![]() ${\mathcal B} \times _{\mathrm {Fun}({\mathrm K},{\mathcal B})} \mathrm {Fun}({\mathrm K},{\mathcal A}) $
along the diagonal functor
${\mathcal B} \times _{\mathrm {Fun}({\mathrm K},{\mathcal B})} \mathrm {Fun}({\mathrm K},{\mathcal A}) $
along the diagonal functor
![]() ${\mathcal B} \to \mathrm {Fun}({\mathrm K},{\mathcal B}).$
${\mathcal B} \to \mathrm {Fun}({\mathrm K},{\mathcal B}).$
Remark 3.7. Note that for every functor
![]() ${\mathcal C} \to {\mathcal B}$
there is a canonical equivalence
${\mathcal C} \to {\mathcal B}$
there is a canonical equivalence
In this sense
![]() ${\mathcal A}^{\mathrm K} \to {\mathcal B}$
is the cotensor of the functor
${\mathcal A}^{\mathrm K} \to {\mathcal B}$
is the cotensor of the functor
![]() ${\mathcal A} \to {\mathcal B}$
with
${\mathcal A} \to {\mathcal B}$
with
![]() ${\mathrm K}$
in the sense of [Reference Heine19, Definition 2.51.] for the action of
${\mathrm K}$
in the sense of [Reference Heine19, Definition 2.51.] for the action of
![]() $\infty \mathrm {Cat} $
on itself. This justifies the Notation 3.7.
$\infty \mathrm {Cat} $
on itself. This justifies the Notation 3.7.
Lemma 3.8.
-
1. The cocartesian fibration
 $\kappa : {\mathcal U} \to \infty \mathrm {Cat}$
classifies the identity.
$\kappa : {\mathcal U} \to \infty \mathrm {Cat}$
classifies the identity.By (1) for every cocartesian fibration
 ${\mathcal D} \to {\mathcal C}$
classifying a functor
${\mathcal D} \to {\mathcal C}$
classifying a functor
 ${\mathcal C} \to \infty \mathrm {Cat}$
there is a canonical embedding of cocartesian fibrations over
${\mathcal C} \to \infty \mathrm {Cat}$
there is a canonical embedding of cocartesian fibrations over
 ${\mathcal C}$
:
${\mathcal C}$
:  $$ \begin{align*}{\mathcal D} \simeq {\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal U} \subset {\mathcal P}^{\mathcal C}({\mathcal D})={\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal R}.\end{align*} $$
$$ \begin{align*}{\mathcal D} \simeq {\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal U} \subset {\mathcal P}^{\mathcal C}({\mathcal D})={\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal R}.\end{align*} $$
-
2. The embedding
 $$ \begin{align*}{\mathcal D} \simeq {\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal U} \subset {\mathcal P}^{\mathcal C}({\mathcal D})={\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal R} \subset {\mathcal C} \times_{\mathrm{Fun}(\{1\},\infty\mathrm{Cat})} \mathrm{Fun}([1],\infty\mathrm{Cat})\end{align*} $$
$$ \begin{align*}{\mathcal D} \simeq {\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal U} \subset {\mathcal P}^{\mathcal C}({\mathcal D})={\mathcal C} \times_{\infty\mathrm{Cat}} {\mathcal R} \subset {\mathcal C} \times_{\mathrm{Fun}(\{1\},\infty\mathrm{Cat})} \mathrm{Fun}([1],\infty\mathrm{Cat})\end{align*} $$
corresponds to a natural transformation of functors
 ${\mathcal D} \to \infty \mathrm {Cat}$
that is classified by the canonical map
${\mathcal D} \to \infty \mathrm {Cat}$
that is classified by the canonical map
 ${\mathcal D}^{[1]} \to {\mathcal D} \times _{\mathcal C} {\mathcal D}$
of cocartesian fibrations over
${\mathcal D}^{[1]} \to {\mathcal D} \times _{\mathcal C} {\mathcal D}$
of cocartesian fibrations over
 ${\mathcal D}.$
${\mathcal D}.$
Proof. (1): Let
![]() ${\mathcal V} \to \infty \mathrm {Cat}$
be the cocartesian fibration classifying the identity. To prove (1) we will construct an equivalence
${\mathcal V} \to \infty \mathrm {Cat}$
be the cocartesian fibration classifying the identity. To prove (1) we will construct an equivalence
![]() ${\mathcal V} \simeq {\mathcal U}$
over
${\mathcal V} \simeq {\mathcal U}$
over
![]() $\infty \mathrm {Cat}$
. By the Yoneda-lemma it will suffice to show that for any
$\infty \mathrm {Cat}$
. By the Yoneda-lemma it will suffice to show that for any
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal A}$
and functor
${\mathcal A}$
and functor
![]() $\theta : {\mathcal A} \to \infty \mathrm {Cat}$
there is a bijection between the sets of equivalence classes of functors
$\theta : {\mathcal A} \to \infty \mathrm {Cat}$
there is a bijection between the sets of equivalence classes of functors
![]() ${\mathcal A} \to {\mathcal V}$
over
${\mathcal A} \to {\mathcal V}$
over
![]() $\infty \mathrm {Cat}$
and
$\infty \mathrm {Cat}$
and
![]() ${\mathcal A} \to {\mathcal U}$
over
${\mathcal A} \to {\mathcal U}$
over
![]() $\infty \mathrm {Cat}$
.
$\infty \mathrm {Cat}$
.
Let
![]() ${\mathcal C} \to {\mathcal A}$
be the cocartesian fibration classified by the functor
${\mathcal C} \to {\mathcal A}$
be the cocartesian fibration classified by the functor
![]() $\theta : {\mathcal A} \to \infty \mathrm {Cat}$
. By naturality of the Grothendieck construction there is a canonical equivalence
$\theta : {\mathcal A} \to \infty \mathrm {Cat}$
. By naturality of the Grothendieck construction there is a canonical equivalence
![]() ${\mathcal C} \simeq {\mathcal A} \times _{\infty \mathrm {Cat}}{\mathcal V}$
over
${\mathcal C} \simeq {\mathcal A} \times _{\infty \mathrm {Cat}}{\mathcal V}$
over
![]() ${\mathrm A}.$
Thus a functor
${\mathrm A}.$
Thus a functor
![]() ${\mathcal A} \to {\mathcal V}$
over
${\mathcal A} \to {\mathcal V}$
over
![]() $\infty \mathrm {Cat}$
corresponds to a functor
$\infty \mathrm {Cat}$
corresponds to a functor
![]() ${\mathcal A} \to {\mathcal A} \times _{\infty \mathrm {Cat}}{\mathcal V} \simeq {\mathcal C}$
over
${\mathcal A} \to {\mathcal A} \times _{\infty \mathrm {Cat}}{\mathcal V} \simeq {\mathcal C}$
over
![]() ${\mathrm A}, $
that is, a section of the cocartesian fibration
${\mathrm A}, $
that is, a section of the cocartesian fibration
![]() ${\mathcal C} \to {\mathcal A}$
.
${\mathcal C} \to {\mathcal A}$
.
Next we identify functors
![]() ${\mathcal A} \to {\mathcal U} $
over
${\mathcal A} \to {\mathcal U} $
over
![]() $\infty \mathrm {Cat}$
. A functor
$\infty \mathrm {Cat}$
. A functor
![]() ${\mathcal A} \to \mathrm {Fun}([1],\infty \mathrm {Cat})$
over
${\mathcal A} \to \mathrm {Fun}([1],\infty \mathrm {Cat})$
over
![]() $\infty \mathrm {Cat}$
is classified by a map of cocartesian fibrations
$\infty \mathrm {Cat}$
is classified by a map of cocartesian fibrations
![]() ${\mathcal D} \to {\mathcal C}$
over
${\mathcal D} \to {\mathcal C}$
over
![]() ${\mathcal A}$
. Since
${\mathcal A}$
. Since
![]() ${\mathcal U} $
is the full subcategory of
${\mathcal U} $
is the full subcategory of
![]() $\mathrm {Fun}([1],\infty \mathrm {Cat})$
spanned by the representable right fibrations, a functor
$\mathrm {Fun}([1],\infty \mathrm {Cat})$
spanned by the representable right fibrations, a functor
![]() ${\mathcal A} \to {\mathcal U} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
over
${\mathcal A} \to {\mathcal U} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
over
![]() $\infty \mathrm {Cat}$
is classified by a map of cocartesian fibrations
$\infty \mathrm {Cat}$
is classified by a map of cocartesian fibrations
![]() ${\mathcal D} \to {\mathcal C}$
over
${\mathcal D} \to {\mathcal C}$
over
![]() ${\mathcal A}$
that induces on the fiber over any
${\mathcal A}$
that induces on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
a representable right fibration.
${\mathrm A} \in {\mathcal A}$
a representable right fibration.
Thus, to complete the proof, we will show that there is a bijection between equivalence classes of sections of the cocartesian fibration
![]() ${\mathcal C} \to {\mathcal A}$
and maps of cocartesian fibrations
${\mathcal C} \to {\mathcal A}$
and maps of cocartesian fibrations
![]() ${\mathcal D} \to {\mathcal C}$
over
${\mathcal D} \to {\mathcal C}$
over
![]() ${\mathcal A}$
that induce on the fiber over any
${\mathcal A}$
that induce on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
a representable right fibration, where
${\mathrm A} \in {\mathcal A}$
a representable right fibration, where
![]() ${\mathcal D} \to {\mathcal A}$
is some cocartesian fibration.
${\mathcal D} \to {\mathcal A}$
is some cocartesian fibration.
A section
![]() $\alpha $
of
$\alpha $
of
![]() ${\mathcal C} \to {\mathcal A}$
gives rise to a map
${\mathcal C} \to {\mathcal A}$
gives rise to a map
![]() ${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
![]() ${\mathcal A}$
that induces on the fiber over any
${\mathcal A}$
that induces on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
the representable right fibration
${\mathrm A} \in {\mathcal A}$
the representable right fibration
![]() $({\mathcal C}_{\mathrm A})_{/\alpha ({\mathrm A})} \to {\mathcal C}_{\mathrm A}$
.
$({\mathcal C}_{\mathrm A})_{/\alpha ({\mathrm A})} \to {\mathcal C}_{\mathrm A}$
.
Conversely, let
![]() $\psi : {\mathcal D} \to {\mathcal C}$
be a map of cocartesian fibrations over
$\psi : {\mathcal D} \to {\mathcal C}$
be a map of cocartesian fibrations over
![]() ${\mathcal A}$
such that for any
${\mathcal A}$
such that for any
![]() ${\mathrm A} \in {\mathcal A}$
the fiber
${\mathrm A} \in {\mathcal A}$
the fiber
![]() ${\mathcal D}_{\mathrm A}$
has a final object. Then the
${\mathcal D}_{\mathrm A}$
has a final object. Then the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal D})$
has a final object
$\mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal D})$
has a final object
![]() $\beta $
such that for any
$\beta $
such that for any
![]() ${\mathrm A} \in {\mathcal A}$
the image
${\mathrm A} \in {\mathcal A}$
the image
![]() $\beta ({\mathrm A})$
is final in
$\beta ({\mathrm A})$
is final in
![]() ${\mathcal D}_{\mathrm A}.$
The composition
${\mathcal D}_{\mathrm A}.$
The composition
![]() $\psi \circ \beta : {\mathcal A} \to {\mathcal C}$
is a section of
$\psi \circ \beta : {\mathcal A} \to {\mathcal C}$
is a section of
![]() ${\mathcal C} \to {\mathcal A}$
.
${\mathcal C} \to {\mathcal A}$
.
We will prove that sending a section
![]() $\alpha $
of
$\alpha $
of
![]() ${\mathcal C} \to {\mathcal A}$
to the map
${\mathcal C} \to {\mathcal A}$
to the map
![]() ${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
![]() ${\mathcal A}$
is inverse to sending a map
${\mathcal A}$
is inverse to sending a map
![]() $\psi : {\mathcal D} \to {\mathcal C} $
of cocartesian fibrations over
$\psi : {\mathcal D} \to {\mathcal C} $
of cocartesian fibrations over
![]() ${\mathcal A}$
such that for any
${\mathcal A}$
such that for any
![]() ${\mathrm A} \in {\mathcal A}$
the fiber
${\mathrm A} \in {\mathcal A}$
the fiber
![]() ${\mathcal D}_{\mathrm A}$
has a final object, to the section
${\mathcal D}_{\mathrm A}$
has a final object, to the section
![]() $\psi \circ \beta : {\mathcal A} \to {\mathcal C}$
of
$\psi \circ \beta : {\mathcal A} \to {\mathcal C}$
of
![]() ${\mathcal C} \to {\mathcal A}$
.
${\mathcal C} \to {\mathcal A}$
.
The map
![]() ${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
![]() ${\mathcal A}$
induces on sections the functor
${\mathcal A}$
induces on sections the functor
![]() $\mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal C})_{/\alpha } \to \mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal C})$
. Consequently,
$\mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal C})_{/\alpha } \to \mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal C})$
. Consequently,
![]() $\alpha : {\mathcal A} \to {\mathcal C} $
is the associated section of the map
$\alpha : {\mathcal A} \to {\mathcal C} $
is the associated section of the map
![]() ${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
of cocartesian fibrations over
![]() ${\mathcal A}$
.
${\mathcal A}$
.
It remains to see that for any map
![]() ${\mathcal D} \to {\mathcal C}$
of cocartesian fibrations over
${\mathcal D} \to {\mathcal C}$
of cocartesian fibrations over
![]() ${\mathcal A}$
that induces on the fiber over any
${\mathcal A}$
that induces on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
a representable right fibration, with associated section
${\mathrm A} \in {\mathcal A}$
a representable right fibration, with associated section
![]() $\beta : {\mathcal A} \to {\mathcal C},$
there is an equivalence
$\beta : {\mathcal A} \to {\mathcal C},$
there is an equivalence
![]() ${\mathcal D} \simeq {\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}} $
over
${\mathcal D} \simeq {\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}} $
over
![]() ${\mathcal C}.$
${\mathcal C}.$
Let
![]() $\psi : {\mathcal D} \to {\mathcal C}$
be a map of cocartesian fibrations over
$\psi : {\mathcal D} \to {\mathcal C}$
be a map of cocartesian fibrations over
![]() ${\mathcal A}$
that induces on the fiber over any
${\mathcal A}$
that induces on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
a representable right fibration. The induced map
${\mathrm A} \in {\mathcal A}$
a representable right fibration. The induced map
of cocartesian fibrations over
![]() ${\mathcal A}$
induces on the fiber over any
${\mathcal A}$
induces on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
the functor
${\mathrm A} \in {\mathcal A}$
the functor
![]() $({\mathcal D}_{\mathrm A})_{/\beta ({\mathrm A})} \to {\mathcal D}_{\mathrm A}$
, which is an equivalence since
$({\mathcal D}_{\mathrm A})_{/\beta ({\mathrm A})} \to {\mathcal D}_{\mathrm A}$
, which is an equivalence since
![]() $\beta ({\mathrm A})$
is a final object in
$\beta ({\mathrm A})$
is a final object in
![]() ${\mathcal D}_{\mathrm A}.$
Therefore the functor (3.5) is an equivalence.
${\mathcal D}_{\mathrm A}.$
Therefore the functor (3.5) is an equivalence.
As we have noted, the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal D})$
admits a final object
$\mathrm {Fun}_{\mathcal A}({\mathcal A},{\mathcal D})$
admits a final object
![]() $\beta $
such that for any
$\beta $
such that for any
![]() ${\mathrm A} \in {\mathcal A}$
the image
${\mathrm A} \in {\mathcal A}$
the image
![]() $\beta ({\mathrm A})$
is final in
$\beta ({\mathrm A})$
is final in
![]() ${\mathcal D}_{\mathrm A}.$
The section
${\mathcal D}_{\mathrm A}.$
The section
![]() $\psi \circ \beta : {\mathcal A} \to {\mathcal C}$
of
$\psi \circ \beta : {\mathcal A} \to {\mathcal C}$
of
![]() ${\mathcal C} \to {\mathcal A}$
and the map
${\mathcal C} \to {\mathcal A}$
and the map
![]() $\psi : {\mathcal D} \to {\mathcal C}$
of cocartesian fibrations over
$\psi : {\mathcal D} \to {\mathcal C}$
of cocartesian fibrations over
![]() ${\mathcal A}$
give rise to a map
${\mathcal A}$
give rise to a map
of cocartesian fibrations over
![]() ${\mathcal A}$
, which induces on the fiber over any
${\mathcal A}$
, which induces on the fiber over any
![]() ${\mathrm A} \in {\mathcal A}$
the functor
${\mathrm A} \in {\mathcal A}$
the functor
![]() $({\mathcal D}_{\mathrm A})_{/\beta ({\mathrm A})} \to ({\mathcal C}_{\mathrm A})_{/\alpha ({\mathrm A})}$
. Since
$({\mathcal D}_{\mathrm A})_{/\beta ({\mathrm A})} \to ({\mathcal C}_{\mathrm A})_{/\alpha ({\mathrm A})}$
. Since
![]() $\psi : {\mathcal D} \to {\mathcal C}$
induces on the fiber over A a right fibration
$\psi : {\mathcal D} \to {\mathcal C}$
induces on the fiber over A a right fibration
![]() ${\mathcal D}_{\mathrm A} \to {\mathcal C}_{\mathrm A}$
, the functor
${\mathcal D}_{\mathrm A} \to {\mathcal C}_{\mathrm A}$
, the functor
![]() $({\mathcal D}_{\mathrm A})_{/\beta ({\mathrm A})} \to ({\mathcal C}_{\mathrm A})_{/\alpha ({\mathrm A})}$
is an equivalence. Consequently, the functor (3.6) is an equivalence.
$({\mathcal D}_{\mathrm A})_{/\beta ({\mathrm A})} \to ({\mathcal C}_{\mathrm A})_{/\alpha ({\mathrm A})}$
is an equivalence. Consequently, the functor (3.6) is an equivalence.
Via the equivalences (3.5) and (3.6) the functor
![]() ${\mathcal D} \to {\mathcal C}$
is equivalent over
${\mathcal D} \to {\mathcal C}$
is equivalent over
![]() ${\mathcal C}$
to
${\mathcal C}$
to
![]() ${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
. The proof of (1) shows (2).
${\mathcal A} \times _{{\mathcal C}^{\{1\}} } {\mathcal C}^{[1]} \to {\mathcal C}^{\{0\}}$
. The proof of (1) shows (2).
Definition 3.9. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a functor. The enveloping cocartesian fibration of
${\mathcal C} \to {\mathcal A}$
be a functor. The enveloping cocartesian fibration of
![]() ${\mathcal C} \to {\mathcal A}$
is the pullback
${\mathcal C} \to {\mathcal A}$
is the pullback
The diagonal embedding
![]() ${\mathcal A} \to \mathrm {Fun}([1],{\mathcal A})$
induces an embedding
${\mathcal A} \to \mathrm {Fun}([1],{\mathcal A})$
induces an embedding
![]() $\theta : {\mathcal C} \to {\mathrm {Env}}({\mathcal C})$
over
$\theta : {\mathcal C} \to {\mathrm {Env}}({\mathcal C})$
over
![]() ${\mathcal A}$
. The following proposition is [Reference Heine17, Proposition A.2.]:
${\mathcal A}$
. The following proposition is [Reference Heine17, Proposition A.2.]:
Proposition 3.10. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a functor. Restriction along
${\mathcal C} \to {\mathcal A}$
be a functor. Restriction along
![]() $\theta $
induces for every cocartesian fibration
$\theta $
induces for every cocartesian fibration
![]() ${\mathcal D} \to {\mathcal A}$
an equivalence
${\mathcal D} \to {\mathcal A}$
an equivalence
where the left hand side is the full subcategory of maps of cocartesian fibrations over
![]() ${\mathcal A}.$
${\mathcal A}.$
Lemma 3.11. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a cocartesian fibration between small
${\mathcal C} \to {\mathcal A}$
be a cocartesian fibration between small
![]() $\infty $
-categories. There is a canonical embedding
$\infty $
-categories. There is a canonical embedding
over
![]() ${\mathcal A}$
that induces on the fiber over every
${\mathcal A}$
that induces on the fiber over every
![]() ${\mathrm A} \in {\mathcal A}$
the embedding
${\mathrm A} \in {\mathcal A}$
the embedding
![]() $(\theta _{\mathrm A})_!: {\mathcal P}({\mathcal C}_{\mathrm A}) \subset {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
.
$(\theta _{\mathrm A})_!: {\mathcal P}({\mathcal C}_{\mathrm A}) \subset {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
.
Proof. By [Reference Heine17, Lemma A.7.] the embedding
![]() $\theta : {\mathcal C} \subset {\mathrm {Env}}({\mathcal C})$
admits a left adjoint
$\theta : {\mathcal C} \subset {\mathrm {Env}}({\mathcal C})$
admits a left adjoint
![]() ${\mathrm L}$
relative to
${\mathrm L}$
relative to
![]() ${\mathcal A}$
, which is a map of cocartesian fibrations over
${\mathcal A}$
, which is a map of cocartesian fibrations over
![]() ${\mathcal A}$
. The relative left adjoint gives rise to a map
${\mathcal A}$
. The relative left adjoint gives rise to a map
![]() ${\mathrm L}_!: {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal P}^{\mathcal A}({\mathcal C})$
of cocartesian fibrations over
${\mathrm L}_!: {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal P}^{\mathcal A}({\mathcal C})$
of cocartesian fibrations over
![]() ${\mathcal A}$
. For every
${\mathcal A}$
. For every
![]() ${\mathrm A} \in {\mathcal A}$
the induced localization
${\mathrm A} \in {\mathcal A}$
the induced localization
![]() ${\mathrm L}_{\mathrm A}: {\mathrm {Env}}({\mathcal C})_{\mathrm A} \rightleftarrows {\mathcal C}_{\mathrm A}: \theta _{\mathrm A}$
induces a localization
${\mathrm L}_{\mathrm A}: {\mathrm {Env}}({\mathcal C})_{\mathrm A} \rightleftarrows {\mathcal C}_{\mathrm A}: \theta _{\mathrm A}$
induces a localization
![]() $({\mathrm L}_!)_{\mathrm A} \simeq ({\mathrm L}_{\mathrm A})_! : {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})\rightleftarrows {\mathcal P}({\mathcal C}_{\mathrm A}): (\theta _{\mathrm A})_! $
. By [Reference Lurie26, Proposition 7.3.2.6.] this implies that the map
$({\mathrm L}_!)_{\mathrm A} \simeq ({\mathrm L}_{\mathrm A})_! : {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})\rightleftarrows {\mathcal P}({\mathcal C}_{\mathrm A}): (\theta _{\mathrm A})_! $
. By [Reference Lurie26, Proposition 7.3.2.6.] this implies that the map
![]() $ {\mathrm L}_!: {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal P}^{\mathcal A}({\mathcal C})$
of cocartesian fibrations over
$ {\mathrm L}_!: {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal P}^{\mathcal A}({\mathcal C})$
of cocartesian fibrations over
![]() ${\mathcal A}$
admits a fully faithful right adjoint relative to
${\mathcal A}$
admits a fully faithful right adjoint relative to
![]() ${\mathcal A}$
that induces on the fiber over
${\mathcal A}$
that induces on the fiber over
![]() ${\mathrm A} \in {\mathcal A}$
the embedding
${\mathrm A} \in {\mathcal A}$
the embedding
![]() $(\theta _{\mathrm A})_!.$
$(\theta _{\mathrm A})_!.$
Lemma 3.11 motivates the following extension of Definition 3.5.
Definition 3.12. For every functor
![]() ${\mathcal C} \to {\mathcal A}$
between small
${\mathcal C} \to {\mathcal A}$
between small
![]() $\infty $
-categories let
$\infty $
-categories let
be the full subcategory spanned by the objects of
![]() ${\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))_{\mathrm A} \simeq {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A}) $
that belong to the essential image of the embedding
${\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))_{\mathrm A} \simeq {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A}) $
that belong to the essential image of the embedding
![]() $(\theta _{\mathrm A})_!: {\mathcal P}({\mathcal C}_{\mathrm A}) \subset {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
for some
$(\theta _{\mathrm A})_!: {\mathcal P}({\mathcal C}_{\mathrm A}) \subset {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
for some
![]() ${\mathrm A} \in {\mathcal A}$
.
${\mathrm A} \in {\mathcal A}$
.
Remark 3.8. For every object
![]() ${\mathrm A}$
of
${\mathrm A}$
of
![]() ${\mathcal A}$
there is a canonical equivalence
${\mathcal A}$
there is a canonical equivalence
Remark 3.9. The embedding
![]() ${\mathcal C} \subset {\mathrm {Env}}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
over
${\mathcal C} \subset {\mathrm {Env}}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
over
![]() ${\mathcal A}$
of Lemma 3.8 induces an embedding
${\mathcal A}$
of Lemma 3.8 induces an embedding
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
over
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
over
![]() ${\mathcal A}$
that induces on the fiber over every object
${\mathcal A}$
that induces on the fiber over every object
![]() ${\mathrm A}$
of
${\mathrm A}$
of
![]() ${\mathcal A}$
the Yoneda-embedding
${\mathcal A}$
the Yoneda-embedding
![]() ${\mathcal C}_{\mathrm A} \to {\mathcal P}({\mathcal C}_{\mathrm A}).$
${\mathcal C}_{\mathrm A} \to {\mathcal P}({\mathcal C}_{\mathrm A}).$
Lemma 3.13. Let
![]() $\phi : {\mathcal D} \to {\mathcal A}$
be a locally cocartesian fibration and
$\phi : {\mathcal D} \to {\mathcal A}$
be a locally cocartesian fibration and
![]() ${\mathcal C} \subset {\mathcal D}$
a full subcategory such that for every
${\mathcal C} \subset {\mathcal D}$
a full subcategory such that for every
![]() ${\mathrm A} \in {\mathcal A}$
the induced embedding
${\mathrm A} \in {\mathcal A}$
the induced embedding
![]() ${\mathcal C}_{\mathrm A} \subset {\mathcal D}_{\mathrm A}$
admits a left adjoint
${\mathcal C}_{\mathrm A} \subset {\mathcal D}_{\mathrm A}$
admits a left adjoint
![]() ${\mathrm L}_{\mathrm A}.$
The restriction
${\mathrm L}_{\mathrm A}.$
The restriction
![]() $\phi ': {\mathcal C} \subset {\mathcal D} \to {\mathcal A}$
is a locally cocartesian fibration. A morphism of
$\phi ': {\mathcal C} \subset {\mathcal D} \to {\mathcal A}$
is a locally cocartesian fibration. A morphism of
![]() ${\mathcal C}$
lying over a morphism
${\mathcal C}$
lying over a morphism
![]() ${\mathrm {f}}: {\mathrm A} \to {\mathrm B} $
of
${\mathrm {f}}: {\mathrm A} \to {\mathrm B} $
of
![]() ${\mathcal A}$
is locally
${\mathcal A}$
is locally
![]() $\phi '$
-cocartesian if and only if it factors as
$\phi '$
-cocartesian if and only if it factors as
![]() ${\mathrm X} \to {\mathrm Y} \to {\mathrm Y}'$
, where
${\mathrm X} \to {\mathrm Y} \to {\mathrm Y}'$
, where
![]() ${\mathrm X} \to {\mathrm Y}$
is
${\mathrm X} \to {\mathrm Y}$
is
![]() $\phi $
-cocartesian and
$\phi $
-cocartesian and
![]() ${\mathrm Y} \to {\mathrm Y}'$
is a
${\mathrm Y} \to {\mathrm Y}'$
is a
![]() ${\mathrm L}_{{\mathrm B}}$
-local equivalence.
${\mathrm L}_{{\mathrm B}}$
-local equivalence.
Proof. For every
![]() ${\mathrm Z} \in {\mathcal C}$
lying over
${\mathrm Z} \in {\mathcal C}$
lying over
![]() ${\mathrm B} \in {\mathcal A}$
the canonical map
${\mathrm B} \in {\mathcal A}$
the canonical map
is an equivalence.
Proposition 3.14. For every functor
![]() ${\mathcal C} \to {\mathcal A}$
of small
${\mathcal C} \to {\mathcal A}$
of small
![]() $\infty $
-categories the functor
$\infty $
-categories the functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cartesian fibration. For every morphism
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cartesian fibration. For every morphism
![]() ${\mathrm A} \to {\mathrm B}$
of
${\mathrm A} \to {\mathrm B}$
of
![]() ${\mathcal A}$
the induced functor
${\mathcal A}$
the induced functor
![]() $ {\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm B} \to {\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm A}$
factors as
$ {\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm B} \to {\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm A}$
factors as
where the last functor is restriction along the functor
![]() ${\mathcal C}_{\mathrm A} \subset {\mathrm {Env}}({\mathcal C})_{\mathrm A} \to {\mathrm {Env}}({\mathcal C})_{\mathrm B},$
and thus is a left adjoint.
${\mathcal C}_{\mathrm A} \subset {\mathrm {Env}}({\mathcal C})_{\mathrm A} \to {\mathrm {Env}}({\mathcal C})_{\mathrm B},$
and thus is a left adjoint.
Proof. The functor
![]() ${\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal A} $
is a cartesian fibration and for every
${\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal A} $
is a cartesian fibration and for every
![]() ${\mathrm A} \in {\mathcal A}$
the induced embedding
${\mathrm A} \in {\mathcal A}$
the induced embedding
![]() $(\theta _{\mathrm A})_!: {\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm A} \simeq {\mathcal P}({\mathcal C}_{\mathrm A}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))_{\mathrm A} \simeq {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
admits a right adjoint. Thus by Lemma 3.13 the restriction
$(\theta _{\mathrm A})_!: {\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm A} \simeq {\mathcal P}({\mathcal C}_{\mathrm A}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))_{\mathrm A} \simeq {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
admits a right adjoint. Thus by Lemma 3.13 the restriction
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal A}$
is a locally cartesian fibration.
${\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal A}$
is a locally cartesian fibration.
Notation 3.15. Let
![]() ${\mathcal C} \to {\mathcal A}, {\mathcal D} \to {\mathcal B}$
be functors. Let
${\mathcal C} \to {\mathcal A}, {\mathcal D} \to {\mathcal B}$
be functors. Let
and
the full subcategory spanned by the commutative squares

such that for every
![]() ${\mathrm A} \in {\mathcal A}$
the induced functor
${\mathrm A} \in {\mathcal A}$
the induced functor
![]() ${\mathcal C}_{\mathrm A} \to {\mathcal D}_{\psi ({\mathrm A})}$
on the fiber over
${\mathcal C}_{\mathrm A} \to {\mathcal D}_{\psi ({\mathrm A})}$
on the fiber over
![]() ${\mathrm A}$
preserves small colimits.
${\mathrm A}$
preserves small colimits.
The following universal property of
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is crucial for our main theorem:
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is crucial for our main theorem:
Proposition 3.16. Let
![]() ${\mathcal D} \to {\mathcal B}$
be a locally cartesian fibration whose fibers admit small colimits.
${\mathcal D} \to {\mathcal B}$
be a locally cartesian fibration whose fibers admit small colimits.
-
1. Let
 ${\mathcal C} \to {\mathcal A}$
be a functor between small
${\mathcal C} \to {\mathcal A}$
be a functor between small
 $\infty $
-categories. Restriction along the embedding
$\infty $
-categories. Restriction along the embedding
 ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
induces an equivalence
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
induces an equivalence  $$ \begin{align*}\theta_{\mathcal D}: \Theta({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \to \Theta({\mathcal C}, {\mathcal D}).\end{align*} $$
$$ \begin{align*}\theta_{\mathcal D}: \Theta({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \to \Theta({\mathcal C}, {\mathcal D}).\end{align*} $$
-
2. Let
 ${\mathcal C} \to {\mathcal A}$
be a functor between
${\mathcal C} \to {\mathcal A}$
be a functor between
 $\infty $
-categories and
$\infty $
-categories and
 ${\mathcal P}^{\mathcal A}({\mathcal C}) $
the full subcategory of
${\mathcal P}^{\mathcal A}({\mathcal C}) $
the full subcategory of
 $\widehat {{\mathcal P}}^{\mathcal A}({\mathcal C})$
such that for every
$\widehat {{\mathcal P}}^{\mathcal A}({\mathcal C})$
such that for every
 ${\mathrm A} \in {\mathcal A}$
the fiber
${\mathrm A} \in {\mathcal A}$
the fiber
 ${\mathcal P}^{\mathrm A}({\mathcal C})_{\mathrm A} \subset \widehat {{\mathcal P}}^{\mathcal A}({\mathcal C})_{\mathrm A} \simeq \widehat {{\mathcal P}}({\mathcal C}_{\mathrm A})$
is generated by
${\mathcal P}^{\mathrm A}({\mathcal C})_{\mathrm A} \subset \widehat {{\mathcal P}}^{\mathcal A}({\mathcal C})_{\mathrm A} \simeq \widehat {{\mathcal P}}({\mathcal C}_{\mathrm A})$
is generated by
 ${\mathcal C}_{\mathrm A}$
under small colimits. Restriction along the induced embedding
${\mathcal C}_{\mathrm A}$
under small colimits. Restriction along the induced embedding
 ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) \subset \widehat {{\mathcal P}}^{\mathcal A}({\mathcal C})$
induces an equivalence
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) \subset \widehat {{\mathcal P}}^{\mathcal A}({\mathcal C})$
induces an equivalence  $$ \begin{align*}\theta_{\mathcal D}: \Theta({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \to \Theta({\mathcal C}, {\mathcal D}).\end{align*} $$
$$ \begin{align*}\theta_{\mathcal D}: \Theta({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \to \Theta({\mathcal C}, {\mathcal D}).\end{align*} $$
Proof. (2) is similar to (1). We prove (1). We first reduce to the case that
![]() ${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration whose fibers admit large colimits.
${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration whose fibers admit large colimits.
By the opposite of Lemma 3.17 (applied to a larger universe) there is an embedding
![]() ${\mathcal D} \subset {\mathcal E}$
over
${\mathcal D} \subset {\mathcal E}$
over
![]() ${\mathcal B}$
that induces on the fiber over every object of
${\mathcal B}$
that induces on the fiber over every object of
![]() ${\mathcal B}$
a small colimits preserving functor, where
${\mathcal B}$
a small colimits preserving functor, where
![]() ${\mathcal E} \to {\mathcal B}$
is a cocartesian and cartesian fibration whose fibers admit large colimits and are locally large. Since the
${\mathcal E} \to {\mathcal B}$
is a cocartesian and cartesian fibration whose fibers admit large colimits and are locally large. Since the
![]() $\infty $
-category of presheaves is generated by the representable presheaves under small colimits [Reference Heine15, Lemma 2.10.], the functor
$\infty $
-category of presheaves is generated by the representable presheaves under small colimits [Reference Heine15, Lemma 2.10.], the functor
![]() $\theta _{\mathcal D}$
is the pullback of the functor
$\theta _{\mathcal D}$
is the pullback of the functor
![]() $\theta _{\mathcal E}$
. So it is enough to check that
$\theta _{\mathcal E}$
. So it is enough to check that
![]() $\theta _{\mathcal E}$
is an equivalence and we can assume that
$\theta _{\mathcal E}$
is an equivalence and we can assume that
![]() ${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration whose fibers admit large colimits and are locally large.
${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration whose fibers admit large colimits and are locally large.
Next we further reduce the statement to show that for every cocartesian and cartesian fibration
![]() ${\mathcal D} \to {\mathcal A}$
whose fibers admit large colimits and are locally large, the canonical functor
${\mathcal D} \to {\mathcal A}$
whose fibers admit large colimits and are locally large, the canonical functor
is an equivalence, where the left hand side is the full subcategory of functors over
![]() ${\mathcal A}$
that induce on every fiber a small colimits preserving functor.
${\mathcal A}$
that induce on every fiber a small colimits preserving functor.
There is a commutative triangle

Because the functor
![]() ${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration, this triangle is a map of cocartesian and cartesian fibrations over
${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration, this triangle is a map of cocartesian and cartesian fibrations over
![]() $\mathrm {Fun}({\mathcal A},{\mathcal B}).$
Since the functor
$\mathrm {Fun}({\mathcal A},{\mathcal B}).$
Since the functor
![]() ${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration, the fiber transports of the cocartesian fibration are left adjoints. This guarantees that the restriction
${\mathcal D} \to {\mathcal B}$
is a cocartesian and cartesian fibration, the fiber transports of the cocartesian fibration are left adjoints. This guarantees that the restriction
![]() $\Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \to \mathrm {Fun}({\mathcal A},{\mathcal B})$
is also a cocartesian fibration and the embedding
$\Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \to \mathrm {Fun}({\mathcal A},{\mathcal B})$
is also a cocartesian fibration and the embedding
![]() $\Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \subset \Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})$
is a map of cocartesian fibrations over
$\Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L} \subset \Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})$
is a map of cocartesian fibrations over
![]() $\mathrm {Fun}({\mathcal A},{\mathcal B}) $
. Hence also the restriction
$\mathrm {Fun}({\mathcal A},{\mathcal B}) $
. Hence also the restriction

is a map of cocartesian fibrations over
![]() $\mathrm {Fun}({\mathcal A},{\mathcal B}) $
.
$\mathrm {Fun}({\mathcal A},{\mathcal B}) $
.
Consequently,
![]() $\theta _{\mathcal D}$
is an equivalence if it induces on the fiber over every functor
$\theta _{\mathcal D}$
is an equivalence if it induces on the fiber over every functor
![]() $\psi : {\mathcal A} \to {\mathcal B}$
an equivalence. The functor
$\psi : {\mathcal A} \to {\mathcal B}$
an equivalence. The functor
![]() $\theta _{\mathcal D}$
induces on the fiber over
$\theta _{\mathcal D}$
induces on the fiber over
![]() $\psi $
the functor
$\psi $
the functor
Therefore it is enough to see that the functor (3.7) is an equivalence.
The functor (3.7) is conservative since for every
![]() ${\mathrm A} \in {\mathcal A}$
the
${\mathrm A} \in {\mathcal A}$
the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm A} \simeq {\mathcal P}({\mathcal C}_{\mathrm A})$
is generated by
${\mathcal P}^{\mathcal A}({\mathcal C})_{\mathrm A} \simeq {\mathcal P}({\mathcal C}_{\mathrm A})$
is generated by
![]() ${\mathcal C}_{\mathrm A}$
under small colimits. Therefore, the functor (3.7) is an equivalence if it admits a fully faithful left adjoint. We devote the remaining proof to showing this.
${\mathcal C}_{\mathrm A}$
under small colimits. Therefore, the functor (3.7) is an equivalence if it admits a fully faithful left adjoint. We devote the remaining proof to showing this.
By Proposition 3.14 the functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cartesian fibration. This implies that
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cartesian fibration. This implies that
![]() ${\mathcal P}^{\mathcal A}({\mathcal C})$
is large because
${\mathcal P}^{\mathcal A}({\mathcal C})$
is large because
![]() ${\mathcal A}$
is large and the fibers of
${\mathcal A}$
is large and the fibers of
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
are large. Let
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
are large. Let
![]() $\iota : {\mathcal C} \subset {\mathcal P}^{\mathcal A}({\mathcal C})$
be the canonical embedding. Since
$\iota : {\mathcal C} \subset {\mathcal P}^{\mathcal A}({\mathcal C})$
be the canonical embedding. Since
![]() ${\mathcal P}^{\mathcal A}({\mathcal C})$
is large and the fibers of the cocartesian fibration
${\mathcal P}^{\mathcal A}({\mathcal C})$
is large and the fibers of the cocartesian fibration
![]() ${\mathcal D} \to {\mathcal A}$
admit large colimits preserved by the fiber transports, by [Reference Lurie27, Corollary 4.3.2.14., Proposition 4.3.2.17.] the induced functor
${\mathcal D} \to {\mathcal A}$
admit large colimits preserved by the fiber transports, by [Reference Lurie27, Corollary 4.3.2.14., Proposition 4.3.2.17.] the induced functor
admits a fully faithful left adjoint
![]() $\iota _!$
, which forms the left Kan extension relative to
$\iota _!$
, which forms the left Kan extension relative to
![]() ${\mathcal A}$
along the embedding
${\mathcal A}$
along the embedding
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}).$
We complete the proof by showing that the fully faithful left adjoint
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}).$
We complete the proof by showing that the fully faithful left adjoint
![]() $\iota _!$
lands in the full subcategory
$\iota _!$
lands in the full subcategory
![]() $\mathrm {Fun}_{\mathcal A}({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L},$
and so is a fully faithful left adjoint of
$\mathrm {Fun}_{\mathcal A}({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L},$
and so is a fully faithful left adjoint of
![]() $\kappa _{\mathcal D}$
. In other words, we have to see that the left Kan extension
$\kappa _{\mathcal D}$
. In other words, we have to see that the left Kan extension
![]() $ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal D}$
relative to
$ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal D}$
relative to
![]() ${\mathcal A}$
of any functor
${\mathcal A}$
of any functor
![]() ${\mathcal C} \to {\mathcal D}$
over
${\mathcal C} \to {\mathcal D}$
over
![]() ${\mathcal A}$
preserves fiberwise small colimits.
${\mathcal A}$
preserves fiberwise small colimits.
Let
![]() ${j}: {\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
be the canonical embedding. Because
${j}: {\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
be the canonical embedding. Because
![]() ${\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
is large, by [Reference Lurie27, Corollary 4.3.2.14., Proposition 4.3.2.17.] the induced functor
${\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
is large, by [Reference Lurie27, Corollary 4.3.2.14., Proposition 4.3.2.17.] the induced functor
admits a fully faithful left adjoint
![]() ${j}_!, $
which forms the left Kan extension relative to
${j}_!, $
which forms the left Kan extension relative to
![]() ${\mathcal A}$
along the embedding
${\mathcal A}$
along the embedding
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})).$
Since
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})).$
Since
![]() ${j}_!$
is fully faithful, the unit
${j}_!$
is fully faithful, the unit
![]() $\mathrm {id} \to {j}^*{j}$
is an equivalence.
$\mathrm {id} \to {j}^*{j}$
is an equivalence.
We want to see that for every functor
![]() ${\mathcal C} \to {\mathcal D}$
over
${\mathcal C} \to {\mathcal D}$
over
![]() ${\mathcal A}$
the left Kan extension
${\mathcal A}$
the left Kan extension
![]() $\iota _!({\mathrm F}) \simeq {j}^*({j}_!(\iota _!({\mathrm F}))): {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal D}$
relative to
$\iota _!({\mathrm F}) \simeq {j}^*({j}_!(\iota _!({\mathrm F}))): {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal D}$
relative to
![]() ${\mathcal A}$
preserves fiberwise small colimits. The embedding
${\mathcal A}$
preserves fiberwise small colimits. The embedding
![]() ${j}: {\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
preserves fiberwise small colimits. Hence it is enough to see that
${j}: {\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
preserves fiberwise small colimits. Hence it is enough to see that
![]() ${j}_!(\iota _!({\mathrm F}))$
preserves fiberwise small colimits.
${j}_!(\iota _!({\mathrm F}))$
preserves fiberwise small colimits.
The functor
![]() ${j} \circ \iota : {\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) $
factors as
${j} \circ \iota : {\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) $
factors as
![]() ${\mathcal C} \to {\mathrm {Env}}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})). $
Therefore by adjointness, the functor
${\mathcal C} \to {\mathrm {Env}}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})). $
Therefore by adjointness, the functor
![]() ${j}_!(\iota _!({\mathrm F}))$
is likewise the left Kan extension of
${j}_!(\iota _!({\mathrm F}))$
is likewise the left Kan extension of
![]() ${\mathrm F}'$
relative to
${\mathrm F}'$
relative to
![]() ${\mathcal A}$
along the embedding
${\mathcal A}$
along the embedding
![]() ${i}:{\mathrm {Env}}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
, where
${i}:{\mathrm {Env}}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
, where
![]() ${\mathrm F}'$
is the left Kan extension of
${\mathrm F}'$
is the left Kan extension of
![]() ${\mathrm F}: {\mathcal C} \to {\mathcal A} $
relative to
${\mathrm F}: {\mathcal C} \to {\mathcal A} $
relative to
![]() ${\mathcal A}$
along the embedding
${\mathcal A}$
along the embedding
![]() ${\mathcal C} \to {\mathrm {Env}}({\mathcal C})$
.
${\mathcal C} \to {\mathrm {Env}}({\mathcal C})$
.
So it suffices to verify that the left Kan extension
![]() ${i}_!({\mathrm H}): {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal D} $
relative to
${i}_!({\mathrm H}): {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C})) \to {\mathcal D} $
relative to
![]() ${\mathcal A}$
of any functor
${\mathcal A}$
of any functor
![]() ${\mathrm H}: {\mathrm {Env}}({\mathcal C}) \to {\mathcal D}$
over
${\mathrm H}: {\mathrm {Env}}({\mathcal C}) \to {\mathcal D}$
over
![]() ${\mathcal A}$
preserves fiberwise small colimits.
${\mathcal A}$
preserves fiberwise small colimits.
Because
![]() ${i}: {\mathrm {Env}}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
is a map of cocartesian fibrations over
${i}: {\mathrm {Env}}({\mathcal C}) \subset {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal C}))$
is a map of cocartesian fibrations over
![]() ${\mathcal A}$
, by [Reference Lurie27, Proposition 4.3.3.10.] for every
${\mathcal A}$
, by [Reference Lurie27, Proposition 4.3.3.10.] for every
![]() ${\mathrm A} \in {\mathcal A}$
the induced functor
${\mathrm A} \in {\mathcal A}$
the induced functor
on the fiber over
![]() ${\mathrm A}$
is computed as the left Kan extension of
${\mathrm A}$
is computed as the left Kan extension of
![]() ${\mathrm H}_{\mathrm A}: {\mathrm {Env}}({\mathcal C})_{\mathrm A} \to {\mathcal D}_{\mathrm A}$
along the induced embedding
${\mathrm H}_{\mathrm A}: {\mathrm {Env}}({\mathcal C})_{\mathrm A} \to {\mathcal D}_{\mathrm A}$
along the induced embedding
![]() $ {\mathrm {Env}}({\mathcal C})_{\mathrm A} \subset {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
, which by [Reference Lurie27, Lemma 5.1.5.5.] preserves small colimits.
$ {\mathrm {Env}}({\mathcal C})_{\mathrm A} \subset {\mathcal P}({\mathrm {Env}}({\mathcal C})_{\mathrm A})$
, which by [Reference Lurie27, Lemma 5.1.5.5.] preserves small colimits.
Lemma 3.17. Let
![]() ${\mathcal D} \to {\mathcal A}$
be a locally cocartesian fibration of small
${\mathcal D} \to {\mathcal A}$
be a locally cocartesian fibration of small
![]() $\infty $
-categories. There is an embedding
$\infty $
-categories. There is an embedding
![]() ${\mathcal D} \subset {\mathcal E}$
over
${\mathcal D} \subset {\mathcal E}$
over
![]() ${\mathcal A}$
that induces on the fiber over every object of
${\mathcal A}$
that induces on the fiber over every object of
![]() ${\mathcal A}$
a small limits preserving functor, where
${\mathcal A}$
a small limits preserving functor, where
![]() ${\mathcal E} \to {\mathcal A}$
is a cocartesian and cartesian fibration whose fibers admit small limits and are locally small.
${\mathcal E} \to {\mathcal A}$
is a cocartesian and cartesian fibration whose fibers admit small limits and are locally small.
Proof. Since
![]() ${\mathcal D} \to {\mathcal A}$
is a locally cocartesian fibration, by [Reference Heine17, Lemma A.7.] the embedding
${\mathcal D} \to {\mathcal A}$
is a locally cocartesian fibration, by [Reference Heine17, Lemma A.7.] the embedding
![]() ${\mathcal D} \subset {\mathrm {Env}}({\mathcal D})$
induces on the fiber over every object of
${\mathcal D} \subset {\mathrm {Env}}({\mathcal D})$
induces on the fiber over every object of
![]() ${\mathcal A}$
a right adjoint functor. Since
${\mathcal A}$
a right adjoint functor. Since
![]() ${\mathcal D} \to {\mathcal A}$
is a locally cocartesian fibration of small
${\mathcal D} \to {\mathcal A}$
is a locally cocartesian fibration of small
![]() $\infty $
-categories, also
$\infty $
-categories, also
![]() ${\mathcal D}$
is small. Take
${\mathcal D}$
is small. Take
![]() ${\mathcal E}:= {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal D})).$
The embedding
${\mathcal E}:= {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal D})).$
The embedding
![]() ${\mathcal D} \subset {\mathrm {Env}}({\mathcal D}) \to {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal D}))$
induces on every fiber a small limits preserving functor.
${\mathcal D} \subset {\mathrm {Env}}({\mathcal D}) \to {\mathcal P}^{\mathcal A}({\mathrm {Env}}({\mathcal D}))$
induces on every fiber a small limits preserving functor.
Remark 3.10. Proposition 3.16 gives for any functors
![]() ${\mathcal A}' \to {\mathcal A}, {\mathcal C} \to {\mathcal A}$
between small
${\mathcal A}' \to {\mathcal A}, {\mathcal C} \to {\mathcal A}$
between small
![]() $\infty $
-categories a canonical functor
$\infty $
-categories a canonical functor
over
![]() ${\mathcal A}',$
which is a map of locally cartesian fibrations over
${\mathcal A}',$
which is a map of locally cartesian fibrations over
![]() ${\mathcal A}'$
, and induces equivalences on fibers and so is an equivalence.
${\mathcal A}'$
, and induces equivalences on fibers and so is an equivalence.
Lemma 3.18. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a locally cartesian fibration between small
${\mathcal C} \to {\mathcal A}$
be a locally cartesian fibration between small
![]() $\infty $
-categories. The embedding
$\infty $
-categories. The embedding
![]() ${\mathcal C} \subset {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cartesian fibrations over
${\mathcal C} \subset {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cartesian fibrations over
![]() ${\mathcal A}.$
The functor
${\mathcal A}.$
The functor
![]() ${\mathcal C} \to {\mathcal A}$
is a cartesian fibration if and only if the functor
${\mathcal C} \to {\mathcal A}$
is a cartesian fibration if and only if the functor
![]() $ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration.
$ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration.
Proof. We first prove that the embedding
![]() ${\mathcal C} \subset {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cartesian fibrations over
${\mathcal C} \subset {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cartesian fibrations over
![]() ${\mathcal A}$
if
${\mathcal A}$
if
![]() ${\mathcal C} \to {\mathcal A}$
is a locally cartesian fibration. By Remark 3.10 for every functor
${\mathcal C} \to {\mathcal A}$
is a locally cartesian fibration. By Remark 3.10 for every functor
![]() ${\mathcal A}' \to {\mathcal A}$
there is a canonical equivalence
${\mathcal A}' \to {\mathcal A}$
there is a canonical equivalence
over
![]() ${\mathcal A}'$
so that we can reduce to the case
${\mathcal A}'$
so that we can reduce to the case
![]() ${\mathcal A}=[1].$
Let
${\mathcal A}=[1].$
Let
![]() ${\mathcal M} \to [1]$
be a functor and
${\mathcal M} \to [1]$
be a functor and
![]() ${\mathcal C}:={\mathcal M}_0,{\mathcal D}:={\mathcal M}_1$
the fibers. The functor
${\mathcal C}:={\mathcal M}_0,{\mathcal D}:={\mathcal M}_1$
the fibers. The functor
![]() ${\mathcal P}({\mathcal M})^{[1]} \to [1]$
is a cartesian fibration classifying the functor
${\mathcal P}({\mathcal M})^{[1]} \to [1]$
is a cartesian fibration classifying the functor
![]() $\phi : {\mathcal P}({\mathcal D}) \subset {\mathcal P}({\mathcal M}) \to {\mathcal P}({\mathcal C})$
, where the first functor takes left Kan extension along the embedding
$\phi : {\mathcal P}({\mathcal D}) \subset {\mathcal P}({\mathcal M}) \to {\mathcal P}({\mathcal C})$
, where the first functor takes left Kan extension along the embedding
![]() ${\mathcal D} \subset {\mathcal M}$
and the second functor restricts along the embedding
${\mathcal D} \subset {\mathcal M}$
and the second functor restricts along the embedding
![]() ${\mathcal C} \subset {\mathcal M}.$
If
${\mathcal C} \subset {\mathcal M}.$
If
![]() ${\mathcal M}\to [1]$
is a cartesian fibration classifying a functor
${\mathcal M}\to [1]$
is a cartesian fibration classifying a functor
![]() ${\mathrm G}: {\mathcal D} \to {\mathcal C},$
then
${\mathrm G}: {\mathcal D} \to {\mathcal C},$
then
![]() $\phi $
is the extension of the functor
$\phi $
is the extension of the functor
![]() ${\mathcal D} \xrightarrow {{\mathrm G}} {\mathcal C} \subset {\mathcal P}({\mathcal C}).$
So the embedding
${\mathcal D} \xrightarrow {{\mathrm G}} {\mathcal C} \subset {\mathcal P}({\mathcal C}).$
So the embedding
![]() ${\mathcal M} \subset {\mathcal P}({\mathcal M})^{[1]}$
is a map of cartesian fibrations over
${\mathcal M} \subset {\mathcal P}({\mathcal M})^{[1]}$
is a map of cartesian fibrations over
![]() $[1].$
$[1].$
A locally cartesian fibration
![]() $\phi $
is a cartesian fibration if and only if the collection of
$\phi $
is a cartesian fibration if and only if the collection of
![]() $\phi $
-cartesian morphisms is closed under composition. Hence
$\phi $
-cartesian morphisms is closed under composition. Hence
![]() ${\mathcal C} \to {\mathcal A}$
is a cartesian fibration if the functor
${\mathcal C} \to {\mathcal A}$
is a cartesian fibration if the functor
![]() $ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration. Conversely, if
$ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration. Conversely, if
![]() ${\mathcal C} \to {\mathcal A}$
is a cartesian fibration, the functor
${\mathcal C} \to {\mathcal A}$
is a cartesian fibration, the functor
![]() $ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration since the fibers of
$ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration since the fibers of
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
are generated by the representable presheaves under small colimits, and the fiber transports of
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
are generated by the representable presheaves under small colimits, and the fiber transports of
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
preserve small colimits.
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
preserve small colimits.
Lemma 3.19. Let
![]() ${\mathcal C} \to {\mathcal D}$
be a map of locally (co)cartesian fibrations over
${\mathcal C} \to {\mathcal D}$
be a map of locally (co)cartesian fibrations over
![]() ${\mathcal A}$
. The functor
${\mathcal A}$
. The functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathcal D})$
is a map of locally (co)cartesian fibrations over
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathcal D})$
is a map of locally (co)cartesian fibrations over
![]() ${\mathcal A}$
.
${\mathcal A}$
.
Proof. By Lemma 3.18 for any locally cartesian fibration
![]() ${\mathcal C} \to {\mathcal A}$
the functor
${\mathcal C} \to {\mathcal A}$
the functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cartesian fibration and the embedding
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cartesian fibration and the embedding
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cartesian fibrations over
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cartesian fibrations over
![]() ${\mathcal A}$
. By Lemma 3.11 and Remark 3.10 for every locally cocartesian fibration
${\mathcal A}$
. By Lemma 3.11 and Remark 3.10 for every locally cocartesian fibration
![]() ${\mathcal C} \to {\mathcal A}$
the functor
${\mathcal C} \to {\mathcal A}$
the functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cocartesian and locally cartesian fibration and the embedding
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a locally cocartesian and locally cartesian fibration and the embedding
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cocartesian fibrations over
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C}) $
is a map of locally cocartesian fibrations over
![]() ${\mathcal A}$
. Since the fibers of
${\mathcal A}$
. Since the fibers of
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
are generated under small colimits by the representables and the fiber transports of the locally (co)cartesian fibration
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
are generated under small colimits by the representables and the fiber transports of the locally (co)cartesian fibration
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
preserve small colimits by Proposition 3.14, the induced functor
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
preserve small colimits by Proposition 3.14, the induced functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathcal D})$
is a map of locally (co)cartesian fibrations over
${\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal P}^{\mathcal A}({\mathcal D})$
is a map of locally (co)cartesian fibrations over
![]() ${\mathcal A}$
.
${\mathcal A}$
.
Definition 3.20. A functor
![]() $\phi : {\mathcal D} \to {\mathcal C}$
of small
$\phi : {\mathcal D} \to {\mathcal C}$
of small
![]() $\infty $
-categories is an exponentiable fibration if the functor
$\infty $
-categories is an exponentiable fibration if the functor
![]() ${\mathcal D} \times _{\mathcal C} (-): \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
taking pullback along
${\mathcal D} \times _{\mathcal C} (-): \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
taking pullback along
![]() $\phi $
preserves small colimits or equivalently admits a right adjoint.
$\phi $
preserves small colimits or equivalently admits a right adjoint.
Notation 3.21. For every exponentiable fibration
![]() $\phi : {\mathcal D} \to {\mathcal C}$
let
$\phi : {\mathcal D} \to {\mathcal C}$
let
![]() $\mathrm {Fun}^{\mathcal C}({\mathcal D},-): \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
be the right adjoint of the functor
$\mathrm {Fun}^{\mathcal C}({\mathcal D},-): \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
be the right adjoint of the functor
![]() ${\mathcal D} \times _{\mathcal C} (-): \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
.
${\mathcal D} \times _{\mathcal C} (-): \infty \mathrm {Cat}_{/{\mathcal C}} \to \infty \mathrm {Cat}_{/{\mathcal C}}$
.
The next remark is [Reference Heine18, Remark 3.69., Remark 3.71.]:
Remark 3.11. The pullback of any exponentiable fibration
![]() ${\mathcal D} \to {\mathcal C}$
along any functor
${\mathcal D} \to {\mathcal C}$
along any functor
![]() ${\mathcal B} \to {\mathcal C}$
is an exponentiable fibration and for every functor
${\mathcal B} \to {\mathcal C}$
is an exponentiable fibration and for every functor
![]() ${\mathcal E} \to {\mathcal C}$
there is a canonical equivalence
${\mathcal E} \to {\mathcal C}$
there is a canonical equivalence
![]() ${\mathcal B} \times _{\mathcal C} \mathrm {Fun}^{\mathcal C}({\mathcal D},{\mathcal E}) \simeq \mathrm {Fun}^{\mathcal B}({\mathcal B} \times _{\mathcal C} {\mathcal D},{\mathcal B} \times _{\mathcal C} {\mathcal E})$
over
${\mathcal B} \times _{\mathcal C} \mathrm {Fun}^{\mathcal C}({\mathcal D},{\mathcal E}) \simeq \mathrm {Fun}^{\mathcal B}({\mathcal B} \times _{\mathcal C} {\mathcal D},{\mathcal B} \times _{\mathcal C} {\mathcal E})$
over
![]() ${\mathcal B}.$
${\mathcal B}.$
Proposition 3.22. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a functor of small
${\mathcal C} \to {\mathcal A}$
be a functor of small
![]() $\infty $
-categories. The following are equivalent:
$\infty $
-categories. The following are equivalent:
-
1. The functor
 ${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration.
${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration. -
2. The locally cartesian fibration
 ${\mathcal P}^{{\mathcal A}}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration.
${\mathcal P}^{{\mathcal A}}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration.
Proof. A functor
![]() ${\mathcal B} \to {\mathcal A}$
is a cartesian fibration if and only if the pullbacks along any functors
${\mathcal B} \to {\mathcal A}$
is a cartesian fibration if and only if the pullbacks along any functors
![]() $[2] \to {\mathcal A}$
are cartesian fibrations by [Reference Lurie27, Corollary 2.4.2.10.]. A functor
$[2] \to {\mathcal A}$
are cartesian fibrations by [Reference Lurie27, Corollary 2.4.2.10.]. A functor
![]() ${\mathcal B} \to {\mathcal A}$
is an exponentiable fibration if and only if the pullbacks along any functors
${\mathcal B} \to {\mathcal A}$
is an exponentiable fibration if and only if the pullbacks along any functors
![]() $[2] \to {\mathcal A}$
are exponentiable fibrations as a consequence of [Reference Lurie27, Proposition B.3.14.] and Remark 3.11.
$[2] \to {\mathcal A}$
are exponentiable fibrations as a consequence of [Reference Lurie27, Proposition B.3.14.] and Remark 3.11.
So by Remark 3.10 we can reduce to the case that
![]() ${\mathcal A}=[2].$
The locally cartesian fibration
${\mathcal A}=[2].$
The locally cartesian fibration
![]() ${\mathcal P}^{[2]}({\mathcal C}) \to [2]$
classifies three functors
${\mathcal P}^{[2]}({\mathcal C}) \to [2]$
classifies three functors
![]() ${\mathrm {f}}: {\mathcal P}({\mathcal C}_2) \to {\mathcal P}({\mathcal C}_1), {g}: {\mathcal P}({\mathcal C}_1) \to {\mathcal P}({\mathcal C}_0), {\mathrm {h}}: {\mathcal P}({\mathcal C}_2) \to {\mathcal P}({\mathcal C}_0)$
, and a natural transformation
${\mathrm {f}}: {\mathcal P}({\mathcal C}_2) \to {\mathcal P}({\mathcal C}_1), {g}: {\mathcal P}({\mathcal C}_1) \to {\mathcal P}({\mathcal C}_0), {\mathrm {h}}: {\mathcal P}({\mathcal C}_2) \to {\mathcal P}({\mathcal C}_0)$
, and a natural transformation
![]() $\alpha : {g} \circ {\mathrm {f}} \to {\mathrm {h}}.$
By [Reference Lurie26, Proposition B.3.2., Proposition B.3.14.] a functor
$\alpha : {g} \circ {\mathrm {f}} \to {\mathrm {h}}.$
By [Reference Lurie26, Proposition B.3.2., Proposition B.3.14.] a functor
![]() ${\mathcal C} \to [2]$
is an exponentiable fibration if and only if
${\mathcal C} \to [2]$
is an exponentiable fibration if and only if
![]() $\alpha $
is an equivalence. By [Reference Lurie27, Proposition 2.4.2.8.] the locally cartesian fibration
$\alpha $
is an equivalence. By [Reference Lurie27, Proposition 2.4.2.8.] the locally cartesian fibration
![]() ${\mathcal P}^{{\mathcal A}}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration if and only if
${\mathcal P}^{{\mathcal A}}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration if and only if
![]() $\alpha $
is an equivalence.
$\alpha $
is an equivalence.
Corollary 3.23. Every functor
![]() ${\mathcal D} \to [1]$
is an exponentiable fibration. So the
${\mathcal D} \to [1]$
is an exponentiable fibration. So the
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \mathrm {Cat}_{/[1]}$
is cartesian closed.
$\infty \mathrm {Cat}_{/[1]}$
is cartesian closed.
Proof. We apply Proposition 3.22 and use that every locally cartesian fibration over
![]() $[1] $
is a cartesian fibration.
$[1] $
is a cartesian fibration.
Corollary 3.24. Let
![]() $\phi :{\mathcal A} \to {\mathcal B}$
be an inclusion of
$\phi :{\mathcal A} \to {\mathcal B}$
be an inclusion of
![]() $\infty $
-categories such that for every morphisms
$\infty $
-categories such that for every morphisms
![]() ${\mathrm X} \to {\mathrm Y}, {\mathrm Y} \to {\mathrm Z}$
in
${\mathrm X} \to {\mathrm Y}, {\mathrm Y} \to {\mathrm Z}$
in
![]() ${\mathcal B}$
we have that
${\mathcal B}$
we have that
![]() ${\mathrm Y} \in {\mathcal A}$
if
${\mathrm Y} \in {\mathcal A}$
if
![]() ${\mathrm X},{\mathrm Z} \in {\mathcal A}.$
Then
${\mathrm X},{\mathrm Z} \in {\mathcal A}.$
Then
![]() $\phi $
is an exponentiable fibration.
$\phi $
is an exponentiable fibration.
Proof. By Proposition 3.22 the functor
![]() $\phi $
is an exponentiable fibration if and only if the locally cartesian fibration
$\phi $
is an exponentiable fibration if and only if the locally cartesian fibration
![]() ${\mathcal P}^{{\mathcal B}}({\mathcal A}) \to {\mathcal B}$
is a cartesian fibration. By [Reference Lurie27, Proposition 2.4.2.8.] the locally cartesian fibration
${\mathcal P}^{{\mathcal B}}({\mathcal A}) \to {\mathcal B}$
is a cartesian fibration. By [Reference Lurie27, Proposition 2.4.2.8.] the locally cartesian fibration
![]() ${\mathcal P}^{{\mathcal B}}({\mathcal A}) \to {\mathcal B}$
is a cartesian fibration if and only if for every morphisms
${\mathcal P}^{{\mathcal B}}({\mathcal A}) \to {\mathcal B}$
is a cartesian fibration if and only if for every morphisms
![]() $\alpha : {\mathrm X} \to {\mathrm Y}, \beta : {\mathrm Y} \to {\mathrm Z} $
the induced natural transformation
$\alpha : {\mathrm X} \to {\mathrm Y}, \beta : {\mathrm Y} \to {\mathrm Z} $
the induced natural transformation
![]() $\theta : \alpha ^* \circ \beta ^* \to (\beta \circ \alpha )^*: {\mathcal P}({\mathcal A}_{\mathrm Z}) \to {\mathcal P}({\mathcal A}_{\mathrm X})$
is an equivalence. If
$\theta : \alpha ^* \circ \beta ^* \to (\beta \circ \alpha )^*: {\mathcal P}({\mathcal A}_{\mathrm Z}) \to {\mathcal P}({\mathcal A}_{\mathrm X})$
is an equivalence. If
![]() ${\mathrm X}$
does not belong to
${\mathrm X}$
does not belong to
![]() ${\mathcal A}$
, the fiber of
${\mathcal A}$
, the fiber of
![]() $\phi $
over
$\phi $
over
![]() ${\mathrm X}$
is empty so that
${\mathrm X}$
is empty so that
![]() ${\mathcal P}({\mathcal A}_{\mathrm X})$
is contractible. So there is nothing to show and we assume that
${\mathcal P}({\mathcal A}_{\mathrm X})$
is contractible. So there is nothing to show and we assume that
![]() ${\mathrm X} $
belongs to
${\mathrm X} $
belongs to
![]() ${\mathcal A}$
so that
${\mathcal A}$
so that
![]() ${\mathcal P}({\mathcal A}_{\mathrm X})\simeq {\mathcal S}.$
If
${\mathcal P}({\mathcal A}_{\mathrm X})\simeq {\mathcal S}.$
If
![]() ${\mathrm Z}$
does not belong to
${\mathrm Z}$
does not belong to
![]() ${\mathcal A}$
, the fiber of
${\mathcal A}$
, the fiber of
![]() $\phi $
over
$\phi $
over
![]() ${\mathrm Z}$
is empty so that
${\mathrm Z}$
is empty so that
![]() ${\mathcal P}({\mathcal A}_{\mathrm Z})$
is contractible. In this case there is nothing to show, too, because
${\mathcal P}({\mathcal A}_{\mathrm Z})$
is contractible. In this case there is nothing to show, too, because
![]() $\alpha ^*,\beta ^*$
preserve small colimits and so the initial object so that
$\alpha ^*,\beta ^*$
preserve small colimits and so the initial object so that
![]() $\theta $
is an endomorphism of the initial object in
$\theta $
is an endomorphism of the initial object in
![]() ${\mathcal P}({\mathcal A}_{\mathrm X})\simeq {\mathcal S}$
and so an equivalence. So we can assume that
${\mathcal P}({\mathcal A}_{\mathrm X})\simeq {\mathcal S}$
and so an equivalence. So we can assume that
![]() ${\mathrm Z}$
belongs to
${\mathrm Z}$
belongs to
![]() ${\mathcal A}$
. By assumption we find that
${\mathcal A}$
. By assumption we find that
![]() ${\mathrm Y}$
belongs to
${\mathrm Y}$
belongs to
![]() ${\mathcal A}$
. In this case the small colimits preserving functors
${\mathcal A}$
. In this case the small colimits preserving functors
![]() $\alpha ^*,\beta ^*:{\mathcal S} \to {\mathcal S}$
are the identity on objects and so preserve the final object. This implies that
$\alpha ^*,\beta ^*:{\mathcal S} \to {\mathcal S}$
are the identity on objects and so preserve the final object. This implies that
![]() $\alpha ^*,\beta ^*:{\mathcal S} \to {\mathcal S}$
are equivalences and
$\alpha ^*,\beta ^*:{\mathcal S} \to {\mathcal S}$
are equivalences and
![]() $\theta $
is an equivalence since the component of
$\theta $
is an equivalence since the component of
![]() $\theta $
at the final space is an endomorphism of the final space and so an equivalence.
$\theta $
at the final space is an endomorphism of the final space and so an equivalence.
Definition 3.25. A map
![]() $[{n}]\to [{m}]$
of
$[{n}]\to [{m}]$
of
![]() $\Delta $
is inert if it is of the form
$\Delta $
is inert if it is of the form
![]() $[{n}] \cong \{{i}+0,\ldots,{i}+{n} \} \subset [{m}]$
for some
$[{n}] \cong \{{i}+0,\ldots,{i}+{n} \} \subset [{m}]$
for some
![]() ${i} \geq 0$
.
${i} \geq 0$
.
Corollary 3.26. Every inert map
![]() $[{n}] \to [{m}]$
of
$[{n}] \to [{m}]$
of
![]() $\Delta $
(viewed as a functor of
$\Delta $
(viewed as a functor of
![]() $\infty $
-categories) is an exponentiable fibration.
$\infty $
-categories) is an exponentiable fibration.
Proof. The result follows from Corollary 3.24 since for every
![]() $ {i} \geq 0$
the ordered subset
$ {i} \geq 0$
the ordered subset
![]() $[{n}] \cong \{{i}+0,\ldots,{i}+{n} \} \subset [{m}]$
is an interval.
$[{n}] \cong \{{i}+0,\ldots,{i}+{n} \} \subset [{m}]$
is an interval.
Corollary 3.27. A locally cartesian fibration of small
![]() $\infty $
-categories is a cartesian fibration if and only if it is an exponentiable fibration.
$\infty $
-categories is a cartesian fibration if and only if it is an exponentiable fibration.
Proof. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a locally cartesian fibration of small
${\mathcal C} \to {\mathcal A}$
be a locally cartesian fibration of small
![]() $\infty $
-categories. By Lemma 3.18 the functor
$\infty $
-categories. By Lemma 3.18 the functor
![]() ${\mathcal C} \to {\mathcal A}$
is a cartesian fibration if and only if the functor
${\mathcal C} \to {\mathcal A}$
is a cartesian fibration if and only if the functor
![]() $ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration. By Proposition 3.22 the functor
$ {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration. By Proposition 3.22 the functor
![]() ${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration if and only if the functor
${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration if and only if the functor
![]() ${\mathcal P}^{{\mathcal A}}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration.
${\mathcal P}^{{\mathcal A}}({\mathcal C}) \to {\mathcal A}$
is a cartesian fibration.
Notation 3.28. Let
be the full subcategory of locally cartesian fibrations.
Notation 3.29. Let
be the subcategory of locally cartesian fibrations whose target is small and whose fibers are presentable and commutative squares

such that for every
![]() ${\mathrm A} \in {\mathcal A}$
the induced functor
${\mathrm A} \in {\mathcal A}$
the induced functor
![]() ${\mathcal C}_{\mathrm A} \to {\mathcal D}_{\psi ({\mathrm A})}$
on the fiber over
${\mathcal C}_{\mathrm A} \to {\mathcal D}_{\psi ({\mathrm A})}$
on the fiber over
![]() ${\mathrm A}$
preserves small colimits.
${\mathrm A}$
preserves small colimits.
For the next corollary we use the notion of adjunction of
![]() $(\infty ,2)$
-categories, that is,
$(\infty ,2)$
-categories, that is,
![]() $\infty $
-categories enriched in
$\infty $
-categories enriched in
![]() $\infty \mathrm {Cat}.$
This is an adjunction in the
$\infty \mathrm {Cat}.$
This is an adjunction in the
![]() $(\infty ,2)$
-category of small
$(\infty ,2)$
-category of small
![]() $(\infty ,2)$
-categories, and a special case of the notion of enriched adjunction (see [Reference Heine20, Definition 2.66.] or [Reference Heine16, 6.2.6] for details).
$(\infty ,2)$
-categories, and a special case of the notion of enriched adjunction (see [Reference Heine20, Definition 2.66.] or [Reference Heine16, 6.2.6] for details).
Corollary 3.30. The inclusion of
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories
admits a left adjoint that sends a functor
![]() ${\mathcal C} \to {\mathcal A}$
between small
${\mathcal C} \to {\mathcal A}$
between small
![]() $\infty $
-categories to
$\infty $
-categories to
![]() ${\mathcal P}^{\mathcal A}({\mathcal C})\to {\mathcal A}.$
${\mathcal P}^{\mathcal A}({\mathcal C})\to {\mathcal A}.$
Proof. By Proposition 3.16 (2) for every locally cartesian fibration
![]() ${\mathcal D} \to {\mathcal B}$
whose fibers admit small colimits, and functor
${\mathcal D} \to {\mathcal B}$
whose fibers admit small colimits, and functor
![]() ${\mathcal C} \to {\mathcal A}$
restriction along the embedding
${\mathcal C} \to {\mathcal A}$
restriction along the embedding
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
induces an equivalence
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
induces an equivalence
This implies the result by [Reference Heine20, Remark 2.75.] since
![]() $\Theta ({\mathcal C}, {\mathcal D})$
is the morphism
$\Theta ({\mathcal C}, {\mathcal D})$
is the morphism
![]() $\infty $
-category of the
$\infty $
-category of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathrm {Fun}([1],\infty \widehat {\mathrm {Cat}})$
and
$\mathrm {Fun}([1],\infty \widehat {\mathrm {Cat}})$
and
![]() $\Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L}$
is the morphism
$\Theta ({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D})^{\mathrm L}$
is the morphism
![]() $\infty $
-category of the
$\infty $
-category of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathrm {LoCART}^{\mathrm L} $
.
$\mathrm {LoCART}^{\mathrm L} $
.
Corollary 3.31. Let
![]() ${\mathcal A}$
be a small
${\mathcal A}$
be a small
![]() $\infty $
-category. The inclusion of
$\infty $
-category. The inclusion of
![]() $(\infty ,2)$
-categories
$(\infty ,2)$
-categories
admits a left adjoint that sends a functor
![]() ${\mathcal C} \to {\mathcal A}$
, where
${\mathcal C} \to {\mathcal A}$
, where
![]() ${\mathcal C}$
is small, to
${\mathcal C}$
is small, to
![]() ${\mathcal P}^{\mathcal A}({\mathcal C})\to {\mathcal A}.$
${\mathcal P}^{\mathcal A}({\mathcal C})\to {\mathcal A}.$
Proof. By Proposition 3.16 (2) for every locally cartesian fibration
![]() ${\mathcal D} \to {\mathcal A} $
whose fibers admit small colimits, and functor
${\mathcal D} \to {\mathcal A} $
whose fibers admit small colimits, and functor
![]() ${\mathcal C} \to {\mathcal A}$
restriction along the embedding
${\mathcal C} \to {\mathcal A}$
restriction along the embedding
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
induces an equivalence
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal C})$
induces an equivalence
The latter equivalence is over
![]() $\mathrm {Fun}({\mathcal A},{\mathcal A})$
and induces on the fiber over the identity of
$\mathrm {Fun}({\mathcal A},{\mathcal A})$
and induces on the fiber over the identity of
![]() ${\mathcal A}$
the canonical functor
${\mathcal A}$
the canonical functor
which therefore also is an equivalence.
This implies the result by [Reference Heine20, Remark 2.75.] since
![]() $\mathrm {Fun}_{\mathcal A}({\mathcal C}, {\mathcal D})$
is the morphism
$\mathrm {Fun}_{\mathcal A}({\mathcal C}, {\mathcal D})$
is the morphism
![]() $\infty $
-category of the
$\infty $
-category of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\infty \widehat {\mathrm {Cat}}_{/{\mathcal A}}$
and
$\infty \widehat {\mathrm {Cat}}_{/{\mathcal A}}$
and
![]() $\mathrm {Fun}_{\mathcal A}^{\mathrm L}({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D}) $
is the morphism
$\mathrm {Fun}_{\mathcal A}^{\mathrm L}({\mathcal P}^{\mathcal A}({\mathcal C}), {\mathcal D}) $
is the morphism
![]() $\infty $
-category of the
$\infty $
-category of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $ \mathrm {LoCART}^{\mathrm L}_{\mathcal A} $
.
$ \mathrm {LoCART}^{\mathrm L}_{\mathcal A} $
.
In the following we compare Definition 3.5 to another one (Corollary 3.37).
Notation 3.32. Let
![]() ${\mathcal L} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
be the full subcategory of left fibrations.
${\mathcal L} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
be the full subcategory of left fibrations.
Remark 3.12. The opposite
![]() $\infty $
-category involution
$\infty $
-category involution
![]() $(-)^{\mathrm {op}}: \infty \mathrm {Cat} \simeq \infty \mathrm {Cat}$
induces an involution
$(-)^{\mathrm {op}}: \infty \mathrm {Cat} \simeq \infty \mathrm {Cat}$
induces an involution
![]() $ \mathrm {Fun}([1],\infty \mathrm {Cat}) \simeq \mathrm {Fun}([1],\infty \mathrm {Cat}), $
which restricts to an equivalence
$ \mathrm {Fun}([1],\infty \mathrm {Cat}) \simeq \mathrm {Fun}([1],\infty \mathrm {Cat}), $
which restricts to an equivalence
![]() ${\mathcal L} \simeq {\mathcal R}$
. There is a commutative square
${\mathcal L} \simeq {\mathcal R}$
. There is a commutative square

where the vertical functors evaluate at the target.
Proposition 3.33. There is a canonical equivalence
over
![]() $\infty \mathrm {Cat},$
where
$\infty \mathrm {Cat},$
where
![]() ${\mathcal L} \to \infty \mathrm {Cat}$
is evaluation at the target.
${\mathcal L} \to \infty \mathrm {Cat}$
is evaluation at the target.
Proof. Let
![]() ${\mathcal C} \to \infty \mathrm {Cat}$
be a functor classifying a cocartesian fibration
${\mathcal C} \to \infty \mathrm {Cat}$
be a functor classifying a cocartesian fibration
![]() ${\mathcal B} \to {\mathcal C}.$
We prove that for any
${\mathcal B} \to {\mathcal C}.$
We prove that for any
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
functors
${\mathcal C}$
functors
![]() ${\mathcal C} \to {\mathcal L}$
over
${\mathcal C} \to {\mathcal L}$
over
![]() $\infty \mathrm {Cat}$
naturally correspond to functors
$\infty \mathrm {Cat}$
naturally correspond to functors
![]() ${\mathcal C} \to \mathrm {Fun}^{\infty \mathrm {Cat}}({\mathcal U},{\mathcal S} \times \infty \mathrm {Cat})$
over
${\mathcal C} \to \mathrm {Fun}^{\infty \mathrm {Cat}}({\mathcal U},{\mathcal S} \times \infty \mathrm {Cat})$
over
![]() $\infty \mathrm {Cat}$
. Functors
$\infty \mathrm {Cat}$
. Functors
![]() ${\mathcal C} \to \mathrm {Fun}^{\infty \mathrm {Cat}}({\mathcal U},{\mathcal S} \times {\mathcal C})$
over
${\mathcal C} \to \mathrm {Fun}^{\infty \mathrm {Cat}}({\mathcal U},{\mathcal S} \times {\mathcal C})$
over
![]() $\infty \mathrm {Cat}$
correspond to sections of the functor
$\infty \mathrm {Cat}$
correspond to sections of the functor
![]() $\mathrm {Fun}^{{\mathcal C}}({\mathcal B},{\mathcal S} \times {\mathcal C}) \to {\mathcal C}$
. Such sections correspond to functors
$\mathrm {Fun}^{{\mathcal C}}({\mathcal B},{\mathcal S} \times {\mathcal C}) \to {\mathcal C}$
. Such sections correspond to functors
![]() ${\mathcal B} \to {\mathcal S} \times {\mathcal C}$
over
${\mathcal B} \to {\mathcal S} \times {\mathcal C}$
over
![]() ${\mathcal C}$
and so to functors
${\mathcal C}$
and so to functors
![]() ${\mathcal B} \to {\mathcal S}.$
A functor
${\mathcal B} \to {\mathcal S}.$
A functor
![]() ${\mathcal B} \to {\mathcal L} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
over
${\mathcal B} \to {\mathcal L} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
over
![]() $\infty \mathrm {Cat}$
is classified by a map of cocartesian fibrations
$\infty \mathrm {Cat}$
is classified by a map of cocartesian fibrations
![]() ${\mathcal A} \to {\mathcal B}$
over
${\mathcal A} \to {\mathcal B}$
over
![]() ${\mathcal C}$
that is fiberwise a left fibration and so a left fibration by [Reference Lurie27, Proposition 2.4.2.4., Proposition 2.4.2.11.]. Such a functor corresponds to a left fibration
${\mathcal C}$
that is fiberwise a left fibration and so a left fibration by [Reference Lurie27, Proposition 2.4.2.4., Proposition 2.4.2.11.]. Such a functor corresponds to a left fibration
![]() ${\mathcal A} \to {\mathcal B}$
classifying a functor
${\mathcal A} \to {\mathcal B}$
classifying a functor
![]() ${\mathcal B} \to {\mathcal S}.$
${\mathcal B} \to {\mathcal S}.$
Corollary 3.34. The cartesian fibration
![]() $\rho : {\mathcal L} \to \infty \mathrm {Cat}$
classifies the functor
$\rho : {\mathcal L} \to \infty \mathrm {Cat}$
classifies the functor
Proof. By Corollary 3.36 there is a canonical equivalence
over
![]() $\infty \mathrm {Cat}.$
By [Reference Gepner, Haugseng and Nikolaus12, Proposition 7.3.] the functor
$\infty \mathrm {Cat}.$
By [Reference Gepner, Haugseng and Nikolaus12, Proposition 7.3.] the functor
![]() $\mathrm {Fun}^{\infty \mathrm {Cat}}({\mathcal U},{\mathcal S} \times \infty \mathrm {Cat}) \to \infty \mathrm {Cat} $
classifies the functor
$\mathrm {Fun}^{\infty \mathrm {Cat}}({\mathcal U},{\mathcal S} \times \infty \mathrm {Cat}) \to \infty \mathrm {Cat} $
classifies the functor
Notation 3.35. Let
![]() ${\mathcal C} \to {\mathcal D}$
be a cocartesian fibration classifying a functor
${\mathcal C} \to {\mathcal D}$
be a cocartesian fibration classifying a functor
![]() $\alpha : {\mathcal D} \to \infty \mathrm {Cat}.$
We write
$\alpha : {\mathcal D} \to \infty \mathrm {Cat}.$
We write
![]() ${\mathcal C}^{\mathrm {rev}} \to {\mathcal D}$
for the cocartesian fibration classifying the composition
${\mathcal C}^{\mathrm {rev}} \to {\mathcal D}$
for the cocartesian fibration classifying the composition
Corollary 3.36. There is a canonical equivalence
over
![]() $\infty \mathrm {Cat},$
where
$\infty \mathrm {Cat},$
where
![]() ${\mathcal R} \to \infty \mathrm {Cat}$
is evaluation at the target.
${\mathcal R} \to \infty \mathrm {Cat}$
is evaluation at the target.
Proof. By Corollary 3.33 there is a canonical equivalence
over
![]() $\infty \mathrm {Cat}.$
Pulling back the latter equivalence along the equivalence
$\infty \mathrm {Cat}.$
Pulling back the latter equivalence along the equivalence
![]() $(-)^{\mathrm {op}}: \infty \mathrm {Cat} \simeq \infty \mathrm {Cat}$
we obtain the desired equivalence
$(-)^{\mathrm {op}}: \infty \mathrm {Cat} \simeq \infty \mathrm {Cat}$
we obtain the desired equivalence
over
![]() $\infty \mathrm {Cat}.$
$\infty \mathrm {Cat}.$
Corollary 3.37. Let
![]() ${\mathcal C} \to {\mathcal A}$
be a cocartesian fibration. There is a canonical equivalence
${\mathcal C} \to {\mathcal A}$
be a cocartesian fibration. There is a canonical equivalence
over
![]() ${\mathcal A}.$
${\mathcal A}.$
Proof. The cocartesian fibration
![]() ${\mathcal D} \to {\mathcal C}$
classifies the functor
${\mathcal D} \to {\mathcal C}$
classifies the functor
![]() $\psi : {\mathcal C} \to \infty \mathrm {Cat}$
. By Corollary 3.36 there is a canonical equivalence
$\psi : {\mathcal C} \to \infty \mathrm {Cat}$
. By Corollary 3.36 there is a canonical equivalence
over
![]() $\infty \mathrm {Cat}.$
The pullback of this equivalence along
$\infty \mathrm {Cat}.$
The pullback of this equivalence along
![]() $\psi $
is the desired equivalence
$\psi $
is the desired equivalence
over
![]() ${\mathcal A}.$
${\mathcal A}.$
Corollary 3.38. Let
![]() ${\mathcal D} \to {\mathcal C}$
be a cocartesian fibration classifying a functor
${\mathcal D} \to {\mathcal C}$
be a cocartesian fibration classifying a functor
![]() $\psi : {\mathcal C} \to \infty \mathrm {Cat}$
.
$\psi : {\mathcal C} \to \infty \mathrm {Cat}$
.
The cartesian fibration
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
classifies the composition
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
classifies the composition
Proof. By definition the functor
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is the pullback of
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is the pullback of
![]() $\rho : {\mathcal R} \to \infty \mathrm {Cat}$
along
$\rho : {\mathcal R} \to \infty \mathrm {Cat}$
along
![]() $\psi : {\mathcal C} \to \infty \mathrm {Cat} $
and so a cartesian fibration, which by Corollary 3.34 classifies the composition
$\psi : {\mathcal C} \to \infty \mathrm {Cat} $
and so a cartesian fibration, which by Corollary 3.34 classifies the composition
Remark 3.13. Evaluation at the target
![]() ${\mathcal R} \to \infty \mathrm {Cat}$
is a cocartesian and cartesian fibration by Lemma 3.4. So for every cocartesian fibration
${\mathcal R} \to \infty \mathrm {Cat}$
is a cocartesian and cartesian fibration by Lemma 3.4. So for every cocartesian fibration
![]() ${\mathcal D} \to {\mathcal C}$
whose fibers are small, the functor
${\mathcal D} \to {\mathcal C}$
whose fibers are small, the functor
![]() ${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is a cocartesian and cartesian fibration.
${\mathcal P}^{\mathcal C}({\mathcal D}) \to {\mathcal C} $
is a cocartesian and cartesian fibration.
Remark 3.14. In [Reference Barwick, Dotto, Glasman, Nardin and Shah6, Example 9.9.] the authors give a different construction of a parametrized
![]() $\infty $
-category of presheaves associated to a cocartesian fibration. Corollary 3.37 implies that our construction of parametrized
$\infty $
-category of presheaves associated to a cocartesian fibration. Corollary 3.37 implies that our construction of parametrized
![]() $\infty $
-category of presheaves associated to a functor
$\infty $
-category of presheaves associated to a functor
![]() $\phi : {\mathcal C} \to {\mathcal A}$
agrees with the one of [Reference Barwick, Dotto, Glasman, Nardin and Shah6] in the case that
$\phi : {\mathcal C} \to {\mathcal A}$
agrees with the one of [Reference Barwick, Dotto, Glasman, Nardin and Shah6] in the case that
![]() $\phi $
is a cocartesian fibration.
$\phi $
is a cocartesian fibration.
4 A local-global principle
Now we are ready to prove the main theorem.
Theorem 4.1. Let
![]() ${\mathcal A}$
be an
${\mathcal A}$
be an
![]() $\infty $
-category. The canonical commutative square of
$\infty $
-category. The canonical commutative square of
![]() $\infty $
-categories
$\infty $
-categories

is a pullback square.
Proof. Let
![]() ${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
be functors of small
${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
be functors of small
![]() $\infty $
-categories. Square (4.1) induces on morphism
$\infty $
-categories. Square (4.1) induces on morphism
![]() $\infty $
-categories the commutative square
$\infty $
-categories the commutative square

which identifies with the commutative square

where we use Remark 3.10. The bottom and top functors of square (4.2) are fully faithful. Therefore the functor from the left upper
![]() $\infty $
-category of square (4.2) to the pullback is fully faithful, too. Consequently, the square (4.2) is a pullback square if the latter functor is essentially surjective. This means that every functor
$\infty $
-category of square (4.2) to the pullback is fully faithful, too. Consequently, the square (4.2) is a pullback square if the latter functor is essentially surjective. This means that every functor
![]() ${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal D})$
over
${\mathcal C} \to {\mathcal P}^{\mathcal A}({\mathcal D})$
over
![]() ${\mathcal A}$
whose pullback to
${\mathcal A}$
whose pullback to
![]() $\iota ({\mathcal A})$
lands in
$\iota ({\mathcal A})$
lands in
![]() ${\mathcal D}$
, already lands in
${\mathcal D}$
, already lands in
![]() ${\mathcal D}, $
which is clear.
${\mathcal D}, $
which is clear.
Consequently, the functor
is fully faithful. So it remains to see that
![]() $\theta $
is essentially surjective.
$\theta $
is essentially surjective.
Let
![]() ${\mathcal B} \to \iota ({\mathcal A})$
be a functor,
${\mathcal B} \to \iota ({\mathcal A})$
be a functor,
![]() $ {\mathcal D} \to {\mathcal A}$
a locally cartesian fibration whose fibers admit small colimits and whose fiber transports preserve small colimits, and
$ {\mathcal D} \to {\mathcal A}$
a locally cartesian fibration whose fibers admit small colimits and whose fiber transports preserve small colimits, and
![]() $\alpha : {\mathcal P}^{\iota ({\mathcal A})}({\mathcal B}) \simeq \iota ({\mathcal A}) \times _{\mathcal A} {\mathcal D} $
an equivalence over
$\alpha : {\mathcal P}^{\iota ({\mathcal A})}({\mathcal B}) \simeq \iota ({\mathcal A}) \times _{\mathcal A} {\mathcal D} $
an equivalence over
![]() $\iota ({\mathcal A})$
. Let
$\iota ({\mathcal A})$
. Let
![]() ${\mathcal C} \subset {\mathcal D}$
be the essential image of the Yoneda-embedding
${\mathcal C} \subset {\mathcal D}$
be the essential image of the Yoneda-embedding
![]() ${\mathcal B} \subset {\mathcal P}^{\iota ({\mathcal A})}({\mathcal B}) \simeq \iota ({\mathcal A}) \times _{\mathcal A} {\mathcal D} \subset {\mathcal D}$
. Then there is a canonical equivalence
${\mathcal B} \subset {\mathcal P}^{\iota ({\mathcal A})}({\mathcal B}) \simeq \iota ({\mathcal A}) \times _{\mathcal A} {\mathcal D} \subset {\mathcal D}$
. Then there is a canonical equivalence
![]() $\iota ({\mathcal A}) \times _{\mathcal A}{\mathcal C} \simeq {\mathcal B}$
over
$\iota ({\mathcal A}) \times _{\mathcal A}{\mathcal C} \simeq {\mathcal B}$
over
![]() $\iota ({\mathcal A})$
and the embedding
$\iota ({\mathcal A})$
and the embedding
![]() ${\mathcal C} \subset {\mathcal D}$
over
${\mathcal C} \subset {\mathcal D}$
over
![]() ${\mathcal A}$
extends to a canonical functor
${\mathcal A}$
extends to a canonical functor
![]() $\beta : {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal D}$
over
$\beta : {\mathcal P}^{\mathcal A}({\mathcal C}) \to {\mathcal D}$
over
![]() ${\mathcal A},$
whose pullback to
${\mathcal A},$
whose pullback to
![]() $\iota ({\mathcal A})$
is the equivalence
$\iota ({\mathcal A})$
is the equivalence
![]() $\alpha : \iota ({\mathcal A}) \times _{\mathcal A}{\mathcal P}^{\mathcal A}({\mathcal C}) \simeq {\mathcal P}^{\iota ({\mathcal A})}({\mathcal B}) \simeq \iota ({\mathcal A}) \times _{\mathcal A}{\mathcal D}.$
Therefore it is enough to see that
$\alpha : \iota ({\mathcal A}) \times _{\mathcal A}{\mathcal P}^{\mathcal A}({\mathcal C}) \simeq {\mathcal P}^{\iota ({\mathcal A})}({\mathcal B}) \simeq \iota ({\mathcal A}) \times _{\mathcal A}{\mathcal D}.$
Therefore it is enough to see that
![]() $\beta $
is an equivalence. For this by Remark 3.10 we can reduce to the case that
$\beta $
is an equivalence. For this by Remark 3.10 we can reduce to the case that
![]() ${\mathcal A}=[1]$
because a functor over
${\mathcal A}=[1]$
because a functor over
![]() ${\mathcal A}$
is an equivalence if all pullbacks along functors
${\mathcal A}$
is an equivalence if all pullbacks along functors
![]() $[1] \to {\mathcal A}$
are equivalences. Since
$[1] \to {\mathcal A}$
are equivalences. Since
![]() $\beta $
is essentially surjective, we need to check that for any
$\beta $
is essentially surjective, we need to check that for any
![]() ${\mathrm X} \in {\mathcal P}({\mathcal C}_0), {\mathrm Y} \in {\mathcal P}({\mathcal C}_1)$
the canonical map
${\mathrm X} \in {\mathcal P}({\mathcal C}_0), {\mathrm Y} \in {\mathcal P}({\mathcal C}_1)$
the canonical map
![]() $\theta _{{\mathrm X},{\mathrm Y}}: {\mathcal P}^{[1]}({\mathcal C})({\mathrm X}, {\mathrm Y}) \to {\mathcal D}(\beta ({\mathrm X}),\beta ({\mathrm Y}))$
induced by
$\theta _{{\mathrm X},{\mathrm Y}}: {\mathcal P}^{[1]}({\mathcal C})({\mathrm X}, {\mathrm Y}) \to {\mathcal D}(\beta ({\mathrm X}),\beta ({\mathrm Y}))$
induced by
![]() $\beta $
is an equivalence. Let
$\beta $
is an equivalence. Let
![]() ${\mathrm G}: {\mathcal P}({\mathcal C}_1) \to {\mathcal P}({\mathcal C}_0)$
be the left adjoint functor classified by the cartesian fibration
${\mathrm G}: {\mathcal P}({\mathcal C}_1) \to {\mathcal P}({\mathcal C}_0)$
be the left adjoint functor classified by the cartesian fibration
![]() ${\mathcal P}^{[1]}({\mathcal C}) \to [1]$
and
${\mathcal P}^{[1]}({\mathcal C}) \to [1]$
and
![]() ${\mathrm G}': {\mathcal D}_1 \to {\mathcal D}_0$
the left adjoint functor classified by the cartesian fibration
${\mathrm G}': {\mathcal D}_1 \to {\mathcal D}_0$
the left adjoint functor classified by the cartesian fibration
![]() ${\mathcal D} \to [1]$
. The unique cartesian lift
${\mathcal D} \to [1]$
. The unique cartesian lift
![]() ${\mathrm G}({\mathrm Y}) \to {\mathrm Y}$
, where
${\mathrm G}({\mathrm Y}) \to {\mathrm Y}$
, where
![]() ${\mathrm G}({\mathrm Y}) \in {\mathcal P}({\mathcal C}_0)$
, is sent to a morphism
${\mathrm G}({\mathrm Y}) \in {\mathcal P}({\mathcal C}_0)$
, is sent to a morphism
![]() $\beta ({\mathrm G}({\mathrm Y})) \to \beta ({\mathrm Y})$
that factors as
$\beta ({\mathrm G}({\mathrm Y})) \to \beta ({\mathrm Y})$
that factors as
![]() $\beta ({\mathrm G}({\mathrm Y})) \xrightarrow {\rho _{\mathrm Y}} {\mathrm G}'(\beta ({\mathrm Y})) \to \beta ({\mathrm Y})$
, where
$\beta ({\mathrm G}({\mathrm Y})) \xrightarrow {\rho _{\mathrm Y}} {\mathrm G}'(\beta ({\mathrm Y})) \to \beta ({\mathrm Y})$
, where
![]() ${\mathrm G}'(\beta ({\mathrm Y})) \in {\mathcal D}_0$
. The map
${\mathrm G}'(\beta ({\mathrm Y})) \in {\mathcal D}_0$
. The map
![]() $\theta _{{\mathrm X},{\mathrm Y}}$
identifies with the map
$\theta _{{\mathrm X},{\mathrm Y}}$
identifies with the map
Since the first map is an equivalence, it is enough to see that
![]() $\rho _{\mathrm Y}$
is an equivalence for every
$\rho _{\mathrm Y}$
is an equivalence for every
![]() ${\mathrm Y} \in {\mathcal P}({\mathcal C}_1).$
Since
${\mathrm Y} \in {\mathcal P}({\mathcal C}_1).$
Since
![]() $\beta _{\mathcal C}$
is fully faithful,
$\beta _{\mathcal C}$
is fully faithful,
![]() $\theta _{{\mathrm X},{\mathrm Y}}$
is an equivalence if
$\theta _{{\mathrm X},{\mathrm Y}}$
is an equivalence if
![]() ${\mathrm X} \in {\mathcal C}_0, {\mathrm Y} \in {\mathcal C}_1$
. Because
${\mathrm X} \in {\mathcal C}_0, {\mathrm Y} \in {\mathcal C}_1$
. Because
![]() ${\mathcal P}({\mathcal C}_0)$
is generated by
${\mathcal P}({\mathcal C}_0)$
is generated by
![]() ${\mathcal C}_0$
under small colimits,
${\mathcal C}_0$
under small colimits,
![]() $\theta _{{\mathrm X},{\mathrm Y}}$
is an equivalence for all
$\theta _{{\mathrm X},{\mathrm Y}}$
is an equivalence for all
![]() ${\mathrm X} \in {\mathcal P}({\mathcal C}_0), {\mathrm Y} \in {\mathcal C}_1$
. Thus
${\mathrm X} \in {\mathcal P}({\mathcal C}_0), {\mathrm Y} \in {\mathcal C}_1$
. Thus
![]() $\rho _{\mathrm Y}$
is an equivalence for every
$\rho _{\mathrm Y}$
is an equivalence for every
![]() ${\mathrm Y} \in {\mathcal C}_1$
. Therefore
${\mathrm Y} \in {\mathcal C}_1$
. Therefore
![]() $\rho _{\mathrm Y}$
is also an equivalence for every
$\rho _{\mathrm Y}$
is also an equivalence for every
![]() ${\mathrm Y} \in {\mathcal P}({\mathcal C}_1)$
because
${\mathrm Y} \in {\mathcal P}({\mathcal C}_1)$
because
![]() ${\mathcal P}({\mathcal C}_1)$
is generated by
${\mathcal P}({\mathcal C}_1)$
is generated by
![]() ${\mathcal C}_1$
under small colimits and the functors
${\mathcal C}_1$
under small colimits and the functors
![]() ${\mathrm G}, {\mathrm G}'$
preserve small colimits and
${\mathrm G}, {\mathrm G}'$
preserve small colimits and
![]() $\rho _{\mathrm Y}$
is natural in
$\rho _{\mathrm Y}$
is natural in
![]() ${\mathrm Y}$
.
${\mathrm Y}$
.
Corollary 4.1. The canonical commutative square

of cartesian fibrations over
![]() $\infty \mathrm {Cat}$
is a pullback square.
$\infty \mathrm {Cat}$
is a pullback square.
Proof. Square (4.3) induces on the fiber over every small
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal A}$
the pullback square (4.1) of Theorem 4.1, and therefore itself is a pullback square.
${\mathcal A}$
the pullback square (4.1) of Theorem 4.1, and therefore itself is a pullback square.
Remark 4.2. We expect that the analogue of Theorem 4.1 also holds for
![]() $(\infty ,n)$
-categories for
$(\infty ,n)$
-categories for
![]() $ 1 \leq n \leq \infty $
for appropriate notions of locally cartesian fibrations. Here the role of the parametrized category of presheaves is taken by a parametrized version of presheaves of higher categories that can be conveniently described via the language of enriched presheaves [Reference Heine18], [Reference Hinich25]. This will be topic of future work.
$ 1 \leq n \leq \infty $
for appropriate notions of locally cartesian fibrations. Here the role of the parametrized category of presheaves is taken by a parametrized version of presheaves of higher categories that can be conveniently described via the language of enriched presheaves [Reference Heine18], [Reference Hinich25]. This will be topic of future work.
Notation 4.2. Let
-
○
 $\mathrm {EXP}\subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
be the full subcategory of exponentiable fibrations,
$\mathrm {EXP}\subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
be the full subcategory of exponentiable fibrations, -
○
 $\mathrm {CART} \subset \mathrm {Fun}([1],\infty \mathrm {Cat}) $
be the full subcategory of cartesian fibrations,
$\mathrm {CART} \subset \mathrm {Fun}([1],\infty \mathrm {Cat}) $
be the full subcategory of cartesian fibrations, -
○
 ${\mathrm {CART}}^{\mathrm L} \subset \mathrm {LoCART}^{\mathrm L} $
be the full subcategory of cartesian fibrations.
${\mathrm {CART}}^{\mathrm L} \subset \mathrm {LoCART}^{\mathrm L} $
be the full subcategory of cartesian fibrations.
Corollary 4.3. The commutative square

of cartesian fibrations over
![]() $\infty \mathrm {Cat}$
is a pullback square.
$\infty \mathrm {Cat}$
is a pullback square.
5 Correspondences as left fibrations
In this section we prove an equivalence between correspondences and left fibrations to a product of two
![]() $\infty $
-categories (Theorem 5.1). An enriched version of this result was proven by Hinich [Reference Hinich25, 8.3.2. Proposition] who proves that for any proto-topos
$\infty $
-categories (Theorem 5.1). An enriched version of this result was proven by Hinich [Reference Hinich25, 8.3.2. Proposition] who proves that for any proto-topos
![]() ${\mathcal V}$
there is an equivalence between
${\mathcal V}$
there is an equivalence between
![]() ${\mathcal V}$
-enriched functors over
${\mathcal V}$
-enriched functors over
![]() $[1]$
and
$[1]$
and
![]() ${\mathcal V}$
-enriched profunctors.
${\mathcal V}$
-enriched profunctors.
The next definition is [Reference Heine, Lopez-Avila and Spitzweck21, Notation 3.3.]:
Definition 5.1. Let
![]() ${\mathcal C}$
be an
${\mathcal C}$
be an
![]() $\infty $
-category. The twisted arrow left fibration
$\infty $
-category. The twisted arrow left fibration
![]() ${\mathrm {Tw}}({\mathcal C})\to {\mathcal C}^{\mathrm {op}} \times {\mathcal C}$
is the left fibration classifying the mapping space functor
${\mathrm {Tw}}({\mathcal C})\to {\mathcal C}^{\mathrm {op}} \times {\mathcal C}$
is the left fibration classifying the mapping space functor
![]() ${\mathcal C}^{\mathrm {op}} \times {\mathcal C} \to {\mathcal S}.$
${\mathcal C}^{\mathrm {op}} \times {\mathcal C} \to {\mathcal S}.$
Theorem 5.1. There is a canonical pullback square of
![]() $\infty $
-categories
$\infty $
-categories

where the right hand vertical functor evaluates at the target. The induced equivalence from the left upper corner of the square to the pullback sends a functor
![]() ${\mathcal M} \to [1]$
to the triple
${\mathcal M} \to [1]$
to the triple
Remark 5.2. Theorem 5.1 says that there is a canonical equivalence between the following
![]() $\infty $
-categories:
$\infty $
-categories:
-
1. The
 $\infty $
-category
$\infty $
-category
 $\infty \mathrm {Cat}_{/[1]}$
of small
$\infty \mathrm {Cat}_{/[1]}$
of small
 $\infty $
-categories
$\infty $
-categories
 ${\mathcal M}$
equipped with a functor
${\mathcal M}$
equipped with a functor
 ${\mathcal M} \to [1]$
.
${\mathcal M} \to [1]$
. -
2. The pullback
 $(\infty \mathrm {Cat} \times \infty \mathrm {Cat})\times _{\infty \mathrm {Cat}}{\mathcal L}$
along the functor
$(\infty \mathrm {Cat} \times \infty \mathrm {Cat})\times _{\infty \mathrm {Cat}}{\mathcal L}$
along the functor
 $(-)^{\mathrm {op}}\times (-): \infty \mathrm {Cat} \times \infty \mathrm {Cat} \to \infty \mathrm {Cat},$
which is the
$(-)^{\mathrm {op}}\times (-): \infty \mathrm {Cat} \times \infty \mathrm {Cat} \to \infty \mathrm {Cat},$
which is the
 $\infty $
-category of two
$\infty $
-category of two
 $\infty $
-categories
$\infty $
-categories
 ${\mathcal C},{\mathcal D}$
equipped with a left fibration
${\mathcal C},{\mathcal D}$
equipped with a left fibration
 ${\mathcal A} \to {\mathcal C}^{\mathrm {op}} \times {\mathcal D}.$
The latter classifies a functor
${\mathcal A} \to {\mathcal C}^{\mathrm {op}} \times {\mathcal D}.$
The latter classifies a functor
 ${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \to {\mathcal S}$
. Such a functor is also known as a profunctor from
${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \to {\mathcal S}$
. Such a functor is also known as a profunctor from
 ${\mathcal D} $
to
${\mathcal D} $
to
 ${\mathcal C}.$
${\mathcal C}.$
Proof. By Theorem 4.1 there is a canonical pullback square of
![]() $\infty $
-categories:
$\infty $
-categories:

Consequently, it is enough to construct an equivalence between the pullbacks

and

We construct this equivalence by giving for every
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal A}$
a bijection between equivalence classes of objects of the
${\mathcal A}$
a bijection between equivalence classes of objects of the
![]() $\infty $
-categories
$\infty $
-categories
![]() $ \mathrm {Fun}({\mathcal A},{\mathcal A}), \mathrm {Fun}({\mathcal A},{\mathcal B})$
natural in
$ \mathrm {Fun}({\mathcal A},{\mathcal A}), \mathrm {Fun}({\mathcal A},{\mathcal B})$
natural in
![]() ${\mathcal A}.$
A functor
${\mathcal A}.$
A functor
![]() ${\mathcal A} \to {\mathcal B}$
is classified by a pair of cocartesian fibrations
${\mathcal A} \to {\mathcal B}$
is classified by a pair of cocartesian fibrations
![]() ${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a map of cocartesian fibrations
${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a map of cocartesian fibrations
![]() ${\mathcal M} \to {\mathcal A} \times [1]$
over
${\mathcal M} \to {\mathcal A} \times [1]$
over
![]() ${\mathcal A}$
that induces on the fiber over every object
${\mathcal A}$
that induces on the fiber over every object
![]() ${\mathrm A}\in {\mathcal A}$
a cartesian fibration
${\mathrm A}\in {\mathcal A}$
a cartesian fibration
![]() ${\mathcal M}_{\mathrm A} \to [1]$
classifying a small colimits preserving functor
${\mathcal M}_{\mathrm A} \to [1]$
classifying a small colimits preserving functor
![]() ${\mathcal M}_{\mathrm A}^1 \to {\mathcal M}_{\mathrm A}^0$
and such that there are equivalences
${\mathcal M}_{\mathrm A}^1 \to {\mathcal M}_{\mathrm A}^0$
and such that there are equivalences
![]() ${\mathcal M}_0 \simeq {\mathcal P}^{\mathcal A}({\mathcal X}), {\mathcal M}_1 \simeq {\mathcal P}^{\mathcal A}({\mathcal Y})$
over
${\mathcal M}_0 \simeq {\mathcal P}^{\mathcal A}({\mathcal X}), {\mathcal M}_1 \simeq {\mathcal P}^{\mathcal A}({\mathcal Y})$
over
![]() ${\mathcal A}$
. By [Reference Heine14, Lemma 2.44.] a functor
${\mathcal A}$
. By [Reference Heine14, Lemma 2.44.] a functor
![]() ${\mathcal W} \to {\mathcal A} \times [1]$
is a map of cocartesian fibrations over
${\mathcal W} \to {\mathcal A} \times [1]$
is a map of cocartesian fibrations over
![]() ${\mathcal A}$
that induces on the fiber over every object
${\mathcal A}$
that induces on the fiber over every object
![]() ${\mathrm A}\in {\mathcal A}$
a cartesian fibration over
${\mathrm A}\in {\mathcal A}$
a cartesian fibration over
![]() $ [1]$
if and only if it is a map of cartesian fibrations over
$ [1]$
if and only if it is a map of cartesian fibrations over
![]() $[1]$
that induces on the fiber over every object of
$[1]$
that induces on the fiber over every object of
![]() $[1]$
a cocartesian fibration over
$[1]$
a cocartesian fibration over
![]() ${\mathcal A}$
. Consequently, a functor
${\mathcal A}$
. Consequently, a functor
![]() ${\mathcal A} \to {\mathcal B}$
is likewise classified by a pair of cocartesian fibrations
${\mathcal A} \to {\mathcal B}$
is likewise classified by a pair of cocartesian fibrations
![]() ${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a map of cartesian fibrations
${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a map of cartesian fibrations
![]() ${\mathcal M} \to {\mathcal A} \times [1]$
over
${\mathcal M} \to {\mathcal A} \times [1]$
over
![]() $[1]$
that induces on the fibers over
$[1]$
that induces on the fibers over
![]() $0,1 \in [1]$
the cocartesian fibrations
$0,1 \in [1]$
the cocartesian fibrations
![]() ${\mathcal P}^{\mathcal A}({\mathcal X}), {\mathcal P}^{\mathcal A}({\mathcal Y})$
, respectively, and induces on the fiber over every object
${\mathcal P}^{\mathcal A}({\mathcal X}), {\mathcal P}^{\mathcal A}({\mathcal Y})$
, respectively, and induces on the fiber over every object
![]() ${\mathrm A}\in {\mathcal A}$
a cartesian fibration
${\mathrm A}\in {\mathcal A}$
a cartesian fibration
![]() ${\mathcal M}_{\mathrm A} \to [1]$
classifying a small colimits preserving functor
${\mathcal M}_{\mathrm A} \to [1]$
classifying a small colimits preserving functor
![]() ${\mathcal M}_{\mathrm A}^1 \to {\mathcal M}_{\mathrm A}^0$
. In other words, a functor
${\mathcal M}_{\mathrm A}^1 \to {\mathcal M}_{\mathrm A}^0$
. In other words, a functor
![]() ${\mathcal A} \to {\mathcal B}$
is classified by a pair of cocartesian fibrations
${\mathcal A} \to {\mathcal B}$
is classified by a pair of cocartesian fibrations
![]() ${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a functor
${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a functor
![]() ${\mathcal P}^{\mathcal A}({\mathcal Y}) \to {\mathcal P}^{\mathcal A}({\mathcal X})$
over
${\mathcal P}^{\mathcal A}({\mathcal Y}) \to {\mathcal P}^{\mathcal A}({\mathcal X})$
over
![]() ${\mathcal A}$
that induces on the fiber over every object of
${\mathcal A}$
that induces on the fiber over every object of
![]() ${\mathcal A}$
a small colimits preserving functor. By Proposition 3.16 the latter is uniquely determined by its restriction, a functor
${\mathcal A}$
a small colimits preserving functor. By Proposition 3.16 the latter is uniquely determined by its restriction, a functor
![]() ${\mathcal Y} \to {\mathcal P}^{\mathcal A}({\mathcal X})$
over
${\mathcal Y} \to {\mathcal P}^{\mathcal A}({\mathcal X})$
over
![]() ${\mathcal A}$
, which corresponds by Proposition 3.37 to a functor
${\mathcal A}$
, which corresponds by Proposition 3.37 to a functor
![]() ${\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y} \to {\mathcal S}$
. The latter is classified by a left fibration
${\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y} \to {\mathcal S}$
. The latter is classified by a left fibration
![]() ${\mathcal A} \to {\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y}$
or equivalently by a map of cocartesian fibrations
${\mathcal A} \to {\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y}$
or equivalently by a map of cocartesian fibrations
![]() ${\mathcal A} \to {\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y} $
over
${\mathcal A} \to {\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y} $
over
![]() ${\mathcal A}$
that induces on the fiber over every object of
${\mathcal A}$
that induces on the fiber over every object of
![]() ${\mathcal A}$
a left fibration. So a functor
${\mathcal A}$
a left fibration. So a functor
![]() ${\mathcal A} \to {\mathcal B}$
is classified by a pair of cocartesian fibrations
${\mathcal A} \to {\mathcal B}$
is classified by a pair of cocartesian fibrations
![]() ${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a map of cocartesian fibrations
${\mathcal X} \to {\mathcal A}, {\mathcal Y} \to {\mathcal A}$
and a map of cocartesian fibrations
![]() ${\mathcal A} \to {\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y} $
over
${\mathcal A} \to {\mathcal X}^{\mathrm {rev}} \times _{\mathcal A} {\mathcal Y} $
over
![]() ${\mathcal A}$
that induces on the fiber over every object of
${\mathcal A}$
that induces on the fiber over every object of
![]() ${\mathcal A}$
a left fibration. The latter is precisely classified by a functor
${\mathcal A}$
a left fibration. The latter is precisely classified by a functor
![]() ${\mathcal A} \to {\mathcal A}.$
${\mathcal A} \to {\mathcal A}.$
Remark 5.3. Under the equivalence
of Theorem 5.1 the opposite
![]() $\infty $
-category involution on
$\infty $
-category involution on
![]() $\infty \mathrm {Cat}_{/[1]}$
corresponds to an involution on the right hand pullback induced by the flip action on the product
$\infty \mathrm {Cat}_{/[1]}$
corresponds to an involution on the right hand pullback induced by the flip action on the product
![]() $\infty \mathrm {Cat} \times \infty \mathrm {Cat}.$
This gives an easy way to understand the opposite
$\infty \mathrm {Cat} \times \infty \mathrm {Cat}.$
This gives an easy way to understand the opposite
![]() $\infty $
-category involution on
$\infty $
-category involution on
![]() $\infty \mathrm {Cat}_{/[1]}$
and is used in [Reference Heine, Lopez-Avila and Spitzweck21, Theorem 5.21.] and [Reference Heine, Spitzweck and Verdugo22, Theorem 6.27.] to compare different models of dualities. In fact in [Reference Heine, Lopez-Avila and Spitzweck21, Proposition 5.23.] equivalence (5.2) is enhanced to a
$\infty \mathrm {Cat}_{/[1]}$
and is used in [Reference Heine, Lopez-Avila and Spitzweck21, Theorem 5.21.] and [Reference Heine, Spitzweck and Verdugo22, Theorem 6.27.] to compare different models of dualities. In fact in [Reference Heine, Lopez-Avila and Spitzweck21, Proposition 5.23.] equivalence (5.2) is enhanced to a
![]() ${\mathrm C}_2$
-equivariant equivalence for the
${\mathrm C}_2$
-equivariant equivalence for the
![]() $C_2$
-actions refining the opposite
$C_2$
-actions refining the opposite
![]() $\infty $
-category involution and the flip action.
$\infty $
-category involution and the flip action.
Notation 5.2. Let
![]() ${\mathrm {Cocart}} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
be the full subcategory of cocartesian fibrations.
${\mathrm {Cocart}} \subset \mathrm {Fun}([1],\infty \mathrm {Cat})$
be the full subcategory of cocartesian fibrations.
Corollary 5.3. Let
![]() ${\mathcal C},{\mathcal D}$
be small
${\mathcal C},{\mathcal D}$
be small
![]() $\infty $
-categories. There is a canonical equivalence
$\infty $
-categories. There is a canonical equivalence
that sends a functor
![]() ${\mathcal M} \to [1]$
and
${\mathcal M} \to [1]$
and
![]() ${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
![]() ${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \subset {\mathcal M}^{\mathrm {op}} \times {\mathcal M} \xrightarrow {{\mathcal M}(-,-)} {\mathcal S}.$
${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \subset {\mathcal M}^{\mathrm {op}} \times {\mathcal M} \xrightarrow {{\mathcal M}(-,-)} {\mathcal S}.$
The latter equivalence restricts to an equivalence
that sends a functor
![]() ${\mathcal M} \to [1]$
and
${\mathcal M} \to [1]$
and
![]() ${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
![]() ${\mathcal C} \to {\mathcal D}$
classified by
${\mathcal C} \to {\mathcal D}$
classified by
![]() ${\mathcal M} \to [1]$
.
${\mathcal M} \to [1]$
.
Proof. By Theorem 5.1 there is a canonical equivalence
that sends a functor
![]() ${\mathcal M} \to [1]$
and
${\mathcal M} \to [1]$
and
![]() ${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
![]() ${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \subset {\mathcal M}^{\mathrm {op}} \times {\mathcal M} \xrightarrow {{\mathcal M}(-,-)} {\mathcal S}.$
${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \subset {\mathcal M}^{\mathrm {op}} \times {\mathcal M} \xrightarrow {{\mathcal M}(-,-)} {\mathcal S}.$
The latter equivalence restricts to an equivalence
that sends a functor
![]() ${\mathcal M} \to [1]$
and
${\mathcal M} \to [1]$
and
![]() ${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
to the functor
![]() ${\mathcal C} \to {\mathcal D}$
classified by
${\mathcal C} \to {\mathcal D}$
classified by
![]() ${\mathcal M} \to [1]$
.
${\mathcal M} \to [1]$
.
For every cocartesian fibration
![]() ${\mathcal M} \to [1]$
and
${\mathcal M} \to [1]$
and
![]() ${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
classifying a functor
${\mathcal M}_0 \simeq {\mathcal C}, {\mathcal M}_1 \simeq {\mathcal D}$
classifying a functor
![]() $\alpha : {\mathcal C} \to {\mathcal D}$
there is a canonical equivalence between the functor
$\alpha : {\mathcal C} \to {\mathcal D}$
there is a canonical equivalence between the functor
![]() ${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \subset {\mathcal M}^{\mathrm {op}} \times {\mathcal M} \xrightarrow {{\mathcal M}(-,-)} {\mathcal S}$
and the functor
${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \subset {\mathcal M}^{\mathrm {op}} \times {\mathcal M} \xrightarrow {{\mathcal M}(-,-)} {\mathcal S}$
and the functor
![]() ${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \xrightarrow {\alpha ^{\mathrm {op}} \times {\mathcal D}} {\mathcal D}^{\mathrm {op}} \times {\mathcal D} \xrightarrow {{\mathcal D}(-,-)} {\mathcal S}$
.
${\mathcal C}^{\mathrm {op}} \times {\mathcal D} \xrightarrow {\alpha ^{\mathrm {op}} \times {\mathcal D}} {\mathcal D}^{\mathrm {op}} \times {\mathcal D} \xrightarrow {{\mathcal D}(-,-)} {\mathcal S}$
.
6 An end formula for mapping spaces of parametrized functor
 $\infty $
-categories
$\infty $
-categories
By Corollary 3.23 the
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \mathrm {Cat}_{/[1]}$
is cartesian closed. In this section we describe the mapping space functor of the internal hom
$\infty \mathrm {Cat}_{/[1]}$
is cartesian closed. In this section we describe the mapping space functor of the internal hom
![]() $\mathrm {Fun}^{[1]}({\mathcal M},{\mathcal N})$
between two functors
$\mathrm {Fun}^{[1]}({\mathcal M},{\mathcal N})$
between two functors
![]() ${\mathcal M} \to [1],{\mathcal N} \to [1]$
(Theorem 6.2). Having this description we relate the mapping spaces of the conditionally existing internal hom
${\mathcal M} \to [1],{\mathcal N} \to [1]$
(Theorem 6.2). Having this description we relate the mapping spaces of the conditionally existing internal hom
![]() $\mathrm {Fun}^{{\mathcal C}}({\mathcal M},{\mathcal N})$
between two functors
$\mathrm {Fun}^{{\mathcal C}}({\mathcal M},{\mathcal N})$
between two functors
![]() ${\mathcal M} \to {\mathcal C},{\mathcal N} \to {\mathcal C}$
to the mapping space functors of
${\mathcal M} \to {\mathcal C},{\mathcal N} \to {\mathcal C}$
to the mapping space functors of
![]() ${\mathcal M},{\mathcal N}$
(Corollary 6.4). As a corollary we compute the mapping space functor of the
${\mathcal M},{\mathcal N}$
(Corollary 6.4). As a corollary we compute the mapping space functor of the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Fun}({\mathcal A},{\mathcal B})$
of functors between two
$\mathrm {Fun}({\mathcal A},{\mathcal B})$
of functors between two
![]() $\infty $
-categories
$\infty $
-categories
![]() ${\mathcal A},{\mathcal B}$
(Corollary 6.6) recovering a global version of a result of [Reference Gepner, Haugseng and Nikolaus12, Proposition 5.1.].
${\mathcal A},{\mathcal B}$
(Corollary 6.6) recovering a global version of a result of [Reference Gepner, Haugseng and Nikolaus12, Proposition 5.1.].
Lemma 6.1. Let
![]() ${\mathcal V}$
be a closed monoidal
${\mathcal V}$
be a closed monoidal
![]() $\infty $
-category,
$\infty $
-category,
![]() ${\mathcal W} \subset \mathrm {Fun}([1],{\mathcal V})$
a full monoidal subcategory satisfying the following conditions:
${\mathcal W} \subset \mathrm {Fun}([1],{\mathcal V})$
a full monoidal subcategory satisfying the following conditions:
-
1. The base change of any object
 ${\mathrm X} \to {\mathrm Y}$
of
${\mathrm X} \to {\mathrm Y}$
of
 ${\mathrm W}$
along any morphism
${\mathrm W}$
along any morphism
 ${\mathrm Z} \to {\mathrm X}$
of
${\mathrm Z} \to {\mathrm X}$
of
 ${\mathcal V}$
exists and is an object of
${\mathcal V}$
exists and is an object of
 ${\mathcal W}$
.
${\mathcal W}$
. -
2. For every object
 ${\mathrm X} \to {\mathrm Y}$
of
${\mathrm X} \to {\mathrm Y}$
of
 ${\mathcal W}$
and every object
${\mathcal W}$
and every object
 ${\mathrm Z}$
of
${\mathrm Z}$
of
 ${\mathcal V}$
the induced morphism
${\mathcal V}$
the induced morphism
 ${\mathrm {Mor}}_{\mathcal V}({\mathrm Z},{\mathrm X}) \to {\mathrm {Mor}}_{\mathcal V}({\mathrm Z},{\mathrm Y})$
in
${\mathrm {Mor}}_{\mathcal V}({\mathrm Z},{\mathrm X}) \to {\mathrm {Mor}}_{\mathcal V}({\mathrm Z},{\mathrm Y})$
in
 ${\mathcal V}$
is an object of
${\mathcal V}$
is an object of
 ${\mathcal W}.$
${\mathcal W}.$
The following holds:
-
1. For every monoidal functor
 $\alpha : {\mathcal A} \to {\mathcal V}$
the pullback
$\alpha : {\mathcal A} \to {\mathcal V}$
the pullback
 ${\mathcal A} \times _{{\mathcal V}} {\mathcal W}$
of the monoidal functor
${\mathcal A} \times _{{\mathcal V}} {\mathcal W}$
of the monoidal functor
 ${\mathcal W} \to {\mathcal V}$
evaluating at the target and
${\mathcal W} \to {\mathcal V}$
evaluating at the target and
 $\alpha $
is a closed monoidal
$\alpha $
is a closed monoidal
 $\infty $
-category.
$\infty $
-category. -
2. The internal hom of every two objects
 $({\mathrm A}, {\mathrm {f}}: {\mathrm X} \to \alpha ({\mathrm A})), ({\mathrm B}, {g}: {\mathrm Y} \to \alpha ({\mathrm B}))\in {\mathcal A} \times _{{\mathcal V}} {\mathcal W} $
consists of the object
$({\mathrm A}, {\mathrm {f}}: {\mathrm X} \to \alpha ({\mathrm A})), ({\mathrm B}, {g}: {\mathrm Y} \to \alpha ({\mathrm B}))\in {\mathcal A} \times _{{\mathcal V}} {\mathcal W} $
consists of the object
 ${\mathrm {Mor}}_{\mathcal A}({\mathrm A},{\mathrm B}) \in {\mathcal A}$
and the projection
${\mathrm {Mor}}_{\mathcal A}({\mathrm A},{\mathrm B}) \in {\mathcal A}$
and the projection  $$ \begin{align*}\alpha({\mathrm{Mor}}_{\mathcal A}({\mathrm A},{\mathrm B})) \times_{{\mathrm{Mor}}_{\mathcal V}({\mathrm X}, \alpha({\mathrm B}))} {\mathrm{Mor}}_{\mathcal V}({\mathrm X},{\mathrm Y}) \to \alpha({\mathrm{Mor}}_{\mathcal A}({\mathrm A},{\mathrm B})).\end{align*} $$
$$ \begin{align*}\alpha({\mathrm{Mor}}_{\mathcal A}({\mathrm A},{\mathrm B})) \times_{{\mathrm{Mor}}_{\mathcal V}({\mathrm X}, \alpha({\mathrm B}))} {\mathrm{Mor}}_{\mathcal V}({\mathrm X},{\mathrm Y}) \to \alpha({\mathrm{Mor}}_{\mathcal A}({\mathrm A},{\mathrm B})).\end{align*} $$
Proof. For every
![]() $({\mathrm A}, {\mathrm {f}}: {\mathrm X} \to \alpha ({\mathrm A})), ({\mathrm B}, {g}: {\mathrm Y} \to \alpha ({\mathrm B}))\in {\mathcal A} \times _{{\mathcal V}} {\mathcal W}, ({\mathrm C}, {\mathrm {h}}: {\mathrm Z} \to \alpha ({\mathrm C}))\in {\mathcal A} \times _{{\mathcal V}} {\mathcal W} $
the canonical morphism
$({\mathrm A}, {\mathrm {f}}: {\mathrm X} \to \alpha ({\mathrm A})), ({\mathrm B}, {g}: {\mathrm Y} \to \alpha ({\mathrm B}))\in {\mathcal A} \times _{{\mathcal V}} {\mathcal W}, ({\mathrm C}, {\mathrm {h}}: {\mathrm Z} \to \alpha ({\mathrm C}))\in {\mathcal A} \times _{{\mathcal V}} {\mathcal W} $
the canonical morphism
in
![]() ${\mathcal A} \times _{{\mathcal V}} {\mathcal W}$
induces a map
${\mathcal A} \times _{{\mathcal V}} {\mathcal W}$
induces a map
over
![]() ${\mathcal A}({\mathrm A}, {\mathrm {Mor}}_{\mathcal A}({\mathrm B},{\mathrm C})) \simeq {\mathcal A}({\mathrm A} \otimes {\mathrm B},{\mathrm C})$
that induces on the fiber over every morphism
${\mathcal A}({\mathrm A}, {\mathrm {Mor}}_{\mathcal A}({\mathrm B},{\mathrm C})) \simeq {\mathcal A}({\mathrm A} \otimes {\mathrm B},{\mathrm C})$
that induces on the fiber over every morphism
![]() $\theta : {\mathrm A} \to {\mathrm {Mor}}_{\mathcal A}({\mathrm B},{\mathrm C})$
corresponding to a morphism
$\theta : {\mathrm A} \to {\mathrm {Mor}}_{\mathcal A}({\mathrm B},{\mathrm C})$
corresponding to a morphism
![]() $\theta ': {\mathrm A} \otimes {\mathrm B} \to {\mathrm C}$
the canonical equivalence
$\theta ': {\mathrm A} \otimes {\mathrm B} \to {\mathrm C}$
the canonical equivalence
Corollary 6.2. The pullback

in cartesian symmetric monoidal
![]() $\infty $
-categories is closed.
$\infty $
-categories is closed.
The internal hom of every
![]() $({\mathcal A},{\mathcal B}, {\mathcal C}, {\mathcal C} \to {\mathcal A}^{\mathrm {op}} \times {\mathcal B}), ({\mathcal A}',{\mathcal B}', {\mathcal C}', {\mathcal C}' \to {\mathcal A}^{\mathrm {\prime {op}}} \times {\mathcal B}')$
consists of
$({\mathcal A},{\mathcal B}, {\mathcal C}, {\mathcal C} \to {\mathcal A}^{\mathrm {op}} \times {\mathcal B}), ({\mathcal A}',{\mathcal B}', {\mathcal C}', {\mathcal C}' \to {\mathcal A}^{\mathrm {\prime {op}}} \times {\mathcal B}')$
consists of
![]() $ \mathrm {Fun}({\mathcal A},{\mathcal A}') $
and
$ \mathrm {Fun}({\mathcal A},{\mathcal A}') $
and
![]() $ \mathrm {Fun}({\mathcal B},{\mathcal B}') $
and the functor
$ \mathrm {Fun}({\mathcal B},{\mathcal B}') $
and the functor
Proof. We apply Lemma 6.1 to
![]() ${\mathcal V}:=\infty \mathrm {Cat}$
and
${\mathcal V}:=\infty \mathrm {Cat}$
and
![]() ${\mathcal W}:= {\mathcal L} \subset \mathrm {Fun}([1], {\mathcal V}).$
${\mathcal W}:= {\mathcal L} \subset \mathrm {Fun}([1], {\mathcal V}).$
Notation 6.3. For every functor
![]() ${\mathcal M} \to [1]$
let
${\mathcal M} \to [1]$
let
![]() $\widetilde {{\mathrm {Tw}}}({\mathcal M})$
be the pullback
$\widetilde {{\mathrm {Tw}}}({\mathcal M})$
be the pullback
Remark 6.1. Let
![]() ${\mathcal C}$
be an
${\mathcal C}$
be an
![]() $\infty $
-category. Projection
$\infty $
-category. Projection
![]() ${\mathcal C} \times [1]\to {\mathcal C}$
induces an equivalence
${\mathcal C} \times [1]\to {\mathcal C}$
induces an equivalence
![]() $\widetilde {{\mathrm {Tw}}}({\mathcal C}\times [1]) \simeq {\mathrm {Tw}}({\mathcal C})$
over
$\widetilde {{\mathrm {Tw}}}({\mathcal C}\times [1]) \simeq {\mathrm {Tw}}({\mathcal C})$
over
![]() $ {\mathcal C}^{\mathrm {op}} \times {\mathcal C}.$
$ {\mathcal C}^{\mathrm {op}} \times {\mathcal C}.$
Theorem 6.2. Let
![]() ${\mathcal M} \to [1], {\mathcal N} \to [1]$
be functors. There is a canonical equivalence
${\mathcal M} \to [1], {\mathcal N} \to [1]$
be functors. There is a canonical equivalence
over
that induces on the fiber over any functors
![]() ${\mathrm F}: {\mathcal M}_0 \to {\mathcal N}_0, {\mathrm G}: {\mathcal M}_1 \to {\mathcal N}_1$
an equivalence
${\mathrm F}: {\mathcal M}_0 \to {\mathcal N}_0, {\mathrm G}: {\mathcal M}_1 \to {\mathcal N}_1$
an equivalence
Proof. By Theorem 5.1 there is a canonical equivalence
![]() $\theta $
between
$\theta $
between
![]() $\infty \mathrm {Cat}_{/[1]}$
and the pullback
$\infty \mathrm {Cat}_{/[1]}$
and the pullback

Consequently, the internal hom of
![]() $\infty \mathrm {Cat}_{/[1]}$
corresponds under
$\infty \mathrm {Cat}_{/[1]}$
corresponds under
![]() $\theta $
to the internal hom of
$\theta $
to the internal hom of
![]() ${\mathcal Q}$
for the cartesian monoidal structures. The description of
${\mathcal Q}$
for the cartesian monoidal structures. The description of
![]() $\theta $
of Theorem 5.1 and the description of the internal hom of Corollary 6.2 imply the result.
$\theta $
of Theorem 5.1 and the description of the internal hom of Corollary 6.2 imply the result.
Corollary 6.4. Let
![]() ${\mathcal A} \to {\mathcal C},{\mathcal B} \to {\mathcal C}$
be functors such that
${\mathcal A} \to {\mathcal C},{\mathcal B} \to {\mathcal C}$
be functors such that
![]() ${\mathcal A} \to {\mathcal C}$
is an exponentiable fibration. Let
${\mathcal A} \to {\mathcal C}$
is an exponentiable fibration. Let
![]() ${\mathrm {f}}: {\mathrm X} \to {\mathrm Y}$
be a morphism in
${\mathrm {f}}: {\mathrm X} \to {\mathrm Y}$
be a morphism in
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() ${\mathrm F}: {\mathcal A}_{\mathrm X} \to {\mathcal B}_{\mathrm X}, {\mathrm G}: {\mathcal A}_{\mathrm Y} \to {\mathcal B}_{\mathrm Y}$
be functors. There is a canonical equivalence
${\mathrm F}: {\mathcal A}_{\mathrm X} \to {\mathcal B}_{\mathrm X}, {\mathrm G}: {\mathcal A}_{\mathrm Y} \to {\mathcal B}_{\mathrm Y}$
be functors. There is a canonical equivalence
Proof. There is a canonical equivalence
Definition 6.5. Let
![]() ${\mathcal C},{\mathcal D}$
be
${\mathcal C},{\mathcal D}$
be
![]() $\infty $
-categories and
$\infty $
-categories and
![]() $\phi : {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \to {\mathcal D}$
be a functor. The end of
$\phi : {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \to {\mathcal D}$
be a functor. The end of
![]() $\phi $
, denoted by
$\phi $
, denoted by
![]() ${\int \phi }$
if it exists, is the limit of the functor
${\int \phi }$
if it exists, is the limit of the functor
![]() ${\mathrm {Tw}}({\mathcal C}) \xrightarrow {{q}} {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \xrightarrow {\phi } {\mathcal D}.$
${\mathrm {Tw}}({\mathcal C}) \xrightarrow {{q}} {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \xrightarrow {\phi } {\mathcal D}.$
Remark 6.3. Let
![]() $\phi : {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \to {\mathcal S}$
be a functor classified by a left fibration
$\phi : {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \to {\mathcal S}$
be a functor classified by a left fibration
![]() ${\mathcal B} \to {\mathcal C}^{\mathrm {op}} \times {\mathcal C}.$
${\mathcal B} \to {\mathcal C}^{\mathrm {op}} \times {\mathcal C}.$
The limit of the functor
![]() ${\mathrm {Tw}}({\mathcal C}) \xrightarrow {{q}} {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \xrightarrow {\phi } {\mathcal S}$
is the space
${\mathrm {Tw}}({\mathcal C}) \xrightarrow {{q}} {\mathcal C}^{\mathrm {op}} \times {\mathcal C} \xrightarrow {\phi } {\mathcal S}$
is the space
Corollary 6.6. Let
![]() ${\mathcal C},{\mathcal D}$
be
${\mathcal C},{\mathcal D}$
be
![]() $\infty $
-categories. There is a canonical equivalence
$\infty $
-categories. There is a canonical equivalence
over
The latter induces on the fiber over every functors
![]() ${\mathrm F},{\mathrm G}:{\mathcal C} \to {\mathcal D}$
an equivalence
${\mathrm F},{\mathrm G}:{\mathcal C} \to {\mathcal D}$
an equivalence
7 A generalized Grothendieck construction
In this section we extend the Grothendieck construction to an equivalence between all
![]() $\infty $
-categories over a base
$\infty $
-categories over a base
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
and lax normal functors from
${\mathcal C}$
and lax normal functors from
![]() ${\mathcal C}$
to a double
${\mathcal C}$
to a double
![]() $\infty $
-category of correspondences.
$\infty $
-category of correspondences.
As the first step we define double
![]() $\infty $
-categories [Reference Gepner and Haugseng11, Definition 2.4.3.].
$\infty $
-categories [Reference Gepner and Haugseng11, Definition 2.4.3.].
Definition 7.1. A double
![]() $\infty $
-category is a cartesian fibration
$\infty $
-category is a cartesian fibration
![]() ${\mathcal B} \to \Delta $
such that for every
${\mathcal B} \to \Delta $
such that for every
![]() $[{n}] \in \Delta $
the induced functor
$[{n}] \in \Delta $
the induced functor
is an equivalence, where the
![]() ${i}$
-th map
${i}$
-th map
![]() $[1] \to [{n}]$
sends
$[1] \to [{n}]$
sends
![]() $0$
to
$0$
to
![]() ${i}-1$
and
${i}-1$
and
![]() $1$
to
$1$
to
![]() ${i}.$
${i}.$
Via the Grothendieck construction double
![]() $\infty $
-categories precisely classify functors
$\infty $
-categories precisely classify functors
![]() $\Delta ^{\mathrm {op}} \to \infty \mathrm {Cat}$
satisfying the Segal condition. In this sense double
$\Delta ^{\mathrm {op}} \to \infty \mathrm {Cat}$
satisfying the Segal condition. In this sense double
![]() $\infty $
-categories are
$\infty $
-categories are
![]() $\infty $
-categories internal to
$\infty $
-categories internal to
![]() $\infty \mathrm {Cat}.$
$\infty \mathrm {Cat}.$
Example 7.1. For every
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
let
${\mathcal C}$
let
![]() $\Delta _{\mathcal C} \to \Delta $
be the cartesian fibration classifying the functor
$\Delta _{\mathcal C} \to \Delta $
be the cartesian fibration classifying the functor
where the first functor forgets the total order. The cartesian fibration
![]() $\Delta _{\mathcal C} \to \Delta $
is a double
$\Delta _{\mathcal C} \to \Delta $
is a double
![]() $\infty $
-category.
$\infty $
-category.
Lemma 7.2. The functor
taking the fiber over
![]() $[0]$
admits a fully faithful right adjoint that sends any
$[0]$
admits a fully faithful right adjoint that sends any
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
to the cartesian fibration
${\mathcal C}$
to the cartesian fibration
![]() $\Delta _{\mathcal C} \to \Delta .$
$\Delta _{\mathcal C} \to \Delta .$
Proof. By the Grothendieck construction there is a canonical equivalence
The functor
![]() $\mathrm {Fun}(\Delta ^{\mathrm {op}}, \infty \mathrm {Cat}) \simeq \infty \mathrm {Cat}^{\mathrm {cart}}_{/\Delta } \xrightarrow {\rho } \infty \mathrm {Cat}$
is the functor evaluating at
$\mathrm {Fun}(\Delta ^{\mathrm {op}}, \infty \mathrm {Cat}) \simeq \infty \mathrm {Cat}^{\mathrm {cart}}_{/\Delta } \xrightarrow {\rho } \infty \mathrm {Cat}$
is the functor evaluating at
![]() $[0]$
. By [Reference Lurie27, Corollary 4.3.2.14., Proposition 4.3.2.17.] this functor admits a right adjoint
$[0]$
. By [Reference Lurie27, Corollary 4.3.2.14., Proposition 4.3.2.17.] this functor admits a right adjoint
![]() $ \gamma $
that sends any
$ \gamma $
that sends any
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
to the right Kan extension of the functor
${\mathcal C}$
to the right Kan extension of the functor
![]() $ [0] \xrightarrow {{\mathcal C}} \infty \mathrm {Cat}$
along the embedding
$ [0] \xrightarrow {{\mathcal C}} \infty \mathrm {Cat}$
along the embedding
![]() $ \{[0] \} \subset \Delta ^{\mathrm {op}}.$
By [Reference Lurie27, Lemma 4.3.2.13., Corollary 4.3.2.14., Proposition 4.3.2.17.] this right Kan extension
$ \{[0] \} \subset \Delta ^{\mathrm {op}}.$
By [Reference Lurie27, Lemma 4.3.2.13., Corollary 4.3.2.14., Proposition 4.3.2.17.] this right Kan extension
![]() $\gamma ({\mathcal C}) $
sends any
$\gamma ({\mathcal C}) $
sends any
![]() $[{n}] \in \Delta $
to the limit of the functor
$[{n}] \in \Delta $
to the limit of the functor
![]() $ \{0,\ldots,{n} \} \simeq (\{[0] \} \times _{\Delta } \Delta _{/[{n}]})^{\mathrm {op}} \to [0] \xrightarrow {{\mathcal C}} \infty \mathrm {Cat}, $
which identifies with
$ \{0,\ldots,{n} \} \simeq (\{[0] \} \times _{\Delta } \Delta _{/[{n}]})^{\mathrm {op}} \to [0] \xrightarrow {{\mathcal C}} \infty \mathrm {Cat}, $
which identifies with
![]() $\mathrm {Fun}(\{0,\ldots,{n} \},{\mathcal C}) \simeq {\mathcal C}^{\times {n}+1}. $
Hence
$\mathrm {Fun}(\{0,\ldots,{n} \},{\mathcal C}) \simeq {\mathcal C}^{\times {n}+1}. $
Hence
![]() $\gamma ({\mathcal C}) $
is the functor
$\gamma ({\mathcal C}) $
is the functor
This implies the result by definition of
![]() $\Delta _{/{\mathcal C}} \to \Delta. $
$\Delta _{/{\mathcal C}} \to \Delta. $
Remark 7.2. The functor
![]() $\rho : \infty \mathrm {Cat}^{\mathrm {cart}}_{/\Delta } \to \infty \mathrm {Cat}$
is a cartesian fibration, where a morphism
$\rho : \infty \mathrm {Cat}^{\mathrm {cart}}_{/\Delta } \to \infty \mathrm {Cat}$
is a cartesian fibration, where a morphism
![]() ${\mathcal B} \to {\mathcal C}$
over
${\mathcal B} \to {\mathcal C}$
over
![]() $\Delta $
is
$\Delta $
is
![]() $\rho $
-cartesian if and only if the following square is a pullback square:
$\rho $
-cartesian if and only if the following square is a pullback square:

This holds since for every cartesian fibration
![]() ${\mathcal A} \to \Delta $
the induced commutative square
${\mathcal A} \to \Delta $
the induced commutative square

is equivalent to the commutative square

In particular, the
![]() $\rho $
-cartesian lift to a double
$\rho $
-cartesian lift to a double
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C} \to \Delta $
of a functor
${\mathcal C} \to \Delta $
of a functor
![]() $ {\mathcal A} \to {\mathcal C}_{[0]}$
is the double
$ {\mathcal A} \to {\mathcal C}_{[0]}$
is the double
![]() $\infty $
-category
$\infty $
-category
![]() $ \Delta _{\mathcal A} \times _{\Delta _{{\mathcal C}_{[0]}}} {\mathcal C}.$
$ \Delta _{\mathcal A} \times _{\Delta _{{\mathcal C}_{[0]}}} {\mathcal C}.$
Notation 7.3. Let
![]() ${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
![]() $\infty $
-categories. We write
$\infty $
-categories. We write
for the full subcategory spanned by the functors over
![]() $\Delta $
preserving cocartesian lifts of morphisms of
$\Delta $
preserving cocartesian lifts of morphisms of
![]() $\Delta .$
$\Delta .$
Definition 7.4. An
![]() $(\infty ,2)$
-precategory is a double
$(\infty ,2)$
-precategory is a double
![]() $\infty $
-category
$\infty $
-category
![]() $\phi : {\mathcal B} \to \Delta $
such that
$\phi : {\mathcal B} \to \Delta $
such that
![]() ${\mathcal B}_0$
is a space.
${\mathcal B}_0$
is a space.
Remark 7.3. By [Reference Hinich25, 5.6.1. Corollary] there is an equivalence between
![]() $(\infty ,2)$
-precategories in the sense of Definition 7.4 and
$(\infty ,2)$
-precategories in the sense of Definition 7.4 and
![]() $\infty $
-precategories enriched in
$\infty $
-precategories enriched in
![]() $\infty \mathrm {Cat}$
, which justifies our terminology.
$\infty \mathrm {Cat}$
, which justifies our terminology.
Example 7.4. For every double
![]() $\infty $
-category
$\infty $
-category
![]() $\phi : {\mathcal B} \to \Delta $
the pullback
$\phi : {\mathcal B} \to \Delta $
the pullback
is an
![]() $(\infty ,2)$
-precategory, which we call the underlying
$(\infty ,2)$
-precategory, which we call the underlying
![]() $(\infty ,2)$
-precategory of
$(\infty ,2)$
-precategory of
![]() $\phi .$
$\phi .$
Example 7.5. Viewing spaces as
![]() $\infty $
-categories any Segal space classifies an
$\infty $
-categories any Segal space classifies an
![]() $(\infty ,2)$
-precategory. For every
$(\infty ,2)$
-precategory. For every
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
the nerve of
${\mathcal C}$
the nerve of
![]() ${\mathcal C}$
defined by
${\mathcal C}$
defined by
![]() ${\mathrm N}({\mathcal C}): \Delta ^{\mathrm {op}} \to {\mathcal S}, [{n}]\mapsto \infty \mathrm {Cat}([{n}],{\mathcal C})$
is a Segal space and so classifies an
${\mathrm N}({\mathcal C}): \Delta ^{\mathrm {op}} \to {\mathcal S}, [{n}]\mapsto \infty \mathrm {Cat}([{n}],{\mathcal C})$
is a Segal space and so classifies an
![]() $(\infty ,2)$
-precategory.
$(\infty ,2)$
-precategory.
Notation 7.5. We define the following
![]() $\infty $
-categories by the following pullback squares:
$\infty $
-categories by the following pullback squares:


Construction 7.6. Let
![]() ${\mathrm H}: {\mathrm K} \to \infty \mathrm {Cat}$
be a functor that admits a colimit
${\mathrm H}: {\mathrm K} \to \infty \mathrm {Cat}$
be a functor that admits a colimit
![]() ${\mathcal A}$
. The canonical
${\mathcal A}$
. The canonical
![]() $\infty \mathrm {Cat}$
-linear functor
$\infty \mathrm {Cat}$
-linear functor
![]() $\mathrm {Cat}_{\infty /{\mathcal A}} \to \lim _{{k} \in {\mathrm K}}\mathrm {Cat}_{\infty /{\mathrm H}({k})}$
induces on morphism
$\mathrm {Cat}_{\infty /{\mathcal A}} \to \lim _{{k} \in {\mathrm K}}\mathrm {Cat}_{\infty /{\mathrm H}({k})}$
induces on morphism
![]() $\infty $
-categories between two functors
$\infty $
-categories between two functors
![]() ${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
a functor
${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
a functor
Lemma 7.7. Let
![]() ${\mathrm H}: {\mathrm K} \to \infty \mathrm {Cat}$
be a functor with colimit
${\mathrm H}: {\mathrm K} \to \infty \mathrm {Cat}$
be a functor with colimit
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
functors. If the functor
${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
functors. If the functor
![]() ${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration, the functor (7.1) is an equivalence.
${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration, the functor (7.1) is an equivalence.
Proof. Since
![]() ${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration, the functor
${\mathcal C} \to {\mathcal A}$
is an exponentiable fibration, the functor
![]() $(-) \times _{{\mathcal A}}{\mathcal C} : \mathrm {Cat}_{\infty /{\mathcal A}} \to \mathrm {Cat}_{\infty /{\mathcal C}} \to \mathrm {Cat}_{\infty /{\mathcal A}}$
preserves small colimits. Hence the canonical functor
$(-) \times _{{\mathcal A}}{\mathcal C} : \mathrm {Cat}_{\infty /{\mathcal A}} \to \mathrm {Cat}_{\infty /{\mathcal C}} \to \mathrm {Cat}_{\infty /{\mathcal A}}$
preserves small colimits. Hence the canonical functor
over
![]() $ \mathrm {colim} ({\mathrm H}) \simeq {\mathcal A} $
is an equivalence. Since the functor
$ \mathrm {colim} ({\mathrm H}) \simeq {\mathcal A} $
is an equivalence. Since the functor
![]() $\mathrm {Fun}_{{\mathcal A}}(-,{\mathcal D}): \mathrm {Cat}_{\infty /{\mathcal A}}^{\mathrm {op}} \to \infty \mathrm {Cat}$
preserves limits, the following canonical functor is an equivalence:
$\mathrm {Fun}_{{\mathcal A}}(-,{\mathcal D}): \mathrm {Cat}_{\infty /{\mathcal A}}^{\mathrm {op}} \to \infty \mathrm {Cat}$
preserves limits, the following canonical functor is an equivalence:
For the next corollary we use that for every
![]() ${n} \geq 0$
the category
${n} \geq 0$
the category
![]() $[{n}]$
is the colimit in
$[{n}]$
is the colimit in
![]() $\infty \mathrm {Cat}$
of the following diagram, in which all maps are inert:
$\infty \mathrm {Cat}$
of the following diagram, in which all maps are inert:

Lemma 7.7 gives the following corollary:
Corollary 7.8. Let
![]() ${n} \geq 0$
and
${n} \geq 0$
and
![]() ${\mathcal B} \to {\mathcal C} $
a functor over
${\mathcal B} \to {\mathcal C} $
a functor over
![]() $[{n}]$
whose pullback along any inert map
$[{n}]$
whose pullback along any inert map
![]() $[1]\to [{n}]$
is an equivalence. For every exponentiable fibration
$[1]\to [{n}]$
is an equivalence. For every exponentiable fibration
![]() ${\mathcal D} \to [{n}]$
the induced functor
${\mathcal D} \to [{n}]$
the induced functor
is an equivalence.
Proof. There is a commutative square:

By Lemma 7.7 both horizontal functors in this square are equivalences. This implies the result.
Notation 7.9. Let
![]() ${n} \geq 0$
and
${n} \geq 0$
and
![]() $\phi : {\mathcal C} \to [{n}]$
be a functor. Pulling back diagram (7) along
$\phi : {\mathcal C} \to [{n}]$
be a functor. Pulling back diagram (7) along
![]() $\phi $
we obtain the following diagram over
$\phi $
we obtain the following diagram over
![]() ${\mathcal C}:$
${\mathcal C}:$

We write
![]() ${\mathcal C}'$
for the colimit of the latter diagram.
${\mathcal C}'$
for the colimit of the latter diagram.
Corollary 7.10. Let
![]() ${n} \geq 0$
and
${n} \geq 0$
and
![]() ${\mathcal C} \to [{n}]$
be a functor.
${\mathcal C} \to [{n}]$
be a functor.
-
1. The functor
 ${\mathcal C}' \to [{n}]$
is an exponentiable fibration.
${\mathcal C}' \to [{n}]$
is an exponentiable fibration. -
2. For every exponentiable fibration
 ${\mathcal D} \to [{n}]$
the induced functor
${\mathcal D} \to [{n}]$
the induced functor  $$ \begin{align*}\mathrm{Fun}_{[{n}]}({\mathcal D},{\mathcal C}') \to \mathrm{Fun}_{[{n}]}({\mathcal D},{\mathcal C})\end{align*} $$
$$ \begin{align*}\mathrm{Fun}_{[{n}]}({\mathcal D},{\mathcal C}') \to \mathrm{Fun}_{[{n}]}({\mathcal D},{\mathcal C})\end{align*} $$
is an equivalence.
Proof. By Corollary 3.26 for every
![]() $1 \leq {i} \leq {n}$
the inert maps
$1 \leq {i} \leq {n}$
the inert maps
![]() $[1]\cong \{{i}-1< {i}\}\subset [{n}]$
are exponentiable fibrations. Hence the pullback of the canonical functor
$[1]\cong \{{i}-1< {i}\}\subset [{n}]$
are exponentiable fibrations. Hence the pullback of the canonical functor
![]() ${\mathcal C}' \to {\mathcal C}$
over
${\mathcal C}' \to {\mathcal C}$
over
![]() $[{n}]$
along the map
$[{n}]$
along the map
![]() $[1]\cong \{{i}-1< {i}\}\subset [{n}]$
identifies with the canonical equivalence
$[1]\cong \{{i}-1< {i}\}\subset [{n}]$
identifies with the canonical equivalence
This implies (2) by Corollary 7.8.
We prove (1). Since the pullback of the canonical functor
![]() ${\mathcal C}' \to {\mathcal C}$
over
${\mathcal C}' \to {\mathcal C}$
over
![]() $[{n}]$
along the map
$[{n}]$
along the map
![]() $[1]\cong \{{i}-1< {i}\}\subset [{n}]$
is an equivalence, the functor
$[1]\cong \{{i}-1< {i}\}\subset [{n}]$
is an equivalence, the functor
![]() ${\mathcal C}' \to [{n}]$
is the colimit of the following diagram:
${\mathcal C}' \to [{n}]$
is the colimit of the following diagram:

This implies (1) by [Reference Ayala and Francis2, Corollary 2.2.13., Corollary 2.2.11.].
We obtain the following proposition:
Proposition 7.11. Let
![]() ${n} \geq 0$
. The embedding
${n} \geq 0$
. The embedding
![]() $\mathrm {EXP}_{[{n}]} \subset \infty \mathrm {Cat}_{/[{n}]}$
admits a right adjoint. A functor
$\mathrm {EXP}_{[{n}]} \subset \infty \mathrm {Cat}_{/[{n}]}$
admits a right adjoint. A functor
![]() ${\mathcal C} \to {\mathcal D}$
over
${\mathcal C} \to {\mathcal D}$
over
![]() $[{n}]$
is a colocal equivalence if and only if it induces an equivalence after pulling back along any inert map
$[{n}]$
is a colocal equivalence if and only if it induces an equivalence after pulling back along any inert map
![]() $[1] \to [{n}].$
$[1] \to [{n}].$
Proof. By 7.10 for every functor
![]() ${\mathcal C} \to [{n}]$
the functor
${\mathcal C} \to [{n}]$
the functor
![]() ${\mathcal C}' \to [{n}]$
is an exponentiable fibration, and for every exponentiable fibration
${\mathcal C}' \to [{n}]$
is an exponentiable fibration, and for every exponentiable fibration
![]() ${\mathcal D} \to [{n}]$
the induced functor
${\mathcal D} \to [{n}]$
the induced functor
is an equivalence. This guarantees that the embedding
![]() $\mathrm {EXP}_{[{n}]} \subset \infty \mathrm {Cat}_{/[{n}]}$
admits a right adjoint that sends any functor
$\mathrm {EXP}_{[{n}]} \subset \infty \mathrm {Cat}_{/[{n}]}$
admits a right adjoint that sends any functor
![]() ${\mathcal C} \to [{n}]$
to the functor
${\mathcal C} \to [{n}]$
to the functor
![]() ${\mathcal C}' \to [{n}]$
.
${\mathcal C}' \to [{n}]$
.
For the next notation let
![]() $\tau :=(-)^{\mathrm {op}}: \infty \mathrm {Cat} \to \infty \mathrm {Cat}$
be the opposite
$\tau :=(-)^{\mathrm {op}}: \infty \mathrm {Cat} \to \infty \mathrm {Cat}$
be the opposite
![]() $\infty $
-category involution.
$\infty $
-category involution.
Proposition 7.12. The cartesian fibration
![]() ${\mathrm {CART}} \to \infty \mathrm {Cat}$
classifies the functor
${\mathrm {CART}} \to \infty \mathrm {Cat}$
classifies the functor
Proof. By Yoneda the cartesian fibration
![]() $\Delta \times _{\infty \mathrm {Cat}} {\mathrm {Cart}}=\tau ^*\infty {\mathrm {CAT}} \to \Delta $
classifies the functor
$\Delta \times _{\infty \mathrm {Cat}} {\mathrm {Cart}}=\tau ^*\infty {\mathrm {CAT}} \to \Delta $
classifies the functor
Since the full subcategory
![]() $\Delta \subset \infty \mathrm {Cat}$
is dense, it is enough to verify that the functor
$\Delta \subset \infty \mathrm {Cat}$
is dense, it is enough to verify that the functor
![]() $ \infty \mathrm {Cat}^{\mathrm {op}} \to \infty \widehat {\mathrm {Cat}}$
classified by the cartesian fibration
$ \infty \mathrm {Cat}^{\mathrm {op}} \to \infty \widehat {\mathrm {Cat}}$
classified by the cartesian fibration
![]() ${\mathrm {CART}} \to \infty \mathrm {Cat}$
and the functor
${\mathrm {CART}} \to \infty \mathrm {Cat}$
and the functor
send for every
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
the colimit of the functor
${\mathcal C}$
the colimit of the functor
![]() $\rho : \Delta \times _{\infty \mathrm {Cat}} \infty \mathrm {Cat}_{/{\mathcal C}} \to \Delta \subset \infty \mathrm {Cat}$
to a limit. We first prove the second statement: because the functor
$\rho : \Delta \times _{\infty \mathrm {Cat}} \infty \mathrm {Cat}_{/{\mathcal C}} \to \Delta \subset \infty \mathrm {Cat}$
to a limit. We first prove the second statement: because the functor
preserves small limits, it suffices to show that the embedding
![]() ${\mathrm N}: \infty \mathrm {Cat} \to \mathrm {Seg}({\mathcal S})\subset \mathrm {Seg}(\infty \mathrm {Cat})$
preserves the colimit of the functor
${\mathrm N}: \infty \mathrm {Cat} \to \mathrm {Seg}({\mathcal S})\subset \mathrm {Seg}(\infty \mathrm {Cat})$
preserves the colimit of the functor
![]() $\Delta \times _{\infty \mathrm {Cat}} \infty \mathrm {Cat}_{/{\mathcal C}} \to \Delta \subset \infty \mathrm {Cat}$
. The embedding
$\Delta \times _{\infty \mathrm {Cat}} \infty \mathrm {Cat}_{/{\mathcal C}} \to \Delta \subset \infty \mathrm {Cat}$
. The embedding
![]() ${\mathrm N}: \infty \mathrm {Cat} \to \mathrm {Seg}({\mathcal S})$
preserves this colimit because
${\mathrm N}: \infty \mathrm {Cat} \to \mathrm {Seg}({\mathcal S})$
preserves this colimit because
![]() $\mathrm {Seg}({\mathcal S})$
is a localization of
$\mathrm {Seg}({\mathcal S})$
is a localization of
![]() ${\mathcal P}(\Delta )$
and so for every
${\mathcal P}(\Delta )$
and so for every
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
the Segal space
${\mathcal C}$
the Segal space
![]() ${\mathrm N}({\mathcal C}) $
is the colimit of the functor
${\mathrm N}({\mathcal C}) $
is the colimit of the functor
which factors as
![]() ${\mathrm N} \rho .$
The embedding
${\mathrm N} \rho .$
The embedding
![]() $ \mathrm {Seg}({\mathcal S}) \subset \mathrm {Seg}(\infty \mathrm {Cat})$
preserves small colimits since the embedding
$ \mathrm {Seg}({\mathcal S}) \subset \mathrm {Seg}(\infty \mathrm {Cat})$
preserves small colimits since the embedding
![]() $\mathrm {Fun}(\Delta ^{\mathrm {op}},{\mathcal S}) \subset \mathrm {Fun}(\Delta ^{\mathrm {op}},\infty \mathrm {Cat})$
preserve small colimits and Segal equivalences: the generating Segal equivalences for
$\mathrm {Fun}(\Delta ^{\mathrm {op}},{\mathcal S}) \subset \mathrm {Fun}(\Delta ^{\mathrm {op}},\infty \mathrm {Cat})$
preserve small colimits and Segal equivalences: the generating Segal equivalences for
![]() $\mathrm {Fun}(\Delta ^{\mathrm {op}},{\mathcal S})$
are the canonical morphisms
$\mathrm {Fun}(\Delta ^{\mathrm {op}},{\mathcal S})$
are the canonical morphisms
for
![]() ${n} \geq 0$
, while the generating Segal equivalences for
${n} \geq 0$
, while the generating Segal equivalences for
![]() $\mathrm {Fun}(\Delta ^{\mathrm {op}},\infty \mathrm {Cat})$
are the canonical morphisms
$\mathrm {Fun}(\Delta ^{\mathrm {op}},\infty \mathrm {Cat})$
are the canonical morphisms
for
![]() ${n} \geq 0$
and
${n} \geq 0$
and
![]() ${\mathcal A}$
a small
${\mathcal A}$
a small
![]() $\infty $
-category.
$\infty $
-category.
We finish the proof by showing that the cartesian fibration
![]() ${\mathrm {CART}} \to \infty \mathrm {Cat}$
classifies a small limits preserving functor
${\mathrm {CART}} \to \infty \mathrm {Cat}$
classifies a small limits preserving functor
![]() $ \infty \mathrm {Cat}^{\mathrm {op}} \to \infty \widehat {\mathrm {Cat}}$
. Let
$ \infty \mathrm {Cat}^{\mathrm {op}} \to \infty \widehat {\mathrm {Cat}}$
. Let
![]() ${\mathrm H}: {\mathrm K} \to \infty \mathrm {Cat}$
be a functor that admits a colimit
${\mathrm H}: {\mathrm K} \to \infty \mathrm {Cat}$
be a functor that admits a colimit
![]() ${\mathcal A}$
. The canonical
${\mathcal A}$
. The canonical
![]() $\infty \mathrm {Cat}$
-linear functor
$\infty \mathrm {Cat}$
-linear functor
![]() $\rho : {\mathrm {CART}}_{{\mathcal A}} \to \lim _{{k} \in {\mathrm K}}{\mathrm {CART}}_{{\mathrm H}({k})}$
induces on morphism
$\rho : {\mathrm {CART}}_{{\mathcal A}} \to \lim _{{k} \in {\mathrm K}}{\mathrm {CART}}_{{\mathrm H}({k})}$
induces on morphism
![]() $\infty $
-categories between two functors
$\infty $
-categories between two functors
![]() ${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
the functor (7.1). The latter is an equivalence by Lemma 7.7 because by Corollary 3.27 every cartesian fibration is an exponentiable fibration. The induced map
${\mathcal C} \to {\mathcal A},{\mathcal D} \to {\mathcal A}$
the functor (7.1). The latter is an equivalence by Lemma 7.7 because by Corollary 3.27 every cartesian fibration is an exponentiable fibration. The induced map
![]() $\iota (\rho )$
is essentially surjective because it identifies with the canonical equivalence
$\iota (\rho )$
is essentially surjective because it identifies with the canonical equivalence
Corollary 7.13. The cartesian fibration
![]() ${\mathrm {CART}}^{\mathrm L} \to \infty \widehat {\mathrm {Cat}}$
classifies the functor
${\mathrm {CART}}^{\mathrm L} \to \infty \widehat {\mathrm {Cat}}$
classifies the functor
Proof. By Proposition 7.12 the cartesian fibration
![]() $\widehat {{\mathrm {CART}}} \to \infty \widehat {\mathrm {Cat}}$
classifies the functor
$\widehat {{\mathrm {CART}}} \to \infty \widehat {\mathrm {Cat}}$
classifies the functor
Hence the cartesian subfibration
![]() ${\mathrm {CART}}^{\mathrm L} \to \infty \widehat {\mathrm {Cat}}$
of
${\mathrm {CART}}^{\mathrm L} \to \infty \widehat {\mathrm {Cat}}$
of
![]() $ \widehat {{\mathrm {CART}}} \to \infty \widehat {\mathrm {Cat}}$
classifies the subfunctor
$ \widehat {{\mathrm {CART}}} \to \infty \widehat {\mathrm {Cat}}$
classifies the subfunctor
We obtain the following theorem:
Theorem 7.6.
-
1. The cartesian fibrations
 $$ \begin{align*}\infty{\mathrm{CAT}} \to \Delta,\end{align*} $$
$$ \begin{align*}\infty{\mathrm{CAT}} \to \Delta,\end{align*} $$
 $$ \begin{align*}\mathrm{PR}^{\mathrm L}\to \Delta,\end{align*} $$
$$ \begin{align*}\mathrm{PR}^{\mathrm L}\to \Delta,\end{align*} $$
 $$ \begin{align*}{\mathrm{CORR}} \to \Delta\end{align*} $$
$$ \begin{align*}{\mathrm{CORR}} \to \Delta\end{align*} $$
are double
 $\infty $
-categories.
$\infty $
-categories. -
2. There is a canonical pullback square of double
 $\infty $
-categories:
$\infty $
-categories: 
Proof. We first prove (2). By Corollary 4.3 there is a canonical pullback square

of cartesian fibrations over
![]() $\infty \mathrm {Cat}$
. Taking the pullback of the latter square along the embedding
$\infty \mathrm {Cat}$
. Taking the pullback of the latter square along the embedding
![]() $\Delta \subset \infty \mathrm {Cat}$
gives a pullback square
$\Delta \subset \infty \mathrm {Cat}$
gives a pullback square

of cartesian fibrations over
![]() $\Delta $
. Since the full subcategory of double
$\Delta $
. Since the full subcategory of double
![]() $\infty $
-categories within the
$\infty $
-categories within the
![]() $\infty $
-category of cartesian fibrations over
$\infty $
-category of cartesian fibrations over
![]() $\Delta $
is closed under small limits, the latter pullback square is a pullback square of double
$\Delta $
is closed under small limits, the latter pullback square is a pullback square of double
![]() $\infty $
-categories after we have proven that the cartesian fibrations
$\infty $
-categories after we have proven that the cartesian fibrations
![]() $\infty {\mathrm {CAT}} \to \Delta , \mathrm {PR}^{\mathrm L}\to \Delta $
are double
$\infty {\mathrm {CAT}} \to \Delta , \mathrm {PR}^{\mathrm L}\to \Delta $
are double
![]() $\infty $
-categories. This will then also imply (1).
$\infty $
-categories. This will then also imply (1).
So it remains to prove that the cartesian fibrations
![]() $\infty {\mathrm {CAT}} \to \Delta , \mathrm {PR}^{\mathrm L}\to \Delta $
are double
$\infty {\mathrm {CAT}} \to \Delta , \mathrm {PR}^{\mathrm L}\to \Delta $
are double
![]() $\infty $
-categories.
$\infty $
-categories.
The cartesian fibration
![]() $\infty {\mathrm {CAT}} \to \Delta $
is a double
$\infty {\mathrm {CAT}} \to \Delta $
is a double
![]() $\infty $
-category if for every
$\infty $
-category if for every
![]() ${n} \geq 0$
the induced functor
${n} \geq 0$
the induced functor
is an equivalence. If this is shown, passing to a larger universe also the functor
is an equivalence, which by definition of
![]() $\mathrm {Pr}^{\mathrm L}$
restricts to an equivalence
$\mathrm {Pr}^{\mathrm L}$
restricts to an equivalence
Therefore the cartesian fibration
![]() $\mathrm {PR}^{\mathrm L}\to \Delta $
is a double
$\mathrm {PR}^{\mathrm L}\to \Delta $
is a double
![]() $\infty $
-category if the cartesian fibration
$\infty $
-category if the cartesian fibration
![]() $\infty {\mathrm {CAT}} \to \Delta $
is a double
$\infty {\mathrm {CAT}} \to \Delta $
is a double
![]() $\infty $
-category.
$\infty $
-category.
So it remains to prove that the functor (7.3) is an equivalence. By Proposition 7.12 the functor (7.3) identifies with the induced functor
The latter induces on maximal subspaces the induced map
which is an equivalence since
![]() $[{n}] \simeq [1] \coprod _{[0]} \ldots \coprod _{[0]} [1]$
in
$[{n}] \simeq [1] \coprod _{[0]} \ldots \coprod _{[0]} [1]$
in
![]() $\infty \mathrm {Cat}.$
$\infty \mathrm {Cat}.$
So it remains to see that the functor (7.3) is fully faithful. The functor (7.3) induces on mapping spaces between cocartesian fibrations
![]() ${\mathcal C} \to [{n}], {\mathcal D} \to [{n}]$
the map on maximal subspaces underlying the canonical functor
${\mathcal C} \to [{n}], {\mathcal D} \to [{n}]$
the map on maximal subspaces underlying the canonical functor
The latter is an equivalence by Lemma 7.7 since every cocartesian fibration is exponentiable by Corollary 3.27.
For the next proposition we view
![]() $\infty \mathrm {Cat}$
as
$\infty \mathrm {Cat}$
as
![]() $(\infty ,2)$
-category via its internal hom:
$(\infty ,2)$
-category via its internal hom:
Proposition 7.14. The
![]() $(\infty ,2)$
-category underlying the double
$(\infty ,2)$
-category underlying the double
![]() $\infty $
-category
$\infty $
-category
![]() $\infty {\mathrm {CAT}}$
is
$\infty {\mathrm {CAT}}$
is
![]() $\infty \mathrm {Cat}$
viewed as enriched in itself via the internal hom.
$\infty \mathrm {Cat}$
viewed as enriched in itself via the internal hom.
Proof. Let
![]() $\infty {\mathrm {CAT}}'$
be the
$\infty {\mathrm {CAT}}'$
be the
![]() $(\infty ,2)$
-category underlying the double
$(\infty ,2)$
-category underlying the double
![]() $\infty $
-category
$\infty $
-category
![]() $\infty {\mathrm {CAT}}$
. Then the space of objects of
$\infty {\mathrm {CAT}}$
. Then the space of objects of
![]() $\infty {\mathrm {CAT}}'$
is
$\infty {\mathrm {CAT}}'$
is
![]() $\iota (\infty {\mathrm {CAT}}_{[0]}) \simeq \iota (\infty \mathrm {Cat})$
and for every
$\iota (\infty {\mathrm {CAT}}_{[0]}) \simeq \iota (\infty \mathrm {Cat})$
and for every
![]() ${\mathrm A},{\mathrm B} \in \infty \mathrm {Cat}$
there is a canonical equivalence
${\mathrm A},{\mathrm B} \in \infty \mathrm {Cat}$
there is a canonical equivalence
By the dual of Corollary 5.3 there is a canonical equivalence
In particular, for any
![]() ${\mathrm A},{\mathrm B},{\mathrm C} \in \infty \mathrm {Cat}$
there is a canonical equivalence
${\mathrm A},{\mathrm B},{\mathrm C} \in \infty \mathrm {Cat}$
there is a canonical equivalence
so that
![]() ${\mathrm A} \times {\mathrm B}$
is the tensor of
${\mathrm A} \times {\mathrm B}$
is the tensor of
![]() ${\mathrm A}$
and
${\mathrm A}$
and
![]() ${\mathrm B}$
in the sense of [Reference Heine19, Definition 2.51.] of the
${\mathrm B}$
in the sense of [Reference Heine19, Definition 2.51.] of the
![]() $\infty \mathrm {Cat}$
-enriched
$\infty \mathrm {Cat}$
-enriched
![]() $\infty $
-category
$\infty $
-category
![]() $\infty {\mathrm {CAT}}'$
. Thus
$\infty {\mathrm {CAT}}'$
. Thus
![]() $\infty {\mathrm {CAT}}'$
admits all tensors. By [Reference Heine18, Remark 3.63., Corollary 6.13.] this implies that there is a unique 2-functor
$\infty {\mathrm {CAT}}'$
admits all tensors. By [Reference Heine18, Remark 3.63., Corollary 6.13.] this implies that there is a unique 2-functor
![]() $\rho : \infty \mathrm {Cat} \to \infty {\mathrm {CAT}}'$
that preserves tensors and sends the final
$\rho : \infty \mathrm {Cat} \to \infty {\mathrm {CAT}}'$
that preserves tensors and sends the final
![]() $\infty $
-category to the final
$\infty $
-category to the final
![]() $\infty $
-category. By [Reference Heine20, Corollary 4.50.] the 2-functor
$\infty $
-category. By [Reference Heine20, Corollary 4.50.] the 2-functor
![]() $\rho $
is an equivalence since the 2-functor
$\rho $
is an equivalence since the 2-functor
![]() ${\mathrm {Mor}}_{\infty {\mathrm {CAT}}'}(*,-): \infty \mathrm {Cat} \to \infty \mathrm {Cat}$
preserves tensors.
${\mathrm {Mor}}_{\infty {\mathrm {CAT}}'}(*,-): \infty \mathrm {Cat} \to \infty \mathrm {Cat}$
preserves tensors.
Notation 7.15. Let
![]() $ \infty \widehat {\mathrm {Cat}}$
be the
$ \infty \widehat {\mathrm {Cat}}$
be the
![]() $(\infty ,2)$
-category of large
$(\infty ,2)$
-category of large
![]() $\infty $
-categories. Let
$\infty $
-categories. Let
![]() $\mathrm {Pr}^{\mathrm L} \subset \infty \widehat {\mathrm {Cat}}$
be the subcategory of the
$\mathrm {Pr}^{\mathrm L} \subset \infty \widehat {\mathrm {Cat}}$
be the subcategory of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\infty \widehat {\mathrm {Cat}}$
of presentable
$\infty \widehat {\mathrm {Cat}}$
of presentable
![]() $\infty $
-categories and left adjoints.
$\infty $
-categories and left adjoints.
Corollary 7.16. The
![]() $(\infty ,2)$
-category underlying the double
$(\infty ,2)$
-category underlying the double
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {PR}}^{\mathrm L}$
is
${\mathrm {PR}}^{\mathrm L}$
is
![]() $\mathrm {Pr}^{\mathrm L}$
.
$\mathrm {Pr}^{\mathrm L}$
.
Proof. By Proposition 7.14 the
![]() $(\infty ,2)$
-category underlying the double
$(\infty ,2)$
-category underlying the double
![]() $\infty $
-category
$\infty $
-category
![]() $\infty \widehat {{\mathrm {CAT}}}$
is
$\infty \widehat {{\mathrm {CAT}}}$
is
![]() $\infty \widehat {\mathrm {Cat}}$
viewed as enriched in itself via the internal hom. Restricting to subcategories gives the result.
$\infty \widehat {\mathrm {Cat}}$
viewed as enriched in itself via the internal hom. Restricting to subcategories gives the result.
The following remark gives another interpretation of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathrm {Pr}^{\mathrm L}:$
$\mathrm {Pr}^{\mathrm L}:$
Remark 7.7. By [Reference Lurie26, Proposition 4.8.1.15.] the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathrm {Pr}^{\mathrm L}$
admits a closed symmetric monoidal structure such that the inclusion
$\mathrm {Pr}^{\mathrm L}$
admits a closed symmetric monoidal structure such that the inclusion
![]() ${j}: \mathrm {Pr}^{\mathrm L} \subset \infty \widehat {\mathrm {Cat}}$
of
${j}: \mathrm {Pr}^{\mathrm L} \subset \infty \widehat {\mathrm {Cat}}$
of
![]() $\infty $
-categories refines to a lax symmetric monoidal functor. Being symmetric monoidal closed, the
$\infty $
-categories refines to a lax symmetric monoidal functor. Being symmetric monoidal closed, the
![]() $\infty $
-category
$\infty $
-category
![]() $\mathrm {Pr}^{\mathrm L}$
is enriched in itself [Reference Heine18, Proposition 6.10.] and so by transfer of enrichment along
$\mathrm {Pr}^{\mathrm L}$
is enriched in itself [Reference Heine18, Proposition 6.10.] and so by transfer of enrichment along
![]() ${j}$
also enriched in
${j}$
also enriched in
![]() $\infty \widehat {\mathrm {Cat}}$
. The lax symmetric monoidal inclusion
$\infty \widehat {\mathrm {Cat}}$
. The lax symmetric monoidal inclusion
![]() ${j}$
gives rise to an inclusion of
${j}$
gives rise to an inclusion of
![]() $(\infty ,2)$
-categories from
$(\infty ,2)$
-categories from
![]() $\mathrm {Pr}^{\mathrm L}$
- endowed with the transfered
$\mathrm {Pr}^{\mathrm L}$
- endowed with the transfered
![]() $\infty \widehat {\mathrm {Cat}}$
-enrichment - to
$\infty \widehat {\mathrm {Cat}}$
-enrichment - to
![]() $\infty \widehat {\mathrm {Cat}}$
endowed with the enrichment in itself by the internal hom, and so induces an equivalence from the transfered
$\infty \widehat {\mathrm {Cat}}$
endowed with the enrichment in itself by the internal hom, and so induces an equivalence from the transfered
![]() $\infty \widehat {\mathrm {Cat}}$
-enrichment on
$\infty \widehat {\mathrm {Cat}}$
-enrichment on
![]() $\mathrm {Pr}^{\mathrm L}$
to the subcategory of the
$\mathrm {Pr}^{\mathrm L}$
to the subcategory of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\infty \widehat {\mathrm {Cat}}$
of presentable
$\infty \widehat {\mathrm {Cat}}$
of presentable
![]() $\infty $
-categories and left adjoint functors.
$\infty $
-categories and left adjoint functors.
Definition 7.17. Let
![]() $\mathrm {Corr}$
be the
$\mathrm {Corr}$
be the
![]() $(\infty ,2)$
-precategory underlying the double
$(\infty ,2)$
-precategory underlying the double
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {CORR}}.$
${\mathrm {CORR}}.$
Corollary 7.18. There is a canonical pullback square of
![]() $(\infty ,2)$
-precategories:
$(\infty ,2)$
-precategories:

Proof. By Theorem 7.6 there is a canonical pullback square of double
![]() $\infty $
-categories:
$\infty $
-categories:

Passing to underlying
![]() $(\infty ,2)$
-categories gives the result since by Corollary 7.16 the
$(\infty ,2)$
-categories gives the result since by Corollary 7.16 the
![]() $(\infty ,2)$
-category underlying the double
$(\infty ,2)$
-category underlying the double
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathrm {PR}}^{\mathrm L}$
is
${\mathrm {PR}}^{\mathrm L}$
is
![]() $\mathrm {Pr}^{\mathrm L}$
.
$\mathrm {Pr}^{\mathrm L}$
.
Corollary 7.19. The univalent completion of the
![]() $(\infty ,2)$
-precategory
$(\infty ,2)$
-precategory
![]() ${\mathrm {Corr}}$
is the full subcategory of the
${\mathrm {Corr}}$
is the full subcategory of the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathrm {Pr}^{\mathrm L}$
spanned by the
$\mathrm {Pr}^{\mathrm L}$
spanned by the
![]() $\infty $
-categories of presheaves.
$\infty $
-categories of presheaves.
Proof. We prove that the canonical 2-functor
![]() $\theta : \mathrm {Corr} \to \mathrm {Pr}^{\mathrm L}$
is fully faithful, that is, induces equivalences on morphism
$\theta : \mathrm {Corr} \to \mathrm {Pr}^{\mathrm L}$
is fully faithful, that is, induces equivalences on morphism
![]() $\infty $
-categories. This implies the result since in this case the 2-functor
$\infty $
-categories. This implies the result since in this case the 2-functor
![]() $\theta $
induces a fully faithful and essentially surjective 2-functor from
$\theta $
induces a fully faithful and essentially surjective 2-functor from
![]() ${\mathrm {Corr}} $
to the full subcategory of
${\mathrm {Corr}} $
to the full subcategory of
![]() $\mathrm {Pr}^{\mathrm L}$
spanned by the
$\mathrm {Pr}^{\mathrm L}$
spanned by the
![]() $\infty $
-categories of presheaves. The latter 2-functor exhibits the target as the univalent completion of the source since by [Reference Heine18, Corollary 6.12.] the local equivalences to a local object for the univalent completion are precisely the fully faithful and essentially surjective 2-functors.
$\infty $
-categories of presheaves. The latter 2-functor exhibits the target as the univalent completion of the source since by [Reference Heine18, Corollary 6.12.] the local equivalences to a local object for the univalent completion are precisely the fully faithful and essentially surjective 2-functors.
So we prove that
![]() $\theta : \mathrm {Corr} \to \mathrm {Pr}^{\mathrm L}$
is fully faithful. Evaluating the pullback square of Corollary 7.18 at
$\theta : \mathrm {Corr} \to \mathrm {Pr}^{\mathrm L}$
is fully faithful. Evaluating the pullback square of Corollary 7.18 at
![]() $[1]\in \Delta $
gives a pullback square
$[1]\in \Delta $
gives a pullback square

of
![]() $\infty $
-categories, which induces on the fiber over any
$\infty $
-categories, which induces on the fiber over any
![]() ${\mathrm X},{\mathrm Y} \in \iota (\infty \mathrm {Cat})$
the induced functor
${\mathrm X},{\mathrm Y} \in \iota (\infty \mathrm {Cat})$
the induced functor
on morphism
![]() $\infty $
-categories. The latter functor is an equivalence since the square is a pullback square.
$\infty $
-categories. The latter functor is an equivalence since the square is a pullback square.
Corollary 7.20. Let
![]() ${\mathcal C}$
be a small
${\mathcal C}$
be a small
![]() $\infty $
-category. There is a canonical equivalence of
$\infty $
-category. There is a canonical equivalence of
![]() $\infty $
-categories
$\infty $
-categories
Proof. By Corollary 4.3 and Proposition 7.13 there is a canonical equivalence
In the following we prove a refinement of Corollary 7.20.
Notation 7.21. Let
![]() $\phi : {\mathcal A} \to \Delta $
be a cartesian fibration. Let
$\phi : {\mathcal A} \to \Delta $
be a cartesian fibration. Let
![]() ${\mathcal A}^\vee \to \Delta ^{\mathrm {op}}$
be the corresponding cocartesian fibration classifying the same functor as
${\mathcal A}^\vee \to \Delta ^{\mathrm {op}}$
be the corresponding cocartesian fibration classifying the same functor as
![]() $\phi .$
$\phi .$
Definition 7.22. Let
![]() ${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
![]() $\infty $
-categories.
$\infty $
-categories.
-
○ A lax map of double
 $\infty $
-categories
$\infty $
-categories
 ${\mathcal A} \to {\mathcal B}$
is a functor
${\mathcal A} \to {\mathcal B}$
is a functor
 ${\mathcal A}^\vee \to {\mathcal B}^\vee $
over
${\mathcal A}^\vee \to {\mathcal B}^\vee $
over
 $\Delta ^{\mathrm {op}}$
preserving cocartesian lifts of inert morphisms of
$\Delta ^{\mathrm {op}}$
preserving cocartesian lifts of inert morphisms of
 $\Delta $
(Definition 3.25).
$\Delta $
(Definition 3.25). -
○ A lax normal map of double
 $\infty $
-categories
$\infty $
-categories
 ${\mathcal A} \to {\mathcal B}$
is a functor
${\mathcal A} \to {\mathcal B}$
is a functor
 ${\mathcal A}^\vee \to {\mathcal B}^\vee $
over
${\mathcal A}^\vee \to {\mathcal B}^\vee $
over
 $\Delta ^{\mathrm {op}}$
preserving cocartesian lifts of inert morphisms of
$\Delta ^{\mathrm {op}}$
preserving cocartesian lifts of inert morphisms of
 $\Delta $
and cocartesian lifts of morphisms of the form
$\Delta $
and cocartesian lifts of morphisms of the form
 $[{n}] \to [0]$
for
$[{n}] \to [0]$
for
 ${n} \geq 0$
.
${n} \geq 0$
.
The embedding
![]() ${\mathrm {CORR}} \subset {\mathrm {CORR}}_{\mathrm {Lax}}$
of cartesian fibrations over
${\mathrm {CORR}} \subset {\mathrm {CORR}}_{\mathrm {Lax}}$
of cartesian fibrations over
![]() $\Delta $
induces an embedding
$\Delta $
induces an embedding
![]() ${\mathrm {CORR}}^\vee \subset {\mathrm {CORR}}^\vee _{\mathrm {Lax}}$
of cocartesian fibrations over
${\mathrm {CORR}}^\vee \subset {\mathrm {CORR}}^\vee _{\mathrm {Lax}}$
of cocartesian fibrations over
![]() $\Delta ^{\mathrm {op}}.$
$\Delta ^{\mathrm {op}}.$
Corollary 7.23. The embedding
![]() ${\mathrm {CORR}}^\vee \subset {\mathrm {CORR}}_{\mathrm {Lax}}^\vee $
of cocartesian fibrations over
${\mathrm {CORR}}^\vee \subset {\mathrm {CORR}}_{\mathrm {Lax}}^\vee $
of cocartesian fibrations over
![]() $\Delta ^{\mathrm {op}}$
admits a right adjoint relative to
$\Delta ^{\mathrm {op}}$
admits a right adjoint relative to
![]() $\Delta ^{\mathrm {op}}.$
$\Delta ^{\mathrm {op}}.$
Proof. To see that the embedding
![]() ${\mathrm {CORR}}^\vee \subset {\mathrm {CORR}}_{\mathrm {Lax}}^\vee $
of cocartesian fibrations over
${\mathrm {CORR}}^\vee \subset {\mathrm {CORR}}_{\mathrm {Lax}}^\vee $
of cocartesian fibrations over
![]() $\Delta ^{\mathrm {op}}$
admits a right adjoint relative to
$\Delta ^{\mathrm {op}}$
admits a right adjoint relative to
![]() $\Delta ^{\mathrm {op}},$
by [Reference Lurie26, Proposition 7.3.2.6.] it suffices to see that for every
$\Delta ^{\mathrm {op}},$
by [Reference Lurie26, Proposition 7.3.2.6.] it suffices to see that for every
![]() $[{n}] \in \Delta $
the induced functor
$[{n}] \in \Delta $
the induced functor
on the fiber over
![]() $[{n}]$
admits a right adjoint. The latter functor is the embedding
$[{n}]$
admits a right adjoint. The latter functor is the embedding
![]() $\mathrm {EXP}_{[{n}]} \subset \infty \mathrm {Cat}_{/[{n}]}$
, which admits a right adjoint by Proposition 7.11.
$\mathrm {EXP}_{[{n}]} \subset \infty \mathrm {Cat}_{/[{n}]}$
, which admits a right adjoint by Proposition 7.11.
Example 7.8. The relative right adjoint
![]() ${\mathrm {CORR}}_{\mathrm {Lax}}^\vee \to {\mathrm {CORR}}^\vee $
preserves cocartesian lifts of inert morphisms because the left adjoint does. So the right adjoint determines a lax map
${\mathrm {CORR}}_{\mathrm {Lax}}^\vee \to {\mathrm {CORR}}^\vee $
preserves cocartesian lifts of inert morphisms because the left adjoint does. So the right adjoint determines a lax map
![]() ${\mathrm {CORR}}_{\mathrm {Lax}} \to {\mathrm {CORR}}$
of double
${\mathrm {CORR}}_{\mathrm {Lax}} \to {\mathrm {CORR}}$
of double
![]() $\infty $
-categories, which is a lax normal map.
$\infty $
-categories, which is a lax normal map.
Remark 7.9. Let
![]() ${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
![]() $\infty $
-categories. There is a canonical equivalence
$\infty $
-categories. There is a canonical equivalence
to the full subcategory of
![]() $ \mathrm {Fun}_{\Delta ^{\mathrm {op}}}({\mathcal A}^\vee ,{\mathcal B}^\vee )$
spanned by the maps
$ \mathrm {Fun}_{\Delta ^{\mathrm {op}}}({\mathcal A}^\vee ,{\mathcal B}^\vee )$
spanned by the maps
![]() ${\mathcal A}^\vee \to {\mathcal B}^\vee $
of cocartesian fibrations over
${\mathcal A}^\vee \to {\mathcal B}^\vee $
of cocartesian fibrations over
![]() $\Delta ^{\mathrm {op}}$
.
$\Delta ^{\mathrm {op}}$
.
Notation 7.24. Let
![]() ${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
${\mathcal A} \to \Delta , {\mathcal B} \to \Delta $
be double
![]() $\infty $
-categories.
$\infty $
-categories.
-
○ Let
 $$ \begin{align*}\mathrm{Lax}\mathrm{Fun}({\mathcal A},{\mathcal B}) \subset \mathrm{Fun}_{\Delta^{\mathrm{op}}}({\mathcal A}^\vee,{\mathcal B}^\vee)\end{align*} $$
$$ \begin{align*}\mathrm{Lax}\mathrm{Fun}({\mathcal A},{\mathcal B}) \subset \mathrm{Fun}_{\Delta^{\mathrm{op}}}({\mathcal A}^\vee,{\mathcal B}^\vee)\end{align*} $$
be the full subcategory spanned by the lax maps of double
 $\infty $
-categories
$\infty $
-categories
 ${\mathcal A} \to {\mathcal B}.$
${\mathcal A} \to {\mathcal B}.$
-
○ Let
 $$ \begin{align*}{\mathrm N}\mathrm{Lax}\mathrm{Fun}({\mathcal A},{\mathcal B}) \subset \mathrm{Fun}_{\Delta^{\mathrm{op}}}({\mathcal A}^\vee,{\mathcal B}^\vee)\end{align*} $$
$$ \begin{align*}{\mathrm N}\mathrm{Lax}\mathrm{Fun}({\mathcal A},{\mathcal B}) \subset \mathrm{Fun}_{\Delta^{\mathrm{op}}}({\mathcal A}^\vee,{\mathcal B}^\vee)\end{align*} $$
be the full subcategory spanned by the lax normal maps of double
 $\infty $
-categories
$\infty $
-categories
 ${\mathcal A} \to {\mathcal B}.$
${\mathcal A} \to {\mathcal B}.$
Notation 7.25. Let
![]() ${\mathrm {Act}} \subset \mathrm {Fun}([1],\Delta )$
be the full subcategory of active morphisms, that is, order preserving maps
${\mathrm {Act}} \subset \mathrm {Fun}([1],\Delta )$
be the full subcategory of active morphisms, that is, order preserving maps
![]() $[{n}]\to [{m}]$
preserving the minimum and maximum.
$[{n}]\to [{m}]$
preserving the minimum and maximum.
Let
![]() ${\mathcal C} \to \Delta $
be a double
${\mathcal C} \to \Delta $
be a double
![]() $\infty $
-category. By [Reference Heine18, Proposition 3.92.] evaluation at the target
$\infty $
-category. By [Reference Heine18, Proposition 3.92.] evaluation at the target
is a cocartesian fibration, where the pullback is formed along evaluation at the source.
Notation 7.26. Let
![]() ${\mathcal C} \to \Delta $
be a double
${\mathcal C} \to \Delta $
be a double
![]() $\infty $
-category. Let
$\infty $
-category. Let
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta $
be the cartesian fibration corresponding to the cocartesian fibration (7.4).
${\mathrm {Env}}({\mathcal C}) \to \Delta $
be the cartesian fibration corresponding to the cocartesian fibration (7.4).
By [Reference Heine18, Proposition 3.92.] the cartesian fibration
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta $
is a double
${\mathrm {Env}}({\mathcal C}) \to \Delta $
is a double
![]() $\infty $
-category and for every double
$\infty $
-category and for every double
![]() $\infty $
-category
$\infty $
-category
![]() $ {\mathcal D} \to \Delta $
the induced functor
$ {\mathcal D} \to \Delta $
the induced functor
is an equivalence.
Example 7.10. The diagonal embedding
![]() $\Delta \subset {\mathrm {Act}}$
induces an embedding
$\Delta \subset {\mathrm {Act}}$
induces an embedding
![]() ${\mathcal C}^\vee \subset {\mathrm {Act}}^{\mathrm {op}} \times _{\Delta ^{\mathrm {op}}} {\mathcal C}^\vee $
over
${\mathcal C}^\vee \subset {\mathrm {Act}}^{\mathrm {op}} \times _{\Delta ^{\mathrm {op}}} {\mathcal C}^\vee $
over
![]() $\Delta ^{\mathrm {op}}$
that determines a lax map of double
$\Delta ^{\mathrm {op}}$
that determines a lax map of double
![]() $\infty $
-categories
$\infty $
-categories
![]() ${\mathcal C} \to {\mathrm {Env}}({\mathcal C}).$
${\mathcal C} \to {\mathrm {Env}}({\mathcal C}).$
Remark 7.11. By [Reference Heine18, Proposition 3.93.] the embedding
![]() ${\mathcal C}^\vee \subset {\mathrm {Act}}^{\mathrm {op}} \times _{\Delta ^{\mathrm {op}}} {\mathcal C}^\vee $
over
${\mathcal C}^\vee \subset {\mathrm {Act}}^{\mathrm {op}} \times _{\Delta ^{\mathrm {op}}} {\mathcal C}^\vee $
over
![]() $\Delta ^{\mathrm {op}}$
admits a left adjoint relative to
$\Delta ^{\mathrm {op}}$
admits a left adjoint relative to
![]() $\Delta ^{\mathrm {op}}$
, which is a map of cocartesian fibrations over
$\Delta ^{\mathrm {op}}$
, which is a map of cocartesian fibrations over
![]() $\Delta ^{\mathrm {op}}.$
So this left adjoint corresponds to a map
$\Delta ^{\mathrm {op}}.$
So this left adjoint corresponds to a map
![]() ${\mathrm {Env}}({\mathcal C}) \to {\mathcal C}$
of cartesian fibrations over
${\mathrm {Env}}({\mathcal C}) \to {\mathcal C}$
of cartesian fibrations over
![]() $\Delta $
, in other words to a map of double
$\Delta $
, in other words to a map of double
![]() $\infty $
-categories.
$\infty $
-categories.
Remark 7.12. Let
![]() ${\mathcal C} \to \Delta $
be a double
${\mathcal C} \to \Delta $
be a double
![]() $\infty $
-category. There is a canonical equivalence
$\infty $
-category. There is a canonical equivalence
![]() ${\mathrm {Env}}({\mathcal C})_{[0]} \simeq {\mathcal C}^\vee _{[0]} \simeq {\mathcal C}_{[0]}$
since
${\mathrm {Env}}({\mathcal C})_{[0]} \simeq {\mathcal C}^\vee _{[0]} \simeq {\mathcal C}_{[0]}$
since
![]() ${\mathrm {Act}}_{[0]/} $
is contractible. Consequently,
${\mathrm {Act}}_{[0]/} $
is contractible. Consequently,
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta $
is an
${\mathrm {Env}}({\mathcal C}) \to \Delta $
is an
![]() $(\infty ,2)$
-precategory if
$(\infty ,2)$
-precategory if
![]() ${\mathcal C} \to \Delta $
is an
${\mathcal C} \to \Delta $
is an
![]() $(\infty ,2)$
-precategory.
$(\infty ,2)$
-precategory.
Remark 7.13. Let
![]() ${\mathcal C} \to \Delta $
be a double
${\mathcal C} \to \Delta $
be a double
![]() $\infty $
-category. Every morphism of
$\infty $
-category. Every morphism of
![]() ${\mathrm {Env}}({\mathcal C})$
, that is, object of
${\mathrm {Env}}({\mathcal C})$
, that is, object of
![]() ${\mathrm {Env}}({\mathcal C})_{[1]}$
, lies in the image of the restricted composition functor
${\mathrm {Env}}({\mathcal C})_{[1]}$
, lies in the image of the restricted composition functor
In other words, any horizontal morphism of
![]() ${\mathrm {Env}}({\mathcal C})\to \Delta $
is of the form
${\mathrm {Env}}({\mathcal C})\to \Delta $
is of the form
![]() $\alpha _1 \circ \ldots \circ \alpha _{n}$
for some
$\alpha _1 \circ \ldots \circ \alpha _{n}$
for some
![]() ${n} \geq 0$
and composable horizontal morphisms
${n} \geq 0$
and composable horizontal morphisms
![]() $\alpha _1 ,\ldots, \alpha _{n}$
of
$\alpha _1 ,\ldots, \alpha _{n}$
of
![]() ${\mathcal C}$
, where
${\mathcal C}$
, where
![]() $\circ $
is the horizontal composition.
$\circ $
is the horizontal composition.
Remark 7.14. Let
![]() ${\mathcal C} \to \Delta $
be an
${\mathcal C} \to \Delta $
be an
![]() $(\infty ,2)$
-category. Then
$(\infty ,2)$
-category. Then
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta $
is an
${\mathrm {Env}}({\mathcal C}) \to \Delta $
is an
![]() $(\infty ,2)$
-category: by Remark 7.12 the canonical map
$(\infty ,2)$
-category: by Remark 7.12 the canonical map
![]() $\iota ({\mathrm {Env}}({\mathcal C})_{[0]}) \to \iota ({\mathrm {Env}}({\mathcal C})_{[1]})$
factors as
$\iota ({\mathrm {Env}}({\mathcal C})_{[0]}) \to \iota ({\mathrm {Env}}({\mathcal C})_{[1]})$
factors as
and so is an embedding if
![]() ${\mathcal C} $
is an
${\mathcal C} $
is an
![]() $(\infty ,2)$
-category. Hence in view of Remark 7.13 it suffices to observe that for every
$(\infty ,2)$
-category. Hence in view of Remark 7.13 it suffices to observe that for every
![]() ${n}, {m} \geq 0$
and composable horizontal morphisms
${n}, {m} \geq 0$
and composable horizontal morphisms
![]() $\alpha _1,\ldots, \alpha _{n}, \beta _1 ,\ldots, \beta _{m}$
of
$\alpha _1,\ldots, \alpha _{n}, \beta _1 ,\ldots, \beta _{m}$
of
![]() $ {\mathcal C}\to \Delta $
such that the horizontal composition
$ {\mathcal C}\to \Delta $
such that the horizontal composition
![]() $\alpha _1 \circ \ldots \circ \alpha _{n} \circ \beta _1 \circ \ldots \circ \beta _{m}$
in
$\alpha _1 \circ \ldots \circ \alpha _{n} \circ \beta _1 \circ \ldots \circ \beta _{m}$
in
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta $
is the 0-fold composition, we find that
${\mathrm {Env}}({\mathcal C}) \to \Delta $
is the 0-fold composition, we find that
![]() ${n}+{m}=0$
so that
${n}+{m}=0$
so that
![]() ${n}={m}=0.$
${n}={m}=0.$
Notation 7.27. Let
![]() $\phi : {\mathcal C} \to \Delta $
be an
$\phi : {\mathcal C} \to \Delta $
be an
![]() $\infty $
-precategory and
$\infty $
-precategory and
![]() ${\mathcal W}$
a set of morphisms of
${\mathcal W}$
a set of morphisms of
![]() ${\mathcal C}_{[1]}$
corresponding to 2-morphisms of
${\mathcal C}_{[1]}$
corresponding to 2-morphisms of
![]() ${\mathcal C} \to \Delta $
. For every
${\mathcal C} \to \Delta $
. For every
![]() ${n} \geq 1$
let
${n} \geq 1$
let
![]() ${\mathcal W}_{n}$
be the set of morphisms of
${\mathcal W}_{n}$
be the set of morphisms of
![]() ${\mathcal C}_{[{n}]}$
whose image under the functor
${\mathcal C}_{[{n}]}$
whose image under the functor
![]() ${\mathcal C}_{[{n}]}\to {\mathcal C}_{[1]} $
induced by the map
${\mathcal C}_{[{n}]}\to {\mathcal C}_{[1]} $
induced by the map
![]() $[1] \cong \{{i}-1<{i}\}\to [{n}]$
for any
$[1] \cong \{{i}-1<{i}\}\to [{n}]$
for any
![]() $0 \leq {i} < {n}$
is a morphism of
$0 \leq {i} < {n}$
is a morphism of
![]() ${\mathcal W}.$
Let
${\mathcal W}.$
Let
![]() ${\mathcal W}_0$
be the set of all morphisms of
${\mathcal W}_0$
be the set of all morphisms of
![]() ${\mathcal C}_{[0]}.$
Let
${\mathcal C}_{[0]}.$
Let
![]() $\bar {{\mathcal W}} $
be the smallest set of morphisms of
$\bar {{\mathcal W}} $
be the smallest set of morphisms of
![]() ${\mathcal C}$
containing all images of morphisms of
${\mathcal C}$
containing all images of morphisms of
![]() ${\mathcal W}_{n}$
in
${\mathcal W}_{n}$
in
![]() ${\mathcal C}$
for
${\mathcal C}$
for
![]() ${n} \geq 0.$
${n} \geq 0.$
Let
![]() $\phi : {\mathcal C} \to \Delta $
be an
$\phi : {\mathcal C} \to \Delta $
be an
![]() $\infty $
-precategory and
$\infty $
-precategory and
![]() ${\mathcal W}$
a set of morphisms of
${\mathcal W}$
a set of morphisms of
![]() ${\mathcal C}_{[1]}$
. Let
${\mathcal C}_{[1]}$
. Let
![]() ${\mathcal C}[{\mathcal W}]:= {\mathcal C}[\bar {{\mathcal W}}]$
be the localization of the
${\mathcal C}[{\mathcal W}]:= {\mathcal C}[\bar {{\mathcal W}}]$
be the localization of the
![]() $\infty $
-category
$\infty $
-category
![]() ${\mathcal C}$
with respect to the set
${\mathcal C}$
with respect to the set
![]() $\bar {{\mathcal W}}$
. The functor
$\bar {{\mathcal W}}$
. The functor
![]() $\phi : {\mathcal C} \to \Delta $
induces a functor
$\phi : {\mathcal C} \to \Delta $
induces a functor
![]() ${\mathcal C}[{\mathcal W}] \to \Delta $
, which by [Reference Hinich24, 2.1.4. Proposition] is a cartesian fibration whose fiber over any
${\mathcal C}[{\mathcal W}] \to \Delta $
, which by [Reference Hinich24, 2.1.4. Proposition] is a cartesian fibration whose fiber over any
![]() $[{n}]\in \Delta $
is the localization
$[{n}]\in \Delta $
is the localization
![]() ${\mathcal C}_{[{n}]}[{\mathcal W}_{n}].$
In particular,
${\mathcal C}_{[{n}]}[{\mathcal W}_{n}].$
In particular,
![]() ${\mathcal C}[{\mathcal W}]_{[0]} \simeq {\mathcal C}_{[0]}[{\mathcal W}_0] \simeq {\mathcal C}_{[0]}.$
By the next lemma the cartesian fibration
${\mathcal C}[{\mathcal W}]_{[0]} \simeq {\mathcal C}_{[0]}[{\mathcal W}_0] \simeq {\mathcal C}_{[0]}.$
By the next lemma the cartesian fibration
![]() ${\mathcal C}[{\mathcal W}] \to \Delta $
is an
${\mathcal C}[{\mathcal W}] \to \Delta $
is an
![]() $\infty $
-precategory.
$\infty $
-precategory.
Lemma 7.28. Let
![]() ${\mathcal C}$
be a space,
${\mathcal C}$
be a space,
![]() ${\mathcal A} \to {\mathcal C}, {\mathcal B} \to {\mathcal C}$
functors and
${\mathcal A} \to {\mathcal C}, {\mathcal B} \to {\mathcal C}$
functors and
![]() ${\mathcal W} $
a set of morphisms of
${\mathcal W} $
a set of morphisms of
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal V}$
a set of morphisms of
${\mathcal V}$
a set of morphisms of
![]() ${\mathcal B}$
containing all equivalences. The canonical functor
${\mathcal B}$
containing all equivalences. The canonical functor
is an equivalence.
Proof. The functor
![]() $\theta $
is a functor over the space
$\theta $
is a functor over the space
![]() ${\mathcal C}$
and so is an equivalence if it induces an equivalence on the fiber over every
${\mathcal C}$
and so is an equivalence if it induces an equivalence on the fiber over every
![]() ${\mathrm Z} \in {\mathcal C}.$
For every
${\mathrm Z} \in {\mathcal C}.$
For every
![]() ${\mathrm Z} \in {\mathcal C}$
let
${\mathrm Z} \in {\mathcal C}$
let
![]() ${\mathcal W}_{\mathrm Z}$
be the set of morphisms of
${\mathcal W}_{\mathrm Z}$
be the set of morphisms of
![]() ${\mathcal A}_{\mathrm Z}$
whose image in
${\mathcal A}_{\mathrm Z}$
whose image in
![]() ${\mathcal A}$
belongs to
${\mathcal A}$
belongs to
![]() ${\mathcal W}.$
Similarly, we define
${\mathcal W}.$
Similarly, we define
![]() ${\mathcal V}_{\mathrm Z}.$
The functor
${\mathcal V}_{\mathrm Z}.$
The functor
![]() $\theta $
induces on the fiber over
$\theta $
induces on the fiber over
![]() ${\mathrm Z}$
the canonical functor
${\mathrm Z}$
the canonical functor
which by [Reference Hinich24, 2.1.4. Proposition] identifies with the canonical functor
The latter is an equivalence by universal property of the localization using that
![]() ${\mathcal W},{\mathcal V}$
contain all equivalences.
${\mathcal W},{\mathcal V}$
contain all equivalences.
Definition 7.29. Let
![]() ${\mathcal C} \to \Delta $
be an
${\mathcal C} \to \Delta $
be an
![]() $\infty $
-precategory. Let
$\infty $
-precategory. Let
![]() ${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
be the localization of
${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
be the localization of
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta $
with respect to the smallest set of
${\mathrm {Env}}({\mathcal C}) \to \Delta $
with respect to the smallest set of
![]() ${\mathrm {Env}}({\mathcal C})_{[1]}$
containing the morphisms
${\mathrm {Env}}({\mathcal C})_{[1]}$
containing the morphisms
![]() $\mathrm {id}^{{\mathrm {Env}}({\mathcal C})}_{\mathrm X} \to \mathrm {id}^{\mathcal C}_{\mathrm X} $
of
$\mathrm {id}^{{\mathrm {Env}}({\mathcal C})}_{\mathrm X} \to \mathrm {id}^{\mathcal C}_{\mathrm X} $
of
![]() ${\mathrm {Env}}({\mathcal C})_{[1]}$
for
${\mathrm {Env}}({\mathcal C})_{[1]}$
for
![]() ${\mathrm X} \in {\mathcal C}_{[0]}$
and all equivalences of
${\mathrm X} \in {\mathcal C}_{[0]}$
and all equivalences of
![]() ${\mathrm {Env}}({\mathcal C})_{[1]}$
and closed under horizontal composition of the
${\mathrm {Env}}({\mathcal C})_{[1]}$
and closed under horizontal composition of the
![]() $\infty $
-precategory
$\infty $
-precategory
![]() ${\mathrm {Env}}({\mathcal C}) \to \Delta .$
${\mathrm {Env}}({\mathcal C}) \to \Delta .$
Remark 7.15. The localization
![]() ${\mathrm {Env}}({\mathcal C})^\vee \to {\mathcal C}^\vee $
relative to
${\mathrm {Env}}({\mathcal C})^\vee \to {\mathcal C}^\vee $
relative to
![]() $\Delta ^{\mathrm {op}}$
whose left adjoint inverts local equivalences, gives rise to a localization
$\Delta ^{\mathrm {op}}$
whose left adjoint inverts local equivalences, gives rise to a localization
![]() ${\mathrm N}{\mathrm {Env}}({\mathcal C})^\vee \to {\mathcal C}^\vee $
relative to
${\mathrm N}{\mathrm {Env}}({\mathcal C})^\vee \to {\mathcal C}^\vee $
relative to
![]() $\Delta ^{\mathrm {op}}.$
Hence the right adjoint is an embedding
$\Delta ^{\mathrm {op}}.$
Hence the right adjoint is an embedding
![]() ${\mathcal C}^\vee \subset {\mathrm N}{\mathrm {Env}}({\mathcal C})^\vee $
that factors as
${\mathcal C}^\vee \subset {\mathrm N}{\mathrm {Env}}({\mathcal C})^\vee $
that factors as
and so corresponds to a lax normal map
![]() ${\mathcal C} \to {\mathrm N}{\mathrm {Env}}({\mathcal C})$
of double
${\mathcal C} \to {\mathrm N}{\mathrm {Env}}({\mathcal C})$
of double
![]() $\infty $
-categories.
$\infty $
-categories.
Remark 7.16. By definition the canonical functor
![]() ${\mathrm {Env}}({\mathcal C}) \to {\mathrm N}{\mathrm {Env}}({\mathcal C})$
over
${\mathrm {Env}}({\mathcal C}) \to {\mathrm N}{\mathrm {Env}}({\mathcal C})$
over
![]() $\Delta $
induces an equivalence
$\Delta $
induces an equivalence
![]() ${\mathrm {Env}}({\mathcal C})_{[0]} \simeq {\mathrm N}{\mathrm {Env}}({\mathcal C})_{[0]}.$
Thus the embedding
${\mathrm {Env}}({\mathcal C})_{[0]} \simeq {\mathrm N}{\mathrm {Env}}({\mathcal C})_{[0]}.$
Thus the embedding
![]() ${\mathcal C}^\vee \subset {\mathrm N}{\mathrm {Env}}({\mathcal C})^\vee $
over
${\mathcal C}^\vee \subset {\mathrm N}{\mathrm {Env}}({\mathcal C})^\vee $
over
![]() $\Delta $
induces an equivalence
$\Delta $
induces an equivalence
![]() ${\mathcal C}_{[0]} \simeq {\mathrm N}{\mathrm {Env}}({\mathcal C})_{[0]}.$
${\mathcal C}_{[0]} \simeq {\mathrm N}{\mathrm {Env}}({\mathcal C})_{[0]}.$
Remark 7.17. Let
![]() ${\mathcal C} \to \Delta $
be an
${\mathcal C} \to \Delta $
be an
![]() $(\infty ,2)$
-category. Then
$(\infty ,2)$
-category. Then
![]() ${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
is an
${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
is an
![]() $(\infty ,2)$
-category by a similar argument like in Remark 7.14: by Remark 7.16 the canonical map
$(\infty ,2)$
-category by a similar argument like in Remark 7.14: by Remark 7.16 the canonical map
![]() $\iota ({\mathrm N}{\mathrm {Env}}({\mathcal C})_{[0]}) \to \iota ({\mathrm N}{\mathrm {Env}}({\mathcal C})_{[1]})$
factors as
$\iota ({\mathrm N}{\mathrm {Env}}({\mathcal C})_{[0]}) \to \iota ({\mathrm N}{\mathrm {Env}}({\mathcal C})_{[1]})$
factors as
and so is an embedding if
![]() ${\mathcal C} $
is an
${\mathcal C} $
is an
![]() $(\infty ,2)$
-category. So it suffices to observe that for every
$(\infty ,2)$
-category. So it suffices to observe that for every
![]() ${n}, {m} \geq 0$
and composable horizontal morphisms
${n}, {m} \geq 0$
and composable horizontal morphisms
![]() $\alpha _1,\ldots, \alpha _{n}, \beta _1 ,\ldots, \beta _{m}$
of
$\alpha _1,\ldots, \alpha _{n}, \beta _1 ,\ldots, \beta _{m}$
of
![]() $ {\mathcal C}\to \Delta $
different from identities such that the horizontal composition
$ {\mathcal C}\to \Delta $
different from identities such that the horizontal composition
![]() $\alpha _1 \circ \ldots \circ \alpha _{n} \circ \beta _1 \circ \ldots \circ \beta _{m}$
in
$\alpha _1 \circ \ldots \circ \alpha _{n} \circ \beta _1 \circ \ldots \circ \beta _{m}$
in
![]() ${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
is the 0-fold composition, we have that
${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
is the 0-fold composition, we have that
![]() ${n}+{m}=0$
and so
${n}+{m}=0$
and so
![]() ${n}={m}=0.$
${n}={m}=0.$
Remark 7.18. Let
![]() ${\mathcal C} \to \Delta , {\mathcal D} \to \Delta $
be double
${\mathcal C} \to \Delta , {\mathcal D} \to \Delta $
be double
![]() $\infty $
-categories. By definition the induced functor
$\infty $
-categories. By definition the induced functor
![]() ${\mathrm {FUN}}({\mathrm N}{\mathrm {Env}}({\mathcal C}),{\mathcal D}) \to {\mathrm {FUN}}({\mathrm {Env}}({\mathcal C}),{\mathcal D})$
is fully faithful and the equivalence
${\mathrm {FUN}}({\mathrm N}{\mathrm {Env}}({\mathcal C}),{\mathcal D}) \to {\mathrm {FUN}}({\mathrm {Env}}({\mathcal C}),{\mathcal D})$
is fully faithful and the equivalence
restricts to an equivalence
Proposition 7.30. Let
![]() ${\mathcal C}$
be a small
${\mathcal C}$
be a small
![]() $(\infty ,2)$
-category. There is a canonical equivalence
$(\infty ,2)$
-category. There is a canonical equivalence
Proof. There is a chain of canonical equivalences of
![]() $\infty $
-categories
$\infty $
-categories
The first equivalence holds by the universal property of
![]() ${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
of Remark 7.18. The second equivalence is straightening of cartesian fibrations. The third equivalence is induced by the canonical equivalence
${\mathrm N}{\mathrm {Env}}({\mathcal C}) \to \Delta $
of Remark 7.18. The second equivalence is straightening of cartesian fibrations. The third equivalence is induced by the canonical equivalence
![]() $\tau ^*{\mathrm N}{\mathrm {Env}}({\mathcal C}) \simeq {\mathrm N}{\mathrm {Env}}(\tau ^*{\mathcal C})$
over
$\tau ^*{\mathrm N}{\mathrm {Env}}({\mathcal C}) \simeq {\mathrm N}{\mathrm {Env}}(\tau ^*{\mathcal C})$
over
![]() $\Delta $
, which follows immediately from the construction of
$\Delta $
, which follows immediately from the construction of
![]() ${\mathrm {Env}}({\mathcal C})\to \Delta .$
The last equivalence is by [Reference Ayala, Mazel-Gee and Rozenblyum3, Theorem B.4.3.].
${\mathrm {Env}}({\mathcal C})\to \Delta .$
The last equivalence is by [Reference Ayala, Mazel-Gee and Rozenblyum3, Theorem B.4.3.].
Corollary 7.31. Let
![]() ${\mathcal C}$
be a small
${\mathcal C}$
be a small
![]() $\infty $
-category. There is a canonical equivalence
$\infty $
-category. There is a canonical equivalence
Proof. By Proposition 7.30 (applied to a larger universe) there is a canonical equivalence
that restricts to an equivalence
Hence by Corollary 4.3 and Proposition 7.13 we obtain a canonical equivalence
Example 7.19. Let
![]() ${\mathcal A} \to {\mathcal C}$
be an exponentiable fibration and
${\mathcal A} \to {\mathcal C}$
be an exponentiable fibration and
![]() ${\mathcal B} \to {\mathcal C}$
a functor. By the defining property of exponentiability the functor
${\mathcal B} \to {\mathcal C}$
a functor. By the defining property of exponentiability the functor
admits a right adjoint
![]() $\mathrm {Fun}^{\mathcal C}({\mathcal A},-).$
The internal hom
$\mathrm {Fun}^{\mathcal C}({\mathcal A},-).$
The internal hom
![]() $\mathrm {Fun}^{{\mathcal C}}({\mathcal A},{\mathcal B})\to {\mathcal C} $
classifies a lax normal functor
$\mathrm {Fun}^{{\mathcal C}}({\mathcal A},{\mathcal B})\to {\mathcal C} $
classifies a lax normal functor
![]() ${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
that sends any morphism
${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
that sends any morphism
![]() $\theta : X \to Y$
in
$\theta : X \to Y$
in
![]() ${\mathcal C}$
to a pro-functor
${\mathcal C}$
to a pro-functor
corresponding to a functor
The functors
![]() ${\mathcal A} \to {\mathcal C}, {\mathcal B} \to {\mathcal C}$
classify lax normal functors
${\mathcal A} \to {\mathcal C}, {\mathcal B} \to {\mathcal C}$
classify lax normal functors
![]() ${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
, where the first classifies a functor that sends the morphism
${\mathcal C}^{\mathrm {op}} \to {\mathrm {CORR}}$
, where the first classifies a functor that sends the morphism
![]() $\theta : X \to Y$
to pro-functors
$\theta : X \to Y$
to pro-functors
![]() $ {\mathrm A}_Y \to {\mathcal A}_X, {\mathcal B}_Y \to {\mathcal B}_X$
corresponding to functors
$ {\mathrm A}_Y \to {\mathcal A}_X, {\mathcal B}_Y \to {\mathcal B}_X$
corresponding to functors
Let
![]() $\rho : {\mathcal W} \to {\mathcal A}_X^{\mathrm {op}} \times {\mathcal A}_Y$
be the left fibration classified by
$\rho : {\mathcal W} \to {\mathcal A}_X^{\mathrm {op}} \times {\mathcal A}_Y$
be the left fibration classified by
![]() $\alpha $
. By construction of the Grothendieck-construction the functor
$\alpha $
. By construction of the Grothendieck-construction the functor
![]() $\gamma $
sends any pair
$\gamma $
sends any pair
![]() $(F,G) \in \mathrm {Fun}({\mathcal A}_X,{\mathcal B}_X)^{\mathrm {op}} \times \mathrm {Fun}({\mathcal A}_Y,{\mathcal B}_Y)$
to the mapping space
$(F,G) \in \mathrm {Fun}({\mathcal A}_X,{\mathcal B}_X)^{\mathrm {op}} \times \mathrm {Fun}({\mathcal A}_Y,{\mathcal B}_Y)$
to the mapping space
where the pullbacks are taken along
![]() $\theta .$
By Theorem 6.2 the mapping space
$\theta .$
By Theorem 6.2 the mapping space
![]() $ \mathrm {Fun}^{[1]}([1] \times _{\mathcal C} {\mathcal A}, [1] \times _{\mathcal C} {\mathcal B})(F,G)$
is the limit of the functor
$ \mathrm {Fun}^{[1]}([1] \times _{\mathcal C} {\mathcal A}, [1] \times _{\mathcal C} {\mathcal B})(F,G)$
is the limit of the functor
![]() $\beta \circ (F^{\mathrm {op}} \times G) \circ \rho : {\mathcal W} \to {\mathcal S}. $
$\beta \circ (F^{\mathrm {op}} \times G) \circ \rho : {\mathcal W} \to {\mathcal S}. $
Competing interests
The author has no competing interest to declare.