We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We provide a short proof that if κ is a regular cardinal with κ < c, then
for any ordinal α < min{
, κ}. In particular,
for any ordinal α < . This generalizes an unpublished result of E. Szemerédi that Martin's axiom implies that
for any cardinal κ with κ < c.
We show that if κ is a weakly compact cardinal, then
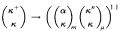
for any ordinals α < κ+ and μ < κ, and any finite ordinals m and n. This polarized partition relation represents the statement that for any partition
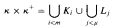
of κ × κ+ into m + μ pieces either there are A ∈ [κ]κ, B ∈ [κ]+]α and i < m with A × B ⊆ Ki or there are C ∈ [κ]κ,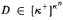 
, and j < μ with C × D ⊆ Lj. Related results for measurable and almost measurable κ are also investigated. Our proofs of these relations involve the use of elementary substructures of set models of large fragments of ZFC.
Working in ZFC, we show that for any infinite cardinal k and ordinal y < (2<k)+ the polarized partition relation
holds. Our proof of this relation involves the use of elementary substructures of set models of large fragments of ZFC.
