We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
To save content items to your account, please confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your account. Find out more about saving content to .
To save content items to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
The study of the S-unit equation for algebraic numbers rests very heavily on Schmidt's Subspace Theorem. Here we prove an effective subspace theorem for the differential function field case, which should be valuable in the proof of results concerning the S-unit equation for function fields. Theorem 1 states that either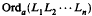 
has a given upper bound where 
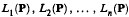are linearly independent linear forms in the polynomials 
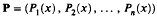with coefficients that are formal power series solutions about x = 0 of non-zero differential equations and where Orda denotes the order of vanishing about a regular (finite) point of functions ƒk, i: (k = 1, n; i = 1, n) or 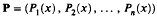lies inside one of a finite number of proper subspaces of (K(x))n. The proof of the theorem is based on the wroskian methods and graded sub-rings of Picard-Vessiot extensions developed by D. V. Chudnovsky and G. V. Chudnovsky in their function field analogues of the Roth and Schmidt theorems. A brief discussion concerning the possibility of a subspace theorem for a product of valuations including the infinite one is also included.
Email your librarian or administrator to recommend adding this to your organisation's collection.