We prove that the classical map comparing Adams’ cobar construction on the singular chains of a pointed space and the singular cubical chains on its based loop space is a quasi-isomorphism preserving explicitly defined monoidal 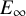 $E_\infty $-coalgebra structures. This contribution extends to its ultimate conclusion a result of Baues, stating that Adams’ map preserves monoidal coalgebra structures.
$E_\infty $-coalgebra structures. This contribution extends to its ultimate conclusion a result of Baues, stating that Adams’ map preserves monoidal coalgebra structures.
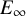 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space