We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We investigate integral means over spherical shell of holomorphic functions in the unit ball 
$\mathbb {B}_n$ of 
$\mathbb {C}^n$ with respect to the weighted volume measures and their relation with the weighted Hadamard product. The main result of this paper has many consequences which improve some well-known estimates related to the Hadamard product in Hardy spaces and weighted Bergman spaces.
We find the lower bound for the norm of the Hilbert matrix operator H on the weighted Bergman space Ap,α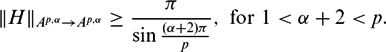We show that if 4 ≤ 2(α + 2) ≤ p, then ∥H∥Ap,α → Ap,α = 
\begin{equation*}\|H\|_{A^{p,\alpha}\rightarrow A^{p,\alpha}}\geq\frac{\pi}{\sin{\frac{(\alpha+2)\pi}{p}}}, \,\, \textnormal{for} \,\, 1<\alpha+2<p.\end{equation*}
$\frac{\pi}{\sin{\frac{(\alpha+2)\pi}{p}}}$, while if 2 ≤ α +2 < p < 2(α+2), upper bound for the norm ∥H∥Ap,α → Ap,α, better then known, is obtained.
