We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Given a ±1 random completely multiplicative function f, we prove by estimating moments that the limiting distribution of the normalized sum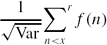
converges to the standard Gaussian distribution as x → ∞ when r restricts summation to n having o(log log log x) prime factors. We also give an upper bound for the large deviations of
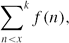with the sum restricted to numbers having a fixed number k of prime factors.
