In this paper we shall prove the following two theorems (the terminology is explained in § 2 below; all rings are assumed to be associative).
THEOREM 1. Suppose that 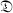 is a division ring of finite order m over its centre Z and let μ(m) denote the factor sequence 1, m, m2, … , mn, … . Then the rings
is a division ring of finite order m over its centre Z and let μ(m) denote the factor sequence 1, m, m2, … , mn, … . Then the rings 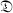 μ(w) and Zμ(m) are isomorphic.
μ(w) and Zμ(m) are isomorphic.