To a finite-dimensional real representation V of a finite group G there are associated its Stiefel–Whitney classes wk (V) (k = 1, 2, 3, …) in the cohomology groups Hk(G; 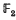). ( 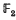is the field with two elements.) The total Stiefel-Whitney class

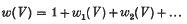
in the ring H*(G; 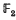is natural with respect to G in the obvious sense, and, in addition,

(a) exponential, i.e. w(V ⊕ W) = w(V).w(W),and

(b) stable, i.e. w(V) = 1 when F is a trivial representation.

The object of this paper is to prove that for a finite abelian group G the natural map is injective, where Â(G) is the completion of the Burnside ring of G and σ0(BG) is the stable cohomotopy of the classifying space BG of G. The map â is detected by means of an M U* exponential characteristic class for permutation representations constructed in (11). The result is a generalization of a theorem of Laitinen (4) which treats elementary abelian groups using ordinary cohomology. One interesting feature of the present proof is that it makes explicit use of the universality of the formal group law of M U*. It also involves a computation of M U*(BG) in terms of the formal group law. This may be of independent interest. Since writing the paper the author has discovered that M U*(BG) has previously been calculated by Land-weber(5).