We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove that if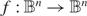 
$f:\mathbb{B}^n \to \mathbb{B}^n$, for n ≥ 2, is a homeomorphism with bounded skew over all equilateral hyperbolic triangles, then f is in fact quasiconformal. Conversely, we show that if 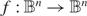$f:\mathbb{B}^n \to \mathbb{B}^n$ is quasiconformal then f is η-quasisymmetric in the hyperbolic metric, where η depends only on n and K. We obtain the same result for hyperbolic n-manifolds. Analogous results in 
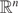$\mathbb{R}^n$, and metric spaces that behave like 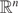$\mathbb{R}^n$, are known, but as far as we are aware, these are the first such results in the hyperbolic setting, which is the natural metric to use on 
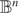$\mathbb{B}^n$.
