We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Perelman established a differential Li-Yau-Hamilton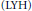 
$\left( \text{LHY} \right)$ type inequality for fundamental solutions of the conjugate heat equation corresponding to the Ricci flow on compact manifolds. As an application of the 
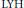$\text{LHY}$ inequality, Perelman proved a pseudolocality result for the Ricci flow on compact manifolds. In this article we provide the details for the proofs of these results in the case of a complete noncompact Riemannian manifold. Using these results we prove that under certain conditions, a finite time singularity of the Ricci flow must form within a compact set. The conditions are satisfied by asymptotically flatmanifolds. We also prove a long time existence result for the Kähler-Ricci flow on complete nonnegatively curved Kähler manifolds.
