We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give a new proof of an unpublished result of Dale Peterson, proved by Lam and Shimozono, which identifies explicitly the structure constants, with respect to the quantum Schubert basis, for the T-equivariant quantum cohomology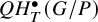 
$QH^{\bullet }_T(G/P)$ of any flag variety 
$G/P$ with the structure constants, with respect to the affine Schubert basis, for the T-equivariant Pontryagin homology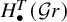 
$H^T_{\bullet }(\mathcal {G}r)$ of the affine Grassmannian 
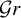$\mathcal {G}r$ of G, where G is any simple simply-connected complex algebraic group.
Our approach is to construct an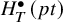 
$H_T^{\bullet }(pt)$-algebra homomorphism by Gromov-Witten theory and show that it is equal to Peterson’s map. More precisely, the map is defined via Savelyev’s generalized Seidel representations, which can be interpreted as certain Gromov-Witten invariants with input 
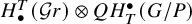$H^T_{\bullet }(\mathcal {G}r)\otimes QH_T^{\bullet }(G/P)$. We determine these invariants completely, in a way similar to how Fulton and Woodward did in their proof of the quantum Chevalley formula.
