Structural rheological modelling of complex fluids developed in Part I of this series and applied to shear thickening systems (Parts II & III), is now used to improve such a modelling in the case of unsteady behaviour, that is, in the presence of thixotropy. The model is based on an explicit viscosity-structure relationship, η(S), between the viscosity and a structural variable S. Under unsteady conditions, characterized by a reduced shear, Γ(t), shear-induced structural change obeys a kinetic equation (through shear-dependent relaxation times). The general solution of this equation is a time-dependent function, S(t) ≡ S[t, Γ(t)]. Thixotropy is automatically modelled by introducing S[t, Γ(t)] into η(S) which leads directly to η(t) ≡ η[t, Γ(t)], without the need for any additional assumptions in the model. Moreover, whilst observation of linear elasticity requires small enough deformation i.e. no change in the structure, larger deformations cause structural buildup/breakdown, i.e. the presence of thixotropy, and hence leads to a special case of non-linear viscoelasticity that can be called “thixoelasticity”.Predictions of a modified Maxwell equation, obtained by using the above-defined η(S) and assuming G = G 0 S (where G 0 is the shear modulus in the resting state defined by S = 1) are discussed in the case of start-up and relaxation tests. Similarly modified Maxwell-Jeffreys and Burger equations are used to predict creep tests and hysteresis loops. Discussion of model predictions Maynly concerns (i) effects of varying model variables or/and applied shear rate conditions and (ii) comparison with some experimental data.

A new structural model of shear-thickening “dilatancy” is proposed for (strongly) stabilized disperse systems. This model is based on the effective volume fraction (EVF) concept, developed in Part I of this series and previously used for the rheological modeling of complex fluids. In such a description, the latter are considered as concentrated dispersions of basic structural units (SUs) — either small, compact clusters or primary particles —, forming large structures at low shear. As shear rate increases, rupturing of these large structures leads to the shear thinning observed prior to dilatancy. The novelty of this model lies in assuming that, beyond the onset of dilatancy, hydrodynamic forces promote, at the expense of basic-SUs, the formation of hydrodynamic clusters as both rheo-optical experiments and numerical simulations recently demonstrated, in contradiction with the (classical) theory based on a shear induced disruption of particle layering. Dilatancy directly results from the increase of the EVF of the dispersion, closely related to the increasing volume of continuous phase imprisoned inside hydroclusters whose size grows as the shear rate increases. Predictions of the model are discussed in comparison with the Mayn features observed in a large number of dilatant dispersions, especially the volume fraction dependences of viscosity and critical shear rates (onset of dilatancy, maximum and discontinuity in viscosity) also the effects of particle size, polydispersity and suspending fluid viscosity.

The structural model discussed in Part I of the present work is applied to "true" behavior – i.e. shear thinning followed by shear thickening (sometimes followed by shear thinning) – very often observed in complex fluids as the applied shear is increased. This model states that the viscosity η of these fluids – described as concentrated dispersions of several classes of Structural Units (SUs) – is a unique function of a flow-dependent effective volume fraction, φ eff. The latter is expressed in terms of S i = fraction of "aggregated" particles contained in all the SUi s (as SUs of i-class) and Ci = (ϕ i −1−1)= "compactness factor", directly related to the mean compactness ϕi of SUi s.Shear induced flocculation (SIF) is the more obvious process capable to explain the shear thickening behavior of partially flocculated suspensions (obviously, another process should be required for stabilized dispersions). After progressive reduction of SUs submitted to shear forces (i.e. leading to a decrease of Si ), such a behavior should be observed if SIF occurs beyond a critical shear rate ${\dot {\gamma}_{\rm C}}$ , then resulting in re-increase of Si , thus of φ eff and η. The simplest "SIF-model" will introduce only one class of SUs, with only one variable S governed by a kinetic equation in which the kinetic rate for SU-formation increases with shear, thus giving the expected shear-thickening behavior if ${\dot {\gamma}}>{\dot {\gamma}_{\rm C}}$ . However, at high shear rates, SIF is limited by a (Smoluchowski-like) shear decreasing sticking probability. Effects of varying model parameters on predictions of the resulting SIF-model are discussed. Finally, this model is tested by comparison with observed rheological behavior, namely viscosity change vs. pH in aqueous styrene-ethylacrylate dispersions, from Laun's data [2].

An analysis of inertia effects in controlled stress rheometry is presented. For Newtonian fluids, this study takes exact account of both the instrumental inertia and the discontinuous stress change in this type of rheometer. In fact, supposedly smooth stress ramps are always approximated by a series of stress steps. The significance of this limitation, which is sometimes critical, is pointed out for the first time. The error induced by assuming that the stress ramps are smooth in Krieger's method for inertia correction [1], is quantitatively evaluated. An improved calculation for non-Newtonian, inelastic fluids is described.

Number of complex fluids (as slurries, drilling muds, paints and coatings,many foods, cosmetics, biofluids...) can approximately be described asconcentrated dispersions of Structural Units (SUs). Due to shear forces,SUs are assumed to be approximately spherical in shape and uniform in size under steady flow conditions, so that a complex fluid can be considered as aroughly monodisperse dispersion of roughly spherical SUs (with ashear-dependent mean radius), what allows to generalize hard sphere modelsof monodisperse suspensions to complex fluids. A rheological model of such dispersions of SUs is based on the concept of the effective volume fraction, $\rm \phi_{eff}$ 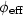which depends on flow conditions. Indeed, in competitionwith particle interactions, hydrodynamic forces can modify (i) S, thenumber fraction of particles that all SUs contain, (ii) both SUsarrangements and their internal structure, especially the SU's compactness,φ. As a structural variable, S is governed by a kinetic equation.Through the shear-dependent kinetic rates involved in the latter, thegeneral solution S depends on Γ, a dimensionless shear variable,leading to $\rm \phi_{eff}$ 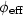(t, Γ; φ). The structural modelling is achieved by introducing this expression of $\rm \phi_{eff}$ 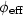into a well-established viscosity model of hard sphere suspensions. Usingthe steady state solution of the kinetic equation, S eq(Γ),allows to model non-Newtonian behaviors of complex fluids under steadyshear conditions, as pseudo-plastic, plastic, dilatant ... ones. In thismodel, the ratio of high shear to low shear limiting viscosities appears asa key variable. Different examples of application will be discussed.