Schmidt [‘Integer points on curves of genus 1’, Compos. Math. 81 (1992), 33–59] conjectured that the number of integer points on the elliptic curve defined by the equation $y^{2}=x^{3}+ax^{2}+bx+c$ , with $a,b,c\in \mathbb{Z}$ , is $O_{\unicode[STIX]{x1D716}}(\max \{1,|a|,|b|,|c|\}^{\unicode[STIX]{x1D716}})$ for any $\unicode[STIX]{x1D716}>0$ . On the other hand, Duke [‘Bounds for arithmetic multiplicities’, Proc. Int. Congress Mathematicians, Vol. II (1998), 163–172] conjectured that the number of algebraic number fields of given degree and discriminant $D$ is $O_{\unicode[STIX]{x1D716}}(|D|^{\unicode[STIX]{x1D716}})$ . In this note, we prove that Duke’s conjecture for quartic number fields implies Schmidt’s conjecture. We also give a short unconditional proof of Schmidt’s conjecture for the elliptic curve $y^{2}=x^{3}+ax$ .

Let 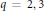$\text{q}\,\text{=}\,\text{2,}\,\text{3}$ and 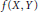$f\left( X,\,Y \right)$ , 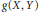$g\left( X,\,Y \right)$ , $h\left( X \right)$ be polynomials with integer coefficients. In this paper we deal with the curve 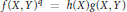$f{{\left( X,\,Y \right)}^{\text{q}}}\,=\,h\left( X \right)g\left( X,\,Y \right)$ , and we show that under some favourable conditions it is possible to determine all of its rational points.

Let K be an algebraic number field with ring of integers OK and f(X) ∈ OK[X]. In this paper we establish improved explicit upper bounds for the size of solutions in OK, of diophantine equations Y2 = f(X), where f(X) has at least three roots of odd order, and Ym = f(X), where m is an integer ≥ 3 and f(X) has at least two roots of order prime to m.

Let F(X, Y) be an absolutely irreducible polynomial with coefficients in an algebraic number field K. Denote by C the algebraic curve defined by the equation F(X, Y) = 0 and by K[C] the ring of regular functions on Cover K. Assume that there is a unit ϕ in K[C] − K such that 1 − ϕ is also a unit. Then we establish an explicit upper bound for the size of integral solutions of the equation F(X, Y) = 0, defined over K. Using this result we establish improved explicit upper bounds on the size of integral solutions to the equations defining non-singular affine curves of genus zero, with at least three points at ‘infinity’, the elliptic equations and a class of equations containing the Thue curves.