We shall study a special case of the following abstract approximation problem: givena normed linear space E and two subspaces, M1 and M2, of E, we seek to approximate f ∈ E by elements in the sum of M1 and M2. In particular, we might ask whether closest points to f from M = M1 + M2 exist, and if so, how they are characterised. If we can define proximity maps p1 and p2 for M1 and M2, respectively, then an algorithm analogous to the one given by Diliberto and Straus [4] can be defined by the formulae

We begin by describing a concrete example from the class of problems to be considered. A continuous bivariate function f defined on the square |t| ≤ 1, |s| ≤ 1 is to be approximated by a tensor-product form involving univariate functions. For example, the approximation may be prescribed to have the form

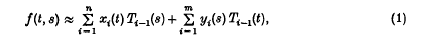
in which the Ti are the Tchebycheff polynomials, and the coefficient functions xi(t) and yi(s) are to be chosen to achieve a good or best approximation. Will a best approximation exist? If so, how can it be obtained?

In Bernstein's proof of the Weierstrass Approximation Theorem, the polynomials

are constructed in correspondence with a function f ∊ C [0, 1] and are shown to converge uniformly to f. These Bernstein polynomials have been the starting point of many investigations, and a number of generalizations of them have appeared. It is our purpose here to consider several generalizations in the form of infinite series and to establish some of their properties.