Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

24 results

Page 1 of 2

Random Walk: A Modern Introduction
  • Gregory F. Lawler, Vlada Limic
  • Published online:
    05 June 2012
    Print publication:
    24 June 2010
  • Random walks are stochastic processes formed by successive summation of independent, identically distributed random variables and are one of the most studied topics in probability theory. This contemporary introduction evolved from courses taught at Cornell University and the University of Chicago by the first author, who is one of the most highly regarded researchers in the field of stochastic processes. This text meets the need for a modern reference to the detailed properties of an important class of random walks on the integer lattice. It is suitable for probabilists, mathematicians working in related fields, and for researchers in other disciplines who use random walks in modeling.

  • Preface

  • Gregory F. Lawler, University of Chicago, Vlada Limic, Université de Provence
  • Book:
    Random Walk: A Modern Introduction
    Published online:
    05 June 2012
    Print publication:
    24 June 2010, pp ix-xii

  • Summary

    Random walk – the stochastic process formed by successive summation of independent, identically distributed random variables – is one of the most basic and well-studied topics in probability theory. For random walks on the integer lattice ℤd, the main reference is the classic book by Spitzer (1976). This text considers only a subset of such walks, namely those corresponding to increment distributions with zero mean and finite variance. In this case, one can summarize the main result very quickly: the central limit theorem implies that under appropriate rescaling the limiting distribution is normal, and the functional central limit theorem implies that the distribution of the corresponding path-valued process (after standard rescaling of time and space) approaches that of Brownian motion.

    Researchers who work with perturbations of random walks, or with particle systems and other models that use random walks as a basic ingredient, often need more precise information on random walk behavior than that provided by the central limit theorems. In particular, it is important to understand the size of the error resulting from the approximation of random walk by Brownian motion. For this reason, there is need for more detailed analysis. This book is an introduction to the random walk theory with an emphasis on the error estimates. Although “mean zero, finite variance” assumption is both necessary and sufficient for normal convergence, one typically needs to make stronger assumptions on the increments of the walk in order to obtain good bounds on the error terms.

  • A Discrete Analogue of a Theorem of Makarov

  • Gregory F. Lawler
  • Journal:
    Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
    Published online by Cambridge University Press:
    12 September 2008, pp. 181-199

  • A theorem of Makarov states that the harmonic measure of a connected subset of ℝ2 is supported on a set of Hausdorff dimension one. This paper gives an analogue of this theorem for discrete harmonic measure, i.e., the hitting measure of simple random walk. It is proved that for any 1/2 < α < 1, β < α − 1/2, there is a constant k such that for any connected subset A ⊂ ℤ2 of radius n,

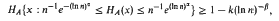
    where HA denotes discrete harmonic measure.

Page 1 of 2