In this paper, we study the sphere packing problem in Euclidean space where we impose additional constraints on the separations of the center points. We prove that any sphere packing in dimension 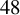$48$, with spheres of radii r, such that no two centers 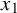$x_1$ and 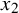$x_2$ satisfy 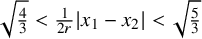$\sqrt {\tfrac {4}{3}} < \frac {1}{2r}|x_1-x_2| <\sqrt {\tfrac {5}{3}}$, has center density less or equal than 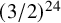$(3/2)^{24}$. Equality occurs for periodic packings if and only if the packing is given by a 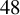$48$-dimensional even unimodular extremal lattice. This shows that any of the lattices 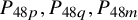$P_{48p},P_{48q},P_{48m}$ and 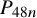$P_{48n}$ are optimal for this constrained packing problem, and gives evidence towards the conjecture that extremal lattices are optimal unconstrained sphere packings in 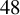$48$ dimensions. We also provide results for packings up to dimension 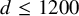$d\leq 1200$, where we impose constraints on the distance between centers and on the minimal norm of the spectrum, showing that even unimodular extremal lattices are again uniquely optimal. Moreover, in the one-dimensional case, where it is not at all clear that periodic packings are among those with largest density, we nevertheless give a condition on the set of constraints that allows this to happen, and we develop an algorithm to find these periodic configurations by relating the problem to a question about dominos.