We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For α ∈ [0, 1] the operator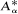 
is the operator formally defined on the Hardy space H2 by
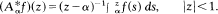
If α = 1, then the usual identification of H2 with l2 takes A 1 onto the discrete Cesàro operator. Here we see that {A α : α ∈ [0, 1]} is not arcwise connected, that Re A α ≥ 0, that A α is a Hilbert-Schmidt operator if α ∈[0, 1), and that A α is neither normaloid nor spectraloid if α ∈(0, 1).
