Luxemburg and Zaanen [5] call an element φ of the topological dual of a normed or seminormed vector space V an integral if
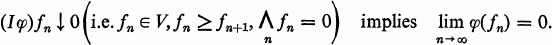
We denote the space of integrals by V I , For the L λ function spaces introduced by Ellis and Halperin [2] another Banach subspace of the dual emerges, namely the conjugate space Lλ* which is the Lλ space determined by the conjugate length function λ*-L λ* is contained in (Lλ)I but need not coincide with it.