Interest in the theory of linear graphs has grown recently in several fields which at first sight seem rather far apart. Recent publications include an excellent review by Bryant(1) of electrical network theory, statistical mechanical work by Sykes(2) and in the field of linear programming a paper by Glicksman, Johnson and Eselson (3). It is in this latter field that the subject of this paper arose, but we shall confine attention here to the graph theoretical aspect alone.

A discussion is given of the convergence of the eigenvalues Λ (N) of two-dimensional finite-difference equations towards the eigenvalues Λ of the corresponding second-order differential equation, and it is shown that

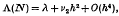
where h = N−1 and ν2 is a constant. As in our previous paper (4), this can be used to make an accurate estimate of λ by extrapolating to h = 0. After an account of the relaxation method used for computing Λ(N) and a discussion of the residual vector, results are presented for an approximation to the lowest spatially symmetric and antisymmetric states of two electrons in a sphere, interacting through their Coulomb potential.

The paper is concerned with linear second-order differential equations in one dimension. The arguments are developed for these equations in general and the examples given are drawn from quantum mechanics, where the accuracies required are in general higher than in classical mechanics and in engineering. An examination is made of the convergence of the eigenvalue Λ(h) of the corresponding finite difference equations towards the eigenvalue λ of the differential equation itself and it is shown that

where h is the size of the interval of the grid covering the range of the independent variable; the constant ν is usually a negative number and consequently Λ(h) may well be a lower bound to λ. This convergence property is used in the numerical calculation of λ by a simple extrapolation technique to a high degree of accuracy. Three examples are given of bounded problems in quantum mechanics. The corresponding eigenfunction can be calculated by a refinement of the familiar relaxation technique by using differences higher than the second, and an example is given.