We investigate the convergence in distribution of integrals of stochastic processes satisfying a functional limit theorem. We allow a large class of continuous Gaussian processes in the limit. Depending on the continuity properties of the underlying process, local Lebesgue or Riemann integrability is required.We are grateful to the referees and Benedikt Pötscher for their helpful and constructive comments. The research of the first author was partially supported by OTKA grants T37668 and T43037 and NSF-OTKA grant INT-0223262. The research of the second author was partially supported by NATO grant PST.EAP.CLG 980599 and NSF-OTKA grant INT-0223262.

We suggest a sequential monitoring scheme to detect changes in the parameters of a GARCH(p,q) sequence. The procedure is based on quasi-likelihood scores and does not use model residuals. Unlike for linear regression models, the squared residuals of nonlinear time series models such as generalized autoregressive conditional heteroskedasticity (GARCH) do not satisfy a functional central limit theorem with a Wiener process as a limit, so its boundary crossing probabilities cannot be used. Our procedure nevertheless has an asymptotically controlled size, and, moreover, the conditions on the boundary function are very simple; it can be chosen as a constant. We establish the asymptotic properties of our monitoring scheme under both the null of no change in parameters and the alternative of a change in parameters and investigate its finite-sample behavior by means of a small simulation study.This research was partially supported by NSF grant INT-0223262 and NATO grant PST.CLG.977607. The work of the first author was supported by the Hungarian National Foundation for Scientific Research, grants T 29621, 37886; the work of the second author was supported by NSERC Canada.

We develop an asymptotic theory for quadratic forms of the autocorrelations of squared residuals from a GARCH(p,q) model. Denoting by 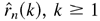, k ≥ 1, these autocorrelations computed from a realization of length n, we show that the statistic 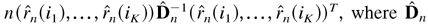is a matrix computed from the data, converges to the chi-square distribution with K degrees of freedom for any 1 ≤ i1 < ··· < iK. Our results are valid under weak assumptions on the innovations and model coefficients that admit that arbitrary low-order moments of the observations can be infinite. The matrix 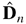and its asymptotic limit D depend on the distribution of the innovations. A small simulation study illustrates the theory and shows, in particular, that using the matrix D computed under the assumption of normal innovations may lead to incorrect conclusions if the innovations have a different distribution.We thank the two referees for their comments and Professor Bruce E. Hansen, the co-editor in charge, for his sound advice on how to improve the paper. The work of István Berkes was supported by the Hungarian National Foundation for Scientific Research, grant T 29621. The work of Lajos Horváth and Piotr Kokoszka was supported by NATO grant PST.CLG.977607.

We propose an estimator for the maximal moment exponent of a GARCH(1,1) sequence. We establish its consistency asymptotic normality with rate n−1/2. Finite sample properties are investigated by means of a small simulation study.The research for this paper was partially supported by NSF grant INT-0223262. István Berkes and Lajos Horváth were supported by the Hungarian National Foundation for Scientific Research, grant T 29621. Piotr Kokoszka and Lajos Horváth were supported by NATO grant PST.CLG.977607.