We prove, in normed linear spaces, the existence of extensions of continuous linear functionals from linear subspaces to the whole space, with arbitrarily prescribed larger norm. Also, we prove that under an additional boundedness assumption, in the known separation theorems for convex sets, there exist hyperplanes which separate and support both sets.

We prove that sup(f-h)(E) = sup(h*-f*)(E*), where f is a proper lower semi-continuous convex functional on a real locally convex space E, h: E → = [-∞, +∞] is an arbitrary-functional and, f*, h* are their convex conjugates respectively. When h = δG, the indicator of a bounded subset G of E, this yields a formula for sup f(G).

We show that there exists a conjugate Banach space E = B* with a basis, such that the distance from E to the collection of all conjugate Banach spaces can be made arbitrarily large, by suitable renorming of E. This solves a problem raised by B.V. Godun, Dokl. Akad. Nauk SSSR. 236 (1977), 18–20.

In previous papers we have proved that if G is a ω*-closed subspace of the conjugate space B* of a normed linear space B, then every b ∈ B can be extended within B, from G to the whole B*, with an arbitrarily small increase of the norm. Here we give some extensions of this result to the case when B* is replaced by a normed linear space E and B by any linear subspace V of E*, and some applications to separation and Helly type theorems.

We introduce some generalizations of Kadec'-Klee norms and use them to study characteristics of subspaces of conjugate spaces and smoothness. We give some connections between such characteristics and basic sequences, which yield, in particular, sharpenings and simpler proofs of some known characterizations of reflexivity.

We prove that if E is a Banach space which has a subspace G such that the conjugate space G* contains a proper norm closed linear subspace V of characteristic 1, then E** is not smooth and there exist in πE(E) points of non-smoothness for E**, where πE: E → E** is the canonical embedding. We show that the spaces E having such a subspace G constitute a large proper subfamily of the family of all non-reflexive Banach spaces.

Consider an open Riemann surface R and a density P(z)dxdy (z = x + iy), well defined on R. As was shown by Myrberg in [3], if P ≢ 0 is a nonnegative α-Hölder continuous density on R (0 < α ≤ 1) then there exists the Green’s functions of the differential equation

p>on R, where Δ means the Laplace operator. As a consequence, there always exists a nontrivial solution on R.

An important problem in the study of the Hilbert space PD(R) of Dirichlet finite solutions of Δu = Pu on a Riemann surface R is to know the behavior of the reproducing kernel in PD(R). The main result of this paper is that the reproducing kernel is strictly positive.

1. Let E be a Banach space (by this we shall mean, for simplicity, a real Banach space) and (xn,fn ) ({xn } ⊂ E, {fn } ⊂ E *) a biorthogonal system, such that {fn } is total on E (i.e. the relations x ∈ E,fn (x) = 0, n = 1, 2, …, imply x = 0). Then it is natural to consider the cone

1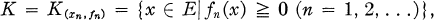

which we shall call “the cone associated with the biorthogonal system (xn,fn )”. In particular, if {xn } is a basis of E and {fn } the sequence of coefficient functional associated with the basis {xn }, this cone is nothing else but

2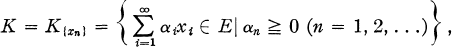

and we shall call it “the cone associated with the basis {xn}”.