Recently Edelman and Reiner suggested two poset structures, 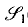 (n, d) and
(n, d) and 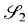 (n, d) on the set of all triangulations of the cyclic d-polytope C(n, d) with n vertices. Both posets are generalizations of the well-studied Tamari lattice. While
(n, d) on the set of all triangulations of the cyclic d-polytope C(n, d) with n vertices. Both posets are generalizations of the well-studied Tamari lattice. While 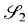 (n, d) is bounded by definition, the same is not obvious for
(n, d) is bounded by definition, the same is not obvious for 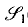 (n, d). In the paper by Edelman and Reiner the bounds of
(n, d). In the paper by Edelman and Reiner the bounds of 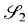 (n, d) were also confirmed for
(n, d) were also confirmed for 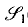 (n, d) whenever d≤5, leaving the general case as a conjecture.
(n, d) whenever d≤5, leaving the general case as a conjecture.