There is a well-known correspondence (due to Mehta and Seshadri in the unitary case, and extended by Bhosle and Ramanathan to other groups), between the symplectic variety 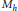${{M}_{h}}$ of representations of the fundamental group of a punctured Riemann surface into a compact connected Lie group $G$ , with fixed conjugacy classes $h$ at the punctures, and a complex variety 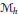${{\mathcal{M}}_{h}}$ of holomorphic bundles on the unpunctured surface with a parabolic structure at the puncture points. For 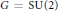$G\,=\,\text{SU}\left( 2 \right)$ , we build a symplectic variety $P$ of pairs (representations of the fundamental group into $G$ , “weighted frame” at the puncture points), and a corresponding complex variety 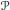$\mathcal{P}$ of moduli of “framed parabolic bundles”, which encompass respectively all of the spaces 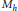${{M}_{h}}$ , 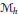${{\mathcal{M}}_{h}}$ , in the sense that one can obtain 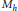${{M}_{h}}$ from $P$ by symplectic reduction, and 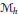${{\mathcal{M}}_{h}}$ from 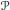$\mathcal{P}$ by a complex quotient. This allows us to explain certain features of the toric geometry of the 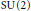$\text{SU(2)}$ moduli spaces discussed by Jeffrey and Weitsman, by giving the actual toric variety associated with their integrable system.

Large classes of integrable Hamiltonian systems can be expressed as systems over coadjoint orbits in a loop algebra defined over a semi-simple Lie algebra [gfr ]. These systems can then be integrated via the classical, symplectic Liouville–Arnold method. On the other hand, the existence of spectral curves as constants of motion allows one to integrate these systems in terms of flows of line bundles on the curves. This note links the symplectic geometry of the coadjoint orbits with the algebraic geometry of these curves for arbitrary semi-simple [gfr ], which then allows us to reconcile the two integration methods.

Cet article de survol est le résumé de la conférence Coxeter-James de l'auteur, prononcée à la réunion d'hiver 1993 de la Société Mathématique du Canada.

La théorie de Morse décrit les liens entre la topologie d'une variété et la topologie des points critiques d'une fonction sur cette variété. La fonctionnelle d'énergie pour les applications d'une surface dans une variété, dont les points critiques seront des applications harmoniques et parfois holomorphes, et la fonctionnelle de Yang-Mills pour des connections sur une variété de dimension quatre sont deux cas en dimension infinie pour lesquels la théorie de Morse ne tient pas. Néanmois, dans les deux cas, on peut récupérer une quantité étonnante d'information, pourvu qu'on stabilise par rapport à un degré ou une charge qui sont des données du problème. Les preuves recyclent des résultats de la théorie de l'homotopie des années '70, et les combinent à des idées de géométrie complexe pour donner de jolis modèles des espaces en cause en termes de "particules". Nous espérons donner un survol général et accessible des idées utilisées.