We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give weighted norm inequalities for the maximal fractional operator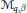 
${{\mathcal{M}}_{q}},\beta $ of Hardy–Littlewood and the fractional integral 
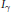${{I}_{\gamma }}$ . These inequalities are established between 
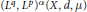${{\left( {{L}^{q}},\,{{L}^{p}} \right)}^{\alpha }}\left( X,\,d,\,\mu\right)$ spaces (which are superspaces of Lebesgue spaces 
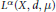${{L}^{\alpha }}\left( X,\,d,\,\mu\right)$ and subspaces of amalgams 
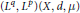$\left( {{L}^{q}},\,{{L}^{p}} \right)\left( X,d,\mu\right)$ ) and in the setting of space of homogeneous type 
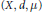$\left( X,d,\mu\right)$ . The conditions on the weights are stated in terms of Orlicz norm.
