This paper looks at the problems faced by the Chinese silver-backed currencies in Manchuria during the period of Northern Expedition (1925–1928), the Chinese attempt to overcome these problems, and the reasons for its failure. Manchuria was a peculiar territory during the interwar period (1919–1939), where several currencies, backed by silver or gold, competed against one another. The Chinese silver banknote, first introduced at the turn of the twentieth century, was challenged by gold-backed Japanese yen issued by the Bank of Korea, and by the Russian ruble. This competition was set in the context of the struggle for political control over the area between China (the Qing Dynasty and its successor, the Chinese Republic), Russia (and its successor the Soviet Union), and the Japanese Empire, as well as the war between the southern Nationalists (Kuomintang) and the militarists (warlords) who controlled the Chinese central government in Beijing and Manchuria. This paper suggests that the difficult financial situation determined the course followed by the warlords, and that their failure was the result of the complex regional context, and the failures in their military strategy rather than of their fiscal policy.

Let 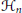${{\mathcal{H}}_{n}}$ be the real linear space of 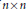$n\,\times \,n$ complex Hermitian matrices. The unitary (similarity) orbit 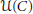$\mathcal{U}\left( C \right)$ of 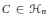$C\,\in \,{{\mathcal{H}}_{n}}$ is the collection of all matrices unitarily similar to 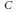$C$ . We characterize those 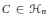$C\,\in \,{{\mathcal{H}}_{n}}$ such that every matrix in the convex hull of 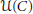$\mathcal{U}\left( C \right)$ can be written as the average of two matrices in 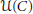$\mathcal{U}\left( C \right)$ . The result is used to study spectral properties of submatrices of matrices in 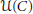$\mathcal{U}\left( C \right)$ , the convexity of images of 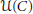$\mathcal{U}\left( C \right)$ under linear transformations, and some related questions concerning the joint 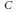$C$ -numerical range of Hermitian matrices. Analogous results on real symmetric matrices are also discussed.