We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We give an explicit raising operator formula for the modified Macdonald polynomials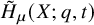 
$\tilde {H}_{\mu }(X;q,t)$, which follows from our recent formula for 
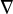$\nabla $ on an LLT polynomial and the Haglund-Haiman-Loehr formula expressing modified Macdonald polynomials as sums of LLT polynomials. Our method just as easily yields a formula for a family of symmetric functions 
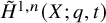$\tilde {H}^{1,n}(X;q,t)$ that we call 
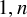$1,n$-Macdonald polynomials, which reduce to a scalar multiple of 
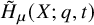$\tilde {H}_{\mu }(X;q,t)$ when 
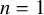$n=1$. We conjecture that the coefficients of 
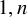$1,n$-Macdonald polynomials in terms of Schur functions belong to 
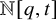${\mathbb N}[q,t]$, generalizing Macdonald positivity.
