Let 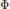$\Phi $ be an algebraically closed field of characteristic zero, 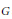$G$ a finite, not necessarily abelian, group. Given a 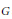$G$ -grading on the full matrix algebra 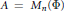$A\,=\,{{M}_{n}}\left( \Phi\right)$ , we decompose 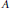$A$ as the tensor product of graded subalgebras 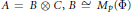$A\,=\,B\,\otimes \,C,\,B\,\cong \,{{M}_{p}}\left( \Phi\right)$ being a graded division algebra, while the grading of 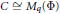$C\,\cong \,{{M}_{q}}\left( \Phi\right)$ is determined by that of the vector space 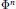${{\Phi }^{n}}$ . Now the grading of 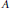$A$ is recovered from those of 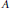$A$ and $B$ using a canonical “induction” procedure.

Let $F$be an algebraically closed field of characteristic $0$, and let $A$ be a $G$-graded algebra over $F$ for some finite abelian group $G$. Through $G$ being regarded as a group of automorphisms of $A$, the duality between graded identities and $G$-identities of $A$ is exploited. In this framework, the space of multilinear $G$-polynomials is introduced, and the asymptotic behavior of the sequence of $G$-codimensions of $A$ is studied.

Two characterizations are given of the ideal of $G$-graded identities of such algebra in the case in which the sequence of $G$-codimensions is polynomially bounded. While the first gives a list of $G$-identities satisfied by $A$, the second is expressed in the language of the representation theory of the wreath product $G \wr S_n$, where $S_n$ is the symmetric group of degree $n$.

As a consequence, it is proved that the sequence of $G$-codimensions of an algebra satisfying a polynomial identity either is polynomially bounded or grows exponentially.