We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the expected value of the length Ln of the minimum spanning tree of the complete graph Kn when each edge e is given an independent uniform [0, 1] edge weight. We sharpen the result of Frieze [6] that limn→∞
$\mathbb{E}$(Ln) = ζ(3) and show thatwhere c1, c2 are explicitly defined constants.
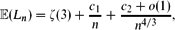$$\mathbb{E}(L_n)=\zeta(3)+\frac{c_1}{n}+\frac{c_2+o(1)}{n^{4/3}},$$
