We are interested in characterising pairs S, T of F-linear subspaces in a field extension L/F such that the linear span ST of the set of products of elements of S and of elements of T has small dimension. Our central result is a linear analogue of Vosper's Theorem, which gives the structure of vector spaces S, T in a prime extension L of a finite field F for which 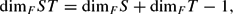 \begin{linenomath}$$\dim_FST =\dim_F S+\dim_F T-1,$$\end{linenomath}
\begin{linenomath}$$\dim_FST =\dim_F S+\dim_F T-1,$$\end{linenomath}