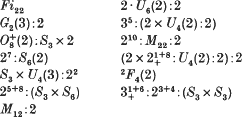In this paper we complete the enumeration, begun in [5], of the maximal subgroups of the Fischer group Fi22 and its automorphism group Fi22:2. It turns out that the lists of maximal subgroups given in [5] and [2] are complete. (Note however that in ([5], theorem (A) (iii)), 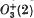 ) should read
) should read 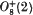 .) More precisely, we prove
.) More precisely, we prove
Main Theorem (i) The simple group Fi22 has exactly 14 conjugacy classes of maximal subgroups, as follows:
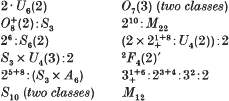
(ii) The group Aut (Fi22) ≅ Fi22: 2 has exactly 13 conjugacy classes of maximal subgroups, as follows: