We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A group G is called a triangle group if it can be presented in the form
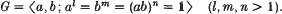
It is well-known that G is isomorphic to a subgroup of PSL2(ℂ), that a is of order l, b is of order m and ab is of order n. If
then G contains the fundamental group of a positive genus orientable surface as a subgroup of finite index whenever s(G) ≤ 1; in particular G is infinite. Furthermore, if s(G) < 1, the genus of the surface is greater than 1 and consequently G contains a free group of rank 2.
