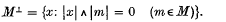In this paper we study the classes of almost f-algebras and d-algebras. Apart from a survey of known properties we present some ‘new’ properties of almost f-algebras and d-algebras and we consider their connection with f-algebras. To be more precise, we show, among other things, in an elementary intrinsic manner, that every Archimedean almost f-algebra is commutative. This result is a considerable improvement upon the fact that every Archimedean f-algebra is commutative. Furthermore, we give a description of the set of nilpotent elements in both an Archimedean d-algebra and an Archimedean almost f-algebra.

A simple proof is given that if X is a normed vector lattice, 1 ≼ p ≼ ∞, and the norm in X is p-additive, then the norm is p-superadditive if p < ∞. If p = ∞, then X satisfies Kakutani's classical M-space condition. The proof uses duality but is otherwise elementary.

A linear operator T on a vector lattice L preserves disjointness if Tx ⊥ y whenever x ⊥ y. If such a T is positive it is automatically order bounded. An ortho-morphism is an order bounded disjointness preserving linear operator on L. In this note we show that the theory of orthomorphisms on archimedean vector lattices admits a totally elementary exposition. Elementary methods are also effective in duality considerations when the order dual separates points of L. For the Jordan decomposition T = T+ − T− with T+x = (Tx+)+ − (Tx−)+ we can dtrop the order boundedness assumption if we assume either that T preserves ideals or that L is normed and T is continuous. Alternatively we may keep order boundedness and assume only |Tx| ⊥ |Ty| whenever x ⊥ y. The main duality results show: T preserves ideals if and only if T** does; T is an orthomorphism if and only if T* is; T is central (|T| is bounded by a multiple of the identity) if and only if T* is central if and only if T and T* preserve ideals.

This paper shows that every lattice group G can be densely embedded in a unique laterally complete lattice group H (the lateral completion of G). All reasonable structure properties of G are inherited by H and we have the following relationships between the ideal radical L(G), the distributive radical D(G) and the radical R(G) of G and the corresponding radicals of H. .

Let H be a complex Hilbert space. Recall that a bounded linear operator A, on H, is positive if (Ax, x) ≥ 0 (x ∈ H) (so that A = A* necessarily) and positive definite if A is positive and invertible.

This note shows that the set of bare points of a compact convex subset of a normed linear space is, in general, a proper subset of its set of exposed points.

One elementary proof of the spectral theorem for bounded self-adjoint operators depends on an elementary construction for the square root of a bounded positive self-adjoint operator. The purpose of this paper is to give an elementary construction for the unbounded case and to deduce the spectral theorem for unbounded self-adjoint operators. In so far as all our results are more or less immediate consequences of the spectral theorem there is little is entirely new. On the other hand the elementary approach seems to the author to provide a deeper insight into the structure of the problem and also leads directly to the spectral theorem without appealing first to the bounded case. Besides this, our methods for proving uniqueness of the square root and of the spectral family seem to be new even in the bounded case. In particular there is no need to invoke representation theorems for linear functionals on spaces of continuous functions.

Recall that the spectrum, σ(T), of a linear operator T in a complex Banach space is the set of complex numbers λ such that T—λI does not have a densely defined bounded inverse. It is known [7, § 5.1] that σ(T) is a closed subset of the complex plane C. If T is not bounded, σ(T) may be empty or the whole of C. If σ(T) ≠ C and T is closed the spectral mapping theorem, is valid for complex polynomials p(z) [7, §5.7]. Also, if T is closed and λ ∉ σ(T), (T–λI)−1 is everywhere defined.

A lattice ring is a lattice group ((l), page 214) and a ring in which ab ≥ 0 whenever a ∧ b ≥ 0.

In any lattice group (commutative or not) we define a+ = a ∨ 0, a− = (−a) ∨ 0 and |a| = a+ + a−. Itisknown((1). pages 219,220) that a+ ∧ a− = 0, a = a+ − a−, |a| = a+ ∨ a−, and that a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c), and a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c). For a non-empty subset M of a lattice group we define

We recall that a bounded linear operator T in a Hilbert space or finite-dimensional unitary space is said to be normal if T commutes with its adjoint operator T*, i.e. TT* = T*T. Most of the proofs given in the literature for the spectral theorem for normal operators, even in the finite-dimensional case, appeal to the corresponding results for Hermitian or unitary operators.