We show that the HNBUE family of life distributions is closed under weak convergence and that weak convergence within this family is equivalent to convergence of each moment sequence of positive order to the corresponding moment of the limiting distribution. A necessary and sufficient condition for weak convergence to the exponential distribution is given, based on a new characterization of exponentials within the HNBUE family of life distributions.

For a Markov chain with optional transitions, except for those to an arbitrary fixed state accessible from all others, Kesten and Spitzer proved the existence of a control policy which minimized the expected time to reach the fixed state and for constructing an optimal policy, proposed an algorithm which works in certain cases. For the algorithm to work they gave a sufficient condition which breaks down if there are countably many states and the minimal hitting time is bounded. We propose a modified algorithm which is shown to work under a weaker sufficient condition. In the bounded case with countably many states, the proposed sufficient condition is not necessary but a similar condition is. In the unbounded case as well as when the state space is finite, the proposed condition is shown to be both necessary and sufficient for the original Kesten–Spitzer algorithm to work. A new iterative algorithm which can be used in all cases is given.

Let {Xn} be a sequence of independent random variables each having a common d.f. V1. Suppose that V1 belongs to the domain of normal attraction of a stable d.f. V0 of index α 0 ≤ α ≤ 2. Here we prove that, if the c.f. of X1 is absolutely integrable in rth power for some integer r > 1, then for all large n the d.f. of the normalized sum Zn of X1, X2, …, Xn is absolutely continuous with a p.d.f. vn such that

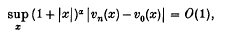
as n → ∞, where v0 is the p.d.f. of Vo.

Let {Xn} be a sequence of iid random variables. If the common charac-teristic function is absolutely integrable in mth power for some integer m ≥ 1, then Zn = n−½(X1 + … + Xn) has a pdf fn for all n ≥ m. Here we give a necessary and sufficient condition for sup asn. → ∞, where φ (x) is the standard normal pdf and M(x) is a non-decreasing function of x ≥ 0 such that M(0) > 0 and M(x)/xδ is non-increasing for 0 < δ ≤ 1.

Let Zn = n−½(X1 + X2 + … + Xn), where {Xn} is a sequence of independent and identically distributed random variables with EX1 = 0, and a common distribution function F and characteristic function ω. Suppose |ω|r is integrable for some integer r ≥ 1. For all n ≥ r, then Zn has a probability density function fn obtained by using the inversion formula.

1. Introduction. We shall employ the customary abbreviations: p.d.f. for probability density function; d.f. for distribution function; c.f. for characteristic function.