We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This paper gives criteria, necessary or sufficient for a vector-valued function F = (f1, f2, …, fk) to be invex. Here each fi is of the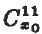 
-class (that is, each fi is a function whose gradient mapping is locally Lipschitz in a neighbourhood of x0) and the invexity of F means that F(x) − F(x0) ⊂ ˚F′(X) + Q for a fixed convex cone Q of Rk and every x near x0 (˚F′ being the Jacobian matrix of F at x0).
