We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that the integral canonical models of Hodge-type Shimura varieties at odd good reduction primes admits ‘
$p$-adic uniformization’ by Rapoport–Zink spaces of Hodge type constructed in Kim [Forum Math. Sigma6 (2018) e8, 110 MR 3812116].
When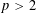 
$p>2$ , we construct a Hodge-type analogue of Rapoport–Zink spaces under the unramifiedness assumption, as formal schemes parametrizing ‘deformations’ (up to quasi-isogeny) of 
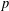$p$ -divisible groups with certain crystalline Tate tensors. We also define natural rigid analytic towers with expected extra structure, providing more examples of ‘local Shimura varieties’ conjectured by Rapoport and Viehmann.
