Let $\pi $ be a set of primes. We say that a group G satisfies $D_{\pi }$ if G possesses a Hall $\pi $-subgroup H and every $\pi $-subgroup of G is contained in a conjugate of H. We give a new $D_{\pi }$-criterion following Wielandt’s idea, which is a generalisation of Wielandt’s and Rusakov’s results.

A subgroup $H$ is called a weak second maximal subgroup of $G$ if $H$ is a maximal subgroup of a maximal subgroup of $G$. Let $m(G,H)$ denote the number of maximal subgroups of $G$ containing $H$. We prove that $m(G,H)-1$ divides the index of some maximal subgroup of $G$ when $H$ is a weak second maximal subgroup of $G$. This partially answers a question of Flavell [‘Overgroups of second maximal subgroups’, Arch. Math.64(4) (1995), 277–282] and extends a result of Pálfy and Pudlák [‘Congruence lattices of finite algebras and intervals in subgroup lattices of finite groups’, Algebra Universalis11(1) (1980), 22–27].

Suppose that $G$ is a finite group and 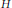$H$ is a subgroup of $G$ . 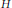$H$ is said to be $s$ -semipermutable in $G$ if 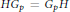$H{{G}_{p}}\,=\,{{G}_{p}}H$ for any Sylow $p$ -subgroup 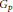${{G}_{p}}$ of $G$ with 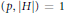$\left( p,\,\left| H \right| \right)\,=\,1$ ; $H$ is said to be $s$ -quasinormally embedded in $G$ if for each prime $p$ dividing the order of $H$ , a Sylow $p$ -subgroup of $H$ is also a Sylow $p$ -subgroup of some $s$ -quasinormal subgroup of $G$ . In every non-cyclic Sylow subgroup 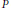$P$ of $G$ we fix some subgroup 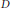$D$ satisfying 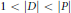$1\,<\,\left| D \right|\,<\,\left| P \right|$ and study the structure of $G$ under the assumption that every subgroup 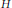$H$ of 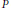$P$ with 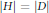$\left| H \right|\,=\,\left| D \right|$ is either $s$ -semipermutable or $s$ -quasinormally embedded in $G$ . Some recent results are generalized and unified.

A subgroup H of a finite group G is called SS-supplemented in G if there exists a subgroup K of G such that HK = G and H ∩ K is S-quasinormal in K. In this paper, we characterize the finite groups in which every subgroup is SS-supplemented and the influence of SS-supplementation of some subgroups on the structure of finite groups is considered. Some recent results on SS-quasinormal subgroups and C-supplemented subgroups are strengthened and enriched.

A subgroup H of a finite group G is said to be c–supplemented in G if there exists a subgroup K of G such that G = HK and H∩K is contained in coreG (H). In this paper some results for finite p–nilpotent groups are given based on some subgroups of Pc–supplemented in G, where p is a prime factor of the order of G and P is a Sylow p–subgroup of G. We also give some applications of these results.

A subgroup H of agroup G is said to be c-supplemented inG if there exists a subgroup K of G such thatHK=G and H \cap K is contained in Core_G (H).We follow Hall's ideas to characterize the structure of the finite groups in which every subgroup isc-supplemented. Properties of c-supplemented subgroups are also applied to determinethe structure of some finite groups.